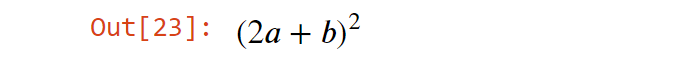Решение линейного уравнения в python
Решение линейного уравнения в Python
В данной статье мы разберем программу на python для решения линейного уравнения Программа решает уравнение вида ax = b. Коэффициенты a и b задаются пользователем с клавиатуры. Программа находит решение и выводит его на экран. Если решений бесконечное количество или их нет, то программа оповещает об этом.
Все возможные решения линейного уравнения можно описать так
Если a = 0 и b = 0, то решений бесконечное количество.
Если a = 0 и b ≠ 0, то решений нет.
Если a ≠ 0, то единственное решение будет равно b / a.
Для задания коэффициентов с клавиатуры в Python используется функция ввода вещественного числа float(input()). Подробно о вводе информации с клавиатуры в python
a = float(input(“Введите коэффициент a “))
b = float(input(“Введите коэффициент b “))
В Python, чтобы проверить равенство двух объектов, используется ==, для проверки неравенства объектов используется !=. Для проверки двух условий одновременно используется оператор and. Подробно об условиях в python
Программа на Python для решения линейного уравнения
a = float(input(“Введите коэффициент a “))
b = float(input(“Введите коэффициент b “))
if (a == 0 and b == 0):
print(“Бесконечное количество решений.”)
if (a == 0 and b != 0):
print(“Решений нет.”)
if (a != 0):
print(b/a))
Полезно почитать по теме условия в Python примеры
Пример анкеты, опроса на Python
Библиотека Sympy: символьные вычисления в Python
Что такое SymPy ? Это библиотека символьной математики языка Python. Она является реальной альтернативой таким математическим пакетам как Mathematica или Maple и обладает очень простым и легко расширяемым кодом. SymPy написана исключительно на языке Python и не требует никаких сторонних библиотек.
Документацию и исходный код этой библиотеки можно найти на ее официальной странице.
Первые шаги с SymPy
Используем SymPy как обычный калькулятор
В библиотеке SymPy есть три встроенных численных типа данных: Real , Rational и Integer . С Real и Integer все понятно, а класс Rational представляет рациональное число как пару чисел: числитель и знаменатель рациональной дроби. Таким образом, Rational(1, 2) представляет собой 1/2 , а, например, Rational(5, 2) — соответственно 5/2 .
Библиотека SymPy использует библиотеку mpmath , что позволяет производить вычисления с произвольной точностью. Таким образом, ряд констант (например, пи, e), которые в данной библиотеке рассматриваются как символы, могут быть вычислены с любой точностью.
Как можно заметить, функция evalf() дает на выходе число с плавающей точкой.
В SymPy есть также класс, представляющий такое понятие в математике, как бесконечность. Он обозначается следующим образом: oo .
Символы
В отличие от ряда других систем компьютерной алгебры, в SymPy можно в явном виде задавать символьные переменные. Это происходит следующим образом:
После их задания, с ними можно производить различные манипуляции.
С символами можно производить преобразования с использованием некоторых операторов языка Python. А именно, арифметических ( + , -` , “* , ** ) и логических ( & , | ,
Библиотека SymPy позволяет задавать форму вывода результатов на экран. Обычно мы используем формат такого вида:
Алгебраические преобразования
SymPy способна на сложные алгебраические преобразования. Здесь мы рассмотрим наиболее востребованные из них, а именно раскрытие скобок и упрощение выражений.
Раскрытие скобок
Чтобы раскрыть скобки в алгебраических выражениях, используйте следующий синтаксис:
При помощи ключевого слова можно добавить поддержку работы с комплексными переменными, а также раскрытие скобок в тригонометрических функциях.
Упрощение выражений
Если вы хотите привести выражение к более простому виду (возможно, сократить какие-то члены), то используйте функцию simplify .
Также надо сказать, что для определенных видов математических функций существуют альтернативные, более конкретные функции для упрощения выражений. Так, для упрощения степенных функций есть функция powsimp , для тригонометрических — trigsimp , а для логарифмических — logcombine , radsimp .
Вычисления
Вычисления пределов
Для вычисления пределов в SymPy предусмотрен очень простой синтаксис, а именно limit(function, variable, point) . Например, если вы хотите вычислить предел функции f(x) , где x -> 0 , то надо написать limit(f(x), x, 0) .
Также можно вычислять пределы, которые стремятся к бесконечности.
Дифференцирование
Для дифференцирования выражений в SymPy есть функция diff(func, var) . Ниже даны примеры ее работы.
Проверим результат последней функции при помощи определения производной через предел.
tan 2 (?)+1 Результат тот же.
Также при помощи этой же функции могут быть вычислены производные более высоких порядков. Синтаксис функции будет следующим: diff(func, var, n) . Ниже приведено несколько примеров.
Разложение в ряд
Для разложения выражения в ряд Тейлора используется следующий синтаксис: series(expr, var) .
Интегрирование
В SymPy реализована поддержка определенных и неопределенных интегралов при помощи функции integrate() . Интегрировать можно элементарные, трансцендентные и специальные функции. Интегрирование осуществляется с помощью расширенного алгоритма Риша-Нормана. Также используются различные эвристики и шаблоны. Вот примеры интегрирования элементарных функций:
Также несложно посчитать интеграл и от специальных функций. Возьмем, например, функцию Гаусса:
Результат вычисления можете посмотреть сами. Вот примеры вычисления определенных интегралов.
Также можно вычислять определенные интегралы с бесконечными пределами интегрирования (несобственные интегралы).
Решение уравнений
При помощи SymPy можно решать алгебраические уравнения с одной или несколькими переменными. Для этого используется функция solveset() .
Как можно заметить, первое выражение функции solveset() приравнивается к 0 и решается относительно х . Также возможно решать некоторые уравнения с трансцендентными функциями.
Системы линейных уравнений
SymPy способна решать широкий класс полиномиальных уравнений. Также при помощи данной библиотеки можно решать и системы уравнений. При этом переменные, относительно которых должна быть разрешена система, передаются в виде кортежа во втором аргументе функции solve() , которая используется для таких задач.
Факторизация
Другим мощным методом исследования полиномиальных уравнений является факторизация многочленов (то есть представление многочлена в виде произведения многочленов меньших степеней). Для этого в SymPy предусмотрена функция factor() , которая способна производить факторизацию очень широкого класса полиномов.
Булевы уравнения
Также в SymPy реализована возможность решения булевых уравнений, что по сути означает проверку булевого выражения на истинность. Для этого используется функция satisfiable() .
Данный результат говорит нам о том, что выражение (x & y) будет истинным тогда и только тогда, когда x и y истинны. Если выражение не может быть истинным ни при каких значениях переменных, то функция вернет результат False .
Линейная алгебра
Матрицы
Матрицы в SymPy создаются как экземпляры класса Matrix :
В отличие от NumPy , мы можем использовать в матрицах символьные переменные:
И производить с ними разные манипуляции:
Дифференциальные уравнения
При помощи библиотеки SymPy можно решать некоторые обыкновенные дифференциальные уравнения. Для этого используется функция dsolve() . Для начала нам надо задать неопределенную функцию. Это можно сделать, передав параметр cls=Function в функцию symbols() .
Теперь f и g заданы как неопределенные функции. мы можем в этом убедиться, просто вызвав f(x) .
Теперь решим следующее дифференциальное уравнение:
Чтобы улучшить решаемость и помочь этой функции в поиске решения, можно передавать в нее определенные ключевые аргументы. Например, если мы видим, что это уравнение с разделяемыми переменными, то мы можем передать в функцию аргумент hint=’separable’ .
Английский для программистов
Наш телеграм канал с тестами по английскому языку для программистов. Английский это часть карьеры программиста. Поэтому полезно заняться им уже сейчас
Математическая библиотека Python SymPy
SymPy — это библиотека Python для выполнения символьных вычислений. Это система компьютерной алгебры, которая может выступать как отдельное приложение, так и в качестве библиотеки для других приложений. Поработать с ней онлайн можно на https://live.sympy.org/. Поскольку это чистая библиотека Python, ее можно использовать даже в интерактивном режиме.
В SymPy есть разные функции, которые применяются в сфере символьных вычислений, математического анализа, алгебры, дискретной математики, квантовой физики и так далее. SymPy может представлять результат в разных форматах: LaTeX, MathML и так далее. Распространяется библиотека по лицензии New BSD. Первыми эту библиотеку выпустили разработчики Ondřej Čertík и Aaron Meurer в 2007 году. Текущая актуальная версия библиотеки — 1.6.2.
Вот где применяется SymPy:
- Многочлены
- Математический анализ
- Дискретная математика
- Матрицы
- Геометрия
- Построение графиков
- Физика
- Статистика
- Комбинаторика
Установка SymPy
Для работы SymPy требуется одна важная библиотека под названием mpmath . Она используется для вещественной и комплексной арифметики с числами с плавающей точкой произвольной точности. Однако pip установит ее автоматически при загрузке самой SymPy:
Такие дистрибутивы, как Anaconda, Enthough, Canopy и другие, заранее включают SymPy. Чтобы убедиться в этом, достаточно ввести в интерактивном режиме команду:
Исходный код можно найти на GitHub.
Символьные вычисления в SymPy
Символьные вычисления — это разработка алгоритмов для управления математическими выражениями и другими объектами. Такие вычисления объединяют математику и компьютерные науки для решения математических выражений с помощью математических символов.
Система компьютерной алгебры же, такая как SymPy, оценивает алгебраические выражения с помощью тех же символов, которые используются в традиционных ручных методах. Например, квадратный корень числа с помощью модуля math в Python вычисляется вот так:
Как можно увидеть, квадратный корень числа 7 вычисляется приблизительно. Но в SymPy квадратные корни чисел, которые не являются идеальными квадратами, просто не вычисляются:
Вот каким будет вывод этого кода: sqrt(7) .
Это можно упростить и показать результат выражения символически таким вот образом:
В случае с модулем math вернется число, а вот в SymPy — формула.
Для рендеринга математических символов в формате LaTeX код SymPy, используйте Jupyter notebook:
Если выполнить эту команду в IDLE, то получится следующий результат:
Квадратный корень неидеального корня также может быть представлен в формате LaTeX с помощью привычных символов:
Символьные вычисления с помощью таких систем, как SymPy, помогают выполнять вычисления самого разного рода (производные, интегралы, пределы, решение уравнений, работа с матрицами) в символьном виде.
В пакете SymPy есть разные модули, которые помогают строить графики, выводить результат (LaTeX), заниматься физикой, статистикой, комбинаторикой, числовой теорией, геометрией, логикой и так далее.
Числа
Основной модуль в SymPy включает класс Number , представляющий атомарные числа. У него есть пара подклассов: Float и Rational . В Rational также входит Integer .
Класс Float
Float представляет числа с плавающей точкой произвольной точности:
SymPy может конвертировать целое число или строку в число с плавающей точкой:
При конвертации к числу с плавающей точкой, также можно указать количество цифр для точности:
Представить число дробью можно с помощью объекта класса Rational , где знаменатель — не 0:
Если число с плавающей точкой передать в конструктор Rational() , то он вернет дробь:
Для упрощения можно указать ограничение знаменателя:
Выведется дробь 1/5 вместо 3602879701896397/18014398509481984.
Если же в конструктор передать строку, то вернется рациональное число произвольной точности:
Также рациональное число можно получить, если в качестве аргументов передать два числа. Числитель и знаменатель доступны в виде свойств:
Класс Integer
Класс Integer в SymPy представляет целое число любого размера. Конструктор принимает рациональные и числа с плавающей точкой. В результате он откидывает дробную часть:
Также есть класс RealNumber , который является алиасом для Float . В SymPy есть классы-одиночки Zero и One , доступные через S.Zero и S.One соответственно.
Другие числовые объекты-одиночки — Half , NaN , Infinity и ImaginaryUnit .
Бесконечность представлена в виде объекта-символа oo или как S.Infinity :
ImaginaryUnit можно импортировать как символ I , а получить к нему доступ — через S.ImaginaryUnit .
Символы
Symbol — самый важный класс в библиотеке SymPy. Как уже упоминалось ранее, символьные вычисления выполняются с помощью символов. И переменные SymPy являются объектами класса Symbol .
Аргумент функции Symbol() — это строка, содержащая символ, который можно присвоить переменной.
Код выше является эквивалентом этого выражения:
Символ может включать больше одной буквы:
Также в SymPy есть функция Symbols() , с помощью которой можно определить несколько символов за раз. Строка содержит названия переменных, разделенные запятыми или пробелами.
В модуле abc можно найти элементы латинского и греческого алфавитов в виде символов. Таким образом вместо создания экземпляра Symbol можно использовать метод:
Однако C, O, S, I, N, E и Q являются заранее определенными символами. Также символы с более чем одной буквы не определены в abc. Для них нужно использовать объект Symbol . Модуль abs определяет специальные имена, которые могут обнаружить определения в пространстве имен SymPy по умолчанию. сlash1 содержит однобуквенные символы, а clash2 — целые слова.
Индексированные символы (последовательность слов с цифрами) можно определить с помощью синтаксиса, напоминающего функцию range() . Диапазоны обозначаются двоеточием. Тип диапазона определяется символом справа от двоеточия. Если это цифра, то все смежные цифры слева воспринимаются как неотрицательное начальное значение.
Смежные цифры справа берутся на 1 больше конечного значения.
Подстановка параметров
Одна из базовых операций в математических выражениях — подстановка. Функция subs() заменяет все случаи первого параметра на второй.
Этот код даст вывод, эквивалентный такому выражению.
А кодом expr.subs(x,a) мы получим туже формулу, но с a вместо x .
Эта функция полезна, когда требуется вычислить определенное выражение. Например, нужно посчитать значения выражения, заменив a на 5 :
Также функция используется для замены подвыражения другим подвыражением. В следующем примере b заменяется на a+b .
Это дает такой вывод:
Функция simplify()
Функция simplify() используется для преобразования любого произвольного выражения, чтобы его можно было использовать как выражение SymPy. Обычные объекты Python, такие как целые числа, конвертируются в SymPy.Integer и так далее. Строки также конвертируются в выражения SymPy:
Любой объект Python можно конвертировать в объект SymPy. Однако учитывая то, что при преобразовании используется функция eval() , не стоит использовать некорректные выражения, иначе возникнет ошибка SimplifyError .
Функция simplify() принимает следующий аргумент: strict=False . Если установить True , то преобразованы будут только те типы, для которых определено явное преобразование. В противном случае также возникнет ошибка SimplifyError . Если же поставить False , то арифметические выражения и операторы будут конвертированы в их эквиваленты SumPy без вычисления выражения.
Функция evalf()
Функция вычисляет данное числовое выражение с точностью до 100 цифр после плавающей точки. Она также принимает параметр subs , как объект словаря с числовыми значениями для символов. Например такое выражение:
Даст такой результат: ?? 2
Вычислим выражение с помощью evalf() и заменим r на 5:
По умолчанию точность после плавающей точки — 15, но это значение можно перезаписать до 100. Следующее выражение вычисляет, используя вплоть до 20 цифр точности:
Функция lambdify()
Функция lambdify() переводит выражения SymPy в функции Python. Если выражение, которое нужно вычислить, затрагивает диапазон значений, то функция evalf() становится неэффективной. Функция lambdify действует как лямбда-функция с тем исключением, что она конвертирует SymPy в имена данной числовой библиотеки, обычно NumPy. По умолчанию же она реализована на основе стандартной библиотеки math.
У выражения может быть больше одной переменной. В таком случае первым аргументом функции является список переменных, а после него — само выражение:
Но чтобы использовать numpy в качестве основной библиотеки, ее нужно передать в качестве аргумента функции lambdify() .
В этой функции использовались два массива numpy: a и b . В случае с ними выполнение гораздо быстрее:
Логические выражения
Булевы функции расположены в модуле sympy.basic.booleanarg . Их можно создать и с помощью стандартных операторов Python: & (And), | (Or),
(Not), а также >> и . Булевы выражения наследуются от класса Basic .
BooleanTrue.
Эта функция является эквивалентом True из Python. Она возвращает объект-одиночку, доступ к которому можно получить и с помощью S.true .
BooleanFalse.
А эта функция является эквивалентом False . Ее можно достать с помощью S.False .
And.
Функция логического AND оценивает два аргумента и возвращает False , если хотя бы один из них является False . Эта функция заменяет оператор & .
Or.
Оценивает два выражения и возвращает True , если хотя бы одно из них является True . Это же поведение можно получить с помощью оператора | .
Not.
Результат этой функции — отрицание булево аргумента. True, если аргумент является False , и False в противном случае. В Python за это отвечает оператор
Xor.
Логический XOR (исключающий OR) возвращает True, если нечетное количество аргументов равняется True , а остальные — False . False же вернется в том случае, если четное количество аргументов True , а остальные — False . То же поведение работает в случае оператора ^ .
В предыдущем примере один(нечетное число) аргумент является True , поэтому Xor вернет True . Если же количество истинных аргументов будет четным, результатом будет False , как показано дальше.
Nand.
Выполняет логическую операцию NAND. Оценивает аргументы и возвращает True , если хотя бы один из них равен False , и False — если они истинные.
Nor.
Выполняет логическую операцию NOR. Оценивает аргументы и возвращает False , если один из них True , или же True , если все — False .
Хотя SymPy и предлагает операторы ^ для Xor ,
для Not , | для Or и & для And ради удобства, в Python они используются в качестве побитовых. Поэтому если операнды будут целыми числами, результаты будут отличаться.
Equivalent.
Эта функция возвращает отношение эквивалентности. Equivalent(A, B) будет равно True тогда и только тогда, когда A и B оба будут True или False . Функция вернет True , если все аргументы являются логически эквивалентными. В противном случае — False .
Запросы
Модуль assumptions в SymPy включает инструменты для получения информации о выражениях. Для этого используется функция ask() .
Следующие свойства предоставляют полезную информацию о выражении:
algebraic(x)
Чтобы быть алгебраическим, число должно быть корнем ненулевого полиномиального уравнения с рациональными коэффициентами. √2, потому что √2 — это решение x2 − 2 = 0. Следовательно, это выражения является алгебраическим.
complex(x)
Предикат комплексного числа. Является истиной тогда и только тогда, когда x принадлежит множеству комплексных чисел.
composite(x)
Предикат составного числа, возвращаемый ask(Q.composite(x)) является истиной тогда и только тогда, когда x — это положительное число, имеющее как минимум один положительный делитель, кроме 1 и самого числа.
even, odd
ask() возвращает True , если x находится в множестве четных и нечетных чисел соответственно.
imaginary
Свойство представляет предикат мнимого числа. Является истиной, если x можно записать как действительное число, умноженное на мнимую единицу.
integer
Это свойство, возвращаемое Q.integer(x) , будет истинным только в том случае, если x принадлежит множеству четных чисел.
rational, irrational
Q.irrational(x) истинно тогда и только тогда, когда x — это любое реальное число, которое нельзя представить как отношение целых чисел. Например, pi — это иррациональное число.
positive, negative
Предикаты для проверки того, является ли число положительным или отрицательным.
zero, nonzero
Предикат для проверки того, является ли число нулем или нет.
[spoiler title=”источники:”]
http://pythonru.com/biblioteki/sympy-v-python
[/spoiler]
SymPy — это библиотека Python для выполнения символьных вычислений. Это система компьютерной алгебры, которая может выступать как отдельное приложение, так и в качестве библиотеки для других приложений. Поработать с ней онлайн можно на https://live.sympy.org/. Поскольку это чистая библиотека Python, ее можно использовать даже в интерактивном режиме.
В SymPy есть разные функции, которые применяются в сфере символьных вычислений, математического анализа, алгебры, дискретной математики, квантовой физики и так далее. SymPy может представлять результат в разных форматах: LaTeX, MathML и так далее. Распространяется библиотека по лицензии New BSD. Первыми эту библиотеку выпустили разработчики Ondřej Čertík и Aaron Meurer в 2007 году. Текущая актуальная версия библиотеки — 1.6.2.
Вот где применяется SymPy:
- Многочлены
- Математический анализ
- Дискретная математика
- Матрицы
- Геометрия
- Построение графиков
- Физика
- Статистика
- Комбинаторика
Для работы SymPy требуется одна важная библиотека под названием mpmath. Она используется для вещественной и комплексной арифметики с числами с плавающей точкой произвольной точности. Однако pip установит ее автоматически при загрузке самой SymPy:
pip install sympyТакие дистрибутивы, как Anaconda, Enthough, Canopy и другие, заранее включают SymPy. Чтобы убедиться в этом, достаточно ввести в интерактивном режиме команду:
>>> import sympy
>>> sympy.__version__
'1.6.2'
Исходный код можно найти на GitHub.
Символьные вычисления в SymPy
Символьные вычисления — это разработка алгоритмов для управления математическими выражениями и другими объектами. Такие вычисления объединяют математику и компьютерные науки для решения математических выражений с помощью математических символов.
Система компьютерной алгебры же, такая как SymPy, оценивает алгебраические выражения с помощью тех же символов, которые используются в традиционных ручных методах. Например, квадратный корень числа с помощью модуля math в Python вычисляется вот так:
import math
print(math.sqrt(25), math.sqrt(7))
Вывод следующий:
5.0 2.6457513110645907Как можно увидеть, квадратный корень числа 7 вычисляется приблизительно. Но в SymPy квадратные корни чисел, которые не являются идеальными квадратами, просто не вычисляются:
import sympy
print(sympy.sqrt(7))
Вот каким будет вывод этого кода: sqrt(7).
Это можно упростить и показать результат выражения символически таким вот образом:
>>> import math
>>> print(math.sqrt(12))
3.4641016151377544
>>> import sympy
>>> print(sympy.sqrt(12))
2*sqrt(3)
В случае с модулем math вернется число, а вот в SymPy — формула.
Для рендеринга математических символов в формате LaTeX код SymPy, используйте Jupyter notebook:
from sympy import *
x = Symbol('x')
expr = integrate(x**x, x)
expr
Если выполнить эту команду в IDLE, то получится следующий результат:
Integral(x**x,x)А в Jupyter:

Квадратный корень неидеального корня также может быть представлен в формате LaTeX с помощью привычных символов:
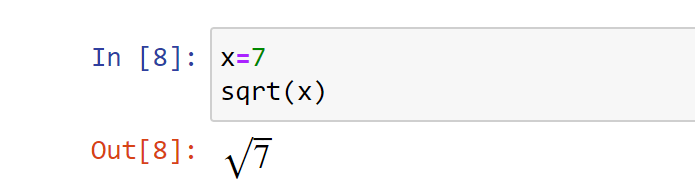
Символьные вычисления с помощью таких систем, как SymPy, помогают выполнять вычисления самого разного рода (производные, интегралы, пределы, решение уравнений, работа с матрицами) в символьном виде.
В пакете SymPy есть разные модули, которые помогают строить графики, выводить результат (LaTeX), заниматься физикой, статистикой, комбинаторикой, числовой теорией, геометрией, логикой и так далее.
Числа
Основной модуль в SymPy включает класс Number, представляющий атомарные числа. У него есть пара подклассов: Float и Rational. В Rational также входит Integer.
Класс Float
Float представляет числа с плавающей точкой произвольной точности:
>>> from sympy import Float
>>> Float(6.32)
6.32
SymPy может конвертировать целое число или строку в число с плавающей точкой:
При конвертации к числу с плавающей точкой, также можно указать количество цифр для точности:
>>> Float('1.33E5')
133000.0
Представить число дробью можно с помощью объекта класса Rational, где знаменатель — не 0:
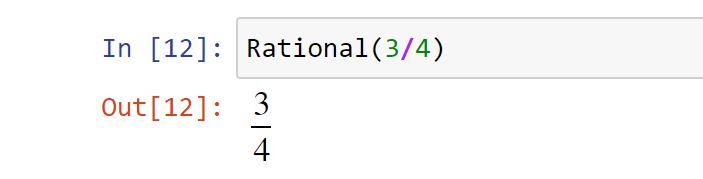
Если число с плавающей точкой передать в конструктор Rational(), то он вернет дробь:

Для упрощения можно указать ограничение знаменателя:
Rational(0.2).limit_denominator(100)
Выведется дробь 1/5 вместо 3602879701896397/18014398509481984.
Если же в конструктор передать строку, то вернется рациональное число произвольной точности:
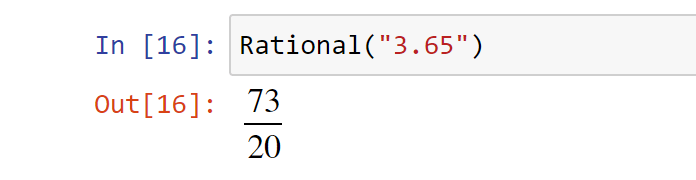
Также рациональное число можно получить, если в качестве аргументов передать два числа. Числитель и знаменатель доступны в виде свойств:
>>> a=Rational(3, 5)
>>> print(a)
3/5
>>> print("числитель:{}, знаменатель:{}".format(a.p, a.q))
числитель:3, знаменатель:5
Класс Integer
Класс Integer в SymPy представляет целое число любого размера. Конструктор принимает рациональные и числа с плавающей точкой. В результате он откидывает дробную часть:
>>> Integer(10)
10
>>> Integer(3.4)
3
>>> Integer(2/7)
0
Также есть класс RealNumber, который является алиасом для Float. В SymPy есть классы-одиночки Zero и One, доступные через S.Zero и S.One соответственно.
Другие числовые объекты-одиночки — Half, NaN, Infinity и ImaginaryUnit.
>>> from sympy import S
>>> print(S.Half)
1/2
>>> print(S.NaN)
nan
Бесконечность представлена в виде объекта-символа oo или как S.Infinity:

ImaginaryUnit можно импортировать как символ I, а получить к нему доступ — через S.ImaginaryUnit.
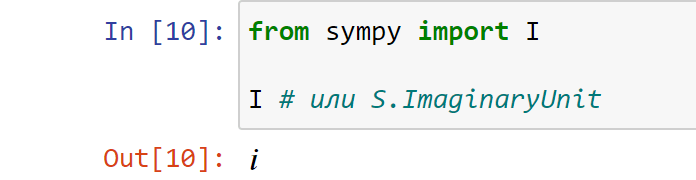
Символы
Symbol — самый важный класс в библиотеке SymPy. Как уже упоминалось ранее, символьные вычисления выполняются с помощью символов. И переменные SymPy являются объектами класса Symbol.
Аргумент функции Symbol() — это строка, содержащая символ, который можно присвоить переменной.
>>> from sympy import Symbol
>>> x = Symbol('x')
>>> y = Symbol('y')
>>> expr = x**2 + y**2
>>> expr
Код выше является эквивалентом этого выражения:
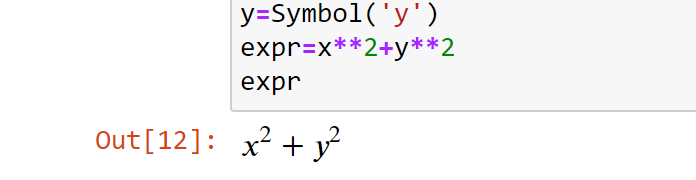
Символ может включать больше одной буквы:
from sympy import Symbol
s = Symbol('side')
s**3
Также в SymPy есть функция Symbols(), с помощью которой можно определить несколько символов за раз. Строка содержит названия переменных, разделенные запятыми или пробелами.
from sympy import symbols
x, y, z = symbols("x, y, z")
В модуле abc можно найти элементы латинского и греческого алфавитов в виде символов. Таким образом вместо создания экземпляра Symbol можно использовать метод:
from sympy.abc import x, z
Однако C, O, S, I, N, E и Q являются заранее определенными символами. Также символы с более чем одной буквы не определены в abc. Для них нужно использовать объект Symbol. Модуль abs определяет специальные имена, которые могут обнаружить определения в пространстве имен SymPy по умолчанию. сlash1 содержит однобуквенные символы, а clash2 — целые слова.
>>> from sympy.abc import _clash1, _clash2
>>> _clash1
{'C': C,'O': O,'Q': Q,'N': N,'I': I,'E': E,'S': S}
>>> _clash2
{'beta': beta,'zeta': zeta,'gamma': gamma,'pi': pi}
Индексированные символы (последовательность слов с цифрами) можно определить с помощью синтаксиса, напоминающего функцию range(). Диапазоны обозначаются двоеточием. Тип диапазона определяется символом справа от двоеточия. Если это цифра, то все смежные цифры слева воспринимаются как неотрицательное начальное значение.
Смежные цифры справа берутся на 1 больше конечного значения.
>>> from sympy import symbols
>>> symbols('a:5')
(a0,a1,a2,a3,a4)
>>> symbols('mark(1:4)')
(mark1,mark2,mark3)
Подстановка параметров
Одна из базовых операций в математических выражениях — подстановка. Функция subs() заменяет все случаи первого параметра на второй.
>>> from sympy.abc import x, a
>>> expr = sin(x) * sin(x) + cos(x) * cos(x)
>>> expr
Этот код даст вывод, эквивалентный такому выражению.
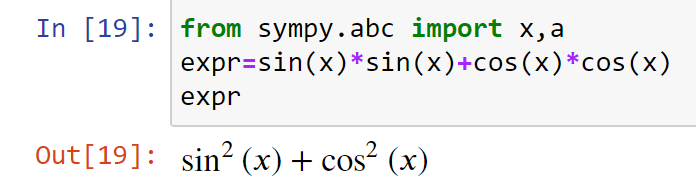
А кодом expr.subs(x,a) мы получим туже формулу, но с a вместо x.
Эта функция полезна, когда требуется вычислить определенное выражение. Например, нужно посчитать значения выражения, заменив a на 5:
>>> from sympy.abc import x
>>> from sympy import sin, pi
>>> expr = sin(x)
>>> expr1 = expr.subs(x, pi)
>>> expr1
0
Также функция используется для замены подвыражения другим подвыражением. В следующем примере b заменяется на a+b.
>>> from sympy.abc import a, b
>>> expr = (a + b)**2
>>> expr1 = expr.subs(b, a + b)
>>> expr1
Это дает такой вывод:
Функция simplify()
Функция simplify() используется для преобразования любого произвольного выражения, чтобы его можно было использовать как выражение SymPy. Обычные объекты Python, такие как целые числа, конвертируются в SymPy.Integer и так далее. Строки также конвертируются в выражения SymPy:
>>> expr = "x**2 + 3*x + 2"
>>> expr1 = sympify(expr)
>>> expr1.subs(x, 2)
12
Любой объект Python можно конвертировать в объект SymPy. Однако учитывая то, что при преобразовании используется функция eval(), не стоит использовать некорректные выражения, иначе возникнет ошибка SimplifyError.
>>> sympify("x***2")
...
SympifyError: Sympify of expression 'could not parse 'x***2'' failed, because of exception being raised:
SyntaxError: invalid syntax (, line 1)
Функция simplify() принимает следующий аргумент: strict=False. Если установить True, то преобразованы будут только те типы, для которых определено явное преобразование. В противном случае также возникнет ошибка SimplifyError. Если же поставить False, то арифметические выражения и операторы будут конвертированы в их эквиваленты SumPy без вычисления выражения.
Функция evalf()
Функция вычисляет данное числовое выражение с точностью до 100 цифр после плавающей точки. Она также принимает параметр subs, как объект словаря с числовыми значениями для символов. Например такое выражение:
from sympy.abc import r
expr = pi * r**2
expr
Даст такой результат: ??2
Вычислим выражение с помощью evalf() и заменим r на 5:
>>> expr.evalf(subs={r: 5})
78.5398163397448
По умолчанию точность после плавающей точки — 15, но это значение можно перезаписать до 100. Следующее выражение вычисляет, используя вплоть до 20 цифр точности:
>>> expr = a / b
>>> expr.evalf(20, subs={a: 100, b: 3})
33.333333333333333333
Функция lambdify()
Функция lambdify() переводит выражения SymPy в функции Python. Если выражение, которое нужно вычислить, затрагивает диапазон значений, то функция evalf() становится неэффективной. Функция lambdify действует как лямбда-функция с тем исключением, что она конвертирует SymPy в имена данной числовой библиотеки, обычно NumPy. По умолчанию же она реализована на основе стандартной библиотеки math.
>>> expr =1 / sin(x)
>>> f = lambdify(x, expr)
>>> f(3.14)
627.8831939138764
У выражения может быть больше одной переменной. В таком случае первым аргументом функции является список переменных, а после него — само выражение:
>>> expr = a**2 + b**2
>>> f = lambdify([a, b], expr)
>>> f(2, 3)
13
Но чтобы использовать numpy в качестве основной библиотеки, ее нужно передать в качестве аргумента функции lambdify().
f = lambdify([a, b], expr, "numpy")
В этой функции использовались два массива numpy: a и b. В случае с ними выполнение гораздо быстрее:
>>> import numpy
>>> l1 = numpy.arange(1, 6)
>>> l2 = numpy.arange(6, 11)
>>> f(l1, l2)
array([ 37, 53, 73, 97, 125], dtype=int32)
Логические выражения
Булевы функции расположены в модуле sympy.basic.booleanarg. Их можно создать и с помощью стандартных операторов Python: & (And), | (Or), ~ (Not), а также >> и <<. Булевы выражения наследуются от класса Basic.
BooleanTrue.
Эта функция является эквивалентом True из Python. Она возвращает объект-одиночку, доступ к которому можно получить и с помощью S.true.
>>> from sympy import *
>>> x = sympify(true)
>>> x, S.true
(True, True)
BooleanFalse.
А эта функция является эквивалентом False. Ее можно достать с помощью S.False.
>>> from sympy import *
>>> x = sympify(false)
>>> x, S.false
(False,False)
And.
Функция логического AND оценивает два аргумента и возвращает False, если хотя бы один из них является False. Эта функция заменяет оператор &.
>>> from sympy import *
>>> from sympy.logic.boolalg import And
>>> x, y = symbols('x y')
>>> x = True
>>> y = True
>>> And(x, y), x & y
Or.
Оценивает два выражения и возвращает True, если хотя бы одно из них является True. Это же поведение можно получить с помощью оператора |.
>>> from sympy import *
>>> from sympy.logic.boolalg import Or
>>> x, y = symbols('x y')
>>> x = True
>>> y = False
>>> Or(x, x|y)
Not.
Результат этой функции — отрицание булево аргумента. True, если аргумент является False, и False в противном случае. В Python за это отвечает оператор ~. Пример:
>>> from sympy import *
>>> from sympy.logic.boolalg import Or,And,Not
>>> x, y = symbols('x y')
>>> x = True
>>> y = False
>>> Not(x), Not(y)
(False, True)
Xor.
Логический XOR (исключающий OR) возвращает True, если нечетное количество аргументов равняется True, а остальные — False. False же вернется в том случае, если четное количество аргументов True, а остальные — False. То же поведение работает в случае оператора ^.
>>> from sympy import *
>>> from sympy.logic.boolalg import Xor
>>> x, y = symbols('x y')
>>> x = True
>>> y = False
>>> Xor(x, y)
True
В предыдущем примере один(нечетное число) аргумент является True, поэтому Xor вернет True. Если же количество истинных аргументов будет четным, результатом будет False, как показано дальше.
Nand.
Выполняет логическую операцию NAND. Оценивает аргументы и возвращает True, если хотя бы один из них равен False, и False — если они истинные.
>>> from sympy.logic.boolalg import Nand
>>> a, b, c = (True, False, True)
>>> Nand(a, c), Nand(a, b)
(False, True)
Nor.
Выполняет логическую операцию NOR. Оценивает аргументы и возвращает False, если один из них True, или же True, если все — False.
>>> from sympy.logic.boolalg import Nor
>>> a, b = False, True
>>> Nor(a), Nor(a, b)
(True, False)
Хотя SymPy и предлагает операторы ^ для Xor, ~ для Not, | для Or и & для And ради удобства, в Python они используются в качестве побитовых. Поэтому если операнды будут целыми числами, результаты будут отличаться.
Equivalent.
Эта функция возвращает отношение эквивалентности. Equivalent(A, B) будет равно True тогда и только тогда, когда A и B оба будут True или False. Функция вернет True, если все аргументы являются логически эквивалентными. В противном случае — False.
>>> from sympy.logic.boolalg import Equivalent
>>> a, b = True, False
>>> Equivalent(a, b), Equivalent(a, True)
( False, True)
Запросы
Модуль assumptions в SymPy включает инструменты для получения информации о выражениях. Для этого используется функция ask().
Следующие свойства предоставляют полезную информацию о выражении:
sympy.assumptions.ask(выражение)
algebraic(x)
Чтобы быть алгебраическим, число должно быть корнем ненулевого полиномиального уравнения с рациональными коэффициентами. √2, потому что √2 — это решение x2 − 2 = 0. Следовательно, это выражения является алгебраическим.
complex(x)
Предикат комплексного числа. Является истиной тогда и только тогда, когда x принадлежит множеству комплексных чисел.
composite(x)
Предикат составного числа, возвращаемый ask(Q.composite(x)) является истиной тогда и только тогда, когда x — это положительное число, имеющее как минимум один положительный делитель, кроме 1 и самого числа.
even, oddask() возвращает True, если x находится в множестве четных и нечетных чисел соответственно.
imaginary
Свойство представляет предикат мнимого числа. Является истиной, если x можно записать как действительное число, умноженное на мнимую единицу.
integer
Это свойство, возвращаемое Q.integer(x), будет истинным только в том случае, если x принадлежит множеству четных чисел.
rational, irrationalQ.irrational(x) истинно тогда и только тогда, когда x — это любое реальное число, которое нельзя представить как отношение целых чисел. Например, pi — это иррациональное число.
positive, negative
Предикаты для проверки того, является ли число положительным или отрицательным.
zero, nonzero
Предикат для проверки того, является ли число нулем или нет.
>>> from sympy import *
>>> x = Symbol('x')
>>> x = 10
>>> ask(Q.algebraic(pi))
False
>>> ask(Q.complex(5-4*I)), ask(Q.complex(100))
(True, True)
>>> x, y = symbols("x y")
>>> x, y = 5, 10
>>> ask(Q.composite(x)), ask(Q.composite(y))
(False, True)
>>> ask(Q.even(x)), ask(Q.even(y))
(True, None)
>>> ask(Q.imaginary(x)), ask(Q.imaginary(y))
(True, False)
>>> ask(Q.even(x)), ask(Q.even(y)), ask(Q.odd(x)), ask(Q.odd(y))
(True, True, False, False)
>>> ask(Q.positive(x)), ask(Q.negative(y)), ask(Q.positive(x)), ask(Q.negative(y))
(True, True)
>>> ask(Q.rational(pi)), ask(Q.irrational(S(2)/3))
(False, False)
>>> ask(Q.zero(oo)), ask(Q.nonzero(I))
(False, False)
Функции упрощения
SymPy умеет упрощать математические выражения. Для этого есть множество функций. Основная называется simplify(), и ее основная задача — представить выражение в максимально простом виде.
simplify
Это функция объявлена в модуле sympy.simplify. Она пытается применить методы интеллектуальной эвристики, чтобы сделать входящее выражение «проще». Следующий код упрощает такое выражение: sin^2(x)+cos^2(x)
>>> x = Symbol('x')
>>> expr = sin(x)**2 + cos(x)**2
>>> simplify(expr)
1
expand
Одна из самых распространенных функций упрощения в SymPy. Она используется для разложения полиномиальных выражений. Например:
>>> a, b = symbols('a b')
>>> expand((a+b)**2)
А тут вывод следующий: ?2+2??+?2.
Вывод: ?2−?2.
Функция expand() делает выражение больше, а не меньше. Обычно это так и работает, но часто получается так, что выражение становится меньше после использования функции:
>>> expand((x + 1)*(x - 2) - (x - 1)*x)
-2
factor
Эта функция берет многочлен и раскладывает его на неприводимые множители по рациональным числам.
>>> x, y, z = symbols('x y z')
>>> expr = (x**2*z + 4*x*y*z + 4*y**2*z)
>>> factor(expr)
Вывод: ?(?+2?)2.
Функция factor() — это противоположность expand(). Каждый делитель, возвращаемый factor(), будет несокращаемым. Функция factor_list() предоставляет более структурированный вывод:
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z)
>>> factor_list(expr)
(1, [(z, 1), (x + 2*y, 2)])
collect
Эта функция собирает дополнительные члены выражения относительно списка выражений с точностью до степеней с рациональными показателями.
>>> expr = x*y + x - 3 + 2*x**2 - z*x**2 + x**3
>>> expr
Вывод: ?3−?2?+2?2+??+?−3.
Результат работы collect():
>>> expr = y**2*x + 4*x*y*z + 4*y**2*z + y**3 + 2*x*y
>>> collect(expr, y)
Вывод: ?3+?2(?+4?)+?(4??+2?).
cancel
Эта функция берет любую рациональную функцию и приводит ее в каноническую форму p/q, где p и q — это разложенные полиномы без общих множителей. Старшие коэффициенты p и q не имеют знаменателей, то есть, являются целыми числами.
>>> expr1=x**2+2*x+1
>>> expr2=x+1
>>> cancel(expr1/expr2)
x + 1
Еще несколько примеров:
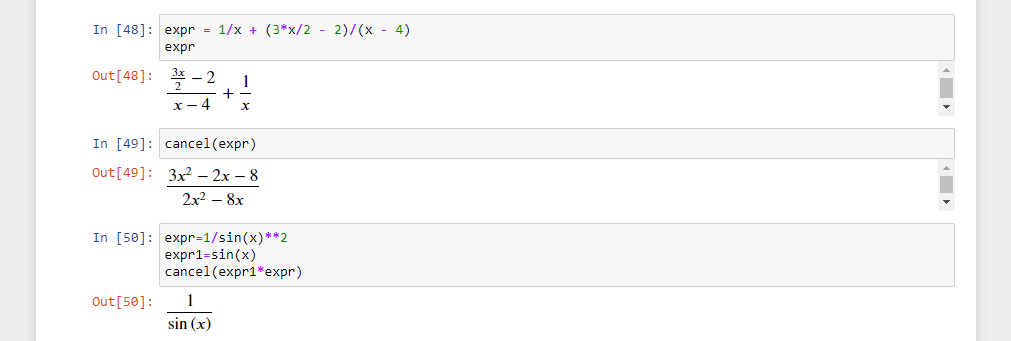
trigsimp
Эта функция используется для упрощения тригонометрических тождеств. Стоит отметить, что традиционные названия обратных тригонометрических функций добавляются в название функции в начале. Например, обратный косинус или арккосинус называется acos():
>>> from sympy import trigsimp, sin, cos
>>> from sympy.abc import x, y
>>> expr = 2*sin(x)**2 + 2*cos(x)**2
>>> trigsimp(expr)
2
Функция trigsimp использует эвристику для применения наиболее подходящего тригонометрического тождества.
powersimp
Эта функция сокращает выражения, объединяя степени с аналогичными основаниями и значениями степеней.
>>> expr = x**y*x**z*y**z
>>> expr
Вывод: ??????.
Можно сделать так, чтоб powsimp() объединяла только основания или степени, указав combine='base' или combine='exp'. По умолчанию это значение равно combine='all'. Также можно задать параметр force. Если он будет равен True, то основания объединятся без проверок.
>>> powsimp(expr, combine='base', force=True)
Вывод: ??(??)?.
combsimp
Комбинаторные выражения, включающие факториал и биномы, можно упростить с помощью функции combsimp(). В SymPy есть функция factorial().
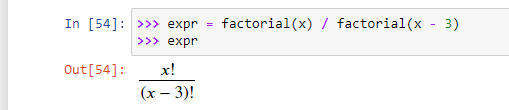
Для упрощения предыдущего комбинаторного выражения эта функция используется следующим образом.
>>> combsimp(expr)
?(?−2)(?−1)
binomial(x, y) — это количество способов, какими можно выбрать элементы y из множества элементов x. Его же можно записать и как xCy.
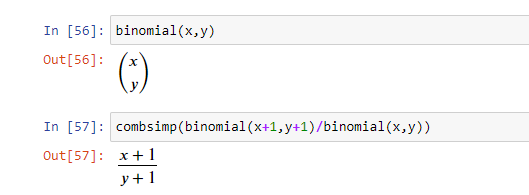
logcombine
Эта функция принимает логарифмы и объединяет их с помощью следующих правил:
log(x) + log(y) == log(x*y)— оба положительные.a*log(x) == log(x**a)если x является положительным и вещественным.
>>> logcombine(a*log(x) + log(y) - log(z))
?log(?)+log(?)−log(?)
Если здесь задать значение параметра force равным True, то указанные выше предположения будут считаться выполненными, если нет предположений о величине.
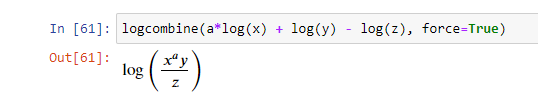
Производные
Производная функции — это ее скорость изменения относительно одной из переменных. Это эквивалентно нахождению наклона касательной к функции в точке. Найти дифференцирование математических выражений в форме переменных можно с помощью функции diff() из SymPy.
>>> from sympy import diff, sin, exp
>>> from sympy.abc import x, y
>>> expr = x*sin(x*x) + 1
>>> expr
Вывод: ?sin(?2)+1.
Чтобы получить несколько производных, нужно передать переменную столько раз, сколько нужно выполнить дифференцирование. Или же можно просто указать это количество с помощью числа.
Также можно вызвать метод diff() выражения. Он работает по аналогии с функцией.
>>> expr = x*sin(x*x) + 1
>>> expr.diff(x)
Вывод: 2?2cos(?2)+sin(?2).
Неоцененная производная создается с помощью класса Derivative. У него такой же синтаксис, как и функции diff(). Для оценки же достаточно использовать метод doit.

Интеграция
SymPy включает и модуль интегралов. В нем есть методы для вычисления определенных и неопределенных интегралов выражений. Метод integrate() используется для вычисления обоих интегралов. Для вычисления неопределенного или примитивного интеграла просто передайте переменную после выражения.
Для вычисления определенного интеграла, передайте аргументы следующим образом:
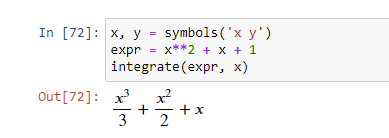
Пример определенного интеграла:
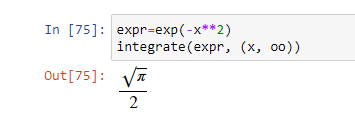
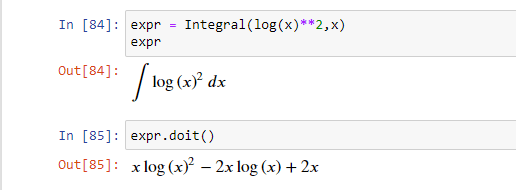
С помощью объекта Integral можно создать неоцененный интеграл. Он оценивается с помощью метода doit().
Трансформации интегралов
SymPy поддерживает разные виды трансформаций интегралов:
- laplace_tranfsorm.
- fourier_transform.
- sine_tranfsorm.
- cosine_transform.
- hankel_transform.
Эти функции определены в модуле sympy.integrals.transforms. Следующие примеры вычисляют преобразования Фурье и Лапласа соответственно:

>>> from sympy.integrals import laplace_transform
>>> from sympy.abc import t, s, a
>>> laplace_transform(t**a, t, s)
(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)
Матрицы
В математике матрица — это двумерный массив чисел, символов или выражений. Теория манипуляций матрицами связана с выполнением арифметических операций над матричными объектами при соблюдении определенных правил.
Линейная трансформация — одно из важнейших применений матрицы. Она часто используется в разных научных областях, особенно связанных с физикой. В SymPy есть модуль matrices, который работает с матрицами. В нем есть класс Matrix для представления матрицы.
Примечание: для выполнения кода в этом разделе нужно сперва импортировать модуль matrices следующим образом.
>>> from sympy.matrices import Matrix
>>> m=Matrix([[1, 2, 3], [2, 3, 1]])
>>> m
⎡1 2 3⎤
⎣2 3 1⎦
Матрица — это изменяемый объект. Также в модуле есть класс ImmutableMatrix для получения неизменяемой матрицы.
Базовое взаимодействие
Свойство shape возвращает размер матрицы.
Методы row() и col() возвращают колонку или строку соответствующего числа.
>>> m.row(0)
[1 2 3]
>>> m.col(1)
⎡2⎤
⎣3⎦
Оператор slice из Python можно использовать для получения одного или большего количества элементов строки или колонки.
У класса Matrix также есть методы row_del() и col_del(), которые удаляют указанные строку/колонку из выбранной матрицы.
>>> m.row(1)[1:3]
[3, 1]
>>> m.col_del(1)
>>> m
⎡1 3⎤
⎣2 1⎦
По аналогии row_insert() и col_insert() добавляют строки и колонки в обозначенные индексы:
>>> m1 = Matrix([[10, 30]])
>>> m = m.row_insert(0, m1)
>>> m
⎡10 30⎤
⎢ 1 3 ⎥
⎣ 2 1 ⎦
Арифметические операции
Привычные операторы +, — и * используются для сложения, умножения и деления.
>>> M1 = Matrix([[3, 0], [1, 6]])
>>> M2 = Matrix([[4, 5], [6, 4]])
>>> M1 + M2
⎡7 5 ⎤
⎣7 10 ⎦
Умножение матрицы возможно лишь в том случае, если количество колонок первой матрицы соответствует количеству колонок второй. Результат будет иметь такое же количество строк, как у первой матрицы и столько же колонок, сколько есть во второй.
Для вычисления определителя матрицы используется метод det(). Определитель — это скалярное значение, которое может быть вычислено из элементов квадратной матрицы.
>>> M = Matrix([[4, 5], [6, 4]])
>>> M.det()
-14
Конструкторы матрицы
SymPy предоставляет множество специальных типов классов матриц. Например, Identity, матрица из единиц, нолей и так далее. Эти классы называются eye, zeroes и ones соответственно. Identity — это квадратная матрица, элементы которой по диагонали равны 1, а остальные — 0.
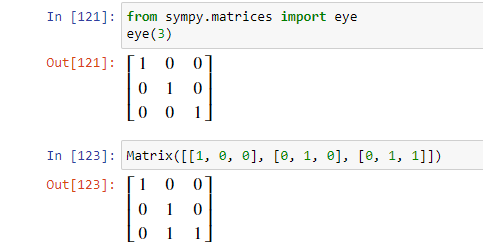
В матрице diag элементы по диагонали инициализируются в соответствии с предоставленными аргументами.
>>> from sympy.matrices import diag
>>> diag(1, 3)
⎡1 0 ⎤
⎣0 3 ⎦
Все элементы в матрице zero инициализируются как нули.
>>> from sympy.matrices import zeros
>>> zeros(2, 3)
⎡0 0 0⎤
⎣0 0 0⎦
По аналогии в матрице ones элементы равны 1:
>>> from sympy.matrices import zeros
>>> ones(2, 3)
⎡1 1 1⎤
⎣1 1 1⎦
Класс Function
В пакете SymPy есть класс Function, определенный в модуле sympy.core.function. Это базовый класс для всех математических функций, а также конструктор для неопределенных классов.
Следующие категории функций наследуются от класса Function:
- Функции для комплексных чисел
- Тригонометрические функции
- Функции целого числа
- Комбинаторные функции
- Другие функции
Функции комплексных чисел
Набор этих функций определен в модуле sympy.functions.elementary.complexes.
re — Эта функция возвращает реальную часть выражения:
>>> from sympy import *
>>> re(5+3*I)
5
>>> re(I)
0
im — Возвращает мнимую часть выражения:
>>> im(5+3*I)
3
>>> im(I)
1
sign — Эта функция возвращает сложный знак выражения..
Для реального выражения знак будет:
- 1, если выражение положительное,
- 0, если выражение равно нулю,
- -1, если выражение отрицательное.
Если выражение мнимое, то знаки следующие:
- l, если выражение положительное,
- -l, если выражение отрицательное.
>>> sign(1.55), sign(-1), sign(S.Zero)
(1,-1,0)
>>> sign (-3*I), sign(I*2)
(-I, I)
Функция abs возвращает абсолютное значение комплексного числа. Оно определяется как расстояние между основанием (0, 0) и точкой на комплексной плоскости. Эта функция является расширением встроенной функции abs() и принимает символьные значения.
Например, Abs(2+3*I), вернет √13.
conjugate — Функция возвращает сопряжение комплексного числа. Для поиска меняется знак мнимой части.
>>> conjugate(4+7*I)
4−7?
Тригонометрические функции
В SymPy есть определения всех тригонометрических соотношений: синуса, косинуса, тангенса и так далее. Также есть обратные аналоги: asin, acos, atan и так далее. Функции вычисляют соответствующее значение данного угла в радианах.
>>> sin(pi/2), cos(pi/4), tan(pi/6)
(1, sqrt(2)/2, sqrt(3)/3)
>>> asin(1), acos(sqrt(2)/2), atan(sqrt(3)/3)
(pi/2, pi/4, pi/6)
Функции целого числа
Набор функций для работы с целым числом.
Одномерная функция ceiling, возвращающая самое маленькое целое число, которое не меньше аргумента. В случае с комплексными числами округление до большего целого для целой и мнимой части происходит отдельно.
>>> ceiling(pi), ceiling(Rational(20, 3)), ceiling(2.6+3.3*I)
(4, 7, 3 + 4*I)
floor — Возвращает самое большое число, которое не больше аргумента. В случае с комплексными числами округление до меньшего целого для целой и мнимой части происходит отдельно.
>>> floor(pi), floor(Rational(100, 6)), floor(6.3-5.9*I)
(3, 16, 6 - 6*I)
frac — Функция представляет долю x.
>>> frac(3.99), frac(10)
(0.990000000000000, 0)
Комбинаторные функции
Комбинаторика — это раздел математики, в котором рассматриваются выбор, расположение и работа в конечной и дискретной системах.
factorial — Факториал очень важен в комбинаторике. Он обозначает число способов, которыми могут быть представлены объекты.
Кватернион
В математика числовая система кватернион расширяет комплексные числа. Каждый объект включает 4 скалярные переменные и 4 измерения: одно реальное и три мнимых.
Кватернион можно представить в виде следующего уравнения: q = a + bi + cj + dk, где a, b, c и d — это реальные числа, а i, j и k — квартенионные единицы, так что i2 == j2 == k2 = ijk.
Класс Quaternion расположен в модуле sympy.algebras.quaternion.
>>> from sympy.algebras.quaternion import Quaternion
>>> q = Quaternion(2, 3, 1, 4)
>>> q
2+3?+1?+4?
Кватернионы используются как в чистой, так и в прикладной математике, а также в компьютерной графике, компьютерном зрении и так далее.

add()
Этот метод класса Quaternion позволяет сложить два объекта класса:
>>> q1=Quaternion(1,2,4)
>>> q2=Quaternion(4,1)
>>> q1.add(q2)
5+3?+4?+0?
Также возможно добавить число или символ к объекту Quaternion.
>>> q1+2
3+2?+4?+0?
>>> q1+x
(?+1)+2?+4?+0?
mul()
Этот метод выполняет умножение двух кватернионов.
>>> q1 = Quaternion(1, 2)
>>> q2 = Quaternion(2, 4, 1)
>>> q1.mul(q2)
(−6)+8?+1?+2?
inverse()
Возвращает обратный кватернион.
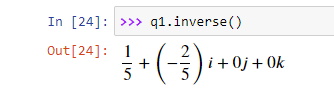
pow()
Возвращает степень кватерниона.
>>> q1.pow(2)
(−3)+4?+0?+0?
exp()
Вычисляет экспоненту кватерниона.
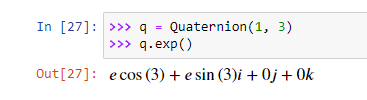
Уравнения
Поскольку символы = и == определены как символ присваивания и равенства в Python, их нельзя использовать для создания символьных уравнений. Для этого в SymPy есть функция Eq().
>>> x, y = symbols('x y')
>>> Eq(x, y)
?=?
Поскольку x=y возможно только в случае x-y=0, уравнение выше можно записать как:
Модуль solver из SymPy предлагает функцию solveset():
solveset(equation,variable,domain)Параметр domain по умолчанию равен S.Complexes. С помощью функции solveset() можно решить алгебраическое уравнение.
>>> solveset(Eq(x**2-9, 0), x)
{−3,3}
>>> solveset(Eq(x**2-3*x, -2), x)
{1,2}
Линейное уравнение
Для решения линейных уравнений нужно использовать функцию linsolve().
Например, уравнения могут быть такими:
- x-y=4
- x+1=1
Функция linsolve() также может решать линейные уравнения в матричной форме:
>>> a, b = symbols('a b')
>>> a = Matrix([[1, -1], [1, 1]])
>>> b = Matrix([4, 1])
>>> linsolve([a, b], y)
Вывод будет тот же.
Нелинейное уравнение
Для таких уравнений используется функция nonlinsolve(). Пример такого уравнения:
>>> a, b = symbols('a b')
>>> nonlinsolve([a**2 + a, a - b], [a, b])
{(−1, −1),(0, 0)}
Дифференциальное уравнение
Для начала создайте функцию, передав cls=Function в функцию symbols. Для решения дифференциальных уравнений используйте dsolve.
>>> x = ymbol('x')
>>> f = symbols('f', cls=Function)
>>> f(x)
?(?)
Здесь f(x) — это невычисленная функция. Ее производная:
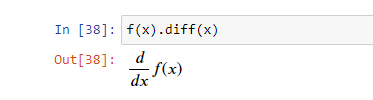
Сначала создается объект Eq, соответствующий следующему дифференциальному уравнению.
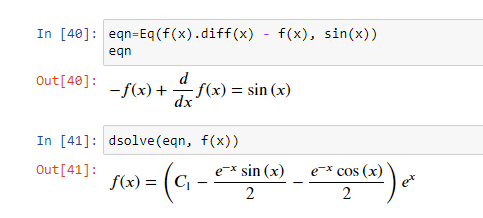
Графики
SymPy использует библиотеку matplotlib в качестве бэкенда для рендеринга двухмерных и трехмерных графиков математических функций. Убедитесь, что на вашем устройстве установлена matplotlib. Если нет, установите с помощью следующей команды.
pip install matplotlib
Функции для работы с графиками можно найти в модуле sympy.plotting:
plot— двухмерные линейные графики.plot3d— трехмерные линейные графики.plot_parametric— двухмерные параметрические графики.plot3d_parametric— трехмерные параметрические графики.
Функция plot() возвращает экземпляр класса Plot. Сам график может включать одно или несколько выражений SymPy. По умолчанию в качестве бэкенда используется matplotlib, но вместе нее можно взять texplot, pyglet или API Google Charts.
plot(expr,range,kwargs)
где expr — это любое валидное выражение SymPy. Если не сказано другое, то по умолчанию значение range равно (-10, 10).
Следующий график показывает квадрат для каждого значения в диапазоне от -10 до 10.
>>> from sympy.plotting import plot
>>> from sympy import *
>>> x = Symbol('x')
>>> plot(x**2, line_color='red')
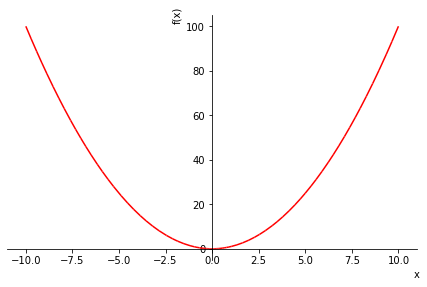
Чтобы нарисовать несколько графиков для одного диапазона, перед кортежем нужно указать несколько выражений.
>>> plot(sin(x), cos(x), (x, -pi, pi))
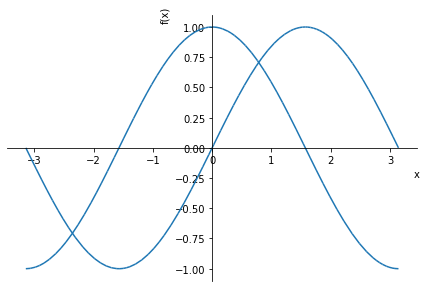
Также для каждого выражения можно задать отдельный диапазон.
plot((expr1,range1),(expr2,range2))
Также в функции plot() можно использовать следующие необязательные аргументы-ключевые слова.
line_color— определяет цвет линии графика.title— название графика.xlabel— метка для оси X.ylabel— метка для оси Y.
>>> plot((sin(x), (x,-pi,pi)), line_color='red', title='Пример графика SymPy')
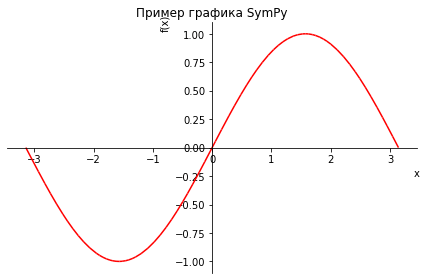
Функция plot3d() рендерит трехмерный график.
>>> from sympy.plotting import plot3d
>>> x, y = symbols('x y')
>>> plot3d(x*y, (x, -10, 10), (y, -10, 10))
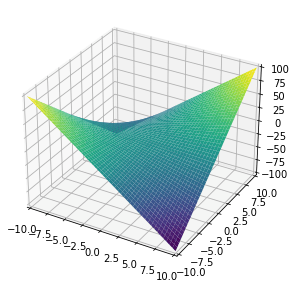
По аналогии с двухмерным трехмерный график может включать несколько графиков для отдельных диапазонов:
>>> plot3d(x*y, x/y, (x, -5, 5), (y, -5, 5))
Функция plot3d_parametric_line() рендерит трехмерный линейный параметрический график:
>>> from sympy.plotting import plot3d_parametric_line
>>> plot3d_parametric_line(cos(x), sin(x), x, (x, -5, 5))
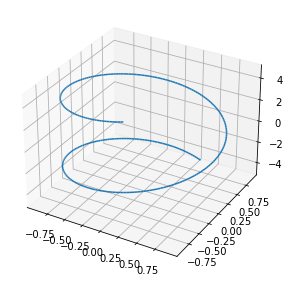
Чтобы нарисовать параметрический объемный график, используйте plot3d_parametric_surface().
Сущности
Модуль geometry в SymPy позволяет создавать двухмерные сущности, такие как линия, круг и так далее. Информацию о них можно получить через проверку коллинеарности или поиск пересечения.
Point
Класс point представляет точку Евклидового пространства. Следующие примеры проверяют коллинеарность точек:
>>> from sympy.geometry import Point
>>> from sympy import *
>>> x = Point(0, 0)
>>> y = Point(2, 2)
>>> z = Point(4, 4)
>>> Point.is_collinear(x, y, z)
True
>>> a = Point(2, 3)
>>> Point.is_collinear(x, a)
False
>>> x.distance(y)
2√2
Метод distance() класса Point вычисляет расстояние между двумя точками.
Line
Сущность Line можно получить из двух объектов Point. Метод intersection() возвращает точку пересечения двух линий.
>>> from sympy.geometry import Point, Line
>>> p1, p2 = Point(0, 5), Point(5, 0)
>>> l1 = Line(p1,p2)
>>> l2 = Line(Point(0, 0), Point(5, 5))
>>> l1.intersection(l2)
[Point2D(5/2, 5/2)]
>>> l1.intersection(Line(Point(0,0), Point(2,2)))
[Point2D(5/2, 5/2)]
>>> x, y = symbols('x y')
>>> p = Point(x, y)
>>> p.distance(Point(0, 0))
Вывод: √?2+?2
Triangle
Эта функция создает сущность Triangle из трех точек.
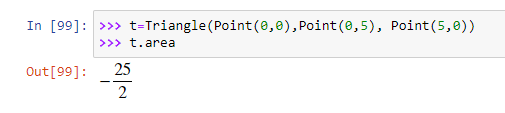
Ellipse
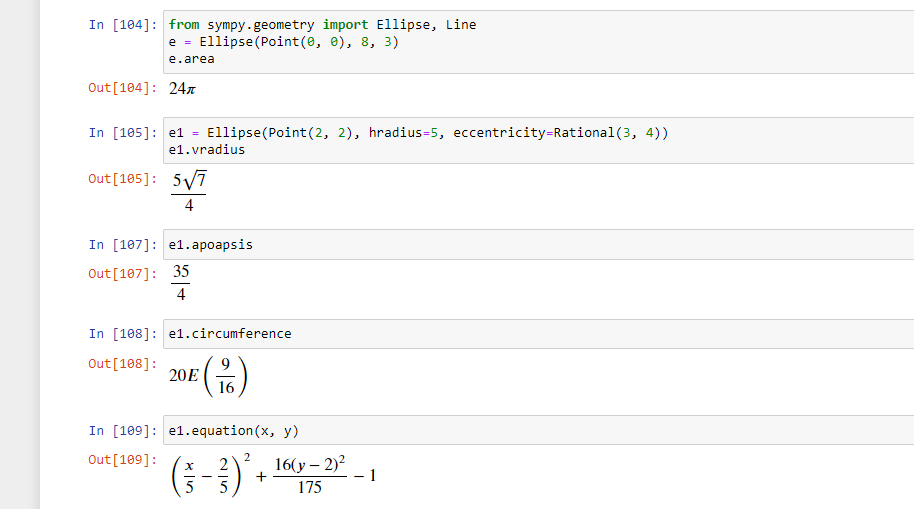
Эллиптическая геометрическая сущность создается с помощью объекта Point, который указывает на центр, а также горизонтальный и вертикальный радиусы.
ellipse(center,hradius,vradius)
>>> from sympy.geometry import Ellipse, Line
>>> e = Ellipse(Point(0, 0), 8, 3)
>>> e.area
24?
- vradius может быть получен косвенно с помощью параметра eccentricity.
apoapsis— это наибольшее расстояние между фокусом и контуром.- метод
equationэллипса возвращает уравнение эллипса.
Множества
В математике множество — это четко определенный набор объектов, которые могут быть числами, буквами алфавита или даже другими множествами. Set — это также один из встроенных типов в Python. В SymPy же есть модуль sets. В нем можно найти разные типы множеств и операции поиска пересекающихся элементов, объединения и так далее.
Set — это базовый класс для любого типа множества в Python. Но стоит отметить, что в SymPy он отличается от того, что есть в Python. Класс interval представляет реальные интервалы, а граничное свойство возвращает объект FiniteSet.
>>> from sympy import Interval
>>> s = Interval(1, 10).boundary
>>> type(s)
sympy.sets.sets.FiniteSet
FiniteSet — это коллекция дискретных чисел. Ее можно получить из любой последовательности, будь то список или строка.
>>> from sympy import FiniteSet
>>> FiniteSet(range(5))
{{0,1,…,4}}
>>> numbers = [1, 3, 5, 2, 8]
>>> FiniteSet(*numbers)
{1,2,3,5,8}
>>> s = "HelloWorld"
>>> FiniteSet(*s)
{?,?,?,?,?,?,?}
По аналогии со встроенным множеством, Set из SymPy также является коллекцией уникальных объектов.
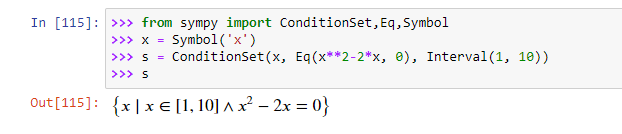
ConditionSet — это множество элементов, удовлетворяющих заданному условию.
Union — составное множество. Оно включает все элементы из двух множеств. Если же какие-то повторяются, то в результирующем множестве будет только одна копия.
>>> from sympy import Union
>>> l1 = [3, 7]
>>> l2 = [9, 7, 1]
>>> a = FiniteSet(*l1)
>>> b = FiniteSet(*l2)
>>> Union(a, b)
{1,3,7,9}
Intersection же включает только те элементы, которые есть в обоих множествах.
>>> from sympy import Intersection
>>> Intersection(a, b)
{7}
ProductSet представляет декартово произведение элементов из обоих множеств.
>>> from sympy import ProductSet
>>> l1 = [1, 2]
>>> l2 = [2, 3]
>>> a = FiniteSet(*l1)
>>> b = FiniteSet(*l2)
>>> set(ProductSet(a, b))
{(1, 2), (1, 3), (2, 2), (2, 3)}
Complement(a, b) исключает те элементы, которых нет в b.
>>> from sympy import Complement
>>> l1 = [3, 1]
>>> a = FiniteSet(*l1)
>>> b = FiniteSet(*l2)
>>> Complement(a, b), Complement(b, a)
(FiniteSet(1), FiniteSet(2))
SymmetricDifference хранит только необщие элементы обоих множеств.
>>> from sympy import SymmetricDifference
>>> l1 = [3, 1]
>>> a = FiniteSet(*l1)
>>> b = FiniteSet(*l2)
>>> SymmetricDifference(a, b)
{1,2}
Вывод в консоль
В SymPy есть несколько инструментов для вывода. Вот некоторые из них:
- str,
- srepr,
- ASCII pretty printer,
- Unicode pretty printer,
- LaTeX,
- MathML,
- Dot.
Объекты SymPy также можно отправить как ввод в другие языки программирования, такие как C, Fortran, JavaScript, Theano.
SymPy использует символы Юникод для рендеринга вывода. Если вы используете консоль Python для работы с SymPy, то лучше всего применять функцию init_session().
>>> from sympy import init_session
>>> init_session()
Python console for SymPy 1.6.2 (Python 3.8.5-64-bit) (ground types: python)
...
Выполним эти команды:
>>> from __future__ import division
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()
>>> Integral(sqrt(1/x), x)
⌠
⎮ ___
⎮ ╱ 1
⎮ ╱ ─ dx
⎮ ╲╱ x
⌡
Если нет LaTeX, но есть matplotlib, то последняя будет использоваться в качестве движка рендеринга. Если и matplotlib нет, то применяется Unicode pretty printer. Однако Jupyter notebook использует MathJax для рендеринга LaTeX.
В терминале, который не поддерживает Unicode, используется ASCII pretty printer (как в выводе из примера).
Для ASCII printer есть функция pprinter() с параметром use_unicode=False.
>>> pprint(Integral(sqrt(1/x), x), use_unicode=False)
/
|
| ___
| / 1
| / - dx
| / x
|
/Также доступ к Unicode printer можно получить из pprint() и pretty(). Если терминал поддерживает Unicode, то он используется автоматически. Если поддержку определить не удалось, то можно передать use_unicode=True, чтобы принудительно использовать Unicode.
Для получения LaTeX-формата используйте функцию latex().
>>> print(latex(Integral(sqrt(1/x), x)))
int sqrt{frac{1}{x}}, dx
Также доступен printer mathml. Для него есть функция pint_mathml().
>>> from sympy.printing.mathml import print_mathml
>>> print_mathml(Integral(sqrt(1/x),x))
x
x
-1
>>> mathml(Integral(sqrt(1/x),x))
xx-1Я хочу написать уравнение на python, которое будет выводить необходимое число.
Выглядит уравнение вот так:
y + 5x = z(x+1)
2 значения уже известны:
y = 3.62
z = 4.5
Но не известен X, который и нужно найти.
3.62 + 5x = 4.5(x+1)
#Потом он решает это уравнение и на вывод я должен получить: 1.76, которое запишу в переменную.
Как мне это сделать?
задан 8 мая 2022 в 15:28
2
Есть такой вариант, но с ходу он работает, если выражение приравнивается к нулю.
То есть мы 3.62 + 5x = 4.5(x+1) приводим к 3.62 + 5x - 4.5(x+1)
Предварительно устанавливаем pip install sympy
from sympy.solvers import solve
from sympy import Symbol
x = Symbol('x')
r = solve(3.62 + 5*x - 4.5*(x+1), x)
print(r)
# [1.76000000000000]
ответ дан 8 мая 2022 в 15:54
AlpensinAlpensin
3,0019 серебряных знаков18 бронзовых знаков
SymPy¶
SymPy – это пакет для символьных вычислений на питоне, подобный системе Mathematica. Он работает с выражениями, содержащими символы.
In [1]:
from sympy import * init_printing()
Основными кирпичиками, из которых строятся выражения, являются символы. Символ имеет имя, которое используется при печати выражений. Объекты класса Symbol нужно создавать и присваивать переменным питона, чтобы их можно было использовать. В принципе, имя символа и имя переменной, которой мы присваиваем этот символ – две независимые вещи, и можно написать abc=Symbol('xyz'). Но тогда при вводе программы Вы будете использовать abc, а при печати результатов SymPy будет использовать xyz, что приведёт к ненужной путанице. Поэтому лучше, чтобы имя символа совпадало с именем переменной питона, которой он присваивается.
В языках, специально предназначенных для символьных вычислений, таких, как Mathematica, если Вы используете переменную, которой ничего не было присвоено, то она автоматически воспринимается как символ с тем же именем. Питон не был изначально предназначен для символьных вычислений. Если Вы используете переменную, которой ничего не было присвоено, Вы получите сообщение об ошибке. Объекты типа Symbol нужно создавать явно.
Можно определить несколько символов одновременно. Строка разбивается на имена по пробелам.
Подставим вместо $x$ выражение $y+1$.
Out[5]:
$$left(y + 1right)^{2} – 1$$
Многочлены и рациональные функции¶
SymPy не раскрывает скобки автоматически. Для этого используется функция expand.
Out[6]:
$$left(x + y – zright)^{6}$$
Out[7]:
$$x^{6} + 6 x^{5} y – 6 x^{5} z + 15 x^{4} y^{2} – 30 x^{4} y z + 15 x^{4} z^{2} + 20 x^{3} y^{3} – 60 x^{3} y^{2} z + 60 x^{3} y z^{2} – 20 x^{3} z^{3} + 15 x^{2} y^{4} – 60 x^{2} y^{3} z + 90 x^{2} y^{2} z^{2} – 60 x^{2} y z^{3} + 15 x^{2} z^{4} + 6 x y^{5} – 30 x y^{4} z + 60 x y^{3} z^{2} – 60 x y^{2} z^{3} + 30 x y z^{4} – 6 x z^{5} + y^{6} – 6 y^{5} z + 15 y^{4} z^{2} – 20 y^{3} z^{3} + 15 y^{2} z^{4} – 6 y z^{5} + z^{6}$$
Степень многочлена $a$ по $x$.
Соберём вместе члены с определёнными степенями $x$.
Out[9]:
$$x^{6} + x^{5} left(6 y – 6 zright) + x^{4} left(15 y^{2} – 30 y z + 15 z^{2}right) + x^{3} left(20 y^{3} – 60 y^{2} z + 60 y z^{2} – 20 z^{3}right) + x^{2} left(15 y^{4} – 60 y^{3} z + 90 y^{2} z^{2} – 60 y z^{3} + 15 z^{4}right) + x left(6 y^{5} – 30 y^{4} z + 60 y^{3} z^{2} – 60 y^{2} z^{3} + 30 y z^{4} – 6 z^{5}right) + y^{6} – 6 y^{5} z + 15 y^{4} z^{2} – 20 y^{3} z^{3} + 15 y^{2} z^{4} – 6 y z^{5} + z^{6}$$
Многочлен с целыми коэффициентами можно записать в виде произведения таких многочленов (причём каждый сомножитель уже невозможно расфакторизовать дальше, оставаясь в рамках многочленов с целыми коэффициентами). Существуют эффективные алгоритмы для решения этой задачи.
Out[10]:
$$left(x + y – zright)^{6}$$
SymPy не сокращает отношения многочленов на их наибольший общий делитель автоматически. Для этого используется функция cancel.
In [11]:
a=(x**3-y**3)/(x**2-y**2) a
Out[11]:
$$frac{x^{3} – y^{3}}{x^{2} – y^{2}}$$
Out[12]:
$$frac{x^{2} + x y + y^{2}}{x + y}$$
SymPy не приводит суммы рациональных выражений к общему знаменателю автоматически. Для этого используется функция together.
Out[13]:
$$frac{x}{x + y} + frac{y}{x – y}$$
Out[14]:
$$frac{x left(x – yright) + y left(x + yright)}{left(x – yright) left(x + yright)}$$
Функция simplify пытается переписать выражение в наиболее простом виде. Это понятие не имеет чёткого определения (в разных ситуациях наиболее простыми могут считаться разные формы выражения), и не существует алгоритма такого упрощения. Функция symplify работает эвристически, и невозможно заранее предугадать, какие упрощения она попытается сделать. Поэтому её удобно использовать в интерактивных сессиях, чтобы посмотреть, удастся ли ей записать выражение в каком-нибудь разумном виде, но нежелательно использовать в программах. В них лучше применять более специализированные функции, которые выполняют одно определённое преобразование выражения.
Out[15]:
$$frac{x^{2} + y^{2}}{x^{2} – y^{2}}$$
Разложение на элементарные дроби по отношению к $x$.
Out[16]:
$$- frac{y}{x + y} + frac{y}{x – y} + 1$$
Подставим конкретные численные значения вместо переменных $x$ и $y$.
Out[17]:
$$- frac{5}{3}$$
А сколько это будет численно?
Out[18]:
$$-1.66666666666667$$
Элементарные функции¶
SymPy автоматически применяет упрощения элементарных функция (которые справедливы во всех случаях).
Out[19]:
$$- sin{left (x right )}$$
Out[20]:
$$left ( frac{sqrt{2}}{2}, quad – frac{sqrt{3}}{3}right )$$
SymPy может работать с числами с плавающей точкой, имеющими сколь угодно большую точность. Вот $pi$ с 100 значащими цифрами.
Out[21]:
$$3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068$$
E – это основание натуральных логарифмов.
Out[22]:
$$left ( 0, quad 1right )$$
Out[23]:
$$left ( x, quad log{left (e^{x} right )}right )$$
А почему не $x$? Попробуйте подставить $x=2pi i$.
Out[25]:
$$left ( x^{2}, quad sqrt{x^{4}}right )$$
А почему не $x^2$? Попробуйте подставить $x=i$.
Символы могут иметь некоторые свойства. Например, они могут быть положительными. Тогда SymPy может сильнее упростить квадратные корни.
In [26]:
p,q=symbols('p q',positive=True) sqrt(p**2)
In [27]:
sqrt(12*x**2*y),sqrt(12*p**2*y)
Out[27]:
$$left ( 2 sqrt{3} sqrt{x^{2} y}, quad 2 sqrt{3} p sqrt{y}right )$$
Пусть символ $n$ будет целым (I – это мнимая единица).
In [28]:
n=Symbol('n',integer=True) exp(2*pi*I*n)
Метод rewrite пытается переписать выражение в терминах заданной функции.
In [29]:
cos(x).rewrite(exp),exp(I*x).rewrite(cos)
Out[29]:
$$left ( frac{e^{i x}}{2} + frac{1}{2} e^{- i x}, quad i sin{left (x right )} + cos{left (x right )}right )$$
Out[30]:
$$- i log{left (i x + sqrt{- x^{2} + 1} right )}$$
Функция trigsimp пытается переписать тригонометрическое выражение в наиболее простом виде. В программах лучше использовать более специализированные функции.
In [31]:
trigsimp(2*sin(x)**2+3*cos(x)**2)
Out[31]:
$$cos^{2}{left (x right )} + 2$$
Функция expand_trig разлагает синусы и косинусы сумм и кратных углов.
In [32]:
expand_trig(sin(x-y)),expand_trig(sin(2*x))
Out[32]:
$$left ( sin{left (x right )} cos{left (y right )} – sin{left (y right )} cos{left (x right )}, quad 2 sin{left (x right )} cos{left (x right )}right )$$
Чаще нужно обратное преобразование – произведений и степеней синусов и косинусов в выражения, линейные по этим функциям. Например, пусть мы работаем с отрезком ряда Фурье.
In [33]:
a1,a2,b1,b2=symbols('a1 a2 b1 b2') a=a1*cos(x)+a2*cos(2*x)+b1*sin(x)+b2*sin(2*x) a
Out[33]:
$$a_{1} cos{left (x right )} + a_{2} cos{left (2 x right )} + b_{1} sin{left (x right )} + b_{2} sin{left (2 x right )}$$
Мы хотим возвести его в квадрат и опять получить отрезок ряда Фурье.
In [34]:
a=(a**2).rewrite(exp).expand().rewrite(cos).expand() a
Out[34]:
$$frac{a_{1}^{2}}{2} cos{left (2 x right )} + frac{a_{1}^{2}}{2} + a_{1} a_{2} cos{left (x right )} + a_{1} a_{2} cos{left (3 x right )} + a_{1} b_{1} sin{left (2 x right )} + a_{1} b_{2} sin{left (x right )} + a_{1} b_{2} sin{left (3 x right )} + frac{a_{2}^{2}}{2} cos{left (4 x right )} + frac{a_{2}^{2}}{2} – a_{2} b_{1} sin{left (x right )} + a_{2} b_{1} sin{left (3 x right )} + a_{2} b_{2} sin{left (4 x right )} – frac{b_{1}^{2}}{2} cos{left (2 x right )} + frac{b_{1}^{2}}{2} + b_{1} b_{2} cos{left (x right )} – b_{1} b_{2} cos{left (3 x right )} – frac{b_{2}^{2}}{2} cos{left (4 x right )} + frac{b_{2}^{2}}{2}$$
In [35]:
a.collect([cos(x),cos(2*x),cos(3*x),sin(x),sin(2*x),sin(3*x)])
Out[35]:
$$frac{a_{1}^{2}}{2} + a_{1} b_{1} sin{left (2 x right )} + frac{a_{2}^{2}}{2} cos{left (4 x right )} + frac{a_{2}^{2}}{2} + a_{2} b_{2} sin{left (4 x right )} + frac{b_{1}^{2}}{2} – frac{b_{2}^{2}}{2} cos{left (4 x right )} + frac{b_{2}^{2}}{2} + left(frac{a_{1}^{2}}{2} – frac{b_{1}^{2}}{2}right) cos{left (2 x right )} + left(a_{1} a_{2} – b_{1} b_{2}right) cos{left (3 x right )} + left(a_{1} a_{2} + b_{1} b_{2}right) cos{left (x right )} + left(a_{1} b_{2} – a_{2} b_{1}right) sin{left (x right )} + left(a_{1} b_{2} + a_{2} b_{1}right) sin{left (3 x right )}$$
Функция expand_log преобразует логарифмы произведений и степеней в суммы логарифмов (только для положительных величин); logcombine производит обратное преобразование.
In [36]:
a=expand_log(log(p*q**2)) a
Out[36]:
$$log{left (p right )} + 2 log{left (q right )}$$
Out[37]:
$$log{left (p q^{2} right )}$$
Функция expand_power_exp переписывает степени, показатели которых – суммы, через произведения степеней.
In [38]:
expand_power_exp(x**(p+q))
Функция expand_power_base переписывает степени, основания которых – произведения, через произведения степеней.
In [39]:
expand_power_base((x*y)**n)
Функция powsimp выполняет обратные преобразования.
In [40]:
powsimp(exp(x)*exp(2*y)),powsimp(x**n*y**n)
Out[40]:
$$left ( e^{x + 2 y}, quad left(x yright)^{n}right )$$
Можно вводить функции пользователя. Они могут иметь произвольное число аргументов.
In [41]:
f=Function('f') f(x)+f(x,y)
Out[41]:
$$f{left (x right )} + f{left (x,y right )}$$
Структура выражений¶
Внутреннее представление выражения – это дерево. Функция srepr возвращает строку, представляющую его.
Out[42]:
"Add(Symbol('x'), Integer(1))"
Out[43]:
"Add(Symbol('x'), Integer(-1))"
Out[44]:
"Add(Symbol('x'), Mul(Integer(-1), Symbol('y')))"
Out[45]:
"Mul(Rational(2, 3), Symbol('x'), Symbol('y'))"
Out[46]:
"Mul(Symbol('x'), Pow(Symbol('y'), Integer(-1)))"
Вместо бинарных операций +, *, ** и т.д. можно использовать функции Add, Mul, Pow и т.д.
Out[48]:
"Function('f')(Symbol('x'), Symbol('y'))"
Атрибут func – это функция верхнего уровня в выражении, а args – список её аргументов.
Out[50]:
$$left ( 2, quad x, quad y^{2}right )$$
In [51]:
for i in a.args: print(i)
Функция subs заменяет переменную на выражение.
Она можнет заменить несколько переменных. Для этого ей передаётся список кортежей или словарь.
Она может заменить не переменную, а подвыражение – функцию с аргументами.
In [55]:
a=f(x)+f(y) a.subs(f(y),1)
Out[55]:
$$f{left (x right )} + 1$$
In [57]:
(x+x**2+x**3+x**4).subs(x**2,y)
Out[57]:
$$x^{3} + x + y^{2} + y$$
Подстановки производятся последовательно. В данном случае сначала $x$ заменился на $y$, получилось $y^3+y^2$; потом в этом результате $y$ заменилось на $x$.
In [58]:
a=x**2+y**3 a.subs([(x,y),(y,x)])
Out[58]:
$$x^{3} + x^{2}$$
Если написать эти подстановки в другом порядке, результат будет другим.
Out[59]:
$$y^{3} + y^{2}$$
Но можно передать функции subs ключевой параметр simultaneous=True, тогда подстановки будут производиться одновременно. Таким образом можно, например, поменять местами $x$ и $y$.
In [60]:
a.subs([(x,y),(y,x)],simultaneous=True)
Out[60]:
$$x^{3} + y^{2}$$
Можно заменить функцию на другую функцию.
In [61]:
g=Function('g') a=f(x)+f(y) a.subs(f,g)
Out[61]:
$$g{left (x right )} + g{left (y right )}$$
Метод replace ищет подвыражения, соответствующие образцу (содержащему произвольные переменные), и заменяет их на заданное выражение (оно может содержать те же произвольные переменные).
In [62]:
a=Wild('a') (f(x)+f(x+y)).replace(f(a),a**2)
Out[62]:
$$x^{2} + left(x + yright)^{2}$$
In [63]:
(f(x,x)+f(x,y)).replace(f(a,a),a**2)
Out[63]:
$$x^{2} + f{left (x,y right )}$$
In [64]:
a=x**2+y**2 a.replace(x,x+1)
Out[64]:
$$y^{2} + left(x + 1right)^{2}$$
Соответствовать образцу должно целое подвыражение, это не может быть часть сомножителей в произведении или меньшая степеть в большей.
In [65]:
a=2*x*y*z a.replace(x*y,z)
In [66]:
(x+x**2+x**3+x**4).replace(x**2,y)
Out[66]:
$$x^{4} + x^{3} + x + y$$
Решение уравнений¶
In [67]:
a,b,c,d,e,f=symbols('a b c d e f')
Уравнение записывается как функция Eq с двумя параметрами. Функция solve возврящает список решений.
Out[68]:
$$left [ frac{b}{a}right ]$$
Впрочем, можно передать функции solve просто выражение. Подразумевается уравнение, что это выражение равно 0.
Out[69]:
$$left [ – frac{b}{a}right ]$$
Квадратное уравнение имеет 2 решения.
Out[70]:
$$left [ frac{1}{2 a} left(- b + sqrt{- 4 a c + b^{2}}right), quad – frac{1}{2 a} left(b + sqrt{- 4 a c + b^{2}}right)right ]$$
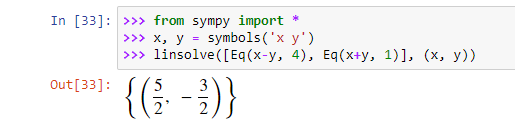
Система линейных уравнений.
In [71]:
solve([a*x+b*y-e,c*x+d*y-f],[x,y])
Out[71]:
$$left { x : frac{- b f + d e}{a d – b c}, quad y : frac{a f – c e}{a d – b c}right }$$
Функция roots возвращает корни многочлена с их множественностями.
Out[72]:
$$left { -2 : 1, quad 1 : 2right }$$
Функция solve_poly_system решает систему полиномиальных уравнений, строя их базис Грёбнера.
In [73]:
p1=x**2+y**2-1 p2=4*x*y-1 solve_poly_system([p1,p2],x,y)
Out[73]:
$$left [ left ( 4 left(-1 – sqrt{- frac{sqrt{3}}{4} + frac{1}{2}}right) sqrt{- frac{sqrt{3}}{4} + frac{1}{2}} left(- sqrt{- frac{sqrt{3}}{4} + frac{1}{2}} + 1right), quad – sqrt{- frac{sqrt{3}}{4} + frac{1}{2}}right ), quad left ( – 4 left(-1 + sqrt{- frac{sqrt{3}}{4} + frac{1}{2}}right) sqrt{- frac{sqrt{3}}{4} + frac{1}{2}} left(sqrt{- frac{sqrt{3}}{4} + frac{1}{2}} + 1right), quad sqrt{- frac{sqrt{3}}{4} + frac{1}{2}}right ), quad left ( 4 left(-1 – sqrt{frac{sqrt{3}}{4} + frac{1}{2}}right) sqrt{frac{sqrt{3}}{4} + frac{1}{2}} left(- sqrt{frac{sqrt{3}}{4} + frac{1}{2}} + 1right), quad – sqrt{frac{sqrt{3}}{4} + frac{1}{2}}right ), quad left ( – 4 left(-1 + sqrt{frac{sqrt{3}}{4} + frac{1}{2}}right) sqrt{frac{sqrt{3}}{4} + frac{1}{2}} left(sqrt{frac{sqrt{3}}{4} + frac{1}{2}} + 1right), quad sqrt{frac{sqrt{3}}{4} + frac{1}{2}}right )right ]$$
Ряды¶
Out[74]:
$$1 + x + frac{x^{2}}{2} + frac{x^{3}}{6} + frac{x^{4}}{24} + mathcal{O}left(x^{5}right)$$
Ряд может начинаться с отрицательной степени.
Out[75]:
$$frac{1}{x} – frac{x}{3} – frac{x^{3}}{45} + mathcal{O}left(x^{5}right)$$
И даже идти по полуцелым степеням.
In [76]:
sqrt(x*(1-x)).series(x,n=5)
Out[76]:
$$sqrt{x} – frac{x^{frac{3}{2}}}{2} – frac{x^{frac{5}{2}}}{8} – frac{x^{frac{7}{2}}}{16} – frac{5 x^{frac{9}{2}}}{128} + mathcal{O}left(x^{5}right)$$
In [77]:
log(gamma(1+x)).series(x,n=6).rewrite(zeta)
Out[77]:
$$- gamma x + frac{pi^{2} x^{2}}{12} – frac{x^{3} zetaleft(3right)}{3} + frac{pi^{4} x^{4}}{360} – frac{x^{5} zetaleft(5right)}{5} + mathcal{O}left(x^{6}right)$$
In [78]:
sinx=series(sin(x),x,0,8) sinx
Out[78]:
$$x – frac{x^{3}}{6} + frac{x^{5}}{120} – frac{x^{7}}{5040} + mathcal{O}left(x^{8}right)$$
In [79]:
cosx=series(cos(x),x,n=8) cosx
Out[79]:
$$1 – frac{x^{2}}{2} + frac{x^{4}}{24} – frac{x^{6}}{720} + mathcal{O}left(x^{8}right)$$
In [80]:
tanx=series(tan(x),x,n=8) tanx
Out[80]:
$$x + frac{x^{3}}{3} + frac{2 x^{5}}{15} + frac{17 x^{7}}{315} + mathcal{O}left(x^{8}right)$$
Произведения и частные рядов не вычисляются автоматически, к ним надо применить функцию series.
Out[81]:
$$x – frac{x^{3}}{6} + frac{x^{5}}{120} – frac{x^{7}}{5040} + mathcal{O}left(x^{8}right)$$
Out[82]:
$$x + frac{x^{3}}{3} + frac{2 x^{5}}{15} + frac{17 x^{7}}{315} + mathcal{O}left(x^{8}right)$$
А этот ряд должен быть равен 1. Но поскольку sinx и cosx известны лишь с ограниченной точностью, мы получаем 1 с той же точностью.
In [83]:
series(sinx**2+cosx**2,n=8)
Out[83]:
$$1 + mathcal{O}left(x^{8}right)$$
Здесь первые члены сократились, и ответ можно получить лишь с меньшей точностью.
In [84]:
series((1-cosx)/x**2,n=6)
Out[84]:
$$frac{1}{2} – frac{x^{2}}{24} + frac{x^{4}}{720} + mathcal{O}left(x^{6}right)$$
Ряды можно дифференцировать и интегрировать.
Out[85]:
$$1 – frac{x^{2}}{2} + frac{x^{4}}{24} – frac{x^{6}}{720} + mathcal{O}left(x^{7}right)$$
Out[86]:
$$x – frac{x^{3}}{6} + frac{x^{5}}{120} – frac{x^{7}}{5040} + mathcal{O}left(x^{9}right)$$
Можно подставить ряд (если он начинается с малого члена) вместо переменной разложения в другой ряд. Вот ряды для $sin(tan(x))$ и $tan(sin(x))$.
In [87]:
st=series(sinx.subs(x,tanx),n=8) st
Out[87]:
$$x + frac{x^{3}}{6} – frac{x^{5}}{40} – frac{55 x^{7}}{1008} + mathcal{O}left(x^{8}right)$$
In [88]:
ts=series(tanx.subs(x,sinx),n=8) ts
Out[88]:
$$x + frac{x^{3}}{6} – frac{x^{5}}{40} – frac{107 x^{7}}{5040} + mathcal{O}left(x^{8}right)$$
Out[89]:
$$frac{x^{7}}{30} + mathcal{O}left(x^{8}right)$$
В ряд нельзя подставлять численное значение переменной разложения (а значит, нельзя и строить график). Для этого нужно сначала убрать $mathcal{O}$ член, превратив отрезок ряда в многочлен.
Out[90]:
$$- frac{x^{7}}{5040} + frac{x^{5}}{120} – frac{x^{3}}{6} + x$$
Производные¶
Out[91]:
$$x cos{left (x + y right )} + sin{left (x + y right )}$$
Out[92]:
$$x cos{left (x + y right )}$$
Вторая производная по $x$ и первая по $y$.
Out[93]:
$$- x cos{left (x + y right )} + 2 sin{left (x + y right )}$$
Можно дифференцировать выражения, содержащие неопределённые функции.
In [94]:
a=x*f(x**2) b=diff(a,x) b
Out[94]:
$$2 x^{2} left. frac{d}{d xi_{1}} f{left (xi_{1} right )} right|_{substack{ xi_{1}=x^{2} }} + f{left (x^{2} right )}$$
Что это за зверь такой получился?
2*x**2*Subs(Derivative(f(_xi_1), _xi_1), (_xi_1,), (x**2,)) + f(x**2)
Функция Derivative представляет невычисленную производную. Её можно вычислить методом doit.
In [96]:
a=Derivative(sin(x),x) Eq(a,a.doit())
Out[96]:
$$frac{d}{d x} sin{left (x right )} = cos{left (x right )}$$
Интегралы¶
In [97]:
integrate(1/(x*(x**2-2)**2),x)
Out[97]:
$$frac{1}{4} log{left (x right )} – frac{1}{8} log{left (x^{2} – 2 right )} – frac{1}{4 x^{2} – 8}$$
In [98]:
integrate(1/(exp(x)+1),x)
Out[98]:
$$x – log{left (e^{x} + 1 right )}$$
Out[99]:
$$x log{left (x right )} – x$$
Out[100]:
$$- x cos{left (x right )} + sin{left (x right )}$$
In [101]:
integrate(x*exp(-x**2),x)
Out[101]:
$$- frac{e^{- x^{2}}}{2}$$
Out[102]:
$$int x^{x}, dx$$
Получился невычисленный интеграл.
In [104]:
a=Integral(sin(x),x) Eq(a,a.doit())
Out[104]:
$$int sin{left (x right )}, dx = – cos{left (x right )}$$
In [105]:
integrate(sin(x),(x,0,pi))
In [106]:
integrate(exp(-x**2),(x,0,oo))
Out[106]:
$$frac{sqrt{pi}}{2}$$
In [107]:
integrate(log(x)/(1-x),(x,0,1))
Out[107]:
$$- frac{pi^{2}}{6}$$
Суммирование рядов¶
In [108]:
summation(1/n**2,(n,1,oo))
Out[108]:
$$frac{pi^{2}}{6}$$
In [109]:
summation((-1)**n/n**2,(n,1,oo))
Out[109]:
$$- frac{pi^{2}}{12}$$
In [110]:
summation(1/n**4,(n,1,oo))
Out[110]:
$$frac{pi^{4}}{90}$$
Невычисленная сумма обозначается Sum.
In [111]:
a=Sum(x**n/factorial(n),(n,0,oo)) Eq(a,a.doit())
Out[111]:
$$sum_{n=0}^{infty} frac{x^{n}}{n!} = e^{x}$$
Пределы¶
In [112]:
limit((tan(sin(x))-sin(tan(x)))/x**7,x,0)
Out[112]:
$$frac{1}{30}$$
Ну это простой предел, считается разложением числителя и знаменателя в ряды. А вот если в $x=0$ существенно особая точка, дело сложнее. Посчитаем односторонние пределы.
In [113]:
limit((tan(sin(x))-sin(tan(x)))/(x**7+exp(-1/x)),x,0,'+')
Out[113]:
$$frac{1}{30}$$
In [114]:
limit((tan(sin(x))-sin(tan(x)))/(x**7+exp(-1/x)),x,0,'-')
Дифференциальные уравнения¶
In [115]:
t=Symbol('t') x=Function('x') p=Function('p')
In [116]:
dsolve(diff(x(t),t)+x(t),x(t))
Out[116]:
$$x{left (t right )} = C_{1} e^{- t}$$
In [117]:
dsolve(diff(x(t),t,2)+x(t),x(t))
Out[117]:
$$x{left (t right )} = C_{1} sin{left (t right )} + C_{2} cos{left (t right )}$$
Система уравнений первого порядка.
In [118]:
dsolve((diff(x(t),t)-p(t),diff(p(t),t)+x(t)))
Out[118]:
$$left [ x{left (t right )} = C_{1} sin{left (t right )} + C_{2} cos{left (t right )}, quad p{left (t right )} = C_{1} cos{left (t right )} – C_{2} sin{left (t right )}right ]$$
Линейная алгебра¶
In [119]:
a,b,c,d,e,f=symbols('a b c d e f')
Матрицу можно построить из списка списков.
In [120]:
M=Matrix([[a,b,c],[d,e,f]]) M
Out[120]:
$$left[begin{matrix}a & b & c\d & e & fend{matrix}right]$$
Out[121]:
$$left ( 2, quad 3right )$$
Out[122]:
$$left[begin{matrix}1 & 2 & 3end{matrix}right]$$
Out[123]:
$$left[begin{matrix}1\2\3end{matrix}right]$$
Можно построить матрицу из функции.
In [124]:
def g(i,j): return Rational(1,i+j+1) Matrix(3,3,g)
Out[124]:
$$left[begin{matrix}1 & frac{1}{2} & frac{1}{3}\frac{1}{2} & frac{1}{3} & frac{1}{4}\frac{1}{3} & frac{1}{4} & frac{1}{5}end{matrix}right]$$
Или из неопределённой функции.
In [125]:
g=Function('g') M=Matrix(3,3,g) M
Out[125]:
$$left[begin{matrix}g{left (0,0 right )} & g{left (0,1 right )} & g{left (0,2 right )}\g{left (1,0 right )} & g{left (1,1 right )} & g{left (1,2 right )}\g{left (2,0 right )} & g{left (2,1 right )} & g{left (2,2 right )}end{matrix}right]$$
Out[126]:
$$g{left (1,2 right )}$$
Out[127]:
$$left[begin{matrix}g{left (0,0 right )} & g{left (0,1 right )} & g{left (0,2 right )}\g{left (1,0 right )} & g{left (1,1 right )} & 0\g{left (2,0 right )} & g{left (2,1 right )} & g{left (2,2 right )}end{matrix}right]$$
Out[128]:
$$left[begin{matrix}g{left (2,0 right )} & g{left (2,1 right )} & g{left (2,2 right )}end{matrix}right]$$
Out[129]:
$$left[begin{matrix}g{left (0,1 right )}\g{left (1,1 right )}\g{left (2,1 right )}end{matrix}right]$$
Out[130]:
$$left[begin{matrix}g{left (0,1 right )} & g{left (0,2 right )}\g{left (1,1 right )} & 0end{matrix}right]$$
Out[131]:
$$left[begin{matrix}1 & 0 & 0\0 & 1 & 0\0 & 0 & 1end{matrix}right]$$
Out[132]:
$$left[begin{matrix}0 & 0 & 0\0 & 0 & 0\0 & 0 & 0end{matrix}right]$$
Out[133]:
$$left[begin{matrix}0 & 0 & 0\0 & 0 & 0end{matrix}right]$$
Out[134]:
$$left[begin{matrix}1 & 0 & 0\0 & 2 & 0\0 & 0 & 3end{matrix}right]$$
In [135]:
M=Matrix([[a,1],[0,a]]) diag(1,M,2)
Out[135]:
$$left[begin{matrix}1 & 0 & 0 & 0\0 & a & 1 & 0\0 & 0 & a & 0\0 & 0 & 0 & 2end{matrix}right]$$
In [136]:
A=Matrix([[a,b],[c,d]]) B=Matrix([[1,2],[3,4]]) A+B
Out[136]:
$$left[begin{matrix}a + 1 & b + 2\c + 3 & d + 4end{matrix}right]$$
Out[137]:
$$left ( left[begin{matrix}a + 3 b & 2 a + 4 b\c + 3 d & 2 c + 4 dend{matrix}right], quad left[begin{matrix}a + 2 c & b + 2 d\3 a + 4 c & 3 b + 4 dend{matrix}right]right )$$
Out[138]:
$$left[begin{matrix}3 b – 2 c & 2 a + 3 b – 2 d\- 3 a – 3 c + 3 d & – 3 b + 2 cend{matrix}right]$$
Out[139]:
$$left[begin{matrix}frac{d}{a d – b c} & – frac{b}{a d – b c}\- frac{c}{a d – b c} & frac{a}{a d – b c}end{matrix}right]$$
Собственные значения и векторы¶
In [142]:
M=Matrix([[(1-x)**3*(3+x),4*x*(1-x**2),-2*(1-x**2)*(3-x)], [4*x*(1-x**2),-(1+x)**3*(3-x),2*(1-x**2)*(3+x)], [-2*(1-x**2)*(3-x),2*(1-x**2)*(3+x),16*x]]) M
Out[142]:
$$left[begin{matrix}left(- x + 1right)^{3} left(x + 3right) & 4 x left(- x^{2} + 1right) & left(- x + 3right) left(2 x^{2} – 2right)\4 x left(- x^{2} + 1right) & – left(- x + 3right) left(x + 1right)^{3} & left(x + 3right) left(- 2 x^{2} + 2right)\left(- x + 3right) left(2 x^{2} – 2right) & left(x + 3right) left(- 2 x^{2} + 2right) & 16 xend{matrix}right]$$
Значит, у этой матрицы есть нулевое подпространство (она обращает векторы из этого подпространства в 0). Базис этого подпространства.
Out[145]:
$$left[begin{matrix}- frac{2}{x – 1}\frac{2}{x + 1}\1end{matrix}right]$$
Out[146]:
$$left[begin{matrix}0\0\0end{matrix}right]$$
Собственные значения и их кратности.
Out[147]:
$$left { 0 : 1, quad – left(x^{2} + 3right)^{2} : 1, quad left(x^{2} + 3right)^{2} : 1right }$$
Если нужны не только собственные значения, но и собственные векторы, то нужно использовать метод eigenvects. Он возвращает список кортежей. В каждом из них нулевой элемент – собственное значение, первый – его кратность, и последний – список собственных векторов, образующих базис (их столько, какова кратность).
In [149]:
for i in range(len(v)): v[i][2][0]=simplify(v[i][2][0]) v
Out[149]:
$$left [ left ( 0, quad 1, quad left [ left[begin{matrix}- frac{2}{x – 1}\frac{2}{x + 1}\1end{matrix}right]right ]right ), quad left ( – left(x^{2} + 3right)^{2}, quad 1, quad left [ left[begin{matrix}frac{x}{2} + frac{1}{2}\frac{x + 1}{x – 1}\1end{matrix}right]right ]right ), quad left ( left(x^{2} + 3right)^{2}, quad 1, quad left [ left[begin{matrix}frac{x – 1}{x + 1}\- frac{x}{2} + frac{1}{2}\1end{matrix}right]right ]right )right ]$$
In [150]:
for i in range(len(v)): z=M*v[i][2][0]-v[i][0]*v[i][2][0] pprint(simplify(z))
⎡0⎤ ⎢ ⎥ ⎢0⎥ ⎢ ⎥ ⎣0⎦ ⎡0⎤ ⎢ ⎥ ⎢0⎥ ⎢ ⎥ ⎣0⎦ ⎡0⎤ ⎢ ⎥ ⎢0⎥ ⎢ ⎥ ⎣0⎦
Жорданова нормальная форма¶
In [151]:
M=Matrix([[Rational(13,9),-Rational(2,9),Rational(1,3),Rational(4,9),Rational(2,3)], [-Rational(2,9),Rational(10,9),Rational(2,15),-Rational(2,9),-Rational(11,15)], [Rational(1,5),-Rational(2,5),Rational(41,25),-Rational(2,5),Rational(12,25)], [Rational(4,9),-Rational(2,9),Rational(14,15),Rational(13,9),-Rational(2,15)], [-Rational(4,15),Rational(8,15),Rational(12,25),Rational(8,15),Rational(34,25)]]) M
Out[151]:
$$left[begin{matrix}frac{13}{9} & – frac{2}{9} & frac{1}{3} & frac{4}{9} & frac{2}{3}\- frac{2}{9} & frac{10}{9} & frac{2}{15} & – frac{2}{9} & – frac{11}{15}\frac{1}{5} & – frac{2}{5} & frac{41}{25} & – frac{2}{5} & frac{12}{25}\frac{4}{9} & – frac{2}{9} & frac{14}{15} & frac{13}{9} & – frac{2}{15}\- frac{4}{15} & frac{8}{15} & frac{12}{25} & frac{8}{15} & frac{34}{25}end{matrix}right]$$
Метод M.jordan_form() возвращает пару матриц, матрицу преобразования $P$ и собственно жорданову форму $J$: $M = P J P^{-1}$.
Out[152]:
$$left[begin{matrix}1 & 0 & 0 & 0 & 0\0 & 2 & 1 & 0 & 0\0 & 0 & 2 & 0 & 0\0 & 0 & 0 & 1 – i & 0\0 & 0 & 0 & 0 & 1 + iend{matrix}right]$$
Out[153]:
$$left[begin{matrix}-2 & frac{10}{9} & 0 & frac{5 i}{12} & – frac{5 i}{12}\-2 & – frac{5}{9} & 0 & – frac{5 i}{6} & frac{5 i}{6}\0 & 0 & frac{4}{3} & – frac{3}{4} & – frac{3}{4}\1 & frac{10}{9} & 0 & – frac{5 i}{6} & frac{5 i}{6}\0 & 0 & 1 & 1 & 1end{matrix}right]$$
In [154]:
Z=P*J*P**(-1)-M simplify(Z)
Out[154]:
$$left[begin{matrix}0 & 0 & 0 & 0 & 0\0 & 0 & 0 & 0 & 0\0 & 0 & 0 & 0 & 0\0 & 0 & 0 & 0 & 0\0 & 0 & 0 & 0 & 0end{matrix}right]$$
Графики¶
SymPy использует matplotlib. Однако он распределяет точки по $x$ адаптивно, а не равномерно.
In [156]:
plot(sin(x)/x,(x,-10,10))
Out[156]:
<sympy.plotting.plot.Plot at 0xaf83218c>
In [157]:
plot(x,x**2,x**3,(x,0,2))
Out[157]:
<sympy.plotting.plot.Plot at 0xb14ab02c>
Другие функции надо импортировать из пакета sympy.plotting.
In [158]:
from sympy.plotting import (plot_parametric,plot_implicit, plot3d,plot3d_parametric_line, plot3d_parametric_surface)
Параметрический график – фигура Лиссажу.
In [159]:
t=Symbol('t') plot_parametric(sin(2*t),cos(3*t),(t,0,2*pi), title='Lissajous',xlabel='x',ylabel='y')
Out[159]:
<sympy.plotting.plot.Plot at 0xaf6a188c>
Неявный график – окружность.
In [160]:
plot_implicit(x**2+y**2-1,(x,-1,1),(y,-1,1))
Out[160]:
<sympy.plotting.plot.Plot at 0xaf71c9cc>
Поверхность. Если она строится не inline, а в отдельном окне, то её можно вертеть мышкой.
In [161]:
plot3d(x*y,(x,-2,2),(y,-2,2))
Out[161]:
<sympy.plotting.plot.Plot at 0xaf6bea8c>
In [162]:
plot3d(x**2+y**2,x*y,(x,-2,2),(y,-2,2))
Out[162]:
<sympy.plotting.plot.Plot at 0xaf64c36c>
Параметрическая пространственная линия – спираль.
In [163]:
a=0.1 plot3d_parametric_line(cos(t),sin(t),a*t,(t,0,4*pi))
Out[163]:
<sympy.plotting.plot.Plot at 0xaf714c0c>
Параметрическая поверхность – тор.
In [164]:
u,v=symbols('u v') a=0.3 plot3d_parametric_surface((1+a*cos(u))*cos(v), (1+a*cos(u))*sin(v),a*sin(u), (u,0,2*pi),(v,0,2*pi))
Out[164]:
<sympy.plotting.plot.Plot at 0xaf646cac>
Что такое SymPy? Это библиотека символьной математики языка Python. Она является реальной альтернативой таким математическим пакетам как Mathematica или Maple и обладает очень простым и легко расширяемым кодом. SymPy написана исключительно на языке Python и не требует никаких сторонних библиотек.
Документацию и исходный код этой библиотеки можно найти на ее официальной странице.
Используем SymPy как обычный калькулятор
В библиотеке SymPy есть три встроенных численных типа данных: Real, Rational и Integer. С Real и Integer все понятно, а класс Rational представляет рациональное число как пару чисел: числитель и знаменатель рациональной дроби. Таким образом, Rational(1, 2) представляет собой 1/2, а, например, Rational(5, 2) — соответственно 5/2.
import sympy as sym a = sym.Rational(1, 2) # дает 1/2 a * 2 # дает 1
Библиотека SymPy использует библиотеку mpmath, что позволяет производить вычисления с произвольной точностью. Таким образом, ряд констант (например, пи, e), которые в данной библиотеке рассматриваются как символы, могут быть вычислены с любой точностью.
sym.pi**2 # результат pi**2 sym.pi.evalf() # результат 3.14159265358979 (sym.pi + sym.exp(1)).evalf() # результат 5.85987448204884
Как можно заметить, функция evalf() дает на выходе число с плавающей точкой.
В SymPy есть также класс, представляющий такое понятие в математике, как бесконечность. Он обозначается следующим образом: oo.
sym.oo > 99999 # результат True sym.oo + 1 # результат oo
Символы
В отличие от ряда других систем компьютерной алгебры, в SymPy можно в явном виде задавать символьные переменные. Это происходит следующим образом:
x = sym.Symbol('x')
y = sym.Symbol('y')
После их задания, с ними можно производить различные манипуляции.
x + y + x - y # результат 2*x (x + y) ** 2 # результат (x + y)**2
С символами можно производить преобразования с использованием некоторых операторов языка Python. А именно, арифметических (+, -`, ``*, **) и логических (&, |, ~) .
Библиотека SymPy позволяет задавать форму вывода результатов на экран. Обычно мы используем формат такого вида:
sym.init_printing(use_unicode=False, wrap_line=True)
Алгебраические преобразования
SymPy способна на сложные алгебраические преобразования. Здесь мы рассмотрим наиболее востребованные из них, а именно раскрытие скобок и упрощение выражений.
Раскрытие скобок
Чтобы раскрыть скобки в алгебраических выражениях, используйте следующий синтаксис:
sym.expand((x + y) ** 3)
?3+3?2?+3??2+?3
3 * x * y ** 2 + 3 * y * x ** 2 + x ** 3 + y ** 3
?3+3?2?+3??2+?3
При помощи ключевого слова можно добавить поддержку работы с комплексными переменными, а также раскрытие скобок в тригонометрических функциях.
sym.expand(x + y, complex=True)#результат re(?)+re(?)+?im(?)+?im(?) sym.expand(sym.cos(x + y), trig=True) # результат −sin(?)sin(?)+cos(?)cos(?)
Упрощение выражений
Если вы хотите привести выражение к более простому виду (возможно, сократить какие-то члены), то используйте функцию simplify.
sym.simplify((x + x * y) / x) # результат y + 1
Также надо сказать, что для определенных видов математических функций существуют альтернативные, более конкретные функции для упрощения выражений. Так, для упрощения степенных функций есть функция powsimp, для тригонометрических —trigsimp, а для логарифмических — logcombine, radsimp.
Вычисления
Вычисления пределов
Для вычисления пределов в SymPy предусмотрен очень простой синтаксис, а именно limit(function, variable, point). Например, если вы хотите вычислить предел функции f(x), где x -> 0, то надо написать limit(f(x), x, 0).
sym.limit(sym.sin(x) / x, x, 0) # результат 1
Также можно вычислять пределы, которые стремятся к бесконечности.
sym.limit(x, x, sym.oo) # результат oo sym.limit(1 / x, x, sym.oo) # результат 0 sym.limit(x ** x, x, 0) # результат 1
Дифференцирование
Для дифференцирования выражений в SymPy есть функция diff(func, var). Ниже даны примеры ее работы.
sym.diff(sym.sin(x), x) # результат cos(?) sym.diff(sym.sin(2 * x), x) # результат 2cos(2?) sym.diff(sym.tan(x), x)
tan2(?)+1
Проверим результат последней функции при помощи определения производной через предел.
sym.limit((sym.tan(x + y) - sym.tan(x)) / y, y, 0)
tan2(?)+1 Результат тот же.
Также при помощи этой же функции могут быть вычислены производные более высоких порядков. Синтаксис функции будет следующим: diff(func, var, n). Ниже приведено несколько примеров.
sym.diff(sym.sin(2 * x), x, 1) # результат 2cos(2?) sym.diff(sym.sin(2 * x), x, 2) # результат −4sin(2?) sym.diff(sym.sin(2 * x), x, 3) # результат −8cos(2?)
Разложение в ряд
Для разложения выражения в ряд Тейлора используется следующий синтаксис: series(expr, var).
sym.series(sym.cos(x), x)
1−?2/2+?4/24+?(?6)
sym.series(1/sym.cos(x), x)
1+?2/2+5?4/24+?(?6)
Интегрирование
В SymPy реализована поддержка определенных и неопределенных интегралов при помощи функции integrate(). Интегрировать можно элементарные, трансцендентные и специальные функции. Интегрирование осуществляется с помощью расширенного алгоритма Риша-Нормана. Также используются различные эвристики и шаблоны. Вот примеры интегрирования элементарных функций:
sym.integrate(sym.sin(x), x) # результат −cos(?) sym.integrate(sym.log(x), x) # результат ?log(?)−?
Также несложно посчитать интеграл и от специальных функций. Возьмем, например, функцию Гаусса:
sym.integrate(sym.exp(-x ** 2) * sym.erf(x), x)
Результат вычисления можете посмотреть сами. Вот примеры вычисления определенных интегралов.
sym.integrate(x**3, (x, -1, 1)) # результат 0 sym.integrate(sym.sin(x), (x, 0, sym.pi / 2)) # результат 1 sym.integrate(sym.cos(x), (x, -sym.pi / 2, sym.pi / 2)) # результат 2
Также можно вычислять определенные интегралы с бесконечными пределами интегрирования (несобственные интегралы).
sym.integrate(sym.exp(-x), (x, 0, sym.oo)) # результат 1
Решение уравнений
При помощи SymPy можно решать алгебраические уравнения с одной или несколькими переменными. Для этого используется функция solveset().
sym.solveset(x ** 4 - 1, x) # результат {−1,1,−?,?}
Как можно заметить, первое выражение функции solveset() приравнивается к 0 и решается относительно х. Также возможно решать некоторые уравнения с трансцендентными функциями.
sym.solveset(sym.exp(x) + 1, x) # результат {?(2??+?)|?∈ℤ}
Системы линейных уравнений
SymPy способна решать широкий класс полиномиальных уравнений. Также при помощи данной библиотеки можно решать и системы уравнений. При этом переменные, относительно которых должна быть разрешена система, передаются в виде кортежа во втором аргументе функции solve(), которая используется для таких задач.
solution = sym.solve((x + 5 * y - 2, -3 * x + 6 * y - 15), (x, y)) solution[x], solution[y] # результат (-3, 1)
Факторизация
Другим мощным методом исследования полиномиальных уравнений является факторизация многочленов (то есть представление многочлена в виде произведения многочленов меньших степеней). Для этого в SymPy предусмотрена функция factor(), которая способна производить факторизацию очень широкого класса полиномов.
f = x ** 4 - 3 * x ** 2 + 1 sym.factor(f)
(?2−?−1)(?2+?−1)
sym.factor(f, modulus=5)
(?−2)2(?+2)2
Булевы уравнения
Также в SymPy реализована возможность решения булевых уравнений, что по сути означает проверку булевого выражения на истинность. Для этого используется функция satisfiable().
sym.satisfiable(x & y) # результат {x: True, y: True}
Данный результат говорит нам о том, что выражение (x & y) будет истинным тогда и только тогда, когда x и y истинны. Если выражение не может быть истинным ни при каких значениях переменных, то функция вернет результат False.
sym.satisfiable(x & ~x) # результат False
Линейная алгебра
Матрицы
Матрицы в SymPy создаются как экземпляры класса Matrix:
sym.Matrix([[1, 0], [0, 1]])
[10]
[01]
В отличие от NumPy, мы можем использовать в матрицах символьные переменные:
x, y = sym.symbols('x, y')
A = sym.Matrix([[1, x], [y, 1]])
A
[1 ?]
[? 1]
И производить с ними разные манипуляции:
A**2
[??+1 2?]
[2? ??+1]
Дифференциальные уравнения
При помощи библиотеки SymPy можно решать некоторые обыкновенные дифференциальные уравнения. Для этого используется функция dsolve(). Для начала нам надо задать неопределенную функцию. Это можно сделать, передав параметр cls=Function в функцию symbols().
f, g = sym.symbols('f g', cls=sym.Function)
Теперь f и g заданы как неопределенные функции. мы можем в этом убедиться, просто вызвав f(x).
f(x) # результат ?(?) f(x).diff(x, x) + f(x)
?(?)+?2/??2?(?)
Теперь решим следующее дифференциальное уравнение:
sym.dsolve(f(x).diff(x, x) + f(x), f(x)) # результат ?(?)=?1sin(?)+?2cos(?)
Чтобы улучшить решаемость и помочь этой функции в поиске решения, можно передавать в нее определенные ключевые аргументы. Например, если мы видим, что это уравнение с разделяемыми переменными, то мы можем передать в функцию аргумент hint='separable'.
sym.dsolve(sym.sin(x) * sym.cos(f(x)) + sym.cos(x) * sym.sin(f(x)) * f(x).diff(x), f(x), hint='separable') # результат [Eq(f(x), -acos(C1/cos(x)) + 2*pi), Eq(f(x), # acos(C1/cos(x)))]