Электромагнитные колебания и волны

Свободные электромагнитные колебания. Колебательный контур
Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.
Колебательный контур — это замкнутый контур, образованный последовательно соединенными конденсатором и катушкой.
Сопротивление катушки ( R ) равно нулю.
Если зарядить конденсатор до напряжения ( U_m ) , то в начальный момент времени ( t_1=0 ) , напряжение на конденсаторе будет равно ( U_m ) . Заряд конденсатора в этот момент времени будет равен ( q_m=CU_m ) . Сила тока равна нулю.
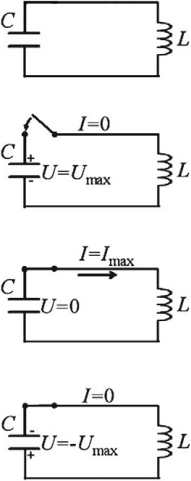
Полная энергия системы будет равна энергии электрического поля:
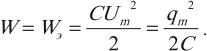
Конденсатор начинает разряжаться, по катушке начинает течь ток. Вследствие самоиндукции в катушке конденсатор разряжается постепенно.
Ток достигает своего максимального значения ( I_m ) в момент времени ( t_2=T/4 ) . Заряд конденсатора в этот момент равен нулю, напряжение на конденсаторе равно нулю.
Полная энергия системы в этот момент времени равна энергии магнитного поля:
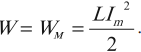
В следующий момент времени ток течет в том же направлении, постепенно (вследствие явления самоиндукции) уменьшаясь до нуля. Конденсатор перезаряжается. Заряды обкладок имеют заряды, по знаку противоположные первоначальным.
В момент времени ( t_3=T/2 ) заряд конденсатора равен ( q_m ) , напряжение равно ( U_m ) , сила тока равна нулю.
Полная энергия системы равна энергии электрического поля конденсатора.
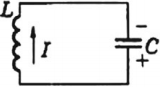
Затем конденсатор снова разряжается, но ток через катушку течет в обратном направлении.
В момент времени ( t_4=3T/4 ) сила тока в катушке достигает максимального значения, напряжение на конденсаторе и его заряд равны нулю. С этого момента ток в катушке начинает убывать, но не сразу (явление самоиндукции). Энергия магнитного поля переходит в энергию электрического поля. Конденсатор начинает заряжаться, и через некоторое время его заряд равен первоначальному, а сила тока станет равной нулю.
Через время, равное периоду ( T ) , система возвращается в начальное состояние. Совершилось одно полное колебание, дальше процесс повторяется.
Важно!
Колебания, происходящие в колебательном контуре, – свободные. Они совершаются без какого-либо внешнего воздействия — только за счет энергии, запасенной в контуре.
В контуре происходят превращения энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно. В любой произвольный момент времени полная энергия в контуре равна:
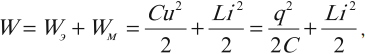
где ( i, u, q ) – мгновенные значения силы тока, напряжения, заряда в любой момент времени.
Эти колебания являются затухающими. Амплитуда колебаний постепенно уменьшается из-за электрического сопротивления проводников.
Вынужденные электромагнитные колебания. Резонанс
Вынужденными электромагнитными колебаниями называют периодические изменения заряда, силы тока и напряжения в колебательном контуре, происходящие под действием периодически изменяющейся синусоидальной (переменной) ЭДС от внешнего источника:
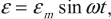
где ( varepsilon ) – мгновенное значение ЭДС, ( varepsilon_m ) – амплитудное значение ЭДС.
При этом к контуру подводится энергия, необходимая для компенсации потерь энергии в контуре из-за наличия сопротивления.
Резонанс в электрической цепи – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением при совпадении частоты вынужденных колебаний внешней ЭДС с частотой собственных колебаний в контуре.
Емкостное и индуктивное сопротивления по-разному изменяются в зависимости от частоты. С увеличением частоты растет индуктивное сопротивление, а емкостное уменьшается. С уменьшением частоты растет емкостное сопротивление и уменьшается индуктивное сопротивление. Кроме того, колебания напряжения на конденсаторе и катушке имеют разный сдвиг фаз по отношению к колебаниям силы тока: для катушки колебания напряжения и силы тока имеют сдвиг фаз ( varphi_L=-pi/2 ) , а на конденсаторе ( varphi_C=pi/2 ) . Это означает, что когда растет энергия магнитного поля катушки, то энергия электрического поля конденсатора убывает, и наоборот. При резонансной частоте индуктивное и емкостное сопротивления компенсируют друг друга и цепь обладает только активным сопротивлением. При резонансе выполняется условие:
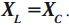
Резонансная частота вычисляется по формуле:
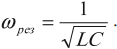
Важно!
Резонансная частота не зависит от активного сопротивления ( R ) . Но чем меньше активное сопротивление цепи, тем ярче выражен резонанс.
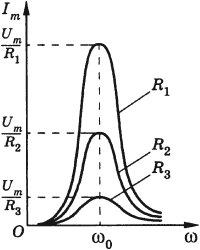
Чем меньше потери энергии в цепи, тем сильнее выражен резонанс. Если активное сопротивление очень мало ( (Rto0) ) , то резонансное значение силы тока неограниченно возрастает. С увеличением сопротивления максимальное значение силы тока уменьшается, и при больших значениях сопротивления резонанс не наблюдается.
График зависимости амплитуды силы тока от частоты называется резонансной кривой. Резонансная кривая имеет больший максимум в цепи с меньшим активным сопротивлением.
Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке. Эти напряжения становятся одинаковыми и во много раз больше внешнего напряжения. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. При резонансе амплитуды этих напряжений одинаковы и они компенсируют друг друга. Падение напряжения происходит только на активном сопротивлении.
При резонансе возникают наилучшие условия для поступления энергии от источника напряжения в цепь: при резонансе колебания напряжения в цепи совпадают по фазе с колебаниями силы тока. Установление колебаний происходит постепенно. Чем меньше сопротивление, тем больше времени требуется для достижения максимального значения силы тока за счет энергии, поступающей от источника.
Явление резонанса используется в радиосвязи. Каждая передающая станция работает на определенной частоте. С приемной антенной индуктивно связан колебательный контур. При приеме сигнала в катушке возникают переменные ЭДС. С помощью конденсатора переменной емкости добиваются совпадения частоты контура с частотой принимаемых колебаний. Из колебаний всевозможных частот, возбужденных в антенне, контур выделяет колебания, равные его собственной частоте.
Резонанс может привести к перегреву проводов и аварии, если цепь не рассчитана на работу в условиях резонанса.
Гармонические электромагнитные колебания
Гармоническими электромагнитными колебаниями называются периодические изменения заряда, силы тока и напряжения, происходящие по гармоническому – синусоидальному или косинусоидальному – закону.
В электрических цепях это могут быть колебания:
- силы тока – ( i=I_mcos(omega t+varphi+frac<pi><2>); )
- напряжения – ( u=U_mcos(omega t+varphi); )
- заряда – ( q=q_mcos(omega t+varphi); )
- ЭДС – ( varepsilon=varepsilon_msinomega t. )
В этих уравнениях ( omega ) –циклическая частота, ( varphi ) – начальная фаза колебаний, амплитудные значения: силы тока – ( I_m ) , напряжения – ( U_m ) и заряда – ( q_m ) .
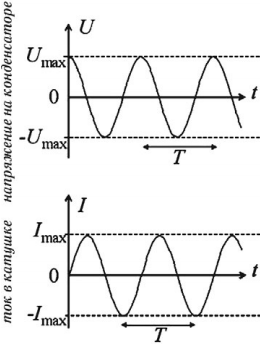
Важно!
Если в начальный момент времени заряд имеет максимальное значение, а сила тока равна нулю, то колебания заряда совершаются по закону косинуса с начальной фазой, равной нулю. Если в начальный момент времени заряд равен нулю, а сила тока максимальна, то колебания заряда совершаются по закону синуса.
Сила тока равна первой производной заряда от времени:
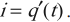
Амплитуда колебаний силы тока равна:
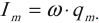
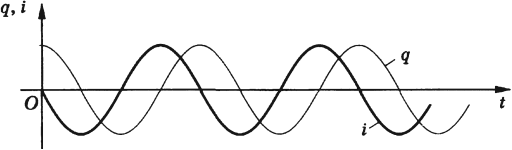
Колебания заряда и напряжения в колебательном контуре происходят в одинаковых фазах. Амплитуда напряжения равна:
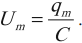
Колебания силы тока смещены по фазе относительно колебаний заряда на ( pi/2 ) .
Период свободных электромагнитных колебаний
Период свободных электромагнитных колебаний находится по формуле Томсона:
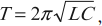
где ( L ) – индуктивность катушки, ( C ) – электроемкость конденсатора.
Важно!
Период и циклическая частота не зависят от начальных условий, а определяются только индуктивностью катушки и электроемкостью конденсатора. Амплитуда колебаний заряда и силы тока определяются начальным запасом энергии в контуре.
При свободных гармонических колебаниях происходит периодическое преобразование энергии. Период колебаний энергии в два раза меньше, чем период колебаний заряда, силы тока и напряжения. Частота колебаний энергии в два раза больше частоты колебаний заряда, силы тока и напряжения.
Переменный ток. Производство, передача и потребление электрической энергии
Переменным называется ток, изменяющийся по величине и направлению по гармоническому закону.
Переменный ток представляет пример вынужденных электромагнитных колебаний. Для описания переменного электрического тока используют следующие величины:
• мгновенное значение силы тока – i;
• мгновенное значение напряжения – u;
• амплитудное значение силы тока – Im;
• амплитудное значение напряжения –Um.
Цепь переменного тока представляет собой колебательный контур, к которому приложена внешняя синусоидальная ЭДС. В цепь переменного тока могут включаться различные нагрузки: резистор, катушка, конденсатор.
Активное сопротивление
Проводник, преобразующий всю энергию электрического тока во внутреннюю, называется активным сопротивлением ( R ) . (Эту величину мы раньше называли сопротивлением.) Активное сопротивление зависит от материала проводника, его длины и площади поперечного сечения и не зависит от частоты переменного тока.
В проводнике с активным сопротивлением колебания силы тока и напряжения совпадают по фазе:
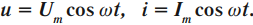
Мгновенное значение мощности: ( p=i^2R, )
среднее значение мощности за период: ( overline
=frac<2>. )
Действующим значением силы переменного тока ( I_Д ) называют значение силы постоянного тока, который в том же проводнике выделяет то же количество теплоты , что и переменный ток за то же время:
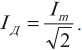
Действующим значением напряжения переменного тока ( U_Д ) называют значение напряжения постоянного тока, который в том же проводнике выделяет то же количество теплоты, что и переменный ток за то же время:
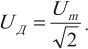
Для цепи с активным сопротивлением выполняется закон Ома для мгновенных, амплитудных и действующих значений.
Индуктивное сопротивление
Катушка в цепи переменного тока имеет большее сопротивление, чем в цепи постоянного тока. В такой цепи колебания напряжения опережают колебания силы тока по фазе на ( pi/2 ) . Колебания силы тока и напряжения происходят по закону:
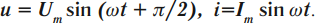
Амплитуда силы тока в катушке:
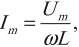
где ( L ) – индуктивность катушки.
Индуктивным сопротивлением ( X_L ) называют физическую величину, равную произведению циклической частоты на индуктивность катушки:
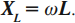
Индуктивное сопротивление прямо пропорционально частоте. Физический смысл индуктивного сопротивления: ЭДС самоиндукции препятствует изменению в ней силы тока. Это приводит к существованию индуктивного сопротивления, уменьшающего силу тока.
Для цепи с индуктивным сопротивлением выполняется закон Ома.
Емкостное сопротивление
В цепи постоянного тока через конденсатор ток не идет. Для переменного тока конденсатор обладает конечным сопротивлением, обратно пропорциональным его емкости. В цепи переменного тока сопротивление конденсатора меньше, чем в цепи постоянного тока.
В такой цепи колебания напряжения отстают от колебаний силы тока по фазе на ( pi/2 ) . Колебания силы тока и напряжения происходят по закону:
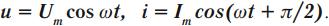
Амплитуда силы тока в катушке: ( I_m=Comega U_m. ) .
Если ввести обозначение ( X_C=frac<1> <omega C>) , то получим соотношение между амплитудными значениями силы тока и напряжения, аналогичное закону Ома: ( I_m=frac. )
Емкостным сопротивлением ( X_C ) называют величину, обратную произведению циклической частоты на электроемкость конденсатора. Емкостное сопротивление обратно пропорционально частоте.
Физический смысл емкостного сопротивления: изменению переменного тока в любой момент времени противодействует электрическое поле между обкладками конденсатора.
В цепи переменного тока колебания силы тока и ЭДС происходят по синусоидальному закону с одинаковой циклической частотой ( omega ) и разностью фаз ( varphi ) :
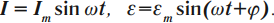
Соотношения амплитудных значений силы тока ( I_m ) и ЭДС ( varepsilon_m ) в цепи переменного тока связаны между собой законом Ома для цепи переменного тока:
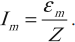
Он гласит: амплитуда силы переменного тока прямо пропорциональна амплитуде ЭДС и обратно пропорциональна полному сопротивлению цепи:
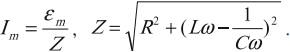
Величина ( Z ) называется полным сопротивлением цепи переменного тока.
Электрическая энергия имеет перед другими видами энергии следующие преимущества:
- можно передавать на большие расстояния с малыми потерями;
- удобно распределять между потребителями;
- легко превращать в другие виды энергии.
В настоящее время производится и используется энергия переменного тока. Это связано с возможностью преобразовывать его напряжение и силу тока с малыми потерями энергии, что особенно важно при передаче электроэнергии на большие расстояния.
Различают следующие типы электростанций:
Получение переменного тока
Переменный ток получают с помощью генератора переменного тока.
Генератор переменного тока (электромеханический генератор переменного тока) – это устройство, преобразующее механическую энергию в электрическую. В основе работы генератора переменного тока лежит явление электромагнитной индукции.
Процесс получения переменного тока можно рассмотреть на примере вращения витка провода в однородном магнитном поле. Магнитный поток через площадь витка равен:
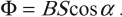
Если период вращения витка ( T ) , то угол ( alpha=frac<2pi t>=omega t ) .
Тогда ( Phi=BScosomega t. )
ЭДС индукции изменяется по закону ( e=-Phi’=BSomegasinomega t=varepsilon_msinomega t. )
Амплитуда ЭДС ( varepsilon_m=BSomega. )
Если рамка содержит ( N ) витков, то ( varepsilon_m=NBSomega. )
Основные части генератора переменного тока:
- обмотка статора с большим числом витков, в ней индуцируется ЭДС. Статор состоит из отдельных пластин из электротехнической стали для уменьшения нагрева от вихревых токов;
- ротор (вращающаяся часть генератора) создает магнитное поле. Для получения нужной частоты переменного тока может иметь несколько пар полюсов. На гидроэлектростанциях в генераторе число пар полюсов равно 40–50, на тепловых электростанциях – 10 -16 ;
- клеммы для снятия напряжения.
Промышленные генераторы вырабатывают напряжение порядка 10 4 В. Промышленная частота переменного тока в нашей стране 50 Гц.
Передача электроэнергии
Электроэнергия производится в основном вдалеке от основных потребителей энергии, там, где есть топливные ресурсы.
С электростанции переменный ток по проводам линии электропередач (ЛЭП) поступает к различным потребителям электрической энергии. Для уменьшения потерь при передаче переменного тока необходимо использовать высокое напряжение. Чем длиннее линия, тем выше должно быть напряжение. В высоковольтных ЛЭП оно может достигать 500 кВ. Генераторы на электростанциях вырабатывают напряжение 16–20 кВ. Потребителям не нужно высокое напряжение. Возникает необходимость преобразования напряжения. С электростанции электрический ток поступает на повышающую подстанцию, затем передается по линии электропередач на понижающую подстанцию, где напряжение понижается до 6–10 кВ, а затем до 220–380 В. Для преобразования напряжения используют трансформатор.
Трансформатор – устройство, преобразующее переменное напряжение без изменения его частоты.
На схемах трансформатор обозначается:
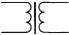
Основные части трансформатора:
- замкнутый сердечник из электротехнической стали;
- две катушки-обмотки.
Катушка, подключаемая к источнику переменного напряжения, называется первичной обмоткой; катушка, к которой подключается нагрузка, – вторичной обмоткой.
Сердечник набирается из отдельных пластин для уменьшения потерь на нагревание вихревыми токами.
Принцип действия основан на явлении электромагнитной индукции. При подключении первичной обмотки к полюсам источника напряжения в ней возникает переменный ток. Напряжение изменяется с течением времени по гармоническому закону. С такой же частотой будут изменяться сила тока в катушке и магнитный поток, создаваемый этим током.
При изменении магнитного потока в каждом витке провода первичной обмотки возникает переменная ЭДС самоиндукции. Этот магнитный поток будет пронизывать и вторую катушку. В каждом ее витке возникает ЭДС индукции, изменяющаяся по гармоническому закону с той же частотой. Число витков в обмотках различно. Отношение ЭДС самоиндукции ( varepsilon_1 ) в первичной обмотке к ЭДС индукции во вторичной обмотке ( varepsilon_2 ) равно отношению числа витков в первичной обмотке ( N_1 ) к числу витков во вторичной обмотке ( N_2 ) :
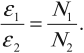
Режим работы
- Режим холостого хода – разомкнута цепь вторичной обмотки. Напряжение ( U_2 ) на ее концах в любой момент времени равно ЭДС индукции ( varepsilon_2 ) , взятой с противоположным знаком. Поэтому можно записать:
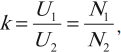
где ( k ) – коэффициент трансформации.
Если ( k>1 ) , то трансформатор понижающий, если ( k , то повышающий.
- Режим нагрузки. При подключении нагрузки к концам вторичной обмотки в ней возникает переменный ток. Напряжение ( U_2 ) на ее концах в любой момент времени отличается от ЭДС индукции ( varepsilon_2 ) на величину падения напряжения на внутреннем сопротивлении вторичной обмотки ( r ) : ( U_2=varepsilon_2-I_2r ) или ( U_2=I_2R ) .
Мощность тока в обмотках одинакова. Поэтому увеличение напряжения на входе повышающего трансформатора в ( k ) раз сопровождается уменьшением силы тока во вторичной катушке во столько же раз.
В трансформаторе нет потерь на трение, так как нет вращающихся частей. Потери в сердечнике состоят из потерь на нагревание и на перемагничивание.
Отношение мощности ( P_2 ) , потребляемой нагрузкой, к мощности ( P_1 ) , потребляемой первичной обмоткой трансформатора, называется коэффициентом полезного действия трансформатора:
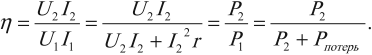
КПД трансформатора – 98%.
Потребление электрической энергии: промышленность – около 70%; сельское хозяйство; транспорт; строительство; средства связи; в быту.
Электромагнитное поле
Электромагнитное поле – это особый вид материи, с помощью которого осуществляется электромагнитное взаимодействие заряженных тел или частиц.
Это понятие было введено Д. Максвеллом, развившим идеи Фарадея о том, что переменное магнитное поле порождает вихревое электрическое поле.
Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты. Вихревое электрическое поле порождает появление вихревого магнитного поля и так далее. Эти переменные электрическое и магнитное поля, существующие одновременно, и образуют единое электромагнитное поле.
Характеристиками этого поля являются вектор напряженности и вектор магнитной индукции.
Если электрический заряд покоится, то вокруг него существует только электрическое поле.
Если напряженность электрического поля равна нулю, а магнитная индукция отлична от нуля, то обнаруживается только магнитное поле.
Если электрический заряд двигается с постоянной скоростью, то вокруг него существует электромагнитное поле.
Максвелл предположил, что при ускоренном движении зарядов в пространстве будет возникать возмущение, которое будет распространяться в вакууме с конечной скоростью. Когда это возмущение достигнет второго заряда, то изменится сила, с которой электромагнитное поле действует на этот заряд.
При ускоренном движении заряда происходит излучение электромагнитной волны. Электромагнитное поле материально. Оно распространяется в пространстве в виде электромагнитной волны.
Свойства электромагнитных волн
Электромагнитная волна – это изменяющееся во времени и распространяющееся в пространстве электромагнитное поле.
Существование электромагнитных волн было теоретически предсказано английским физиком Дж. Максвеллом в 1864 году. Электромагнитные волны были открыты Г. Герцем.
Источник электромагнитной волны – ускоренно движущаяся заряженная частица – колеблющийся заряд.
Важно!
Наличие ускорения – главное условие излучения электромагнитной волны. Интенсивность излученной волны тем больше, чем больше ускорение, с которым движется заряд.
Источниками электромагнитных волн служат антенны различных конструкций, в которых возбуждаются высокочастотные колебания.
Электромагнитная волна называется монохроматической, если векторы ( vec ) и ( vec ) совершают гармонические колебания с одинаковой частотой (частотой волны).
Длина электромагнитной волны: ( lambda=cT=frac<nu>, )
где ( c ) – скорость электромагнитной волны, ( T ) – период, ( nu ) – частота электромагнитной волны.
Свойства электромагнитных волн
- В вакууме электромагнитная волна распространяется с конечной скоростью, равной скорости света 3·10 8 м/с.
- Электромагнитная волна поперечная. Колебания векторов напряженности переменного электрического поля и магнитной индукции переменного магнитного поля взаимно перпендикулярны и лежат в плоскости, перпендикулярной к вектору скорости волны.
- Электромагнитная волна переносит энергию в направлении распространения волны.
Важно!
Электромагнитная волна в отличие от механической волны может распространяться в вакууме.
Плотность потока или интенсивность – это электромагнитная энергия, переносимая через поверхность единичной площади за единицу времени.
Обозначение – ( I ) , единица измерения в СИ – ватт на квадратный метр (Вт/м 2 ).
Важно!
Плотность потока излучения электромагнитной волны от точечного источника убывает обратно пропорционально квадрату расстояния от источника и пропорциональна четвертой степени частоты.
Электромагнитная волна обладает общими для любых волн свойствами, это:
- отражение,
- преломление,
- интерференция,
- дифракция,
- поляризация.
Электромагнитная волна производит давление на вещество. Это означает, что у электромагнитной волны есть импульс.
Различные виды электромагнитных излучений и их применение
Электромагнитные излучения имеют длины волн от 10 -12 до 10 4 м или частоты от 3·10 4 до 3·10 20 .
Различают следующие виды электромагнитных излучений:
- радиоволны;
- инфракрасное излучение;
- видимое излучение (свет);
- ультрафиолетовое излучение;
- рентгеновское излучение;
- гамма-излучение.
Границы между диапазонами условны, но излучения имеют качественные различия в свойствах. При переходе от излучений с малой частотой к излучениям с большей частотой волновые свойства проявляются слабее, а корпускулярные (квантовые) – сильнее.
Радиоволны
( lambda ) = 10 3 –10 -3 м, ( nu ) = 10 5 –10 11 Гц. Источники радиоволн – колебательный контур, вибратор.
Радиоволны делятся на:
- длинные (длина больше 1 км);
- средние (от 100 м до 1 км);
- короткие (от 10 до 100 м);
- ультракороткие (меньше 10 м).
Свойства: отражение, поглощение, интерференция, дифракция. Применение: радиосвязь, телевидение, радиолокация.
Радиосвязью называется передача информации с помощью радиоволн. Радиосвязь осуществляется с помощью модулированных радиоволн. Модуляцией радиоволны называется изменение ее параметров (амплитуды, частоты, начальной фазы) с частотой, меньшей частоты передаваемой волны.
Схема радиосвязи показана на рисунке:
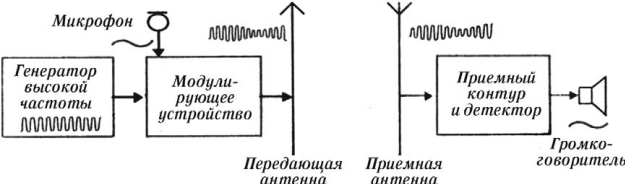
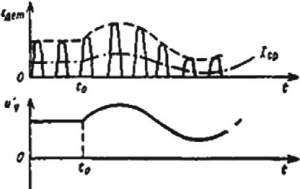
Передача радиоволн. Генератор высокой частоты вырабатывает высокочастотные колебания несущей частоты. Звуковые колебания поступают в микрофон, где преобразуются в электромагнитные колебания. В модуляторе эти колебания преобразуются в модулированные колебания. После усиления модулированные колебания поступают в передающую антенну, которая излучает электромагнитные волны. На рисунке показан звуковой сигнал низкой частоты и модулированный высокочастотный сигнал.
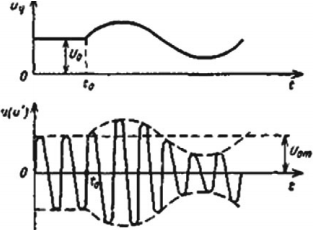
Прием радиоволн. Электромагнитные колебания поступают в приемную антенну и вызывают электромагнитные колебания в приемном контуре. Эти колебания поступают в усилитель, а затем в детектор. В качестве детектора используют устройство с односторонней проводимостью. Это может быть полупроводниковый диод. В детекторе сигнал демодулируют (детектируют). Процесс детектирования заключается в выделении из высокочастотных модулированных колебаний колебаний низкой (звуковой) частоты. После сглаживания и усиления сигнал поступает в динамик. На рисунке показаны процессы детектирования (демодуляции) и сглаживания.
Радиолокацией называют обнаружение и определение местоположения объектов с помощью радиоволн. Излучение осуществляется короткими импульсами. В интервале времени между излучением двух последовательных импульсов осуществляется прием отраженного от объекта сигнала. Для радиолокации используют ультракороткие радиоволны.
Инфракрасное (тепловое) излучение
( lambda ) = 10 -3 – 10 -7 м, ( nu ) = 10 11 – 10 14 Гц. Источники – атомы и молекулы вещества.
Это излучение испускают все тела при температуре, отличной от 0 К. Свойства: нагревает вещество при поглощении; интерференция; дифракция; проходит через дождь, снег, дымку; невидимо; преломление, отражение. Применение: в приборах ночного видения, в физиотерапии, промышленности (для сушки). Регистрируют с помощью термопары, болометра, фотографическим методом.
Видимое излучение
( lambda ) = 8·10 -7 – 4·10 -7 м, ( nu ) = 4·10 11 – 8·10 14 Гц.
Это излучение воспринимается глазом. Свойства: отражение, преломление, поглощение, интерференция, дифракция.
Ультрафиолетовое излучение
( lambda ) = 10 -8 – 4·10 -7 м, ( nu ) = 8·10 14 – 3·10 15 Гц. Источники – кварцевые лампы.
Ультрафиолетовое излучение дают светящиеся пары ртути и твердые тела, у которых температура выше 1000°С. Свойства: химическое действие; большая проникающая способность; биологическое действие; невидимо. Применение: в медицине, промышленности. Регистрируют фотографическими методами.
Рентгеновское излучение
( lambda ) = 10 -8 – 10 -11 м, ( nu ) = 3·10 16 – 3·10 19 Гц. Источник – рентгеновские трубки.
Возникает при торможении быстрых электронов. Свойства: высокая химическая активность; биологическое действие; интерференция; дифракция на кристаллической решетке; высокая проникающая способность. Применение: в медицине, промышленности, науке.
Гамма-излучение
Длина волны меньше 10 -11 м, частота от 10 20 Гц и выше. Источник – ядерные реакции.
Свойства: высокая проникающая способность, сильное биологическое действие. Применение: в медицине, промышленности (дефектоскопия), науке.
Шкала электромагнитных излучений позволяет сделать вывод: все электромагнитные излучения обладают одновременно волновыми и квантовыми свойствами, которые дополняют друг друга.
Важно!
Волновые свойства сильнее выражены при малых частотах и больших длинах волн, а квантовые – при больших частотах и малых длинах волн.
Решение задач по теме «Электромагнитные колебания и волны»
По этой теме можно выделить четыре группы задач:
- на определение параметров колебательного контура;
- на уравнения гармонических электромагнитных колебаний;
- на применение закона Ома;
- на расчет мощности и КПД трансформатора.
Решение первой группы задач на определение параметров колебательного контура основано на использовании формулы Томсона (формулы периода свободных электромагнитных колебаний) и закона сохранения и превращения энергии в колебательном контуре. Поэтому необходимо записать уравнения для мгновенных значений заряда и напряжения на конденсаторе и силы тока в катушке; записать уравнение для полной энергии колебательного контура в произвольный момент времени. В качестве дополнительных формул могут понадобиться формулы электроемкости плоского конденсатора, индуктивности катушки и длины электромагнитной волны. Помните, что скорость распространения электромагнитной волны в вакууме равна скорости света – 3·10 8 м/с. В среде с показателем преломления ( n ) скорость света можно рассчитать по формуле: ( v=frac. )
Важно!
Амплитудное значение напряжения – ( U_m=frac ) , амплитудное значение силы тока – ( I_m=q_momega ) .
При решении второй группы задач на уравнения гармонических электромагнитных колебаний рекомендуется записать заданное в задаче уравнение и уравнение гармонических колебаний в общем виде. Сравнить эти уравнения и определить основные характеристики: амплитуду, частоту, фазу.
При решении задач на закон Ома нужно помнить, что электроизмерительные приборы показывают действующие значения напряжения и силы тока. Действующие значения величин пропорциональны амплитудным значениям. Важно помнить, что резонанс возникает при равенстве индуктивного и емкостного сопротивлений.
Решение четвертой группы задач на расчет мощности и КПД трансформатора опирается на знание формул КПД и мощности в цепи.
Электромагнитные колебания
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.
Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.
Колебательный контур
Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.
Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.
Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.
Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.
Начальный момент: . Заряд конденсатора равен , ток через катушку отсутствует (рис. 1 ). Конденсатор сейчас начнёт разряжаться.

Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.
Аналогия. Маятник оттянут вправо на величину и в начальный момент отпущен. Начальная скорость маятника равна нулю.
Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2 ).

Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.
Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.
Конец первой четверти : . Конденсатор полностью разрядился. Сила тока достигла максимального значения (рис. 3 ). Сейчас начнётся перезарядка конденсатора.

Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.
Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения . Деформация пружины равна нулю.
Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4 ).

Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.
Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.
Конец второй четверти . Конденсатор полностью перезарядился, его заряд опять равен (но полярность другая). Сила тока равна нулю (рис. 5 ). Сейчас начнётся обратная перезарядка конденсатора.

Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна .
Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6 ).

Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.
Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен , но на сей раз имеет другое направление (рис. 7 ).

Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью , но на сей раз в обратном направлении.
Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8 ).

Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.
Конец четвёртой четверти и всего периода: . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9 ).

Данный момент идентичен моменту , а данный рисунок — рисунку 1 . Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.
Аналогия. Маятник вернулся в исходное положение.
Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!
Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.
В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.
Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.
Энергетические превращения в колебательном контуре
Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .
Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.
Возьмём момент времени, когда заряд конденсатора максимален и равен , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:
Теперь, наоборот, рассмотрим момент, когда ток максимален и равен , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:
В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:
Соотношение (1) применяется при решении многих задач.
Электромеханические аналогии
В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.
Для пружинного маятника мы имеем соотношение, аналогичное (1) :
Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, и — их наибольшие значения.
Сопоставляя друг с другом равенства (1) и (2) , мы видим следующие соответствия:
Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.
В самом деле, период колебаний пружинного маятника, как мы знаем, равен:
B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость . Получим:
Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.
Гармонический закон колебаний в контуре
Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».
Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.
Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10 ).

Рис. 10. Положительное направление обхода
Сила тока считается положительной 0)’ alt='(I > 0)’ /> , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной .
Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.
При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если 0′ alt=’I > 0′ /> , то заряд левой пластины возрастает, и потому 0′ alt=’dot > 0′ /> .
Величины и меняются со временем, но энергия контура остаётся неизменной:
Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8) ; не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ):
Подставляя сюда и , получим:
Но сила тока не является функцией, тождественно равной нулю; поэтому
Перепишем это в виде:
Мы получили дифференциальное уравнение гармонических колебаний вида , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:
Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:
Мы снова пришли к формуле Томсона.
Гармоническая зависимость заряда от времени в общем случае имеет вид:
Циклическая частота находится по формуле (10) ; амплитуда и начальная фаза определяются из начальных условий.
Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при заряд конденсатора максимален и равен (как на рис. 1 ); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой :
Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12) , опять-таки не забывая о правиле нахождения производной сложной функции:
Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:
Амплитуда силы тока равна:
Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2 ).
Ток течёт в отрицательном направлении: . Поскольку , фаза колебаний находится в первой четверти: . Синус в первой четверти положителен; стало быть, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (13) .
А теперь посмотрите на рис. 8 . Ток течёт в положительном направлении. Как же работает наш «минус» в этом случае? Разберитесь-ка, в чём тут дело!
Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13) . Для наглядности представим эти графики в одних координатных осях (рис. 11 ).

Рис. 11. Графики колебаний заряда и тока
Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.
Используя формулу приведения
запишем закон изменения тока (13) в виде:
Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная , больше фазы заряда на величину . В таком случае говорят, что ток опережает по фазе заряд на ; или сдвиг фаз между током и зарядом равен ; или разность фаз между током и зарядом равна .
Опережение током заряда по фазе на графически проявляется в том, что график тока сдвинут влево на относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз ).
Вынужденные электромагнитные колебания
Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.
Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12 ).

Рис. 12. Вынужденные колебания
Если напряжение источника меняется по закону:
то в контуре происходят колебания заряда и тока с циклической частотой (и с периодом, соответственно, ). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте .
Амплитуда вынужденных колебаний заряда и тока зависит от частоты : амплитуда тем больше,чем ближе к собственной частоте контура .При наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.
Электромагнитные колебания — основные понятия, формулы и определения с примерами
Содержание:
Электромагнитные колебания:
Мы проживаем в различных городах и селах нашей республики. Они находятся в сотнях и тысячах километров от столицы. Несмотря на большие расстояния между населенными пунктами, мы постоянно поддерживаем связь. Кроме этого, нам известна информация о событиях со всего мира. Эти новости мы узнаем по телевизору, радио, мобильным телефонам. Каким образом информация доходит до нас по телевидению, через радиоприемники, мобильные телефоны?
Передача на большие расстояния речи, музыки, изображений или другой информации в виде электромагнитных сигналов называется телекоммуникацией. Передача информации в виде электрических сигналов с помощью проводников была изобретена в 1837 году английскими учеными У. Куком и Ч. Уитсоном. Американский художник С. Морзе изобрел передачу информации с помощью специального алфавита, состоящего из точек и тире. Этот метод в дальнейшем стал широко применяться во всем мире. В 1876 году А.Г. Белл изобрел телефон. В настоящее время, если телефоны в наших домах и различных ведомствах связаны со станцией через металлические проводники, то междугородные и международные телефонные станции связаны кабелями оптических волокон. Информация по этим кабелям передается с помощью лазерных лучей. По одной паре кабель одновременно может поддерживать связь 6000 телефонных абонентов. Наши радиоприемники и телевизоры могут получать информацию вообще без проводов. Мобильные телефоны также поддерживают беспроводную связь. В этих случаях информация передается с помощью электромагнитных волн.
Как поступает информация по проводам и воздуху в виде речи, изображения и звука в мобильные телефоны, радиоприемники и телевизоры? Ответы на эти вопросы вы, уважаемые ученики, найдете в данной главе.
Свободные электромагнитные колебания
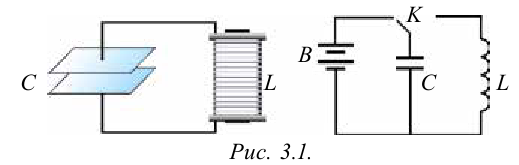
Простые электромагнитные колебания можно создать в электрической цепи, состоящей из конденсатора и катушки индуктивности. Построим электрическую цепь, состоящую из конденсатора, катушки индуктивности, источника постоянного тока и включателя (рис. 3.1). Для упрощения не будем учитывать сопротивление электрической цепи. При включении включателя с левой стороны батареи пластинки конденсатора С заряжаются. При этом между обкладками конденсатора создается электрическое поле с максимальной энергией 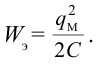
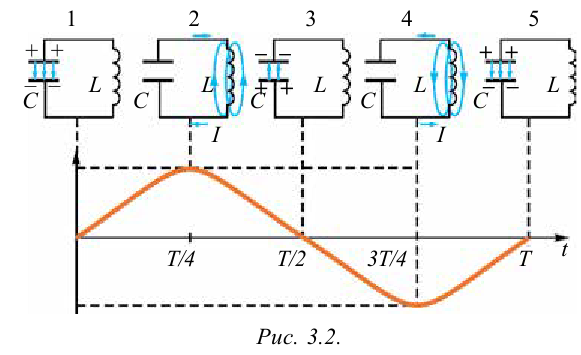
В результате зарядки верхней обкладки конденсатора положительным, а нижней обкладки отрицательным зарядом он становится источником тока (1 случай). В результате с положительной обкладки конденсатора наблюдается перемещение зарядов на отрицательную обкладку через катушку индуктивности, т.е. образуется ток. Вокруг этого тока создается магнитное поле. Этот ток из-за индуктивности катушки постепенно увеличивается и достигает максимального значения (смотрите график на рисунке). Магнитное поле, созданное вокруг тока, протекающего через катушку, будет тоже растущим (2 случай). В этом случае энергия электрического поля между обкладками конденсатора уменьшается до нуля. Энергия магнитного поля вокруг катушки постепенно растет и достигает своего максимального значения 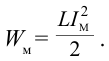 Как известно из предыдущих тем, согласно явлению электромагнитной индукции на концах катушки, расположенной в изменяющемся магнитном поле, появляется разность потенциалов. Уменьшая значение тока эта разность потенциалов заряжает обкладки конденсатора противоположными зарядами (3 случай). Заряженный конденсатор через катушку индуктивности снова создает ток (4 случай). Этот ток тоже является растущим, его магнитное поле на концах катушки создает разность потенциалов. Уменьшается ток, и разность потенциалов снова заряжает конденсатор (5 случай). В 5-ом и 1-ом случаях знаки зарядов конденсатора одинаковы. Значит, последующие процессы повторяются, как было описано выше.
Как известно из предыдущих тем, согласно явлению электромагнитной индукции на концах катушки, расположенной в изменяющемся магнитном поле, появляется разность потенциалов. Уменьшая значение тока эта разность потенциалов заряжает обкладки конденсатора противоположными зарядами (3 случай). Заряженный конденсатор через катушку индуктивности снова создает ток (4 случай). Этот ток тоже является растущим, его магнитное поле на концах катушки создает разность потенциалов. Уменьшается ток, и разность потенциалов снова заряжает конденсатор (5 случай). В 5-ом и 1-ом случаях знаки зарядов конденсатора одинаковы. Значит, последующие процессы повторяются, как было описано выше.
Из рассмотренных процессов сделаем следующие выводы:
- В цепи, состоящей из конденсатора и катушки индуктивности, заряд, переданный конденсатору из источника тока, в замкнутой цепи создаст переменный ток.
- Энергия, полученная от источника, сначала концентрируется в качестве энергии электрического поля между обкладками конденсатора, а затем превращается в энергию магнитного поля внутри катушки. Далее энергия магнитного поля превращается в энергию электрического поля и т.д., периодически происходят превращения.
Мы узнали, что любые процессы, которые периодически повторяются, называются колебаниями.
Значит, процесс в цепи, состоящей из конденсатора с и катушки, тоже имеет колебательный характер. Это явление называется электромагнитные колебания. Замкнутая цепь, состоящая из катушки (L) и конденсатора (С), в которой создаются электромагнитные колебания, называется колебательным контуром (рис. 3.3).
Формула определения периода (частоты) электромагнитного колебания в колебательном контуре найдена английским физиком У. Томсоном.
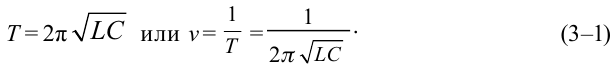
Здесь: Т-период колебания в секундах, 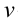 -частота колебания измеряется в 1 /с = 1 Гц.
-частота колебания измеряется в 1 /с = 1 Гц.
Когда происходят электромагнитные колебания в контуре, энергия электрического поля периодически превращается в энергию магнитного поля и наоборот. В идеальном колебательном контуре из-за отсутствия расхода энергии колебания не затухают. Полная энергия сохраняется и ее величина в любой момент времени равна:
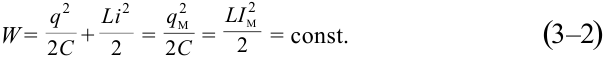
Здесь: L- индуктивность катушки, С-емкость конденсатора, 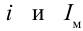 -мгновенные и максимальные значения силы тока соответственно:
-мгновенные и максимальные значения силы тока соответственно: 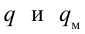 — мгновенные и максимальные значения заряда в конденсаторе соответственно.
— мгновенные и максимальные значения заряда в конденсаторе соответственно.
Явления, происходящие в колебательном контуре, — это превращение энергии электрического поля конденсатора в энергию магнитного поля катушки и наоборот — энергии магнитного поля катушки в энергию электрического поля конденсатора. Это явление можно сравнить с рассмотренным в 10-м классе примером, где потенциальная энергия растянутой пружины, пружинного маятника, превращается в кинетическую энергию груза и наоборот. Согласно этому в следующей таблице приведем аналогию величин, характеризующих механические и электрические колебания.
Следует отметить, что электромагнитные и механические колебания имеют разную природу, но выражаются аналогичными уравнениями.
Пример №1
Емкость конденсатора колебательного контура равна 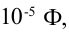 индуктивность катушки — 0,4 Гн. Максимальное напряжение конденсатора -2 В. Найдите период собственного колебания контура и максимальную энергию контура.
индуктивность катушки — 0,4 Гн. Максимальное напряжение конденсатора -2 В. Найдите период собственного колебания контура и максимальную энергию контура.
Дано: 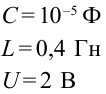 Найти:
Найти: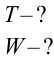
Формула: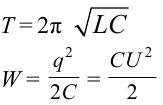
Решение: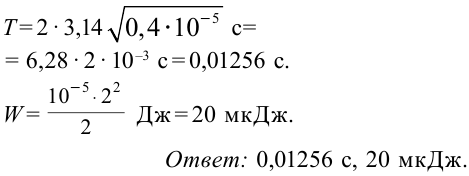
Графическое изображение колебания затухающие электромагнитные колебания
В рассмотренном колебательном контуре для создания возникающих электромагнитных колебаний сначала в момент времени t=0 на конденсатор подается заряд qM, не оказывая других внешних воздействий. Колебания, возникающие при отсутствии внешних воздействий, называются свободными колебаниями.
Учитывая схожесть электромагнитных колебаний с механическими колебаниями, изученными в 10-м классе, изменение заряда конденсатора можно записать следующей формулой:

Если учесть, что 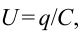 для изменения напряжения конденсатора получим
для изменения напряжения конденсатора получим

Сила тока в катушке определяется согласно следующей закономерности: 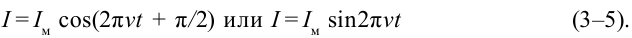
Периодическое изменение физических параметров с течением времени по закону синуса или косинуса называется гармоническими колебаниями.
Модуль наибольшего значения колеблющейся величины называется амплитудой колебания, или амплитудной величиной.
Амплитуда в механических колебаниях равна наибольшему отклонению тела от положения равновесия, а в электромагнитных колебаниях — наибольшему значению электрического заряда 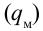 на обкладках конденсатора.
на обкладках конденсатора.
Для изображения зависимости величин гармонических колебаний от времени удобен графический метод.
Нарисуем графики зависимости заряда, напряжения и силы тока электромагнитных колебаний от времени. Для этого воспользуемся формулами (3-3), (3-4) и (3-5). Сравнивая эти уравнения, можно увидеть, что колебания отличаются друг от друга по фазовым смещениям, т.е. имеют сдвиг по фазе.
Нарисуем графики вышеназванных уравнений. Ось абсцисс указывает в долях период времени, над ним соответствующие фазы колебания. По оси ординат выставлены величины 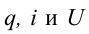 (рис. 3.4).
(рис. 3.4). 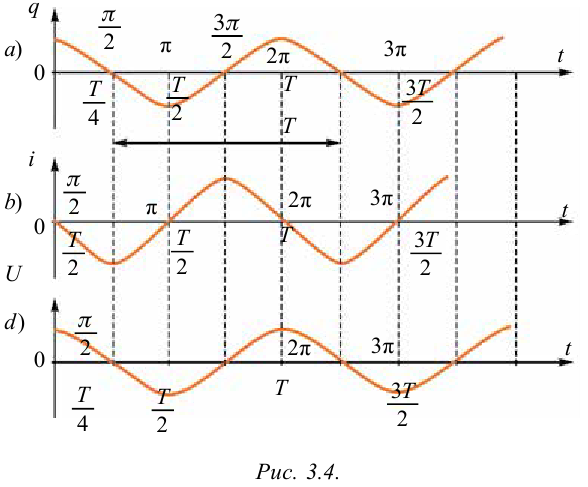
Если на этих графиках будет известен масштаб, то по оси абсцисс можно найти период (время), а по оси ординат — амплитуду или мгновенное значение колеблющихся величин. Таким же образом сравнивая графики, можно найти сдвиг по фазе. Например, при максимальном значении заряда и напряжения на обкладках конденсатора сила тока равна нулю.
Колебания силы тока в контуре по фазам опережают колебания заряда на 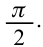 Заряд и напряжение изменяются в одной фазе.
Заряд и напряжение изменяются в одной фазе.
Как было сказано выше, колебания, возникающие в идеальных колебательных контурах, не затухают. В реальных контурах из-за того, что сопротивление R не равняется нулю, электрическая энергия превращается в тепло и амплитуда колебания со временем уменьшается (рис. 3.5).
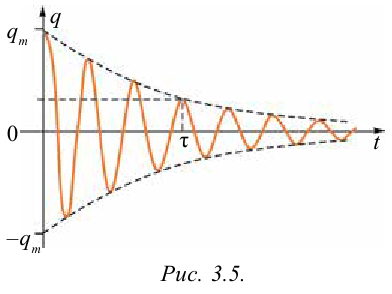
Такие колебания называются затухающим и колебаниями.
Следует отметить, что согласно формуле 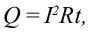 чем больше сопротивление контура, тем больше расходуется энергия. С увеличением сопротивления контура увеличится период колебания. Значит, затухающие колебания не являются гармоническими.
чем больше сопротивление контура, тем больше расходуется энергия. С увеличением сопротивления контура увеличится период колебания. Значит, затухающие колебания не являются гармоническими.
Затухающие колебания относятся к непериодичным колебаниям. Их уравнения выражаются через дифференциальные уравнения и являются сложными задачами, поэтому, не приводя их решения, ограничимся приведением их графиков.
Пример №2
На рисунке приведен график изменения тока в колебательном контуре. Объясните изменение энергии в промежутке времени: 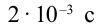 и
и 
Решение: За приведенный промежуток времени 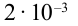 с и
с и 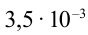 с сила тока, протекающего через катушку, растет и достигает своего максимального значения.
с сила тока, протекающего через катушку, растет и достигает своего максимального значения.
Значит, энергия электрического поля конденсатора уменьшается до нуля и растет энергия магнитного поля катушки, достигая максимального значения. 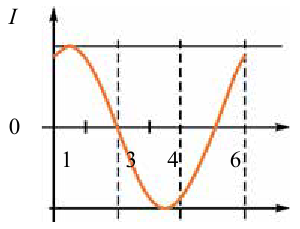
Генераторы электромагнитных колебаний на транзисторах
Мы узнали, что в колебательном контуре возникают высокочастотные электромагнитные колебания. Если наблюдать на экране осциллографа колебания, возникающие в колебательном контуре, то увидим, что с течением времени амплитуда колебания уменьшается (рис. 3.6). 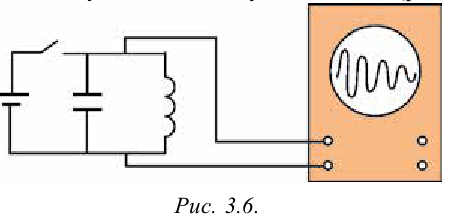
Причиной этого является электрическое сопротивление проводников катушки контура, используемых для соединения. Известно, что, имея сопротивление, проводник нагревается. Электрическая энергия превращается в тепловую энергию. Поэтому возникающие в контуре свободные электромагнитные колебания являются затухающими колебаниями.
Для того чтобы колебания не затухали, израсходованную энергию нужно периодически передавать колебательному контуру с помощью батарейки. Это означает, что включатель в контуре не должен постоянно оставаться включенным, его надо периодически выключать. Вспомните из 10-го класса фазы колебания. Согласно этому, во время перезарядки обкладки конденсатора включатель должен соединиться в тот момент, когда знаки зарядов на обкладках соответствуют полюсам батарейки.
Как при этом должен работать включатель? Представим себе, что частота колебания контура равна 1 МГц. В этом случае потребуется включатель включать-выключать миллион раз в секунду! Эту задачу не смогут выполнить никакие механические или электромеханические устройства.
Такую задачу может выполнить только электронный прибор, т.е. транзистор. Вспомним приведенный в 10-м классе принцип работы транзистора 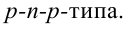 Чтобы через транзистор протекал ток, подключаются отдельные батарейки между базой-эмиттером и коллектором-эмиттером. В случае подсоединения к базе отрицательного полюса батарейки, к эмиттеру положительного полюса через транзистор протекает ток (включатель включен). Если поменять полюсы батарейки, ток не протекает (включатель выключен). Значит, транзистор может выполнять функцию включателя. Поэтому для создания незатухающего колебания в контуре его нужно подсоединить к источнику через транзистор.
Чтобы через транзистор протекал ток, подключаются отдельные батарейки между базой-эмиттером и коллектором-эмиттером. В случае подсоединения к базе отрицательного полюса батарейки, к эмиттеру положительного полюса через транзистор протекает ток (включатель включен). Если поменять полюсы батарейки, ток не протекает (включатель выключен). Значит, транзистор может выполнять функцию включателя. Поэтому для создания незатухающего колебания в контуре его нужно подсоединить к источнику через транзистор.
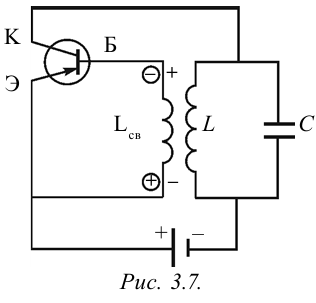
На рис. 3.7 приводится схема генератора, в котором создаются высокочастотные незатухающие колебания. Здесь контур, состоящий из L и С, подсоединен к источнику тока через транзистор. В момент включения протекающий через катушку L ток имеет растущий характер. Магнитное поле, возникающее вокруг нее, тоже будет расти. Это магнитное поле, проходящее сквозь катушку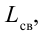 создает электродвижущую силу взаимной индукции. На рис. 3.7 знаки внутри на концах катушки показаны в кружочках. Здесь на базу транзистора (Б) подастся напряжение с отрицательным знаком, на эмиттер (Э) — с положительным знаком и по транзистору протекает полный ток. В это время конденсатор С в контуре заряжается. Из-за индуктивности катушки (L) протекающий по нему ток перестанет увеличиваться. В
создает электродвижущую силу взаимной индукции. На рис. 3.7 знаки внутри на концах катушки показаны в кружочках. Здесь на базу транзистора (Б) подастся напряжение с отрицательным знаком, на эмиттер (Э) — с положительным знаком и по транзистору протекает полный ток. В это время конденсатор С в контуре заряжается. Из-за индуктивности катушки (L) протекающий по нему ток перестанет увеличиваться. В 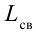 не возникает электродвижущей силы и по транзистору ток не протекает. Теперь ключ выключим. Конденсатор С начинает разряжаться через катушку L, и в контуре появляются электромагнитные колебания. Когда в контуре происходят электромагнитные колебания, меняется и величина, и направление тока, протекающего по катушке L. Значит, знак электродвижущей силы, возникающей в
не возникает электродвижущей силы и по транзистору ток не протекает. Теперь ключ выключим. Конденсатор С начинает разряжаться через катушку L, и в контуре появляются электромагнитные колебания. Когда в контуре происходят электромагнитные колебания, меняется и величина, и направление тока, протекающего по катушке L. Значит, знак электродвижущей силы, возникающей в 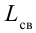 , изменяется. Транзистор находится то в открытом, то в закрытом положении.
, изменяется. Транзистор находится то в открытом, то в закрытом положении.
Таким образом, конденсатор С в контуре периодически заряжается от батарейки. Однако если источник напряжения подсоединяется в колебательный контур периодически, в те интервалы времени, когда обкладки конденсатора, подсоединенные к положительному полюсу, заряжаются положительно, конденсатор непрерывно заряжается. В этом случае колебания не затухнут. В противном случае колебания не возникнут. Значит, включение-выключение транзистора должно управляться колебаниями в контуре. Цепь база-эмиттер в транзисторе называется входной цепью, цепь коллектор-эмиттер — выходной цепью. Обычно напряжение (ток), приложенное во входной части на транзисторе, управляет выходным током. В транзисторных генераторах наоборот, напряжение при выходе (в контуре) управляет входным напряжением 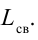 . Такие процессы называются обратной связью. Благодаря этой обратной связи контур периодически обеспечивается энергией.
. Такие процессы называются обратной связью. Благодаря этой обратной связи контур периодически обеспечивается энергией.
Чтобы обратная связь обеспечила колебания, напряжение входных и выходных цепей по фазе должно отличаться на 180°.
Частота электромагнитных колебаний, вырабатываемых генератором, выражается по формуле Томсона (3-1).
Таким образом, в генераторе образуются незатухающие автоколебания. Автоколебания являются вторым типом незатухающих колебаний. Основная их разница от вынужденных колебаний заключается в том, что им не нужны внешние периодичные действия. В этих системах имеется собственный источник энергии. Система сама обеспечивает и управляет пополнением израсходованной энергии. Любая система автоколебания состоит из следующих частей: источник энергии, колебательная система и электронный ключ.
Частоты автоколебания изменяются в очень широком диапазоне. Они используются для радиосвязи, телевидения, ЭВМ и в других устройствах.
Электромагнитные колебания могут быть как полезными, так и вредными для живых организмов. Каждый орган человеческого организма имеет свойственную ему резонансную частоту. Когда частота внешнего колебания равняется этой резонансной частоте, действия будут сильными. Доказано, что электромагнитные излучения влияют на психику человека.
В современной медицине все шире распространяются методы лечения с помощью высокочастотных электромагнитных колебаний. Кроме того, электромагнитные излучения оптического диапазона (УФ-излучения) используются для лечения и диагностики различных заболеваний.
Активное сопротивление в цепи переменного тока
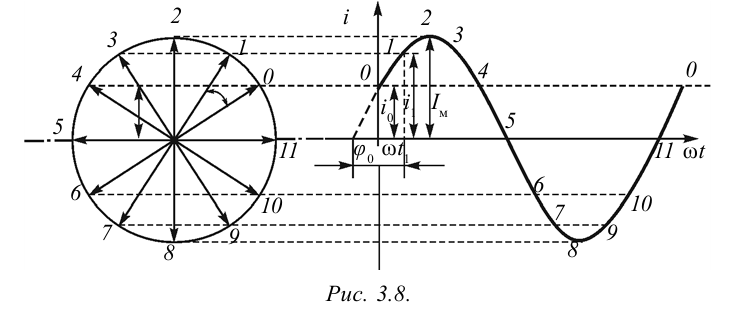
В предыдущих темах мы познакомились с графическими изображениями изменения некоторых физических величин в зависимости от времени. Для их описания также широко применяется метод векторной диаграммы. Скажем, изменение тока в цепи задается уравнением
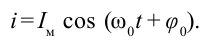
Возьмем вектор длиной 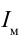 и приведем в движение по направлению против часовой стрелки. Пусть время для одного вращения равно периоду изменения величины
и приведем в движение по направлению против часовой стрелки. Пусть время для одного вращения равно периоду изменения величины 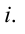 . В этом случае проекция на вертикальной оси вектора м равна мгновенному значению величины
. В этом случае проекция на вертикальной оси вектора м равна мгновенному значению величины 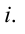
В повседневной жизни, быту и технике к цепи переменного тока подсоединяются различные бытовые приборы. Утюг, электрическая лампочка, вентилятор и т.д — в этих приборах электрическая энергия превращается в тепловую, световую, механическую и другие виды энергии. Когда эти приборы подсоединяются к источнику напряжения, то они оказывают различное сопротивление протеканию тока. Для изучения их природы попробуем подсоединить разные приборы к цепи переменного тока.
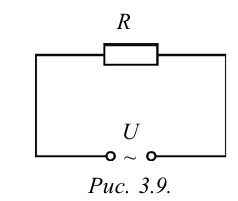
Сначала рассмотрим случай, когда к цепи переменного тока подсоединено заранее известное нам сопротивление (рис. 3.9). Пусть это сопротивление будет активным сопротивлением. Такое сопротивление называется активным, потому что когда через него протекает ток, электрическая энергия полностью превращается в другие виды (тепло, свет и др.) энергии. Проводник подсоединен к источнику переменного тока, имеющего сопротивление R и напряжение U. Это напряжение задается уравнением 
Используя закон Ома для участка цепи, находим мгновенное значение силы тока, протекающего по сопротивлению R 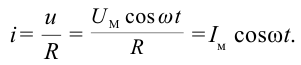
Здесь 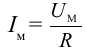 амплитудное значение силы тока. Таким образом, изменение силы тока в цепи, состоящей только активного сопротивления, будет иметь вид
амплитудное значение силы тока. Таким образом, изменение силы тока в цепи, состоящей только активного сопротивления, будет иметь вид 
Если сопоставить уравнение изменения напряжения (3-6) с полученным уравнением для силы тока (3-7), можно прийти к выводу, что колебания напряжения и силы тока в активном сопротивлении будут происходить в одинаковой фазе. Графики колебания напряжения и силы тока приведены на рис. 3.10.
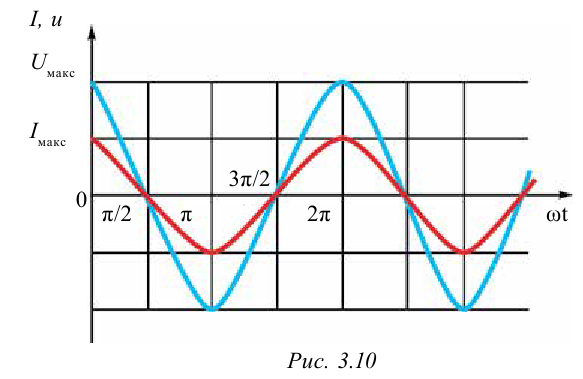
Зависимость между колебаниями напряжения и силы тока можно показать через векторную диаграмму (рис. 3.11).
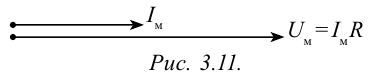
На диаграмме амплитуда переменного тока и амплитуда переменного напряжения изображены в виде параллельных векторов, а угол между ними, т.е. разница фазы колебания равна нулю.
Частота потребляемого в быту электрического напряжения равна 50 Гц. Это означает, что в секунду электрическая лампочка накаливания 100 раз включается и выключается. Чувствительность человеческого глаза такова, что он способен уловить изменение процесса только до 16-20 раз в секунду, поэтому мы не чувствуем включение-выключение электрической лампочки с такой частотой. По этой причине важно знать мощность переменного тока.
Мощность цепи с активным сопротивлением
Мгновенная мощность переменного тока определяется как 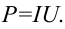 Если выражения (3-7) и (3-6) использовать для определения мгновенных значений силы тока и напряжения, получим,
Если выражения (3-7) и (3-6) использовать для определения мгновенных значений силы тока и напряжения, получим,
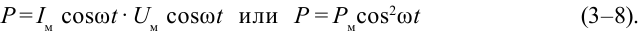
Здесь: 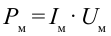 называется максимальным значением мощности переменного тока. Из-за того что выражение
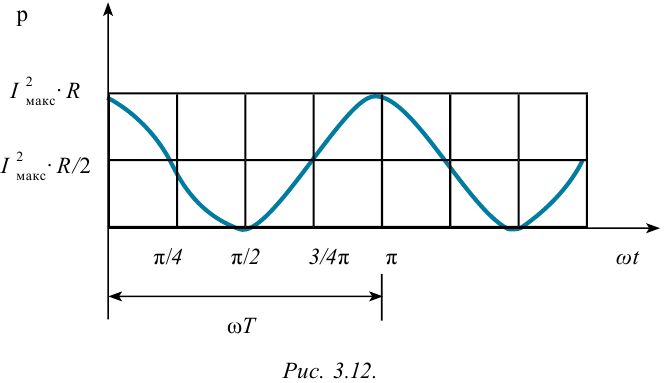
называется максимальным значением мощности переменного тока. Из-за того что выражение 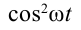 имеет постоянно положительный знак, мгновенное значение мощности переменного тока тоже будет иметь положительный знак (рис. 3.12).
имеет постоянно положительный знак, мгновенное значение мощности переменного тока тоже будет иметь положительный знак (рис. 3.12).
Как видно из рис. 3.12, величина мгновенной мощности переменного тока меняется периодически. По какой формуле в этом случае можно определить количество тепла, выделенного при протекании переменного тока в электрической плите? Для этого введем понятие эффективного значения переменного тока.
Эффективным значением переменного тока 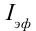 называется величина, равная количеству тепла, выделяемому при протекании переменного тока через активное сопротивление, равное силе постоянного тока, при котором выделяется такое же количество тепла за единицу времени.
называется величина, равная количеству тепла, выделяемому при протекании переменного тока через активное сопротивление, равное силе постоянного тока, при котором выделяется такое же количество тепла за единицу времени.
Опыты показывают, что эффективное значение силы тока связано с его максимальным значением и определяется следующей формулой:

Эффективное значение переменного напряжения можно записать формулой (3-9):

Пример №3
При подсоединении резистора в цепь переменного тока с максимальным напряжением 30 В по нему протекает максимальный ток 2 А. Найдите среднюю мощность, выделяемую в резисторе.
Дано: 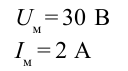 Найти:
Найти: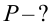
Формула: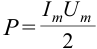
Решение:
Конденсатор в цепи переменного тока
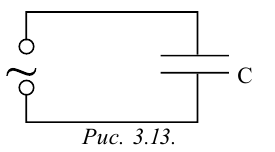
Опыты показывают, что, подсоединяя конденсатор к цепи постоянного тока, по ней ток не протекает, так как пространство между обкладками конденсатора разделено диэлектриком. Если конденсатор подсоединить к цепи переменного тока, то по ней ток течет.
Для изучения вопроса, от каких физических параметров зависит сила тока, протекающего через конденсатор, рассмотрим случай, когда к цепи переменного тока подсоединен только конденсатор (рис. 3.13).
Пусть емкость конденсатора равна С и приложенное напряжение изменяется согласно закономерности

сопротивление соединительных проводов R = 0. В этом случае напряжение конденсатора будет: 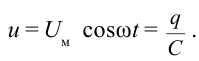 Здесь: q — заряд обкладок конденсатора и его значение
Здесь: q — заряд обкладок конденсатора и его значение 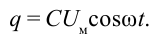 Чтобы найти силу тока в цепи, возьмем производную первого порядка формулы заряда:
Чтобы найти силу тока в цепи, возьмем производную первого порядка формулы заряда: 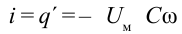
sinco= 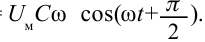 Если это сопоставить с мгновенным значением силы тока, получим:
Если это сопоставить с мгновенным значением силы тока, получим: 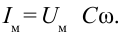 Здесь
Здесь 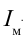 — максимальное значение силы тока. Тогда уравнение силы тока, протекающего через конденсатор, будет иметь вид:
— максимальное значение силы тока. Тогда уравнение силы тока, протекающего через конденсатор, будет иметь вид:

Если сопоставить это уравнение с напряжением, приложенным к конденсатору (3-11), мы увидим, что колебания силы тока в цепи опережают колебания напряжения на 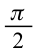 (рис. 3.14). На рис. 3.15 приводится векторная диаграмма силы переменного тока и напряжения для случая, когда к цепи подсоединен только конденсатор. Емкостное сопротивление конденсатора в цепи:
(рис. 3.14). На рис. 3.15 приводится векторная диаграмма силы переменного тока и напряжения для случая, когда к цепи подсоединен только конденсатор. Емкостное сопротивление конденсатора в цепи:

В этом случае значение амплитуды силы тока будет следующим:
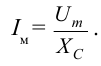
Это выражение является законом Ома для участка цепи переменного тока с конденсатором. На месте активного сопротивления стоит величина 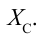 . Поэтому его называют емкостным сопротивлением (реактивным сопротивлением). Емкостное сопротивление тоже измеряется в омах.
. Поэтому его называют емкостным сопротивлением (реактивным сопротивлением). Емкостное сопротивление тоже измеряется в омах.
Отсюда вытекает, что сила тока, протекающего через конденсатор, зависит от емкости конденсатора и частоты переменного тока. Чем больше емкость и частота, тем меньше сопротивление цепи, и соответственно сила тока будет больше. 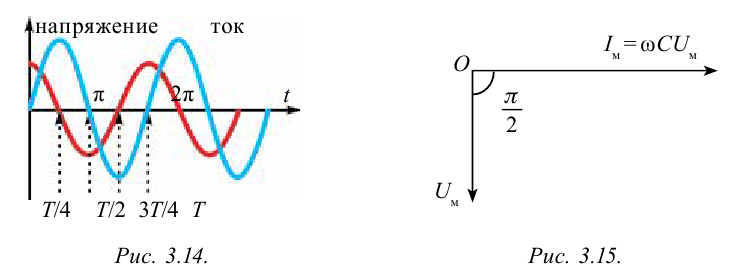
Пример №4
К цепи переменного тока с частотой 50 Гц подсоединен конденсатор емкостью 50 мкФ. Чему равно емкостное сопротивление цепи?
Дано: 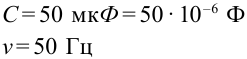 Найти:
Найти: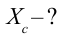
Формула: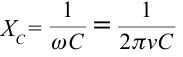
Решение: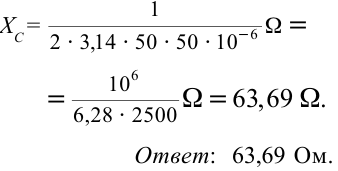
Катушка индуктивности в цепи переменного тока
Проведем такой опыт. К источнику постоянного тока последовательно подсоединим электрическую лампочку и катушку индуктивности. Обратим внимание на яркость лампочки. Затем последовательно подсоединим электрическую лампочку и катушку индуктивности к источнику с эффективным напряжением, равным постоянному напряжению 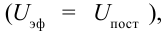 обратим внимание на яркость лампочки. Тогда яркость лампочки, соединенная с цепью переменного тока, будет меньше. Для определения этого явления рассмотрим случай, когда подсоединена только катушка индуктивности (рис. 3.16).
обратим внимание на яркость лампочки. Тогда яркость лампочки, соединенная с цепью переменного тока, будет меньше. Для определения этого явления рассмотрим случай, когда подсоединена только катушка индуктивности (рис. 3.16).
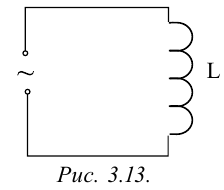
Сила тока, протекающего по катушке с индуктивностью L, изменяется согласно закономерности

Сопротивление соединительных проводов и катушки пусть будет 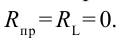
Ток, протекающий по катушке, из-за индуктивности катушки создаст электродвижущую силу (ЭДС) самоиндукции. Ее мгновенное значение определяется выражением

Здесь: 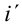 — производная первого порядка, взятая от силы тока по времени. Если учесть
— производная первого порядка, взятая от силы тока по времени. Если учесть 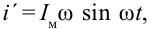 мгновенное значение ЭДС равно
мгновенное значение ЭДС равно
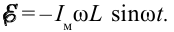
ЭДС цепи, напряжение на концах катушки и падение потенциала на активном сопротивлении связаны через следующее соотношение

Если учесть, что R = 0, формула (3-16) примет вид
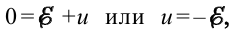
тогда напряжение определяется следующей формулой:
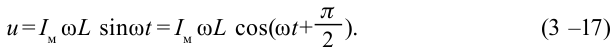
Если сопоставить напряжение с мгновенным значением напряжения, то вытекает 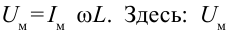 — амплитудное значение напряжения. В
— амплитудное значение напряжения. В
таком случае уравнение напряжения, приложенного к концам катушки, будет выглядеть так:

Если сопоставить это уравнение с выражением (3-14) силы тока, протекающего по катушке, можем увидеть, что колебания напряжения, приложенного к концам катушки, по фазе опережают колебания силы тока на 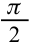 (рис.3.17). На рис. 3.18 приводится векторная диаграмма силы тока и напряжения для случая, где в цепь переменного тока подсоединена только катушка индуктивности.
(рис.3.17). На рис. 3.18 приводится векторная диаграмма силы тока и напряжения для случая, где в цепь переменного тока подсоединена только катушка индуктивности.
Если амплитудное значение напряжения катушки сопоставимо с законом Ома, написанным для участка цепи, известно, что произведение 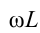 выражает сопротивление. Введем знак:
выражает сопротивление. Введем знак: 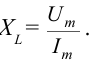
Тогда сопротивление катушки будет: 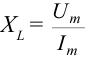
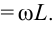
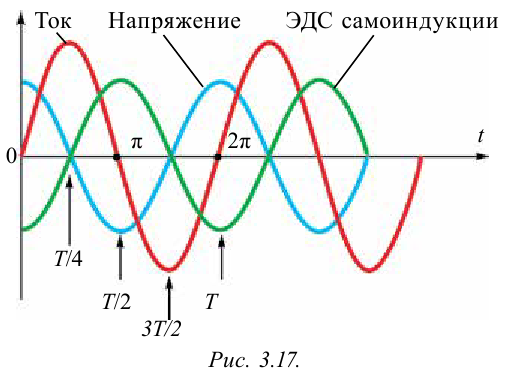
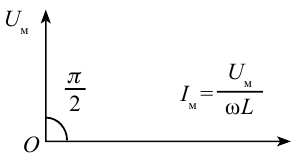
В таком случае амплитудное значение силы тока будет следующим: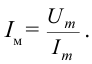
Это выражение является законом Ома для участка цепи переменного тока с катушкой. На месте активного сопротивления стоит величина 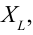 поэтому его называют индуктивным сопротивлением (реактивным сопротивлением). Индуктивное сопротивление тоже измеряется в омах.
поэтому его называют индуктивным сопротивлением (реактивным сопротивлением). Индуктивное сопротивление тоже измеряется в омах.
Отсюда вытекает, что сила тока, протекающего по катушке, зависит от индуктивности катушки и частоты переменного тока. Чем больше индуктивность и частота, тем больше будет сопротивление цепи, а сила протекающего тока соответственно будет меньше.
Пример №5
К цепи переменного тока с частотой 10 кГц подсоединена катушка с индуктивностью 5 Гн. Чему равно индуктивное сопротивление цепи?
Дано: 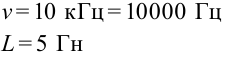 Найти:
Найти: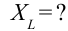
Формула: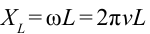
Решение: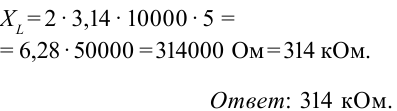
Закон ома для цепи переменного тока при последовательном соединении активного, индуктивного и емкостного сопротивления
Составим цепь, последовательно соединяя резистор с сопротивлением R, катушку индуктивности с индуктивностью L и конденсатор с емкостью С (рис. 3.19). На концы подаем переменное напряжение 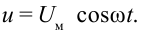 По причине последовательного соединения составных частей цепи сила тока, протекающего по ним, будет одинаковой. Пусть эта сила тока изменяется закономерностью
По причине последовательного соединения составных частей цепи сила тока, протекающего по ним, будет одинаковой. Пусть эта сила тока изменяется закономерностью

общее напряжение равно сумме векторов падения напряжения в потребителях:

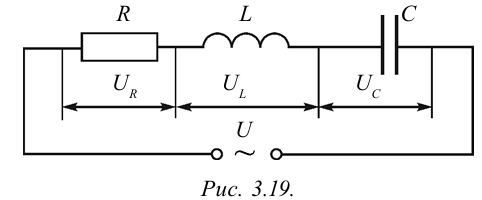
Здесь: 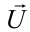 — общее напряжение в цепи,
— общее напряжение в цепи, 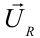 — напряжение на резисторе,
— напряжение на резисторе,
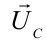 напряжение на конденсаторе и
напряжение на конденсаторе и 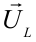 — напряжение на катушке. Их амплитудные значения обозначим как
— напряжение на катушке. Их амплитудные значения обозначим как 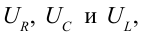 и построим векторную диаграмму.
и построим векторную диаграмму.
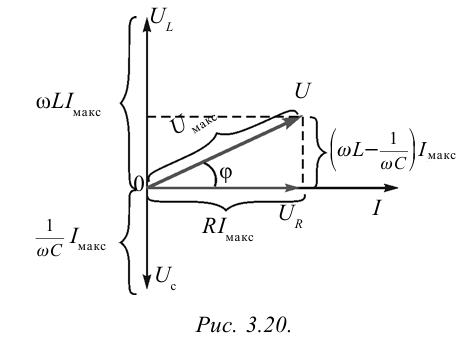
Амплитуду силы тока возьмем как вектор, направленный по горизонтальной оси (рис. 3.19). Фаза колебания напряжения в активном сопротивлении соответствует фазе колебания силы тока. Колебания напряжения в конденсаторе по фазе отстают на — от колебания силы тока. В катушке колебания напряжения опережают колебания силы тока на 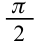 . В векторной диаграмме напряжение в конденсаторе
. В векторной диаграмме напряжение в конденсаторе 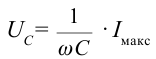 и напряжение в катушке
и напряжение в катушке 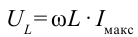 направлены противоположно. Итоговое напряжение будет
направлены противоположно. Итоговое напряжение будет 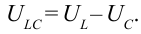
Чтобы найти общее напряжение (U), вектор 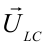 сложим с вектором
сложим с вектором 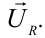 . Из рис. следует
. Из рис. следует 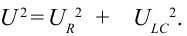 Отсюда находим выражение максимального значения общего напряжения:
Отсюда находим выражение максимального значения общего напряжения:
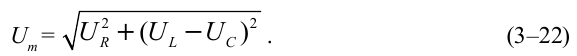
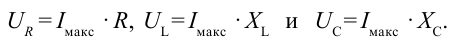
Подставим в выражение (3-22)
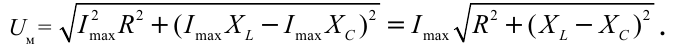
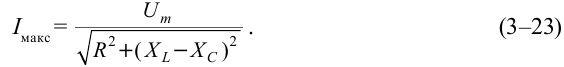
Это выражение называют законом Ома для полной цепи переменного тока.
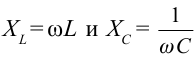 подставим в выражение (3-23) и получим
подставим в выражение (3-23) и получим
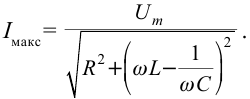
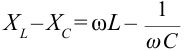 сопротивление называется реактивным сопротивлением.
сопротивление называется реактивным сопротивлением.
Выражение 
называется полным сопротивлением цепи переменного тока.
Разницу фаз между колебаниями тока и колебаниями напряжения в цепи можно определить, используя векторную диаграмму:
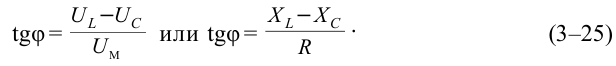
Характерные свойства цепи переменного тока заключаются в том, что энергия, получаемая от генератора, выделяется в качестве тепловой энергии только в активном сопротивлении. В реактивном сопротивлении энергия не выделяется.
В реактивном сопротивлении энергия электрического поля периодически превращается в энергию магнитного поля и наоборот. В первой четверти периода, когда конденсатор заряжается, энергия передастся в цепь и накапливается в виде энергии электрического поля. В следующей четверти периода эта энергия снова передается в источник в виде энергии магнитного поля.
Пример №6
К источнику переменного тока с максимальным значением напряжения 120 В и частотой 100 Гц подсоединены активное сопротивление 200 Ом, конденсатор емкостью 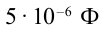 и катушка с индуктивностью 400 мГн. Найдите максимальное значение силы тока в цепи.
и катушка с индуктивностью 400 мГн. Найдите максимальное значение силы тока в цепи.
Дано: 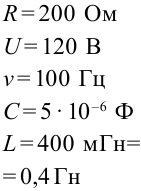 Найти:
Найти: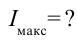
Формула: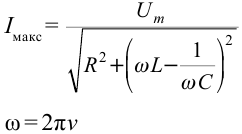
Решение:
Явление резонанса в цепи переменного тока
Полное сопротивление электрической цепи в случае последовательного соединения цепи переменного тока, сопротивления R, катушки с индуктивностью L и конденсатора с емкостью С определяется выражением
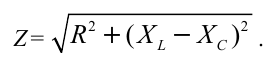
Если 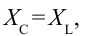 то разность
то разность 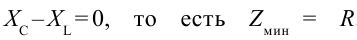 Тогда сопротивление цепи достигнет своего минимального значения. Амплитуда силы тока цепи будет
Тогда сопротивление цепи достигнет своего минимального значения. Амплитуда силы тока цепи будет

Значит, в этих условиях амплитуда силы тока резко возрастет. Это явление называется резонансом в электрической цепи. Для наблюдения резонанса должны выполняться следующие условия 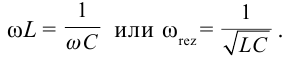
Мы знаем, что частота свободного колебания в контуре колебания, где активное сопротивление равно нулю,определяется из выражения 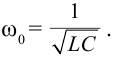 В этом случае получается, что для появления резонанса в цепи частота внешнего периодического напряжения, приложенного к цепи, должна быть равной собственной частоте цепи
В этом случае получается, что для появления резонанса в цепи частота внешнего периодического напряжения, приложенного к цепи, должна быть равной собственной частоте цепи 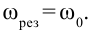
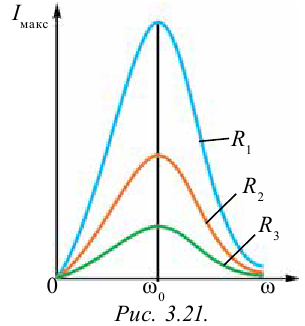
На рис. 3.21 приводится график зависимости амплитудного значения силы тока цепи от частоты внешних напряжений, приложенных к нему. График зависимости 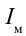 кривой резонанса.
кривой резонанса.
На рис. 3.21 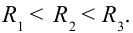 С увеличением частоты внешнего напряжения растет амплитудное значение тока в цепи и при
С увеличением частоты внешнего напряжения растет амплитудное значение тока в цепи и при 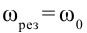 достигает максимального значения. Затем с увеличением частоты значение тока уменьшается.
достигает максимального значения. Затем с увеличением частоты значение тока уменьшается.
Рассмотренное явление резонанса называется резонансом напряжения.
Во время резонанса с увеличением тока напряжение в катушке и конденсаторе быстро растет. Их значение может быть больше, чем величины внешнего напряжения.
Во время резонанса амплитуда колебания напряжения индуктивной катушки и конденсатора будет: 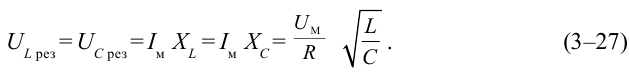
В колебательных контурах выполняются условия 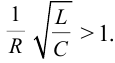 Поэтому
Поэтому
напряжение катушки и конденсатора будет больше, чем напряжение,
приложенное к цепи, а с уменьшением R оно будет увеличиваться. Другими словами, при больших значениях активного сопротивления резонанс на практике не наблюдается.
В период резонанса амплитудное значение переменного тока и амплитуда общего напряжения колеблется в одинаковой фазе.
Явление резонанса широко используют в технике. В радиоприемниках принцип выделения нужных сигналов среди множества радиосигналов основан на явлении резонанса. При этом значение емкости или индуктивности в колебательном контуре входной части приемника изменяется и его собственная частота настраивается на частоту сигнала той станции, которую необходимо принять. В контуре происходит резонанс именно для сигнала выбранной частоты, и созданное им напряжение будет самым большим. В электротехнических приборах тоже применяется явление резонанса, так как во время увеличения напряжения в катушке или конденсаторе может возникнуть электрический пробой.
Пример №7
К цепи переменного тока с частотой 50 Гц подсоединена катушка с индуктивностью 100 мГн и конденсатор емкостью С. При каком значении емкости конденсатора происходит явление резонанса?
Дано: 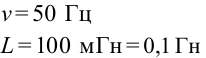 Найти:
Найти: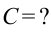
Формула 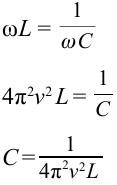
Решение: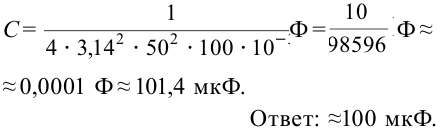
Сила и мощность переменного тока
Как вам известно, работа, выполненная постоянным током, определяется как произведение напряжения, силы тока и времени прохождения тока:

Для определения работы, выполненной переменным током за короткий промежуток времени, его значение рассматриваем как постоянное. В таком случае мгновенное значение выполненной работы переменного тока тоже находится из похожей формулы:

Если напряжение, приложенное к концам цепи, изменяется согласно закономерности
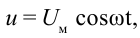
то сила тока в нем тоже меняется по гармоническому закону со сдвигом по фазе: 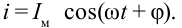 Тогда для мгновенного значения выполненной работы переменного тока напишем следующее выражение:
Тогда для мгновенного значения выполненной работы переменного тока напишем следующее выражение:
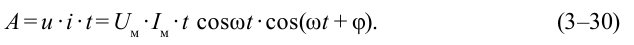
Работа, выполненная за единицу времени, называется мощностью. Поэтому мгновенное значение мощности переменного тока можно записать в виде
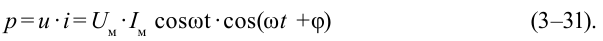
Здесь мощность с истечением времени меняется и по модулю, и по знаку. В первой половине периода, если мощность передается в цепь (р>0), то во второй половине часть мощности обратно передается в сеть питания (р
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
источники:
http://ege-study.ru/ru/ege/materialy/fizika/elektromagnitnye-kolebaniya/
http://www.evkova.org/elektromagnitnyie-kolebaniya
Запишите уравнение зависимости силы тока в колебательном контуре от времени, если изменение заряда на пластинах конденсатора описывается уравнением (Кл).
Найди верный ответ на вопрос ✅ «Запишите уравнение зависимости силы тока в колебательном контуре от времени, если изменение заряда на пластинах конденсатора описывается …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Физика » Запишите уравнение зависимости силы тока в колебательном контуре от времени, если изменение заряда на пластинах конденсатора описывается уравнением (Кл).
Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.
Определение
Переменный ток — вынужденные электромагнитные колебания.
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:
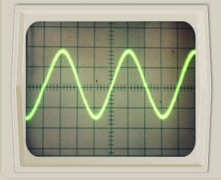
Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.
Определение
Частота переменного тока — это количество колебаний за 1 с.
Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.
Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.
Внимание!
При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙108 м/с).
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).
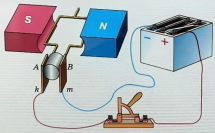
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.
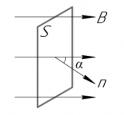
Численно магнитный поток определяется формулой:
Φ=BScosα
При равномерном вращении рамки угол α увеличивается пропорционально времени:
α=2πnt
где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:
Φ=BScos2πnt
Здесь множитель 2πn представляет собой число колебаний магнитного потока за 2π секунд. Это не что иное, как циклическая частота колебаний:
ω=2πn
Следовательно:
Φ=BScosωt
Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:
e=−Φ´=−BS(cosωt)´=BSωsinωt=εmaxsinωt
εmax — амплитуда ЭДС индукции, равная:
εmax=BSω
Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:
u=Umaxsinωt
u=Umaxcosωt
где Umax — амплитуда напряжения (максимальное по модулю значение напряжения).
Сила тока меняется с той частотой, что и напряжение — ω. Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:
i=Imaxsin(ωt+φс)
где Imax — амплитуда силы тока (максимальное по модулю значение силы тока), φс — разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.
u=Umaxcosωt=12cos300,25π=12√22≈8,5 (В).
Активное сопротивление в цепи переменного тока
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).
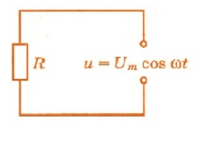
Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:
u=Umaxcosωt
Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:
i=uR=UmaxcosωtR=Imaxcosωt
В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:
Imax=UmaxR
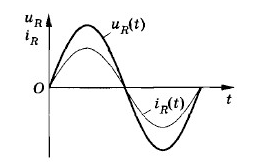
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Определение
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
P=I2R
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
p=i2R
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
p=(Imaxcosωt)2R
Вспомним из курса математики:
cos2α=1+cos2α2
Отсюда:
p=I2max2R(1+cos2ωt)=I2maxR2+I2maxR2cos2ωt
График зависимости мгновенной мощности от времени:
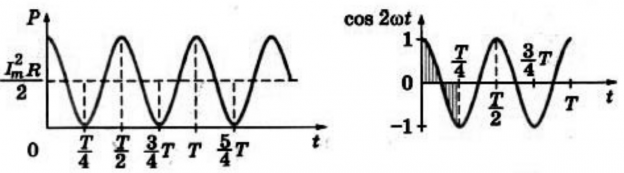
На протяжении первой четверти периода, когда cos2ωt>0, мощность в любой момент времени больше величины I2maxR2. На протяжении второй четверти периода, когда cos2ωt<0, мощность в любой момент времени меньше этой величины. Среднее за период значение cos2ωt=0, следовательно, средняя за период мощность равна I2maxR2.
Средняя мощность −p равна:
−p=I2maxR2=−i2R
Пример №2. Сила переменного тока в цепи меняется по закону i=Imaxcosωt. Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.
p=(Imaxcosωt)2R=10(1·cos(100π·1)2=10 (Дж)
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
−i2=I2max2
Определение
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I=√−i2=Imax√2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
U=√−u2=Umax√2
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
P=I2R=UI
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
P=I2R
I=Imax√2
P=(Imax√2)2R=I2max2R=222·5=10 ⎛⎝Дж⎞⎠
Задание EF22720
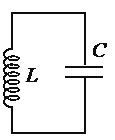 В идеальном колебательном контуре (см. рисунок) напряжение между обкладками конденсатора меняется по закону UC = U0cos ωt, где U0 = 5 В, ω = 1000π с–1. Определите период колебаний напряжения на конденсаторе.
В идеальном колебательном контуре (см. рисунок) напряжение между обкладками конденсатора меняется по закону UC = U0cos ωt, где U0 = 5 В, ω = 1000π с–1. Определите период колебаний напряжения на конденсаторе.
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу Томсона.
3.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• Закон изменения напряжения между обкладками конденсатора: UC=U0cosωt.
• Амплитуда напряжения: U0=5 В.
• Циклическая частота колебаний: ω = 1000π с–1.
Запишем формулу Томсона:
T=2πω=2π1000π=21000=0,002 (с)
Ответ: 0,002
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18735
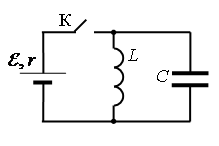 В электрической цепи, показанной на рисунке, ключ К длительное время замкнут, E=6 В, r = 2 Ом, L = 1 мГн. В момент t = 0 ключ К размыкают. Амплитуда напряжения на конденсаторе в ходе возникших в контуре электромагнитных колебаний равна ЭДС источника. В какой момент времени напряжение на конденсаторе в первый раз достигнет значения E? Сопротивлением проводов и активным сопротивлением катушки индуктивности пренебречь. Ответ запишите в мкс.
В электрической цепи, показанной на рисунке, ключ К длительное время замкнут, E=6 В, r = 2 Ом, L = 1 мГн. В момент t = 0 ключ К размыкают. Амплитуда напряжения на конденсаторе в ходе возникших в контуре электромагнитных колебаний равна ЭДС источника. В какой момент времени напряжение на конденсаторе в первый раз достигнет значения E? Сопротивлением проводов и активным сопротивлением катушки индуктивности пренебречь. Ответ запишите в мкс.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Описать, что происходит в момент замыкания и размыкания цепи.
3.Выполнить решение задачи в общем виде.
4.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε=5 В.
• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.
• Сопротивление ЭДС источника тока: r = 2 Ом.
• Индуктивность катушки: L = 1 мГн.
1 мГн = 10–3 Гн
Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:
I0=εr
Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.
После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:
u=−UCmaxsinωt
Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.
Циклическую частоту выразим из формулы Томсона:
ω=2πT=1√LC
Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:
W=Li22+Cu22=CU2Cmax2=LI202
Выразим максимальное напряжение на конденсаторе:
CU2Cmax=LI20
UCmax=I0√LC
Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:
UCmax=ε=I0r=I0√LC
Отсюда:
√LC=r
C=Lr2
Период колебаний в контуре определим через формулу Томсона:
T=2π√LC=2π√LLr2=2πLr
Вспомним зависимость напряжения от времени:
u=−UCmaxsinωt
Подставим известные данные для искомого момента времени:
5=−5sinωt
Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:
t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)
Ответ: 7,85
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18116
Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?
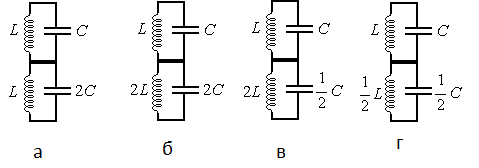
Алгоритм решения
- Выделить цель эксперимента.
- Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
- Выбрать верную пару контуров
Решение
Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18656
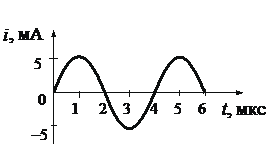 На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.
На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.
Алгоритм решения
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.5k
