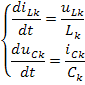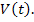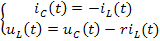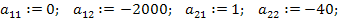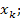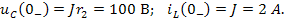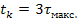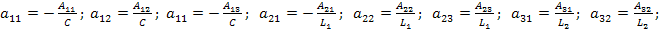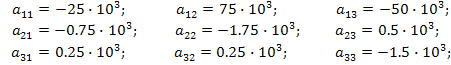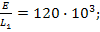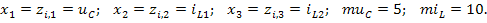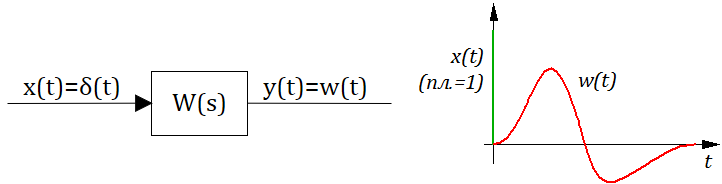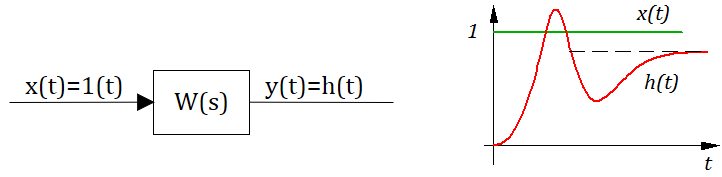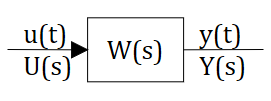Метод переменных состояния
Уравнениями состояния можно назвать любую систему уравнений, определяющих режим цепи. В более узком смысле — это система дифференциальных уравнений первого порядка, разрешенная относительно производных.
Методом переменных состояния назовем анализ цепи, основанный на решении уравнений состояния (первого порядка), записанных в форме Коши. Таким образом, метод переменных состояния — один из методов расчета прежде всего переходных процессов. Далее предполагается, что цепь имеет только независимые источники и не содержит индуктивных сечений и емкостных контуров. В противном случае составление уравнений становится намного сложнее.
Для линейной цепи с постоянными сосредоточенными параметрами ток каждой ветви, напряжение между выбранными выводами, заряд на обкладках конденсатора и т. д. всегда можно найти как решение составленного для этого тока, напряжения, заряда и т. д. дифференциального уравнения (например, исключением других токов и напряжений из системы уравнений Кирхгофа):
Введением переменных это уравнение сводится к эквивалентной системе дифференциальных уравнений первого порядка:
Здесь переменными, которые называются переменными состояния, служат переменная х и ее производные.
Как известно, переходный процесс в любой цепи, кроме ее параметров (значений r, L, С, М) и действующих источников [e(t) и J(t)], определяется независимыми начальными (t = 0) условиями — токами в индуктивных элементах и напряжениями на емкостных элементах
, которые должны быть известны или рассчитаны. Через них выражаются искомые величины во время переходного процесса. Они же определяют энергетическое состояние цепи. Поэтому в качестве переменных состояния целесообразно выбирать токи
и напряжения
. Действующие источники можно назвать входными величинами
, искомые величины — выходными
. Для цепи с n независимыми токами
и напряжениями
должны быть заданы еще n независимых начальных условий.
Сокращенно дифференциальные уравнения состояния запишем в матричной форме так:
или короче
где X матрица-столбец (размера n x 1) переменных состояния (вектор переменных состояния); F — матрица-столбец (размера m x 1) ЭДС и токов источников (внешних возмущений); А — квадратная матрица порядка n (основная); В — матрица размера п х m (матрица связи). Элементы этих матриц определяются топологией и параметрами цепи.
Для выходных величин (если определяются не токи в индуктивных и напряжения на емкостных элементах) в матричной форме система алгебраических уравнений имеет вид
или короче
где W — матрица-столбец (размера l x 1); M — матрица связи (размера l x n); N — матрица связи (размера l x m).
Элементы матриц зависят от топологии и параметров цепи. Для уравнений состояния разработаны и машинные алгоритмы формирования на основе топологии и значений параметров.
Уравнения в матричной форме (14.91) можно составить, например, с применением метода наложения. Для получения зависимостей между производными переменных состояния, т. е. и переменными состояния
, а также ЭДС и токами источников, действующими в цепи, будем считать, что переменные состояния заданы. Рассматриваемую цепь, например на рис. 14.41, а, заменим после коммутации эквивалентной (рис. 14.41,6), у которой каждый заданный ток
представлен источником тока
, а каждое заданное напряжение
— источником напряжения (ЭДС)
. Применив метод наложения (положительные направления выбраны), запишем напряжения
и токи
(сначала учитываем действие источников
затем
и далее источников, действующих в цепи):
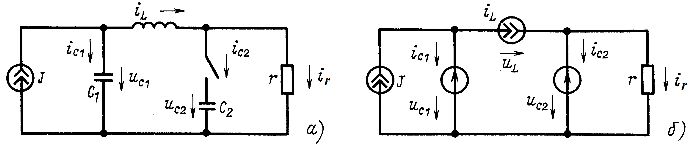
Рис. 14.41
Так как , то
т. e.
Конечно, уравнения (14.93) можно получить и из уравнений Кирхгофа исключением токов и напряжений ре-зистивных элементов. Однако совместное решение уравнений Кирхгофа с увеличением числа ветвей цепи становится все более громоздким.
Уравнения состояния можно формировать и сразу в матричной форме.
Если источников тока и ЭДС нет, т. е. F = 0, то уравнения (14.91) упрощаются
и характеризуют свободные процессы в цепи. Решение запишем в виде
где X (0) — матрица-столбец начальных значений переменных состояния; — матричная экспоненциальная функция.
Подставив (14.94) в (14.91в), убедимся, что получается тождество.
При решение уравнения (14.91) представим в виде
где Ф(t) — некоторая матричная функция цепи. После дифференцирования (14.95) получим
Сравним (14.96) с (14.91а)
и, умножив на , после интегрирования найдем, что
где θ — переменная интегрирования, или
Подставим это выражение в (14.95):
В частности, при t = 0 имеем
Следовательно, решение для переменных состояния записывается в виде
(реакция цепи равна сумме реакций при нулевом входе и при нулевом начальном состоянии).
Это решение можно получить и применив операторный метод расчета переходных процессов, рассматриваемый в разделе.
Выходные величины можно найти по (14.92).
Если состояние цепи задано не при t = 0, а при , то в (14.97) первое слагаемое записывается так:
, а нижний предел интеграла не 0, а τ.
Главная трудность расчета заключается в вычислении матричной экспоненциальной функции. Один из путей такой: сначала находим собственные значения λ матрицы А, т. е. корни уравнения
где 1 — единичная матрица порядка n, которые определяются из уравнения
где — элементы матрицы А.
Собственные значения совпадают с корнями характеристического уравнения цепи.
Матричная экспонента, аргумент которой — матрица Аt, имеющая порядок n, представима конечным числом n слагаемых. Если собственные значения различны, то
где — функции времени;
и т. д.
Далее для определения составляем алгебраическую систему n уравнений
Наконец, определив из (14.100), по (14.99) находим
и затем X (t) по (14.97).
Пример 14.6. Определить ток в цепи на рис. 14.42 после коммутации при
.
Решение. Выбираем положительные направления токов в индуктивных элементах, т. е. переменных состояния, и тока
. Независимые начальные условия:
. Дифференциальные уравнения цепи
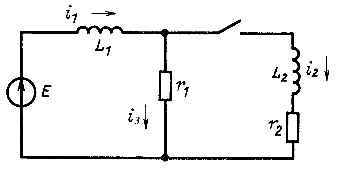
Рис. 14.42
Исключив ток , получим уравнения относительно производных переменных состояния:
т. е. согласно (14.91)
и матрица-столбец начальных значений
Вычислим собственные значения; по (14.98)
откуда . Если приравнять нулю главный определитель уравнений с переменными состояния, то получим те же значения
.
Находим коэффициенты ак по (14.100), т. е. из системы уравнений
откуда
и по (14.99)
Ток
Значения тока вычисленные в моменты
секунд для интервала времени 0 — 0,1 с, в конце которого ток отличается от установившегося
менее чем на 1,5%, приведены в табл. 14.1. При вычислениях цифры записывались с 8 разрядами, а во всех приведенных в примере формулах и в табл. 14.1 указаны с округлением.
| Таблица 14.1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0,005 | 0,01 | 0,015 | 0,02 | 0,025 | 0,03 | 0,035 | 0,04 | 0,045 | 0,05 | |
| 1,079 | 1,213 | 1,343 | 1,455 | 1,55 | 1,628 | 1,692 | 1,746 | 1,79 | 1,827 | |
| k | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 0,055 | 0,06 | 0,065 | 0,07 | 0,075 | 0,08 | 0,085 | 0,09 | 0,095 | 0,1 | |
| 1,857 | 1,882 | 1,902 | 1,919 | 1,933 | 1,945 | 1,954 | 1,962 | 1,97 | 1,974 |
Если среди n собственных значений матрицы А есть q кратных , то для n — q разных корней составляется система (14.100), а для q кратных уравнения получаются после вычисления первых q — 1 производных по
от обеих частей уравнения с корнем
, т. е.
Если в цепи действует только один источник ЭДС (или тока), представляющий единичный скачок 1(t), т. е. F(t)=1(t), и начальные условия нулевые, то решение (14.97) запишется в виде
Для выходных величин по (14.92а) получим
Это будут переходные функции цепи h(t). Импульсные переходные функции k(t) определяются по (14.84) или (14.85).
Более общим путем вычисления матричной экспоненциальной функции служит ее представление бесконечным рядом
но ряд при больших t медленно сходится. При ограничении конечным числом слагаемых вычисление сводится к умножению и суммированию матриц. Такие операции есть в математическом обеспечении ЭВМ. Известен метод вычисления матричной экспоненциальной функции, основанный на критерии Сильверста.
Уравнения состояния цепей, порядок которых больше двух-трех, проще решаются не аналитическими, а численными методами, дающими возможность автоматизировать расчет в случае применения ЭВМ.
Все страницы раздела на websor
Расчет
переходных процессов в линейных
электрических цепях
методом переменных состояния
Это наиболее
универсальный метод расчета цепей как
них, так и нелинейных. Метод используется
для расчета цепей высокого порядка,
когда применение других методов расчета
нецелесообразно
или практически невозможно. Метод
переменных состояния основан на
решении уравнений состояния (первого
порядка) записанных
в форме Коши. Для решения системы
уравнений первого порядка разработаны
численные методы, позволяющие
автоматизировать расчет переходных
процессов с ЭВМ. Таким образом, метод
переменных состояния – один из расчета
переходных процессов, ориентированный
прежде всего на применение
ЭВМ.
Для линейной цепи
с постоянными сосредоточенными
параметрами ток
каждой ветви, напряжение между выводами,
заряд на обкладках,
конденсатора и т. д. можно найти как
решение дифференциального уравнения,
составленного для этого тока, напряжения,
заряда и т.д., исключением других токов
и напряжений из системы уравнений
Кирхгофа:
(1.1)
Введением переменных
.
уравнение (1.1)
сводится к эквивалентной системе
дифференциальных уравнений первого
порядка:

Здесь
переменными,
которые называются переменными состояния,
служит переменная X
и ее производные. При этом предполагается,
что цепь имеет только независимые
источники и не содержит
индуктивных сечений и емкостных контуров.
В противном случае составление уравнений
становится намного сложнее
1. Формирование
уравнений переменных состояния
Энергетическое
состояние цепи, а следовательно, и
переходный
процесс в любой цепи определяется
энергией магнитного поля, запасенной
в индуктивностях, и энергией электрического
поля, запасенной
в емкостях. Запасы энергии в реактивных
элементах определяют
токи в индуктивностях и напряжения
емкостей, т.е. они определяют энергетическое
состояние цепи и поэтому принимаются
в качестве независимых переменных
состояния.
Любая
система уравнений, определяющая состояние
цепи, называется уравнениями
состояния. Токи в индуктивных элементах
и напряжения на емкостных элементах
представляют независимые начальные
условия
цепи и должны быть известны или рассчитаны.
Через них выражаются искомые величины
во время переходного
процесса.
Действующие
источники энергии принято называть
входными величинами
,
а
искомые величины (токи и напряжения)
– выходными величинами
.
Для
цепи с n
независимыми токами
и напряжениями
должны быть заданы еще n
независимых начальных условий. Для
операций
с большим числом переменных используют
методы матричного
исчисления.
Сокращенно
дифференциальные уравнения состояния,
описывающие цепь по законам Кирхгофа,
записываются в матричной форме:
, (1.3)
где
X
– вектор-столбец (размером n
х 1) произвольных переменных
состояния; V
– вектор-столбец (размером m
х 1) внешних воздействий
(ЭДС и токов источников); А – квадратная
матрица порядка
n
(основная); В – матрица связи между входами
цепи и переменными
состояния (размера n
х m).
Элементы этих матриц определяются
топологией и параметрами цепи
,
m
– число входов,
n
– число переменных состояния.
Для
выходных величин (если определяются не
токи в индуктивностях и напряжения на
емкостных элементах) необходимо добавить
еще уравнение в матричной форме:
(1.4)
где
Y
– вектор – столбец искомых токов и
напряжений на выходе (размерен
1 х 1), 1 – число выходов; С – матрица связи
переменных
состояния с выходами цепи (п х 1); D
– матрица непосредственной
связи входов и выходов цепи (размером
1 х m).
Элементы
матриц зависят от топологии и значений
параметров цепи.
Систему матричных
уравнений
;
(1.5)
можно
представить в виде структурной схемы
(рис.1.3).
Рис.1
1.1.
Составление уравнений состояния цепи
методом наложения
Пусть дана схема
цепи после коммутации
Рис.2
Будем
считать, что переменные состояния
заданы. Рассматриваемую
цепь (рис.2) заменим после коммутации
эквивалентной (рис.3), у которой заданный
ток
представлен источником тока
,
заданное
напряжение
источником напряжения
.
Рис.3
Применив
метод наложения (положительные направления
выбраны
), запишем напряжения
и токи
(сначала учитываем действие
источника
затем
и далее источников, действующих
в цепи ).
От
действия
:
;
;
от
действия
:
;
;
от действия е :
;
,
а полный ток
и напряжение
.
Тогда

Учитывая, что
и
получим
т.е в матричном
виде уравнение (1.7) запишемся
(1.8)
где
1.2. Составление
уравнений состояния цепи с помощью
законов Кирхгофа
Уравнения
(1.7) можно получить и из уравнений Кирхгофа
исключением
токов и напряжений резистивных элементов.
По законам Кирхгофа
уравнения для цепи (см.рис. 2) запишем в
виде

Разрешим
первое уравнение системы относительно
,
а третье,
учитывая, что
,
относительно
.
Тогда

Переменные
и
являются переменными состояния для
рассматриваемой
цепи. В правой части системы (1.10)
присутствует переменная
,
не
являющаяся независимой переменной
состояния. Для
ее исключения перепишем второе уравнение
системы (1.9) в виде
(1.11)
и подставим сюда
.
Полученное
из (1.11) значение тока
(1.12)
подставим в систему
(1.10).
Получим
систему уравнений в переменных состояния
для
исследуемой цепи

где
X,
X,
V,
А, В соответствуют системе уравнений
(1.7).
Пусть
в рассматриваемом примере требуется
определить токи
и
.
Следовательно
и
будут выходными величинами цепи и
их необходимо представить в виде
,
.
Ток
уже определен в требуемом виде (1.12), а
ток
.
Тогда
вторая система уравнений в переменных
состояния
примет
вид

В матричной форме
система уравнений (1.14) запишется в виде
(1.15)
где
В
частном случае, если выходными переменными
является переменные
состояния
то матрица С принимает вид диагональной
матрицы, а элементы матрицы D
равны нулю.
Уравнения состояния
решаются на компьютерах численными
методами.
8
Соседние файлы в папке ТЭЦ – ФРЭ Part II
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
№74 Расчет переходных процессов методом переменных состояния.
Уравнениями состояния электрической цепи называют любую систему дифференциальных уравнений, которая описывает состояние (режим) данной цепи. Например, система уравнений Кирхгофа является уравнениями состояния цепи, для которой она составлена.
В более узком смысле в математике уравнениями состояния называют систему дифференциальных уравнений 1-го порядка, разрешенных относительно производных (форма Коши). Система уравнений состояния в обобщенной форме имеет вид:
Та же система уравнений в матричной форме:
или в обобщённой матричной форме:
Система уравнений состояния формы Коши решается методом численного интегрирования (метод Эйлера или метод Рунге-Кутта) на ЭВМ по стандартной программе, которая должна быть в пакете стандартных программ. При отсутствии такой программы в пакете она легко может быть составлена по следующему алгоритму (метод Эйлера) для к-го шага:
Значения производных на к-ом шаге:
Значения переменных на к-ом шаге:
Для определения значений переменных и их производных на 1-м шаге ин¬тегрирова¬ния используются их значения на момент t=0, т.е. их начальные условия x1(0), x2(0). xn(0).
Уравнения состояния формы Коши для заданной схемы могут быть получены из системы уравнений Кирхгофа путем их преобразования. Для этой цели: а) из системы уравнений Кирхгофа методом подстановки исключаются ”лишние” переменные, имеющие зависимые начальные условия, и оставляют переменные iL(t) и uC(t), которые не изменяются скачком и имеют независи-мые начальные условия iL(0) и uC(0); б) оставшиеся уравнения решаются относительно производных и приводятся их к форме Коши.
В случае сложных схем уравнения состояния формы Коши могут быть составлены топологическими методами с использованием матриц соединений [A] и [B].
Последовательность расчета переходного процесса методом переменных состояния выглядит так:
1. Производится расчет схемы в установившемся режиме до коммутации и определяются независимые начальные условия iL(0) и uC(0).
2. Составляется система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации.
3. Методом исключения ”лишних” переменных система уравнений Кирхгофа преобразуется в систему уравнений Коши, составляются матрицы коэффициентов.
4. Выбирается расчетное время (продолжительность переходного процесса) и число шагов интегрирования N.
5. Решение задачи выполняется на ЭВМ по стандартной программе. Выходную функцию получают в виде графической диаграммы x=f(t)или в виде таблицы координат функций для заданных моментов времени.
Пример. Для схемы рис. 74.1 с заданными параметрами элементов (e(t)=Emsin(ωt+ψE), R, R1, R2, R3, L1, L2, C) выполнить расчет переходного процесса и определить функцию uab(t).
1. Выполняется расчет схемы в установившемся режиме переменного тока до коммутации и определяются начальные условия i1(0), i2(0), uC(0).
2. Составляется система дифференциальных уравнений по законам Кирхгофа:
3. Система уравнений Кирхгофа преобразуется в систему уравнений Коши.
Для этой цели из (1) выражаем
и делаем подстановку в (1) и (2), а из (4) делаем подстановку в (1). Тогда получим:
Подсчитаем значения отднльных коэфициэнтов:
Составляем матрицы коэффициентов:
В качества исследуемого промежутка времени выбираем период переменного тока
Число шагов интегрирования принимаем N = 1000,
Вводим исходные данные в ЭВМ и выполняем рассчет.
В качестве выходной функции принимаем:
Для выходной функции Uab(T) строим графическую диаграмму в интервале периода Т.
Как составить уравнения переменных состояния
Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости 

При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как 
Пусть в момент времени 



В момент времени t составляющая общего тока, определяемая начальным скачком напряжения 

В момент времени 


Полный ток 


Заменяя конечный интервал приращения времени 
 . . |
(1) |
Соотношение (1) называется интегралом Дюамеля.
Следует отметить, что с использованием интеграла Дюамеля можно определять также напряжение. При этом в (1) вместо переходной проводимости 
Последовательность расчета с использованием
интеграла Дюамеля
- Определение функции
(или
) для исследуемой цепи.
- Запись выражения
(или
) путем формальной замены t на
.
- Определение производной
.
- Подстановка найденных функций в (1) и интегрирование определенного интеграла.
В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.
Исходные данные для расчета: 



 .
. .
.

Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.
Метод переменных состояния
Уравнения элекромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.
Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники.
Количество переменных состояния, а следовательно, число уравнений состояния равно числу независимых накопителей энергии.
К уравнениям состояния выдвигаются два основных требования:
-возможность восстановления на основе переменных состояния (переменных, относительно которых записаны уравнения состояния) любых других переменных.
Первое требование удовлетворяется специальной методикой составления уравнений состояния, которая будет рассмотрена далее.
Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах. Действительно, зная закон изменения этих переменных во времени их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная цепь оказывается резистивной, а следовательно, всегда рассчитывается при известных параметрах источников. Кроме того, начальные значения этих переменных относятся к независимым, т.е. в общем случае рассчитываются проще других.
При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные 



Таким образом, полная система уравнений в матричной форме записи имеет вид
 ; ; |
(2) |
 . . |
(3) |
Здесь 







Начальные условия для уравнения (2) задаются вектором начальных значений 
В качестве примера составления уравнений состояния рассмотрим цепь на рис. 4,а, в которой требуется определить токи 

По законам Кирхгофа для данной цепи запишем
 ; ; |
(4) |
 ; ; |
(5) |
 . . |
(6) |
Поскольку 
или в матричной форме записи
Матричное уравнение вида (3) вытекает из соотношений (4) и (6):
Вектор начальных значений 

Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используют специальную методику упорядоченного составления уравнений состояния.
Методика составления уравнений состояния
Эта методика включает в себя следующие основные этапы:
1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники напряжения (ЭДС). Резисторы включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви связи включаются катушки индуктивности, источники тока и оставшиеся резисторы.
2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).
3. Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы (см. табл. 1) перечисляются емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные и индуктивные элементы ветвей связи, а также источники тока.
Метод переменных состояния
Факультет автоматики и электромеханики
Кафедра теоретической и общей электротехники
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
(Метод переменных состояния)
Методические указания к выполнению курсовой работы
Составил Башев А.А.
Ред. проф. Алтунин Б.Ю.
Н.Новгород, 2010
Метод переменных состояния.
В основу метода переменных состояния положена принципиальная возможность замены дифференциального уравнения n-го порядка электрической цепи n дифференциальными уравнениями первого порядка. В качестве переменных состояния принимают токи индуктивностей 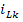
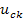
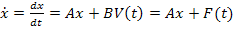
где: 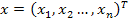
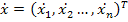
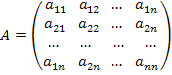
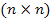
V(t) – столбцовая матрица (вектор) m независимых воздействий;
B – матрица размером 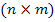
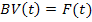
Формирование системы дифференциальных уравнений цепи основано на использовании дифференциальных уравнений для переменных состояния, согласно которым
Расчёт цепей методом переменных состояний можно разделить на два этапа:
1) На первом этапе составляют систему дифференциальных уравнений цепи;
2) На втором этапе решают составленную систему дифференциальных уравнений;
Решение системы дифференциальных уравнений, составленных методом переменных состояния, можно выполнить двумя способами: аналитическим и численным.
При аналитическом способе решение уравнений состояния записывают в виде суммы матриц принуждённой 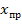
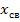
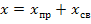
где: 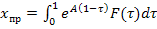
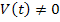

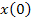
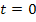
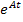
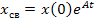
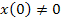
Если в цепи после коммутации нет источников энергии, т.е. 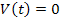
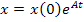
Если же после коммутации есть источники независимых воздействий, то матрица 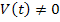
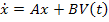
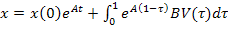
которое состоит из суммы двух слагаемых – реакции цепи при ненулевых начальных условиях и реакции цепи при нулевых начальных условиях и наличии источников внешних воздействий
При численном способе решения уравнений состояния используют различные программы численного интегрирования на ЭВМ: метод Рунге-Кутта, метод Эйлера, метод трапеций и др. Так, например, в пакете программ MathCAD приведены программы численного решения дифференциальных уравнений модифицированном методом Эйлера и методом Рунге-Кутта. Поскольку погрешность решения методом Эйлера достигает нескольких процентов, то более предпочтительным является метод Рунге-Кутта, который при решении уравнений четвёртого порядка даёт погрешность 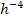
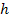
В системе MatchCAD программа интегрирования уравнений по методу Рунге-Кутта имеет имя rkfixed. Обращение к ней производится через операцию присваивания какой-либо переменной (в дальнейшем z) имени программы:
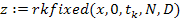
где: x – вектор переменных состояния, размер которого определяется вектором начальных значений 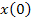
0 и 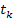
N – число точек на интервале интегрирования;
D – функция, которая описывает правую часть уравнений, разрешённых относительно первых производных.
Для линейных цепей функция D имеет вид линейного матричного преобразования 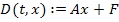
Матрица z имеет размер 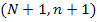
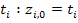
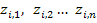
Для контоля правильности задания исходных данных можно (но не обязательно) обратиться к программе определения собственных чисел матрицы A: eigenvals (A). Эта программа выводит информацию о собственных числах, которые совпадают с корнями характеристического уравнения цепи. Необходимым, но недостаточным условием правильности ввода данных, является набор отрицательных собственных чисел (или комплексно-сопряжённых чисел с отрицательно вещественной частью).
Рассмотрим теперь некоторые способы составления дифференциальных уравнений цепи по методу переменных состояния. Для этих целей наиболее часто применяют два основных способа:
1) использование законов Кирхгофа;
2) использование метода наложения.
Рассмотрим применение этих способов на некоторых примерах.
Пример 1. Требуется составить уравнения состояния и решить их для одноконтурной цепи второго порядка при отключении источника напряжения Е. Схема цепи приведена на рисунке 1(а), а параметры её элементов имеют следующие значения: Е=40 В; r=40 Ом; L=1 Гн; С=500мкФ.
Решение. Посмотрим схему замещения цепи для произвольного момента времени t, которая приведена на рисунке 1(б). На этой схеме ёмкость С заменена источником постоянного напряжения 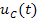
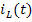
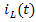
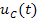
Рисунок 1. Исходная (а) и расчётная (б) схемы цепи к примеру 1.
Для полученной схемы можно составить уравнения, пользуясь законами Кирхгофа:
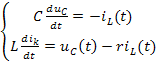
Из этих уравнений получаем значение первых производных переменных состояния:
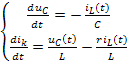
Пользуясь которыми, запишем матричное уравнение цепи:
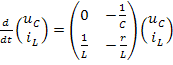
При использовании программы rkfixedэто уравнение записывают в виде:
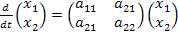
где 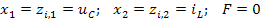
Это матричное уравнение необходимо ещё дополнить матрицей начальных состояний цепи, которая включает напряжение на ёмкости и ток в индуктивности на момент коммутации (т.е. при t=0_):
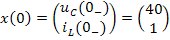
используемой для начала процесса интегрирования дифференциальных уравнений цепи.
Перед обращением к программе интегрирования rkfixed определяем через операцию присваивания значения следующих величин:
1) коэффициентов матрицы А:
2) значений вектора начальных состояний переменных
3) число точек интегрирования 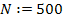
4) формализованную матричную запись уравнений состояния 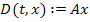
5) конечное значение временного интервала 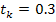
Необходимый временной интервал интегрирования 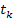
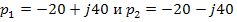
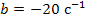
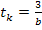
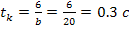
Форма записи исходных данных для программы rkfixed и результаты расчёта приведены на рисунке 2. Поскольку переменные состояния 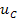
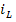
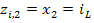
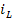
Из полученных графиков следует, что переходный процесс в цепи носит колебательных характер, а обе функции постепенно затухают до нулевого значения при увеличении времени t.
Рисунок 2. Результаты расчёта к примеру 1.
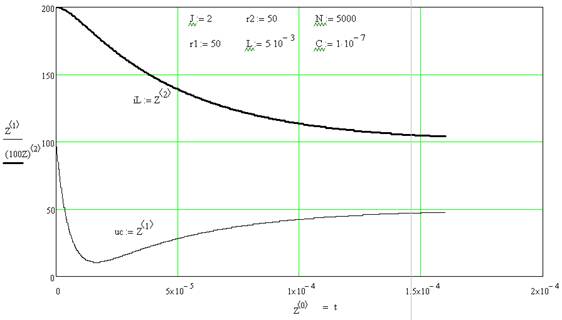
Пример 2. Составить уравнения для переменных состояния и рассчитать их при замыкании ключа К в цепи второго порядка, изображённой на рисунке 3(а). Параметры элементов цепи имеют следующие значения: А; r1=r2=50 Ом; L=5 мГн; С=0,1 мкФ.
Решение. Переходный процесс в рассматриваемой цепи возникает в результате перераспределения энергии между индуктивностью L и ёмкостью C после подключения сопротивления r1. Используя первый закон Кирхгофа, определим ток в ёмкости С:
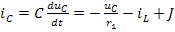
Рисунок 3. Исходная (а) и расчётная (б) схемы к примеру 2.
Аналогично, используя второй закон Кирхгофа, найдём напряжение на индуктивности:
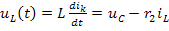
Объединим эти уравнения в систему для переменных состояния:
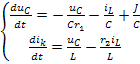
Полученную систему уравнений запишем в матричной форме:
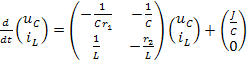
После подстановки числовых значений параметров элементов получим уравнения состояния в виде:
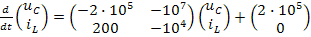
Для определения вектора начальных значений найдём напряжение на ёмкости и ток в индуктивности до замыкания ключа К:
Таким образом, вектор начальных значений переменных состояния имеет вид:
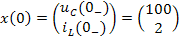
Схемы замещения для расчёта значений переменных состояния приведена на рисунке 3(б). На этой схеме ёмкость заменена источником напряжения 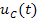
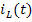
Решение уравнений состояния выполним по программе rkfixed, входящей в систему MathCAD. Для этого присвоим переменным состояния следующие значения: 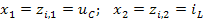
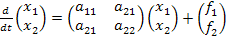
где значения коэффициентов можно взять из уравнений состояния, рассчитанных выше, и включить в программу констант или определить через операции присваивания в самой программе.
Форма задания исходных данных для расчёта по программе rkfixed приведена на рисунке 4. Значение N=5000 указано произвольно, так как оно влияет только на время выполнения расчёта и точность. Косвенно оценить точность расчёта можно, сравнив результаты интегрирования для двух значений N=N1 и N1/2. Если результаты расчета в этих точках совпадают, то точность вычислений и число точек интегрирования на интервале tk находится в приемлемых пределах.
Через операцию присваивания определяем также вектор начальных значений х и вектор независимых источников F. Временной интервал tk может быть указан произвольно или приближённо выбран с помощью анализа чисел матрицы А.
Для апериодического процесса, который существует в рассматриваемой цепи, следует выбрать наименьшее по модулю собственное число pmin и воспользоваться формулой tk =3/pmin. Из двух собственных чисел p1=-1.888E5 1/c; p2=-2.118E4 1/c меньшее значение имеет p2, поэтому tk =3/2,118Е4=1,42Е-4 с.
Выбор интервала tk можно также выполнить, анализируя постоянные времени цепей первого порядка, которые можно построить на основе исходной цепи путём последовательного исключения реактивных элементов. При этом из найденных постоянных времени следует выбрать ту, которая имеет максимальное значение, и, используя её, рассчитать
Графики временных зависимостей 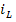
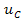
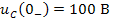
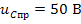

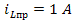
Рисунок 4. Результаты расчёта к примеру 2.
Пример 3. Составить уравнения для переменных состояния и выполнить расчёт переходного процесса в цепи третьего порядка, приведённой на рисунке 5(а) при замыкании ключа К. Параметры элементов цепи имеют следующие значения: Е=120 В; r1=r3=r4=1 Ом; r2=r5=2 Ом; L1=1 мГн; L2=2 мГн; С=10 мкФ.
Рисунок 5. Исходная (а) и расчётная (б) схемы к примеру 3.
Решение. Переходный процесс в схеме обусловлен перераспределением энергии реактивными элементами цепи после коммутации ключа К. На рисунке 5(б) изображена схема замещения цепи, на которой реактивные элементы заменены источниками напряжения и тока. Положительные направления этих источников согласованы с исходной схемой. При расчёте схемы замещения определению подлежат напряжения на источниках тока 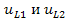
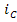
Расчёт схемы, приведённой на рисунке 6(а), позволяет определить искомые величины от действия источника напряжения 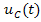
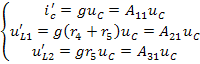
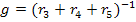
Аналогично выполняется расчёт схемы, изображённой на рисунке 6(б), пользуясь которой, определим те же величины от действия источника тока 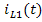
Рисунок 6. Схемы для расчёта цепи от напряжения 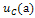
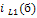

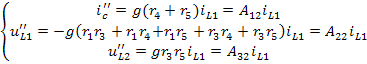
Выполнив расчёт схемы, приведённой на рисунке 6(в), найдём искомые величины при действии 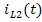
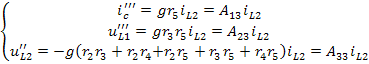
Расчёт схемы, изображённой на рисунке 6(г), позволяет определить искомые величины от действия напряжения Е:
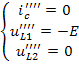
Суммируя частные решения для отдельных источников с учётом выбранных положительных направлений напряжений и токов, находим полные значения искомых величин:
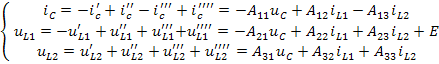
Полученные уравнения позволяют сформулировать нормальную систему дифференциальных уравнений для переменных состояния и записать её в матричной форме:
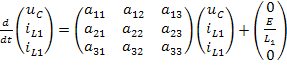
где
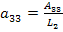
После подстановки значений параметров элементов цепи найдём числовые значения коэффициентов уравнений:
К системе уравнений, записанной в нормальной форме, необходимо добавить вектор, который отражает начальное состояние цепи в момент 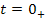
Так как переменные состояния подчиняются законам коммутации, то этот вектор можно получить из анализа состояния цепи до коммутации, т.е. при 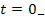
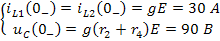
Таким образом, вектор начальных состояний цепи имеет вид:
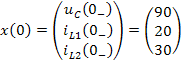
При обращении к программе rkfixed, входящей в систему MathCAD, можно использовать найденные выше значения коэффициентов дифференциальных уравнений или задать их в виде расчётных формул с указанием значений исходных параметров схемы. На рисунке 7 приведён результат расчёта по программе rkfixed. При построении графиков приняты следующие обозначения и масштабные коэффициенты:
Рисунок 7. Результаты к примеру 3.
Кроме этого, при вводе данных указано время интегрирования, которое, как и раньше, выбрано по формуле tk =3/bmin, где bmin – минимальное значение модуля вещественной части собственных чисел матрицы eigenvals (A). Для рассматриваемого примера это число имеет значение b=1.268E3, откуда находим значение tk=2E-3 с.
[spoiler title=”источники:”]
http://toehelp.ru/theory/toe/lecture29/lecture29.html
http://mydocx.ru/1-78244.html
[/spoiler]
Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной
проводимости 
напряжению 
воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла
Дюамеля – лежит принцип наложения.
При использовании интеграла Дюамеля для разделения переменной, по которой производится
интегрирование, и переменной, определяющей момент времени, в который определяется
ток в цепи, первую принято обозначать как , а вторую – как t.

Пусть в момент времени к цепи с нулевыми начальными
условиями (пассивному двухполюснику ПД на рис. 1) подключается источник
с напряжением произвольной формы. Для нахождения
тока в цепи заменим исходную кривую
ступенчатой (см. рис. 2), после чего с учетом, что цепь линейна, просуммируем
токи от начального скачка напряжения и всех ступенек напряжения до
момента t, вступающих в действие с запаздыванием по времени.
В момент времени t составляющая общего тока, определяемая начальным скачком
напряжения , равна
.
В момент времени имеет место скачок напряжения
, который с учетом временного
интервала от начала скачка до интересующего момента времени t обусловит составляющую
тока .
Полный ток в момент времени t равен, очевидно,
сумме всех составляющих тока от отдельных скачков напряжения с учетом , т.е.
.
Заменяя конечный интервал приращения времени на бесконечно малый, т.е. переходя
от суммы к интегралу, запишем
 . . |
(1) |
Соотношение (1) называется интегралом Дюамеля.
Следует отметить, что с использованием интеграла Дюамеля можно определять также
напряжение. При этом в (1) вместо переходной проводимости будет входить переходная функция
по напряжению.
Последовательность расчета с использованием
интеграла Дюамеля
- Определение функции
(или
) для исследуемой цепи.
- Запись выражения
(или
) путем формальной замены t на
.
- Определение производной
.
- Подстановка найденных функций в (1) и интегрирование определенного интеграла.
В качестве примера использования
интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.
Исходные данные для расчета: ,
,
.
- Переходная проводимость
-
.
-
.
-


Полученный результат аналогичен выражению тока, определенному в предыдущей
лекции на основе формулы включения.
Метод переменных состояния
Уравнения элекромагнитного состояния – это система уравнений, определяющих
режим работы (состояние) электрической цепи.
Метод переменных состояния основывается на упорядоченном составлении и решении
системы дифференциальных уравнений первого порядка, которые разрешены относительно
производных, т.е. записаны в виде, наиболее удобном для применения численных
методов интегрирования, реализуемых средствами вычислительной техники.
Количество переменных состояния, а следовательно, число уравнений состояния
равно числу независимых накопителей энергии.
К уравнениям состояния выдвигаются два основных требования:
-независимость уравнений;
-возможность восстановления на основе переменных состояния (переменных, относительно
которых записаны уравнения состояния) любых других переменных.
Первое требование удовлетворяется специальной методикой составления уравнений
состояния, которая будет рассмотрена далее.
Для выполнения второго требования в качестве переменных состояния следует принять
потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения)
на конденсаторах. Действительно, зная закон изменения этих переменных во времени
их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная
цепь оказывается резистивной, а следовательно, всегда рассчитывается при известных
параметрах источников. Кроме того, начальные значения этих переменных относятся
к независимым, т.е. в общем случае рассчитываются проще других.
При расчете методом переменных состояния, кроме самих уравнений состояния,
связывающих первые производные и
с самими переменными
и
и источниками внешних воздействий
– ЭДС и тока, необходимо составить систему алгебраических уравнений, связывающих
искомые величины с переменными состояния и источниками внешних воздействий.
Таким образом, полная система уравнений в матричной форме записи имеет вид
| (2) |
| (3) |
Здесь и
– столбцовые матрицы соответственно
переменных состояния и их первых производных по времени; – матрица-столбец источников
внешних воздействий; – столбцовая матрица выходных
(искомых) величин; – квадратная размерностью
n x n (где n – число переменных
состояния) матрица параметров, называемая матрицей Якоби; – прямоугольная матрица связи
между источниками и переменными состояния (количество строк равно n, а столбцов
– числу источников m); – прямоугольная матрица связи
переменных состояния с искомыми величинами (количество строк равно числу искомых
величин к, а столбцов – n); – прямоугольная размерностью
к x mматрица связи входа с выходом.
Начальные условия для уравнения (2) задаются вектором начальных значений (0).
В качестве примера составления уравнений состояния рассмотрим цепь на рис.
4,а, в которой требуется определить токи и
.

По законам Кирхгофа для данной цепи запишем
| (4) |
| (5) |
| (6) |
Поскольку с учетом соотношения (6) перепишем
уравнения (4) и (5) в виде

или в матричной форме записи
Матричное уравнение вида (3) вытекает из соотношений (4) и (6):
Вектор начальных значений (0)=
.
Непосредственное использование законов Кирхгофа при составлении уравнений состояния
для сложных цепей может оказаться затруднительным. В этой связи используют специальную
методику упорядоченного составления уравнений состояния.
Методика составления уравнений состояния
Эта методика включает в себя следующие основные этапы:
1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется
дерево, охватывающее все конденсаторы и источники напряжения (ЭДС). Резисторы
включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви
связи включаются катушки индуктивности, источники тока и оставшиеся резисторы.
2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая
в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами,
затем резисторами, включенными в дерево, следующими нумеруются ветви связи с
резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).
3. Составляется таблица, описывающая соединение элементов в цепи. В первой
строке таблицы (см. табл. 1) перечисляются емкостные и резистивные элементы
дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные
и индуктивные элементы ветвей связи, а также источники тока.
Таблица 1. Таблица соединений
|
11 |
22 |
u |
|
|
33 |
-1 |
0 |
0 |
|
44 |
1 |
1 |
1 |
|
J |
1 |
0 |
Процедура заполнения таблицы заключается в поочередном мысленном замыкании
ветвей дерева с помощью ветвей связи до получения контура с последующим обходом
последнего согласно ориентации соответствующей ветви связи. Со знаком «+» записываются
ветви графа, ориентация которых совпадает с направлением обхода контура, и со
знаком «-» ветви, имеющие противоположную ориентацию.
Осуществляется расписывание таблицы по столбцам и по строкам. В первом случае
получаются уравнения по первому закону Кирхгофа, во втором – по второму.
В рассматриваемом случае (равенство тривиально)
,
откуда в соответствии с нумерацией токов в исходной цепи

При расписывании таблицы соединений по строкам напряжения на пассивных элементах
необходимо брать со знаками, противоположными табличным:
 |
(7) |
Эти уравнения совпадают соответственно с соотношениями (6) и (5).
Из (7) непосредственно вытекает
.
Таким образом, формализованным способом получены уравнения, аналогичные составленным
выше с использованием законов Кирхгофа.
Литература
- Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. - Матханов П.Н. Основы анализа электрических цепей. Линейные цепи.:
Учеб. для электротехн. радиотехн. спец. вузов. 3-е изд., перераб. и доп. –М.:
Высш. шк., 1990. –400с.
Контрольные вопросы и задачи
- Какой принцип лежит в основе метода расчета переходных процессов с использованием
интеграла Дюамеля, и для каких цепей может быть использован данный метод? - В каких случаях целесообразно использовать метод расчета с использованием
интеграла Дюамеля? - В цепи на рис. 3 при
напряжение на входе цепи мгновенно
спадает до нуля. Определить ток в цепи. - Какие требования и почему выдвигаются к уравнениям состояния?
- Что включает в себя система уравнений при расчете переходного процесса в
цепи методом переменных состояния? - Перечислите основные этапы методики составления уравнений состояния.
- Записать матрицы А и В для цепи на рис. 5, если
,
,
,
,
,
.
Ответ: при
;
при
.
Ответ:
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
В это части будут рассмотрены:
2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.
Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.
2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)
Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1
Рис. 2.9.1 — Звено САР
Предположим, что уравнение динамики имеет вид:
где:
— постоянные времени;
— коэффициент усиления.
Пусть известны отображения:
Найдем изображения для производных:
Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:
B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.
Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.
После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.
Пример
Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:
начальные условия:
входное воздействие:
— единичное ступенчатое воздействие.
Выполним преобразование Лапласа:
Подставим в уравнение динамики и получим уравнение динамики в изображениях:
Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:
Рисунок 2.9.2 График переходного процесса.
2.10. Весовая и переходная функции звена (системы).
Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.
Рисунок 2.10.1 Весовая функция.
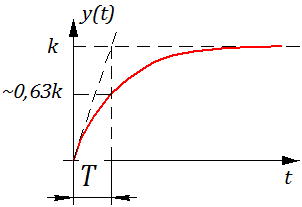
Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.
Рисунок 2.10.2 Переходная функция.
Рисунок 2.10.3 Пример весовой функции.
Рисунок 2.10.4 Пример перходной функции.
На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:
Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.
Рисунок 2.10.5 Весовая функция как передаточная в изображениях.
Рисунок 2.10.6 Ступенчатое воздействие.
Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):
тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:
Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона
Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).
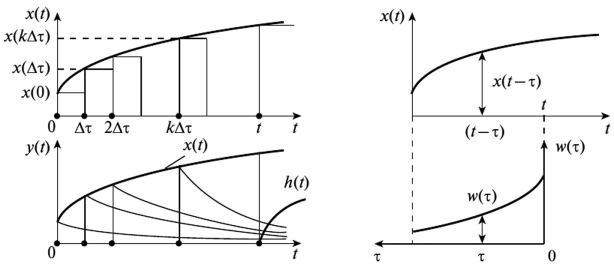
Рисунок 2.11 Демонстрация расчета по формуле Дюамеля-Карсона
Решение.
Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:
где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.
Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:
Переходя к пределам
получаем интеграл:
если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:
где — вспомогательное время
Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:
Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:
2.12. Mетод переменных состояния.
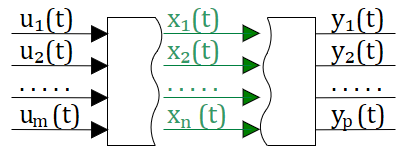
До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)
Рисунок 2.12.1 Моногомерная система автоматического управления.
В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2
Рисунок 2.12.2 Перменные состояния в многомерной системе.
В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:
Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:
где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;
Данная система уравнений может быть записана в матричной форме:
где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;
В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.
Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования
Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.
Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики
Пример решения задачи в форме коши.
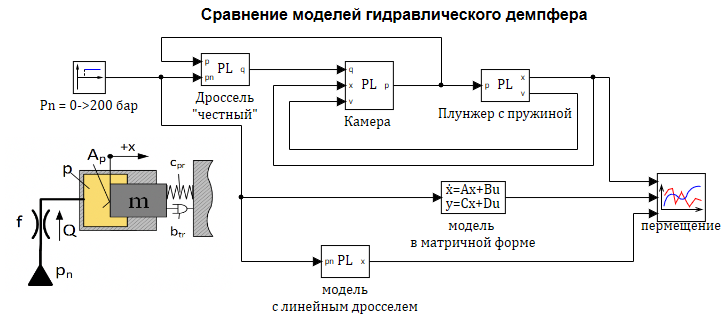
Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:
Дано:
Цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Полость начальным объемом 20 см3 соединяется с источником давлния дросселем диаметром диаметр которого 0,2 мм. Коэффициент расхода дросселя 0.62. Плотность рабочей жидкости ρ = 850 кг/м3.
Определить:
Перемещение дросселя, если в источнике давление происходит скачек 200 бар. см. рис. 2.12.13
Рисунок 2.12.3 Гидравлическая система.
Уравенение движение плунжера:
Где:
– площадь плунжера,
– жесткость пружины,
– коэффициент вязкого трения, p – давление в камере.
Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда
Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:
Где: Q – расход в камеру, V — объем камеры.
Расход через дроссель:
Где: f– площадь дросселя,
– давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:
Подставляем линеаризованную формул расхода в формулу давления:
Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:
Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:
Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.
Рисунок 2.12.4 Расчетная схема .
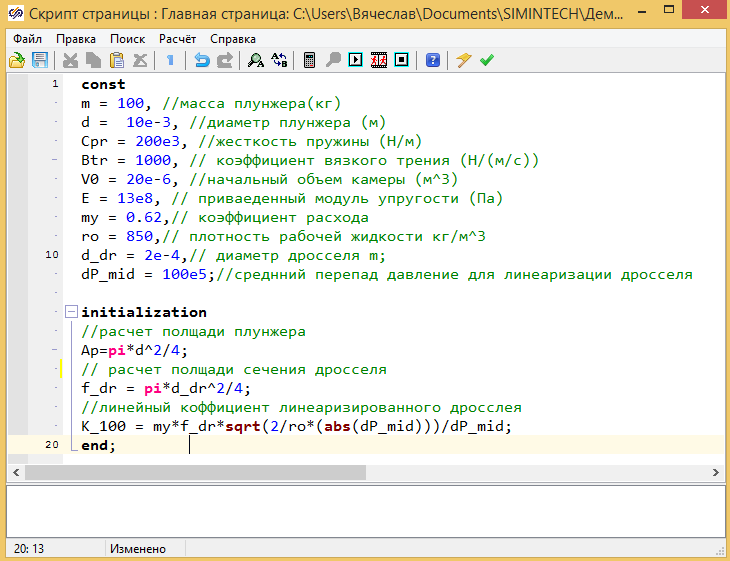
Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:
Рисунок 2.12.5 Глобальный скрипт проекта.
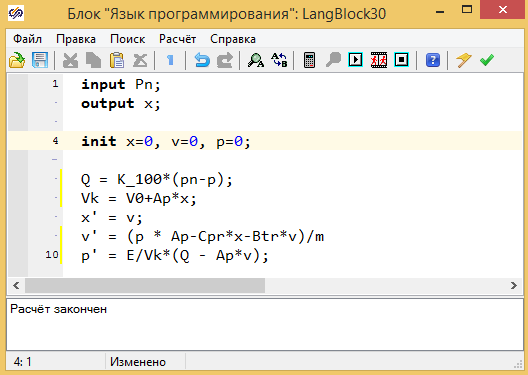
Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)
Рисунок 2.12.6 Скрипт расчета модели в форме Коши.
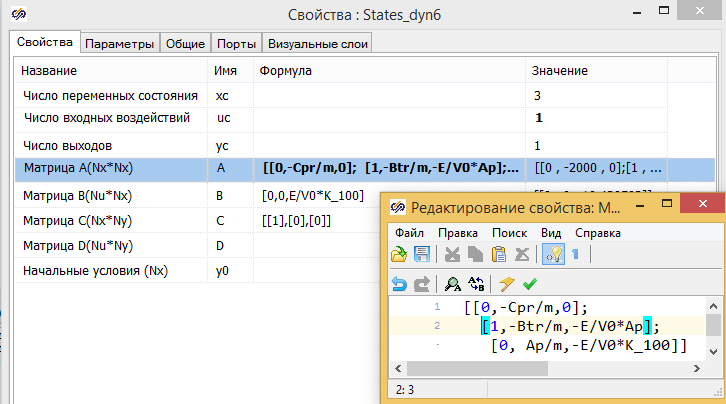
Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7
Рисунок 2.12.7 Настройка блока расчета системы уравнений в пременных состояния в матричной форме.
Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)
Рисунок 2.12.8 Результаты расчета трех моделей гидравлического плунжера.
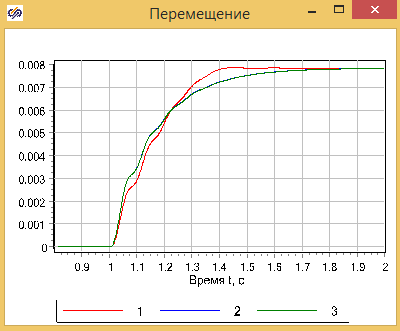
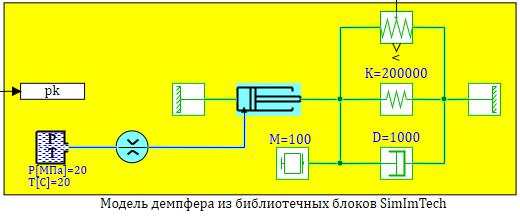
Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10
Рисунок 2.12.9 Модель демпфера из библиотечных блоков.
Рисунок 2.12.10 Результаты рассчета моделей демпфера. График 4 — модель из библиотечных блоков.
На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.
2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно
Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:
Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:
2.13.1. Правая часть содержит только b0*u(t)
В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.
Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:
Для перехода к форме Коши ведем новые переменные:
И перепишем уравнение относительно y”'(t):
Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:
Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:
2.13.2. Правая часть общего вида
Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:
Сделаем преобразования: перейдем к уравнениям динамики в изображениях:
Тогда можно представить уравнение в изображениях в виде:
где:
Разделим уравнение в изображениях на произведение полиномов , получим:
Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что
отображение величины
. Тогда входная величина может быть в изображениях представлена как:
Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.
А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:
Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния :
А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:
Перейдем от изображения к оригиналам:
Если обозначить вектор , то мы получим уравнения переменных состояниях в матричной форме, где D = 0:
Пример:
Рисунок 2.13.1 Передаточная функция.
Имеется передаточная функция (рис. 2.13.1) в изображениях :
Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши
В изображения реакция системы связана с входным воздействие соотношением:
Разделим в последнем правую и левую часть на произведения , и введем новую перменную
:
Полиномы N(s) и L(s) равны:
Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):
Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:
Или в матричной форме:
Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:
Перейдем от изображений к оригиналу:
Таким образом второе уравнение матричной системы выглядит так:
Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2
Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.
Продолжение лекций находится здесь:
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (РЕГУЛИРОВАНИЯ).
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ.
3.2. Типовые звенья систем автоматического управления (регулирования). Классификация типовых звеньев. Простейшие типовые звенья.
3.3. Апериодическое звено 1–го порядка (инерционное звено). На примере входной камеры ядерного реактора.
3.4. Апериодическое звено 2-го порядка.
3.5. Колебательное звено.
3.6. Инерционно-дифференцирующее звено.
3.7. Форсирующее звено.
3.8. Инерционно-интегрирующее (звено интегрирующее звено с замедлением).
3.9 Изодромное звено (изодром).
Полезные ссылки:
Модель демпфера из лекции можно взять здесь…
Волченко Ю.М. Теоремы операционного исчисления.
Интеграл Дюамеля и физический смысл функции веса
Лекция. «Векторно-матричные модели систем управления в непрерывном времени»
Л. С. Шихобалов. Учебное пособие «МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ»
Характеристическое уравнение матрицы
Подробное описание моделирования гидравлического демпфера.
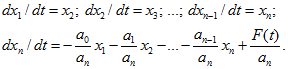
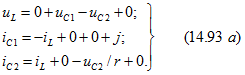
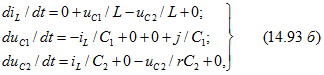
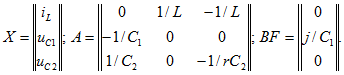
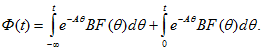

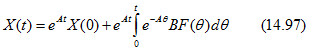
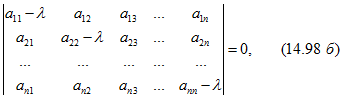
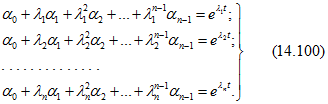
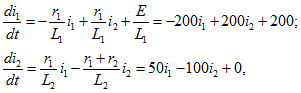
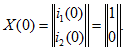
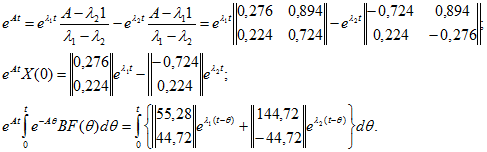
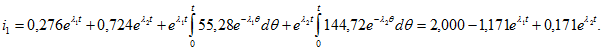
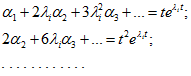
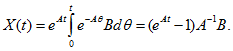






















 (или
(или  ) для исследуемой цепи.
) для исследуемой цепи. (или
(или  ) путем формальной замены t на
) путем формальной замены t на  .
. .
.