Мы уже писали про закон Ома, а также параллельное и последовательное соединение проводников. Но это были цветочки. Сегодня разберемся с задачами посложнее: посмотрим, как решаются задачи на правила Кирхгофа.
Не забывайте подписаться на наш телеграм-канал: там вас ждут актуальные новости сферы образования, полезные лайфхаки и скидки для студентов.
Задачи на правило Кирхгофа с решением
Как решать задачи по правилу Кирхгофа? Прежде, чем приступать к решению задач, обязательно изучите теорию. Также мы подготовили для вас универсальную памятку по решению физических задач.
Задача №1 на эквивалентные преобразования соединений проводников.
Условие
Преобразуйте схему с помощью эквивалентных преобразований.
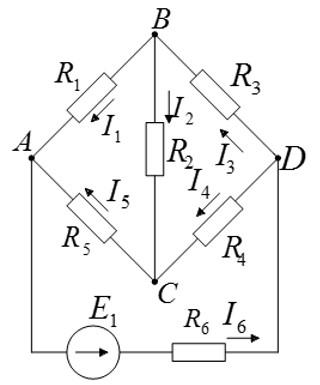
Решение
Кроме основных формул для последовательного и параллельного соединения проводников, существуют формулы для преобразования звезды резисторов в эквивалентный треугольник и наоборот. Треугольник резисторов R2 R3 R4 можно преобразовать в эквивалентную звезду RB RB RD по формулам:
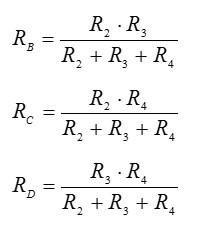
Преобразованная схема будет выглядеть следующим образом:
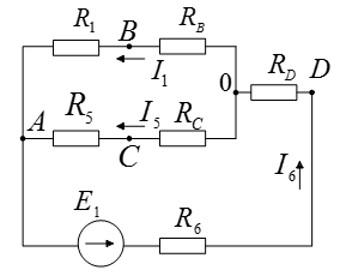
Ответ: см. выше.
Правила Кирхгофа применяются для сложных цепей(например, для цепей с несколькими источниками питания), когда эквивалентные преобразования не приносят результата.
Задача №2 на первое правило (закон) Кирхгофа
Условие
Необходимо составить уравнения по первому закону Кирхгофа для следующей цепи:
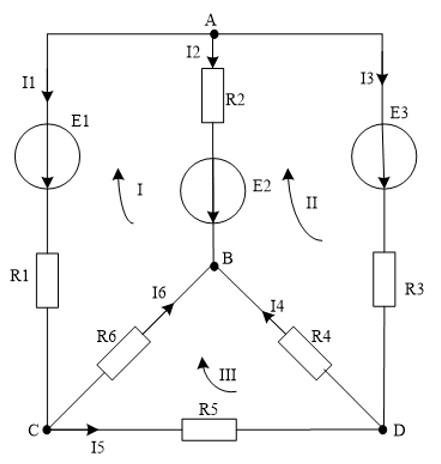
Решение
В данной цепи 4 узла. По первому закону составляем 3 уравнения (на 1 уравнение меньше, чем количества узлов):
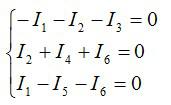
Ответ: см. выше.
Для решения задач на правила Кирхгофа необходимо уметь решать системы линейных уравнений. Для решения сложных систем удобно использовать специальные программы: MathCad, MatLab и т.д.
Далее для наглядности рассмотрим задачу с более простой схемой.
Задача №3 на правила Кирхгофа
Условие
Два источника питания E1=2В и E2=1В соединены по схеме, показанной на рисунке. Сопротивление R=5 Ом. Внутреннее сопротивление источников одинаково и равно r1=r2=1 Ом. Определить силу тока, который проходит через сопротивление.
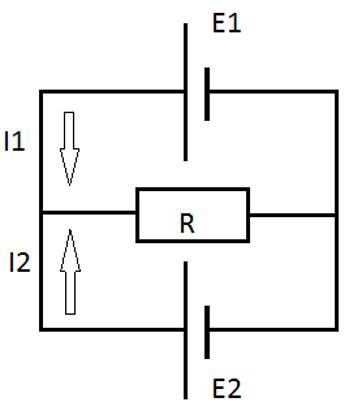
Решение
По первому закону Кирхгофа сумма токов, сходящихся в узле, равна нулю (токи обозначим произвольно):
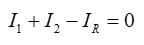
Выберем направление обхода верхнего контура против часовой стрелки. По второму закону Кирхгофа, сумма падений напряжений в контуре равна сумме ЭДС:
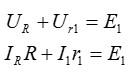
Запишем то же самое для второго контура, обходя его по часовой стрелке:
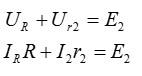
Объединим уравнения с неизвестными токами в систему:
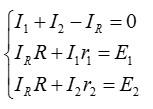
Чтобы решить систему, выразим силу тока I1 из второго уравнения, а силу тока I2 – из третьего:
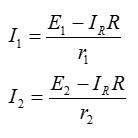
Первое уравнение теперь можно записать в виде:
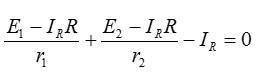
Выражая искомый ток и подставляя значения из условия, получаем:
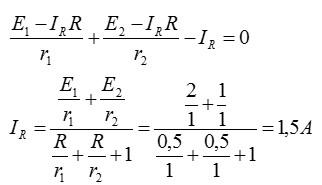
Ответ: 1,5 А.
Задача №4 на правила Кирхгофа
Условие
Дана схема электрической цепи. Необходимо:
- обозначить сопротивления, над каждой ветвью указать свой ток и источники ЭДС;
- указать на схеме направления токов и ЭДС;
- составить уравнения по первому и второму закону Кирхгофа.
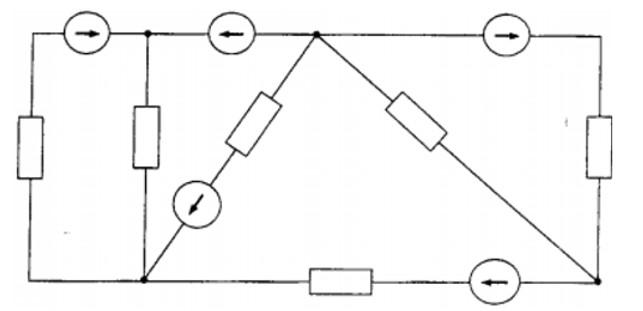
Решение
Приведем схему, обозначив сопротивления, ЭДС и токи:
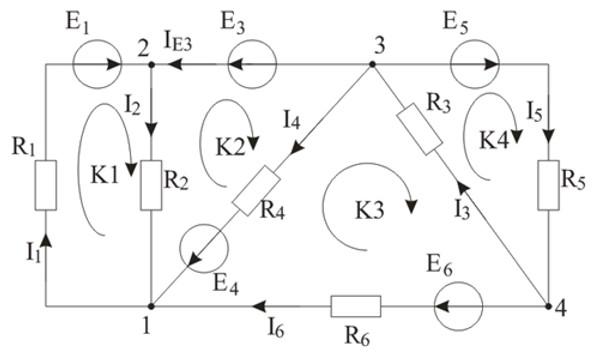
В схеме 7 токов и 4 узла. Необходимо составить 4 – 1 = 3 уравнения по первому закону Кирхгофа и 7 – 3 = 4 уравнения по второму закону Кирхгофа.
Первый закон Кирхгофа:
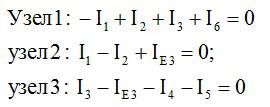
Второй закон Кирхгофа (выбранные контуры К1, К2, К3, К4 указаны на рисунке):
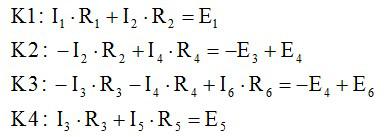
Ответ: см. выше.
Задача №5 на правила Кирхнофа
Условие
Определить все токи в ветвях, составив систему уравнений по законам Кирхгофа.
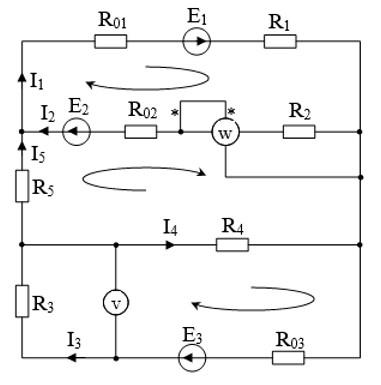
Параметры цепи: E1 = 40 В, E2 = 50 В, E3 = 60 В, R01 = 0,1 Ом, R02 = 0,3 Ом, R03 = 0,2 Ом, R1 = 4,4 Ом, R2 = 4,7 Ом, R3 = 4,6 Ом, R4 = 5,2 Ом, R5 = 7,6 Ом.
Решение
Направления токов в ветвях цепи и направления обхода контуров указаны на схеме. Цепь содержит 3 узла и 3 независимых контура. Таким образом, для расчета токов в ветвях необходимо составить два уравнения по первому закону Кирхгофа и три по второму:
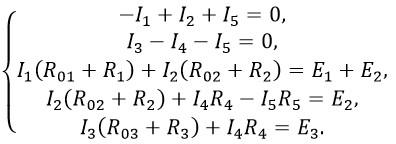
Подставим числовые значения и решим систему уравнений:
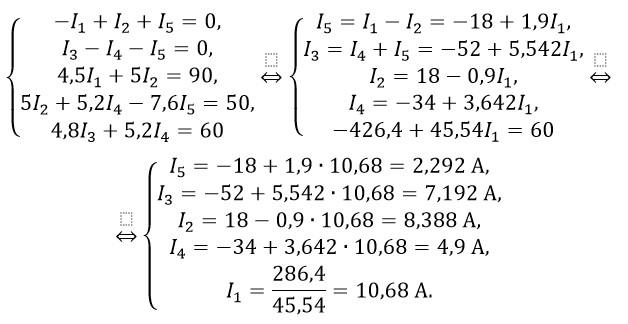
Ответ: I1=10,68 А; I2=8,388 А; I3=7,192 А; I4=4,9 А; I5=2,292 А.
Вопросы на правила Кирхгофа
Вопрос 1. Сформулируйте первый закон Кирхгофа.
Ответ. Первый закон Кирхгофа связан с сохранением заряда и формулируется следующим образом:
Для любого узла электрической цепи алгебраическая сумма токов ветвей, подключенных к данному узлу, равна нулю.
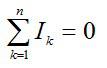
Первое правило Кирхгофа является следствием закона сохранения электрического заряда, согласно которому ни в какой точке заряды не могут безгранично накапливаться: количество электричества, притекающее к данной точке за определенный промежуток времени, должно быть равно количеству электричества, оттекающему от неё.
Вопрос 2. Как следует выбирать направления токов в ветвях электрической цепи?
Ответ. Направления токов во всех ветвях электрической цепи задаются произвольно до составления уравнений. Токи, входящие в узел, принято считать положительными, а выходящие из узла – отрицательными.
Вопрос 3. Как формулируется второй закон Кирхгофа?
Ответ. Второй закон Кирхгофа связан с законом сохранения энергии и формулируется следующим образом:
Алгебраическая сумма всех ЭДС контура электрической цепи равна алгебраической сумме напряжений и алгебраической сумме падений напряжений на всех его участках.
Вопрос 4. Что следует учитывать при составлении уравнений второго закона Кирхгофа для цепи и ее конкретного контура.
Ответ. Перед составлением уравнений второго закона Кирхгофа для цепи необходимо произвольно выбрать направления токов во всех ветвях цепи и определить направление обхода контура.
При составлении уравнения для конкретного контура учитываются:
- токи, входящие в узлы принимаются положительными;
- ЭДС источников принимаются положительными, если
- направления их действия (стрелка) совпадает с выбранным направлением обхода (независимо от направления тока в них);
- падения напряжений в ветвях (IkRk) принимаются положительными, если положительное направление тока совпадает с выбранным направлением обхода;
- напряжения Uk, включенные в контур, принимаются положительными, если эти напряжения создают ток, направленный также как и направление обхода (направление напряжения, определяемое стрелкой, совпадает с направлением обхода).
Вопрос 5. Что такое эквивалентные преобразования последовательного и параллельного соединения пассивных элементов?
Ответ. Задачей эквивалентного преобразования последовательного и параллельного соединения пассивных элементов, является последовательное упрощение исходной схемы и нахождение эквивалентного сопротивления схемы.
Нужна помощь в решении задач и других студенческих заданий? Профессиональный сервис помощи учащимся окажет оперативную помощь с выполнением любой работы.
Для расчета электрической цепи применяют два закона Кирхгофа. (Скорее их можно отнести не к законам, а к правилам. Но в большинстве учебников пишут именно о “законах” Кирхгофа. Поэтому и здесь будем обращаться к законам).
Первый закон Кирхгофа
Первый закон Кирхгофа применяют к узлам электрической цепи и выражают баланс токов в них. Первый закон Кирхгофа гласит:
Алгебраическая сумма токов сходящихся в узле электрической цепи равна 0.
Под словом “алгебраическая” имеется в виду, что учитывается знак перед током: “плюс” или “минус”.
В общем виде первый закон Кирхгофа можно записать как:
Для примера возьмем узел, в котором протекают токи, указанные стрелками (далее рассмотрим это все на конкретных схемах).
Токи, втекающие и вытекающие из узла, берутся с противоположными знаками. Втекающие в узел токи берутся со знаком, например, “+”, а вытекающие с “-“ (можно вытекающие брать с “+”, а втекающие с “-“). Главное, чтобы втекающие и вытекающие токи отличались по знаку.
Будем считать токи положительными, если они втекают в узел, а вытекающие из узла – отрицательными. Тогда первый закон Кирхгофа для узла, представленного на рисунке 2, запишется:
I1-I2+I3+I4=0
Это выражение можно записать и в следующем виде:
I2=I1+I3+I4;
Ток I2 мы перенесли за знак равенства, его знак поменялся на противоположный (был с “минусом”, стал с “плюсом”).
Остальные токи мы не переносим, поэтому их знаки не меняются.
Согласно последнему выражению, первый закон Кирхгофа можно сформулировать по-другому:
Сумма токов, втекающих (подходящих) в узел, равна сумме токов, вытекающих (отходящих) из узла.
Все это говорит о том, что в узле эти токи не остаются и заряд в узле не накапливается.
Для более полного понимания, представим электрическую цепь (схему электрической цепи), для которой запишем первый закон Кирхгофа.
Запишем для этой цепи первый закон Кирхгофа для узла “a” (о том, как определить количество уравнений по первому и второму законам Кирхгофа, рассмотрим в конце ).
I1+I2-I3=0 или I3=I1+I2.
Второй закон Кирхгофа
Этот закон применяется к контурам электрической цепи и выражает баланс напряжений в них. Второй закон Кирхгофа звучит так:
Алгебраическая сумма ЭДС в замкнутом контуре (с учетом направления обхода контура) равна алгебраической (учитывается знак “+” или “-“) сумме падений напряжений на всех сопротивлениях (элементах) этого контура.
Для того, чтобы правильно составить уравнения по второму закону Кирхгофа, нужно пользоваться следующим правилом:
ЭДС берется со знаком “+”, если ее действие совпадает с направлением обхода контура. Напряжение на элементе контура берется со знаком “+”, если направление тока через данный элемент совпадает с направлением обхода контура. Если не совпадает направление обхода контура с направлением тока через элемент, то напряжение этого элемента берется со знаком “-“.
Запишем второй закон Кирхгофа для цепи, представленной ниже:
Выбираем направление обхода контура по часовой стрелке. В данном случае направление тока и направление обхода контура совпадают, поэтому I·R1 и I·R2 взяли со знаком “+”. А также совпадает направление обхода контура и действие ЭДС, поэтому ЭДС также записали со знаком “+”.
Возьмем еще один пример.
Запишем для этой цепи второй закон Кирхгофа. Обход выбираем по часовой стрелке (указали обход контура на схеме круговой стрелкой внутри контура). Как видим, направление обхода контура и направление тока I1 совпадают, а ток I2 направлен напротив обхода контура.
Следовательно, падение напряжения на резисторе R1 запишется со знаком “+”, т. е. +I1·R1. А падение напряжения на R2 запишется со знаком “-“, т. е. –I2·R2.
Направление действия ЭДС совпадает с обходом контура, поэтому ЭДС E берем со знаком “+”.
Запишем второй закон Кирхгофа для этой цепи:
I1·R1-I2·R2=E
Ну и напоследок рассмотрим сложную электрическую цепь, состоящую из нескольких источников и резисторов.
Введем произвольно направление токов в ветвях, а также укажем на схеме в виде круговых стрелок направление обхода контуров.
Токи в ветвях направили произвольно, обход контура выбрали по часовой стрелке, а также узлы в этой схеме обозначили буквами a и b. Для того, чтобы понять, как и сколько уравнений по первому и второму законам Кирхгофа нужно составить для данной цепи, необходимо посчитать количество ветвей, узлов и независимых контуров.
Подробно вышесказанные понятия электрической цепи мы рассмотрим в следующих статьях. А пока вкратце.
Узел – это место соединения трех и более ветвей в электрической цепи (в данном случае таких узлов два. Это узлы “a” и “b”.
Ветвь – это участок электрической цепи, который образуется одним или несколькими последовательно соединенными элементами и через все эти элементы протекает один и тот же ток.
Контур – это любой замкнутый путь электрической цепи, проходящий по двум или нескольким ветвям.
Так же есть такое понятие как независимый контур.
Независимый контур должен включать в себя хотя бы одну ветвь, не входящую в другие контуры.
На рисунке 9 будет три контура, два из которых независимые. Если контур 1 независимый, контур 2 независимый(таким образом все три ветви этой схемы цепи вошли в эти независимые контуры). Тогда контур 3 уже независимым не будет, поскольку все ветви “заняты” остальными двумя контурами.
Или если контур 1 независимый (он включает в себя ветви с элементами E и R1). Контур 3 независимый (он включает в себя ветви с элементом E и ветвь с элементом R3. Элемент R3 ранее не входил в первый независимый контур), поэтому контур 3 считается независимым.
Получается, что все ветви “заняты”. Тогда контур 2 независимым уже не будет, поскольку в него не входят ветви или ветвь ранее не входящую в другие контура. Все ветви вошли в ранее независимые контуры 1 и 3.
В цепи на рисунке 9, в общем случае, три ветви, два узла и два независимых контура. Общее количество уравнений по законам(правилам) Кирхгофа составляется столько, сколько ветвей в схеме цепи за вычетом количества ветвей, где есть источник тока (именно источник тока, а не ЭДС). В нашей схеме нет источников тока, следовательно, составляются три уравнения по законам Кирхгофа. Теперь осталось определить, сколько уравнений нужно составить по первому и второму законам Кирхгофа. Общее количество уравнений будет три. Формула для определения количества уравнений по первому закону Кирхгофа следующая:
N1з.к.=Ny-1, где Ny – количество узлов.
Ny=2, тогда
N1.з.к.=Ny-1=2-1=1
Т. е. по первому закону Кирхгофа составляется одно уравнение для данной цепи, а общее количество уравнений – три. Таким образом, мы получаем, что по второму закону Кирхгофа нужно составить два уравнения. Или для определения количества уравнений по второму закону Кирхгофа есть формула:
N2.з.к.=Nв-(Ny-1), где Nв – количество ветвей
Nв=3, тогда:
N2.з.к.=3-(2-1)=2
По второму закону Кирхгофа составляется два уравнения. Составим систему, состоящую из трех уравнений. Одно уравнение по первому закону Кирхгофа (это уравнение составляется для любого узла a или b) и двух уравнений по второму закону Кирхгофа для двух любых независимых контуров, например, составим для контуров 1 и 2.
Неизвестными в данной системе являются токи I1, I2 и I3. Решая данную систему, находят эти неизвестные.
О том, как решаются задачи с более сложными цепями, мы поговорим в следующих статьях.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;
Пример . Методом
непосредственного применения законов
Кирхгофа рассчитать токи в схеме на
рис.
Число ветвей
обозначим m, а число узлов n. Произвольно
выбираем положительные направления
токов в ветвях и направления обхода
контуров. Поскольку в каждой ветви
протекает свой ток, то число токов,
которое следует определить, а следовательно,
и число уравнений, которое нужно
составить, равно m. По первому закону
Кирхгофа составляем n-1 уравнений.
Недостающие m-(n-1) уравнений следует
составить по второму закону Кирхгофа
для взаимно независимых контуров.
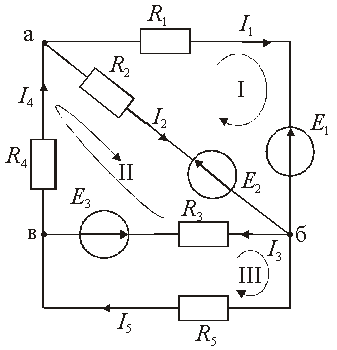
Рис.
2.20. Схема замещения сложной электрической
цепи
с несколькими источниками энергии:
I,
II, III – номера контуров
1. Проводим
топологический анализ.
Она содержит пять
ветвей и три узла, m = 5, n = 3. Составляем
два уравнения по первому закону Кирхгофу,
т. к. n – 1 = 2 (например, для узлов а и б).
2. Составляем
уравнения по певому и второму законам
Кирхгофа
Для
узла
“а”
– I1
– I2
+ I4
= 0.
Для
узла
“б”
– I1
+ I2
– I3
– I5
= 0.
Остальные m – (n – 1)
= 3 уравнения составляем по второму
закону Кирхгофа.
Для
контура
I – R1·I1
– R2·I2
= – E1
+ E2.
Для
контура
II – R2·I2
+ R3·I3
+ R4·I4
= – E2
– E3.
Для контура III –
– R3·I3
+ R5·I5
= E3.
Решив систему,
состоящую из пяти уравнений, находим
пять неизвестных токов. Если какие-либо
значения токов оказались отрицательными,
то это означает, что действительные
направления этих токов противоположны
первоначально выбранным.
При расчётах
сложных цепей с использованием ЭВМ
удобна матричная форма записи. Уравнения,
составленные по законам Кирхгофа,
запишем в виде
– I1
– I2
+ 0 + I4
+ 0 = 0
I1
+ I2
– I3
+ 0 – I5
= 0
R1·I1
– R2·I2
+ 0 + 0 + 0 = – E1
+ E2
0 + R2·I2
+ R3·I3
+ R4·I4
+ 0 = – E2
– E3
0 + 0 + –
R3·I3
+ 0 + R5·I5
= E3.
В матричной форме
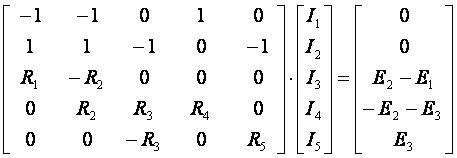
или [R]·[I]
= [Е],
где [R]
– квадратная (5 х 5) матрица, элементами
которой являются коэффициенты при
неизвестных токах в исходных уравнениях;
[I]
– матрица – столбец неизвестных токов;
[E]
– матрица – столбец, элементами которой
могут быть алгебраическая сумма ЭДС.
Решение матричного
уравнения ищут в виде
[I]
= [R]-1·[E],
где [R]-1
– матрица, обратная матрице [R].
Рассмотренный
метод расчета неудобен, если в цепи
имеется большое количество узлов и
контуров, поскольку потребуется решать
громоздкую систему уравнений. В таких
случаях рекомендуется применять метод
контурных токов, позволяющий значительно
сократить число расчетных уравнений
2.
Метод контурных
токов
Метод основан на 2-м законе Кирхгофа.
При его использовании в составе
анализируемой схемы выбирают независимые
контуры и предполагают, что в каждом
из контуров течет свой контурный ток.
Для каждого из независимых контуров
составляют уравнение по 2-му закону
Кирхгофа и их решают. Токи в ветвях
находят как алгебраическую сумму
контурных токов, протекающих по данной
ветви.
Все источники сигналов, представленные
источниками тока, заменяют источниками
ЭДС (рис. 4.29).
Э та
та
схема эквивалентна, если
а
 )E = IZiI;
)E = IZiI;
б) ZiII = ZiI.
1) Топологический анализ схемы.
а) Как и в предыдущем методе, определяют
число ветвей b.
б) Определяют число узлов у.
в) Подсчитывают число независимых
контуров Nk
= b – y
+ 1.
Все независимые контуры обозначены
дугами со стрелками на них, которые
показывают положительное направление
обхода.
Все контуры нумеруют и каждому контуру
присваивают свой контурный ток: Ik1;
Ik2;IkNk.
За положительное направление контурного
тока принимают положительное направление
обхода контура.
2) По второму закону Кирхгофа относительно
контурных токов записывают уравнения,
которые после приведения подобных
членов образуют систему линейных
уравнений Nk
= Nkпорядка:
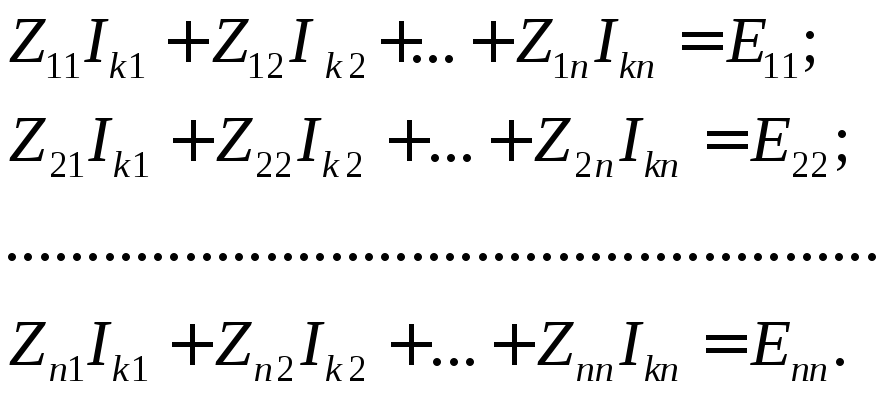
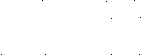
где Iki– контурный токi-го
контура;
Zii– собственное сопротивлениеi-го
контура и равно алгебраической сумме
сопротивлений, входящих вi-й
контур;
Zji– сопротивление смежных ветвей междуi-м иj-м
контурами. Оно представляет собой
алгебраическую сумму, причем ее члены
берутся со знаком «+», если контурные
токи направлены одинаково, и со знаком
«–», если они направлены встречно;
Eki– контурная ЭДСi-ого
контура. Она равна алгебраической сумме
ЭДС, входящих вi-й
контур. Контурная ЭДСEkiберется со знаком «+», когда направление
источника ЭДС и направление тока
совпадают, и со знаком «–», если они
направлены встречно.
3 )
)
По правилу Крамера находят контурные
токиIki=![]() .
.
4) Токи в ветвях находят как алгебраическую
сумму контурных токов, протекающих
через данную ветвь. В алгебраической
сумме контурные токи берутся со знаком
«+» , если ток ветви и совпадает с контурным
током и «–» если не совпадает.
Если токи ветви оказались положительными,
то выбранное направление тока совпадает
с истинным и наоборот.
Пример.Дана комплексная схема
замещения электрической цепи (рис. 4.30).
Определить токи во всех ветвях.
1. Проводим топологический анализ
а) b= 6; б)y= 4;в)Nk= 6 – 4 + 1=3.
2) Составим систему уравнений по методу
МКТ
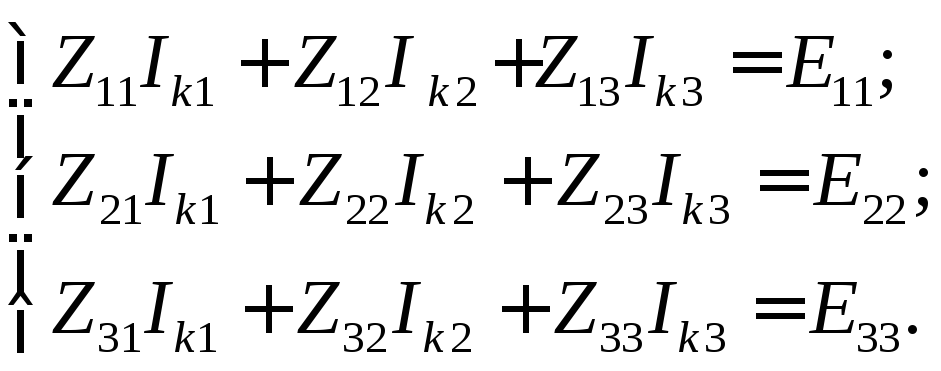
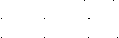
г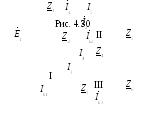 де:
де:
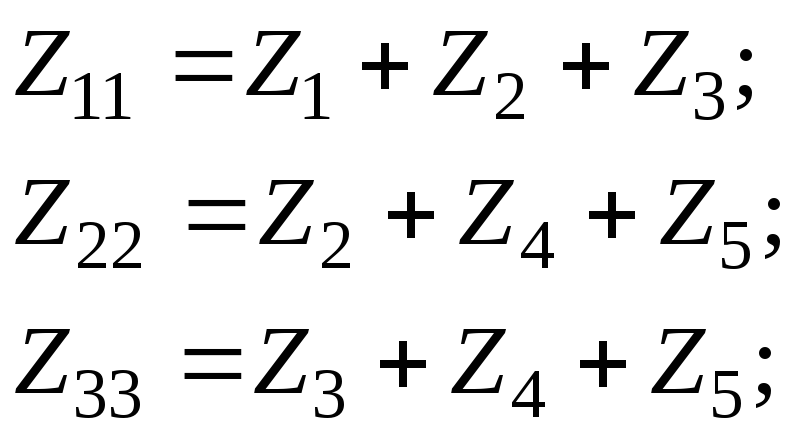
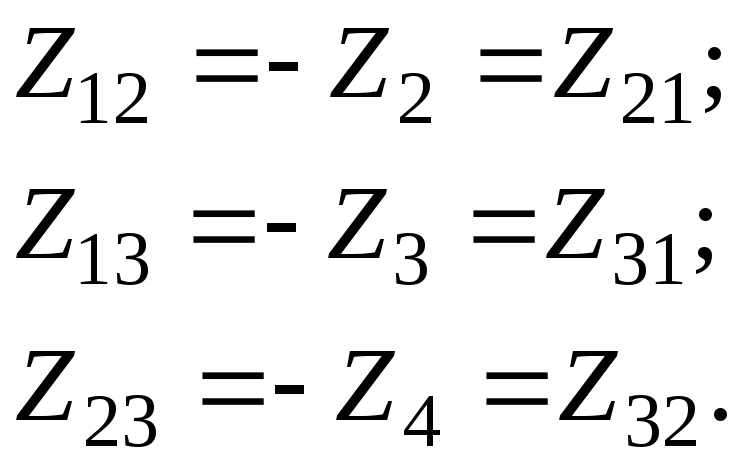
E


 11=
11=
E1; E22
= 0;E33 = 0.
3) По методу Крамера находим контурные
токи Iki
=
![]() .
.
4













 )
)
Находим токи
в ветвях:
I1 = Ik1;
I2 =
= Ik1 – Ik2;
I3 =
Ik1
– Ik3;
I4 =
–Ik2 + Ik3;
I5
= Ik2;
I6 =
Ik3.
Пример 2. Рассмотрим
электрической цепи постоянного тока,
рис. 2.21.
1. Проводим топологический анализ
а) b= 5; б)y= 3;в)Nk= 5 – 3 + 1=3.
2) Для каждого
контура записывают уравнение второго
закона Кирхгофа,
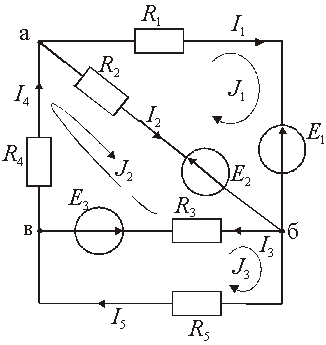
Рис.
2.21. – Расчетная схема для метода контурных
токов
В каждом из трех
контуров протекает свой контурный ток
J1,
J2,
J3.
Произвольно выбираем направление этих
токов, например, по часовой стрелке.
Составляем уравнения по второму закону
Кирхгофа для каждого контура с учетом
соседних контурных токов, протекающих
по смежным ветвям
(R1
+ R2)·J1
– R2·J2
= E2
– E1
– R2·J1
+ (R2
+ R3
+ R4)·J2
– R3·J3
= – E2
– E3
– R3·J2
+ (R3
+ R5)·J3
= E3.
Решив систему
уравнений, находят контурные токи J1,
J2,
J3.
Затем определяют реальные токи в ветвях,
причем токи во внешних ветвях равны
контурным, а в смежных – алгебраической
сумме 2-х контурных токов, протекающих
в данной ветви
I1
= J1;
I2
= J2
– J1;
I3
= J2
– J3;
I4
= J2;
I5
= J3.
Исходная система
уравнений в матричной форме
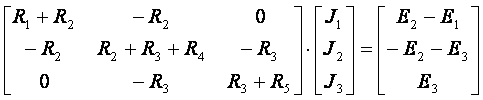
или
[R]·[J]
= [E],
где [R]
– квадратная матрица коэффициентов
контурных токов;
[J]
– матрица – столбец контурных токов;
[E]
– матрица – столбец ЭДС.
Решением матричного
уравнения является матрица
[J]
= [R]-1
·[E],
где [R]-1
– матрица, обратная матрице [R]
-
Пример 3. Для
электрической цепи, схема которой
приведена на рис. 1.1, получим следующие
уравнения:
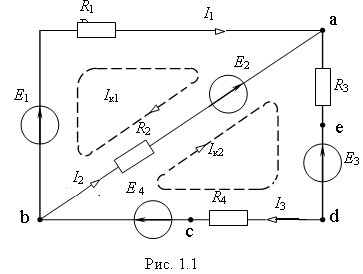
получим следующие
уравнения:
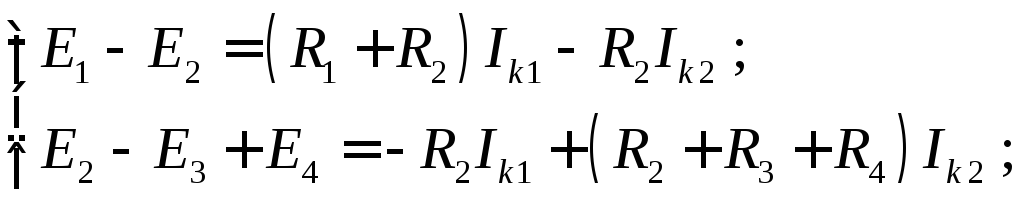
П![]() о
о
методу Крамера найдем контурные токи:
Действительные
токи в ветвях: I1
= Ik1;
I2
= Ik2
– Ik1;
I3
= Ik2.
Пример 4. Расчет
цепи методом контурных токов на рис.
2.22.
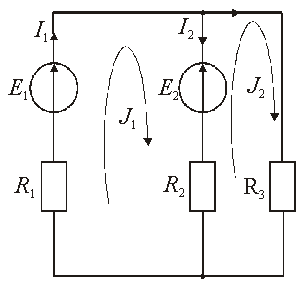
Рис.
2.22. – Расчет цепи методом контурных
токов
Для схемы замещения
электрической цепи, показанной на рис.
2.22, задано: E1
= 30 B; E2
= 10 В; R1
= 8 Ом; R2
= 15 Ом; R3
= 36 Ом. Требуется определить токи в ветвях
методом контурных токов. Составить
баланс мощности.
Схема содержит
три ветви (m = 3), два узла (n = 2). Выбираем
положительные направления токов в
ветвях произвольно. Число уравнений,
составленных по методу контурных токов,
равно m – (n – 1) = 2. Задаем направление
контурных токов (например, по часовой
стрелке) и составляем систему уравнений
(R1
+ R2)·J1
– R2·J2
= E1
– E2
– R2·J1
+ (R2
+ R3)·J2
= E2.
Подставляя численные
значения сопротивлений резисторов и
ЭДС в приведённые уравнения, находим
контурные токи J1,
J2
(Например, методом определителей)
20 = 23·J1
– 15·J2
10 = – 15·J1
+ 51·J2
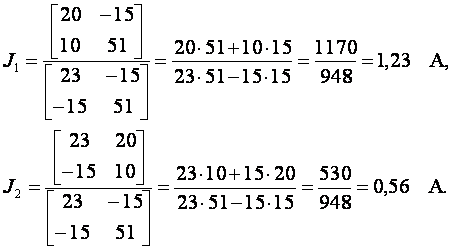
Токи в ветвях
I1
= J1
= 1,23 А; I2
= – J2
+ J1
= 1,23 – 0,56 = 0,67 А; I3
= J2
= 0,56 А.
Составляем баланс
мощностей.
Мощность генераторов
(источников)
РИ
= Е1·I1
– Е2·I2
= 30·1,23 – 10·0,67 = 30,2 Вт,
где произведение
Е2·I2
имеет знак минус (ток через источник не
совпадает с ЭДС, значит источник ЭДС
работает в режиме потребителя электрической
энергии).
Мощность, потребляемая
нагрузкой, составляет
РН
= R1·I12
+ R2·I22
+ R3·I32
= 8·1,232
+ 15·0,562
+ 36·0,562
= 30,13 Вт.
Погрешность
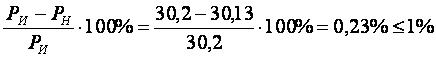
составляет менее
1%, т. е. токи найдены верно.
Метод узловых
потенциалов (МУП)
Метод основан на применении первого
закона Кирхгофа. В нем за неизвестные
величины принимают потенциалы узлов.
По закону Ома определяют токи во всех
ветвях схемы.
Все источники ЭДС, имеющиеся в схеме,
заменяют источниками тока (рис. 4.31).
а) I
= E/ZiI;
б) ZiII
= ZiI.
1) Топологический анализ.
а) Подсчитывают число ветвей bи число узловy.Определяется количество независимых
узловNy =y – 1.
б) Нумеруют все узлы. Один из узлов, к
которому сходится наибольшее число
ветвей, считают нулевым, где
![]() – потенциал нулевого узла.
– потенциал нулевого узла.
2) По 1-му закону Кирхгофа составляют
уравнения для Nузлов
схемы и решают их относительно потенциалов
узлов:
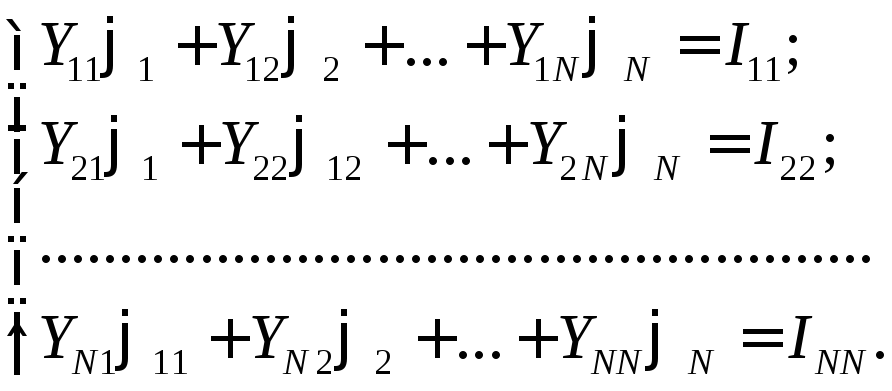


 ,
,
где Yii– собственная узловая проводимость.
Она равна сумме проводимостей всех
ветвей, сходящихся вi-м
узле, все они берутся со знаком «+»;
Yij– межузловая проводимость междуi-м
иj-м узлами. Проводимости
всех узлов берутся со знаком «–»;
Iii– алгебраическая сумма токов источников
тока, сходящихся вi-м
узле. Втекающие токи записываются в эту
сумму со знаком «+», а вытекающие – со
знаком «–».
3) Потенциалы узлов находят по формуле
Крамера
![]() .
.
4) Токи в ветвях находят по закону Ома
I= (1
–2)/Z.
Пример.Дана электрическая цепь
(рис. 4.32). Рассчитать токи во всех ветвях.
П
I2
Z2
редварительно преобразуем все
источники напряжения (рис. 4.32) в источники
тока (рис. 4.33).

Z1
Z2
Z3
Z4
E1
E2
I
I1
I2
I4
I
I3
I1
Z1
Z3
Z4
Рис. 4.32 Рис. 4.33
Проведем топологический анализ.
а) число ветвей b= 4;
б) число независимых узлов Nу= 2, их потенциалы: φ1и φ2(рис. 4.33).
Составим систему уравнений по методу
узловых потенциалов:









 ;
;![]()
![]() .
.
По методу Крамера найдем потенциалы
узлов
![]() .
.
По закону Ома найдем токи во всех ветвях
схемы:
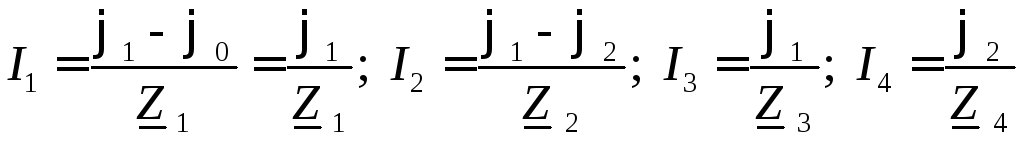



 .
.
-
МЕТОДИЧЕСКИЕ
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ по
теме цепи переменного тока
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.
Учёный Густав Киргхоф сформулировал два правила [1], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.
Первое правило Кирхгофа
Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.
Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.
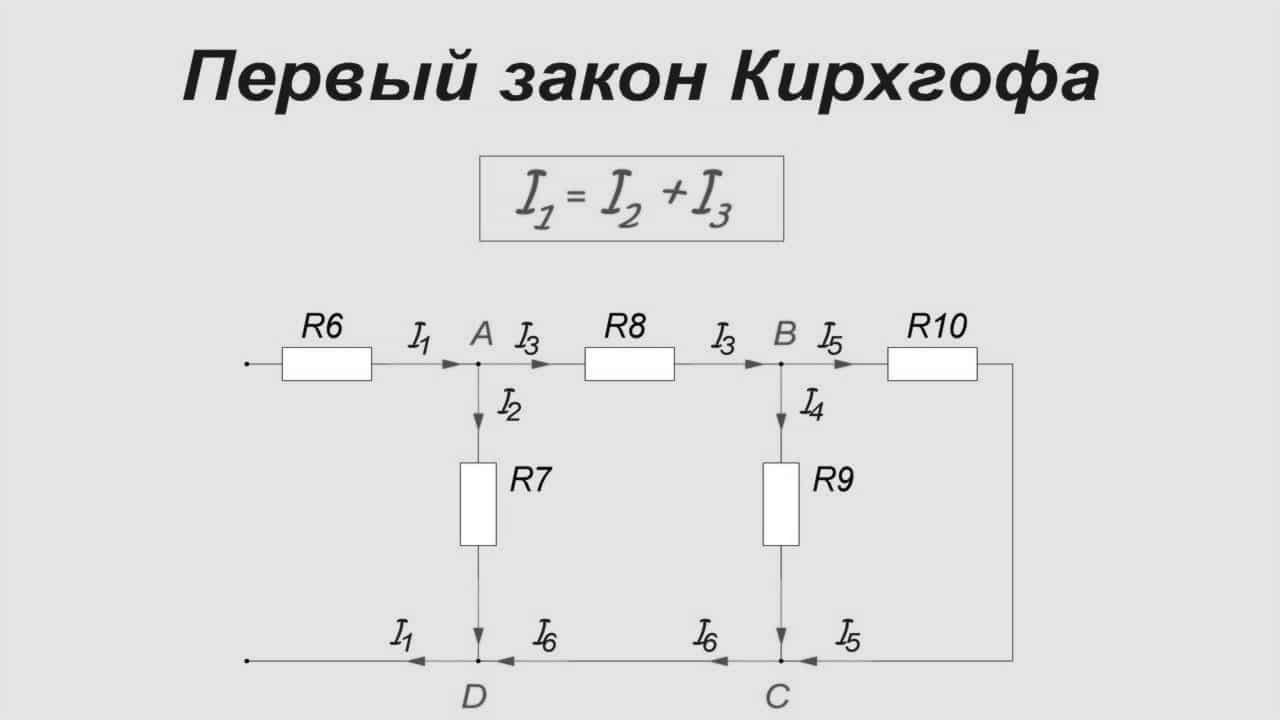
Ток I1 входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I1 = I2 + I3.
На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i1, i2, i3, i4 то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i1 + i2 + i3 + i4 = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.

Запишем наши выводы в алгебраической форме, для общего случая:

Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.
Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.
Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».
Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.
Второе правило Киргхофа
Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.
Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.
При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.

Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.
Формулировки уравнений общего характера:

, где где Lk и Ck – это индуктивности и ёмкости, соответственно.
Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.
Закон Кирхгофа для магнитной цепи
Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.

В частности: ∑Ф=0.
То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.
Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).
Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.
Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.
При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».
Примеры расчета цепей
Рассмотрим ещё раз рисунок 3. На нём изображено 4 разнонаправленных вектора: i1, i2, i3, i4. Из них – два входящие ( i2, i3) и два исходящие из узла (i1, i4). Положительными будем считать те векторы, которые направлены в точку соединения ветвей, а остальные – отрицательными.
Тогда, по формуле Кирхгофа, составим уравнение и запишем его в следующем виде: – i1 + i2 + i3 – i4 = 0.
На практике такие узлы являются частью контуров, обходя которые можно составить ещё несколько линейных уравнений с этими же неизвестными. Количество уравнений всегда достаточно для решения задачи.
Рассмотрим алгоритм решения на примере рис. 5.

Схема содержит 3 ветви и два узла, которые образуют три пары по два независимых контура:
- 1 и 2.
- 1 и 3.
- 2 и 3.
Запишем независимое уравнение, выполняющееся, например, в точке а. Из первого правила Кирхгофа вытекает: I1 + I2 – I3 = 0.
Воспользуемся вторым правилом Кирхгофа. Для составления уравнений можно выбрать любой из контуров, но нам необходимы контуры с узлом а, так как для него мы уже составили уравнение. Это будут контуры 1 и 2.
Пишем уравнения:
- I1R1 + I3 R3 = E1;
- I2R2 + I3R3 = E2.
Решаем систему уравнений:

Так как значения R и E известны (см. рисунок 5), мы придём к системе уравнений:

Решая эту систему, получим:
- I1 = 1,36 (значения в миллиамперах).
- I2 = 2,19 мА.;
- I3 = 3,55 мА.
Потенциал узла а равен: Ua = I3*R3 = 3,55 × 3 = 10,65 В. Чтобы убедиться в верности наших расчётов, проверим выполнение второго правила по отношению к контуру 3:
E1 – E2 + I1R1+ I2R2 = 12 – 15 + 1,36 – 4,38 = – 0,02 ≈ 0 (с учётом погрешностей, связанных с округлениями чисел при вычислениях).
Если проверка выполнения второго правила успешно завершена, то расчёты сделаны правильно, а полученные данные являются достоверными.
Применяя правила (законы) Кирхгофа можно вычислять параметры электрической энергии для магнитных цепей.
Примеры решения задач на законы Кирхгофа
Рассмотрим на примерах как можно использовать законы Кирхгофа при решении задач.
Задача 1
Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найти токи в ветвях, используя законы Кирхгофа.
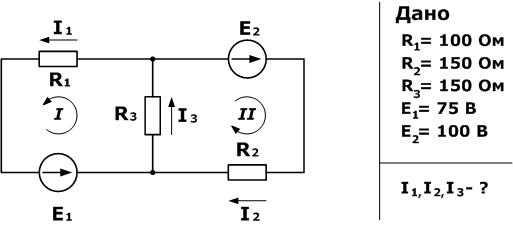
Используя первый закон Кирхгофа, можно записать n-1 уравнений для цепи. В нашем случае количество узлов n=2, а значит нужно составить только одно уравнение.
Напомним, что по первому закону, сумма токов сходящихся в узле равна нулю. При этом, условно принято считать входящие токи в узел положительными, а выходящими отрицательными. Значит для нашей задачи
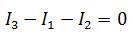
Затем используя второй закон (сумма падений напряжения в независимом контуре равна сумме ЭДС в нем) составим уравнения для первого и второго контуров цепи. Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус. Аналогично с источниками ЭДС.
На примере первого контура – ток I1 и I3 совпадают с направлением обхода контура (против часовой стрелки), ЭДС E1 также совпадает, поэтому берем их со знаком плюс.
Уравнения для первого и второго контуров по второму закону будут:
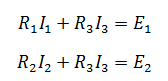
Все эти три уравнения образуют систему
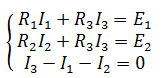
Подставив известные значения и решив данную линейную систему уравнений, найдем токи в ветвях (способ решения может быть любым).
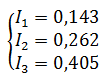
Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка балансом мощностей.
Задача 2
Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.
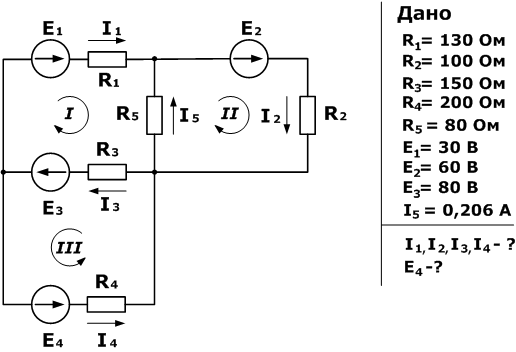
Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2
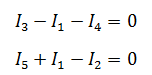 Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.
Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.
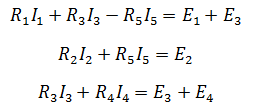
На основании этих уравнений составляем систему с 5-ью неизвестными

Решив эту систему любым удобным способом, найдем неизвестные величины
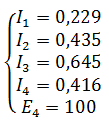 Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками.
Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками.
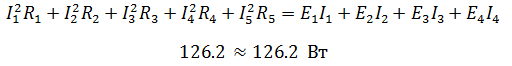 Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.
Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.
Читайте также – расчет простых цепей постоянного тока
