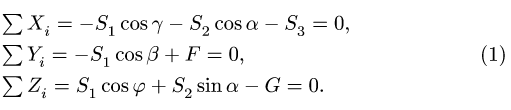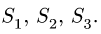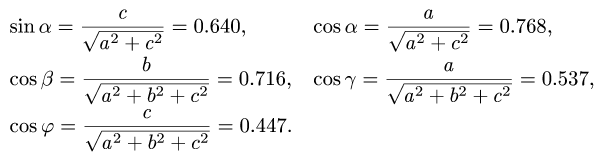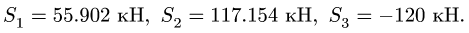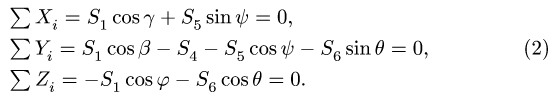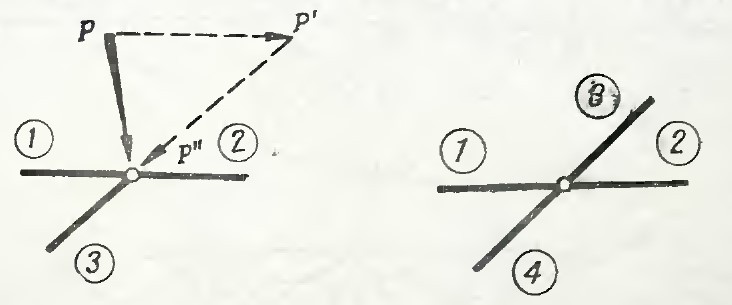Особое место в ряду статических
задач занимает расчёт ферм. Фермой
называется жёсткая конструкция из
прямолинейных стержней. Если все стержни
фермы и вся приложенная к ней нагрузка
расположены в одной плоскости, ферма
называется плоской. В дальнейшем будем
рассматривать только плоские фермы.
Соединения стержней называются узлами
фермы.
В результате полного расчёта фермы
необходимо определить реакции опор и
усилия во всех стержнях фермы.
При расчёте ферм приложенную внешнюю
нагрузку (включая весовую нагрузку)
заменяют эквивалентной системой, силы
которой приложены к узлам фермы. В
реальных фермах соединения стержней,
как правило, жёсткие (сварка, клёпка и
т.д.), так что они не допускают относительного
поворота стержней. В расчётной схеме
крепления стержней считаются шарнирными,
причём, трение в шарнирах считается
пренебрежимо малым.
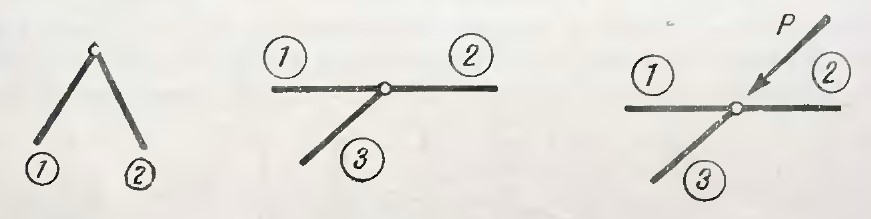
В результате сделанных упрощающих
предположений оказывается, что каждый
стержень находится в равновесии под
действием двух сил, приложенных к его
концам. Эти силы должны иметь общую
линию действия, т.е. они направлены вдоль
стержня. Таким образом, считается, что
каждый стержень фермы работает или на
растяжение, или на сжатие, но не может
испытывать кручения или изгиба. Усилие
в стержне считается положительным, если
он растянут.
Для определения усилий в стержнях
фермы используются два основных метода.
Пример
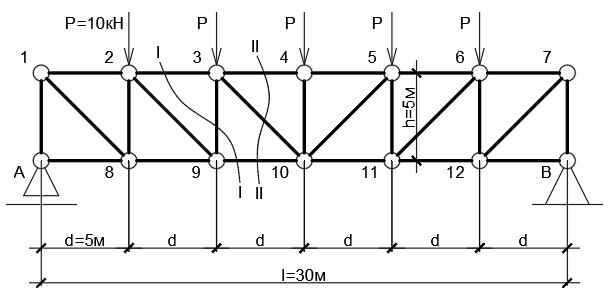
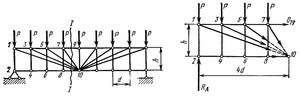
Рассчитать ферму, изображённую на Рис.
2.18.
Дано:
кН;
м.
|
|
|
Рис. 2.18 |
Прежде всего обозначим все узлы и
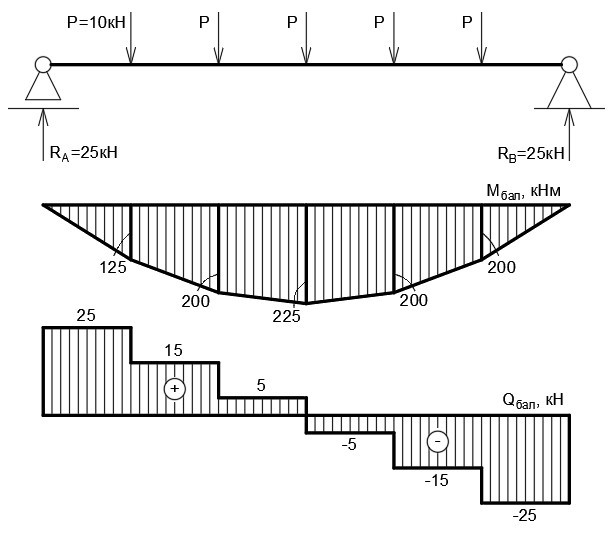
все стержни фермы. Определим реакции
опор. Для этого рассмотрим равновесие
фермы в целом (Рис. 2.19). Составим условия
равновесия:
Отсюда:
|
|
|
Рис. 2.19 |
Поскольку вычисленные величины
опорных реакций определяют весь
дальнейший расчёт, имеет смысл проверить
полученные результаты, составив,
например, уравнение моментов относительно
оси
(чтобы в это уравнение вошли все
вычисленные величины):
Для определения усилий в стержнях фермы
используются два основных метода.
Метод вырезания узлов.Метод
состоит в том, что рассматривается
равновесие каждого узла фермы в
определённой последовательности. На
узел действует плоская система сходящихся
сил, для которой можно составить два
уравнения равновесия, что позволяет
определить две неизвестные. Поэтому
расчёт начинают с узла, соединяющего
два стержня фермы. Затем переходят к
соседним узлам в определённой
последовательности, которая позволяет
на каждом шаге определять усилия в
очередных двух стержнях. Первоначально
предполагается, что стержни растянуты,
т.е. их реакции направлены от узлов. Если
усилие в каком-либо стержне оказывается
отрицательным, то это означает, что
данный стержень сжат.
Заметим, что уравнения равновесия
фермы в целом являются прямым следствием
полной системы уравнений равновесия
узлов, так что методом вырезания узлов
можно определить в том числе и реакции
опор фермы. Но в этом случае часто
приходится совместно решать систему,
содержащую значительное число уравнений.
Предварительное определение реакций
опор упрощает решение задачи, а
неиспользованные уравнения равновесия
узлов можно рассматривать как проверочные.
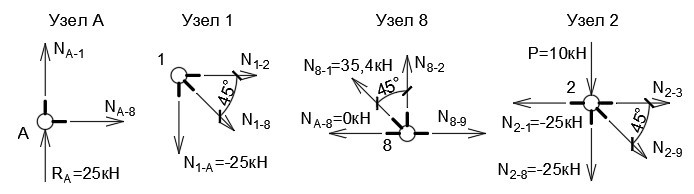
Рассмотрим
равновесие узла
Отсюда:
(стержень сжат)
(стержень сжат).
Рассмотрим
равновесие узла
Отсюда:
(стержень растянут)
(стержень сжат).
Рассмотрим
равновесие узла
Значения
тригонометрических функций определим
из треугольника
:
Таким
образом,
(стержень растянут)
(стержень сжат).
Рассмотрим
равновесие узла
Отсюда:
(стержень сжат).
(стержень сжат).
Р
равновесие узла
Отсюда:
(стержень растянут)
(стержень сжат).
Рассмотрим
равновесие узла
Отсюда:
(стержень растянут)
Таким образом, определены усилия во
всех стержнях фермы. Оставшиеся уравнения
используем для проверки полученных
результатов.
Р
равновесие узла
Метод сквозных сечений (метод
Риттера).Этим методом удобно
пользоваться для определения усилий в
отдельных стержнях фермы, в частности
для проверочных расчётов. Идея метода
состоит в том, что ферма разделяется
сечением на две части и рассматривается
равновесие одной из этих частей. Сечение
проводится по трём стержням фермы, в
которых (или в одном из которых) требуется
определить усилие. Действие отброшенной
части фермы заменяют соответствующими
реакциями, направляя их вдоль разрезанных
стержней от узлов, т.е. считая стержни
растянутыми (как и в методе вырезания
узлов). Условия равновесия составляются
так, чтобы в каждое уравнение входила
только одна неизвестная величина.
Если сечение проводится более, чем
по трём стержням, то усилия в “лишних”
стержнях должны быть определены
предварительно. В противном случае
будет необходимо рассмотреть комбинацию
из нескольких сечений или комбинацию
метода сечений и метода вырезания узлов.
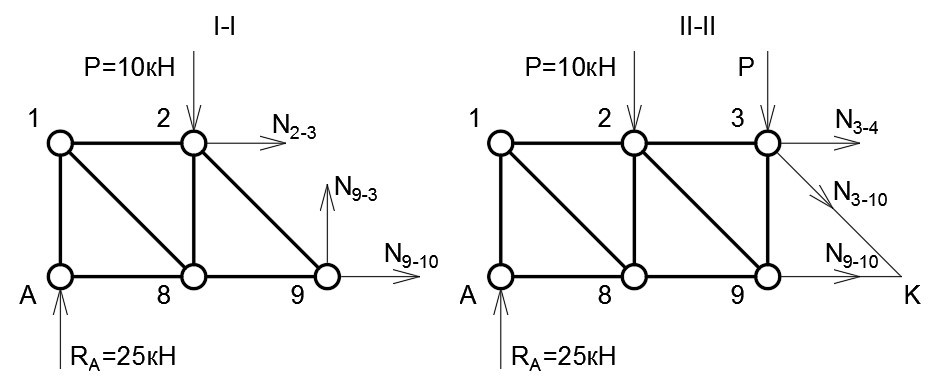
В качестве примера проведём сечение
через шестой, седьмой и восьмой стержни.
Рассмотрим равновесие правой части
фермы (Рис. 2.20).
Уравнения равновесия имеют вид:
Отсюда:
|
|
|
Рис. 2.20 |
Условие жёсткости фермы.Найдём
минимальное число стержней,
которое необходимо для образования
плоской фермы, имеющейузлов. Простейшая ячейка фермы
(треугольник) имеет три стержня и три
узла. Для присоединения каждого из
оставшихсяузлов необходимо два стержня. Таким
образом, условие жёсткости фермы имеет
вид:
Условие статической определимости
фермы.Ферма является статически
определимой, если число неизвестных
совпадает с числом независимых уравнений
равновесия, в которые эти неизвестные
входят. Для плоской фермы, имеющейузлов, можно составить
уравнений равновесия, три из которых
расходуются на определение трёх
составляющих реакций опор. Для определения
усилий в стержнях фермы остаётсяуравнения. Таким образом, условие
статической определимости фермы
совпадает с условием её жёсткости.
Методы расчёта фермы рассмотрим на
примере.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ:
-
В
чём суть упрощающих предположений,
принимаемых при расчёте фермы? -
В
чём состоит метод вырезания узлов? -
В
чём состоит метод сквозных сечений? -
Каково
условие жёсткости фермы? -
Каково
условие статической определимости
фермы?
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из
сборника задач И.В.Мещерского: 4.66; 4.67;
4.68; 4.70; 4.71; 4.73; 4.74.
Из
учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплекты СР-8; СР-9;
СР-10; СР-11.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2015560.03 Кб15PSY – recommendation.pdf
- #
- #
Содержание:
- Ферма и их расчет
- Метод вырезания узлов
- Метод Риттера
- Расчет плоских ферм
- Основные понятия о плоских фермах
- Условие жесткости фермы
- Статически определенные фермы
- Метод вырезания узлов
- Метод Риттера
- Фермы. Способы определения усилий в стержнях ферм
- Простейшие фермы
- Определение усилий в стержнях фермы
- Способ вырезания узлов
- Способ Риттера
Фермой называется шарнирно-стержневая геометрически неизменяемая конструкция.
Плоская ферма – частный случай пространственной конструкции, у которой один из поперечных размеров либо мал по сравнению с другими размерами, либо не существенен для распределения внутренних усилий.
Реальная ферма, может не иметь идеальных шарнирных соединений в узлах, соединения стержней между собой в узлах являются жесткими, а не шарнирными, с помощью сварки, заклепок, болтов или других скреплений.
Плоские фермы конструируют таким образом, что приложенная к ферме нагрузка передается в узлах, вследствие чего, в сечениях элементов ферм не возникают поперечные силы и изгибающие моменты, стержень работает только на продольные усилия – растяжение или сжатие, и, следовательно, реакции стержней будут направлены вдоль этих стержней.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Ферма и их расчет
Ферма — это жесткая конструкция, которая состоит из прямолинейных стержней, соединенных между собой шарнирами. Место, где стержни соединяются друг с другом, носит название узла фермы. Внешняя нагрузка прикладывается к ферме только в ее узлах. Ферма состоит из идеальных стержней, то есть тонких, однородных, невесомых
стержней, на концах которых шарниры, которые работают на растяжение или на сжатие.
Мы будем рассматривать фермы, в которых оси всех стержней и векторы внешних сил содержатся в одной плоскости, то есть, плоские фермы. Помимо этого, конструктивно ферма состоит из стержней, которые образуют собой треугольники, то есть в конструкции фермы нет лишних стержней. такие фермы являются жесткими и статически определенными. В них число стержней n и число узлов m всегда связано таким соотношением
n = 2m – 3 .
Расчет фермы сводится к определению ее опорных реакций и усилий в стержнях.
Рассмотрим простую плоскую ферму (рис. 1.26).
Как видно из схемы — это плоская конструкция, которая состоит из 7 стержней, которые соединяются в 5 узлах. В узлах I и V ферма имеет опоры (в I-ом узле — неподвижная шарнирная опора; в V-м — подвижная шарнирная опора), к II и к IV узлу фермы приложены внешние нагрузки в виде сосредоточенных сил 



Первый этап расчета фермы — это определение ее опорных реакций. Определяют опорные реакции, рассматривая ферму в целом, как твердое тело с приложенными внешними силами. Тогда, условно освобождая ферму от связей (опор) и заменяя их соответствующими реакциями (в узле I это реакции 


Из первого уравнения системы вычисляем неизвестную реакцию XI. она равна
XI = P2 = 10 kH.
Из последнего уравнения вычисляем реакцию RV:
Далее, из второго уравнения является возможность вычислить последнюю неизвестную
величину YI. Она будет равняться
YI = P1 – RV = 30 – 5 = 25 kH.
Таким образом, вычислено искомые реакции опор фермы. Теперь необходимо определить неизвестные усилия в стержнях фермы. существует несколько способов определения этих усилий, графические и аналитические. Мы рассмотрим два аналитические методы: метод вырезания узлов и метод сечений (или метод Риттера). Рассмотрим последовательно эти методы.
Метод вырезания узлов
Этот метод заключается в последовательном вырезании (мысленно) узлов фермы,
начиная с узла где совпадают два стержня с неизвестными внутренними усилиями. Таким образом, каждый узел — это плоская система сходящихся сил, для которой можно составить два уравнения равновесия, из которых определяют неизвестные усилия в этих двух стержнях.
При применении этого метода принимается правило, согласно которому реакции
стержней направляются от узлов. Если же при определении реакции стержня произойдет, что она имеет отрицательный знак, то этот стержень сжат и действительное направление его реакции ориентировано к узлу.
Определим данным методом усилия в стержнях фермы, приведенной на рис. 1.26. Вырезаем сначала узел I (рис. 1.27). Кроме реакций 





используя условия равновесия для плоской системы сходящихся сил в виде. Будем иметь
Из второго уравнения определяем усилия S1. Оно равно
Как видим, стержень 1 сжатый усилиям 35,3 kH. С первого уравнения определим неизвестное усилие S2
S2 = – XI – S1 sinα = –10 – (– 35,3 · 0,707) = – 10 + 25,00 = 15,00 kH .
Таким образом, стержень 2 растянутый усилием 15,00 kH.
Далее вырезаем узел ІІ (рис. 1.28). В этом узле сосредоточены внешняя сила 






направлены от узла ІІ. Усилия же в стержне 1 уже определено ранее, при вырезании первого узла, и не только установлено его значение, но и то, что он сжат, поэтому направление его реакции 
Составим для узла ІІ уравнения равновесия, также используя условия, аналогичные предыдущим.
Из второго уравнения определяем усилия S3. Оно будет равняться
Как видим, стержень 3 сжатый усилиям 7,00 kH. Направление реакции S3 — к узлу ІІ.
Из первого уравнения находим усилия S4. Оно равно
S4 = –S1 sinα – S3 cosα = – 35,30 · 0,707 – (–7,00)0,707 = – 25,00 + 5,0 = – 20,00 kH.
Таким образом, стержень 4 сжатый усилием 20,00 kH.
Далее вырезаем узел IV (рис. 1.29). Он находится под действием внешней силы 


Решаем систему, для чего из второго уравнения выразим усилия S5 через усилия S7. Оно будет равняться
Теперь подставим значение S5 в первое уравнение системы. Будем иметь
S7 cosα – (– S7)cosα – P2 + S4 = 0.
Отсюда
Стержень 7 сжатый усилием 7,00 kH. Теперь есть возможность найти усилие S5. Оно равно
S5 = – S7 = 7,00 kH.
Стержень 5 растянутый усилием 7,00 kH.
Теперь, для окончательного определения усилий в стержнях фермы, что рассматривается, необходимо вырезать узел V. К узлу V приложена реакция 


Как видим, для определения последнего неизвестного усилия S6 достаточно решить первое уравнение системы. Найдем S6 :
S6 = S7 cosα = 7,00 · 0,707 = 5,00 kH.
Стержень 6 растянутый усилием 5,00 kH.
Данные расчетов заносим в таблицу 1.1. Знак при определенном усилии в стержне показывает характер его нагрузки. Если он положительный (“+”), То стержень растянут, если отрицательный (“–”), то стержень сжат.
Метод Риттера
Рассмотрим второй аналитический метод определения усилий в стержнях плоской фермы. Это метод Риттера, или метод сечений.
Данный метод имеет несколько преимуществ по сравнению с рассмотренным ранее
методом вырезания узлов. Здесь нет необходимости составлять большое количество уравнений равновесия узлов, особенно когда ферма многостержневая. Кроме того, в случае неточности расчета какого-то стержня, в дальнейшем эта ошибка накапливается при расчетах других стержней. Метод Риттера лишен этих неудобств.
Особенность применения этого метода состоит в том, что условно делается сечение всей фермы, при этом в сечении должно быть не больше, чем три стержня с неизвестными усилиями. Тогда рассматривается равновесие одной из частей фермы, а вторая часть отбрасывается. Действие стержней, которые попали в сечение, заменяем их реакциями. предварительно считается, что эти стержни также растянуты, то есть их усилия направлены от узлов. Опорные реакции фермы определяются так же, как и при
применении метода вырезания узлов.
Определим усилия в 4, 5 и 6 стержнях фермы, сделав сечение и рассматривая равновесие правой части фермы (рис. 1.31). Вместо указанных стержней прикладываем в узле IV усилия 




фермы находится в равновесии под действием плоской системы произвольных сил, а
для этого составим для нее уравнения равновесия, используя условия равновесия. Согласно методу Риттера надо составлять уравнения равновесия, как суммы моментов сил относительно тех точек, где пересекаются линии действия большего количества неизвестных усилий. В данном случае такими точками будут точки ІІІ и IV. В отношении этих точек возьмем моменты сил.
Будем иметь
Вычислим неизвестные усилия. Из первого уравнения — усилия S5:
Из второго уравнения — усилия S4. Оно будет равняться
Таким образом, стержень 4 сжатый усилиям 20,00 kH, направление усилия S4 будет противоположный тому, который был показан на рис. 1.31.
Расчет плоских ферм
Фермой называется конструкция, состоящая из стержней, соединённых между собой на концах шарнирами и образующих геометрически неизменяемую систему. Шарнирные соединения стержней фермы называют её узлами. Если оси всех стержней фермы лежат в одной плоскости, то ферма называется плоской.
Основные понятия о плоских фермах
Фермой называется геометрически неизменная конструкция, состоящая из прямолинейных стержней, соединенных в узлах шарнирами (рис. 8.1).
Основная задача, о которой будет идти речь далее, заключается в определении внутренних усилий, возникающих в стержнях фермы под действием внешних активных сил.
Приведенное определение фермы имеет одно существенное упрощение, которое позволяет усилия в стержнях фермы находить методами теоретической механики. Этим упрощением является допущение о шарнирном соединение стержней фермы.
В реальных фермах стержни соединены жестко с помощью электросварки, клепки и тому подобное. Однако, как показывают исследования в строительной механике, сделано допущение о способе соединения стержней фермы позволяет найти приближенное значение усилий с достаточной точностью.
Фермы используются в качестве несущих конструкций в различных сооружениях: в мостах, в перекрытиях зданий, в подъемных кранах, каркасах самолетов тому подобное.
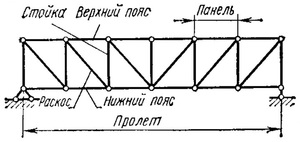
Места соединения стержней фермы называются узлами, а те узлы, которыми ферма опирается на основу – опорными узлами. Стержни, размещены по верхнему контуру фермы, образуют верхний пояс, а по нижнем – нижний пояс (См. Рис. 8.1).
Вертикальные стержни называются стойками, а наклонены – раскосами.
Фермы бывают пространственные и плоские. Если оси всех стержней фермы лежат в одной плоскости, такая ферма называется плоской, если нет – то пространственной. В этом разделе ограничимся рассмотрением только плоских ферм.
Расчет ферм существенно упрощается, если сделать такие допущения:
1) трения в шарнирах отсутствует;
2) заданные силы, действующие на ферму, лежат в плоскости фермы и приложенные в узлах;
3) собственный вес стержней малый по сравнению с заданными силами и ею можно пренебречь.
Если выполнять эти условия, каждый стержень фермы будет работать на растяжение или сжатие и не испытывать деформации изгиба, в чем и есть преимущество фермы как строительной конструкции. Действительно, при условии, что все усилия приложены в узлах фермы и отсутствует трение в шарнирах, каждый стержень будет находиться под действием только двух сил, которые приложены к его концов. Согласно с первой аксиомой статики, при равновесии линия действия этих сил должна проходить через их точки приложения. Итак, силы, приложенные к стержню фермы, будут обязательно направлены вдоль стержня, и поэтому приводить его сжатие или растяжение.
Сделанные допущения оправданы тем, что, во-первых, трения в шарнирах малое по сравнению с заданными силами и им можно пренебречь; во-вторых, если сила приложена не у узле фермы, то ее можно разложить на составляющие, которые будут приложены в узлах.
Для того чтобы ферму можно было использовать как несущую конструкцию в инженерных сооружениях, необходимо обеспечить ее жесткость.
Определим условия, при которых ферма будет жесткой (геометрически неизменной).
Условие жесткости фермы
Найдем наименьшее число стержней N, необходимых для построения геометрически неизменяемой (жесткой) фермы, которая имеет n узлов.
Простой, геометрически неизменной фермой является конструкция, состоит из трех узлов, соединенных тремя стержнями. для жесткого присоединения каждого из последующих 
Следовательно, для обеспечения жесткости фермы (т.е. исключения относительных
перемещений стержней) необходимо, чтобы число стержней равнялось
то есть
Пример неизменной жесткой фермы показано на рис. 8.3, а.
Если число стержней 

Уравнение (8.1) называется условием жесткости фермы. Заметим, что равенство (8.1) является необходимым условием жесткости фермы, но не достаточным. Для конструкции, изображенной на рис. 8.3, г, условие (8.1) выполняется, но эта система геометрически переменная. Для обеспечения геометрической неизменности фермы условие (8.1) должно выполняться как для всей фермы, так и для отдельных ее частей (решеток).
Статически определенные фермы
Статическую определенность фермы устанавливают по количеству реакций опор и числом стержней фермы.
Заметим, что ферма является неизменной системой, поэтому, как известно из предыдущего, неизвестных опорных реакций не должно быть более трех. В противном случае задача определения опорных реакций для данной фермы является статически неопределенной.
Рассчитывая фермы, кроме трех неизвестных реакций, нужно еще определить усилия в стержнях фермы. Выясним, сколько независимых уравнений статики можно составить для определения этих неизвестных сил. для этого используем метод вырезания узлов.
На каждый вырезанный узел фермы будет действовать плоская система сходящихся сил, которая состоит из внешних сил (активных и реакций связей) и внутренних усилий в стержнях. Поэтому система сил, приложенная к узлу, должна удовлетворять двум уравнениям равновесия 
Следовательно, при равновесии фермы, которая имеет n узлов, все действующие на ферму
внешние силы и усилия в стержнях должны удовлетворять 2n уравнением.
С равновесия отдельных узлов фермы следует равновесие фермы в целом, а потому три уравнения равновесия 
К 2n уравнениям будут входить три неизвестные реакции связей и внутренние усилия в стержнях. Из этих уравнений можно найти 


Методы нахождения усилий в стержнях статически неопределенных ферм рассматриваются в курсах сопротивления материалов и строительной механики. В курсе
теоретической механики рассматривают только статически определенные фермы.
Существует три основных метода нахождения усилий в стержнях статически определенных ферм: вырезания узлов Риттера и графический (построения
диаграммы Максвелла-Кремоны).
Остановимся только на двух аналитических методах.
Метод вырезания узлов
Суть метода вырезания узлов заключается в том, что рассматриваем равновесие каждого узла в отдельности. Для этого вырезаем узлы фермы, прикладываем к ним соответствующие внешние силы и реакции стержней и составляем уравнение
равновесия сил, приложенных к каждому узлу. Поскольку в начале расчета фермы неизвестно, какие стержни фермы растянуты, а какие сжаты, условно допускаем, что все стержни растянуты. В этом случае реакции стержней направляем от узлов. Если в результате вычислений получим значение реакций некоторых стержней со знаком минус, то это будет означать, что эти стержни сжаты. Найденные реакции стержней по модулю равны внутренним усилием в стержнях.
Последовательность рассмотрения узлов определяется по условию: число неизвестных сил, приложенных к узлу, не должно превышать количества уравнений равновесия сил, то есть двух.
Проиллюстрируем этот метод на конкретном примере.
Задача 1. Найти усилия в стержнях фермы, изображенной на рис. 8.4, методом вырезания узлов, если к узлу D фермы приложено вертикальную силу
Решение. В этой ферме число узлов n = 8, а число стержней N = 13. Итак, условие (8.1) выполняется и ферма является жесткой без лишних стержней, то есть статически определенной.
Составим уравнения равновесия для всей фермы и найдем реакции опор А и В:
Переходим к определению усилий в стержнях. Условно вырежем все узлы фермы, сохраняя последовательность, указанную выше. реакции стержней обозначим через 
Для сил, которые совпадают в каждом узле, составим последовательно уравнения равновесия. Расчет начнем с узла А, в котором приложены только две неизвестные силы 
Равновесие последнего узла В можно не рассматривать, поскольку все усилия 
Полученные усилия в стержнях 1, 4, 8 и 12 отрицательные, и это означает, что стержни сжаты.
Усилия в отдельных стержнях загруженной фермы, как видно из приведенного примера, могут равняться нулю. Такие стержни принято называть нулевыми.
Сформулируем леммы, которые позволяют найти нулевые стержни плоской фермы, не проводя ее расчета.
Лемма 1. Если в незагруженном узле плоской фермы сходятся два стержни, то усилия в этих стержнях равны нулю.
Лемма 2. Если в незагруженном узле плоской фермы сходятся три стержни, два из которых расположены на одной прямой, то усилия в третьем стержни равна нулю. Усилия в первых двух стержнях равны между собой.
Лемма 3. Если в узле плоской фермы сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилия в этом стержни равна по модулю приложенной силе, а усилия во втором стержне равна нулю.
Довести эти леммы предлагается самостоятельно.
Методом вырезания узлов выгодно пользоваться тогда, когда нужно найти усилия во всех стержнях фермы. Этот метод хоть и простой, но громоздкий и нерациональный в тех случаях, когда нужно найти усилия не во всех стержнях фермы, а только в отдельных. Например, для нахождения усилий только в одном стержне приходится рассматривать
последовательно равновесие определенного количества узлов, пока не будет найдено усилия в нужном стержни. Этот недостаток отсутствует в методе Риттера.
Метод Риттера
Метод Риттера состоит в том, что после нахождения реакций опор ферму условно разрезают на две части так, чтобы в сечении было не более трех стержней с неизвестными усилиями, и рассматривают равновесие одной из частей фермы. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, то есть считают, что стержни розтянути (как в методе вырезания узлов).
На часть фермы, которую рассматриваем в равновесии, будут действовать внешние силы и реакции разрезанных стержней. Для полученной плоской системы сил составляем три уравнения равновесия.
Уравнение выгодно записывать в виде равенства нулю суммы моментов всех сил относительно трех разных центров,которые являются точками, в которых попарно пересекаются разрезанные стержни или их продолжение. Эти точки носят название точек Риттера. В каждое из уравнений моментов относительно трех точек Риттера будет входить лишь одно неизвестное, а именно усилия в том стержни, ось которого через эту точку не проходит. Покажем это на примере.
Задача 2. Методом Риттера найти усилия в стержнях 4, 5 и 6 фермы, изображенной на рис. 8.4.
Решение.Реакции опор фермы найдены в предыдущем примере 

Действие правой части на левую заменяем реакциями 

Для плоской системы сил, которая действует на левую часть фермы, составляем три уравнения равновесия:
где 

Индексация точек Риттера 


Решая эту систему уравнений, получим:
Величины найденных усилий
Аналогично можно найти усилия и в других стержнях фермы. Из приведенного примера видно, что уравнение равновесия не связаны между собой, а потому для нахождения усилий в одном стержне достаточно составить лишь одно из этих уравнений.
Фермы. Способы определения усилий в стержнях ферм
Основными способами определения усилий в стержнях ферм являются: – способ вырезания узлов; – способ сечений Риттера; – графический способ определения усилий в стержнях фермы с помощью построения диаграммы Максвелла-Кремоны; – метод построения веревочного многоугольника.
Простейшие фермы
Фермами называются конструкции, которые состоят из прямолинейных стержней, которые соединены между собой шарнирами и образуют неизменную геометрическую фигуру (рис. 4.1). При расчете ферм весом стержней пренебрегают и считают, что шарниры размещены только на концах стержней; нагрузки, действующие на ферму, приложенные в шарнирах (т.е. в узлах фермы). В этом случае каждый стержень фермы испытывает усилия, действующие вдоль оси стержня, то есть будет растянут или сжат.
С всего класса геометрически неизменных ферм без лишних стержней выделим простые фермы. Их построение происходит так: рассматривается основной треугольник, к нему двумя стержнями присоединяется новый шарнир (узел) и и. д. В дальнейшем будем изучать простые, плоские фермы, где их стержни расположены в одной плоскости.
По своему назначению зачастую фермы делятся на мостовые, стропильные и крановые (рис. 4.1). Установим зависимость между количеством 

Рассуждаем так: для образования основного треугольника нужно три стержня и три шарнира. Для образования каждого из остальных 

Основной задачей расчета простых ферм является определение усилий в стержнях фермы, которые являются внутренними силами, возникающими в стержнях под действием внешних сил. Эту задачу можно решить методами теоретической механики.
Определение усилий в стержнях фермы
Ограничимся двумя способами определения усилий в стержнях простой фермы: способом
вырезания узлов (графически-аналитический метод) и способом Риттера (аналитический метод).
Способ вырезания узлов
Этот способ заключается в том, что каждый узел вырезается из
фермы и рассматривается отдельно как таковой, что находится в равновесии под действием приложенных к нему внешних сил и усилий разрезанных стержней. Система сил, действующей на узел, является плоской системой сходящихся сил, которая находится в равновесии; следовательно, силовой многоугольник, построенный из этих сил, должен быть замкнутым. Построение силовых многоугольников (треугольников) следует начинать с узла, в которых сходятся два стержня, тогда построением замкнутого треугольника (третья сторона отвечает известной заданной силе, прилагаемой в узле) найдутся усилия в этих двух стержнях. После этого можно переходить к следующему узлу и т. Д. Каждый следующий узел выбирается так, чтобы в нем сходилось не более двух стержней с неизвестными усилиями. Так графически будут определены усилия во всех стержнях. Если усилия разрезанных стержней направлены по стержнях в сторону узла, то они сжимающие, в противном случае – растяжимые.
Формально условия равновесия узлов фермы включают в себя условия равновесия фермы в целом, то есть позволяют найти и внешние реакции. Более того, предварительное определение внешних реакций фермы существенно упрощает решения задачи. Рассмотрим способ вырезания узлов на примере расчета усилий в стержнях фермы, показанной на рис. 4.2.
Пример 1. В узле В фермы приложена сила 

Решение. Рассмотрим ферму как твердое тело, которое находится в равновесии под действием плоской системы параллельных сил 





откуда найдем
Определение усилий в стержнях начнем с рассмотрения узла А, в котором сходятся два стержня: 1 и 7. Строим замкнутый треугольник из сил 












Неудобство этого способа заключается в его громоздкости, поскольку приходится строить столько многоугольников, сколько узлов в ферме. Объединение разных многоугольников сил в одну диаграмму осуществили независимо друг от друга английский физик Максвелл и итальянский геометр Кремона, в честь которых эту диаграмму назван диаграммой Максвелла – Кремоны.
Способ Риттера
Этот способ позволяет найти усилия в любом стержни фермы независимо от усилий в других стержнях. Однако предварительно необходимо определить реакции опор фермы.
Способ Риттера состоит в том, что ферма рассекается на две части так, чтобы в сечении было не более трех стержней с неизвестными усилиями, которые не сходятся в одном узле. Отвергая отсеченную часть фермы и рассматривая равновесие той части, оставшейся под действием приложенных внешних сил и усилий, которые заменяют действие рассеченных стержней, получим для этой части фермы три уравнения равновесия с тремя неизвестными усилиями. Чаще всего эти уравнения являются условиями равенства нулю алгебраических сумм моментов сил относительно трех разных центров моментов, за которые выбирают точки парного пересечения рассеченных стержней с числа перерезанных. Эти точки называются точками Риттера.
Если два стержня из трех рассеченных параллельны, то одна точка Риттера удаляется в бесконечность. Тогда составляют два уравнение моментов сил и одно уравнение проекций сил на ось, перпендикулярную к параллельным стержням.
Пример 2. Определить усилия в стержнях 1, 2, 3 фермы, если

Решение. Найдем реакции в опорах фермы 



Отсюда находим 
Для определения усилия 
Для определения усилия 

Подставляя необходимые данные, находим
Итак, усилия 


Но, с другой стороны, взаимосвязь между построением новых вершин диаграммы Максвелла – Кремоны и положением предыдущих, следует рассматривать как определенное ограничение погрешностей, позволяет избежать грубых
ошибок.
Метод Риттера в отличие от предыдущего не приводит к накоплению ошибок, так как все усилия определяются независимо друг от друга, но одновременно не дает возможности заметить грубые ошибки, которые могут случиться при исчислении.
Очевидно, лучшая методика определения усилий в стержнях фермы заключаться в сочетании методов Максвелла – Кремоны и Риттера. Например, все усилия определяются по методу Максвелла – Кремоны и некоторые из них проверяются методом Риттера.
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Содержание:
Расчет ферм:
При устройстве перекрытий, постройке мостов, кранов, мачт для высоковольтных линий и т. п. применяются конструкции, называемые фермами.
Фермой называется геометрически неизменяемая система, состоящая из невесомых стержней, соединенных между собой по концам шарнирами. Места соединения стержней между собой называются узлами фермы.
Обычно в фермах соединение стержней в узлах осуществляется при помощи клепки или сварки, шарнирное же соединение стержней вводится лишь для облегчения расчета ферм, что приводит к сравнительно небольшим ошибкам в вычислении по сравнению с действительными конструкциями.
Фермы, у которых оси всех стержней расположены в одной плоскости, называются плоскими. В дальнейшем мы ограничимся рассмотрением плоских ферм.
Всякая ферма состоит из ряда стержневых треугольников, соединенных в узлах шарнирно (рис. 79).
Рис. 79.
Для образования фермы мы должны взять основной треугольник, хотя бы abc, и к нему последовательно присоединять каждый узел d, е и т. д. двумя стержнями. Если ферма состоит из
При расчете фермы, т. е. при определении усилий во всех ее стержнях, мы можем для каждого узла составить два уравнения равновесия, а для 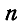
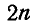
Отсюда следует, что число неизвестных усилий, определяемое числом стержней, сложение с числом опорных реакций не должно превышать общего числа уравнений статики 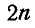
Для определения усилий в стержнях ферм обычно применяют один из следующих трех способов: последовательное вырезание узлов, построение диаграммы Кремона, проведение сквозных сечений (Риттера).
При применении каждого из перечисленных способов следует предварительно по заданным силам, приложенным к ферме, определить опорные реакции (аналитически или графически) и только после этого переходить к определению усилий в стержнях фермы.
Определение усилий по способу последовательного вырезания узлов
Определение усилий по способу последовательного вырезания узлов заключается в том, что последовательно рассматривают равновесие каждого узла фермы и для рассматриваемого узла либо составляют два уравнения равновесия в форме 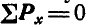
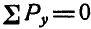
При этом порядок рассмотрения равновесия узлов безразличен, лишь бы в рассматриваемом узле число неизвестных усилий не превышало двух.
Выясним применение этого способа на отдельных примерах.
Задача №1
Найти усилия 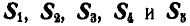
Рис. 80.
Решение. Начнем с рассмотрения равновесия узла А, так как здесь сходятся два неизвестных усилия. Вырежем узел А и взамен пересеченных стержней введем силы 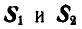
Вырежем теперь узел В и рассмотрим его равновесие (рис. 80, в):
откуда получаем:
Переходим к рассмотрению равновесия узла С (рис. 80, г):
откуда находим:
Составляя уравнения равновесия для точки D (рис. 80, д), имеем:
откуда
Для усилия 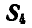
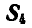
Правильное направление стрелок усилий показано на рисунке 80, а.
Иногда при определении усилий в стержнях полезно сразу выделить те стержни, усилия в которых равны нулю (нулевые стержни). Из рассмотрений равновесия узлов А и С (рис. 80, б и. 80, г) заключаем:
1. Если имеется узел А, в котором сходятся два стержня, то при отсутствии других сил, приложенных к узлу, усилия в этих стержнях равны нулю.
2. Если имеется узел С, где сходятся три стержня, из которых два направлены по одной прямой, а третий примыкает к узлу под любым углом, то при отсутствии других сил, приложенных к узлу, усилие в третьем стержне равно нулю. На основании этого можно сказать, что усилия в стержнях 1, 2, 3, 4, 5 и 6 фермы (рис. 79) равны нулю.
Задача №2
Сцепка состоит из четырех тросов АО, ВО, АС и ВС, образующих квадрат (рис. 81, а).
Между точками А и В по диагонали квадрата вставлен брус, а в точках А, В и С приложены вертикальные силы Q = 500 кГ каждая. Определить натяжения 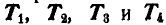
Решение. Из рассмотрения равновесия точки С (рис. 81, б) имеем:
откуда:
Переходим к рассмотрению равновесия узла А (рис. 81, в):
откуда
Рис. 81.
В силу симметрии узлов А и В заключаем, что 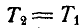
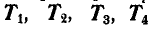
Задача №3
В точках А и F шарнирной стержневой системы (рис. 82, а), внешний контур которой совпадает со сторонами правильного шестиугольника, приложены силы 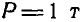
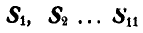
Рис. 82.
Решение. Эту задачу проще всего решить геометрическим способом, построив для каждого из узлов замкнутый треугольник сил. Рассмотрим сначала равновесие точки А (можно F). Отложим в выбранном масштабе силу Р (рис. 82, б) и из начала и конца этой силы проведем направления, параллельные стержням 1 и 6, до их взаимного пересечения. В полученном треугольнике равновесия стрелки сил 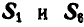
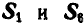
При построении треугольника равновесия для точки В известной нам силой является реакция 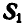
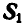
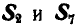
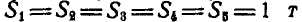
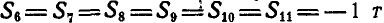
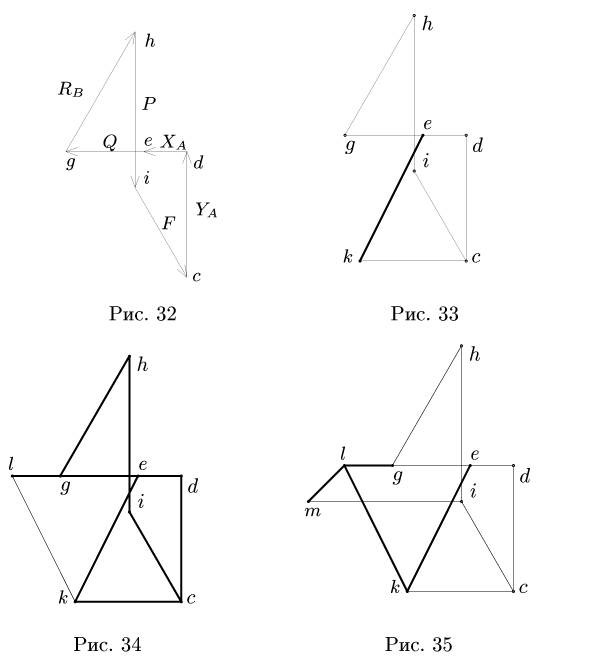
Задача №4
Способом последовательного вырезания узлов определить усилия во всех стержнях ферм (рис. 83 и 84).
Рис. 83. Рис. 84.
Ответ (к рис. 83).
Таблица 1
Ответ (к рис. 84).
Таблица 2
Определение усилий в стержнях ферм по способу построения диаграммы Кремона
Идея этого графического способа проста и заключается в построении для узлов фермы, находящихся в равновесии, замкнутых многоугольников сил, образующих диаграмму.
Пусть требуется найти усилия во всех стержнях фермы (рис. 85, а) при действии на нее заданных сил 2 т и 8 т. Известными нам способами находим, что левая опорная реакция равна 4 т, а правая 6 т.
Для облегчения построения диаграммы введем в рассмотрение внешние и внутренние поля. Под внешними полями будем понимать части плоскости, ограниченные с боков внешними силами (заданными и реактивными) и внешним контуром фермы, под внутренними полями — части плоскости, ограниченные стержнями фермы.
Рис. 85.
Условимся нумерацию внешних полей 1, 2, 3 и 4 (рис. 85, а) производить по направлению движения стрелки часов, внутренних 5, 6, 7, 8 — слева направо, а усилия, сходящиеся в каждом узле обозначать двойными цифрами смежных полей, производя обход усилий в каждом узле по часовой стрелке. Так, например, в узле а сходятся три усилия: 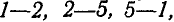
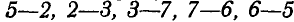
Выбрав масштаб сил, например 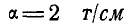
Построение диаграммы следует начинать для того узла, в котором сходятся не более двух стержней. В нашем случае такими узлами являются 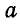
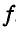
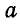
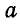
Теперь можно перейти к следующему узлу, где сходятся два неизвестных усилия; таким узлом является 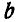
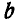
Переходим к узлу с. Здесь сходятся усилия 6—5, 5—2, 2—3, имеющиеся на диаграмме, и неизвестные 3—7 и 7—6. Проводим из точки 3 диаграммы направление, параллельное стержню 3—7, а из точки 6 направление, параллельное стержню 7—6; в пересечении этих направлений получаем на диаграмме точку 7. Подобные построения можно провести для остальных узлов. Узел 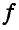
Имея диаграмму Кремона (рис. 85, б), можно:
1. Проверять правильность построенной диаграммы, основываясь на том, что многоугольник сил для каждого узла должен быть замкнут. Возьмем, например, узел d, в котором сходятся усилия 7—3, 3—4, 4—8, 8—7. Мы видим, что эти усилия на диаграмме образуют замкнутый многоугольник.
2. Определять величину и знак усилия в любом стержне, примыкающем к какому-либо узлу. Так, например, если возьмем стержень 3—7, примыкающий к узлу с (если бы мы переставили цифры и рассматривали стержень 7—3, то тогда мы обязаны были бы его отнести к узлу d), то на диаграмме величина усилия, возникающего в этом стержне, выражается отрезком 3—7, умноженным на масштаб, а направление будет к узлу с, так как на диаграмме усилие 3—7 читается от 3 к 7, т. е. справа налево. Точно так же усилие в стержне 7—6 изобразится на диаграмме отрезком 7—6, умноженным на масштаб α , а направление усилия будет от узла с, так как при чтении усилия 7—6 на диаграмме оно направлено от 7 к 6, т. е. сверху вниз по диагонали. Следовательно, в первом случае мы имеем сжатие (—), во втором — растяжение (+).
Задача №5
Определить усилия в стержнях ферм путем построения диаграммы Кремона (рис. 86, а и 87, а).
Рис. 86.
Рис. 87.
Решение. На рисунках 86, б и 87, б приведено построение диаграмм.
Определение усилий в стержнях ферм по способу сквозных сечений
Особенность этого способа состоит в том, что он позволяет определять усилие в любом стержне фермы, не определяя усилий в остальных стержнях, что во многих случаях является удобным.
Выясним применение этого способа на отдельном примере.
Пусть дана ферма (рис. 88, а), стержни которой образуют между собой углы в 45° и 90°. Определим сначала величины опорных реакций аналитически или способом веревочного многоугольника. Нетрудно видеть, что
Пронумеровав стержни, можно перейти к определению усилий, возникающих в стержнях, по способу сквозных сечений. Положим, требуется найти усилие 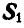
Рассмотрим теперь равновесие одной из частей фермы, расположенной слева или справа от проведенного сечения. В данной задаче удобнее выделить левую часть, так как на нее действует меньше сил (рис. 88, б).
Взамен отброшенной правой части прикладываем реакции стержней 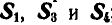
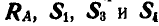

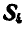

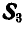
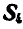
Рис. 88.
Нетрудно видеть, что таким. уравнением является уравнение моментов относительно той точки, где пересекаются линии действия усилий 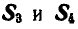
откуда
Чтобы определить усилие 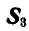
откуда
Для определения усилия 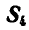
откуда
Знак минус указывает на то, что стержень 4 сжат,
Точки 1, 3; 3, 4 и 1, 4, выбранные таким образом, приводят нас к уравнениям равновесия (36, б).
При определении усилия 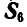
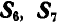
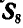
Для определения усилия 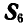
откуда
При определении усилия в стержне 7 следовало бы составить уравнение моментов относительно точки 6, 8, пересечения стержней 6 и 8, но эти стержни параллельны и точка 6, 8 получается в бесконечности; в этом случае вместо уравнения моментов составляют уравнение проекций на ось, перпендикулярную к линиям действия тех реакций стержней, которые параллельны:
откуда
Подобным же способом можно определить усилия и в остальных стержнях.
Преимущество изложенного способа заключается в том, что здесь мы можем определить усилие в любом стержне, не определяя усилий в остальных стержнях.
Рис. 89.
Задача №6
Определить по способу сквозных сечений усилия во всех стержнях фермы (рис. 89).
Указание: предварительно определяем реакцию 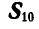
Ответ (к рис. 89) см. в таблице 3.
Таблица 3
Задача №7
По известному усилию в стержне 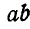
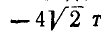
Рис. 90.
Ответ (к рис. 90) см. таблицу 4.
Таблица 4
Статически определимые фермы. Методы вырезания узлов и сквозного сечения
Плоская или пространственная неизменяемая конструкция, составленная из шарнирно соединенных между собой стержней, называется фермой.
На рис. 135 изображена простая плоская ферма (пример пространственной фермы приведен в § 19-4).
Если число узлов (шарниров) фермы n, а число стержней k, то в простой плоской ферме соблюдается условие
k=2n + 3
Ферма называется статически определимой, если усилия во всех стержнях фермы, нагруженной в шарнирах, можно определить при помощи уравнений равновесия.
Все. плоские простые фермы статически определимы.
Для определения усилий в стержнях ферм употребляются графические или аналитические методы. Рассмотрим только аналитические методы: метод вырезания узлов (задача 103-17) и метод сквозного сечения—метод Риттера (задача 104-17).
При использовании метода вырезания узлов необходимо придерживаться следующего порядка:
- а) выяснить, какие нагрузки действуют на ферму, как они направлены и где приложены, а затем определить реакции связей, используя уравнения равновесия Правильность этой части решения нужно обязательно проверить: для проверки можно использовать любое дополнительно составленное уравнение равновесия;
- б) затем следует определить усилия в стержнях фермы, начиная с того узла, на который действуют не более двух неизвестных сил, так как в каждом случае на узел действует система сходящихся сил и, следовательно, для одного узла можно составить лишь два уравнения равновесия;
- в) вырезав узел, необходимо заменить действие на узел отброшенной части фермы усилиями, действующими вдоль стержней, считая при этом, что все стержни растянуты, а затем составить уравнения равновесия;
- г) путем перехода от узла к узлу определяют усилия во всех стержнях, один из узлов при этом остается нерассмотренным; составив уравнения равновесия для этого узла, можно проверить правильность решения задачи.
При определении усилий в стержнях ферм по методу сквозного сечения необходимо придерживаться следующего порядка:
- а) прежде всего, так же как и при методе вырезания узлов, выявив все нагрузки, определить реакции опор;
- б) мысленно разрезать фермы на две части таким образом, чтобы разрез проходил не более чем через три стержня, усилия в которых неизвестны”1, и, отбросив одну из частей, заменить действие отброшенной части на оставшуюся усилиями, направленными вдоль стержней, предполагая при этом, что все разрезанные стержни (с неизвестными усилиями) растянуты;
- в) составить три уравнения равновесия; при выборе направлений осей проекций, а также центра моментов нужно исходить из того, чтобы в каждое из уравнений по возможности входило не более одной неизвестной силы.
Задача №8
Определить усилия в стержнях фермы, нагруженной, как показано на рис. 136, а, тремя силами: 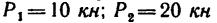
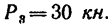
Решение — методом вырезания узлов.
1. Освободим ферму от связей и заменим связи их реакциями. Действие подвижного шарнира А заменим реакцией 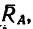
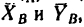
Составим три уравнения равновесия:
Подставив в эти уравнения числовые значения и решив находим (вычисления рекомендуем произвести самостоятельно):
* При разрезании фермы через четыре и большее число стержней образуется плоская система сил с четырьмя или соответственно большим числом неизвестных. Так как для произвольной плоской системы сил можно составить только три уравнения равновесия, задачу решить нельзя.
Для проверки можно использовать уравнение проекций сил на ось у или уравнение моментов сил относительно точки С (или D, или Е, или F).
2. Вырежем узел А, заменив действие на узел отброшенной части фермы силами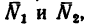
силы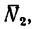
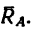
Из уравнения (2)
(стержень 1 сжат).
Из уравнения (1)
(стержень 2 растянут).
3. Вырежем узел С, заменив действие на узел отброшенной части фермы силами 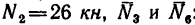
Отсюда
(стержень 6 растянут);
(стержень 3 растянут).
4. Вырежем узел D. В этом случае узел находится в равновесии иод действием пяти сил, три из них известны: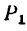
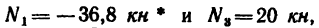
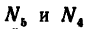
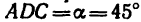
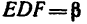
определить, что 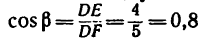
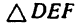
FE=3 л, катет DЕ = 4 м и, следовательно, гипотенуза DF=5 м), a
Составим уравнение равновесия:
Из уравнения (6)
(стержень 5 растянут).
Из уравнения (5)
(стержень 4 сжат).
5. Вырежем узел Е, к которому приложены четыре силы: две из них известны (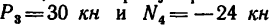
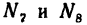
Расположив оси проекций, как показано на рис. 140, и замечая, что угол 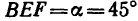
* Хотя из рассмотрения условия равновесия узла А установлено, что усилие в стержне 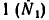
Из уравнения (7)
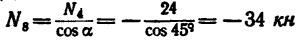
Из уравнения (8)
(стержень 7 сжат).
6. Вырежем узел В, к которому приложены четыре силы: реакции 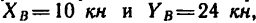

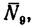
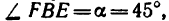
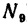
из которого
(стержень 9 растянут).
Усилия, возникающие во всех стержнях под действием внешних нагрузок, определены. Теперь_ рассмотрим узел F. Вырезав этот узел и составив для сил 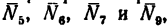
Найденные значения усилий в стержнях целесообразно представить в виде таблицы:
Задача №9
Определить усилия в стержнях 4, 5 и 6 фермы, нагруженной тремя силами: 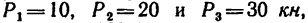
Решение.
1. Так же как и при решении методом вырезания узлов, прежде всего определяем реакции опор; в данном случае они те же, что и в предыдущем примере:
2. Разрежем ферму через стержни 4, 5 и 6 и, отбросив правую ее часть, заменим действие правой части на левую силами 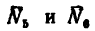
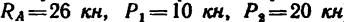
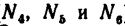
3. Составим три уравнения равновесия:
Из уравнения (1)
(стержень 5 растянут).
Из уравнения (2)
(стержень 6 растянут).
Из уравнения (3)
(стержень 4 сжат).
Сравнивая найденные числовые значения усилий в 4, 5 и 6 стержнях фермы с теми, которые для этих же стержней получены в задаче 103-17, видим, что они одинаковы.
Правильность решения здесь можно проверить, составив уравнение проекций сил на ось х. Для проверки это уравнение вполне надежно, так как в него входят все три искомые силы. Проверку решения этим способом рекомендуется произвести самостоятельно.
- Заказать решение задач по теоретической механике
Ферма и аналитические методы расчета
Постановка задачи:
Плоская ферма опирается на неподвижный и подвижный шарниры. К узлам фермы приложены нагрузки. Найти усилия в стержнях фермы методом Риттера
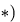
Эта задача является усложненным вариантом задачи, где усилия в стержнях можно было легко определить только из уравнений проекций, не находя реакции опор и не привлекая понятие момента силы. Аналогично можно поступить и в этой задаче, однако порядок системы линейных уравнений, описывающей равновесие всех узлов, будет велик, поэтому, во-первых, надежно решить такую систему можно только с помощью компьютера, во-вторых, таким образом будет проделана лишняя работа, так как система уравнений содержит усилия всех стержней, в том числе и тех, которые по условию задачи не требуется определять. Поэтому для решения сложных ферм, содержащих большое число стержней, применим метод Риттера, основная идея которого — независимое определение усилий в стержнях. Эту же идею можно с успехом применять и в других задачах статики.
План решения:
1. Освобождаем ферму от внешних связей. Действие опорных шарниров заменяем их реакциями. Для определения реакций опор составляем три уравнения равновесия.
2. Проверяем найденные реакции, составляя еще одно уравнение равновесия фермы.
3. В тех стержнях, где это возможно, усилия находим методом Риттера
Рассматриваем равновесие одной из частей фермы (как правило, где меньше нагрузок). Для стержней, усилия в которых необходимо определить, находим точки Риттера (моментные точки). Они являются точками попарного пересечения линий действия сил в рассеченных стержнях. Искомые усилия определяем из уравнений моментов рассматриваемой части относительно точек Риттера.
Если два стержня в сечении параллельны, то точки Риттера для третьего стержня не существует, и для определения усилия в нем необходимо составить уравнение проекций на ось, перпендикулярную параллельным стержням.
В уравнение метода Риттера всегда входит усилие только одного стержня. Это позволяет искать усилия независимо одно от другого,
уменьшая тем самым возможность ошибок и избегая накопления неизбежных погрешностей округления в численных расчетах.
4. Определяем усилия методом вырезания узлов. Этот метод применяют в тех случаях, когда сечения Риттера для нужного стержня не существует. Вырезаем узел фермы, к которому подходит стержень с искомым усилием. Выбираем оси и составляем уравнения равновесия узла в проекциях. Решаем уравнения относительно искомого усилия. Если к узлу подходит более двух стержней с неизвестными усилиями, то метод вырезания узлов можно комбинировать с методом Риттера.
Задача №10
Плоская ферма опирается на неподвижный и подвижный шарниры (рис. 22). К узлам фермы приложены две вертикальные нагрузки Р — 90 кН и две наклонные 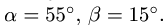
Решение
1. Освобождаем ферму от внешних связей. Действие опор заменяем их реакциями. Левую (неподвижную) шарнирную опору заменяем двумя составляющими реакции 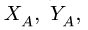
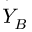
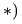
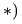
Система уравнений состоит из трех независимых друг от друга уравнений, решение которых легко найти, подставив численные значения нагрузок и углов из условия
2. Проверяем найденные вертикальные реакции, составляя уравнение проекций всех сил на ось у:
Горизонтальную реакцию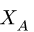
3. Методом Риттера находим усилия в стержнях 1, 2, 3. Сечением I-I (рис. 23) мысленно разделяем ферму на две части, пересекая три стержня.Действие разрезанных частей заменяем их усилиями.
Рассматриваем левую часть (рис. 24), на которую действуют четыре известных силы 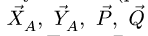
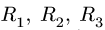
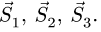
Точка 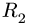
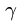
Уравнения метода Риттера имеют вид
Находим решение системы:
4. Методом вырезания узлов определяем 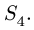
Усилие больше нуля, следовательно, стержень 4 растянут. Усилие в стержне 5 методом Риттера определить нельзя — не существует сечения, делящего ферму на две части и пересекающего при этом три стержня. В этом состоит недостаток метода. Поэтому воспользуемся методом вырезания узлов совместно с методом Риттера. Находим 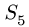
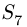
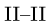
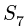
Находим 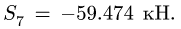
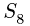
Вырезаем узел D и составляем уравнения равновесия (рис. 27):
Исключая 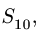
Результаты расчетов в кН занесем в таблицу:
Второе свойство имеет исключения. Существуют фермы, которые одним сечением можно разделить на две, рассекая N > 3 стержней. При этом для одного из стержней существует точка Риттера — точка пересечения остальных N — 1 стержней (подумайте, как выглядит такая ферма).
2. Сечение Риттера не обязательно должно изображаться непрерывной линией. В ферме на рис. 4, с. 15 для определения усилия в стержне АВ надо выполнить разрывное сечение (какое?). Экспериментируя с сечениями, не забывайте про три его основных свойства.
3. Рассматривая одну из частей рассеченной фермы, забудьте на время о существовании другой. Иначе в уравнения равновесия вы можете случайно включить внешние силы или реакции опор отброшенной части.
4. Не стоит беспокоиться, если точка Риттера находится на отрезанной части, располагается где-нибудь далеко или попадает на шарнир. Ее положение может быть где угодно.
5. В уравнения метода Риттера (моментов или проекций) должно войти только одно усилие стержня фермы. В этом основной смысл метода Риттера. Очень часто встречается следующая ошибка. Составляя уравнение, студент неправильно выбирает точку Риттера или составляет не то уравнение, например, уравнение проекций вместо уравнения моментов. При этом в уравнение кроме одного неизвестного усилия входят и другие, ранее найденные. В принципе такое уравнение может быть и верно, и ответ получится верным, но это не метод Риттера, где определение усилий производится независимо одно от другого во избежание накопления ошибок.
6. Положение точки Риттера для каждого стержня не зависит от рассматриваемой части. Однако степень сложности уравнения моментов для разных частей фермы может существенно отличаться. Для большей надежности решения уравнение Риттера (в форме уравнения моментов или уравнения проекций) для одной части может служить проверочным для другой.
7. Проверить расчет можно на компьютере.
Ферма и графический расчет
Постановка задачи:
С помощью диаграммы Максвелла-Кремоны найти усилил в стержнях фермы.
План решения:
Графический метод расчета ферм является дополнением к аналитическим методам расчета, которые вы изучили в предыдущем параграфе. Диаграмма Максвелла-Кремоны состоит из отдельных силовых многоугольников. Каждый многоугольник соответствует равновесию какого-либо узла фермы.
1. Обозначаем усилия в стержнях фермы.
2. Освобождаем ферму от связей. Действие опор заменяем их реакциями. Составляем три уравнения равновесия. Находим реакции.
3. Проверяем найденные реакции, составляя еще одно уравнение равновесия.
4. Изображаем все силы, действующие на ферму (включая найденные аналитически реакции опор), в виде векторов вне фермы. Если реакция опоры отрицательная, то заменяем ее направление на противоположное. Для графического способа требуются только реальные направления реакций.
5. Обозначаем буквами или цифрами внешние поля — области чертежа, разделенные силами и стержнями фермы.
6. Обозначаем буквами или цифрами внутренние поля — области, ограниченные стержнями фермы.
7. Внешним нагрузкам и усилиям в стержнях даем новые имена — по соседним с силой (или стержнем) полям.
8. Построение диаграммы Максвелла-Кремоны начинаем с многоугольника внешних сил. Выберем направление обхода фермы (по часовой стрелке или против). Начинаем с произвольной силы. Откладывая ее в масштабе и соблюдая направление, обозначаем на диаграмме начальную и конечную точку строчными буквами, соответствующими ее новому обозначению по направлению обхода. Следующая сила пристраивается к концу первой и т.д. до замыкания многоугольника внешних сил и реакций опор.
9. Строим точки внутренних полей на диаграмме. Точку, соответствующую внутреннему полю, можно найти, если у этого поля построены точки двух соседних с ней полей.
Таким образом, начинать графический расчет можно с поля, у которого имеется два соседних с ним внешних поля, уже отмеченные на диаграмме. Искомая точка лежит на пересечении прямых, параллельных стержням, имена которых состоят из имени искомой точки и точек найденных внешних полей. Этот пункт выполняем многократно, до полного построения диаграммы. Модули усилий в стержнях равны длинам соответствующих отрезков на диаграмме.
10. Определяем знаки усилий. Рассматриваем шарнир фермы, к которому подходит какая-либо внешняя нагрузка или стержень с усилием известного знака. Равновесие шарнира изображено на диаграмме замкнутым силовым многоугольником с заданным направлением обхода. Сопоставляя направление усилия на диаграмме и его направление в вырезанном узле, определяем знак усилия. Если направление вектора на многоугольнике совпадает с направлением вектора, приложенного к узлу, то усилие больше нуля. В противном случае — усилие меньше нуля, т.е. стержень сжат.
Задача №11
С помощью диаграммы Максвелла-Кремоны найти усилия в стержнях фермы (рис. 28).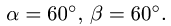
Решение
1. Обозначаем усилия в стержнях фермы так, как это принято в строительной механике. Усилия в стержнях верхнего пояса (слева направо) — 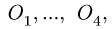
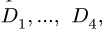
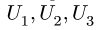
2. Определяем реакции опор фермы. Реакцию 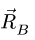
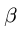
Решаем уравнения и получаем следующие значения:
3. Проверяем вертикальные реакции, составляя уравнение проекций на вертикальную ось:
4. Изображаем все силы, действующие на ферму. Реакцию 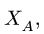
5. Обозначаем внешние поля — области чертежа, разделенные силами и стержнями фермы, — 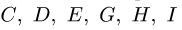
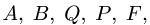
6. Обозначаем внутренние поля 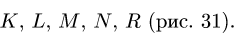
7. Внешним нагрузкам и усилиям в стержнях даем новые имена — по соседним с силой (или стержнем) полям. Приведем таблицу соответствия имен.
8. Строим многоугольник внешних сил. Выберем направление обхода фермы по часовой стрелке. Начинаем с произвольной силы, например, F = 20 кН. Откладывая в масштабе эту силу и соблюдая ее направление, обозначаем начальную и конечную точку строчными буквами г и с, соответствующими направлению обхода — из поля I в поле С. Следующая по часовой стрелке нагрузка — вертикальная реакция опоры 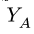
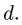
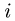
9. Строим точки внутренних полей на диаграмме. Точку, соответствующую внутреннему полю, можно найти, если у этого поля построены два соседних с ним поля. Таким образом, начинать графический расчет можно с поля у которого соседние поля Н и G определены на диаграмме, или К с известными соседними полями Е и С (рис. 31). Рассматриваем поле К. По направлению стержней ЕК и КС проводим линии через точки ей с диаграммы. Точка их пересечения — 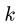
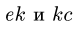
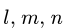
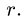
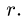
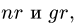
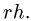
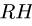
10. Определяем знаки усилий. Рассмотрим, например, усилие Ох. Вырезаем узел А, к которому приложено усилие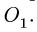
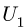
Здесь обход cdek против часовой стрелки задает реакция опоры 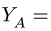
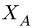
Если направление вектора на многоугольнике совпадает с направлением вектора, приложенного к узлу, то усилие больше нуля — стержень растянут. В противном случае — усилие 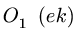
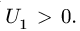
Окончательные результаты в кН заносим в таблицу:
- Замечание 1. Точность, с которой можно получить усилия графическим способом, обычно невысока. Результаты с тремя знаками после запятой, данные в таблицах, получены, конечно, не графически, а из решения задачи аналитическим методом вырезания узлов
.
- Замечание 2. Графический способ расчета ферм в реальной инженерной практике безнадежно устарел, для расчета пространственных ферм он вообще не годится. Однако в учебных целях, для проверки аналитического решения и как пример изящного и быстрого определения усилий с помощью карандаша и линейки, диаграмма Максвелла-Кремоны сохраняет свое значение.
- Замечание 3. В качестве необычной задачи программирования, предлагаем попробовать найти алгоритм автоматического построения диаграммы Максвелла-Кремоны в системе Maple V, Maple 7, Mathematics 4 или в любом другом пакете, позволяющем работать с графикой. Основное требование к программе — не составлять уравнения равновесия узлов фермы в проекциях. Допустимо найти аналитическим методом реакции опор.
Пространственная ферма
Постановка Задачи. Определить усилия е стержнях пространственной фермы, нагруженной в одном узле силами.
План решения:
Задача является естественным обобщением задачи § 1.1, с. 14, в которой методом вырезания узлов определялись усилия в простейшей плоской ферме. Этот же метод применим и здесь, единственное отличие — вместо двух уравнений равновесия узла в проекциях на оси в пространственной задаче будет три уравнения.
1. Узлы фермы находятся в равновесии. Вырезаем узлы, заменяя действие стержней их реакциями. Реакцию незагруженного стержня направляем вдоль его оси. Используя правило знаков, согласно которому усилие растянутого стержня считается положительным, реакцию каждого стержня направляем из шарнира по направлению внешней нормали сечения стержня. Расчет начинаем с узла, к которому подходят три стержня с неизвестными усилиями.
2. Для каждого из шарниров составляем по три уравнения равновесия в проекциях. Решаем полученную систему.
Задача №12
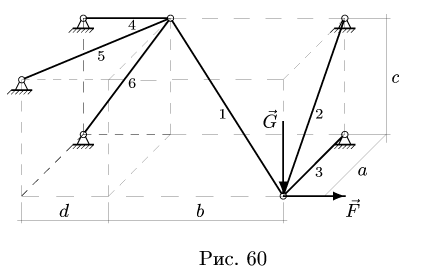
Найти усилия в стержнях 1-6 пространственной фермы, нагруженной в одном узле вертикальной силой G = 100 кН и горизонтальной F = 40 кН. Даны размеры а = 12 м, b = 16 м, с = 10 м, d = 5 м (рис. 60).
Решение
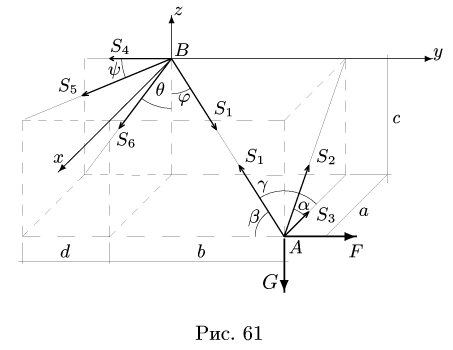
1. Узлы А и В находятся в равновесии. Вырезаем эти узлы, заменяя действие стержней их реакциями, направленными из узла к стержню(рис 61.)
Стержень 1 является общим для обоих узлов, поэтому на рисунке есть два противоположно направленных вектора с усилием 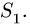
2. Расчет начинаем с узла А, к которому подходят три стержня с неизвестными усилиями. Составляем уравнения равновесия узла в проекциях на три оси координат:
Система уравнений (1) содержит три неизвестных усилия
Вычисляем тригонометрические функции, входящие в уравнения.
Решение системы (1):
Знаки найденных усилий показывают, что стержни 1 и 2 растянуты, а стержень 3 сжат. Составляем уравнения равновесия узла В:
Уравнения (2) содержат три неизвестных усилия 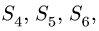
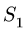
Решение системы (2):
Знаки найденных усилий показывают, что стержни 5 и 6 сжаты, а стержень 4 растянут.
Результаты расчета (в кН) заносим в таблицу:
- Пространственная система сходящихся сил
- Момент силы относительно точки и относительно оси
- Теория пар, не лежащих в одной плоскости
- Произвольная пространственная система сил
- Параллельные силы
- Произвольная плоская система сил
- Равновесие системы, состоящей из нескольких тел
- Графостатика в теоретической механике
Раздел 1. Теоретическая
механика
Тема 1.6. Равновесие системы тел
Лекция 1. Равновесие системы тел. Расчет
плоских ферм. Равновесие при наличии трения скольжения
Цель: изучение равновесия
системы тел и равновесия при наличии трения скольжения. Знакомство с методикой
расчета плоских ферм.
Задачи:
1.
Изучить равновесие системы тел, научиться
рассчитывать плоские фермы. Ознакомиться с видами трения и равновесием
тел при наличии трения скольжения.
2.
Совершенствовать умение применять основные термины
и формулы на практике.
3.
Способствовать пониманию
сущности и социальной значимости своей будущей профессии, проявлению к ней
устойчивого интереса.
Информационное
обеспечение:
Основная литература:
1.
Олофинская В.П. Техническая механика. Курс лекций с
вариантами практических и тестовых заданий. – М.: ФОРУМ-ИНФРА-М, 2013.
2.
Сафонова Г.Г., Артюховская Т.Ю., Ермаков Д.А.
Техническая механика. – М.: ИНФРА-М, 2013.
3.
Эрдеди А.А. Техническая механика.- М.: Изд. центр
«Академия», 2017.
Дополнительная
литература:
1.
Аркуша
А.И., Фролов М.И. Техническая механика. – М.: Высшая школа, 1983.
2.
Аркуша
А.И. Руководство к решению задач по теоретической механике. – М.: Высшая
школа, 1976.
3.
Эрдеди
А.А., Медведев Ю.А., Эрдеди Н.А. Техническая механика. – М.: Высшая школа,
1991.
Интернет-ресурсы:
http:/antigtu.ru/video–l–p/ –
видеолекции по теоретической механике, по деталям машин; электронные лекции по
механике и сопромату; готовые решения задач из различных задачников.
Содержание
1.
Равновесие системы тел
2.
Расчет плоских ферм
3.
Понятие о трении. Виды трения
4.
Равновесие тел при наличии трения скольжения
1. Равновесие системы тел
Система тел – это несколько тел, соединенных
между собой каким-то образом. На эти тела действуют внутренние и внешние силы.
Внутренние – силы взаимодействия между
телами одной и той же системы.
Внешние – силы, с которыми на тела
данной системы действуют тела, не входящие в нее.
Система тел, для которых число неизвестных реакций связей равно
числу уравнений равновесия,
называются статически определимыми. Система тел, для которых число
неизвестных реакций связей больше числа уравнений равновесия,
называются статически
неопределимыми.
Если при отбрасывании
внешних связей (опор) конструкция остается жесткой, то для нее задача о
равновесии решается как для абсолютно твердого тела (при действии плоской
системы сил число неизвестных реакций связей не должно быть больше трех).
Если после отбрасывания
внешних связей конструкция не считается жесткой, то наиболее рациональным
способом решения подобных задач является расчленение конструкции на отдельные
тела и составление уравнений равновесия для каждого из тел в отдельности.
Для конструкции
из n тел, на каждое из которых
действует произвольная плоская система сил, получится таким путем 3n уравнений равновесия, позволяющих найти 3n неизвестных.
Рассмотрим равновесие трехшарнирной арки
(рисунок1).
Рис.1 Трехшарнирная арка
F1, F2, F3 – силы, действующие на арку; XA, YA, XB, YB – реакции
опор А и В; m – момент
Например, если отбросить опоры А и В трехшарнирной
арки, то она не будет жесткой: ее части могут поворачиваться вокруг
шарнира С.
Для определения реакций внешних
связей ХА, YА, ХВ,YВ расчленим
конструкцию по соединительному шарниру С на две части и
рассмотрим равновесие каждой из частей в отдельности (рисунок 2).
Рис.2. Расчленение арки на две части
При действии на трехшарнирную арку
произвольной плоской системы сил для каждой части можно записать три уравнений
равновесия:
для АС для СВ
Присоединив к этой системе шести уравнений,
на основании закона о действии и противодействии, уравнения для узла С (), получим систему уравнений, из которой можно найти реакции
внешних связей ХА, YА, ХВ, YВ и реакции
внутренних связей ХС, YС.
2. Расчет плоских ферм
Фермой называется жесткая
конструкция из прямолинейных стержней, соединенных на концах шарнирами. Если
все стержни фермы лежат в одной плоскости, ферма называется плоской.
Места соединения стержней фермы называют узлами. Все внешние нагрузки к
ферме прикладываются только в узлах. При расчете фермы трением в узлах и весом
стержней (по сравнению с внешними нагрузками) пренебрегают или распределяют
веса стержней по узлам. Тогда на каждый из стержней фермы будут действовать две
силы, приложенные к его концам, которые при равновесии могут быть направлены
только вдоль стержня. Следовательно, можно считать, что стержни фермы работают
только на растяжение или на сжатие. Ограничимся рассмотрением жестких плоских
ферм, без лишних стержней, образованных из треугольников. В таких фермах число
стержней k и число узлов n связаны соотношением
k=2n-3
Расчет фермы сводится к определению
опорных реакций и усилий в ее стержнях.
Опорные реакции можно найти обычными
методами статики, рассматривая ферму в целом как твердое тело.
Усилия в стержнях можно определить двумя
методами: методом вырезания узлов и методом сечений (метод Риттера).
Метод вырезания узлов. Этим методом удобно
пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному
рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы. Ход
расчетов поясним на конкретном примере для плоской фермы (рисунок 3).
Рисунок 3. Плоская ферма
а) – расчетная схема; б) – схема узла III
Рассмотрим изображенную на рис. 3,а ферму,
образованную из одинаковых равнобедренных прямоугольных треугольников; действующие
на ферму силы параллельны оси х и равны: F1 = F2 = F3 = 2Н.
В этой ферме число узлов n =
6, а число стержней k = 9. Следовательно, соотношение между
ними выполняется, и ферма является жесткой без лишних стержней.
Составляя уравнения равновесия
для фермы в целом, найдем, что реакции опор направлены, как показано на
рисунке, и численно равны;
XA=3F=6 H.
YA=N=3/2F=3 H.
Переходим к определению усилий в
стержнях.
Пронумеруем узлы фермы римскими
цифрами, а стержни — арабскими. Искомые усилия будем обозначать S1 (в стержне 1), S2 (в стержне 2) и т. д. Отрежем
мысленно все узлы вместе со сходящимися в них стержнями от остальной фермы.
Действие отброшенных частей стержней заменим силами, которые будут направлены
вдоль соответствующих стержней и численно равны искомым усилиям S1, S2,
… Изображаем сразу все эти силы на рисунке, направляя их от узлов, т. е.
считая, все стержни растянутыми (рис. 3,а). Изображенную картину надо
представлять себе для каждого узла так, как это показано на рис. 3,б для
узла III. Если в результате расчета величина усилия в каком-нибудь стержне
получится отрицательной, это будет означать, что данный стержень не растянут, а
сжат. Буквенных обозначений для сил, действующих вдоль стержней, на рис. 2 не
вводим, поскольку ясно, что силы, действующие вдоль стержня 1, равны
численно S1, вдоль стержня 2 — равны S2 и т. д.
Теперь для сил, сходящихся в
каждом узле, составляем последовательно уравнения равновесия
Начинаем с узла 1, где сходятся
два стержня, так как из двух уравнений равновесия можно определить только два
неизвестных усилия.
Составляя уравнения равновесия для
узла 1, получим
F1+S2cos450=0, N+S1+S2sin450=0.
Отсюда находим
Теперь, зная S1, переходим к узлу II. Для него уравнения равновесия дают
S3+F2=0, S4–S1=0,
откуда
S3=-F=-2 H, S4=S1=-1 H.
Определив S4, составляем аналогичным путем уравнения
равновесия сначала для узла III, а
затем для узла IV. Из этих уравнений находим:
Наконец, для вычисления S9 составляем уравнение равновесия сил,
сходящихся в узле V, проекцируя их на ось By. Получим YA+S9cos450=0 откуда
Второе уравнение равновесия для
узла V и два уравнения для узла VI можно составить как проверочные. Для
нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них
были использованы три уравнения равновесия всей фермы в целом при
определении N, ХА, и YА.
Окончательные результаты расчета
можно свести в таблицу 1:
Таблица 1. Результаты
расчета усилий в стержнях
|
№ стержня |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Усилие, Н |
-1 |
-2,82 |
-2 |
-1 |
+1,41 |
-3 |
0 |
-3 |
-4,23 |
Как показывают знаки усилий,
стержень 5 растянут, остальные стержни сжаты; стержень 7 не нагружен (нулевой стержень).
Наличие в ферме нулевых стержней,
подобных стержню 7, обнаруживается сразу, так как если в узле, не нагруженном
внешними силами, сходятся три стержня, из которых два направлены вдоль одной
прямой, то усилие в третьем стержне равно нулю. Этот результат получается из
уравнения равновесия в проекции на ось, перпендикулярную к упомянутым двум
стержням.
Если в ходе расчета встретится узел, для
которого число неизвестных больше двух, то можно воспользоваться методом
сечений.
Метод сечений (метод Риттера). Этим методом удобно пользоваться
для определения усилий в отдельных стержнях фермы, в частности, для
проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две
части сечением, проходящим через три стержня, в которых (или в одном из
которых) требуется определить усилие, и рассматривают равновесие одной из этих
частей. Действие отброшенной части заменяют соответствующими силами, направляя
их вдоль разрезанных стержней от узлов, т. е. считая стержни растянутыми (как
и в методе вырезания узлов). Затем составляют уравнения равновесия, беря
центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только
одно неизвестное усилие.
Пример: для плоской фермы
(рисунок 4) определить усилия в стержнях 6, 7 и 8, если реакции опор RA =40
кН, RB =20 кН и нагрузка F = 60
кН.
Рисунок 4. Расчетная схема плоской фермы
А, В – опоры фермы, 1, 2, …11 – стержни фермы
При определении усилий
все стержни фермы условимся считать растянутыми, знак «минус» в ответе будет
означать, что стержень сжат. Определяем усилие в стержне 6 фермы. Для этого
проводим сечение I-I, рассекая не более трех стержней, в том числе стержень 6,
усилие в котором определяется. Мысленно отбрасываем левую часть фермы, заменяя
ее действие на оставшуюся правую часть усилиями N6, N7 и N8,
приложенными в соответствующих сечениях стержней и направленными в сторону
отброшенной части (рисунок 5).
Рисунок 5. Расчетная
схема для определения усилия в 6-м стержне
Чтобы определить усилие N6 независимо
от усилий N7 и N8,
составляем уравнение моментов сил, действующих на правую часть фермы,
относительно точки К, в которой пересекаются линии действия
сил N7 и N8. Эту точку
называют точкой Риттера.
Т.к. то
кН.
Воспользуемся тем же сечением для
определения усилия N7, независимо от усилий N6 и N8.
Спроецируем все силы, действующие на правую часть фермы, на вертикальную
ось Y, так как проекции сил N6 и N8 на
эту ось равны нулю:
кН.
Для определения усилия N8 составим
уравнение моментов этих же сил относительно точки Риттера L, в
которой пересекаются линии действия сил N6 и N7:
кН.
Знаки полученных ответов
показывают, что стержень 6 растянут, а стержни 7 и 8 сжаты.
3.Понятие о трении. Виды трения
Трение
или фрикционное взаимодействие (англ. friction) –
процесс взаимодействия тел при их относительном движении (смещении), или при движении тела в газообразной или жидкой среде.
По виду
относительного движения тел различают:
·
Трение покоя – оба тела неподвижны относительно друг друга;
·
Трение скольжения – одно тело поступательно перемещается по поверхности
другого;
·
Трение качения – одно из тел катится по поверхности другого тела
(рисунок 6).
Рисунок 6. Виды трения
По характеру взаимодействия трение принято разделять на:
§
Сухое – когда взаимодействующие тела не разделены никакими дополнительными
слоями (смазками). Редко встречается на практике;
§
Граничное – когда в области контакта могут содержаться слои и участки
различной природы (окисные пленки, жидкость и т.д.). Характерно для трения
скольжения;
§
Жидкостное (вязкое) – когда между контактирующими телами существуют слои
твердого тела, жидкости или газа различной толщины. Встречается обычно при
трении качения;
§
Смешанное – когда между телами есть участки сухого и жидкостного трения.
Прикладное значение трения.
В механизмах и машинах (двигатели внутреннего сгорания (ДВС),
автомобили, механические передачи и пр.) трение играет отрицательную роль,
приводя к быстрому износу узлов и деталей и снижая КПД (коэффициент полезного действия).
Для уменьшения трения применяют специальные масла и смазки, используют
напыление покрытий на детали.
В то же время за счет трения осуществляется сцепление с
поверхностью. Благодаря этому, мы можем передвигаться по земле, движется
транспорт, предметы сохраняют неподвижность (мебель в доме относительно пола,
здания относительно поверхности Земли и т.п.).
4.Равновесие
тел при наличии трения скольжения
Если к твердому телу, покоящемуся на шероховатой
горизонтальной поверхности, приложить горизонтальную силу F,
то действие этой силы вызовет появление силы трения Fтр = -F.
Сила трения (Fтр) – сила,
возникающая в плоскости касания тел и противодействующая перемещению тела.
Благодаря силе трения тело остается в покое при
изменении модуля силы F от нуля до некоторого
значения Fmax.
Модуль силы трения также
изменяется от 0 до Fтрmax в
момент начала движения. Модуль максимальной силы трения пропорционален
нормальному давлению N тела на плоскость, т.е. Fтрmax = fтрN.
Коэффициент
пропорциональности fтр является безразмерной
величиной и называется коэффициентом трения, который зависит
от материала и физического состояния соприкасающихся тел и определяется
экспериментально.
Может показаться удивительным, но именно
сила трения покоя разгоняет автомобиль. Ведь при движении автомобиля колеса не
проскальзывают относительно дороги, и между шинами и поверхностью дороги
возникает сила трения покоя (рис.7). Как легко видеть, она направлена в сторону
движения автомобиля. Величина этой силы не может превосходить максимального
значения трения покоя. Поэтому если на скользкой дороге резко нажать на газ, то
автомобиль начнет буксовать. А вот если нажать на тормоза, то вращение колёс
прекратится, и автомобиль будет скользить по дороге. Сила трения изменит своё
направление и начнёт тормозить автомобиль.
Рисунок 7. Схема движения колеса автомобиля
Сила трения при скольжении твёрдых тел
зависит не только от свойств поверхностей и силы давления (это зависимость
качественно такая же, как для трения покоя), но и от скорости движения. Часто с
увеличением скорости сила трения сначала резко падает, а затем снова начинает
возрастать.
При скольжении тела по
шероховатой поверхности возникает сила реакции, которая имеет
две составляющие – нормальную и силу трения скольжения (рисунок 8). Сила
трения скольжения, приложенная к одному из трущихся тел, направлена
противоположно его скорости относительно второго тела.
Рисунок 8. Схема
скольжения тела
N – нормальная
составляющая реакции , Fтр – сила трения скольжения
Рассмотрим твердое
тело на шероховатой поверхности (рисунок 9), находящееся под действием активных
сил в предельном состоянии равновесия, т.е. когда сила трения достигает своего
наибольшего значения при данном значении нормальной реакции.
Рисунок 9. Равновесие тела при максимальной силе
трения скольжения
В этом случае полная
реакция шероховатой поверхности отклонена от нормали к общей касательной
плоскости трущихся поверхностей на наибольший угол (Rmax).
Этот наибольший угол между полной реакцией, построенной на наибольшей силе
трения при данной нормальной реакции и направлением нормальной реакции,
называется углом трения φ:
tgφ = Fтрmax/N = fN/N = f.
Конус трения – поверхность, образованная
линией действия максимальной реакции опорной поверхности при движении тела в
различных направлениях (рисунок 9).
При равновесии тела на шероховатой
поверхности под действием силы P (рисунок 10) можно
составить два уравнения равновесия:
ΣFkx = 0;
Psinα – Fтр = 0;
ΣFky = 0;
-Pcosα + N = 0.
Рисунок 10. Схема равновесия тела на шероховатой
поверхности
Следовательно,
Для равновесия тела на шероховатой
поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на
тело, проходила внутри конуса трения или по его образующей через его вершину.
Никакая сила, лежащая внутри конуса трения, не
может вывести тело из состояния равновесия.
Контрольные вопросы
1. Какая система тел называется
статически определимой?
2. Приведите пример статически
неопределимой системы тел.
3. Какая конструкция называется
фермой?
4. Назовите основные составные
элементы фермы.
5. Как определить жесткость фермы?
6. Какой стержень фермы называется
нулевым?
7. Как определяется нулевой стержень
фермы?
8. В чем заключается сущность способа
вырезания узлов?
9. В чем заключается сущность способа
Риттера?
10. Что называется силой трения?
11. Что такое коэффициент трения, угол трения
и от чего зависит их значение?
12. Брус находится в равновесии, опираясь на
гладкую вертикальную стену и шероховатый горизонтальный пол; центр тяжести
бруса находится в его середине. Можно ли определить направление полной реакции
пола?
13. Назовите размерность коэффициента трения
скольжения.
14. Что такое предельная сила трения
скольжения.
15. Что характеризует конус трения?

- Способ проекций
- Метод вырезания узла
- Метод сечений
- Способ моментной точки
- Признаки нулевого стержня
- Расчёт ферм на персональном компьютере
- Порядок работы в программе Полюс
Рисунок 1
Фермы классифицируются:
- по очертанию внешнего контура;
- по виду решётки;
- по способу опирания;
- по назначению;
- по уровню проезда транспорта.
Также выделяют простейшие и сложные фермы. Простейшими называют фермы, образованные последовательным присоединением шарнирного треугольника. Такие конструкции отличаются геометрической неизменяемостью, статической определимостью. Фермы со сложной структурой, как правило, статически неопределимы.
Для успешного расчёта необходимо знать виды связей и уметь определять реакции опор. Эти задачи подробно рассматриваются в курсе теоретической механики. Разницу между нагрузкой и внутренним усилием, а также первичные навыки определения последних дают в курсе сопротивления материалов.
Рассмотрим основные методы расчёта статически определимых плоских ферм.
Способ проекций
На рис. 2 симметричная шарнирно-опёртая раскосная ферма пролётом L = 30 м, состоящая из шести панелей 5 на 5 метров. К верхнему поясу приложены единичные нагрузки P = 10 кН. Определим продольные усилия в стержнях фермы. Собственным весом элементов пренебрегаем.
Рисунок 2
Опорные реакции определяются путём приведения фермы к балке на двух шарнирных опорах. Величина реакций составит R (A) = R (B) = ∑P/2 = 25 кН. Строим балочную эпюру моментов, а на её основе — балочную эпюру поперечных усилий (она понадобится для проверки). За положительное направление принимаем то, что будет закручивать среднюю линию балки по часовой стрелке.
Рисунок 3
Метод вырезания узла
Метод вырезания узла заключается в отсечении отдельно взятого узла конструкции с обязательной заменой разрезаемых стержней внутренними усилиями с последующим составлением уравнений равновесия. Суммы проекций сил на оси координат должны равняться нулю. Прикладываемые усилия изначально предполагаются растягивающими, то есть направленными от узла. Истинное направление внутренних усилий определится в ходе расчёта и обозначится его знаком.
Рационально начинать с узла, в котором сходится не более двух стержней. Составим уравнения равновесия для опоры, А (рис. 4).
∑ F (y) = 0: R (A) + N (A-1) = 0
∑ F (x) = 0: N (A-8) = 0
Очевидно, что N (A-1) = -25кН. Знак «минус» означает сжатие, усилие направлено в узел (мы отразим это на финальной эпюре).
Условие равновесия для узла 1:
∑ F (y) = 0: -N (A-1) — N (1−8)∙cos45° = 0
∑ F (x) = 0: N (1−2) + N (1−8)∙sin45° = 0
Из первого выражения получаем N (1−8) = –N (A-1)/cos45° = 25кН/0,707 = 35,4 кН. Значение положительное, раскос испытывает растяжение. N (1−2) = -25 кН, верхний пояс сжимается. По этому принципу можно рассчитать всю конструкцию (рис. 4).
Рисунок 4
Метод сечений
Ферму мысленно разделяют сечением, проходящим как минимум по трём стержням, два из которых параллельны друг другу. Затем рассматривают равновесие одной из частей конструкции. Сечение подбирают таким образом, чтобы сумма проекций сил содержала одну неизвестную величину.
Проведём сечение I-I (рис. 5) и отбросим правую часть. Заменим стержни растягивающими усилиями. Просуммируем силы по осям:
∑ F(y) = 0: R(A) — P + N(9−3)
N(9−3) = P — R(A) = 10 кН — 25 кН = -15 кН
Стойка 9−3 сжимается.
Рисунок 5
Способ проекций удобно применять в расчётах ферм с параллельными поясами, загруженными вертикальной нагрузкой. В этом случае не придётся вычислять углы наклона усилий к ортогональным осям координат. Последовательно вырезая узлы и проводя сечения, мы получим значения усилий во всех частях конструкции. Недостатком способа проекций является то, что ошибочный результат на ранних этапах расчёта повлечёт за собой ошибки во всех дальнейших вычислениях.
Способ моментной точки
Способ моментной точки требует составлять уравнение моментов относительно точки пересечения двух неизвестных сил. Как и в методе сечений, три стержня (один из которых не пересекается с остальными) разрезаются и заменяются растягивающими усилиями.
Рассмотрим сечение II-II (рис. 5). Стержни 3−4 и 3−10 пересекаются в узле 3, стержни 3−10 и 9−10 пересекаются в узле 10 (точка K). Составим уравнения моментов. Суммы моментов относительно точек пересечения будут равняться нулю. Положительным принимаем момент, вращающий конструкцию по часовой стрелке.
∑ m(3) = 0: 2d∙R(A) — d∙P — h∙N(9−10) = 0
∑ m(K) = 0: 3d∙R(A) — 2d∙P — d∙P + h∙N(3−4) = 0
Из уравнений выражаем неизвестные:
N(9−10) = (2d∙R(A) — d∙P)/h = (2∙5м∙25кН — 5м∙10кН)/5м = 40 кН (растяжение)
N(3−4) = (-3d∙R(A) + 2d∙P + d∙P)/h = (-3∙5м∙25кН + 2∙5м∙10кН + 5м∙10кН)/5м = -45 кН (сжатие)
Способ моментной точки позволяет определить внутренние усилия независимо друг от друга, поэтому влияние одного ошибочного результата на качество последующих вычислений исключено. Данным способом можно воспользоваться в расчёте некоторых сложных статически определимых ферм (рис. 6).
Рисунок 6
Требуется определить усилие в верхнем поясе 7−9. Известны размеры d и h, нагрузка P. Реакции опор R(A) = R(B) = 4,5P. Проведём сечение I-I и просуммируем моменты относительно точки 10. Усилия от раскосов и нижнего пояса не попадут в уравнение равновесия, так как сходятся в точке 10. Так мы избавляемся от пяти из шести неизвестных:
∑ m(10) = 0: 4d∙R(A) — d∙P∙(4+3+2+1) + h∙O(7−9) = 0
O(7−9) = -8d∙P/h
Аналогично можно рассчитать остальные стержни верхнего пояса.
Признаки нулевого стержня
Нулевым называют стержень, в котором усилие равно нулю. Выделяют ряд частных случаев, в которых гарантированно встречается нулевой стержень.
- Равновесие ненагруженного узла, состоящего из двух стержней, возможно только в том случае, если оба стержня нулевые.
- В ненагруженном узле из трёх стержней одиночный (не лежащий на одной прямой с остальными двумя) стержень будет нулевым.
Рисунок 7
- В трехстержневом узле без нагрузки усилие в одиночном стержне будет равно по модулю и обратно по направлению приложенной нагрузке. При этом усилия в стержнях, лежащих на одной прямой, будут равны друг другу, и определятся расчётом N(3) = -P, N(1) = N(2).
- Трехстержневой узел с одиночным стержнем и нагрузкой, приложенной в произвольном направлении. Нагрузка P раскладывается на составляющие P’ и P” по правилу треугольника параллельно осям элементов. Тогда N(1) = N(2) + P’, N(3) = -P”.
Рисунок 8
- В ненагруженном узле из четырёх стержней, оси которых направлены по двум прямым, усилия будут попарно равны N(1) = N(2), N(3) = N(4).
Пользуясь методом вырезания узлов и зная правила нулевого стержня, можно проводить проверку расчётов, проведённых другими методами.
Расчёт ферм на персональном компьютере
Современные вычислительные комплексы основаны на методе конечного элемента. С их помощью осуществляют расчёты ферм любого очертания и геометрической сложности. Профессиональные программные пакеты Stark ES, SCAD Office, ПК Лира обладают широким функционалом и, к сожалению, высокой стоимостью, а также требуют глубокого понимания теории упругости и строительной механики. Для учебных целей и подойдут бесплатные аналоги, например Полюс 2.1.1.
В Полюсе можно рассчитывать плоские статически определимые и неопределимые стержневые конструкции (балки, фермы, рамы) на силовое воздействие, определять перемещения и температурное воздействие. Перед нами эпюра продольных усилий для фермы, изображённой на рис. 2. Ординаты графика совпадают с полученными вручную результатами.
Рисунок 9
Порядок работы в программе Полюс
- На панели инструментов (слева) выбираем элемент «опора». Размещаем помещаем элементы на свободное поле кликом левой кнопки мыши. Чтобы указать точные координаты опор, переходим в режим редактирования, нажав на значок курсора на панели инструментов.
- Двойной клик по опоре. Во всплывающем окне «свойства узла» задаём точные координаты в метрах. Положительное направление осей координат — вправо и вверх соответственно. Если узел не будет использоваться в качестве опоры, установите флажок «не связан с землёй». Здесь же можно задать приходящие в опору нагрузки в виде точечной силы или момента, а также перемещения. Правило знаков такое же. Удобно разместить крайнюю левую опору в начале координат (точка 0, 0).
- Далее размещаем узлы фермы. Выбираем элемент «свободный узел», кликаем по свободному полю, точные координаты прописываем для каждого узла в отдельности.
- На панели инструментов выбираем «стержень». Кликаем на начальном узле, отпускаем кнопку мышки. Затем кликаем на конечном узле. По умолчанию стержень имеет шарниры на двух концах и единичную жёсткость. Переходим в режим редактирования, двойным кликом по стержню открываем всплывающее окно, при необходимости изменяем граничные условия стержня (жёсткая связь, шарнир, подвижный шарнир для опорного конца) и его характеристики.
- Для загружения ферм используем инструмент «сила», нагрузка прикладывается в узлах. Для сил, прикладываемых не строго вертикально или горизонтально, устанавливаем параметр «под углом», после чего вводим угол наклона к горизонтали. Альтернативно можно сразу ввести значение проекций силы на ортогональные оси.
- Программа считает результат автоматически. На панели задач (вверху) можно переключать режимы отображения внутренних усилий (M, Q, N), а также опорных реакций (R). Результатом будет эпюра внутренних усилий в заданной конструкции.
В качестве примера рассчитаем сложную раскосную ферму, рассмотренную в методе моментной точки (рис. 6). Примем размеры и нагрузки: d = 3м, h = 6м, P = 100Н. По выведенной ранее формуле значение усилия в верхнем поясе фермы будет равно:
O(7−9) = -8d∙P/h = -8∙3м∙100Н/6м = -400 Н (сжатие)
Эпюра продольных усилий, полученная в Полюсе:
Рисунок 10
Значения совпадают, конструкция смоделирована верно.
Список литературы
- Дарков А. В., Шапошников Н. Н. — Строительная механика: учебник для строительных специализированных вузов — М.: Высшая школа, 1986.
- Рабинович И. М. — Основы строительной механики стержневых систем — М.: 1960.






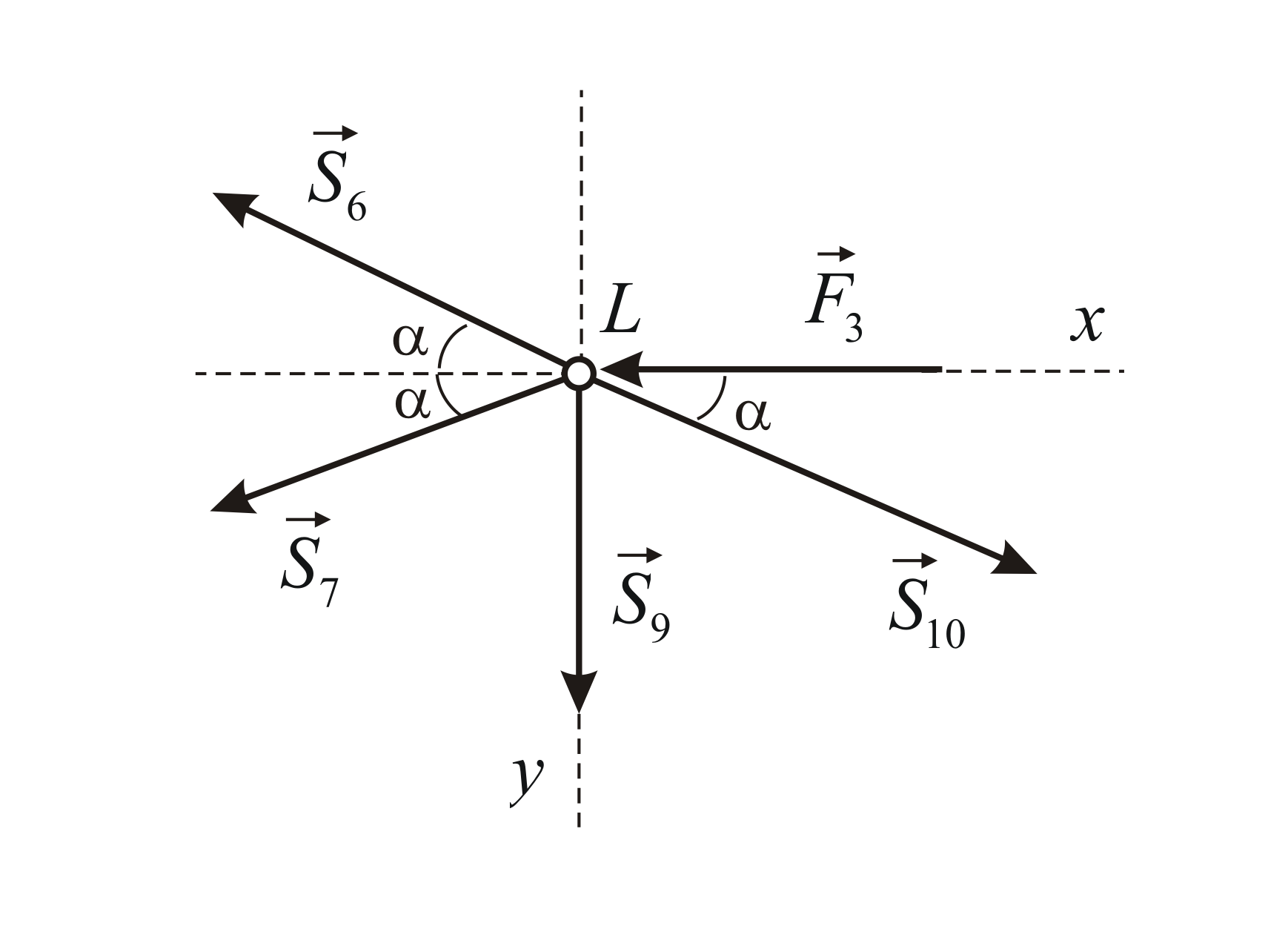
























































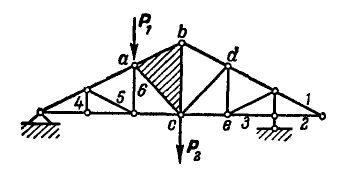
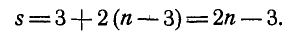
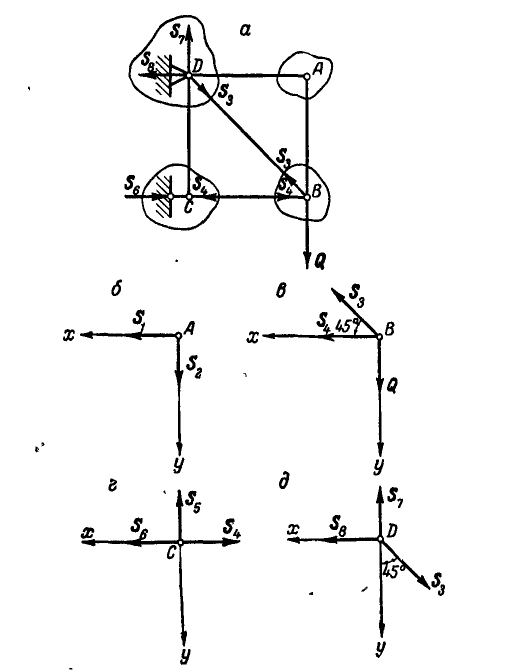
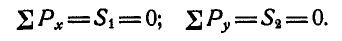
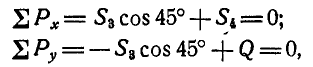
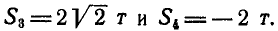
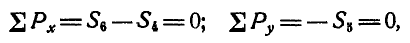
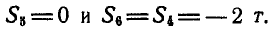

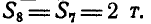
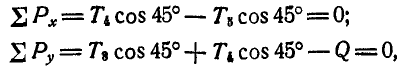
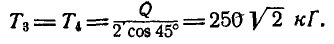
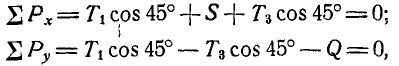
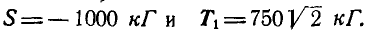
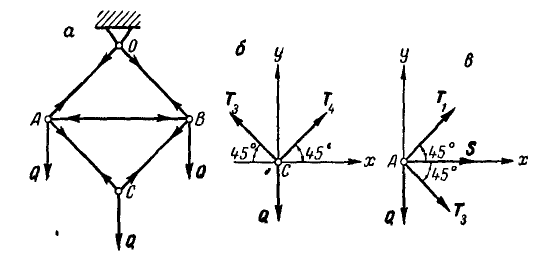
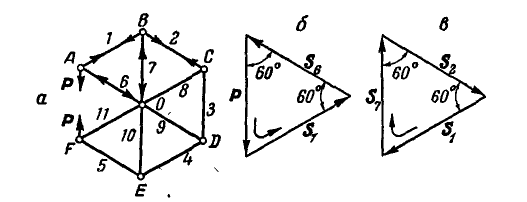
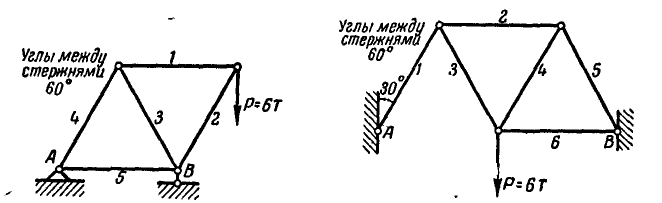
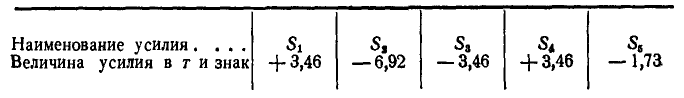
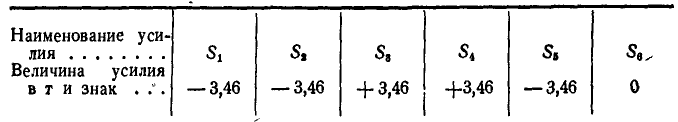
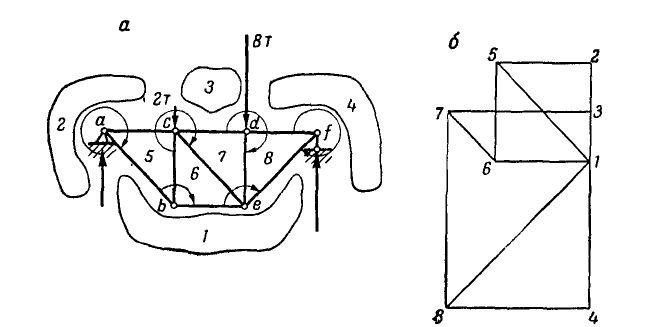
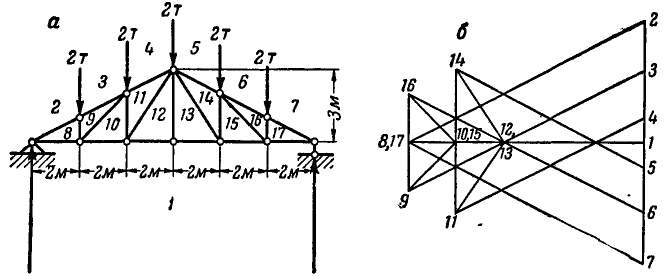
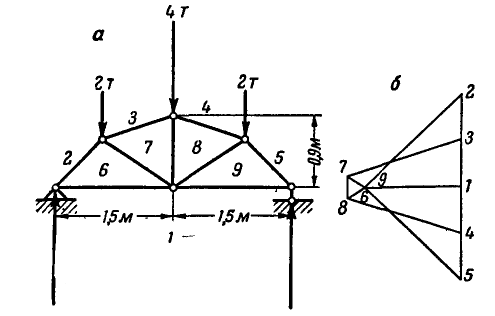
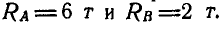
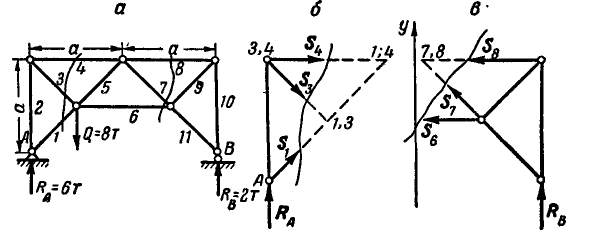
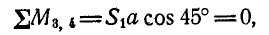
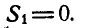
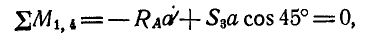
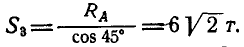
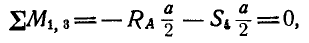
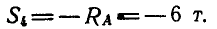
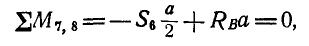
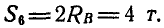

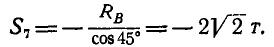
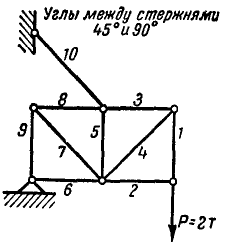
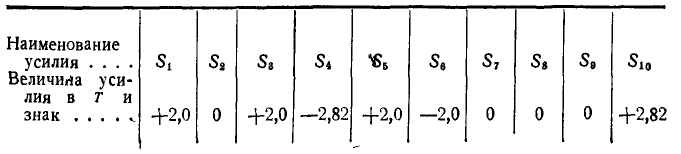
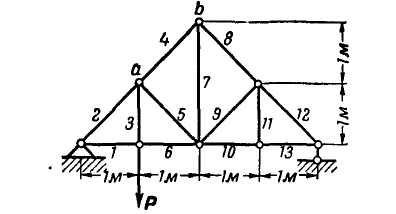
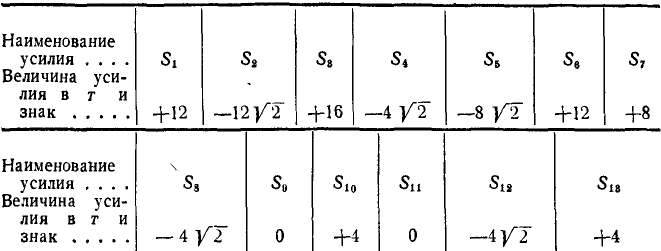
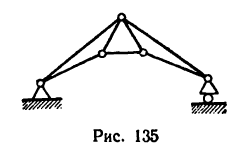
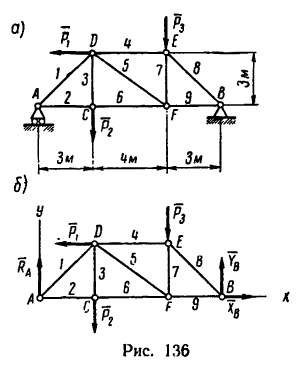
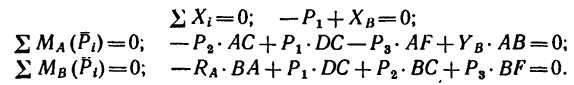
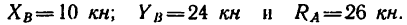
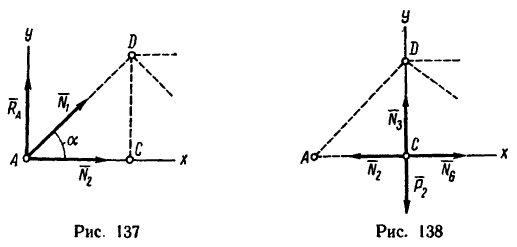
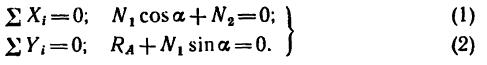
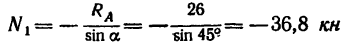
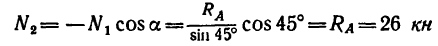
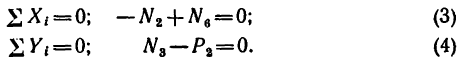
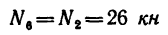
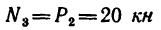
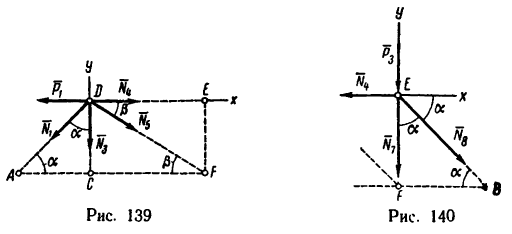
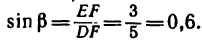
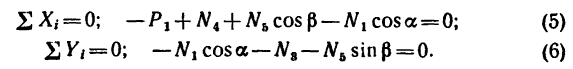
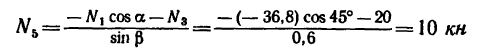
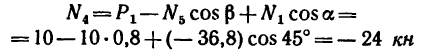
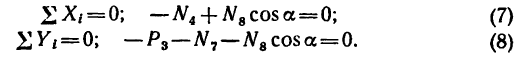
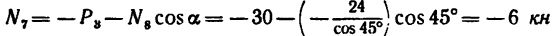
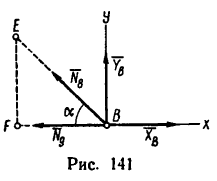
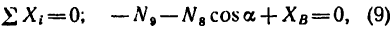
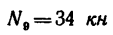

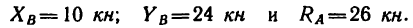
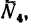
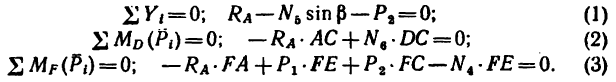
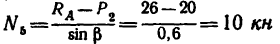
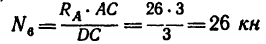
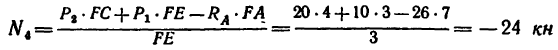
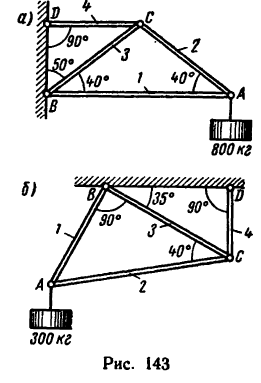
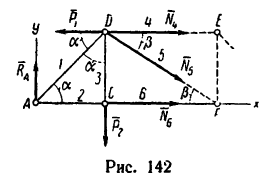
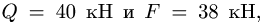
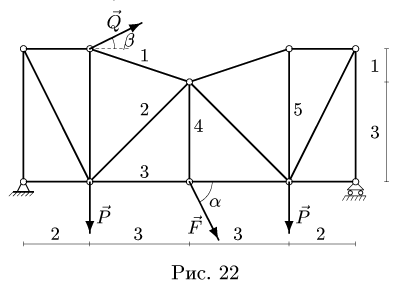
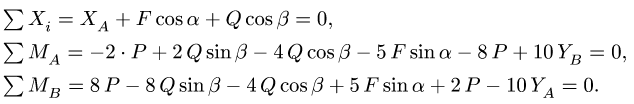
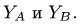
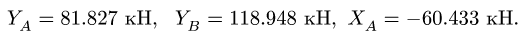
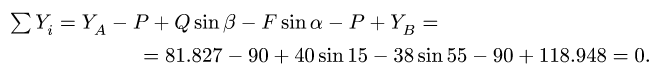
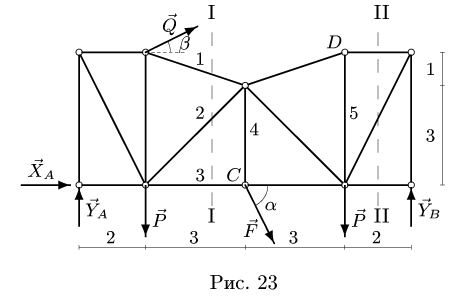
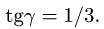
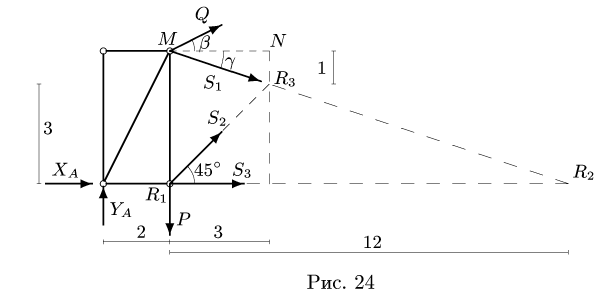
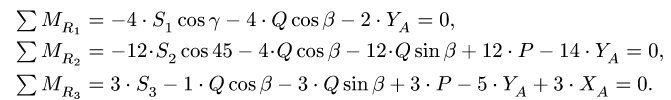
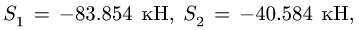
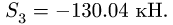
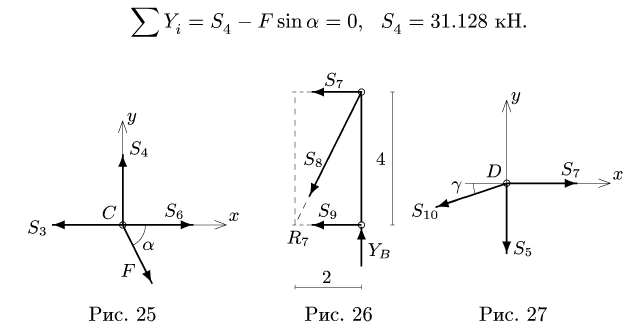
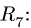
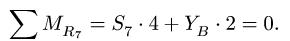
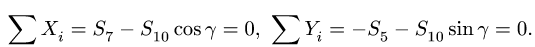
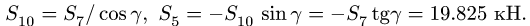

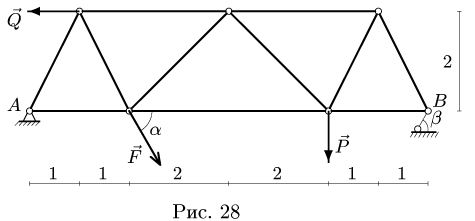
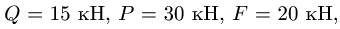
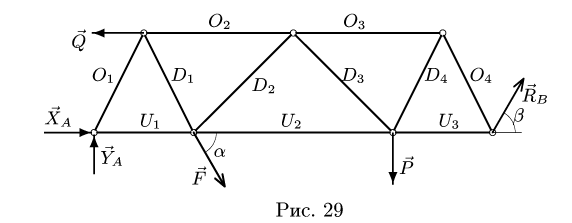
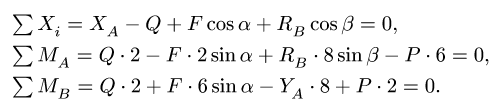
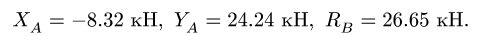
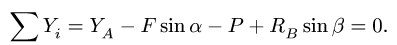
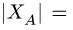

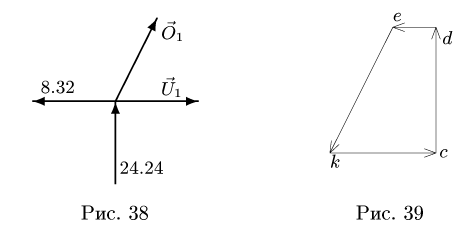

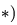 .
.