Как составить уравнения сторон треугольника по заданным вершинам

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

По известным координатам вершин треугольника  А(4;4), В(-6;-1), С(-2;-4) записать для его сторон уравнения в общем виде и уравнение в общем виде биссектрисы угла АВС. 

Решение

Так как нам известны координаты вершин, то проще всего получить уравнение стороны в канонической форме – формула, от которого легко перейти к уравнению в общей форме. Для канонического уравнения нам нужны координаты точки, принадлежащей стороне и координаты направляющего вектора (параллельного рассматриваемому).

1. Найдем уравнение стороны АВ. В качестве точки прямой можно взять точку А с заданными координатами, а в качестве направляющего вектора – вектор АВ. Найдем координаты вектора АВ:

2. Тогда каноническое уравнение стороны АВ запишется:

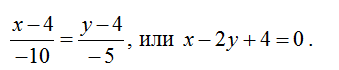
3. Аналогично можно получить уравнения остальных сторон треугольника: для стороны ВС: координаты вектора 

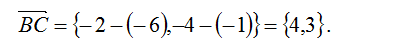
4. Откуда каноническое уравнение: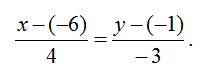

Следовательно, общее уравнение: 3x+4y+22=0.

5. Для стороны CА: координаты направляющего вектора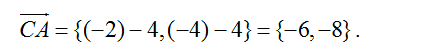

6. Каноническое уравнение: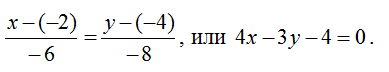 

7. Выведем общее уравнение для биссектрисы. Известно, что биссектриса делит угол пополам. Если на сторонах АВ и ВС треугольника отложить орты (соответственно a и b) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов a и b).

8. Для нахождения орта a необходимо знать координаты вектора BA:

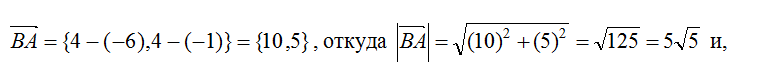
соответственно a определится как:

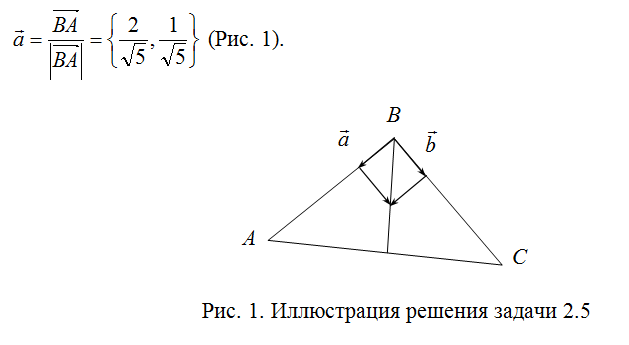
9. Аналогично определим орт b:

Теперь определим их сумму:

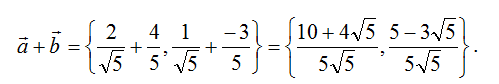
10. Тогда каноническое уравнение биссектрисы:

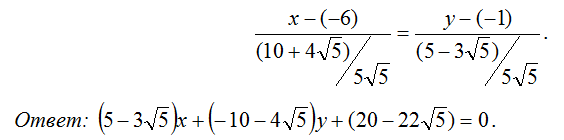
Как по координатам вершин треугольника найти уравнения его сторон

В аналитической геометрии треугольник на плоскости можно задать в декартовой системе координат. Зная координаты вершин, вы можете составить уравнения сторон треугольника. Это будут уравнения трех прямых, которые, пересекаясь, образуют фигуру.

Вам понадобится

• – ручка;
• – бумага для записей;
• – калькулятор.

Инструкция

Прямая на плоскости описывается уравнением: ax+bу+с = 0, где х,y – координаты по оси 0х и оси 0у какой-либо точки прямой; a, b, с – числовые коэффициенты. Причем a и b не могут равняться нулю одновременно. Такой вид записи называется общим уравнением прямой.

Также прямую можно задать выражением вида: y = kx+c. Это уравнение прямой с угловым коэффициентом k, который является тангенсом угла, образующегося при пересечении данной прямой с осью 0х.

Зная координаты двух точек А (х1;y1), В (х2;у2), вы можете записать уравнение прямой, проведенной через эти точки, используя пропорцию: (у-у1)/(у1-у2)=(х-х1)/(у1-у2). Далее, преобразовав это равенство, приведите его к виду как в шаге 1 или 2.

Рассмотрите алгоритм решения задачи на конкретном примере. Даны три вершины треугольника с известными координатами: А (9;8), В (7;-6), С (-7;4). Напишите уравнение прямых, образующих его.

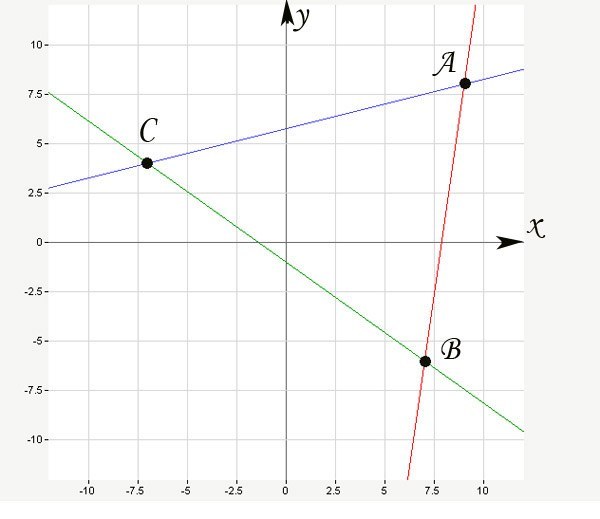
Найдите уравнение для прямой АВ. Примените формулу из шага 3, подставив значения координат точек А и В: (у-8)/(8-(-6)) = (х-9)/(9-7). Преобразуйте его: (у-8)/14 = (х-9)/2 или 2(у-8) = 14(х-9). Сократите уравнение, разделив левую и правую части на два, и раскройте скобки: у = 7х-63+8 = 7х-55.
Уравнение для АВ: у = 7х-55. Или: 7х-у-55 = 0 (АВ).

Аналогично напишите уравнение для прямой ВС: (у-(-6))/(-6-4) = (х-7)/7-(-7)). (у+6)/(-10) = (х-7)/14. 7(у+6) = -5(х-7). 7у+42 = -5х+35. 7у = -5х-7. у = -5/7х-1.
Уравнение для ВС: y = -5/7х-1. Или: -5х-7у-7 = 0 (ВС).

Затем уравнение для прямой СА: (у-8)/(8-4) = (х-9)/(9-(-7)). 16(у-8) = 4(х-9). 4у-32 = х-9. 4у = х-9+32. у = 0,25х+5,75.
Уравнение для СА: у = 0,25х+5,75. Или: х-4у+23 = 0 (СА).

Вы составили уравнения трех сторон фигуры. Для самопроверки постройте треугольника в системе координат. Найдите на чертеже значения пересечений прямых с осью 0у. Сравните эти координаты с полученными в уравнении. Например, для (BC) при y = 0, х = -1,4.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Уравнения сторон треугольника

Как составить уравнение сторон треугольника по координатам его вершин?

Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.

Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)

Составить уравнения сторон треугольника.

1) Составим уравнение прямой AB, проходящей через 2 точки A и B.

Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:

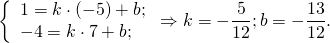
Таким образом, уравнение стороны AB

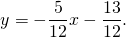
2) Прямая BC проходит через точки B(7;-4) и C(3;7):

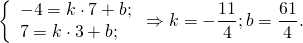
Отсюда уравнение стороны BC —

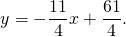
3) Прямая AC проходит через точки A(-5;1) и C(3;7):

Уравнение прямой в отрезках: описание, примеры, решение задач

Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.

Уравнение прямой в отрезках – описание и примеры

Пусть на плоскости расположена прямоугольная система координат O x y .

Прямая линия на плоскости в декартовой системе координат O x y задается уравнением вида x a + y b = 1 , где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях O x и O y . Длины отрезков считаются от начала координат.

Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a , 0 и 0 , b принадлежат данной прямой линии, так как a a + 0 b = 1 ⇔ 1 ≡ 1 и 0 a + b b = 1 ⇔ 1 ≡ 1 . Точки a , 0 и b , 0 расположены на осях координат O x и O y и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b . Знак « — » обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.

Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат O x y на схематическом чертеже. Уравнение прямой в отрезках x a + y b = 1 применяется для построения прямой линии в декартовой системе координат O x y . Для этого нам необходимо отметить на осях точки a , 0 и b , 0 , а затем соединить эти точки линией при помощи линейки.

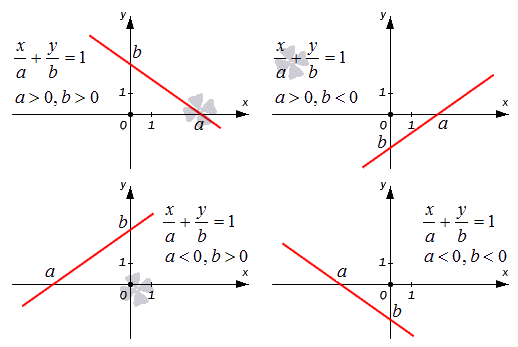
На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.

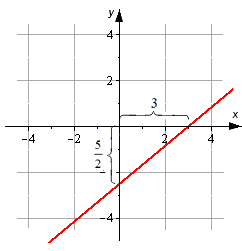
Прямая линия задана уравнением прямой в отрезках вида x 3 + y — 5 2 = 1 . Необходимо построить эту прямую на плоскости в декартовой системе координат O x y .

Решение

Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3 , 0 , 0 , — 5 2 . Отметим их и проведем линию.

Приведение общего уравнения прямой к уравнению прямой в отрезках

Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.

Полное общее уравнение прямой линии на плоскости имеет вид A x + B y + C = 0 , где А , В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на – С . При этом, коэффициенты при x и y мы отправляем в знаменатели:

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Для осуществления последнего перехода мы воспользовались равенством p q = 1 q p , p ≠ 0 , q ≠ 0 .

В результате, мы осуществили переход от общего уравнения прямой A x + B y + C = 0 к уравнению прямой в отрезках x a + y b = 1 , где a = — C A , b = — C B .

Разберем следующий пример.

Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x — 7 y + 1 2 = 0 .

Решение

Переносим одну вторую в правую часть равенства x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Делим обе части равенства на — 1 2 : x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Преобразуем полученное равенство к нужному виду: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .

Мы получили уравнение прямой в отрезках.

Ответ: x — 1 2 + y 1 14 = 1

В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.

Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида x a + y b = 1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y .

x a + y b = 1 ⇔ x a + y b — 1 = 0 ⇔ 1 a · x + 1 b · y — 1 = 0

Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».

Уравнение прямой в отрезках имеет вид x 2 3 + y — 12 = 1 . Необходимо написать общее уравнение прямой на плоскости.

Решение

Действует по заранее описанному алгоритму:

x 2 3 + y — 12 = 1 ⇔ 1 2 3 · x + 1 — 12 · y — 1 = 0 ⇔ ⇔ 3 2 · x — 1 12 · y — 1 = 0

Ответ: 3 2 · x — 1 12 · y — 1 = 0

Уравнение длины сторон треугольника

Средняя оценка: 4.7

Всего получено оценок: 133.

Средняя оценка: 4.7

Всего получено оценок: 133.

Уравнение длин сторон треугольника – это первые вкрапления высшей математики в математику школьного курса. Понимание данной тематики приближает ученика к университетскому уровню, вместе с тем делая более понятной тему функции.

Функция

Что такое функция? Это зависимость одной величины от другой. В математической функции чаще всего две неизвестных: независимая и зависимая или х и у соответственно.

Что это значит? Это значит, что х может принимать абсолютно любое значение, а у будет под него подстраиваться, меняясь в соответствии с коэффициентами функции.

Существуют ситуации, когда функция имеет несколько переменных. Зависимая у всегда 1, но факторов, которые влияют на неё может быть несколько. Не всегда такую функцию получается отразить на графике. В лучшем случае графически можно отобразить зависимость у от 2 переменных.

Как проще всего представить зависимость у(х)?

Да очень просто. Представьте себе избалованного ребенка и богатую любящую мать. Они вместе приходят в магазин и начинают клянчить конфеты. Кто знает, сколько конфет мальчик потребует сегодня?

Очень важно понимать, что одному значению функции у, всегда соответствует 1 значение аргумента х. Но, как и с корнями квадратного уравнения, эти значения могут совпадать.

Уравнение прямой линии

Зачем нам нужно уравнение прямой, если мы говорим об уравнении длин сторон треугольника?

Да затем, что каждая из сторон треугольника это отрезок. А отрезок это ограниченная часть прямой. То есть мы можем задать уравнения прямых. А в точках их пересечения ограничить линии, тем самым обрезав прямые и превратив их в отрезки.

Уравнение прямой выглядит следующим образом:

Уравнение сторон треугольника

Необходимо найти уравнение длин сторон треугольника с вершинами в точках А(3,7) ; В(5,3); С(12;9)

Все координаты положительны, значит, треугольник будет расположен в 1 координатной четверти.

Поочередно составим уравнения каждой из линий треугольника.

• Первой будет линия АВ. Координаты точек подставим в уравнение прямой на место х и у. Таким образом мы получим систему из двух линейных уравнений. Решив ее можно найти значение коэффициентов для функции:

Из первого уравнения выразим b и подставим во второе.

Подставим значение а и найдем b.

Составим уравнение прямой.

• Аналогично составим два оставшихся уравнения.