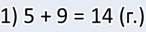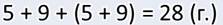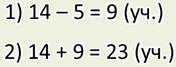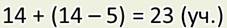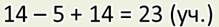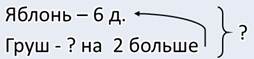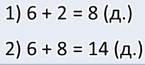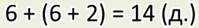Чтобы составить задачу, которая приведёт к этим выражениям, например, с двумя неизвестными, нужно сначала поиграться с числами.
Берём две машины. Одна движется со скоростью 60 км/час, а вторая на 20 быстрее 80 км/час. У этих скоростей оптимальный общий множитель 48. Увеличиваем его в 10 раз получится 480 км.
Первой машине потребуется 8 часов, для преодоления этого расстояния, а второй 6 на 2 часа меньше. 480 км – это известное расстояние. Неизвестные величины — это скорость и время.
Напускаем туману. Определяемся, что скорость 1-й машины на 20 км/час меньше второй машины. Но вторая выехала на 2 часа позже и догнала первую на расстоянии 480 км. Задача готова. Нужно хитро задать вопрос. Например: Через какое время 2-я машина будет на расстоянии в 100 км от первой после из встречи.
Чтобы решить такую задачу потребуется составлять выражение. Принимать за “х” скорость первой или второй машины до встречи. За “у” время первой или второй машины также до встречи. Или обходиться одним “х”, а можно и просто обойтись числами. Но это не для составителя. Составитель оперирует известными ему числами, а “решала” составляет выражения.
Конечно это интересно. Составить хитрую математическую задачку, и чтобы её не быстро решили. А выдёргивать с интернета любой может. Я составляю сама. Бывает до взрыва мозга, а не такую легкотню, как написала выше. Например вот эта: про курагу, чернослив и инжир.
Методическая
разработка Соловей Виктории Анатольевны, учителя начальных классов МБОУ
Пяозерская СОШ.
Разработка рассчитана на учащихся 1 –
4 классов.
Обучение
составлению задач по выражению.
Образование перешло на стандарты
второго поколения, по требованиям которых целью образования становится
общекультурное, личностное и познавательное развитие обучающихся,
обеспечивающее такую ключевую компетенцию, как умение учиться. В основе данного
умения лежат универсальные учебные действия, которые требуют специальной работы
по их формированию. Работа по составлению и решению задач в значительной
степени позволяет формировать у учащихся познавательные и регулятивные
универсальные учебные действия. Из познавательных УУД формируются логические
действия (анализ с целью выделения признаков, построение логической цепи
рассуждений), действия постановки и решения проблем (формулирование проблем).
Из регулятивных УУД формируются целеполагание (постановка учебной задачи на
основе соотнесения того, что уже известно и усвоено, и того, что еще
неизвестно), планирование (составление плана и последовательности действий),
прогнозирование (предвосхищение результатами уровня усвоения, его временных
характеристик), контроль (в форме сличения способа действия и его результата с
заданным эталоном с целью обнаружения отклонений и отличий от эталона),
коррекция (внесение необходимых дополнений и корректив в план и способ действия
в случае расхождения эталона, реального действия и его продукта), оценка
(выделение и осознание учащимися того, что уже усвоено и что еще подлежит
усвоению, осознание качества и уровня усвоения), волевая саморегуляция
(способность к мобилизации сил и энергии; способность к волевому усилию – к
выбору в ситуации мотивационного конфликта и к преодолению препятствий).
Обучаясь работе над задачей, ученик
учится решать любую жизненную задачу, т.к. при решении и математической, и
жизненной задачи он проходит те же этапы.
Обучение составлению задач по выражению
очень важно для обучения решению задач. Обучаясь составлять задачи, ученик
более глубоко осознает установленные связи между величинами, учится
представлять себе связь между числовыми данными и реальными объектами,
переносить математические объекты на объекты реального мира. Это кропотливая и
сложная работа, в ходе которой учитель развивает у обучающихся важное умение –
умение решать задачи.
Этапы обучения составлению задач по выражению.
1. Подготовительный этап – обучение составлению задач
по выражениям, включающим одно действие.
На данном этапе перед нами стоит цель обучить составлению
задач по выражениям, включающим одно действие. Чтобы обучающиеся осознали, что
одним и тем же арифметическим действием можно решить разные виды задач,
предлагаются следующие задачи:
1.
решающиеся действием сложения (задача разбирается
устно всем классом, решения записываются на доске в столбики)
«Девочка вымыла 25 глубоких тарелок и 16 мелких. Сколько
всего тарелок вымыла девочка?»
«Один дом построили за 3 недели, а на строительство
второго дома затратили на 2 недели больше. Сколько недель затратили на
строительство второго дома?»
2.
решающиеся действием вычитания
«У Миши было 7 рублей. Он купил тетрадь за 4 рубля. Сколько
денег осталось у Миши?»
«Мальчики слепили из пластилина 4 медведя и несколько
слонов. Всего они слепили 7 животных. Сколько слонов слепили мальчики?»
3.
решающиеся действием умножения
«У бабушки жили кролики в трех клетках, по 2 кролика в
каждой. Сколько кроликов жило у бабушки?»
«Учитель задумал число, которое при делении на 3 дает число
2. Какое число задумал учитель?»
«За каникулы один ученик прочитал 2 книги, а второй ученик
– в 2 раза больше. Сколько книг прочитал за каникулы второй ученик?»
4.
решающиеся действием деления
«Двум классам подарили 10 скакалок, каждому поровну.
Сколько скакалок подарили каждому классу?»
«В магазин привезли 10
кг яблок, а груш – в два раза меньше. Сколько кг груш привезли в магазин?»
«На конкурсе самодеятельности выступили 10 чтецов и 2
певца. Во сколько раз больше выступило чтецов, чем певцов?»
После решения всех задач необходимо сделать вывод о том,
что одним и тем же выражением можно записать решения различных задач. Для этого
предлагается посмотреть на записи в столбиках и подумать, что можно сказать о
записях в каждом столбике, какие задачи решались.
Следующий шаг – составление всевозможных задач по одному
выражению.
Чтобы облегчить поиск сюжета, на доску вывешивается таблица
с перечнем глаголов, которая была составлена совместно с учащимися в ходе
беседы о том, какие действия можно совершать с игрушками, покупками, книгами,
тканями и т.д.
|
Подарили |
Вылепили |
Покрасили |
|
Заплатили |
Отрезали |
Погрузили |
|
Убрали |
Вырастили |
Прочитали |
|
Начертили |
Принесли |
Разложили |
|
Полили |
Уехали |
Привезли |
Так же следует отметить, что сюжет задачи, а,
следовательно, и слова, обозначающие действия, обучающиеся могут придумать
сами.
Для того чтобы добиться результативности в работе,
необходимо предусмотреть при обучении составлению текстовых задач следующие этапы.
 |
Поэтому вынесем на доску готовый алгоритм составления
задачи:
1) придумаю сюжет задачи
2.назову объекты, о которых будет говориться в задаче
3.дам количественную характеристику объектам
4.сформулирую требование задачи
5.смоделирую текст задачи.
На доске записывается выражение а + в. Дается задание
придумать как можно больше задач, которые можно решить с помощью данного
выражения. Далее идет обсуждение придуманных задач.
Такая же работа проводится с выражениями а – в, а * в, а :
в.
2. Обучение составлению задач по выражениям,
включающим два действия.
Работа проводится в несколько этапов.
1, 2, 3, 4 этапы – фронтальная работа.
5 этап – групповая работа.
6 этап – индивидуальная работа.
1 этап – составление задачи по
образцу учителя.
Предлагается решить задачу «В книжном шкафу на трех полках
стоит по 10 книг, а на четвертой полке 5 книг. Сколько книг в шкафу?»
-О чем говорится в задаче? (О книгах.)
-Зная, что на трех полках по 10 книг, что можно найти?
(Сколько всего книг на трех полках.)
-Зная, сколько всего книг на трех полках и сколько книг на
четвертой полке, что можно найти? (Сколько всего книг в шкафу.)
-Запишем решение в виде выражения.
На доске появляется запись 10*3+5
Следующий шаг – объяснение учителем, как он будет
составлять задачу.
Опять используется таблица со словами-подсказками.
-Посмотрите внимательно на выражение. Какое действие
выполняем первым? (Действие умножения)
-По 10 взяли три раза.
-В решенной задаче назовите объект, к которому относится
число 3? (Количество полок, на которых было по 10 книг).
-В решенной задаче назовите объект, к которому относится
число 10? (Число книг на каждой из трех полок).
-Что обозначает число 5? (Отдельное число книг на четвертой
полке).
-Таким образом, было книг по 10 три раза да еще 5.
-Придумаем задачу с такими же количественными
характеристиками.
1. Придумаю сюжет задачи: привоз в магазин.
2. Выберу объекты: пачки с печеньем.
3.Дам объекту количественную характеристику: по 10 три раза
– по 10 пачек печенья в трех коробках, да еще 5 пачек отдельно.
4.Сформулирую требование задачи: сколько пачек печенья
привезли в магазин?
5.Смоделирую текст задачи: «В магазин привезли три коробки
с печеньем по 10 пачек в каждой коробке, да еще 5 пачек отдельно. Сколько пачек
печенья привезли в магазин?»
Текст задачи появляется на доске. Предлагается разобрать
задачу, чтоб убедиться, будет ли предложенное выражение являться решением
составленной задачи. После решения задачи подводится итог, что учитель составил
задачу по предложенному выражению верно.
Следующий шаг – составление учащимися аналогичных задач по
образцу, данному учителем, но предлагается изменить числовые данные.
Предлагается выражение 8*4+6. [Приложение № 2].
2 этап – самостоятельное
составление аналогичной задачи по выражению предварительно решенной задачи.
На этом этапе предлагаются две задачи: в записи решения
первой содержится действие умножения, в записи решения второй – действие
деления.
Задача 1: «Девочки посадили на клумбы 6 астр, 4 мака, а
ромашек в 2 раза больше, чем астр и маков вместе. Сколько ромашек посадили
девочки на клумбы?»
-О чем говорится в задаче?
-Что сказано о каждом виде цветов?
-Что нужно найти в задаче?
-Можем ли мы сразу ответить на вопрос задачи? Почему?
-Узнав, сколько астр и маков вместе, можем ли мы найти,
сколько ромашек посадили?
-Составьте словесную краткую запись:
А. – 6 шт.
М. – 4 шт.
Р. – ?, в 2 раза больше, чем —-
-Решите задачу, записав решение в виде выражения.
На доске появляется выражение вида (6+4)*2.
Вывод: в данном выражении одну количественную
характеристику сложили со второй количественной характеристикой и увеличили в
два раза.
Следующее, что предстоит сделать, это составить задачу по
этому же выражению.
-Сколько групп объектов должно быть в задаче? (три)
-Что известно о количестве объектов первой группы? (их 6)
-Что сказано о количестве объектов второй группы? (их 4)
-А что можно будет сказать про количество объектов третьей
группы? (их в два раза больше, чем первых и вторых вместе)
-Составьте аналогичную задачу по этому же выражению,
подобрав объекты сами. Можно сюжет изменить [Приложение № 2].
Задача 2: «В школьном концерте выступили 8 чтецов, певцов –
в 2 раза меньше, а танцоров – на 3 больше, чем певцов. Сколько танцоров
выступило в школьном концерте?»
-О чем говорится в задаче?
-Кто выступал в концерте?
-Что сказано о чтецах?
-Что сказано о певцах? Можем ли мы найти, сколько их было?
Как?
-Что сказано о танцорах? Можем ли мы узнать, сколько их
было? Как?
-Ответили мы на вопрос задачи?
-Составьте краткую запись.
Чтецы-8
чел.
Певцы-?, в 2 раза меньше, чем
Танцоры-?,
на 3 больше, чем
– Решите задачу, записав решение в виде выражения.
На доске появляется запись 8:2+3.
Вывод: одну количественную характеристику уменьшили в 2
раза, тем самым нашли вторую количественную характеристику. Затем ко второй
количественной характеристике прибавили еще 3, тем самым нашли третью (искомую)
характеристику.
Предлагается составить аналогичную задачу.
-Сколько групп объектов должно быть в вашей задаче? (три)
-Что известно о количестве представителей первой группы
объектов? (их 8)
-Что можете сказать о количестве представителей второй
группы объектов? (мы не знаем сколько их, но знаем, что их в 2 раза меньше, чем
первых)
-Что можете сказать о количестве представителей третьей
группы? (не знаем, сколько их, но знаем, что их на 3 больше, чем вторых)
-Составьте аналогичную задачу по этому же выражению,
подобрав другие объекты. Сюжет можно изменить [Приложение № 2].
3 этап – составление задач с
описанием новой ситуации.
На данном этапе обучающиеся должны научиться составлять
задачи с описанием иной ситуации сначала по образцу учителя, а затем
самостоятельно. Поэтому здесь можно выделить два шага.
1 шаг – составление задач по образцу задачи учителя.
Решается задача: «Два мальчика разделили подаренные им 80
рублей поровну. Один из мальчиков истратил 15 рублей. Сколько денег у него
осталось?»
-О ком говорится в задаче?
-Что сказано про мальчиков?
-Как разделили деньги мальчики?
-Можем сразу ответить на вопрос задачи? Почему?
-Можно узнать, сколько было денег у каждого мальчика?
-Составим краткую запись в виде чертежа.
1 м.
2 м.
? 15 руб.
-Что найдем сначала? Каким действием?
-Теперь можно ответить на вопрос задачи? Каким действием?
Задача решается, решение записывается в виде выражения
80:2-15
Делается вывод: определенное число группы объектов
разделили на две равные части, и из одной части сняли определенное их
количество.
Теперь учитель составляет по этому выражению задачу другого
вида и объясняет учащимся, как он это делает.
-Какое действие в данном выражении выполняется первым?
(действие деления)
-Действие деления можно связать:
1) с разбиением множества на равнозначные подмножества:
на равные части – что мы и делали в решенной задаче;
по содержанию – каждый ученик вырезал 4 снежинки, а всего они
вырезали 16 снежинок. Сколько учеников вырезали снежинки? 16:4=4 (уч.)
2) с уменьшением числа в несколько раз:
например, кроликов 20, а курочек в два раза меньше; сколько
курочек? 20:2=10 (к.)
или, у Васи 20 марок, а у Ромы в два раза меньше, сколько у
Ромы? 20:2=10.
Таким образом, в первом случае мы имеем дело с разными
объектами, а во втором случае – с одинаковыми объектами.
3) с кратным сравнением. Но
этот случай мы не рассматриваем, т.к. ученику трудно составить задачу в два
действия, где встречается кратное сравнение.
Так как перед нами стоит цель составить иную задачу по
данному выражению, обратимся к случаю, в котором необходимо число уменьшить в
несколько раз.
Итак, количество каких-то объектов уменьшили в несколько
раз, получив новую группу объектов, которую еще уменьшили на несколько единиц.
1. придумаю сюжет: покупка мебели в школу.
2. выберу объекты: парты и стулья.
3. дам количественную характеристику: стульев – 80.
Количество парт «связываем» с выражением. Неизвестно, но можно найти: 80 : 2.
Далее в выражении выполняется действие вычитания, значит, количество парт
уменьшилось на 15.
4. сформулирую требование задачи: сколько парт из
привезенных осталось?
5. смоделирую текст задачи: «В школу привезли 80 стульев, а
парт – в 2 раза меньше. 15 парт отдали в музыкальную школу. Сколько парт из
привезенных осталось в школе?»
Следует сравнить два вида задач, тексты которых написаны на
доске.
|
«Два мальчика разделили подаренные им 80 рублей поровну. |
«В школу привезли 80 стульев, а парт – в 2 раза меньше. |
|
Объект Действием Из |
Объект Действием Из |
-Глядя на выражение, с помощью которого записано решение
этих двух задач, и судя по сравнению содержания этих задач, к какому выводу
можно прийти? (с помощью одного и того же выражения записано решение двух
совершенно разных задач)
Далее детям предлагается составить задачу, аналогичную той,
которая составлена учителем (Приложение № 2).
2 шаг – самостоятельное составление задачи другого вида по
выражению ранее решенной задачи.
Всем классом разбирается задача: «У Мити 3 игрушечных
динозаврика, у Саши – в 2 раза больше, чем у Мити, а у Славы – на 4 динозаврика
больше, чем у Саши. Сколько динозавриков у Саши?»
В итоге получается выражение 3*2+4.
-Что обозначает действие умножения в этой задаче?
(количество динозавриков Мити увеличили в два раза)
-Что означает действие умножения в высказывании «карандаши
разложили в 2 коробки по 3 штуки»? (по 3 взяли два раза)
-Попробуйте составить задачу, в которой какие-либо 3
объекта возьмут два раза, да еще добавят 4 такие же объекта [Приложение № 2].
4 этап – составление памятки.
На данном этапе необходимо составить алгоритм, которым
смогут пользоваться учащиеся при составлении задач по выражению.
-С чего начинаем, когда нам предложено то или иное
выражение? (смотрим, какие действия в этом выражении, какое действие
выполняется первым, вторым)
-Вспомним, что мы находим действием умножения (сумму
одинаковых слагаемых, либо увеличиваем число в несколько раз).
-Вспомним, что мы находим действием деления (деление на
равные части, деление по содержанию, уменьшение числа в несколько раз).
-Теперь необходимо выбрать, что мы будем делать с будущими
объектами, используя данное действие.
-Можно приступить непосредственно к придумыванию задачи?
(да, можно)
-Что теперь нам необходимо придумать? (сюжет задачи)
-Далее что делаем? (придумываем объекты)
-Как теперь связать объекты с выражением? (подумать, какой
объект связать с той или иной числовой данной)
-Условие задачи практически готово, чего еще не хватает в будущей
задаче? (требования)
-Составив требование, что нужно сделать? (сформулировать
текст задачи)
-Сформулируем памятку в виде пунктов плана:
1. Посмотрю на действие, которое выполняется первым, и
подумаю, что я могу найти этим действием.
2. Придумаю сюжет задачи.
3. Придумаю объекты задачи.
4. Свяжу объекты с числовыми данными выражения.
5. Составлю требование задачи.
6. Сформулирую текст задачи.
Учащиеся готовят для себя памятки в виде карточек, чтобы
иметь возможность использовать их в дальнейшей работе.
5 этап – составление задач в
парах.
1. Первый ученик решает задачу, составляя выражение. Второй
ученик составляет аналогичную задачу. Затем меняются ролями [Приложение № 3].
Задача 1: «Мама сварила 33
кг варенья. 5 кг варенья она налила в одну банку, а остальное – в 7 банок
поровну. Сколько килограммов варенья она налила в каждую банку?»
Задача 2: «Засолили 89
кг огурцов, 65 кг поместили в бочку, а остальные разложили поровну в 8 банок.
Сколько килограммов огурцов положили в каждую банку?»
2. Первый ученик решает задачу, составляя выражение. Второй
ученик составляет по этому выражению задачу с описанием новой ситуации. Затем
меняются ролями [Приложение № 3].
Задача 1: «18 учеников сели по 2 ученика за парту. Еще 4
парты остались свободными. Сколько всего парт?»
Задача 2: «20 яблок разложили по 5 яблок на тарелки. Еще 5
тарелок остались пустыми. Сколько всего тарелок?»
6 этап – индивидуальная работа.
Каждому учащемуся предлагается решить задачу, составив
выражение. А затем дается задание составить задачу по этому выражению, но с
описанием новой ситуации. Задачи даются по вариантам.
Задача 1: «В школьный хор из первых классов взяли 9
учеников, из вторых классов – в 2 раза больше, чем из первых классов, а из
третьих – на 3 ученика меньше, чем из вторых классов. Сколько учеников взяли в
школьный хор из третьих классов?»
Задача 2: «На молочной ферме работало 8 школьников, в поле
– в 4 раза больше, чем на ферме, а в саду – на 10 школьников меньше, чем в
поле. Сколько школьников работало в саду?»
Есть в задачах (для второго класса) на умножение небольшой подвох. Скажу честно, пока не поняла сути, сама делала подобные ошибки.
Доброго всем времени суток!
Разберем на примерах:
Задача 1.
В трех вазах лежит по два апельсина. Сколько всего апельсинов в трех вазах?
Задача 2.
Катя читала книгу три часа. За один час она прочитывала пять страниц. Сколько страниц прочла Катя за три часа?
Задача 3.
В магазин привезли шесть коробок конфет. В каждой коробке пять килограмм конфет. Сколько всего килограмм конфет привезли в магазин ?
Также во втором классе встречаются задания с формулировкой «составить выражение». Что же это значит? А это значит, что необходимо составить решение задачи в одно действие.
Пример 1.
Составь выражение и вычисли.
Катя купила три набора карандашей по шесть штук в каждом. Из всех наборов восемь карандашей она отдала брату. Сколько карандашей у Кати осталось ?
Пример2.
Составь выражение и вычисли.
У Вани было 30 рублей. Он купил два ластика по 3 рубля каждый. Сколько денег осталось у Вани?
! Иногда требуется просто составить выражение, иногда пишут составь и вычисли.
На этом у меня всё. Возможно мои маленькие заметки стали полезными для Вас.
С уважением Tasha.I
Спасибо за лайки и отзывы.
Содержание
- Числовые и буквенные выражения
- Числовые выражения: что это
- Буквенные выражения
- Выражения с переменными
- Запись решения задачи выражением
- Урок 15. Математика 2 класс ФГОС
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Запись решения задачи выражением»
Числовые и буквенные выражения
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
- 23 + 5 = 28
- 5 — 2 = 3
- 52 * 3 = 156
- 28 : 7 = 4
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
- (5 * 3) — (5 * 2) = 5
- 6 : (7 — 4) = 2
- (45 + 45) : 9 = 10
- 11 * (5 * 5) = 275
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
- Сначала выполняется действие, записанное в скобках.
- Затем выполняется деление/умножение.
- В последнюю очередь выполняется сложение/вычитание.
Пример 1. Найдите значение числового выражения: 3 * (2 + 8) — 4
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
(6 + 7) * (13 + 2) = 195
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
- Сначала находим значение первого выражения:
6 + 8 = 14
Затем находим значение второго выражения:
2 * 2 = 4
Сравниваем получившиеся результаты:
14 больше 4
14 > 4
6 + 8 > 2 * 2
Пример 2. Сравните следующие числовые выражения:
5 * (12 — 2) — 7 и (115 + 9) — (7 — 3)
- Находим значение первого выражения, соблюдая порядок выполнения арифметических действий:
12 — 2 = 10
5 * 10 = 50
50 — 7 = 43
5 * (12 — 2) — 7 = 43
Затем находим значение:
115 + 9 = 124
7 — 3 = 4
124 — 4 = 120
Сравниваем полученные результаты:
43 меньше 120
43
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
- Сначала следует прочитать его полностью.
- Затем оно записывается.
- Третьим шагом идет подстановка значения неизвестного в выражение.
- А затем производится вычисление, согласно очередности выполнения арифметических действий.
Пример 1. Найдите значение выражения: 5 + x.
- Читаем: найдите сумму числа 5 и x.
- Подставляем вместо неизвестного x число 4.
- Вычисляем: 5 + 4 = 9.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
- Читаем: найдите произведение суммы числа 4 и а и суммы числа 2 и x.
- Подставляем вместо неизвестного a число 2.
- Вычисляем 4 + 2 = 6.
- Подставляем вместо неизвестного x число 5.
- Вычисляем 2 + 5 = 10.
- Находим произведение 6 * 10 = 60.
- Записываем результат: (4 + 2) * (2 + 5) = 60.
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
- Например, в выражении x + a — 8
x — переменная
a — переменная
Если вместо переменных подставить числа, то буквенное выражение x + a — 8 станет числовым выражением. Вот так:
- подставляем вместо переменной x число 5, а вместо переменной a — число 10, получаем 5 + 10 — 8.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
После подстановки значения переменных находим значение x + a — 8 = 5 + 10 — 8 = 7.
Часто можно встретить буквенные выражения, записанные следующим образом:
5x — 4a
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
- Сумма 6 и a.
- Разность 8 и x.
- Сумма x — 2 и 6
- Разность 15 и x — y
- Сумма 45 + 5 и 12 — 6
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: (b — 345) + (180 + x).
Задание три.
Составьте буквенное выражение:
Разность разности 30 и y и разности a и b.
Ответ: (30 — y) — (a — b).
Задание четыре.
Составьте выражение для решения задачи и найдите его значение.
Ролл «Калифорния» стоит 480 рублей — это на 40 рублей меньше, чем ролл «Филадельфия». Сколько будут стоить оба ролла?
Как решаем:
Калифорния — 480 рублей.
Филадельфия — 480 + 40.
Калифорния + Филадельфия = ?
480 + (480 + 40).
Мы помним, что выполнение арифметических действий в числовом выражении имеет строгую последовательность. Сначала — действие в скобках:
480 + 520 = 1 000.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
Маша — 150 видео.
Лена — 150 + 13 видео.
Маша + Лена = ? видео.
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Задание шесть.
Вычислите:
(500 + 300) : a — 15,
при условии, что a = 10.
Подставляем число 10 (значение переменной) вместо переменной
(500 + 300) : 10 — 15
Затем выполняем сначала арифметическое действие в скобках: 500 + 300 = 800.
Затем выполняем деление 800 : 10 = 80.
Выполняем вычитание 80 — 15 = 65.
Ответ: (500 + 300) : 10 — 15 = 65.
Задание семь.
Вычислите:
(270 — 120) * (x — 10),
при условии, что x = 45.
Как решаем: подставляем число 45 (значение переменной) вместо переменной x
(270 — 120) * (45 — 10).
Затем выполняем сначала арифметическое действие в скобках: 270 — 120 = 150.
Выполняем арифметическое действие во вторых скобках: 45 — 10 = 35.
Затем выполняем умножение 150 * 35 = 5 250
Ответ: (270 — 120) * (45 — 10) = 5 250.
Задание восемь.
Вычислите:
(50 * x) — (3 * y)
при условии, что x = 2; y = 10
Подставляем число 2 вместо переменной x
(50 * 2) — (3 * y).
Подставляем число 10 вместо переменной y
(50 * 2) — (3 * 10).
Затем выполняем сначала арифметическое действие в скобках: 50 * 2 = 100.
Выполняем арифметическое действие во вторых скобках: 3 * 10 = 30.
Затем выполняем вычитание 100 — 30 = 70
Источник
Запись решения задачи выражением
Урок 15. Математика 2 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Запись решения задачи выражением»
— Плюс. Плююююс! Ты где?
Привет, Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор с царицей Математикой.
— Здравствуй, Минус. Как это я забыл! Включаю.
— Здравствуйте, Дорогие Плюс и Минус!
Сегодня я хочу проверить, как вы умеете решать задачи. Я дам несколько задач и предлагаю вам устроить соревнование — кто сможет их решить быстрее, но при этом, конечно, правильно.
— Да, царица, мы Вас внимательно слушаем.
— Мы очень внимательно слушаем.
— Ну что же, приступим. Итак, вот первая задача:
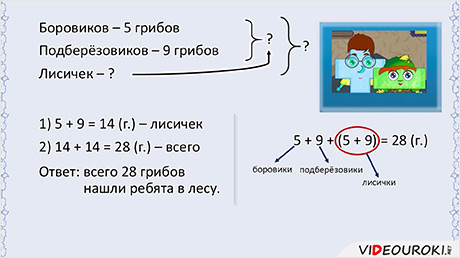
Ребята в лесу собирали грибы. Они нашли 5 боровиков, 9 подберёзовиков, а лисичек столько, сколько боровиков и подберёзовиков вместе. Сколько всего грибов нашли ребята в лесу?
Ну, Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас смотрят, попробуют решить эту задачу.
— Всё, я готов! Могу даже объяснить, как я решал эту задачу.
Нам даны два числа: количество боровиков — их 5, и количество подберёзовиков — их 9. Но неизвестно количество лисичек. Про них сказано, что их столько, сколько боровиков и подберёзовиков вместе. А ещё неизвестно, сколько всего грибов.
В задаче два неизвестных, значит, задача составная, то есть в ней не одно действие, а два. В первом действии я узнаю, сколько лисичек.
А так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то общее количество грибов я нашёл вот так:
Ответ: всего 28 грибов нашли ребята в лесу.
— А я решал задачу другим способом. Вот посмотрите:
— Да, Минус, чувствуется, что сложение — это не твой конёк. Конечно, задачу ты решил правильно. Но при этом у тебя получилось не два, а три действия. При этом первое и второе действия повторяются. Для этой задачи такой способ записи не очень удобен. Хотя некоторые задачи действительно удобно записывать не по действиям, как это сделал я, а числовым выражением. А вот, кстати, царица Математика уже даёт нам новую задачу.
— Тихо, Плюс, слушаем!
— На уроке физкультуры присутствовало 14 мальчиков. А девочек — на 5 меньше. Сколько всего учащихся присутствовало на уроке физкультуры?
— Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!
— Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.
А в задаче надо узнать количество девочек, и только потом — сколько всего детей. Я так и узнавал:
Ответ: всего 23 учащихся присутствовало на уроке физкультуры.
— А вот я записал решение этой задачи по-другому:
И ещё можно вот так:
— Но ведь ты мне только что говорил, что такой способ решения неудобен! Зачем же ты решил задачу другим способом — записью выражения.
— В первой задаче он действительно был неудобен, а в этой — очень даже удобен. Во-первых, это не другой способ решения задачи. Посмотри, в моём решении есть те же действия, что и в твоём, и даже в той же последовательности.
Ты первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я записал в скобках. А то, что записано в скобках, всегда выполняется первым.
Во втором действии к 14 прибавляем полученное в первом действии число 9. А в этой записи слагаемые меняются местами — к 9 прибавляется 14.
И получается, что это не другой способ решения задачи — ведь все действия одинаковы, а другой способ записи решения. Ты решал по действиям, а я — выражением. Способ решения одинаковый, а способ записи этого решения — разный. Но посмотри, моя запись получилась короче. В ней нет номеров действий и пояснений. Поэтому такая запись помогает экономить и время, и бумагу.
— Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую запись задачи выражением.
Ваше величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?
— Ну что же, слушайте:
В моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш растёт в моём саду?
Я хочу видеть у вас оба способа записи решения — и по действиям, и выражением.
— Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш, необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2 больше, чем яблонь.
Значит, в саду царицы растёт 14 яблонь и груш.
А вот как получилась запись выражением:
Сначала я нашёл, количество груш. Но, так как это действие стоит не в начале записи, я выделил его скобками. А потом нашёл сумму чисел. Ответ такой же, как и при записи по действиям — 14.
— Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.
— Можно я начну первый.
Записывать решение задачи можно по действиям и выражением.
— При записи по действиям мы пишем номер действия и пояснения к каждому действию, а при записи выражением только пояснение к значению записанного выражения.
— При записи выражения первое действие часто записываем в скобках, и конечно, не забываем записать ответ задачи.
— Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете пойти погулять в мой сад и полакомиться яблоками и грушами.
Источник
Для того, чтобы наглядно представить задачу и облегчить себе процесс ее решения, составляется краткая запись условия задачи. В краткой записи фиксируются величины, числа – данные и искомые, а также некоторые слова, показывающие, о чем говорится в задаче: «было», «положили», «стало» и т. п. и знаки, означающие отношения: «больше», «меньше», «одинаково» и т. п.
Краткую запись задачи можно выполнять в виде опорной схемы, таблицы, чертежа, с помощью геометрических фигур.
Для того чтобы краткая запись в максимальной степени способствовала решению задачи, нужно:
1) Краткую запись составлять на основе анализа текста задачи;
2) В краткой записи должно быть минимальное количество условных обозначений;
3) Количество вопросительных знаков в краткой записи должно соответствовать количеству действий в задаче;
4) Форму краткой записи выбирать такую, чтобы она более наглядно представляла условие задачи.
Основные виды краткой записи в начальной школе
Краткая запись в зависимости от типа задач:

Возможны вариации перечисленных вариантов краткой записи в зависимости от условия задачи. Возможна и запись в виде таблиц и рисунков.
Примеры задач:
– Витя собрал коллекцию из 18 камней и разложил на коробки поровну. Сколько камней в каждой банке?
Простая задача на деление на равные части, оформляем такие задачи в виде таблицы
В 1 коробке Количество коробок Всего камней
? к. 3 к. 18 к.
– 8 приглашений разложили в конверты, по 2 в каждый. Сколько использовали конвертов?
В 1 конверте Количество конвертов Всего приглашений
2 пр. ? к. 8 пр.
– Трое друзей решили сложится поровну и купить мяч стоимостью 60 рублей. Сколько денег должен дать каждый из них?
На 1 чел. денег Количество чел. Всего денег
поровну 3 чел. 60 руб.
– Одну деталь мастер должен делать за 45 мин, а делает за 38 мин. Сколько времени сэкономит мастер, когда он сделает 8 деталей?
Составная задача на разностное сравнение, лучше оформить в виде таблицы.
– Вера посадила 9 луковиц, по 3 луковицы в ряд. Сколько получилось рядов?
Это простая задача на деление по содержанию. Такую задачу нагляднее оформить картинкой.
– В детский сад привезли два бидона с молоком, по 20 л в каждом. За завтраком дети выпили 12 л молока. Сколько литров молока осталось?
Задача на нахождение остатка.
Было – 20 л и 20 л
Выпили – 12 л
Осталось – ? л
– В куске ткани было 24 м ткани. Из 10 м этой ткани сшили одинаковые детские костюмы, а из остальной ткани-7 одинаковых детских пальто. Сколько метров ткани расходовали на одно пальто.
Было -24 м
Израсходовали – 10 м
Осталось – 7 к. по ? м
– Когда брат полил 5 грядок, а сестра -3 грядки, им осталось полить 4 грядки. Сколько всего грядок должны полить дети?
Было – ? гр.
Полили – 5 гр. и 3 гр.
Осталось – 4 гр.
– В парк привезли 33 куста роз. Когда на нескольких клумбах посадили по 6 кустов, то осталось еще 15 кустов. Сколько было клумб?
Было – 33 к.
Посадили – ? кл. по 6 к.
Осталось – 15 к.
– В прятки играли 12 ребят. К ним присоединились 3 девочки и 4 мальчика. Сколько всего ребят стали играть в прятки?
Было – 12 р.
Пришли – 3 д. и 4 м.
Стало – ? р.
– У Саши было 6 наклеек. Он подарил другу 2 наклейки. Потом Саша купил еще 5 наклеек. Сколько наклеек стало у Саши?
Было – 6 н.
Подарил – 2 н.
Купил – 5 н.
Стало – ? н.
– На полянке паслись 14 коров, а овец на 10 больше. Сколько животных паслись на полянке?
– В первый день вырыли 5м траншеи, во второй на 3м меньше, чем в первый, в третий на 1м больше, чем во второй. На сколько больше вырыли траншей в первый и во второй день вместе, чем в третий?
– На двух полках было 17 кг меда. Со второй полки продали 5 кг и на 2 полках стало поровну. Сколько кг меда было на 1 полке?
Нагляднее представит задачу запись в виде схемы.
Пояснения к решению задач
Эта форма работы над составной задачей предусматривает проверку умения учащихся по данным действиям решения задачи пояснить, на какой вопрос и с какой целью отвечает действие. Таким образом, в конце каждого действия пишем пояснение, что именно мы нашли этим действием. Такая форма работы помогает учащимся увидеть другие отношения, вести необходимую цепочку логических рассуждений, анализировать и делать выводы.
Ответ задачи
Если использовались пояснения, ответ можно записать кратко. Если же не использовались, пишем полный ответ.