Как составить условия задачи по сказке

Латыпова Ляйсан Раисовна

гимназия № 25

учитель начальных классов

г. Нижнекамск

Республика Татарстан

Домашний адрес: улица Бызова, дом 5^а, квартира 143

(дом. тел. 43-58-60)

Использование игрового материала

на уроках математики

Использование занимательных задач

со сказочными сюжетами на уроках математики.

Часто родители и учителя жалуются, что дети не любят решать задачи. В своей работе на уроках математики я использую задачи со сказочными сюжетами. Являясь занимательными по форме, они усиливают интерес к самой задаче, побуждают ребенка решать проблему, вызывают желание помочь полюбившимся героям. Красота решения, неожиданный поворот мысли, логика рассуждений, все это усиливает эмоциональное восприятие детей.

Очень важно подобрать посильные для учеников задания, соответствующие их возможностям, развитию. Полезно и дать первый толчок для побуждения ребенка заняться решением, а затем усилить его сопротивляемость перед встающими трудностями. Ведь часто бывает, что даже смышленый ученик не хочет просто прочитать задачу, не то что решать ее, а поэтому целесообразно использовать внешнюю занимательность текстов. Цель может быть достигнута, если условие задачи будет похоже на сказку.

Казалось бы, сказка и математика – понятия несовместимые. Свежий сказочный образ и сухая абстрактная мысль! Однако нередко именно такая форма позволяет удачно ввести ребят в мир математики, причем через посредство увлекательной ситуации. Такое сочетание благоприятно для обучения, поскольку через сказочные элементы учитель может найти пути в сферу эмоций ребенка. Желание помочь попавшему в беду любимому герою, стремление разобраться в сказочной ситуации – все это стимулирует умственную деятельность ребенка.

В то же время важна и обратная связь: в ряде случаев встреча со сказочными героями в мире математики побуждает ученика еще раз прочитать литературное произведение, поразмышлять, глубже заглянуть в него. При составлении задач надо добиваться, чтобы поведение сказочных героев соответствовало духу самой сказки: борьба за справедливость Ивана- царевича и коварство Кощея Бессмертного, верность дружбе неунывающего Буратино и желание поживиться за чужой счет лисы Алисы и кота Базилио и т.д. симпатии детей на стороне положительных героев. Добро торжествует, зло наказано, отрицательные качества высмеиваются. Сказки и через задачи продолжают воспитывать детей.

Условия задач со сказочными сюжетами во многих случаях громоздки. Но это сказка! Выбранная форма влечет за собой относительно большой ее объем – ведь очень часто при составлении задачи приходится следовать литературному тексту сказки. Зато в таком случае дети с большим удовольствием читают условие, вникают в его смысл – а работа над текстом является существенной частью психологической подготовки ребенка к олимпиаде.

Вместе с тем надо сохранять чувство меры, разумно дозировать разные виды заданий. Предлагаю ряд задач. Они могут быть полезны на различных этапах олимпиады, подготовительных занятиях, на уроке.

«Режим дня для попрыгуньи Стрекозы»

Попрыгунья Стрекоза половину времени каждых суток красного лета спала, третью часть времени каждых суток танцевала, шестую часть – пела. Остальное время она решила посвятить подготовке к зиме. Сколько часов в сутки Стрекоза готовилась к зиме?

Ответ: В течение суток Стрекоза ни часу не готовилась к зиме.

В сутках 24 часа. Из них Стрекоза спала 24:2 =12 (ч), танцевала 24:3=8 (ч), пела 24:6=4 (ч). Всего она на эти дела тратила 12+8+4=24 (ч. в сутки). Так что на подготовку к зиме у Стрекозы не хватало времени.

«Квартет»

Проказница мартышка,

Осел,

Козел

Да косолапый Мишка

Затеяли сыграть Квартет.

Для этого они сели кружком, Мартышка расположилась напротив Медведя, а рядом с нею – Осел и Козел.

Ударили в смычки, дерут, толку нет. Тогда Осел и Козел поменялись местами.

Расселись, начали Квартет.

Он все-таки на лад нейдет.

Таким образом, они перепробовали все возможные варианты, причем медведь всегда оставался на одном и том же месте.

Сколько всего было вариантов расположения незадачливых музыкантов?

Ответ: 6 вариантов.

«Кто победил Змея Горыныча»

– Змей Горыныч побежден! – такая молва дошла до Микулы Селяниновича. Он знал, что это мог сделать кто-то из богатырей: либо Илья Муромец, либо Алеша Попович, либо Добрыня Никитич.

Вскоре Микуле Селяниновичу сообщили:

1. Змея Горыныча победил не Илья Муромец;

2. Змея Горыныча победил Алеша Попович.

Спустя некоторое время выяснилось, что одно из этих сообщений неверное, другое верное.

Догадайся, кто из трех богатырей победил Змея Горыныча.

Ответ: Змея Горыныча победил Добрыня Никитич.

Предположим, что Змея Горыныча победил Илья Муромец. Тогда оба сообщения неверные – результат не соответствует условию задачи.

Предположим, что Змея Горыныча победил Алеша Попович. Тогда оба сообщения верные. И этот результат условию задачи не соответствует.

Предположим, что Змея Горыныча победил Добрыня Никитич. Тогда первое сообщение верное, а второе – неверное. Результат соответствует условию задачи.

«Иван против Кощея Бессмертного»

– Помогу тебе, Иван, вызволить Василису Прекрасную, – сказала Баба Яга. – По душе ты мне пришелся. Да и от Кощеева коварства много я страдала, уж очень хочется его проучить.

Вот тебе, Иван, клубок. Приведет он тебя прямо к Кощею Бессмертному. В подземелье у него три темницы. В одной из них томится Василиса Прекрасная, в другой находится Змей Горыныч, а третья темница – пустая. Учти, что все надписи на дверях темниц неверные.

Бросил Иван клубок на землю. Покатился клубок, а Иван – за ним. Долго ли, коротко ли, он дошел до Кощея Бессмертного. Потребовал Иван у него Василису Прекрасную.

Повел Кощей Ивана в подземелье. Показал там три темницы, на дверях которых написано:

темница I – «Здесь Василиса Прекрасная»;

темница II – «Темница III не пустая»;

темница III – «Здесь Змей Горыныч».

– Отпущу, Иван, с тобой Василису Прекрасную, если угадаешь, в какой она темнице. Покажешь на дверь, за которой Змей Горыныч, – быть тебе им растерзанным. Покажешь на пустую темницу – быть тебе в ней узником до конца дней своих.

Задумался Иван… Ребята, посоветуйте Ивану, на какую дверь ему показать.

Ответ: Василиса Прекрасная во II темнице.

Надпись на двери темницы II неверная, т.е. темница III пустая. Значит, I и II темницы не пустые. Надпись на двери I темницы тоже неверная. Значит, там Змей Горыныч. Тогда во II темнице Василиса Прекрасная.

«Дедушка Мазай спасает зайцев»

Во время наводнения дедушка Мазай снял с острова зайцев.

Только уселась команда косая, Весь островочек пропал под водой.

Далее дедушка Мазай спас еще некоторое количество зайцев, снимая их с пней. Интересно, что это число записывается теми же цифрами, что и число зайцев, спасенных с острова, но в обратном порядке. Число зайцев с острова больше, чем число зайцев, снятых с пней. Оба числа двузначные.

Мимо бревно суковатое плыло, Сидя, и стоя, и лежа пластом, Зайцев десяток спасалось на нем.

Мазай и этих зайцев взял с собой. Всего Мазай спас 43 зайца. Сколько зайцев спас дедушка Мазай с острова?

Ответ: Дедушка Мазай спас с острова 21 зайца.

Сказочная эта задача или нет – пусть решат сами дети, соотнеся ее реальными фактами. Пусть дети вспомнят случаи, когда они или их знакомые спасли кого-либо из «братьев меньших».

«Буратино и его друзья»

Буратино, Мальвина и Пьеро, спасаясь от Карабаса Барабаса, выбежали на берег озера. Мальвина и Пьеро сели на черепаху Тортилу. Буратино же места не хватило, поэтому он бросился вплавь. Буратино может переплыть озеро через 30 мин, а Тортила в 3 раза быстрее (с грузом или без него). Карабас Барабас побежал вокруг озера, и на это ему потребуется 30 мин.

Как быстрее переплыть озеро всем беглецам?

Успеют ли Буратино и его друзья убежать от Карабаса Барабаса, если от озера до папы Карло им надо бежать 18 мин?

Карабас бежит в два раза быстрее, чем Буратино и его друзья.

Ответ: Буратино и его друзья успеют убежать от Карабаса Барабаса.

Когда Буратино доплывает до середины озера, то Тортила успеет доплыть до берега (высадив Мальвину и Пьеро) и встретить на середине Буратино – ведь Тортила плывет в 3 раза быстрее, чем он. На середине озера Буратино будет через 30:2=15 (мин). Значит, Тортила с Буратино достигнут берега через 15:3=5 (мин). Буратино достигнет берега через 15+15:3=20 (мин). Через 30-20=10 (мин) после этого на место высадки прибежит Карабас Барабас. За это время будут у папы Карло в 18-10=8 (мин) бега. Карабасу Барабасу бежать до папы Карло 18:2=9 (мин). 8

«Винни – Пух и пятачок идут в гости»

Винни – Пух с Пятачком отправились к Сове на день рождения. Сова жила на высоком превысоком дубе. Пятачок нес в подарок 5 одинаковых баночек меда, а Винни – Пух – воздушный шарик. Этот шарик может за один раз поднять либо Винни – Пуха и 2 баночки меда, либо Пятачка и 3 баночки меда, либо 5 баночек меда (больше этого груза шарик не может поднять).

Когда друзья подошли к дубу, Винни – Пух сказал:

– Шарик не может поднять нас с банками меда. Давай-ка, подарим Сове
лишь воздушный шарик! Кстати, скоро у меня день рождения…

Пятачок вежливо спросил:

– А может ли воздушный шарик поднять нас обоих за один раз?

Как бы ты ответил на этот вопрос?

Ответ: Да, может.

Масса Винни – Пуха не больше массы 5-2 = 3 (баночек меда). Масса Пятачка не больше массы 5-3 = 2 (баночек меда). Масса Винни – Пуха и Пятачка не больше 3+2 = 5 (баночек меда). Значит, шарик может поднять Винни – Пуха и Пятачка.

С детьми можно обсудить моральную сторону предложения Винни – Пуха, а затем рассмотреть, что же делать с баночками меда и шариком. Дети могут предложить свои варианты подарков Сове и Винни – Пуху к их дням рождения.

«Золушка»

Злая мачеха дала кроме прочей работы Золушке непосильную математическую. Надо помочь.

1. Расставь знаки и скобки так, чтобы получилось верное равенство.

9 9 9 = 2 9 9 9 = 10

9 9 9 = 9 9 9 9 = 90

2. Какое число было вначале?

х3 -19 +10 :9 +86 +3 -32 :2

3. Самый длинный бал королевства продолжался с 15 августа по 7 сентября включительно. Сколько дней продолжался праздник?

4. Восстанови запись. Одинаковые фигурки обозначают одинаковые цифры.

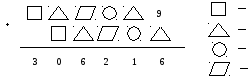
5. В каждом из четырех ящиков лежит волшебный порошок: белый, красный, черный, зеленый.

На каждом ящике указаны надписи, но ни одна из них неверная. Отгадай цвет порошка в каждом ящике?

Белый

Зеленый или белый

Красный или зеленый

Черный, или зеленый, или красный

6. Можно ли найти 2 целых числа, одно из которых больше другого на 10, а их произведение равно 96? Докажи.

7. Сумма длин сторон комнаты 28 м. Может ли ее площадь быть равной 36 м², 24м²? Докажи.

8. «Домино». Продолжи.

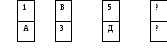
Ответы:

1. (9+9) : 9 = 2

9 х 9 : 9 = 9

2. 48

3. 24 дня

4.

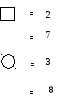
5.

6. 16 – 6 = 10, 16 х 6 = 96

7. 24 м²; (S = 12 х 2; Р = (12 + 2) х 2

8. 1/А В/3 5/Д Ё/7

«Теремок»

1. У мышки, лягушки, петушка и ежа дни рождения 2 марта, 17 мая, 2 июля, 20 марта. Лягушка и петушок родились в одном месяце, а у петушка и мышки день рождения на одну цифру. Кто когда родился?

2. Жители теремка должны дежурить у ворот каждую ночь по 3, а один в это время спал, чтобы днем делать нужную работу. Сколькими способами можно составить график дежурства?

3. Число яблок в корзине двузначное. Яблоки можно разделить поровну между двумя, тремя или пятью детьми. Сколько яблок в корзине?

4. Во сколько раз лестница на 4-ый этаж в теремке длиннее на 2 этаж?

5. Во сколько раз станет больше площадь теремка, если все его стороны увеличить в 2 раза?

6. Решили жители теремка сделать себе волшебный кодовый замок. На световом табло высвечивалось четырехзначное число, у которого цифра тысяч такая же, как цифра сотен, а цифра десятков такая же, как цифра единиц. Сумма этих цифр равна 16, причем сотен в этом числе больше, чем десятков. Что это за число?

7. Ночной сторож Еж взял легко гнущуюся проволоку длиной 1 м 35 см разрезал ее на равные куски. Путем сгибания он получил равносторонние треугольники, длины сторон которых выражаются целыми числами сантиметров, не превышающих 5 см. Сколько таких треугольников он мог получить?

Ответы:

1. Петушок – 2 марта, Лягушка – 20 марта, Мышка – 2 июля, Еж – 17 мая

2. 444

3. 30 яблок

4. В 4 раза

5. В 4 раза

6. 6622 или 7711 или 5533

7. 45

«Три поросенка»

1. Три поросенка бежали от волка 3 км. Сколько километров пробежал каждый поросенок?

2. Ниф-ниф и Нуф-нуф жили в домиках с большим окном, а Нуф-нуф и Наф-наф в домиках с высокой крышей. Кто в каком домике живет?

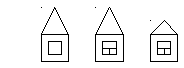
Найдите решения

D

D

Н

А

Г

Н

Б

Н

О

Б

О

Л

Н

О

1. В книжке вырваны страницы – с 5-ой по 18-ю. Сколько листов не хватает в книге?

2. Три поросенка, празднуя победу над Волком, открыли большую коробку конфет. Сколько конфет в ней было, если Ниф-ниф съел одну третью часть всех конфет, Наф-наф – сколько же, А Нуф-нуф – оставшиеся 17 штук?

3. Поросята Ниф-ниф и Нуф-нуф бежали от Волка к домику Наф-нафа. Волку бежать до поросят (если они стоят на месте) 4 мин. поросятам бежать до домика Наф-нафа 6 мин. Волк бежит в 2 раза быстрее поросят. Успеют ли поросята убежать?

4. Три поросенка имеют по некоторому количеству желудей. Первый дает двум другим столько желудей, сколько каждый из них имеет. Затем второй поросенок дает двум другим столько желудей, сколько каждый из них теперь имеет, в свою очередь и третий поросенок дает своим братьям столько, сколько есть у каждого в этот момент. После у каждого оказывается 8 желудей. Сколько желудей было у каждого поросенка первоначально?

5. Шоколадку разделили на 3 равные части. Как это сделать?

Ответы:

1. 3 км

– Нуф – нуф; Наф – наф; Ниф – Ниф;

– – D

– –

нега, село, небо

1. 7 листов

2. 51 конфета

3. Успеют (4 + 3 = 7 6)

6.

«Курочка Ряба»

1. 4 яйца сварили за 4 мин. Сколько минут варится 1 яйцо?

2. У бабушки было 3 десятка яиц. Чтобы приготовить завтрак, она истратила шестую часть яиц. Сколько яиц осталось? Запиши выражение.

3. За 20 секунд мышка пронеслась 60 метров. Сколько метров она успеет пробежать за 1 минуту?

4. Два десятка умножили на три десятка. Сколько десятков получили?

5. Во дворе по вертикальному столбу высотой 6 м движется улитка. За день она поднимается на 4 м, за ночь опускается на 3 м. Сколько дней ей потребуется, чтобы добраться до вершины?

6. Во дворе куры и поросята. У них всех 5 голов и 14 ног. Сколько кур и поросят? (20 голов и 52 ноги?)

7. На квадратном огороде, периметр которого равен 80 м, посадили собаку на цепь длиной 9 м 70 см и прикрепили цепь к столбу, торчащему самом центре огорода. Длина собаки от ошейника до передних зубов 30 см. Смогут ли пробраться в огород мыши?

8. С соседней птицефабрики сбежали 6 738 кур и 12 петухов. На ловлю каждой курицы директор птицефабрики тратит 3 мин., а на ловлю петуха – 15 мин. Сколько времени потребуется директору, чтобы переловить всех сбежавших, если остальные сотрудники птицефабрики уйдут в отпуск?

Ответы:

1. 4 мин

2. 30 – (30 : 6) = 25

3. 180 м

4. 60 м

5. 3 дня

6. 3 курицы и 2 поросенка (6 поросят 14 кур)

7. Только в самые уголки

8. 20 394 мин (15 дней)

«Семеро козлят»

1. Вокруг клумбы квадратной формы надо разместить 14 камешков так, чтобы вдоль каждой стороны было одинаковое количество. Нарисуй, как это сделать.

2. Запиши ответы к выражениям числами.

1. Кузнецу принесли 4 обрывка цепи, по 3 звена в каждом, и попросили соединить в одну цепь. Кузнец выполнил заказ, раскрыв только 3 звена. Как он это сделал?

2. Сколько будет 7 + 7 деленное на 7?

3. Волку и козе с капустой надо переправиться через реку. В лодке может поместиться только перевозчик, а с ним или волк, или коза, или капуста. Если оставить волка с козой, то волк съест козу, если оставить волка с капустой, то волк выбросит капусту, а козе – кормить козлят. Как им переправиться?

4. Переправилась коза, пришла в избушку. Как ей поделить 7 кочанов капусты, чтобы каждый козленок получил по кочану и один кочан остался в корзине?

5. Семеро козлят спешили на день рождения и поэтому двигались с одинаковой скоростью. Один козленок нигде не задерживался и пришел вовремя, а остальные 5 раз останавливались, чтобы подкрепиться травкой. В первый раз козлята подкрепились за 18 секунд, во второй – в 2 раза дольше, а в третий раз – на полминуты меньше, чем во второй. На сколько минут опоздали козлята?

Ответы:

1.

1. 2; 0; 0; 4

3.

1. 2

коза

капуста

коза

волк

коза

1. Один вместе с корзиной

2. 18 + 36 + + 6 = 1 мин

«Снеговик»

1. Расшифруй: АА + А = БОВ

2. Если какой-нибудь мальчик съест 5 порций мороженого за раз – он заболеет ангиной. Петя на свой день рождения пригласил 19 мальчиков из своего класса и купил 90 порций мороженого. Может ли завтра в классе оказаться 20 больных?

3. В феврале 2004 г. 5 воскресений, а всего 29 дней. На какой день приходится 23 февраля 2004 года?

4. Часы за сутки убегают вперед на 3 мин. Их поставили точно. Через какой промежуток часы снова покажут точное время?

5. Отца Деда Мороза зовут Николай Петрович, а сына Деда Мороза – Алексей Владимирович. Как зовут самого Деда Мороза?

6. Сумма трех чисел равна их произведению. Эти числа различные и однозначные. Какие это числа?

7. Хоккейная команда провела 3 матча, забив ворота противника всего 3 шайбы и пропустив одну шайбу. Один из матчей она выиграла, другой свела вничью, а третий проиграла. С каким счетом закончился каждый матч?

8. Как изменится площадь снежной крепости, если каждую стену достроить, увеличив в 3 раза?

Ответы:

1. 99 + 9 = 108

2. Им достанется по 4,5 порции. Нет

3. Понедельник

4. 240 суток

5. Владимир Николаевич

6. 1, 2, 3

7. 3 : 0; 0 : 0; 0 : 1

8. В 9 раз

«Чебурашка»

1. Гена угостил Чебурашку яблоками. Он дал ему 8 яблок, что составило 2/10 части яблок в корзине. Сколько яблок осталось у Гены?

2. У Гены на дне рожденья было непослушных мальчиков столько же, сколько послушных девочек. Кого больше: послушных девочек или мальчиков?

3. Чебурашка и Гена едут на поезде, если считать от начала, их вагон – четвертый, если от конца – то 12 –й. Сколько вагонов в поезде?

4. В день рожденья Гены Чебурашка показал, всем уникальные способности: он у каждого гостя угадал число его дня рождения. Он действовал так: просил свое число, являвшееся у каждого днем рождения, утроить, затем полученные результаты разделить на 9, частное умножить на 3, а остаток разделить на 3 . Попросив, чтобы было объявлено это произведение и это частное, он мог сказать, какого числа у человека день рожденья. Как найти день рожденья?

5. Деревянный окрашенный куб с ребром 3 см распилили на кубические сантиметры. сколько среди них кубиков, которые окрашены с трех сторон?

6. На квадратном пустыре решили построить наибольшую круглую танцплощадку. радиус полученного круга 3 см. Найдите периметр пустыря?

7. Вместо звездочек поставь нужные цифры.

+ * 3 * 69* * х 7 *

3 * 3 * 7 * * *

* 0 0 0 * *

* *

* *

* * * 9

Ответы:

1. 32 яблока

2. Поровну

3. 15 вагонов

4. К умноженному частному прибавить разделенный остаток

5. 4 сверху, 4 снизу

6. 24 м

7. _х637 _–693 9 _х79

363 63 77 111

1000 _–63 ₊79

63 79

0 79

8769

«Муха – цокотуха»

1. Муха – цокотуха купила самовар, пригласила гостей, испекла к чаю 20 булочек и 40 крендельков. Каждому гостю досталось по 2 кренделька и по одной булочке. Сколько гостей было?

2. У пчелки глаз столько, сколько у тебя да еще полстолько. Сколько глаз у пчелки?

3. Над болотцем тихо, тихо…

В теплом воздухе парят

Сам комар да Комариха,

С ними – туча комарят!

Комариха с Комаром говорят:

– Сосчитай-ка, Комар, комарят.

– Как же счесть, Комариха, комарят?

Не поставишь комарят наших в ряд.

Насчитала Комариха сорок пар.

А продолжил этот счет сам Комар.

Комарят Комар до вечера считал.

Насчитал 13 тысяч и устал.

А теперь считайте сами вы, друзья:

Велика ли комариная семья?

1. У мухи угощенье – нектар 19 различных цветов весом в 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 г. Как разложить его в 10 тарелочек, чтобы все они одинаково весили?

2. Муха-цокотуха нашла денежку и на нее купила на базаре самовар, крендельки и конфеты. Самовар и крендельки стоят 48 чуков. За крендельки и конфеты Муха уплатила 3 чука. Причем конфеты дорожу крендельков. Сколько чуков составляет денежка, которую нашла Муха?

3. Решили сделать из Мухи слона – накормить ее до слоновьего веса. Сколько нужно еды, если муха весит 1/10 часть грамма, а слон – 14 т?

4. Муху пригласили в гости. Туда она шла пешком с подарком и в новых сапожках, а обратно ехала. Первую половину пути она ехала на гусенице – ехала в 2 раза медленнее, чем шла пешком. А другую половину – на Кузнечике – в 5 раз быстрее, чем пешком. На какой путь потрачено времени меньше: в гости или обратно?

Ответы:

1. 19 гостей

2. 3

3. 13082

4. 19 г, 18 + 1, 17 + 2, 16 + 3, 15 + 4, 14 + 5, 13 + 6, 12 + 7, 11 + 8, 10 + 9

5. 50 чуков

6. 12 т 600кг

7. В гости

«Колобок»

1. Колобок вышел из дома и покатился по дорожке. До дома зайца он катился 4 мин со скоростью 5 м/мин, до волка катился 10 мин со скоростью 4 м/мин, до медведя 15 мин со скоростью 3 м/мин, до лисы 10 мин со скоростью 3 м/мин. Какое расстояние прокатился колобок от дома до встречи с лисой?

2. Решил колобок показать Лисе, какой он неглупый и заинтересовать:

Напиши число любое,

На него я погляжу

И затем клочок бумаги

При тебе в конверт вложу.

Под своим числом любое

Напиши число опять,

И число одно позволю

Сам себе я написать.

Подведем черту и сложим

Наших чисел стройный ряд.

Нет ошибки? Осторожней!

Все в порядке? Очень рад!

Сумма – я прошу, проверьте!

У меня давно в конверте!

В чем тут фокус? В чем секрет?

Сообщи мне свой ответ.

1. Найди пропущенное число.

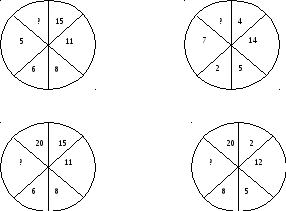
1. Пирог прямоугольной формы двумя разрезами разделили на 4 части так, чтобы две из них были четырехугольной формы, две – треугольной.

2. Заяц, Волк, Медведь и Лиса решили стать союзниками и всем вместе напасть на Колобка. Они обменялись лапопожатиями. Сколько было всего лапопожатий?

3. Как переложить 10 колобков в обратном порядке, трогая только 3 из них?

1. Во сколько раз больше число, выраженное четырьмя единицами пятого разряда, чем число, выраженное четырьмя единицами первого разряда?

Ответы:

1. 135 м

2. Взять третье число такое, чтобы его цифры дополнили до девяток одно число. Для суммы выполнить преобразования: слева в ответе ко второму числу приписать 1, число единиц уменьшить на 1, остальные цифры без изменения

3. 20; 10; 5; 3

4.

5. 6

6.

1. В 10 000 раз

«Паровозик из Ромашково»

1. Машина за 40 мин проехала 40 км, а катер за 30 мин 35 км. Чья скорость больше?

2. Паровозик выехал в полночь, а в 8 ч прибыл на станцию назначения. В 19 ч он отправился обратно. Когда он вернется назад?

3. Бюро прогнозов сообщило в 3 ч дня, что в ближайшую неделю сохранится безоблачная погода. Можно ли ожидать, что через 60 ч будет светить солнце?

4. От пристани одновременно в одном направлении отчалили пароход и катер со скоростью 24 км/ч и 15 км/ч. Через 4 ч пароход сел ан мель. Снявшись через некоторое время с мели, он догнал катер через час. Сколько времени простоял пароход на мели?

5. Игрушечный паровозик из детской железной дороги может тянуть груз в 1 кг. Сколько таких паровозиков нужно, Чтобы утащить настоящий вагон весом 100т?

6. Колесо имеет 10 спиц. Сколько промежутков между спицами?

7. Счетчик автомобиля показывал 12 921 км. Через 2 ч на счетчике опять появилось число, которое читалось одинаково в обоих направлениях. С какой скоростью ехал автомобиль?

Ответы:

1. Катера

2. 3 ч. ночи

3. Нет, будет ночь

4. 3 часа

5. 10 000 паровозиков

6. 10 промежутков

7. 55 км/ч

Загадки на занятиях математики

Загадки расширяют кругозор детей, развивают любознательность и пытливость, тренируют внимание, память, мышление. Они могут быть использованы учителем на уроке, во внеклассной работе, во время отдыха, так как всегда интересны детям.

На уроках математики и во внеклассных занятиях можно использовать загадки, содержащие, например:

различные числа: математические отношения:

У него четыре лапки, Лапки – цап – царапки, Пара чутких ушей. Он – гроза для мышей. (Кот.)	Чем больше из нее берешь, Тем больше она становится. (Яма.)
Черненькая, хвостаттенькая, Не лает, не кусает, А из класса в класс Не пускает. (Двойка.)	Говорит она беззвучно, А понятно и нескучно. Ты беседуй чаще с ней – Станешь в 10 раз умней. (Книга.)
единицы измерения величины:
К нам во двор забрался крот, Роет землю у ворот. Тонна в рот земли войдет, Если крот откроет рот (Экскаватор.)

При знакомстве с новой цифрой загадка может служить исходным материалом для выделения изучаемого числа. Например, учитель предлагает детям отгадать загадку:

Вспушит она свои бока,

Свои четыре уголка,

И тебя, как ночь настанет,

Все равно к себе притянет.

(Подушка.)

После того как дети назвали отгадку, учитель просит их вспомнить, какое число прозвучало в загадке, объясняет, как изображается число 4; предлагает найти это число в кассе цифр и счетного материала и показать соответствующую карточку. Сконцентрировав внимание на числе 4, учитель может провести обычную для урока математики работу – попросить детей назвать предыдущие и последующие числа или сказать, между какими числами расположено 4 в числовом ряду; сказать все примеры на сложение с ответом 4 (изучение состава числа), сделать соответствующие записи в тетради или составить с помощью разрезных цифр.

Приведем загадки, с которыми можно познакомить детей при изучении нумерации чисел в первом десятке.

Отгадайте–ка ребятки, Что за цифра-акробатка? Если на голову встанет, Ровно на три меньше станет. (Девять.)

Говорит она беззвучно, А понятно и нескучно. Ты беседуй чаще с ней – Станешь в 10 раз умней. (Книга.)

Особенно полезны загадки, по тексту которых надо догадаться, о какой цифре идет речь, и написать или показать ее. Такие загадки, как стихотворения С.Я. Маршака «От 1 до 10» («Веселый счет»), помогают детям запомнить графическое изображение цифр, учат узнавать из по описанию. Первоклассники с удовольствием откликаются на предложение учителя подумать, какая цифра о себе сказала: Или отгадать что это за цифра:

Я так мила, я так кругла, Я состою из двух кружочков, Как рада я, что я нашла Себе таких, как вы, дружочков! (Восемь.)

Вид ее – как запятая, Хвост крючком, и не секрет: Любит всех она лентяев, А ее лентяи – нет. (Двойка.)

Задачи, имеющие форму загадок, также вызывают большой интерес, активность, стремление правильно ответить на вопрос, например:

Отгадайте–ка ребятки,

Что за цифра-акробатка?

Если на голову встанет,

Ровно на три больше станет.

(Шесть.)

После того как кто-нибудь из учащихся даст правильный ответ на вопрос, можно продолжить работу с загадкой. Попросить детей найти в классе карточку с цифрой 6, перевернуть ее и ответить, какая цифра получилась. На сколько 9 больше 6? Каким действием можно узнать, на сколько одно число больше другого? После этого дети могут записать пример в тетради или составить его с помощью разрезных цифр.

Любая загадка – это логическое упражнение, при выполнении которого ребенок учится выделять различные стороны предмета (абстрагирование), а также находить предмет по нескольким перечисленным признакам (синтез). Загадки могут быть различной степени сложности, это зависит от числа признаков (детям трудно учитывать все признаки предмета) и от того, насколько характерны для данного объекта. Поэтому чем младше дети, тем меньшее количество признаков должно содержаться в загадке, но они должны быть характерными для данного предмета, например:

Я пыхчу, пыхчу, пыхчу, Сто вагонов я тащу. (Паровоз.)

Ем я уголь, пью я воду. Как напьюсь прибавлю ходу. Везу обоз на сто колес И называюсь … (Паровоз.)

Первая из загадок более легкая, так как небольшое количество условий и имитация звуков помогают быстро найти отгадку; вторая содержит больше признаков, которые необходимо учесть, но рифмованность текста с отгадкой тоже облегчает поиск правильного ответа.

Если загадка вызывает затруднение детей, то не следует торопиться говорить ответ. Надо попытаться помочь детям: сказать, что в загадке рассказывается о животном или предмете домашнего обихода, о явлении природы ли ягоде. Например, после чтения загадки:

Танцует крошка,

А всего одна ножка.

(Волчок, юла.)

– можно спросить учащихся, о какой детской игрушке идет речь. Это указание сужает поиски и облегчает нахождение отгадки.

Для того чтобы дети отгадали загадку, они должны быть знакомы с предметом или явлением, о котором идет речь, наблюдать его. С другой стороны, загадки про один и тот же предмет, позволяющие показать его с разных сторон, способствуют расширению знаний об окружающем мире, например:

Овсом его не кормят, Кнутом его не гонят, А как пашет – Семь плугов тащит. (Трактор.)

Я сильней десяти коней. Где в полях пройду весной, Летом станет хлеб стеной. (Трактор.)

При дальнейшем изучении нумерации чисел можно предложить детям следующие загадки:

Двенадцать братьев Друг за другом ходят, Друг друга не обходят. (Месяцы.)

Тридцать три родных сестрицы – Писаных красавицы, На одной живут странице, А повсюду славятся! (Буквы.)

После того как дети отгадают загадку и хотя бы кратко пояснят, какие слова в тексте помогли им в этом, можно предложить с помощью сигнальных блокнотов показать число, которое встретилось в загадке: определить, сколько в нем десятков и единиц, назвать число каждого разряда, предыдущее и последующее числа, представить число в виде суммы разрядных слагаемых и т.п.

Загадки могут использоваться при изучении темы «Меры времени». Так, загадка:

Две сестрицы друг за другом

Пробегают круг за кругом.

Коротышка – только раз,

Та, что выше, – каждый час.

(Стрелки часов.) –

– может привлечь внимание учащихся к движению стрелок, послужить началом работы с моделью часов (подвижные стрелки). Например, можно попросить поставить стрелки часов так, чтобы они показывали 9 часов, а затем определить, какой угол образовался между стрелками (прямой), какую долю циферблата отделяют стрелки (1/4).

На руке, и на стене, И на башне в вышине Ходят с боем и без боя. Всем нужны – и нам с тобою. (Часы.)

Что за птицы пролетают? По семерке в каждой стае. Вереницею летят, Не воротятся назад. (Дни недели.)

При знакомстве учащихся с календарем уместно будет прочитать следующие загадки:

Годовой кусточек Каждый день роняет листочек, Год пройдет – Весь лист опадет. (Календарь.)

Выходило 12 молодцов, Выносили 52 сокола, Выпускали 365 лебедей. (Месяцы, недели, дни.)

В этой загадке в иносказательной форме описывается год, а количественные соотношения между мерами времени служат основными (характеристиками) признаками, по которым учащиеся определяют отгадку. Очень часто дети стараются запомнить загадку, чтобы загадать ее друзьям или родителям, подчас не подозревая, что тем самым заучивают таблицу мер времени.

Такая работа развивает логическое мышление, математическую речь, учит видеть в окружающем мире общие свойства и различия предметов и явлений. Все это в дальнейшем будет способствовать формированию обобщений, умению давать определения понятиям (по ближайшему роду и видовому отличию), развитию мыслительных операций (абстрагирование, анализ, синтез).

Осень и математика

Структура заданий:

1. четверостишие об осени;

2. фамилии поэтов и соответствующие им числа;

3. логико-математическое упражнение.

Образный, немногословный и эмоциональный язык поэзии может больше сказать детям об осени, чем многословный и длинный рассказ об этом времени года. Среди фамилий поэтов одна принадлежит автору четверостишия, другие даны для создания условий выбора. Дети слышат и запоминают имена русских поэтов и на уроках математики. Одно из чисел является ответом к логико-математическому упражнению развивающего характера. Условия математических заданий предполагают развитие умения сравнивать объекты (числа, выражения, уравнения, фигуры и т.д.), находить связи между ними, формулировать гипотезы и применять их для нахождения неизвестного числа.

Работу с предлагаемыми заданиями можно организовать по-разному, используя фронтальную, групповую и индивидуальную формы совместной деятельности учителя и учащихся. На уроке русского языка, например, читают стихотворение, переписывать его в тетрадь, работают над правописанием отдельных слов, запоминают наизусть. На уроке математики работа продолжается: дети выполняют математическое упражнение, отвечают на вопросы, связанные с ним, и узнают имя автора стихотворения.

1. Поспевает брусника, А.Н. Плещеев 104

Стали дни холоднее. К.Д. Бальмонт 108

И от птичьего крика Ф.И. Тютчев 106

В сердце только грустнее.

1. Встает заря во мгле холодной; К.Д. Бальмонт 76

На нивах шум работ умолк; А.С. Пушкин 84

С своей волчихою голодной А.Н. Майков 95

Выходит на дорогу волк…

3. Стаи птиц улетают А.С. Пушкин 140

Прочь, за синее море. Ф.И. Тютчев 150

Все деревья блистают К.Д. Бальмонт 160

В разноцветном уборе.

Указание: ×87 ×2 −14 +34 :50

4. Скучная картина! Тучи без конца, А.Н. Майков 15

Дождик так и льется, лужи А.Н. Плещеев 25

у крыльца… К.Д. Бальмонт 35

: 4 = : 4 = + 61 =

− 1500 = 8 × 207 =

5. Осень! Летит по дорогам К.Д. Бальмонт 304

Осени стужа и стон! А.С. Пушкин 406

Каркает около стога Н.М. Рубцов 508

Стая озябших ворон.

6. Есть в осени первоначальной Ф.И. Тютчев 60

Короткая, но длинная пора – Н.А. Некрасов 120

Весь день стоит как бы хрустальный, А.С. Пушкин 180

И лучезарны вечера…

7. Ласточки пропали, Н.М. Рубцов 15

А вчера зарей А.А. Фет 30

Все грачи летали К.Д. Бальмонт 45

Да, как сеть, мелькали

Вон над той горой.

8. Роняет лес багряный свой убор. А.С. Пушкин 15

Сребрит мороз увянувшее поле, А.А. Блок 16

Проглянет день, как будто поневоле, А.Н. Майков 17

И скроется за край окружных гор.

9. Октябрь уж наступил – уж роща И.А. Бунин 13

отряхает А.Н. Майков 14

Последние листы с нагих своих А.С. Пушкин 15

ветвей;

Дохнул осенний хлад – дорога

промерзает.

Журча еще, бежит за мельницу

ручей…

10. Осенние листья по ветру кружат, А.Н. Плещеев 95

Осенние листья в тревоге вопят: А.Н. Майков 75

«Все гибнет, все гибнет! Ты А.А. Блок 85

черен и гол,

О лес наш родимый, конец твой

пришел!»

: 14

: 14

: 14

11. Что ты рано в гости, А.Н. Майков 43

Осень, к нам пришла? А.А. Фет 57

Еще просит сердце А.Н. Плещеев 26

Света и тепла!

12. Чахлая рябина А.Н. Плещеев 14

мокнет под окном; С.А. Есенин 16

Смотрит деревушка А.Н. Майков 18

сереньким пятном

96 24

78 39

84 ?

13. Осыпал лес свои вершины, М.Ю. Лермонтов 26

Сад обнажил свое чело, А.Н. Плещеев 30

Дохнул сентябрь, и георгины Ф.И. Тютчев 24

Дыханьем ночи обожгло. А.А. Фет 32

х + 13 = 19	42	48
15 – х = 6	38	47
х + 12 = 20	24	?

14. Пустеет воздух, птиц не слышно И.А. Бунин 16

боле, Ф.И. Тютчев 28

Но далеко еще до первых зимних А.А. Блок 24

бурь –

И льется чистая и теплая лазурь

На отдыхающее поле…

5a + 2	27 : x = 9	17
20 − 3a	25 : x = 5	5
4 + 3a	4 × x =32	?

15. Лес, точно терем расписной, К.Д. Бальмонт 36

Лиловый, золотой, багряный, И.А. Бунин 25

Веселой, пестрою стеной М.Ю. Лермонтов 49

Стоит над светлою поляной.

96 : x = 16	y × 15 = 75	65
84 : x = 21	y × 22 = 66	43
27 × x = 54	17 × y = 85	?

16. Бедный зайчик прыгает А.А. Блок 2

Возле мокрых сосен. С.А. Есенин 3

Страшно в лапы волку Ф.И. Тютчев 4

Серому попасть…

В + Е	9
Ж : Б	?

17. Осень. Обсыпается весь наш А.К Толстой 42

бедный сад, М.Ю. Лермонтов 54

Листья пожелтелые по ветру И.А. Бунин 68

летят;

Лишь вдали красуются, там на дне

Ж	(96)	К
И	(50)	Д
М	(?)	В

долин,

Кисти ярко- красные вянущих

рябин.

18. С вечера все снится, Н.М. Рубцов 7

На дворе темно. А.А. Фет 5

Лист сухой валится, А.Н. Плещеев 9

Ночью ветер злится

Да стучит в окно…

К	(9)	В
И	(6)	Г
Т	(?)	Н

19. Солнце реже смеется, К.Д. Бальмонт 23

Нет в цветах благовонья. А.А. Фет 28

Скоро осень проснется Н.М. Рубцов 25

И заплачет спросонья.

К	Д	М	Р	У
14	7	16	20	?

20. Около леса, как в мягкой постели, А.Н. Плещеев 28

Выспаться можно – покой Н.А. Некрасов 75

и простор! – А.Н. Майков 35

Листья поблекнуть еще не успели,

Желты и свежи лежат, как ковер.

84	48
32	23
57	?

21. На улице стало безлюдно, С.Д. Дрожжин 4

Не слышится шума ребят, К.Д. Бальмонт 8

И жёлтые листья на землю А.К. Толстой 7

С берёз, как червонцы, летят.

385	3
91	2
4752	?

22. Уж небо осенью дышало, С.А. Есенин 19

Уж реже солнышко блистало, А.С. Пушкин 17

Короче становился день, А.А. Блок 21

Лесов таинственная сень

С печальным шумом обнажалась,

Ложился на поля туман…

94	13
16	7
98	?

23. На ручей, рябой и пестрый, Н.А. Некрасов 3

За листком летит листок, А.А. Блок 5

И струей, сухой и острой, А.С. Пушкин 7

Набегает холодок.

77	(10)	13
86	(4)	91
59	(?)	38

24. Осинник желтый бьет тревогу; А.А. Фет 14

Осыпался с березы лист А.Н. Майков 13

И, как ковер, устлал дорогу… Н.А. Некрасов 15

709	(7)	153
499	(11)	218
568	(?)	312

25. Лес пахнет дубом и сосной, А.К. Толстой 40

За лето высох он от солнца, И.А. Бунин 30

И осень тихою вдовой А.А. Блок 50

Вступает в пестрый терем свой.

38	x × 6 = 132	60
12	x : 4 = 17	80
25	125 : x = 25	?

26. Кроет уж лист золотой А.Н. Майков 51

Влажную землю в лесу… С.Д. Дрожжин 63

Смело топчу я ногой А.С. Пушкин 45

Вешнюю леса красу.

17 × 4 − 2 1× 3	a + 37	42
21 × 5 − 7 ×14	83 − a	76
16 × 6 − 23 × 4	a + 47	?

27. Люблю дымок спаленной жнивы, С.А. Есенин 5

В степи ночующий обоз, М.Ю. Лермонтов 3

И на холме средь жёлтой нивы А.А. Блок 12

Чету белеющих берёз.

Клёст	2
Королёк	5
Колибри	?

28. Хмурая, дождливая А.А. Блок 3

Наступила осень. С.Д. Дрожжин 5

Всю капусту сняли, Н.А. Некрасов 7

Нечего украсть…

сЛон	кЛуб	2
водА	мерА	4
смЕх	плЕн	?

29. Мой сад с каждым днём увядает; А.Н.Майков 25

Помят он, поломан и пуст, С.Д.Дрожжин 18

Хоть пышно ещё доцветает А.С.Пушкин 24

Настурций в нём огненный куст…

Стул − 16

Бак − 9

Пирог − ?

30. Славная осень! Здоровый, ядрёный К.Д.Бальмонт 30547

Воздух усталые силы бодрит; А.К.Толстой 24

Лёд неокрепший на речке студёной Н.А.Некрасов 201

Словно как тающий сахар лежит…

5 3541 30 547 201 24

Ребус − 30 547

Яр − 24

Бук − ?

31. Унылая пора! Очей очарованье! С.А.Есенин 91

Приятна мне твоя А.А.Блок 537

прощальная краса − А.С.Пушкин 2370

Люблю я пышное природы

увяданья,

В багрец и в золото одетые леса…

716 312 2370 91 537 95 468

Киоск − 95 468

Бумага − 716 312

Аист − ?

Ответы:

1.108.2.84.3.160.4.25.5.508.6.60.7.30.8.15.9.15.10.75.11.26.12.14.13.32.14.28.15.25.16.4.17.42.18.5.19.23.20.75.21.4.22.17.23.3.24.13.25.30.26.51.27.3.28.3.29.25.30.201.31.2370

Внеклассная работа на уроках математики

Настоящее сотрудничество учителя и ученика возможно при условии, что учиться не заставляют, а увлекают.

Чтобы активизировать познавательную деятельность учащихся начальных классов, надо использовать элемент занимательности в методах изложения материала.

Качество знаний и навыков учащихся по математике, формирование интереса, увлеченности обеспечиваются прежде всего организацией обучения на уроке, ибо урок, по словам В.А. Сухомлинсокго, первая искра, зажигающая факел любознательности. Наиболее эффективны те методы изложения материала, которые позволяют усваивать новые знания путем самостоятельного поиска, а это возможно при построении урока в виде соревнования, путешествия, сказочного сюжета.

Урок в занимательной форме позволяет способным ребятам раскрыть и активизировать свои способности. Неуверенным или ленивым учащимся – развить инициативу, сообразительность, математическое мышление. Даже самые незначительные достижения порождают в ученике веру в свои возможности. Учителю надо поддержать любознательность ребят, показывать, что он верит в их силы, вместе с ними радуется успеху каждого.

На внеклассных занятиях также идет развитие внимания, навыков устных вычислений, умений ориентироваться в пространстве Особое внимание надо обращать на эмоциональную окраску занятий, на развитие интереса к ним, инициативы, самостоятельности учащихся, творческой фантазии.

Цель – решение нестандартных заданий, интерес к предмету, показать возможность участия в этих занятиях каждого учащегося.

Викторина по учебно-воспитательному курсу

«Правила дорожного движения»

Умные знаки

Вставив пропущенные знаки, вы узнаете правильный ответ.

1. Как называется та часть улицы, по которой идут пешеходы?

3…10…2…= 15

+ – -мостовая

х : -тротоуар

2. По какой части улицы движется транспорт?

70…30…7 = 107

+ -по мостовой

– -по тротуару

3. Что такое перекресток?

6…3…4… = 72

х -место пересечения дорог

: -место перехода через улицу

4. Что такое светофор?

6…8…2 = 24

+ – -дорожный знак, запрещающий движение транспорта

х : -прибор для регулирования движения машин и пешеходов

5. Для чего служит красный сигнал светофора?

90…30…3 = 1

х -разрешает движение

: -запрещает движение

6. На какой сигнал светофора можно переходить улицу?

56…23…11 = 22

+ -на красный сигнал

– -на зеленый сигнал

7. В каком месте можно переходить проезжую часть?

800 : 8…20 х 5

-в любом месте

8. Как нужно обходить трамвай?

100…27…8 = 81

+ – -спереди

х : -сзади

9. Можно ли детям моложе 14 лет выезжать на велосипеде за пределы двора?

107 – 29…56+ 24

-да

= -иногда

10. Можно ли играть рядом с проезжей частью?

78 + 24… 56 + 56

-да

= -изредка

11. Как нужно обходить автобус и троллейбус?

94…6…90 = 10

+ – -сзади

х : -спереди

12. Когда ты переходишь улицу с двусторонним движением, куда надо посмотреть сначала?

81 : 9…90 : 10

-прямо

= -налево

13. Кого называют пешеходами?

7…7…2 = 98

х -людей, передвигающихся по улице пешком

: -людей, находящихся в общественном транспорте

14. Что такое улица с односторонним движением?

93…3…17 = 73

+ -улица, по которой пешеходы движутся только в одну сторону

– -улица, по которой машины движутся только в одну сторону

15. По какой стороне тротуара нужно идти?

50…2…3 = 75

+ – -по левой

х : -по правой

16. Как нужно идти по обочине на загородной дороге?

58…(70…40)…7 = 95

+ – -навстречу движению транспорта

х : -по направлению движения транспорта

17. Можно ли кататься рядом с проезжей частью на роликовых коньках?

75 + 17…107 – 14

-да, конечно

= -иногда можно

18. Как называется группа дорожных знаков в виде треугольников с красным окаймлением?

48 + 48…54 + 32

-предупреждающие знаки

= -предписывающие знаки

19. Как выглядят запрещающие дорожные знаки?

56…24…18 = 14

+ -голубые прямоугольники с рисунками

– -круги с красной каймой или красным фоном

20. Через какую дверь нужно входить в троллейбус, автобус, трамвай?

80…(20…5) = 20

х -через переднюю дверь

: -через заднюю дверь

21.Как называется место ожидания пассажирами общественного транспорта?

(5…8)…(30…3) = 4

+ – -стоянка

х : -остановка

22. Можно ли высовываться из окна автомобиля, автобуса, троллейбуса?

57…18…25 = 100

+ -нельзя

– -можно

23. В какую сторону нужно выходить из легкого автомобиля?

5 х 4 : 2…2 х 9 : 3

-в сторону тротуара

24. Что такое подземный переход?

58…(32…19) = 45

+ -специальная разметка на проезжей части, по которой пешеход может перейти на другую сторону улицы

– -специальное сооружение под проезжей частью, по которому пешеход может перейти на другую сторону улицы

25. Почему нельзя переходить дорогу на желтый сигнал светофора?

63…19…(14…12) = 84

+ – -некоторые автомобили при этом могут продолжить или начать движение

х : -этот сигнал горит недолго, и пешеход может не успеть перейти дорогу

26. В чем опасность перехода дороги с собакой на поводке?

(36…9)…(48…6) = 32

+ – -собака может лаять на автомобили, пугая этим водителей

х : -собака может испугаться автомобилей и броситься под машину, увлекая за собой ребенка

27. Какой автомобиль хуже виден: приближающийся сбоку или следующий на встречу?

26…26…29 = 81

+ -приближающийся сбоку

– -едущий навстречу

28.О чем надо думать, когда, находясь на дороге, ты увидел что-то необычное или интересное?

25 : 5 х 3…72 : 8 х 2

-в о том, что нужно запомнить увиденное и рассказать об этом папе и маме

за дорожной обстановкой

Нестандартные задачи

Известно, что решение текстовых задач представляет собой большие трудности для учащихся. Известно и то, какой именно этап решения особенно труден. Это самый первый этап – анализ текста задачи.

Умение ориентироваться в тексте математической задачи – важный результат и важное условие общего развития ученика. И заниматься этим нужно не только на уроках математики, но и на уроках чтения и изобразительного искусства. Некоторые задачи – хорошие темы для рисунков. И любая задача – хорошая тема для пересказа. А если в классе есть уроки театра, то некоторое математические задачи можно инсценировать.

Но достаточно ли для этого тех задач, которые имеются в ныне действующих учебниках и решение которых входит в обязательный минимум? Нет, недостаточно. В обязательный минимум входит умение решать задачи определенных типов:

• о числе элементов некоторого множества;

• о движении, его скорости, пути и времени;

• о цене и стоимости;

• о работе, ее времени, объеме и производительности труда.

Указанные четыре темы являются стандартными. Считается, что умение решать задачи на эти темы может научить решать задачи вообще. К сожалению, это не так. Хорошие ученики, умеющие решить практически любую задачу из учебника на перечисленные темы, часто бывают не в состоянии понять условие задачи на другую тему.

Выход заключается в том, чтобы не ограничиваться какой-либо тематикой задач, а решать и нестандартные задачи, то есть задачи, тематика которых не является сама по себе объектом изучения. Ведь не ограничиваем мы сюжеты рассказов на уроках чтения!

Нужно воспитывать в детях любовь к красоте логических рассуждений. Можно также предложить сильным ученикам построить рассуждение, понятное для других.

Среди задач есть совершенно однотипные в математическом отношении. Если дети увидят это, – замечательно. Учитель может и сам показать это. Однако, недопустимо говорить: решаем эту задачу, как ту, и ответ будет такой же. Дело в том, что, во-первых, не все учащиеся в первом классе способны к таким аналогиям. А во-вторых, в нестандартных задачах фабула не менее важна, чем математическое содержание. Поэтому лучше подчеркивать связи между задачами со сходной фабулой.

Задача 1. Портфель Коли помещается в портфеле Васи, а портфель Васи можно спрятать в портфель Севы. Какой из этих портфелей самый большой?

Эта задача – о свойствах предметов. Но о размерах портфелей сообщается опосредственно – через возможность одному из них поместиться в другом. Заметим, что эти свойства не эквиваленты: если один портфель не помещается в другом, то из этого следует, что он больше. Но если портфель помещается в другом, то из этого следует, что он меньше. Нужно добиться четкого решения задачи в три ступени:

1) так как портфель Коли помещается в портфеле Васи, то портфель Коли меньше портфеля Васи;

2) так как портфель Васи можно спрятать в портфеле Севы, то портфель Васи меньше портфеля Севы;

3) так как портфель Коли меньше портфеля Васи, а портфель Васи меньше портфеля Севы, то портфель Севы самый большой.

При анализе решения желательно сопроводить этот сюжет рисунком на доске и в тетрадях: изобразить портфели в виде отрезков с буквами К, В, и С:

К

В

С

С самого начала нужно приучать детей изображать отрезками любые объекты, о которых известно, что один из них больше другого или равен ему.

Задача 2. Если провести стеклом по мрамору, на мраморе окажется царапина. А если провести алмазом по стеклу, царапина останется на стекле. Какой из этих материалов самый твердый?

В этой задаче известны результаты взаимодействия веществ, а вывод требуется сделать об их сравнительной твердости. Решение трехзвенное:

1. стекло тверже мрамора, так как оставляет на нем царапину;

2. алмаз тверже стекла, так как оставляет на нем царапину;

3. следовательно, алмаз – самый твердый из этих трех материалов.

Задача 3. Мама вымыла пять тарелок, а две уже вытерла. Сколько тарелок еще мокрые?

Ответ: 3.

Тарелки надо нарисовать, под двумя

С С написать С(сухие).

Записать действие: 5 – 2 = 3.

Задача 4. Вася переломил плитку шоколада, потом переломил одну из получившихся частей. На сколько частей переломил Вася плитку шоколада?

Ответ: 3.

После первого разлома стало две части, а после второго – три. Необходимо продемонстрировать это на любом примере: разорвать лист или разломать палочку.

Задача 5. Один нехороший человек всегда говорит неправду. Что он ответит на вопрос: «У Вас один нос или два?»?

Ответ: Два.

Он ответит так потому, что всегда говорит неправду. Хорошо бы выслушать такой аргументированный ответ и у наиболее слабых учащихся.

Задача 6. На сколько частей можно разделить лист бумаги двумя непересекающимися прямыми линиями?

Ответ: На 3.

Это сразу видно на рисунке.

Задача 7. В классе 24 человека. Сколькими способами можно выбрать из них дежурного на 1 сентября?

Смысл задачи в том, чтобы на простом примере разобраться в терминологии комбинаторных задач. Что значит «Сколькими способами»? Можно сказать, что одним: ведь выбрать надо одного дежурного. Но в качестве него можно выбрать любого из 24 человек. В этих случаях и говорят: «Сколькими способами? – двадцатью четырьмя». Это ответ задачи. Полезно вначале не разбирать ее в классе, а задать на дом и посмотреть, кто как понял вопрос. И после этого объявить, что значат слова «Сколькими способами?»

Задача 8. Юля сидит на парте, второй спереди и четвертой сзади. Сколько парт в ряду?

Ответ: 5.

Это можно понять из рисунка:

Задача 9. Сколько нулей во всех числах от 1 до 100?

Ответ: 11.

По одному нулю имеется в числах 10, 20, 30, 40, 50, 60, 70, 80, 90 – девять нулей. Еще два нуля в числе 100. Итого 11 нулей.

Задача 10. Расшифруй этот пример: А + А = 6. В нем буква А обозначает в обоих случаях одну и ту же цифру.

Ответ: 3 + 3 = 6

Задача решается подбором. Нужно лишь понять, что вместо буквы А надо писать какую-нибудь цифру, одну и ту же в обоих случаях. Можно спросить, почему не годится цифра 1 (потому что 1 + 1 = 6 – неверно). Далее можно проверить цифру 2 и, наконец, цифру 3. Полезно заменить, что если взять цифру 3, то результат будет больше 6. То есть ответ здесь единственный.

Задача 11. Как с помощью сосудов емкостью 4 л и 6 л налить из водопроводного крана 2 л воды?

Ответ: Наполнить 6-литровый сосуд и из него наполнить 4-литровый сосуд; тогда в 6-литровом останется ровно 2 литра.

Задача 12. Маша купила две поздравительные открытки к Новому году для Веры и Люси. Сколькими способами она может определить, какой из подруг надписать какую открытку?

Ответ: двумя способами.

Первый способ: Первую Вере, вторую Люсе, Второй способ: первую Люсе, вторую Вере.

Задача 13. Витя, Коля и Петя ездят в школу на трамвае вместе. Петя тратит на поездку 10 минут. Сколько времени они едут в школу вместе?

Это задача – шутка, направленная против бездумного сложения при слове «вместе». Конечно, все дети едут одновременно 10 минут.

Задача 14. Каждый из трех городов соединили дорогой с двумя другими. Сколько получилось дорог?

Здесь необходим чертеж, из которого сразу виден ответ: 3.

Возможна «живая картина». К доске вызываются жители трех городов: Москвы, Санкт-Петербурга и Казани (хорошо, если им на грудь будут приколоты знаки: М, С – Пб и К). Они выстраиваются у доски треугольником и между ними протягиваются веревки, обозначающие дороги. Все видят, что дорог три.

Задача 15. Из клетки взяли 3 цыплят и посадили в нее 3 кроликов. Как изменилось число ног в клетке?

Ответ: Увеличилось на 6.

Каждый кролик взамен цыпленка даст лишние две ноги.

Задача 16. Каждую из четырех точек соединили отрезками с тремя другими. Сколько получилось отрезков?

Здесь необходим чертеж, из которого сразу виден ответ: 6.

Задача 17. У Гали и Кости 8 игрушек. Гале подарили еще 2 игрушки. Сколько стало игрушек у Гали и Кости вместе?

Ответ: 10 игрушек.

Ведь если одно из слагаемых увеличить на 2, а второе не менять, то сумма увеличится на 2.

Задача 18. Петя и Вася обменялись рукопожатиями и подарили друг другу по одной свой фотографии. Сколько было рукопожатий? Сколь понадобилось фотографий?

Ответ: одно рукопожатие; две фотографии.

Это выясняется инсценировкой. Надо вызвать к доске учеников (лучше всего, если это будет Петя и Вася, а если нет, то полезно переименовать действующие лица в задаче). Они держат в руках фотографии (или что-нибудь другое). Кроме того, нужно вызвать к доске еще одного ученика – счетчика. Пусть Петя и Вася пожмут друг другу руку, счетчик объявит, что произошло одно рукопожатие, и все дети запишут этот результат. Потом Петя и Вася обменяются фотографиями, а счетчик отметит, что фотографии понадобилось две, и все запишут этот результат.

Задача 19. Какая из этих сумм больше:

1 + 3 + 5 + 5 + 7 + 9 или 2 + 4 + 6 + 4 + 6 + 8 ?

Ответ: Суммы одинаковы.

Это можно получить простым подсчетом (и там, и там 30), а можно и таким рассуждением: во второй сумме каждое из первых трех слагаемых на единицу больше, чем в первой сумме, а каждое из последних трех на единицу меньше. Заметим, что не нужно говорить, какой из двух способов лучше: оба они одинаково быстрые, а значит, лучше тот, который придумал ты сам.

Задача 20. Из клетки с зайцами торчат 12 ушей. Сколько в ней зайцев?

Ответ: 6.

Для решения нужно нарисовать 12 ушей и считать их парами.

2. Герои любимых сказок в математических задачах

Многие согласятся с тем, что задачи с участием любимых сказочных персонажей решать намного интереснее. Среди этих задач видное место занимают задачи со сказочными героями, сюжетами и сказочными образами, которые мы находим в интернете.

Сказочная форма позволяет ввести необычные, увлекательные ситуации в математические задачи со сказочным сюжетом. Тем самым эти задачи оживляются. Мы решили «оживить» задачи с помощью сказочных героев.

Занимательные задачи сказочного характера, придуманные нами самостоятельно, в которых есть необычные увлекательные ситуации, помогают лучше понять текстовые задачи, осмыслить и найти правильное решение. Мы с огромным удовольствием решаем задачи в занимательной форме, которые теперь составляем самостоятельно.

При самостоятельном составлении задач в сказочной форме надо стремиться к тому, чтобы условие задачи соответствовала духу самой действительности сказки: верность дружбы Буратино, сварливость старухи, хитрость лисы и т.д. Мы всегда симпатизируем положительным героям: Золушке, Колобку, Емеле, Маше и т.д. Отрицательные качества высмеиваются. Сказки и через задачи должны учить нас добру.

В этом году мы решили составить пробный сборник задач с любимыми сказочными героями собственного сочинения. Мы думаем, что этот сборник заинтересует ребят не только нашего класса, но и других.

Задачи, составленные одноклассниками

Решение сказочных задач

Сказочные задачи непременно должны отвечать
следующим требованиям:

• Задачу задает сказочный герой (например, фея
  или Баба – Яга). В роли сказочного героя, загадывающего загадки, может
  выступать кукла или переодевшийся  в «волшебную» одежду ведущий;
• Условиями сказочной  задачи являются
  сказочные испытания;
• Задача не должна иметь  единственного
  правильного/ неправильного ответа;
• Образы, герои и проблематика задач должны
  быть близкими и понятны ребенку. Согласитесь, кукла Гамлет, задающая
  известный  вопрос «быть или не быть», детсадовцам будет совсем непонятна,
  в отличие от причины слез Царевны – Несмеяны.

В результате осмысления сказочных задач у
ребят развивается  умение находить оригинальные, свободные от стереотипов  
способы решения тех проблем, которые  неизбежно появятся на их  жизненном  пути.
При   этом с навыками, полученными      в результате решения сказочных задач,
жизненные трудности   будут преодолены ребенком с наименьшими энергозатратами и
с творческим подходом. Приведу   лишь несколько классических  сказочных  задач,
а  вы, опираясь на мой  пример, можете придумать их сами.

• Подъехал богатырь Илья – Муромец к распутью
  трех  дорог и увидел на нем огромный камень. На камне было написано:
  «Направо пойдешь – коня потеряешь. Налево пойдешь – сам погибнешь. Прямо
  пойдешь – ничего не найдешь». Какую из трех дорог выбрал именно её?
• Трудный путь  пришлось пройти Ивану-
  царевичу, чтобы найти невесту свою Василису, которую похитил злой Кощей
  Бессмертный. Нашел, в конце  концов, Иванушка  мрачный замок Кощея, да вот
  беда, окружает замок огненная река. Как же перебраться Иванушке через эту
  реку?
• Как  вы думаете, что случится с тем, кто
  искупается в молочной речке с кисельными берегами?
• Победил  Иванушка  Кощея, и все Кощеево
  богатство Иванушке досталось: и монеты, и золото, и драгоценные камни, и
  украшения всякие. Как вы думаете, что потом Иванушка сделал со всем этим
  богатством?
• В далекой сказочной стране есть Хрустальный
  город. Всё, всё,  всё в нём хрустальное. Как вы думаете, каким этот город
  был раньше? Кто его заколдовал, и почему? Почему именно в хрусталь все
  превратилось?
• Жил да был в далекой  сказочной стране
  король, и была у него дочка- принцесса. Король любимой дочке все разрешал,
  кроме одного: подниматься в маленькую башенку на самой вершине замка. Как
  вы думаете, почему принцессе не разрешалось подниматься в эту башенку?
  Однажды король уехал по своим королевским  делам. А как поступила
  принцесса в отсутствие короля?
• К одной сказочной принцессе – а она была
  очень красивой – сваталось очень много женихов. Но прекрасная принцесса
  всем отказывала и ни за кого не хотела выходить замуж. Как вы думаете,
  почему? Чего хотела принцесса?

Условия задачи
таковы. Для того чтобы целыми и невредимыми пройти по
сказочной стране, с собой нужно взять множество самых  разных вещей, ведь в
дороге может случиться множество неожиданных приключений. Но так как мы много
вещей унести не можем, то всем вместе необходимо подумать, что нам необходимо
взять с собой в дорогу. Каждый из ребят должен назвать вещь, объяснив, в каких
ситуациях и для чего она может пригодиться. С собой мы берем только  ту  вещь,
которая может пригодиться во множестве сказочных ситуаций. Дети, предлагая
какую- либо вещь, должны назвать не менее трех (а дети после 7 лет не менее
пяти) вариантов её использования в сказочном путешествии. Заканчивая эту тему,
хочется отметить следующее. Методик огромное множество. Но какой бы способ вы
не выбрали для общения с ребенком, необходимо помнить о двух вещах.

1. Психологическая интерпретация должна
   быть безоценочной. Всё сказанное ребенком
   (например, сочиненная им сказка или решение предложенной сказочной
   задачи) не должно раскладываться на «плохое» и «хорошее». Нужно принимать
   всё сказанное им как данность. Сказкотерапия  позволила нам заглянуть в
   душу ребенка, в самые сокровенные  её  уголки.
2. Необходим анализ сказки и её обсуждение. Кроме всего прочего, это поможет ребенку научиться формулировать
   свои мысли, а самое главное, дает  ему  возможность говорить о своих
   мыслях, о своих  чувствах, о своих эмоциях и переживаниях – и быть
   услышанными другими людьми. В наш век отчаянного одиночества подобное
   значение очень важно.

Анализ сказки
заключается в обсуждении её сюжета по определенным вопросам. Все их можно
разбить на три большие группы.

1.     
Почему в сказке произошли  именно эти
события?

2.     
Могло ли быть по – другому?

3.     
Что в этой сказке  ребенку кажется похожим
на его жизнь?

Приведем примерный
перечень вопросов для каждой группы:

1.     
Почему в сказке произошли  именно эти события?

·        
О чем  эта сказка?

·        
Чему она учит?

·        
Почему герои совершали те или  иные  поступки?

·        
Почему герой потерял (приобрел) что-то важное?

·        
Почему победа, в конце концов, осталась за героем?

2.     
Могло ли быть по – другому?

·        
Как бы сложилась сказка, если бы герой выбрал
другой?

·        
Что было бы, если бы в сказке были одни
отрицательные герои?

·        
Какой была бы сказка, если бы не было отрицательных
героев?

·        
Могла ли сказка окончиться как- нибудь по- другому?
Если ребенок ответит  на этот вопрос утвердительно, то следует уточнить, каким
он видит окончание этой сказки.

3.     
Что в этой сказке  ребенку кажется похожим на его
жизнь?

При этом в процессе анализа наиболее важно,
чтобы дети прочувствовали и проговорили не сюжетную канву сказки (кто и куда
пошел, кто и что принес), а её смысл. А именно, почему произошло то или иное
событие, зачем это нужно, как это повлияло на персонажей, можно ли провести
аналогию с реальной жизнью.

Урок – проект «Задачки из сказок»

по математике в 7 «в» классе.

Руководитель проекта Лебедева Татьяна Анатольевна

2018/19 учебный год

Цели проекта:

В направлении личностного развития:

формирование у учащихся умения распознавать, обследовать и разрешать проблемные ситуации из области математики, способности к преодолению мыслительных стереотипов, навыков публичного выступления;

формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

развитие интереса к математическому творчеству и математических способностей;

В метапредметном направлении:

развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

В предметном направлении:
• овладение математическими знаниями и умениями, необходимыми для практического применения;
• формирования механизмов мышления, характерных для математической деятельности, навыков конструирования и моделирования.

Задачи проекта:

1. Формировать интересы, склонности учащихся к познавательной деятельности, практические умения и навыки проведения проектной деятельности.

2. Развивать интерес к математике.

3. Развивать умение самостоятельно творчески мыслить и использовать это умение на практике.

4. Развивать способность излагать и защищать собственную точку зрения по проблеме.

Содержание деятельности:

Подобрать и исследовать содержание некоторых сказок, распечатать и раскрасить картинку из сказки

Сконструировать и решить задачи разных типов для участия в неделе вспомогательных классов

Этапы работы над проектом:

Обоснование цели и задач проекта.

Самоопределение в группы.

Работа с информационными источниками.

Исследование и отбор содержания сказок для различных типов задач

Конструирование и оформление задач.

Оформление результата.

Защита проекта.

1 этап. Аннотация проекта:

Мы с вами познакомились с содержанием некоторых сказок.

Мы знаем, что задача состоит из условия и вопроса. В условии должны быть числовые данные. Вопрос должен спрашивать о том, о чем мы хотим узнать.

Для того, чтобы придумать задачу, мы попробуем определить, про что может быть эта задача, исходя из содержания сказки, выполним проект «Задачки из сказки». А результатом нашей работы будут:

1.Новые и интересные задачи, составленные по сказкам.

2.Создание стенгазеты

Чтобы работа над проектом была интересной, а результат качественным, мы будем работать тремя командами: одна команда будет раскрашивать иллюстрации, вторая команда будет придумывать задачи, третья команда распечатает их на компьютере.

Цель каждой команды – качественно выполнить свою работу.

2 этап. Самоопределение.

Каждый учащийся выбирает группу, в которой будет работать.

3 этап. Работа с информационными источниками.

Найти в интернете картинки и отрывки из предложенных сказок и распечатать их.

4 этап. Исследование и отбор содержания сказок для различных типов задач

Инструкция:

Прочитайте предложенные отрывки из сказок «Красная Шапочка», «Три поросенка», «Волк и семеро козлят», «Три медведя».

Выделите все объекты, о которых идет речь в тексте.

Какие количественные отношения связывают эти объекты? (больше…, меньше…, поровну, …часть от…).

Придумайте вопросы про эти объекты. (Формулируем вопрос задачи).

Что нужно знать, чтобы ответить на эти вопросы? (Составляем условие задачи).

Сформулируйте тексты задач.

5 этап. Конструирование и оформление задач.

Пример 1:

Сказка «Красная Шапочка».

Что несла бабушке Красная Шапочка? Давайте придумаем, сколько было пирожков в корзине. Кто ей повстречался? Давайте представим, что девочка угостила волка несколькими пирожками. Пирожков у девочки стало больше или меньше? Итак, давайте придумаем текст задачи..А теперь придумаем вопрос. Что мы должны узнать?

Далее дети составляют задачи по другим сказкам, записывают их содержание. Третья группа печатает их на компьютере.

6 этап. Оформление результата.

Учащиеся оформляют стенгазету.

7 этап. Защита проекта

На неделе математики для вспомогательных классов учащиеся представляют свой продукт и проводят конкурс среди сверстников по решению данных задач.

Муниципальное бюджетное общеобразовательное учреждение

«Козловская средняя общеобразовательная школа №2»

Козловского района Чувашской Республики

ПРОЕКТ

Выполнил: Беспалов Роман,

ученик 7 класса

Руководитель: Фаттахова Диляра Хазибовна, учитель математики

Козловка-2016

Цель проекта:

Повышение интереса учащихся к математике посредством русских народных сказок.

Задачи проекта:

– вспомнить некоторые русские народные сказки; привлечь к ним внимание;

– составить к этим сказкам математические задачи;

– использовать составленные задачи на уроках математики и дополнительных занятиях;

– способствовать духовному, нравственному, патриотическому воспитанию школьников.

Введение.

«Предмет математики настолько серьёзен,

что полезно не упускать случаев делать его

немного занимательным»

(Б. Паскаль)

Многие считают, что математика – скучная сухая наука, но я так не считаю. Я решил оживить математику сказками. Русские народные сказки в математических задачах помогут поддержать интерес на уроке, разовьют любознательность. Сказка позволяет привить вкус к самостоятельным рассуждениям, которые способствуют развитию математического мышления. Русские народные сказки – явление уникальное. В сказочном мире все необычно: животные, наделенные человеческими качествами, предметы, имеющие волшебные свойства и помогающие человеку, и многое другое. В течение многих столетий сказки учат добру, справедливости, героизму, любви, дают знания об окружающем мире, воспитывают нравственно.

Основная часть.

Колобок.

Жили- были старик со старухой. Замесила как-то старуха муку на сметане, состряпала Колобок, изжарила его в масле и на окошко студить положила.

Колобок полежал, взял и покатился. С окна на лавку, с лавки на пол, по полу к двери, прыг через порог и во двор. Со двора за ворота и дальше по тропинке в лес. В это время Лиса грелась у своей норы на расстоянии 40 км от Колобка, Заяц чистил морковку на расстоянии 30 км, а голодный Волк мечтал о еде на расстоянии 28 км. Уловив запах свежей выпечки, они одновременно помчались навстречу ему. Лиса бежала со скоростью 7 км/ч., Заяц со скоростью 6 км/ч., Волк со скоростью 4 км/ч. Кто первым встретился с Колобком, если он катился со скоростью 1 км/ч?

Решение:

1) находим скорости сближения зверей с Колобком:

7-1= 6км/ч – с Лисой

6-1= 5 км/ч – с Зайцем

4-1= 3км/ч – с Волком

2) 40:6 = 6 ч 40 мин – предполагаемое время встречи Лисы с Колобком

30:5 = 6 ч- предполагаемое время встречи Зайца с Колобком

28:3 = 9 ч 20 мин – предполагаемое время встречи Волка с Колобком

Ответ: первым с Колобком встретился Заяц

Золотая рыбка.

Жил старик со своей старухой. Старик ловил рыбу, старуха пряла пряжу. Раз старик кинул невод в море. Пришел невод с травой морскою, второй раз кинул, пришел невод с одной тиною, но старик не расстраивался. Бросал невод в море он полтора часа, пока не поймалась золотая рыбка: три раза через каждые 10 минут, после каждые пять минут. Сколько раз старику пришлось бросить невод в море, прежде чем поймать золотую рыбку?

Решение:

1) 10 х 3= 30 мин

2) 1 час = 60 мин. 60:5= 12 раз

3) 12+3= 15 раз

Ответ: старик бросал невод в море 15 раз, прежде чем поймал рыбку.

Баба Яга.

Баба Яга утверждает, что Змей Горыныч не пролетит 1000 км без дозаправки. Кощей Бессмертный поспорил с ней на бочку меда, что пролетит. Змей Горыныч пролетел 4 часа со скоростью 247 км/ч и, совершив вынужденную посадку, съел Ивана Царевича. Проспорила Баба Яга бочку меда или не проспорила?

Решение: за 4 часа Змей Горыныч пролетел 247 х 4 = 988 км

Ответ: Баба Яга не проспорила.

Сивка – бурка.

В некотором царстве, в некотором государстве жил- был старик и было у него три сына. Младшего все Иванушкой-дурачком звали. Однажды собрались братья ехать к царскому двору, посмотреть на Елену Прекрасную. Иванушку с собой не взяли. Сели на коней и поехали. По 12 верст в день. А Иванушка вышел в тот же день и шел так: в первый день прошел 1 версту, во второй день – две версты, в третий – 3 версты и так, прибавляя каждый день по одной версте. Через сколько дней он настиг братьев, которые к тому времени уже дошли до дворца, и покорил сердце Елены Прекрасной?

Решение: в первый день Иванушка отстанет на 12 -1 = 11 верст, во второй еще на 12 – 2 = 10 верст, в третий еще на 12 -3=9 верст и так далее. На 12-й день отставание составит ( 11+10+9+…+2+1+0) верст.

А затем расстояние между ними начнет сокращаться. В 13 –й день на 13-12=1 версту, в 14-й день еще на 14-12=2 версты, в 15-й день еще на 15-12=3 версты и наконец, в 23 –й день на 23-12 = 11 верст. На 23 –й день расстояние между ними уменьшится на (1+1+3+…+10+11) верст.

Ответ: Иванушка догонит братьев по прошествии 23 дней.

Хаврошечка.

Жила – была семья, и росли в семье три дочери одна другой ленивей. Взяли они в свой дом сиротку, Крошечку-Хаврошечку. Она их обшивала, для них пряла и ткала и слова доброго никогда не слыхивала. Совсем заморили ее работой.

Пожаловалась Крошечка-Хаврошечка на свое житье любимой коровушке. А коровушка ей в ответ: «Красавица – девица, влезь ко мне в ушко, а в другое вылези, все будет сработано». Так все и сбывалось. Отнесет она хозяйке рулоны сукна, та их спрячет и еще больше работы задаст. Набрался у хозяйки целый сундук сукна, и решила она его продать. Разложили они около дома разноцветные рулоны сукна. 20 рулонов белого сукна, 13 рулонов черного сукна, 5 красного, 19 зеленого и 7 синего. А в то время ехал мимо молодой богатый купец. Залюбовался он красивым товаром и решил купить. А дочери с ним так и заигрывают. Заплатил купец за все рулоны 486 рублей. Цена рулонов была не равная: за черный рулон он платил на 4 рубля больше, чем за белый, за красный – на 3 рубля меньше, чем за черный, за зеленый на 2 рубля меньше, чем за красный, а за синий на 1 руб. больше, чем за зеленый. Сколько денег он заплатил за один рулон каждого цвета? Этот вопрос он задал хозяйским дочерям. Долго думали девицы, но ни одна из них не смогла ответить. Только Крошечка-Хаврошечка несмело ответила на вопрос купца. Услышав правильный ответ, он обрадовался и увез ее с собой. Так и стали они жить вместе в добре и лиха не знать.

Решение: (способ 1)

Легко видеть, что самое дешевое сукно зеленое, синее стоит дороже его на 1 рубль , красное на 2 рубля, черное на 5 рублей, белое на рубль. Если бы за каждый вид сукна было уплачено столько же сколько за зеленое, то при этом было бы уплачено меньше на 20 х 1 + 13 х 5 + 5 х 2 + 7 х 1 = 102 рубля. Вся покупка стоила бы 486 – 102 = 384 рубля. А так как куплено 64 рулона сукна, то рулон зеленого сукна стоит 384: 64 = 6 рублей. Зная это, легко находим стоимость остальных рулонов.

6+1=7 рублей- синее сукно; 6+2=8 рублей- красное сукно; 8+3=11 рублей-чёрное сукно; 11-4=7 рублей- белое сукно.

Решение: (способ 2)

Пусть один рулон белого сукна стоит Х рублей. Черного – (Х + 4) рублей, красного -(Х+1)рублей, зеленого -(Х-1) рублей, синего- Х рублей. Тогда 20 Х + 13 (Х+4) + 5 (Х+1) + 19 (Х-1) + 7Х = 486. Решив уравнение получаем, что один рулон белого цвета стоит 7 рублей, черного – 11 рублей, красного – 8 рублей, зеленого – 6 рублей, синего – 7 рублей.

Заключение

Составив задачи к некоторым русским народным сказкам, я доказал, что математика совсем нескучная наука. Я думаю, что решение задач с необычными сюжетами способствует развитию интереса учащихся к математике, повысит активность учащихся на уроке. Мне хочется, чтобы мои одноклассники попробовали составить свои задачи, которые можно было бы рассмотреть на уроках или дополнительных занятиях.