Параметры
| Подпись | Описание | Тип данных |
|
Входной класс пространственных объектов |
Класс пространственных объектов, для которого пространственные отношения объектов будут оценены. |
Feature Class |
|
Поле уникального ID |
Целочисленное поле, содержащее по уникальному значению для каждого объекта во входном классе объектов. Если у вас нет поля Уникальный ID, вы можете создать его путем добавления нового целого поля в вашу таблицу классов объектов и вычислив значения полей, которые были бы равны полям FID или OBJECTID. |
Field |
|
Выходной файл матрицы пространственных весов |
Полный путь к создаваемому файлу матрицы пространственных весов (.swm). |
File |
|
Определение пространственных взаимоотношений |
Определяет, как формируются пространственные отношения между объектами.
|
String |
|
Метод определения расстояния (Дополнительный) |
Определяет, как рассчитываются расстояния от одного объекта до соседнего объекта.
|
String |
|
Порядок (Дополнительный) |
Параметр для расчета обратного расстояния. Типичные значения – 1 или 2. |
Double |
|
Пороговое расстояние (Дополнительный) |
Определяет предельное расстояние для пространственных взаимоотношений Обратное расстояние и Фиксированное расстояние. Введите это значение, используя единицы, определенные во входящей системе координат. Задает размер пространственного окна при определении пространственных взаимоотношений Пространственно-временное окно. Значение 0 указывает на то, что пороговое расстояние не применяется. Когда этот параметр остается пустым, пороговое значение по умолчанию будет вычислено исходя из экстента и количества объектов во Входном классе объектов. |
Double |
|
Число соседей (Дополнительный) |
Целое число, показывающее или минимально или точное количество соседей. В случае K ближайших соседей каждый объект будет иметь число соседей, в точности равное заданному. В случае Обратного расстояния или Фиксированного расстояния каждый объект будет иметь количество соседей, равное указанному значению или превышающее его (для этого, если потребуется, пороговое расстояние будет временно увеличено). Когда выбран один из вариантов смежности для параметра Определение пространственных взаимоотношений, каждому из полигонов будет присвоено минимальное число соседей. Для полигонов с меньшим числом соседей, чем число соседей с совпадающими границами, дополнительное количество соседей определяется по принципу близости центроидов объектов. |
Long |
|
Стандартизация строк (Дополнительный) |
Нормализация ряда рекомендуется, независимо от того, распределены ли объекты потенциально предвзято в зависимости от дизайна примера или от установленной схемы агрегации.
|
Boolean |
|
Входная таблица (Дополнительный) |
Таблица, содержащая числовые веса, связывающие объекты друг с другом во Входном классе объектов. Требуемые поля – Входной класс объектов, Поле уникального ID, NID (соседний ID) и WEIGHT. |
Table |
|
Поле даты/времени (Дополнительный) |
Поле даты с временной отметкой для каждого объекта. |
Field |
|
Тип интервала даты/времени (Дополнительный) |
Единицы измерения времени.
|
String |
|
Значение интервала даты/времени (Дополнительный) |
Целочисленное значение количества единиц измерения времени, составляющее временной диапазон. Например, если в качестве Типа интервала даты/времени выбрано Часы, а Значение интервала даты/времени равно 3, временной диапазон составит 3 часа; объекты, попадающие в указанный временной диапазон и в указанный пространственный диапазон, будут считаться соседями. |
Long |
|
Использовать Z-значения |
Если входные объекты содержат z-значения, вы можете использовать или игнорировать их. Позволяет выбрать, будут ли z-координаты включаться в построение матрицы пространственных весов.
|
Boolean |
arcpy.stats.GenerateSpatialWeightsMatrix(Input_Feature_Class, Unique_ID_Field, Output_Spatial_Weights_Matrix_File, Conceptualization_of_Spatial_Relationships, {Distance_Method}, {Exponent}, {Threshold_Distance}, {Number_of_Neighbors}, {Row_Standardization}, {Input_Table}, {Date_Time_Field}, {Date_Time_Interval_Type}, {Date_Time_Interval_Value}, Use_Z_values)
| Имя | Описание | Тип данных |
|
Input_Feature_Class |
Класс пространственных объектов, для которого пространственные отношения объектов будут оценены. |
Feature Class |
|
Unique_ID_Field |
Целочисленное поле, содержащее по уникальному значению для каждого объекта во входном классе объектов. Если у вас нет поля Уникальный ID, вы можете создать его путем добавления нового целого поля в вашу таблицу классов объектов и вычислив значения полей, которые были бы равны полям FID или OBJECTID. |
Field |
|
Output_Spatial_Weights_Matrix_File |
Полный путь к создаваемому файлу матрицы пространственных весов (.swm). |
File |
|
Conceptualization_of_Spatial_Relationships |
Определяет, как формируются пространственные отношения между объектами.
|
String |
|
Distance_Method (Дополнительный) |
Определяет, как рассчитываются расстояния от одного объекта до соседнего объекта.
|
String |
|
Exponent (Дополнительный) |
Параметр для расчета обратного расстояния. Типичные значения – 1 или 2. |
Double |
|
Threshold_Distance (Дополнительный) |
Определяет предельное расстояние для пространственных взаимоотношений Обратное расстояние и Фиксированное расстояние. Введите это значение, используя единицы, определенные во входящей системе координат. Задает размер пространственного окна при определении пространственных взаимоотношений Пространственно-временное окно. Значение 0 указывает на то, что пороговое расстояние не применяется. Когда этот параметр остается пустым, пороговое значение по умолчанию будет вычислено исходя из экстента и количества объектов во Входном классе объектов. |
Double |
|
Number_of_Neighbors (Дополнительный) |
Целое число, показывающее или минимально или точное количество соседей. В случае K_NEAREST_NEIGHBORS каждый объект будет иметь это точно заданное число соседей. В случаях INVERSE_DISTANCE или FIXED_DISTANCE каждый объект будет иметь по крайней мере это заданное количество соседей, (для этого, если потребуется, пороговое расстояние будет временно увеличено). Когда выбран один из вариантов смежности для параметра Определение пространственных взаимоотношений, каждому полигону будет присвоено это минимальное число соседей. Для полигонов с меньшим числом соседей, чем число соседей с совпадающими границами, дополнительное количество соседей определяется по принципу близости центроидов объектов. |
Long |
|
Row_Standardization (Дополнительный) |
Нормализация ряда рекомендуется, независимо от того, распределены ли объекты потенциально предвзято в зависимости от дизайна примера или от установленной схемы агрегации.
|
Boolean |
|
Input_Table (Дополнительный) |
Таблица, содержащая числовые веса, связывающие объекты друг с другом во Входном классе объектов. Требуемые поля – Входной класс объектов, Поле уникального ID, NID (соседний ID) и WEIGHT. |
Table |
|
Date_Time_Field (Дополнительный) |
Поле даты с временной отметкой для каждого объекта. |
Field |
|
Date_Time_Interval_Type (Дополнительный) |
Единицы измерения времени.
|
String |
|
Date_Time_Interval_Value (Дополнительный) |
Целочисленное значение количества единиц измерения времени, составляющее временной диапазон. Например, если в качестве Типа интервала даты/времени выбрано Часы, а Значение интервала даты/времени равно 3, временной диапазон составит 3 часа; объекты, попадающие в указанный временной диапазон и в указанный пространственный диапазон, будут считаться соседями. |
Long |
|
Use_Z_values |
|
Boolean |
Пример кода
Следующий скрипт окна Python демонстрирует, как использовать инструмент GenerateSpatialWeightsMatrix.
import arcpy
arcpy.env.workspace = "C:/data"
arcpy.GenerateSpatialWeightsMatrix_stats("911Count.shp", "MYID", "euclidean6Neighs.swm", "K_NEAREST_NEIGHBORS", "#", "#", "#", 6, "NO_STANDARDIZATION")Следующий автономный Python скрипт демонстрирует, как использовать инструмент GenerateSpatialWeightsMatrix.
# Analyze the spatial distribution of 911 calls in a metropolitan area
# using the Hot-Spot Analysis Tool (Local Gi*)
# Import system modules
import arcpy
# Set property to overwrite existing output, by default
arcpy.env.overwriteOutput = True
# Local variables...
workspace = "C:/Data"
try:
# Set the current workspace (to avoid having to specify the full path to the feature classes each time)
arcpy.env.workspace = workspace
# Copy the input feature class and integrate the points to snap
# together at 500 feet
# Process: Copy Features and Integrate
cf = arcpy.CopyFeatures_management("911Calls.shp", "911Copied.shp",
"#", 0, 0, 0)
integrate = arcpy.Integrate_management("911Copied.shp #", "500 Feet")
# Use Collect Events to count the number of calls at each location
# Process: Collect Events
ce = arcpy.CollectEvents_stats("911Copied.shp", "911Count.shp", "Count", "#")
# Add a unique ID field to the count feature class
# Process: Add Field and Calculate Field
af = arcpy.AddField_management("911Count.shp", "MyID", "LONG", "#", "#", "#", "#",
"NON_NULLABLE", "NON_REQUIRED", "#",
"911Count.shp")
cf = arcpy.CalculateField_management("911Count.shp", "MyID", "[FID]", "VB")
# Create Spatial Weights Matrix for Calculations
# Process: Generate Spatial Weights Matrix...
swm = arcpy.GenerateSpatialWeightsMatrix_stats("911Count.shp", "MYID",
"euclidean6Neighs.swm",
"K_NEAREST_NEIGHBORS",
"#", "#", "#", 6,
"NO_STANDARDIZATION")
# Hot Spot Analysis of 911 Calls
# Process: Hot Spot Analysis (Getis-Ord Gi*)
hs = arcpy.HotSpots_stats("911Count.shp", "ICOUNT", "911HotSpots.shp",
"GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "NONE",
"#", "#", "euclidean6Neighs.swm")
except:
# If an error occurred when running the tool, print out the error message.
print(arcpy.GetMessages())В математике, весовая матрица 









Для удобства весовую матрицу порядка 




Свойства[править | править код]
Некоторые свойства следуют непосредственно из определения:
Две весовые матрицы считаются эквивалентными, если одна может быть получена из другой, посредством ряда перестановок и умножений строк и столбцов исходной матрицы на минус единицу. Весовые матрицы полностью классифицированы для случаев, когда 

Примеры[править | править код]
Отметим, что при отображении весовых матрицы используется символ 
Приведём два примера: 



Открытые вопросы[править | править код]
Существует множество открытых вопросов о весовых матрицах. Главным из них является их существование: для каких чисел n и w существует W(n,w)? Многое в этом вопросе остаётся неизвестным. В равной степени важным, но часто неисследованным вопросом является их подсчёт: для заданных n и w, сколько существует матриц W(n,w)? Более глубоко, можно задаться вопросом классификации с точки зрения структуры, но на сегодняшний день это далеко выходит за рамки наших возможностей, даже для матриц Адамара или конференс-матриц.
Ссылки[править | править код]
- On Hotelling’s Weighing Problem, Alexander M. Mood, Ann. Math. Statist. Volume 17, Number 4 (1946), 432-446.
Примечания[править | править код]
- ↑ M. Harada, A. Munemasa, On the classification of weighing matrices and self-orthogonal codes, 2011, http://arxiv.org/abs/1011.5382 Архивная копия от 21 января 2022 на Wayback Machine.

Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
(2) ТИС комплексное.docx
Скачиваний:
0
Добавлен:
20.08.2019
Размер:
211.41 Кб
Скачать
Данная матрица
является идентичной матрице смежностей,
только в данном случае при связи
определенных узлов между собой мы
характеризуем весом этой связи. То есть
если в матрице смежностей при соединении
первого и второго узла соответствующая
ячейка принимала значение 1, то в матрице
весов она будет принимать значение,
соответствующее весу данного соединения.
При отсутствии
связи, в пустых ячейках можно записать
знак бесконечности (∞),
что соответствует о бесконечно большом
расстоянии и невозможности установить
связь.
Приведем матрицу
весов для графа, отображенного на рисунке
2.1.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
0 |
10 |
∞ |
12 |
71 |
∞ |
30 |
21 |
∞ |
∞ |
|
2 |
10 |
0 |
7 |
9 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
|
3 |
∞ |
7 |
0 |
∞ |
∞ |
14 |
3 |
∞ |
∞ |
∞ |
|
4 |
12 |
9 |
∞ |
0 |
∞ |
20 |
∞ |
∞ |
∞ |
∞ |
|
5 |
71 |
∞ |
∞ |
∞ |
0 |
31 |
∞ |
18 |
∞ |
∞ |
|
6 |
∞ |
∞ |
14 |
20 |
31 |
0 |
20 |
9 |
51 |
∞ |
|
7 |
30 |
∞ |
3 |
∞ |
∞ |
20 |
0 |
∞ |
∞ |
21 |
|
8 |
21 |
∞ |
∞ |
∞ |
18 |
9 |
∞ |
0 |
18 |
34 |
|
9 |
∞ |
∞ |
∞ |
∞ |
∞ |
51 |
∞ |
18 |
0 |
19 |
|
10 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
21 |
34 |
19 |
0 |
2.4 Матрица инцидентности
Для построения
данной матрицы необходимо произвольным
образом пронумеровать связи заданные
индивидуальным заданием, сделаем это:
|
Начало |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
5 |
5 |
6 |
6 |
6 |
7 |
8 |
8 |
9 |
|
Конец |
2 |
4 |
5 |
7 |
8 |
3 |
4 |
6 |
7 |
6 |
6 |
8 |
7 |
8 |
9 |
10 |
9 |
10 |
10 |
|
Вес |
10 |
12 |
71 |
30 |
21 |
7 |
9 |
14 |
3 |
20 |
31 |
18 |
20 |
9 |
51 |
21 |
18 |
34 |
19 |
|
Нумерация |
1 |
11 |
2 |
12 |
3 |
13 |
4 |
14 |
5 |
15 |
6 |
16 |
7 |
17 |
8 |
18 |
9 |
19 |
10 |
Суть матрицы
состоит в том, что каждая связь (их всего
будет 19-ть) будет отображается таким
образом: начало связи и конец будет
отмечено единицами для соответствующих
узлов. Соответственно пустые ячейки с
отсутствием связи, возможно заполнить
нулями.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
3 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
4 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
7 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
8 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
11 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
12 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
13 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
14 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
15 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
16 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
17 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
18 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
19 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
17. 2. Части графа
Граф  является частью графа
является частью графа  , если
, если  и
и  , т.е. граф содержит все вершины и рёбра любой его части.
, т.е. граф содержит все вершины и рёбра любой его части.
Часть, которая наряду с некоторым подмножеством рёбер графа содержит и все инцидентные им вершины, называется подграфом.
Часть, которая наряду с некоторым подмножеством рёбер графа содержит все вершины графа (  ,
,  ), называется суграфом.
), называется суграфом.
Исходный граф по отношению к его подграфу называют надграфом, а по отношению к суграфу – сверхграфом.
Совокупность всех рёбер графа, не принадлежащих его подграфу (вместе с инцидентными вершинами ), образует дополнение подграфа (рис. 17.12).

Рис.
17.12.
Граф и его составляющие: а) граф; б) часть графа; в) подграф; г) суграф
Связный неориентированный граф, не содержащий циклов, называют деревом.
Несвязный граф без циклов, отдельные компоненты связности которого являются деревьями, называют лесом.
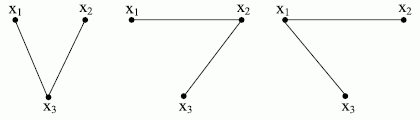
Рис.
17.13.
Три различных дерева, которые можно построить на множестве из трёх вершин
Все приведённые деревья изоморфны друг другу, т.е. на трёх вершинах можно построить только одно неизоморфное дерево.
17. 3. Способы задания графов
Уже отмечалось, что произвольный граф можно задать совокупностью двух множеств:  – множества вершин и
– множества вершин и  – множества рёбер ( дуг ) графа или множества
– множества рёбер ( дуг ) графа или множества  и отображения
и отображения 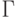 множества
множества  в
в  .
.
Условные обозначения таких графов  и
и 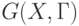 , соответственно.
, соответственно.
Другой удобной формой описания графов является представление их с помощью матриц, методика формальной разработки которых хорошо разработана.
Матрица смежности
Из ранее сказанного известно, что две вершины  и
и  графа
графа  называются смежными, если они являются граничными вершинами ребра
называются смежными, если они являются граничными вершинами ребра 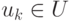 .
.
Отношение смежности на множестве вершин графа можно определить, представив каждое ребро как пару смежных вершин, т.е.

Для неориентированных графов такие пары неупорядочены, так что
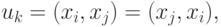
а для орграфов – упорядочены, причём,  и
и  означают, соответственно, начальную и конечную вершины дуги
означают, соответственно, начальную и конечную вершины дуги  .
.
Петля при вершине  в обоих случаях представляется неупорядоченной парой
в обоих случаях представляется неупорядоченной парой  .
.
Множество вершин  вместе с определённым на нём отношением смежности полностью определяет граф.
вместе с определённым на нём отношением смежности полностью определяет граф.
Граф можно представить матрицей смежности.
Строки и столбцы матрицы соответствуют вершинам графа, а её  элемент равен числу кратных рёбер, связывающих вершины
элемент равен числу кратных рёбер, связывающих вершины 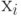 и
и  (или направленных от вершины
(или направленных от вершины  к вершине
к вершине  для орграфов).
для орграфов).
Например, для графа рис. 17.2, а, матрица смежности имеет вид
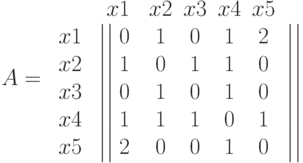
Матрица смежности неориентированного графа всегда симметрична, а орграфа – в общем случае несимметрична. Неориентированным рёбрам соответствуют пары ненулевых элементов, симметричных относительно главной диагонали матрицы, а петлям – ненулевые элементы главной диагонали.
В столбцах и строках, соответствующих изолированным вершинам, все элементы равны нулю. Элементы матрицы простого графа равны 0 или 1, причём, элементы главной диагонали равны 0.
Правильность составления матрицы легко проверить: для неориентированного графа сумма элементов в каждом i -том столбце или строке соответствует степени вершины 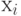 . Если элементы матрицы
. Если элементы матрицы  расположенные на главной диагонали, отличны от нуля, то это свидетельствует о наличии петель в вершине
расположенные на главной диагонали, отличны от нуля, то это свидетельствует о наличии петель в вершине  .
.
Для неориентированного графа матрица смежности  симметрична относительно главной диагонали, так как
симметрична относительно главной диагонали, так как  .
.
При решении целого класса задач проектирования РЭС приходится оперировать матрицами, которые строятся аналогично матрицам смежности, но значения их элементов определяются мерой (весом), связанной с ребром ( дугой ) графа.
В САПР широко используют две разновидности таких матриц: матрицу весовых соотношений и матрицу длин.
Матрица весовых соотношений
Это квадратная матрица  , общий элемент которой
, общий элемент которой
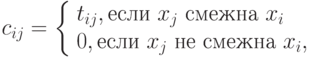
где  – вес связи
– вес связи  .
.
Применение матриц весовых соотношений позволяет учитывать различные требования к сокращению длины тех или иных электрических соединений в конструкциях РЭС, условия тепловой и электромагнитной совместимости отдельных элементов схемы и другие.
Матрица длин
Это квадратная матрица 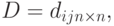 общий элемент которой
общий элемент которой

где  – длина ребра
– длина ребра  .
.
В евклидовой метрике расстояние между двумя точками на плоскости

где  и
и  – координаты вершин
– координаты вершин  и
и  , соответственно.
, соответственно.
Это выражение неудобно для использования в машинных программах, так как извлечение квадратного корня на ЭВМ требует больших затрат времени. Поэтому часто пользуются линейной метрикой, тем более, что при решении многих конструкторских задач она вполне оправдана.
Пример. При проектировании многослойных печатных плат трассировка соединений ведётся в каждом из слоёв во взаимно перпендикулярных направлениях, в связи с чем длина электрических связей между элементами с координатами 

Линейная метрика оказывается непригодной для решения задач, в которых имеет место вычисление производных по координатам (оптимизация нелинейных функций).
В этом случае расстояние между двумя точками представляется в виде степенной функции:

где  – показатель степени (как правило,
– показатель степени (как правило,  ).
).
Матрицу длин используют при решении задач оптимизации размещения конструктивных элементов на плате, когда одним из критериев качества является минимум суммарной длины соединений.
Матрица инцидентности
Если вершина  является концом ребра
является концом ребра  то говорят, что они инцидентны: вершина
то говорят, что они инцидентны: вершина  инцидентна ребру
инцидентна ребру  и ребро
и ребро  инцидентно вершине. В то время как смежность представляет собой отношение между однородными объектами ( вершинами ), инцидентность – это отношение между разнородными объектами ( вершинами и рёбрами).
инцидентно вершине. В то время как смежность представляет собой отношение между однородными объектами ( вершинами ), инцидентность – это отношение между разнородными объектами ( вершинами и рёбрами).
При рассмотрении орграфов различают положительную инцидентность ( дуга исходит из вершины ) и отрицательную инцидентность ( дуга заходит в вершину ).
Рассматривая инцидентность вершин и рёбер графа, можно представить его матрицей инцидентности размера  , строки которой соответствуют вершинам, а столбцы – рёбрам.
, строки которой соответствуют вершинам, а столбцы – рёбрам.
Для неориентированного графа элементы этой матрица определяются по следующему правилу: ij – элемент равен 1, если вершина  инцидентна ребру
инцидентна ребру  и равен нулю, если
и равен нулю, если  и
и 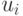 не инцидентны.
не инцидентны.
В случае орграфа ненулевой 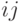 – элемент равен
– элемент равен  , если
, если  – начальная вершина дуги
– начальная вершина дуги 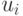 , и равен
, и равен  , если
, если  – конечная вершина дуги
– конечная вершина дуги 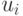 .
.
Приведём пример: составим матрицу инцидентности для рис. 17.2,а.

Каждый столбец матрицы содержит обязательно два единичных элемента (для орграфа эти элементы всегда имеют различные знаки и равны, соответственно,  и
и  ).
).
Количество единиц в строке равно степени соответствующей вершины (для орграфа количество положительных единиц определяет положительную степень, а количество отрицательных единиц – отрицательную степень).
Нулевая строка соответствует изолированной вершине, а нулевой столбец – петле.
Следует иметь в виду, что нулевой столбец матрицы инцидентности лишь указывает на наличие петли, но не содержит сведений том, с какой вершиной эта петля связана (в практических приложениях это может быть несущественно).
Правильность составления матрицы  легко проверить: число единиц в i-ой строке матрицы соответствует степени вершины
легко проверить: число единиц в i-ой строке матрицы соответствует степени вершины  графа, а число единиц в каждом столбце – двум, так как каждое ребро соединяет две вершины графа. Единственное исключение составляет петля, дважды инцидентная одной и той же вершине.
графа, а число единиц в каждом столбце – двум, так как каждое ребро соединяет две вершины графа. Единственное исключение составляет петля, дважды инцидентная одной и той же вершине.
Столбец, соответствующий петле, состоит из нулей, в результате чего матрица  не указывает на существование петель. Поэтому при изучении свойств графа с помощью этой матрицы необходимо исключить из него петли.
не указывает на существование петель. Поэтому при изучении свойств графа с помощью этой матрицы необходимо исключить из него петли.
Граф однозначно задаётся матрицами смежности и инцидентности. В свою очередь, каждая из этих матриц полностью определяет граф.
Существуют простые приёмы перехода от одной матрицы к другой.
Кроме выше перечисленных разновидностей матриц используются также матрицы контуров, сечений и так далее. Эти матрицы используются, как правило, при анализе электронных схем, поэтому далее они не будут рассматриваться.
Контрольные вопросы
- На какие понятия опираются понятия теории графов?
- Для каких целей используются графы?
- Сформулируйте понятие графа.
- Как представляется граф геометрически?
- Что представляют собой ориентированные и неориентированные графы?
- В каких случаях и почему используются ориентированные и неориентированные графы?
- Какие вершины называют смежными?
- Какие вершины называют инцидентными?
- Что называют локальной степенью вершины?
- Что называют несвязным графом?
- Что называют маршрутом?
- Что входит в понятие ” цепь “?
- Как составляется матрица смежности графа?
- Как составляется матрица инцидентности?
Весовая матрица
Cтраница 2
Далее по формуле ( VI 56) находим весовую матрицу логарифмов скоростей, которая является общей для серии опытов при постоянных подачах и температуре.
[16]
Матрица W ( К х А) называется весовой матрицей.
[17]
В версиях ДАН, рассматриваемых до сих пор, весовая матрица вычисляется в виде суммы произведений пар векторов. Эти вычисления полезны, поскольку они демонстрируют функции, которые может выполнять ДАН. Однако это определенно не тот способ, посредством которого производится определение весов нейронов мозга.
[18]
Так как ограничения (6.125) и (6.131) предполагаются независимыми, а весовая матрица W невырожденная, то матрицы коэффициентов ц, в уравнении (6.139) и v в уравнении (6.140) также невырожденны.
[19]
Это выражение для Г выведено для общего случая, когда весовая матрица W и матрица, обратная корреляционной матрице измерений Г, не равны между собой. Однако на практике матрицы W и IV1 стараются сделать как можно более близкими между собой, выбирая при этом такую систему измерений, которая исключает автокорреляцию, в результате чего все недиагональные элементы матрицы Гг становятся равными нулю. В худшем случае матрица Г2 и, следовательно, матрица W содержат небольшие недиагональные блоки, определяющие взаимную корреляцию между различными типами измерений. Обычно все же в уравнении ( 6) принимают FZ W – l, имея в виду, что полученное выражение для Гх справедливо в той же степени, в которой удалось сформировать соответствующую весовую матрицу.
[20]
Система задана своими характеристиками вход – выход, под которыми понимается весовая матрица G ( t) ( gij ( t)) nxm или передаточная матрица G ( p) gtj ( p)) nxm – При этом элементы последней являются рациональными функциями р и имеют вид правильных дробей.
[21]
Выход каждого фотодетектора является сверткой между входным вектором и соответствующим столбцом весовой матрицы. Таким образом, набор выходов представляет собой вектор, равный произведению входного вектора на весовую матрицу.
[23]
Непосредственно генетический алгоритм работает на 4 – м этапе для вычисления весовой матрицы сети. Предварительно на этапе 3 пользователь, обучив с помощью BrainMaker несколько сетей, выбирает две лучшие, которые составляют исходную популяцию алгоритма. Таким образом, размер популяции равен двум.
[25]
Это показывает, что двухслойная линейная сеть эквивалентна одному слою с весовой матрицей, равной произведению двух весовых матриц. Следовательно, любая многослойная линейная сеть может быть заменена эквивалентной однослойной сетью. Таким образом, для расширения возможностей сетей по сравнению с однослойной сетью необходима нелинейная активационная функция.
[26]
Допустим, что ковариационная матрица наблюдаемых величин, а следовательно, и весовая матрица выбраны плохо. Возникает вопрос, можно ли предугадать, как это скажется на результатах лшв-анализа и при последующей проверке гипотез.
[27]
Таким образом, мы получили замечательный результат – оптимальная оценка не зависит от весовой матрицы.
[28]
При этом хорошо реализована схема организации связей: можно задать одну векторную связь с заданной весовой матрицей, а не набор скалярных связей с весовыми коэффициентами.
[29]
Для многомерных линейных операторов верны при соответствующем матричном обобщении приведенные выше формулы связи между передаточными и весовыми матрицами.
[30]
Страницы:
1
2
3
4


