1 июля 2011
Elitarium.ru, 1 июля 2011г.
Предисловие редакции HT.ru:
Данная статья адресована, в первую очередь, маркетологам и социологам, которые занимаются проведением массовых опросов и исследований. Но нам бы хотелось, чтобы с этим материалом были знакомы наши hr-ы. Даже если Вы еще никогда не занимались проведением опросов в своей организации, поверьте, Вам предстоит когда-нибудь столкнуться с этой интереснейшей областью работы. И одной из первых проблем, которая встанет перед Вами, будет вопрос “Кого привлекать к опросу?”. Скажем так, данная статья не даст простого и четкого ответа на этот, в действительности, непростой вопрос. Но, прочитав ее, Вы сможете по-новому, осмысленнее и более профессионально взглянуть на тот фронт работ, который представляет собой проведение опросов. Например, Вы сможете предугадать, чьи ответы Вы получите в случае, когда опрос в организации будут проходить “все желающие”.
Редакция HT.ru
Автор статьи: Игopь Cтанислaвович Бepeзин, консультант по маркетинговым стратегиям, президент Гильдии мapкетoлoгов (г. Моcква).  Опрос и анкетирование являются ведущими, универсальными методами проведения социологических и маркетинговых исследований. Чаше всего, когда говорят о маркетинговом исследовании — сборе первичной информации, имеют в виду именно опрос или анкетирование, предполагающие прямое выяснение, непредвзятого мнения достаточно многочисленной группы респондентов.
Опрос и анкетирование являются ведущими, универсальными методами проведения социологических и маркетинговых исследований. Чаше всего, когда говорят о маркетинговом исследовании — сборе первичной информации, имеют в виду именно опрос или анкетирование, предполагающие прямое выяснение, непредвзятого мнения достаточно многочисленной группы респондентов.
Массовым считается опрос, в ходе которого путем личной беседы сотрудника исследовательской компании — интервьюера с носителями информации (респондентами), состоящей из нескольких десятков коротких вопросов, изучаются мнения нескольких сотен (тысяч) человек. Под анкетированием понимают безличную форму общения исследователей с носителями информации, при которой респонденты самостоятельно отвечают на вопросы анкеты, следуя содержащейся в ней инструкции и не вступая в непосредственный контакт с интервьюерами.
Конечной целью анкетирования и массового опроса является получение данных, характеризующих так называемую генеральную совокупность. Генеральная совокупность — это все представители какой-либо группы, носители какого-либо важного признака, например:
-
все российские избиратели;
-
все потенциальные потребители пива, проживающие в Перми;
-
все подростки (12-16 лет) Поволжского региона;
-
все учителя физики и химии, работающие в средних школах;
-
все домохозяйства, имеющие доход от 500 до 1 500 долл. в месяц;
-
все компании, занимающиеся розничной торговлей в Самаре и т. д. и т. п.
Для того чтобы опросить десятки или сотни тысяч, а тем более — миллионы человек (компаний), из которых может состоять генеральная совокупность, нужны сотни или даже тысячи интервьюеров. На проведение подобного исследования могут понадобиться десятки, если не сотни миллионов долларов и не менее полугода напряженной работы. Такое возможно только при переписи населения (проводящейся не чаще одного раза в 10 лет).
Однако в маркетинге этого и не требуется. Достаточно того, чтобы относительно небольшая выборка (от нескольких сотен до нескольких тысяч представителей) репрезентировала (выразила) мнение генеральной совокупности. Как такое возможно? На каком основании можно распространять данные, полученные от небольшой группы людей, на существенно (в десятки и сотни раз) большую группу? На основании гипотезы о том, что на поведение, знания, отношение потребителей к компании, товару, услуге или отдельных их компонентов оказывают влияние социально-демографические характеристики самих потребителей.
Иными словами, большинство представителей четко определенной социально-демографический группы будут сходным образом реагировать на внешние, в данном случае — рыночные стимулы: товар, цену, упаковку, рекламу и т. д. и т. п. И нет никакой необходимости опрашивать всех представителей этой группы, поскольку ее мнение (с допустимой погрешностью) может представить (репрезентировать) небольшая выборка из ее представителей.
Способы построения выборки
Существуют две группы методов построения выборки, в той или иной степени реализующих репрезентацию мнений и позиций генеральной совокупности: вероятностные и детерминированные.
Первая группа методов (вероятностные) базируется на использовании теории вероятности. В основе ее применения лежит постулат, что репрезентация будет достигнута в случае, если каждой единице генеральной совокупности обеспечено равновероятное попадание в выборку. Например, если генеральной совокупностью является все взрослое (16-85 лет) население города (200 тыс. человек), то каждому жителю должна быть обеспечена вероятность стать участником исследования(попасть в выборку), равная 1 / 200 000. В противном случае выборка будет не случайной, а смещенной, т. е. менее репрезентативной.
Реализовать это можно в случае, если все элементы генеральной совокупности могут быть тем или иным образом пронумерованы, а затем эти номера будут выбраны в определенной последовательности — «по воле случая». Например, в Москве около 2 500 средних школ, каждаяиз которых имеет свой номер. Мы могли бы выбрать наугад 100 номеров и провести опрос 100 директоров (завучей, учителей физики, классных руководителей 11-х классов и т. п.) в этих школах.
Эти 100 номеров мы можем выбрать с помощью таблицы или «генератора случайных чисел» (есть такая специальная компьютерная программа), а также с помощью «барабана» но принципу того, как это делается при проведении лотереи. Такие способы построения выборки называются «простой случайной выборкой». Каждый ее элемент отбирается независимо и имеет равную вероятность попасть в выборку.
Мы могли бы выбрать наугад любое число от 1 до 25, например— 12, а затем взять в выборку школы с номерами: 12, 37, 62, 87, 112, 137 и т. д. Такой метод построения называемся «систематической выборкой», первый элемент которой выбирается произвольно, а затем выбирают каждый i-й элемент.
Мы также могли бы сначала разделить эти школы на несколько страт (возможно, и пересекающихся), например, на школы физико-математические, спортивные, лингвистические и гуманитарные, а затем произвести случайную или систематическую выборку (по 20-30 школ) из каждой страты. Такой метод построения называется «стратифицированной выборкой».
Разновидностью стратифицированной выборки является «маршрутная выборка», суть реализации которой состоит в следующем. Город делится на 20-40 «секторов» по числу интервьюеров, задействованных и исследовании. Каждый интервьюер получает один сектор, маршрут обследования «своего» сектора и инструкцию по реализации простой случайной выборки. Например такую: «Начать обход с улицы Баумана, с дома № 2, третьего подъезда, второго этажа сверху, первой квартиры слева. Затем — дом № 4, второй подъезд, третий этаж, вторая квартира справа… Потом — переулок Комсомольский, нечетная сторона… Потом — тупик Коммунизма… и т. д.»
Наконец, мы могли бы разделить генеральную совокупность на непересекающиеся кластеры, к примеру, по муниципальным районам (их в Москве 125, и в каждом в среднем по 20 школ). Затем случайным образом выбрать пять районов и произвести обследование всех школ данного муниципального района. Такой метод построения называется «кластерной выборкой».
Тем не менее у вероятностных методов построения выборки есть один весьма существенный недостаток. Каждый из них исходит из предположения о том, что все элементы генеральной совокупности являются равнодоступными: и в «техническом» смысле (у всех есть телефон для телефонного опроса или доступ в Интернет), и в «психологическом», т. е. все респонденты с примерно равной вероятностью согласятся или откажутся принимать участие в исследовании. Однако это не так.
Граждане с относительно высокими доходами менее доступны для исследователей, чем те, чьи доходы невысоки. И нет никакой силы, которая могла бы заставить этих люден отвечать им вопросы социологов или маркетологов. Поэтому все выборки всегда смещены в сторону средне- и малообеспеченных групп населения. Во всех без исключения странах мира.
Менее образованные граждане идут на контакт с социологами менее охотно, чем лица с высшим образованием. Поэтому в большинстве выборок доля хорошо образованных граждан как правило существенно выше, чем в генеральной совокупности.
Никто из сотрудников исследовательских компаний не желает общаться с бомжами, алкоголиками, наркоманами, психо- и социопатами и прочими маргиналами. И у руководителя исследования нет решительно никаких возможностей заставить своих сотрудников делать это. А между прочим, к этим группам в России по взвешенным оценкам относится от 12 до 15% жителей Следовательно, любая выборка смещена в сторону «вменяемых» граждан.
Некоторые граждане боятся отвечать на вопросы, даже самые невинные. Таких людей немного, но они есть. А вот способов заставить их участвовать в опросе нет.
Наконец, есть люди, которые просто не желают участвовать в исследовании. У них есть время, они ничего не боятся, они все понимают, но на вопросы отвечать отказываются. И точка.
Таким образом, все выборки в маркетинге и социологии являются смещенными в сторону средне- и малообеспеченных, более образованных, контактных и вменяемых граждан. Они и репрезентируют общее мнение генеральной совокупности. И все исследователи рынка прекрасно это знают.
Преодолеть наложенные выше проблемы можно с помощью метода «квот», относящегося к детерминированным методам, при котором априори обеспечивается пропорциональное представительство носителей существенных признаков (пол, возраст, доход, образование и т. п.) генеральной совокупности в выборке.
Это наиболее эффективный, на наш взгляд, метод проведения массовых опросов. При его использовании существенно облегчается задача поиска корреляционных связей, сравнения различных типов (групп) потребителей между собой и экстраполяции выявленных закономерностей на генеральную совокупность.
Единственная, но весьма существенная трудность при реализации него метода состоит в том, что не всегда доподлинно известно распределение всех важных параметров в самой генеральной совокупности. В этом случае исследователь или консультант исследовательского проекта должен взять на себя смелость распределить квоты по своему усмотрению, в соответствии со своим видением, пониманием рынка.
Задача достижения строгой репрезентативности не всегда является важной. Иногда целесообразно воспользоваться существенно более простыми в реализации детерминированными методами:
-
нерепрезентативным, или произвольным, когда опрашивают того, кто «попался под руку» интервьюеру и согласился участвовать в опросе. Естественно, этот метод дает крайне ненадежные результаты. А вдруг под руку попадется рота солдат или команда баскетболисток! Однако его использование допустимо в исследованиях, носящих поисковый характер, не требующих большой точности, при проведении «пилотажа» анкеты. «Произвольность» можно компенсировать большим объемом выборки, из которой затем можно будет попробовать отобрать необходимое число «подходящих» анкет и составить уже из них репрезентативную в каких-то отношениях выборку;
-
поверхностным — когда отбор осуществляется по самым общим признакам, задаваемым исследователем интервьюерам в виде не очень строгого задания;
-
« воронки» — когда сначала отбираются наиболее «контактные», а затем среди них — наиболее «компетентные», подходящие респонденты;
-
« концентрации» — на представителях отдельных, сопоставимых сегментов рынка, среди которых проводят «сплошной» опрос. Например, школьный 11 «А» класс может представлять всех старшеклассников школы или даже города как «обычный», «типичный класс»;
-
«снежного кома» — когда начальная группа подбирается случайным образом, а дальнейший отбор ведется из кандидатов, указанных первыми респондентами, и т. д.
Достоверность и погрешности измерений
Под «достоверностью», уровнем достоверности понимают показатель вероятности того, что истинное значение изучаемого параметра генеральной совокупности попадет в доверительный интервал. Чем выше задаваемый уровень достоверности, тем больше должна быть выборка. Под доверительным интервалом понимают диапазон, в который попадет истинное значение изучаемого параметра генеральной совокупности при данном уровне достоверности. Чем он меньше, тем больше должна быть выборка.
К примеру, общероссийская городская выборка (14-65 лет) в 1 200 респондентов имеет доверительный интервал 4 процентных пункта при уровне достоверности 0,95. При ее проведении 15% участников опроса заявили, что за последние три месяца были в кинотеатре хотя бы один раз.
Эти данные позволяют нам утверждать с заданным уровнем достоверности, что от 11 до 19% жителей российских городов в возрасте от 14 до 65 лет были в кинотеатре хотя бы один раз за последние три месяца. Иными словами, можно сказать, что все значения между 11 и 19% в данном случае находятся в пределах «допустимой статистической погрешности». Если бы мы хотели задать доверительный интервал в 2 процентных пункта, то выборку (при прочих равных условиях) пришлось бы увеличить примерно в четыре раза.
Со стороны уровня достоверности эти данные означают, что если бы было проведено 100 независимых измерении (опросов) по 1200 респондентов в каждом, то в 95 из них значение доли ответов на вопрос о посещении кинотеатра не вышло бы за пределы доверительного интервала (в этом конкретном случае — 11-19%). А в пяти исследованиях или бы получены значения, выходящие за пределы доверительного интервала. Если бы нас устраивала достоверность на уровне 0,9, то опросить можно было бы 200 человек. Если нам нужна достоверность на уровне 0,99, то пришлось бы опросить более 10 тыс. человек.
Оптимальный размер выборки
Вот одна из формул расчета необходимого объема выборки, используемая при известном среднем отклонении (дисперсии) и заданных уровнях достоверности и точности:
N = (g2 * z2) / d2
где: N — искомый объем выборки; g — дисперсия признака, ожидаемое среднее отклонение получаемых результатов от ожидаемого среднего значения; z — коэффициент уровня достоверности (2 — для 0,95, 3 — для 0,99); d — уровень точности.
Допустим, мы изучаем поведение покупателей в продовольственном магазине, в частности, мы хотим определить среднюю сумму чека. Из бесед с владельцем магазина мы узнаем, что она может быть в районе 500-700 руб., а среднее отклонение (g) может составить 200 руб. В ходе опроса мы хотели бы определить среднее значение с точностью (d) до 20 руб. при уровне достоверности (z) в 0,95. Подставляем значения формулу и получаем:
40000 * 4 / 400 = 400.
То есть нам достаточно опросить 400 покупателей. Если бы мы хотели узнать среднюю сумму чека с точностью до 10 руб.. то нам пришлось бы опросить 1600 покупателей. Если бы при этом мы хотели получить уровень достоверности в 0,99, то количество покупателей, которых необходимо опросить, составило бы 3 500 человек. И наоборот: если нас устроила бы точность ±50 руб., то нам достаточно было бы опросить в заданных условиях всего 65 человек.
Практическое использование этой и других формул, которые здесь не будут приводиться, весьма затруднено следующими обстоятельствами:
-
Что делать, если мы не знаем даже приблизительно «ожидаемую среднюю» и среднюю дисперсию признака?
-
Что делать, если в анкете у нас 10 вопросов, по которым ожидаются различные средние, с различными средними дисперсиями?
-
Как быть в случае использования номинальных шкал?
-
Как быть в случае, если один вопрос предполагает два или три варианта ответа и т. д. и т. п.?
-
Для простых альтернативных вопросов по принципу «да/нет» используются одни формулы, для более сложных — другие.
-
Формулы необходимо корректировать в зависимости от количества столбцов в таблице «факторных распределении», а также в зависимости от распределения ответов (10 на 90 — это одно, а 45 на 55 — совсем другое дело).
-
Одни формулы учитывают размер генеральной совокупности, а другие (как приведенная выше) — нет. Есть много иных нюансов.
На практике сначала определяют количество респондентов, которое исследователи предполагают опросить с учетом временных и финансовых ограничений, задают уровень достоверности (обычно — 0,95), а затем уже рассчитывают доверительный интервал.
Определение необходимого и достаточного объема выборки происходит на основе опыта и неформальных «конвенций» исследователей между собой. Считается, и это многократно проверено на практике, что опрос 30-50 представителей конкретной, «узкой» социально-демографической группы населения, например «ярославских замужних женщин в возрасте 30-45 лет, имеющих одного ребенка, высшее образование и совокупный семейный доход в пределах от 1 500 до 3 000 долл. в месяц», можно распространять на всю эту группу, и допустимая ошибка (доверительный интервал) не превысит 4 процентных пунктов при уровне достоверности около 0,95.
Однако полученные данные нельзя распространять, например, на незамужних женщин того же возраста, имеющих такой же доход и уровень образования. А также на женщин, имеющих иной доход, возраст или уровень образования. И уж тем более — на мужчин.
Таким образом, если в задачу исследователя входит получение информации о мнениях, знаниях, поведении или отношении к некой проблеме всех ярославских женщин, и при этом все перечисленные выше социально-демографические факторы являются значимыми, необходимо построить такую выборку, в которой были бы представлены все «узко определенные» группы. В данном случае — две группы по семейному положению, три — по наличию и количеству детей, три возрастные, три доходные, две образовательные. Итого 108 групп, в каждой из которых должно быть не менее 30 представительниц. Всего — более 3 000 респондентов.
На самом деле едва ли найдется вопрос или проблема, на которые все пять факторов будут оказывать взаимное перекрестное воздействие. В большинстве случаев вполне можно было бы обойтись опросом 400-600 респонденток, а затем провести попарный (а не перекрестный) факторный анализ. То есть отдельно исследовать влияние факторов «возраст», «образование», «доход», «семейное положение», «дети». При этом выборка каждый раз разбивалась бы на две-три группы, наполнение которых было бы не меньше 100-150 респондентов.
Репрезентативная выборка, представляющая все население России, должна состоять из 3 600-9 000 человек и 180 групп (два пола, три возраста, два образовательных уровня, три доходные группы, пять типов поселений). Доверительный интервал будет в пределах ±3 процентных пункта. Это означает, что, к примеру, если 30% (12% или 45%) наших респондентов заявили, что регулярно употребляют в пищу майонез, то долю потребителей майонеза в России можно оценить в 27-33% (9-15 или 42-48% соответственно).
Размер выборки практически не зависит от размера генеральной совокупности. И в мегаполисе с населением более миллиона человек, и в уездном городе с населением в 35 тыс. человек для построения выборки, репрезентативной по одинаковому числу параметров, потребуется опросить одинаковое число респондентов.
От чего действительно зависит размер выборки — так это от числа параметров, по которым мы желаем добиться репрезентативности. Если нас устраивает репрезентативность только по полу и возрасту, то выборки в 400 человек в одном населенном пункте будет более чем достаточно. Если параметров три, количество респондентов придется увеличить до 600. Добиться репрезентативности выборки одновременно по пяти параметрам: полу, возрасту, доходу, образованию, сфере профессиональной деятельности — можно лишь на выборке из 1 000-1 200 человек в одном населенном пункте.
В вашей почте раз в неделю. А еще: новости, акции и мероприятия для HR.
Схемы отбора в выборку
Время на прочтение
4 мин
Количество просмотров 12K
Схема отбора в выборку — это детальное описание того, какие данные и каким способом будут получены. Есть много схем для отбора в выборку, поэтому нужно выбрать для исследований такую, которая даст наиболее репрезентативные результаты. Репрезентативность выборки — это соответствие характеристик выборки характеристикам популяции.
В идеале лучше работать со всей генеральной совокупностью, но это занимает много времени и ресурсов. Поэтому можно исследовать только ее часть, что и называется выборкой. Затем исследуются элементы, которые попали в выборку. На основе полученных значений оцениваются неизвестные элементы выборки.

Основные принципы отбора в выборку
Идея состоит в том, чтобы перенести результаты на всю генеральную совокупность. Поэтому выборка должна быть репрезентативной. Другими словами она пропорциональна как подгруппам, так и всей совокупности, и не исключает каких-либо отдельных групп.
Выборка должна быть настолько большой, насколько это возможно, чтобы избежать ошибочных суждений. По сути выборкой может быть любое подмножество генеральной совокупности.
Если выборка недостаточно репрезентативна — исследование будет считаться предвзятым. Если она будет недостаточно большой — неточным.
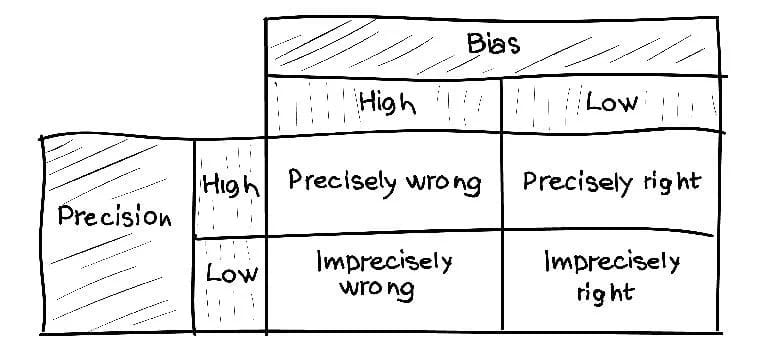
Если правильно подобрать связь между выборкой и совокупностью, тогда можно сделать правильные заключения о природе всей совокупности. Лучше быть возможно правым, чем точно не правым.
Схемы отбора для вероятностных выборок
Вероятностные выборки подразумевают, что исследователь абсолютно уверен в связях выборки с генеральной совокупностью. Если же связи не прослеживаются или в наличии имеются не все элементы генеральной совокупности используется невероятностная выборка.
На основе жеребьевки
Схема отбора состоит в том, чтобы провести ряд испытаний без возвращения элемента в генеральную совокупность. Каждый элемент совокупности имеет одинаковые шансы попасть в выборку.
Из генеральной совокупности N случайным образом отбирается один элемент, вероятность попадания элемента в выборку равна 1/N. Затем из выборки N-1 выбирается второй элемент с вероятностью 1/(N-1) и так далее до n-го элемента с вероятностью 1/(N-n).
Отбор Бернулли
Отбор происходит из упорядоченного списка из N элементов. Пусть наперед задано некоторое число ε (1<ε<0) и набор N независимых реализаций равномерно распределенной на [0,1] случайной величины ε1…εN. Каждому элементу k ставится в соответствие значение. Если εк<π, то этот элемент отбирается, в другом случае — нет. Возможность того, что элемент будет выбран равна π для каждого из N элементов. Таким образом каждый элемент, который попал в выборку является биномиально распределенной величиной.
Систематический отбор
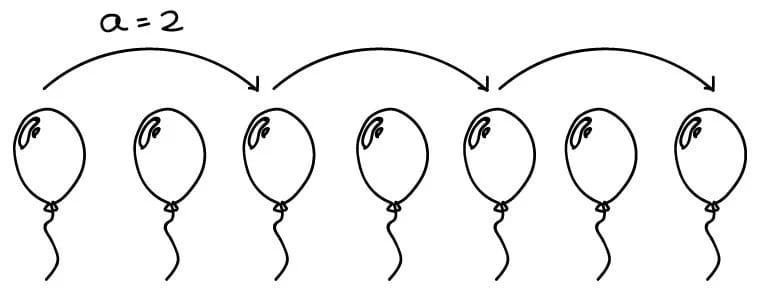
Пусть N — размер генеральной совокупности. а — некоторое фиксированное число. а ∈ N. Первый элемент выборки выбирается случайным образом среди первых a элементов совокупности. Выбранное число r 1≤ r ≤a называется случайным стартом (началом), а число а — выборочным интервалом. Каждый элемент [1,2… а] имеет одинаковую вероятность быть выбранным, равную 1/а. Далее в выборку попадают элементы с шагом а.
Можно получить а разных выборок, каждая из которых имеет одинаковую вероятность быть выбранной.
Простой случайный отбор с возвращением
Во всех вышеизложенных схемах у элемента не было возможности попасть в выборку более 1 раза.
Это логично, так как при повторном включении элемента новая информация не добавляется. Но в этом случае некоторые оценки имеют очень простые статистические свойства, что дает возможность исследовать довольно сложные процедуры отбора.
Например, выполняется m независимых отборов элементов из генеральной совокупности размера N с одинаковыми вероятностями 1/N. Отобранный элемент возвращается в совокупность. Таким образом все N элементов участвуют в отборе постоянно.
Пропорциональный отбор: с возвращением и без
Предполагает, что все числа генеральной совокупности должны быть хорошо перемешаны. Тогда исследователь берет каждый а-й элемент из списка.
Стратифицированный отбор
При этом отборе генеральная совокупность делится на группы, которые не пересекаются. Эти группы называются стратами. Элементы в каждой страте однородны по определенным признакам. В каждой страте проводится отбор элементов. Метод отбора может быть любым, при чем не обязательно одинаковым в каждой страте. Отбор из одной страты не зависит от других страт.
Стратегия отбора в этом случае становится более эффективной. Чем больше изменяется исследуемая характеристика, тем большей будет выборка для более точной оценки. А если разбить совокупность на страты, в которых характеристики мало отличаются, то небольшой выборки из каждой страты будет достаточно для оценки всей совокупности.
Пример: исследование уровня доходов по миру. Вначале весь мир делится на страты, а именно страны. Это области, которые не пересекаются между собой, затем исследование проводится по каждой стране отдельно.
Схемы отбора для невероятностных выборок
В этом случае сложно оценить вероятность попадания каждого элемента совокупности в сэмпл. Исследователи, использующие эти методы, не могут сделать точные выводы о генеральной совокупности.
Кластерный отбор
Если непосредственный отбор из совокупности невозможен, элементы генеральной совокупности объединяются в кластеры.
Кластерный отбор может проходить в одну стадию, тогда сначала отбирают кластеры, а потом исследуют все элементы отобранных кластеров. Например, при исследовании города, кластером может быть семья или жители одного дома.
Если отбор осуществляется в две стадии, то совокупность делят на кластеры, которые состоят из других, более мелких кластеров. На первой стадии получают вероятностную выборку первичных кластеров. На второй стадии — из первичных кластеров отбирают элементы.
Процедура может состоять из трех и более стадий, тогда такая схема называется многостадийной.
Типовой отбор
Элементы отбираются исходя из того, находятся ли они в простом доступе. Такие выборки очень легко составлять, но нет ни единой гарантии что она будет репрезентативной.
Снежный ком
Обычно используется при отборе кандидатов в специфической небольшой группе экспертов. Выбирается один человек для опроса, затем он должен посоветовать несколько других людей и так далее.
Конспект
- Выборки бывают вероятностные и невероятностные.
- Если неправильно выбран метод отбора в выборку. исследование может стать предвзятым или неточным.
- Лучше быть возможно правым, чем точно не правым.
Методы выборки: Типы с примерами
Опубликовано 2023-02-11 19:53 пользователем

Выборка является важной частью любого исследовательского проекта. Правильный метод выборки может сделать или разрушить достоверность вашего исследования, и очень важно выбрать правильный метод для вашего конкретного вопроса. В этой статье мы подробно рассмотрим некоторые из наиболее популярных методов выборки и приведем реальные примеры того, как их можно использовать для сбора точных и надежных данных.
От простой случайной выборки до сложной стратифицированной выборки, мы рассмотрим плюсы, минусы и лучшие практики каждого метода. Итак, независимо от того, являетесь ли вы опытным исследователем или только начинаете свой путь, эта статья – обязательное чтение для всех, кто хочет освоить методы выборки. Давайте начнем!
Индекс содержания
- Что такое выборка?
- Типы выборки: методы выборки
- Типы вероятностной выборки с примерами:
- Использование вероятностной выборки
- Типы не вероятностной выборки с примерами
- Использование не вероятностной выборки
- Как вы решаете, какой тип выборки использовать?
- Разница между вероятностной и не вероятностной выборкой
- Вывод
Что такое выборка?
Выборка – это техника отбора отдельных членов или подмножества населения для того, чтобы сделать на их основе статистические выводы и оценить характеристики всего населения. Различные методы выборки широко используются исследователями в маркетинговых исследованиях, так что им не нужно изучать все население, чтобы получить действенные выводы.
Это также удобный и экономически эффективный метод, и поэтому он составляет основу любого плана исследования. Методы выборки могут быть использованы в программном обеспечении для проведения исследовательских опросов для получения оптимальных результатов.
Например, предположим, производитель лекарств хотел бы исследовать неблагоприятные побочные эффекты лекарства на население страны. В этом случае практически невозможно провести исследование, в котором участвовали бы все. В этом случае исследователь определяет выборку людей из каждой демографической группы и затем исследует их, получая ориентировочные данные о поведении препарата.
Узнайте больше об Аудитории
Типы выборки: Методы выборки
Выборка в исследованиях рыночных действий бывает двух типов – вероятностная и не вероятностная выборка. Давайте подробнее рассмотрим эти два метода выборки.
- Вероятностная выборка: Вероятностная выборка – это метод выборки, при котором исследователь выбирает несколько критериев и отбирает членов популяции случайным образом. При таком параметре отбора все члены имеют равную возможность участвовать в выборке.
- Невероятностная выборка: При невероятностной выборке исследователь случайным образом выбирает членов для исследования. Этот метод выборки не является фиксированным или заранее определенным процессом отбора. Это затрудняет для всех элементов населения равные возможности быть включенными в выборку.
В этом блоге обсуждаются различные вероятностные и не вероятностные методы выборки, которые вы можете применить в любом исследовании рынка.
Типы вероятностной выборки с примерами:
Вероятностная выборка – это метод, при котором исследователи выбирают образцы из большей совокупности на основе теории вероятности. Этот метод выборки учитывает каждого члена популяции и формирует выборки на основе фиксированного процесса.
Например, в популяции из 1000 человек каждый член имеет шанс 1/1000 быть отобранным для включения в выборку. Вероятностная выборка устраняет смещение выборки в популяции и позволяет включить в выборку всех членов.
Существует четыре типа методов вероятностной выборки:

- Простая случайная выборка: Одним из лучших методов вероятностной выборки, который помогает экономить время и ресурсы, является метод простой случайной выборки. Это надежный метод получения информации, при котором каждый отдельный член популяции выбирается случайно, чисто случайно. Например, в организации из 500 сотрудников, если команда HR решит провести мероприятия по сплочению коллектива, они, скорее всего, предпочтут выбирать фишки из миски. В этом случае каждый из 500 сотрудников имеет равную возможность быть отобранным.
- Кластерная выборка: Кластерная выборка – это метод, при котором исследователи делят всю совокупность на части или кластеры, представляющие совокупность. Кластеры определяются и включаются в выборку на основе таких демографических параметров, как возраст, пол, местоположение и т.д. Это позволяет создателю опроса сделать эффективные выводы из полученных данных.
Например, предположим, правительство Соединенных Штатов хочет оценить количество иммигрантов, проживающих на материковой части США. В этом случае они могут разделить его на кластеры, основанные на таких штатах, как Калифорния, Техас, Флорида, Массачусетс, Колорадо, Гавайи и т. д. Такой способ проведения опроса будет более эффективным, так как результаты будут распределены по штатам и предоставят глубокие данные об иммиграции. - Систематическая выборка: Исследователи используют метод систематической выборки для отбора членов выборки из популяции через регулярные промежутки времени. Он требует выбора начальной точки для выборки и размера выборки, который можно повторять через регулярные промежутки времени. Этот метод выборки имеет заранее определенный диапазон; следовательно, этот метод выборки наименее трудоемкий.
Например, исследователь намеревается собрать систематическую выборку из 500 человек в популяции численностью 5000 человек. Он/она пронумерует каждый элемент популяции от 1 до 5000 и выберет каждого 10-го человека для включения в выборку (Общая популяция/Размер выборки = 5000/500 = 10). - Стратифицированная случайная выборка: Стратифицированная случайная выборка – это метод, при котором исследователь делит популяцию на более мелкие группы, которые не пересекаются, но представляют всю популяцию. Например, исследователь, желающий проанализировать характеристики людей, принадлежащих к различным группам по годовому доходу, создает страты (группы) в соответствии с годовым доходом семьи. Например, менее $20 000, $21 000 – $30 000, $31 000 – $40 000, $41 000 – $50 000 и т. д. Таким образом, исследователь делает вывод о характеристиках людей, принадлежащих к различным группам доходов. Маркетологи могут проанализировать, на какие группы доходов ориентироваться, а какие исключить, чтобы создать дорожную карту, которая принесет плодотворные результаты.
Uses of probability sampling
Существует множество вариантов использования вероятностной выборки:
- Снижение погрешности выборки: При использовании метода вероятностной выборки погрешность выборки, полученной из совокупности, незначительна или вообще отсутствует. Выборка в основном отражает понимание и умозаключения исследователя. Вероятностная выборка приводит к более качественному сбору данных, поскольку выборка адекватно представляет население.
- Разнородное население: Когда население обширно и разнообразно, важно иметь адекватное представительство, чтобы данные не были перекошены в сторону одной демографической группы. Например, предположим, что компания Square хотела бы понять, какие люди могли бы использовать ее устройства в точках продаж. В этом случае поможет опрос, проведенный на выборке людей по всей территории США из разных отраслей промышленности и социально-экономического положения.
- Создание точной выборки: Выборка вероятностей помогает исследователям планировать и создавать точную выборку. Это помогает получить четко определенные данные.
Типы не вероятностной выборки с примерами
Не вероятностный метод – это метод выборки, который предполагает сбор обратной связи на основе возможностей исследователя или статистика по отбору выборки, а не на основе фиксированного процесса отбора. В большинстве ситуаций результаты опроса, проведенного с использованием не вероятностной выборки, приводят к искаженным результатам, которые могут не представлять желаемую целевую совокупность. Однако существуют ситуации, например, на предварительных этапах исследования или при ограничении затрат на проведение исследования, когда не вероятностная выборка будет гораздо полезнее, чем другой тип.
Четыре типа непроизводственной выборки лучше объясняют цель этого метода выборки:
- Выборка удобства: Этот метод зависит от легкости доступа к испытуемым, например, опрос покупателей в торговом центре или прохожих на оживленной улице. Обычно его называют выборкой удобства из-за того, что исследователю легко проводить его и вступать в контакт с испытуемыми. Исследователи практически не имеют полномочий для отбора элементов выборки, и он осуществляется исключительно на основе близости, а не репрезентативности. Этот метод не вероятностной выборки используется, когда существуют ограничения по времени и затратам на сбор обратной связи. В ситуациях с ограниченными ресурсами, например, на начальных этапах исследования, используется выборка по удобству.
Например, стартапы и НПО обычно проводят выборку по удобству в торговом центре для распространения листовок о предстоящих событиях или продвижения дела – они делают это, стоя у входа в торговый центр и раздавая брошюры случайным образом. - Суждение или целенаправленная выборка: Суждение или целенаправленная выборка формируется по усмотрению исследователя. Исследователи в обязательном порядке учитывают цель исследования, а также понимание целевой аудитории. Например, когда исследователи хотят понять ход мыслей людей, заинтересованных в получении степени магистра. Критерием отбора будет: “Заинтересованы ли вы в получении степени магистра в …?”, а те, кто ответит “нет”, будут исключены из выборки.
- Выборка снежного кома: Выборка снежного кома – это метод выборки, который исследователи применяют, когда субъектов трудно отследить. Например, опрос людей без жилья или нелегальных иммигрантов будет чрезвычайно сложным. В таких случаях, используя теорию снежного кома, исследователи могут отследить несколько категорий для опроса и получить результаты. Исследователи также применяют этот метод выборки, когда тема очень чувствительна и не обсуждается открыто – например, опросы для сбора информации о ВИЧ СПИДе. Не многие жертвы охотно ответят на вопросы. Тем не менее, исследователи могут связаться с людьми, которых они могут знать, или с волонтерами, связанными с этим делом, чтобы установить контакт с жертвами и собрать информацию.
- Квотная выборка: В квотной выборке при этом методе отбор участников происходит на основе заранее установленного стандарта. В этом случае, поскольку выборка формируется по определенным признакам, созданная выборка будет обладать теми же качествами, которые встречаются в генеральной совокупности. Это быстрый метод сбора выборки.
Uses of non-probability sampling
Невероятностная выборка используется для следующего:
- Создание гипотезы: Исследователи используют метод непропорциональной выборки для создания предположения, когда имеется ограниченная или вообще отсутствует предварительная информация. Этот метод помогает немедленно получить данные и создает базу для дальнейшего исследования.
- Исследовательские исследования: Исследователи широко используют этот метод выборки при проведении качественных исследований, пилотных исследований или исследовательских работ.
- Бюджет и временные ограничения: Невероятностный метод применяется, когда есть бюджетные и временные ограничения, и необходимо собрать некоторые предварительные данные. Поскольку схема опроса не является жесткой, проще выбрать респондентов случайным образом и попросить их пройти опрос или анкетирование.
Как вы решаете, какой тип выборки использовать?
Для любого исследования важно точно выбрать метод выборки, чтобы он соответствовал целям вашего исследования. Эффективность выборки зависит от различных факторов. Вот несколько шагов, которым следуют опытные исследователи, чтобы выбрать оптимальный метод выборки.
- Запишите цели исследования. Как правило, это должно быть сочетание стоимости, точности или аккуратности.
- Определите эффективные методы выборки, которые потенциально могут достичь целей исследования.
- Протестируйте каждый из этих методов и проверьте, помогают ли они достичь цели.
- Выберите метод, который лучше всего подходит для исследования.
Откройте силу точной выборки!
Разница между вероятностной и не вероятностной выборкой
Выше мы рассмотрели различные типы методов выборки и их подтипы. Однако, чтобы подытожить все обсуждение, ниже приведены существенные различия между вероятностными и не вероятностными методами выборки:
| Вероятностные методы выборки | Невероятностные методы выборки. | |
| Определение | Вероятностная выборка – это метод выборки, при котором выборки из большей совокупности отбираются с помощью метода, основанного на теории вероятности. | Невероятностная выборка – это метод выборки, при котором исследователь отбирает образцы на основе субъективного суждения исследователя, а не случайного отбора. |
| Альтернативно известный как | Случайный метод выборки. | Неслучайный метод выборки |
| Отбор популяции | Популяция отбирается случайным образом. | Население выбрано произвольно. |
| Натура | Исследование является окончательным. | Исследование является исследовательским. |
| Выборка | Поскольку существует метод определения выборки, демографические характеристики населения представлены убедительно. | Поскольку метод выборки произволен, демографические характеристики населения представлены почти всегда искаженно. |
| Время, затрачиваемое | На проведение исследования требуется больше времени, поскольку план исследования определяет параметры отбора до начала маркетингового исследования. | Этот тип выборочного метода является быстрым, поскольку ни выборка, ни критерии отбора выборки не определены. |
| Результаты | Данный тип выборки является полностью беспристрастным, следовательно, результаты также являются убедительными. | Данный тип выборки является полностью необъективным, следовательно, результаты также являются необъективными, что делает исследование спекулятивным. |
| Гипотеза | При вероятностной выборке существует основная гипотеза до начала исследования, и этот метод направлен на доказательство гипотезы. | При не вероятностной выборке гипотеза выводится после проведения исследования. |
Вывод
Теперь, когда мы узнали, как работают различные методы выборки, которые широко используются исследователями в маркетинговых исследованиях, чтобы им не нужно было исследовать все население для сбора действенных выводов, давайте рассмотрим инструмент, который может помочь вам управлять этими выводами.
понимает необходимость точного, своевременного и экономически эффективного метода отбора нужной выборки; именно поэтому мы предлагаем программное обеспечение Software – набор инструментов, позволяющих эффективно отбирать целевую аудиторию, управлять полученными данными в организованном, настраиваемом хранилище и управлять сообществом для обратной связи после проведения опроса.
Не упустите шанс повысить ценность исследований.
Попробуйте сегодня!
Рубрика:
- Бизнес
Ключевые слова:
- исследование рынка
Автор:
- Dan Fleetwood
Источник:
- questionpro
Перевод:
- Дмитрий Л

Автор: Игopь Cтанислaвович Бepeзин, консультант по маркетинговым стратегиям, президент Гильдии мapкетoлoгов (г. Моcква).
Опрос и анкетирование являются ведущими, универсальными методами проведения социологических и маркетинговых исследований. Чаше всего, когда говорят о маркетинговом исследовании — сборе первичной информации, имеют в виду именно опрос или анкетирование, предполагающие прямое выяснение, непредвзятого мнения достаточно многочисленной группы респондентов.
Массовым считается опрос, в ходе которого путем личной беседы сотрудника исследовательской компании — интервьюера с носителями информации (респондентами), состоящей из нескольких десятков коротких вопросов, изучаются мнения нескольких сотен (тысяч) человек. Под анкетированием понимают безличную форму общения исследователей с носителями информации, при которой респонденты самостоятельно отвечают на вопросы анкеты, следуя содержащейся в ней инструкции и не вступая в непосредственный контакт с интервьюерами.
Конечной целью анкетирования и массового опроса является получение данных, характеризующих так называемую генеральную совокупность. Генеральная совокупность — это все представители какой-либо группы, носители какого-либо важного признака, например:
- все российские избиратели;
- все потенциальные потребители пива, проживающие в Перми;
- все подростки (12-16 лет) Поволжского региона;
- все учителя физики и химии, работающие в средних школах;
- все домохозяйства, имеющие доход от 500 до 1 500 долл. в месяц;
- все компании, занимающиеся розничной торговлей в Самаре и т. д.
Чтобы опросить десятки или сотни тысяч, а тем более — миллионы человек (компаний), из которых может состоять генеральная совокупность, нужны сотни или даже тысячи интервьюеров. На проведение подобного исследования могут понадобиться десятки, если не сотни миллионов долларов и не менее полугода напряженной работы. Такое возможно только при переписи населения (проводящейся не чаще одного раза в 10 лет).
Однако в маркетинге этого и не требуется. Достаточно того, чтобы относительно небольшая выборка (от нескольких сотен до нескольких тысяч представителей) репрезентировала (выразила) мнение генеральной совокупности. Как такое возможно? На каком основании можно распространять данные, полученные от небольшой группы людей, на существенно (в десятки и сотни раз) большую группу? На основании гипотезы о том, что на поведение, знания, отношение потребителей к компании, товару, услуге или отдельных их компонентов оказывают влияние социально-демографические характеристики самих потребителей.
Иными словами, большинство представителей четко определенной социально-демографический группы будут сходным образом реагировать на внешние, в данном случае — рыночные стимулы: товар, цену, упаковку, рекламу и т. д. Нет никакой необходимости опрашивать всех представителей этой группы, поскольку ее мнение (с допустимой погрешностью) может представить (репрезентировать) небольшая выборка из ее представителей.
Способы построения выборки
Существуют две группы методов построения выборки, в той или иной степени реализующих репрезентацию мнений и позиций генеральной совокупности: вероятностные и детерминированные.
Первая группа методов (вероятностные) базируется на использовании теории вероятности. В основе ее применения лежит постулат, что репрезентация будет достигнута в случае, если каждой единице генеральной совокупности обеспечено равновероятное попадание в выборку. Например, если генеральной совокупностью является все взрослое (16-85 лет) население города (200 тыс. человек), то каждому жителю должна быть обеспечена вероятность стать участником исследования(попасть в выборку), равная 1 / 200 000. В противном случае выборка будет не случайной, а смещенной, т. е. менее репрезентативной.
Реализовать это можно в случае, если все элементы генеральной совокупности могут быть тем или иным образом пронумерованы, а затем эти номера будут выбраны в определенной последовательности — «по воле случая». Например, в Москве около 2 500 средних школ, каждая из которых имеет свой номер. Мы могли бы выбрать наугад 100 номеров и провести опрос 100 директоров (завучей, учителей физики, классных руководителей 11-х классов и т. п.) в этих школах.
Эти 100 номеров мы можем выбрать с помощью таблицы или «генератора случайных чисел» (есть такая специальная компьютерная программа), а также с помощью «барабана» но принципу того, как это делается при проведении лотереи. Такие способы построения выборки называются «простой случайной выборкой». Каждый ее элемент отбирается независимо и имеет равную вероятность попасть в выборку.
Мы могли бы выбрать наугад любое число от 1 до 25, например — 12, а затем взять в выборку школы с номерами: 12, 37, 62, 87, 112, 137 и т. д. Такой метод построения называемся «систематической выборкой», первый элемент которой выбирается произвольно, а затем выбирают каждый i-й элемент.
Мы также могли бы сначала разделить эти школы на несколько страт (возможно, и пересекающихся), например, на школы физико-математические, спортивные, лингвистические и гуманитарные, а затем произвести случайную или систематическую выборку (по 20-30 школ) из каждой страты. Такой метод построения называется «стратифицированной выборкой».
Разновидностью стратифицированной выборки является «маршрутная выборка», суть реализации которой состоит в следующем. Город делится на 20-40 «секторов» по числу интервьюеров, задействованных и исследовании. Каждый интервьюер получает один сектор, маршрут обследования «своего» сектора и инструкцию по реализации простой случайной выборки. Например такую: «Начать обход с улицы Баумана, с дома № 2, третьего подъезда, второго этажа сверху, первой квартиры слева. Затем — дом № 4, второй подъезд, третий этаж, вторая квартира справа… Потом — переулок Комсомольский, нечетная сторона… Потом — тупик Коммунизма… и т. д.»
Наконец, мы могли бы разделить генеральную совокупность на непересекающиеся кластеры, к примеру, по муниципальным районам (их в Москве 125, и в каждом в среднем по 20 школ). Затем случайным образом выбрать пять районов и произвести обследование всех школ данного муниципального района. Такой метод построения называется «кластерной выборкой».
Тем не менее у вероятностных методов построения выборки есть один весьма существенный недостаток. Каждый из них исходит из предположения о том, что все элементы генеральной совокупности являются равнодоступными: и в «техническом» смысле (у всех есть телефон для телефонного опроса или доступ в Интернет), и в «психологическом», т. е. все респонденты с примерно равной вероятностью согласятся или откажутся принимать участие в исследовании. Однако это не так.
Граждане с относительно высокими доходами менее доступны для исследователей, чем те, чьи доходы невысоки. И нет никакой силы, которая могла бы заставить этих люден отвечать им вопросы социологов или маркетологов. Поэтому все выборки всегда смещены в сторону средне- и малообеспеченных групп населения. Во всех без исключения странах мира.
Менее образованные граждане идут на контакт с социологами менее охотно, чем лица с высшим образованием. Поэтому в большинстве выборок доля хорошо образованных граждан как правило существенно выше, чем в генеральной совокупности.
Никто из сотрудников исследовательских компаний не желает общаться с бомжами, алкоголиками, наркоманами, психо- и социопатами и прочими маргиналами. У руководителя исследования нет решительно никаких возможностей заставить своих сотрудников делать это. А между прочим, к этим группам в России по взвешенным оценкам относится от 12 до 15% жителей. Следовательно, любая выборка смещена в сторону «вменяемых» граждан.
Некоторые граждане боятся отвечать на вопросы, даже самые невинные. Таких людей немного, но они есть. А вот способов заставить их участвовать в опросе нет.
Наконец, есть люди, которые просто не желают участвовать в исследовании. У них есть время, они ничего не боятся, они все понимают, но на вопросы отвечать отказываются. И точка.
Таким образом, все выборки в маркетинге и социологии являются смещенными в сторону средне- и малообеспеченных, более образованных, контактных и вменяемых граждан. Они и репрезентируют общее мнение генеральной совокупности. Все исследователи рынка прекрасно это знают.
Преодолеть наложенные выше проблемы можно с помощью метода «квот», относящегося к детерминированным методам, при котором априори обеспечивается пропорциональное представительство носителей существенных признаков (пол, возраст, доход, образование и т. п.) генеральной совокупности в выборке.
Это наиболее эффективный, на наш взгляд, метод проведения массовых опросов. При его использовании существенно облегчается задача поиска корреляционных связей, сравнения различных типов (групп) потребителей между собой и экстраполяции выявленных закономерностей на генеральную совокупность.
Единственная, но весьма существенная трудность при реализации него метода состоит в том, что не всегда доподлинно известно распределение всех важных параметров в самой генеральной совокупности. В этом случае исследователь или консультант исследовательского проекта должен взять на себя смелость распределить квоты по своему усмотрению, в соответствии со своим видением, пониманием рынка.
Задача достижения строгой репрезентативности не всегда является важной. Иногда целесообразно воспользоваться существенно более простыми в реализации детерминированными методами:
- нерепрезентативным, или произвольным, когда опрашивают того, кто «попался под руку» интервьюеру и согласился участвовать в опросе. Естественно, этот метод дает крайне ненадежные результаты. А вдруг под руку попадется рота солдат или команда баскетболисток! Однако его использование допустимо в исследованиях, носящих поисковый характер, не требующих большой точности, при проведении «пилотажа» анкеты. «Произвольность» можно компенсировать большим объемом выборки, из которой затем можно будет попробовать отобрать необходимое число «подходящих» анкет и составить уже из них репрезентативную в каких-то отношениях выборку;
- поверхностным — когда отбор осуществляется по самым общим признакам, задаваемым исследователем интервьюерам в виде не очень строгого задания;
- «воронки» — когда сначала отбираются наиболее «контактные», а затем среди них — наиболее «компетентные», подходящие респонденты;
- «концентрации» — на представителях отдельных, сопоставимых сегментов рынка, среди которых проводят «сплошной» опрос. Например, школьный 11 «А» класс может представлять всех старшеклассников школы или даже города как «обычный», «типичный класс»;
- «снежного кома» — когда начальная группа подбирается случайным образом, а дальнейший отбор ведется из кандидатов, указанных первыми респондентами, и т. д.
Достоверность и погрешности измерений
Под «достоверностью», уровнем достоверности понимают показатель вероятности того, что истинное значение изучаемого параметра генеральной совокупности попадет в доверительный интервал. Чем выше задаваемый уровень достоверности, тем больше должна быть выборка. Под доверительным интервалом понимают диапазон, в который попадет истинное значение изучаемого параметра генеральной совокупности при данном уровне достоверности. Чем он меньше, тем больше должна быть выборка.
К примеру, общероссийская городская выборка (14-65 лет) в 1 200 респондентов имеет доверительный интервал 4 процентных пункта при уровне достоверности 0,95. При ее проведении 15% участников опроса заявили, что за последние три месяца были в кинотеатре хотя бы один раз.
Эти данные позволяют нам утверждать с заданным уровнем достоверности, что от 11 до 19% жителей российских городов в возрасте от 14 до 65 лет были в кинотеатре хотя бы один раз за последние три месяца. Иными словами, можно сказать, что все значения между 11 и 19% в данном случае находятся в пределах «допустимой статистической погрешности». Если бы мы хотели задать доверительный интервал в 2 процентных пункта, то выборку (при прочих равных условиях) пришлось бы увеличить примерно в четыре раза.
Со стороны уровня достоверности эти данные означают, что если бы было проведено 100 независимых измерении (опросов) по 1200 респондентов в каждом, то в 95 из них значение доли ответов на вопрос о посещении кинотеатра не вышло бы за пределы доверительного интервала (в этом конкретном случае — 11-19%). А в пяти исследованиях или бы получены значения, выходящие за пределы доверительного интервала. Если бы нас устраивала достоверность на уровне 0,9, то опросить можно было бы 200 человек. Если нам нужна достоверность на уровне 0,99, то пришлось бы опросить более 10 тыс. человек.
Оптимальный размер выборки
Вот одна из формул расчета необходимого объема выборки, используемая при известном среднем отклонении (дисперсии) и заданных уровнях достоверности и точности:
N = (g2 * z2) / d2
где: N — искомый объем выборки; g — дисперсия признака, ожидаемое среднее отклонение получаемых результатов от ожидаемого среднего значения; z — коэффициент уровня достоверности (2 — для 0,95, 3 — для 0,99); d — уровень точности.
Допустим, мы изучаем поведение покупателей в продовольственном магазине, в частности, мы хотим определить среднюю сумму чека. Из бесед с владельцем магазина мы узнаем, что она может быть в районе 500-700 руб., а среднее отклонение (g) может составить 200 руб. В ходе опроса мы хотели бы определить среднее значение с точностью (d) до 20 руб. при уровне достоверности (z) в 0,95. Подставляем значения формулу и получаем:
40000 * 4 / 400 = 400.
То есть нам достаточно опросить 400 покупателей. Если бы мы хотели узнать среднюю сумму чека с точностью до 10 руб.. то нам пришлось бы опросить 1600 покупателей. Если бы при этом мы хотели получить уровень достоверности в 0,99, то количество покупателей, которых необходимо опросить, составило бы 3 500 человек. И наоборот: если нас устроила бы точность ±50 руб., то нам достаточно было бы опросить в заданных условиях всего 65 человек.
Практическое использование этой и других формул, которые здесь не будут приводиться, весьма затруднено следующими обстоятельствами:
- Что делать, если мы не знаем даже приблизительно «ожидаемую среднюю» и среднюю дисперсию признака?
- Что делать, если в анкете у нас 10 вопросов, по которым ожидаются различные средние, с различными средними дисперсиями?
- Как быть в случае использования номинальных шкал?
- Как быть в случае, если один вопрос предполагает два или три варианта ответа и т. д. и т. п.?
- Для простых альтернативных вопросов по принципу «да/нет» используются одни формулы, для более сложных — другие.
- Формулы необходимо корректировать в зависимости от количества столбцов в таблице «факторных распределении», а также в зависимости от распределения ответов (10 на 90 — это одно, а 45 на 55 — совсем другое дело).
- Одни формулы учитывают размер генеральной совокупности, а другие (как приведенная выше) — нет. Есть много иных нюансов.
На практике сначала определяют количество респондентов, которое исследователи предполагают опросить с учетом временных и финансовых ограничений, задают уровень достоверности (обычно — 0,95), а затем уже рассчитывают доверительный интервал.
Определение необходимого и достаточного объема выборки происходит на основе опыта и неформальных «конвенций» исследователей между собой. Считается, и это многократно проверено на практике, что опрос 30-50 представителей конкретной, «узкой» социально-демографической группы населения, например «ярославских замужних женщин в возрасте 30-45 лет, имеющих одного ребенка, высшее образование и совокупный семейный доход в пределах от 1 500 до 3 000 долл. в месяц», можно распространять на всю эту группу, и допустимая ошибка (доверительный интервал) не превысит 4 процентных пунктов при уровне достоверности около 0,95.
Однако полученные данные нельзя распространять, например, на незамужних женщин того же возраста, имеющих такой же доход и уровень образования. А также на женщин, имеющих иной доход, возраст или уровень образования. И уж тем более — на мужчин.
Таким образом, если в задачу исследователя входит получение информации о мнениях, знаниях, поведении или отношении к некой проблеме всех ярославских женщин, и при этом все перечисленные выше социально-демографические факторы являются значимыми, необходимо построить такую выборку, в которой были бы представлены все «узко определенные» группы. В данном случае — две группы по семейному положению, три — по наличию и количеству детей, три возрастные, три доходные, две образовательные. Итого 108 групп, в каждой из которых должно быть не менее 30 представительниц. Всего — более 3 000 респондентов.
На самом деле едва ли найдется вопрос или проблема, на которые все пять факторов будут оказывать взаимное перекрестное воздействие. В большинстве случаев вполне можно было бы обойтись опросом 400-600 респонденток, а затем провести попарный (а не перекрестный) факторный анализ. То есть отдельно исследовать влияние факторов «возраст», «образование», «доход», «семейное положение», «дети». При этом выборка каждый раз разбивалась бы на две-три группы, наполнение которых было бы не меньше 100-150 респондентов.
Репрезентативная выборка, представляющая все население России, должна состоять из 3 600-9 000 человек и 180 групп (два пола, три возраста, два образовательных уровня, три доходные группы, пять типов поселений). Доверительный интервал будет в пределах ±3 процентных пункта. Это означает, что, к примеру, если 30% (12% или 45%) наших респондентов заявили, что регулярно употребляют в пищу майонез, то долю потребителей майонеза в России можно оценить в 27-33% (9-15 или 42-48% соответственно).
Размер выборки практически не зависит от размера генеральной совокупности. И в мегаполисе с населением более миллиона человек, и в уездном городе с населением в 35 тыс. человек для построения выборки, репрезентативной по одинаковому числу параметров, потребуется опросить одинаковое число респондентов.
От чего действительно зависит размер выборки — так это от числа параметров, по которым мы желаем добиться репрезентативности. Если нас устраивает репрезентативность только по полу и возрасту, то выборки в 400 человек в одном населенном пункте будет более чем достаточно. Если параметров три, количество респондентов придется увеличить до 600. Добиться репрезентативности выборки одновременно по пяти параметрам: полу, возрасту, доходу, образованию, сфере профессиональной деятельности — можно лишь на выборке из 1 000 — 1 200 человек в одном населенном пункте.
Изучите полный цикл маркетинговых исследований в практическом курсе «Маркетинговые исследования»:

Выборочный метод: определение и истоки
Задача построения выборки возникает
всякий раз, когда необходимо собрать
информацию о некоторой группе или
большой совокупности людей. Выборку в
той или иной форме используют в
ориентированных на «жесткие»
статистические методы опросах, в
исследованиях политических и культурных
элит и даже при отборе «случаев» для
включенного наблюдения и качественного
анализа.
Статистические (или квазистатистические)
обследования населения и ресурсов,
судя по всему, зародились одновременно
с первыми формами централизованной
социальной и политической организации:
развитые аграрные общества и древние
города-государства нуждались в такой
информации и использовали ее при решении
разнообразнейших управленческих задач
—от фискальной политики до
строительства общественных бань. Эти
обследования иногда принимали форму
сплошных переписей населения. (Об одной
такой переписи, имевшей, правда, самые
печальные последствия, рассказывает
нам книга пророка Самуила: когда
царь Давид (Xв. до н. э.)
осуществил перепись населения древнего
Израиля, в стране разразилась страшная
эпидемия (2Цар.
24).Однако значительно чаще приходилось
довольствоваться сведениями о какой-то
части совокупности: об урожайности
судили по пробному обмолоту, о партии
товара —по образцу,
а о прихожанах —по их
духовному наставнику.
Выборка —это
подмножество заданной совокупности
(популяции), позволяющее делать более
или менее точные выводы относительно
совокупности в целом. Зачем нужно
строить выборки? Прежде всего, из
практических соображений, так как
выборкаэкономит силы и средстваисследователей. Проведение полномасштабной
переписи или сплошного опроса населения
требует значительных финансовых и
трудовых затрат, которые к тому же могут
пропасть впустую в случае, если в
разработке методики исследования были
допущены принципиальные просчеты.
Другая причина заинтересованности в
выборках связана с тем, что выборочная
процедура представляет собой удобную
и экономичную форму индуктивного
вывода1.Третья
причина заключается в том, что эта
процедура реализует фундаментальныйпринцип рандомизации,т. е. случайного
отбора (от англ.random—
случайный, выбранный наугад).
Представление о том, что отбор наблюдений
должен носить случайный, непредумышленный
характер, в общем соответствует нашему
интуитивному знанию об условиях
вынесения объективного и непредвзятого
суждения. Однако стро-
1Напомним, что под индуктивным
выводом обычно понимают рассуждение
по схеме «от частных наблюдений
—к общей эмпирической закономерности».
гая, т. е. математико-статистическая,
теория случайной выборки вплоть до
конца XIX —начала
XXвв. не пользовалась популярностью
в среде профессиональных статистиков.
Многим исследователям казалось, что в
основе отбора должна лежать не «игра
случая», а поиск типичных, характерных
наблюдений. Это убеждение препятствовало
применению в массовых обследованиях
методов теории вероятности, достигшей
высочайшего уровня развития уже в
XVIII— первой половине XIXвв. Применимость выборочного метода
для изучения случайно распределенных
признаков, например дохода или размера
семьи, была впервые обоснована в работах
норвежца А. Киэра, англичан А. Боули и
К. Пирсона, а также русского статистика
А. И. Чупрова2.
Следующим принципиально важным шагом
в развитии выборочного метода стала
осуществленная Р. Фишером разработка
техники рандомизациив эксперименте
и выборочном наблюдении3. О роли
рандомизации в планировании эксперимента
говорится в главе 4.Что
же касается выборочного обследования,
то оно часто используется как «замена»
экспериментального метода. Нельзя
провести эксперимент, в котором людям
в случайном порядке присваиваются
определенные значения переменных «пол»
или «цвет кожи». Однако применение
выборочного метода и статистического
анализа, как мы увидим в дальнейшем,
позволяет справляться с этими ограничениями
и делать выводы о взаимосвязях между
самыми разными переменными, включая
вышеупомянутые. Но для того, чтобы такие
выводы были обоснованы, нужно устранить
любое систематическое влияние
«посторонних», смешивающих факторов
на изучаемые переменные. Единственным
средством для достижения этой цели
является абсолютно случайный характер
отбора наблюдений. Лишьравенство
шансов попадания в выборку для каждого
наблюдения,т. е. отбор «наугад»,
гарантирует от намеренных или ненамеренных
искажений. Пусть, например, в ходе опроса
мы изучаем влияние пола и рода занятий
респондента на его отношение к
планированию семьи и ограничению
рождаемости. Если используемая нами
выборочная процедура ведет к тому,
что работающие женщины имеют несколько
меньшие шансы стать респондентами, чем
домохозяйки и пенсионерки (последних,
как известно, проще застать дома), наши
результаты наверняка окажутся смещенными.
Поэтому наилучшей моделью отбора
считается вероятностная, или случайная,
выборка4,в которой
строго соблюдаетсяпринцип равенства
шансов попадания в выборку и для всех
единиц изучаемой совокупности, и для
любых последовательностей таких
единиц.
Именно с рассмотрения разных подходов
к построению вероятностной выборки
мы и начнем наше обсуждение, чтобы в
дальнейшем перейти к не столь совершенным
видам целевого,т. е. не основанного
на вероятностях отбора, и их роли в
практике социологических исследований.
Выше мы определили, что такое выборка.
Сейчас нам необходимо строго определить
еще несколько элементарных понятий.
Переписьюназывают процедуру
2Более детальные
сведения о развитии выборочного метода
можно найти, в частности, в интересной
и доступной книге:Дружинин Н. К.Выборочное наблюдение и эксперимент.
М.: Статистика,
1979.
3 См.:
Fisher R. A.
The Design of Experiment. 3rd
ed. L.: Oliver &
Boyd, 1942.
4В дальнейшем мы
будем использовать термины «случайная
выборка» и «вероятностная выборка»
как взаимозаменяемые.
сбора информации о каждом члене изучаемой
группы или популяции. Все члены
интересующей исследователя группы
(популяции) составляют генеральную
совокупность. Выборочная процедураобеспечивает обоснованность и
«законность» выводов о генеральной
совокупности, сделанных на основании
небольшой выборки.
Типы вероятностных выборок и их
реализация
Первым шагом в построении любой модели
отбора, включая вероятностную, является
определение генеральной совокупности.Решение этой задачи далеко не всегда
бывает очевидным. Прежде всего, генеральная
совокупность, т. е. множество интересующих
социолога объектов исследования, может
быть задана и описана лишь на основе
каких-то содержательных представлений.
Если, например, нас интересуют политические
пристрастия избирателей, естественно
включить в генеральную совокупность
лишь тех, кто уже достиг 18-летнего
возраста. Изучение факторов, влияющих
на формирование семейного бюджета
горожан, потребует иного определения
генеральной совокупности: интересующая
исследователя популяция в данном случае
будет состоять из городских семей.
Полезно также помнить о том, что идеальная
генеральная совокупность,задаваемая
теоретическим описанием предмета
исследования, почти никогда не будет
полностью совпадать среальной
совокупностью.Реальная генеральная
совокупность подвержена постоянным
колебаниям: «взрослое население города
Воронежа на 00час
15ноября 1996года»
будет отличаться от «взрослого населения
города Воронежа на 00час
16ноября 1996года».
Некоторые люди за день уедут из города,
попадут в больницу, некоторые
—вернутся домой из командировки
и т. п. Поэтому столь важно при описании
изучавшейся в исследовании генеральной
совокупности указывать время и место
проведения исследования. Следует
также помнить, что идеальная генеральная
совокупность — это
теоретическая абстракция, более или
менее совпадающая с реальной совокупностью.
Выборка осуществляется из реальной
популяции, переход от которой к
идеальной совокупности обеспечивается
не только правилами статистического
вывода, но и некоторой долей теоретического
воображения.
Если исследователь построил выборку,
которая представляет интересующую его
совокупность с приемлемой степенью
точности, то полученная выборка является
репрезентативной(представительной).
В противоположном случае можно говорить
о наличии существеннойвыборочной
ошибки.Более строго выборочную ошибку
определяют какрасхождение между
оценкой некоторого показателя, получаемой
на основании исследования выборки, и
истинным значением этого показателя
в генеральной совокупности.
К счастью, существуют точные методы для
учета и оценки случайной выборочной
ошибки, связанной с не носящими
систематического характера колебаниями
изучаемой переменной в разных подвыборках
из одной и той же генеральной
совокупности. Подробнее эти методы мы
будем обсуждать ниже (в частности,
формулы для расчета случайной ошибки
выборки будут рассмотрены в главе
8).Значительно более серьезную
проблему создает наличиесистематических
смещений,возникающих в результатенарушения случайного характера
выборочной процедуры.Результаты
такого «не вполне случайного» отбо-
paмогут выглядеть более
или менее правдоподобно, однако сами
по себе они никогда не позволят обнаружить
смещение или оценить его величину.
Последнее утверждение можно
проиллюстрировать на примере классического
опыта с рулеткой. Если нам скажут, что
вчера десять раз подряд выпало «красное»,
мы сможем назвать такую серию событий
крайне маловероятной. Однако этот
субъективно подозрительный результат
сам по себе не дает оснований для каких-то
суждений о величине и характере ошибок,
порождаемых выборочной процедурой, т.
е. об исправности механизма самой
рулетки.
Систематическая ошибка выборки не
обязательно является результатом злого
умысла. Например, в США во время войны
во Вьетнаме (до введения контрактной
системы набора на армейскую службу)
правительство проводило специальные
лотереи для отбора призывников. Фактически
случайно отбирались даты рождения: все
годные к несению строевой службы юноши,
родившиеся в день, который определялся
в ходе такого «розыгрыша», призывались
в армию. В 1970г. результаты
отбора были подвергнуты острой критике.
Проведенное специальной комиссией
расследование показало, что в выборочной
процедуре действительно присутствовало
смещение. Билетики с напечатанными
датами были заключены в специальные
капсулы, которые затем опускали в
лотерейный барабан в порядке следования
месяцев, начиная с января. Из-за
недостаточного перемешивания капсул
внутри барабана капсулы с ноябрьскими
и декабрьскими датами концентрировались
в верхней части и, естественно, выпадали
с заметно большей частотой5.
Самым знаменитым примером смещенной
выборочной процедуры в истории социологии
стал предвыборный опрос, проведенный
американским журналом «TheLiteraryDigest»
в 1936г. Результаты опроса
показывали, что Ф. Д. Рузвельт получит
40,9%голосов и уступит президентское
кресло республиканцу А. Ф. Лэндону. В
действительности Рузвельт получил
60,2%голосов избирателей. Расхождение
в 19,3%в значительной
степени объяснялось характером выборочной
процедуры. Дело в том, что на практикедля построения любой выборки используют
какой-то список всех членов изучаемой
совокупности, называемый основой
выборки.В опросе, проведенном «TheLiteraryDigest»,
в качестве основы выборки использовались
телефонные справочники, а также
регистрационные списки владельцев
автомобилей6. Во второй половине
1930-х гг. такие списки включали в себя
почти исключительно представителей
экономически благополучных классов.
Беднейшие слои населения, избирательная
активность которых, кстати, существенно
увеличилась в годы Великой Депрессии,
оказались недостаточно представлены
в выборке, что и послужило причиной
столь значительной ошибки. (Интересно
отметить, что объем выборки в описываемом
случае был просто огромным
—свыше двух миллионов человек!)
Существует несколько типов вероятностной
выборки, различающихся характером
выборочной процедуры. Мы рассмотрим
лишь пять: простую случайную,
систематическую, стратифицированную,
кластерную и многоступенчатую.
Процедура построения простой случайной
выборкивключает в себя следующие
шаги.
5
RouncefieldM., HolmesP.
Practical Statistics. Basingstoke: Macmillan Education Ltd,
1989. P. 122.
6 Galiup
G. A. Guide to Public Opinion Polls.
Princeton: Princeton University Press,1948.
|
Таблица |
|||||||||||
|
Номер |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
98 |
08 |
62 |
48 |
26 |
45 |
24 |
02 |
84 |
04 |
|
|
2 |
33 |
18 |
51 |
62 |
32 |
41 |
94 |
15 |
09 |
49 |
|
|
3 |
80 |
95 |
10 |
04 |
06 |
96 |
38 |
27 |
07 |
74 |
|
|
4 |
79 |
75 |
24 |
91 |
40 |
71 |
96 |
12 |
82 |
96 |
|
|
5 |
18 |
63 |
33 |
25 |
37 |
98 |
14 |
50 |
65 |
71 |
|
|
6 |
74 |
02 |
94 |
39 |
02 |
77 |
.55 |
73 |
22 |
70 |
|
|
7 |
54 |
17 |
84 |
56 |
11 |
80 |
99 |
33 |
71 |
43 |
|
|
8 |
11. |
66 |
44 |
98 |
83 |
52 |
07 |
98 |
48 |
27 |
|
|
9 |
48 |
32 |
47 |
79 |
28 |
31 |
24 |
96 |
47 |
10 |
|
|
10 |
69 |
07 |
49 |
41 |
38 |
87 |
63 |
79 |
19 |
76 |
|
|
11 |
09 |
18 |
82 |
00 |
97 |
32 |
82 |
53 |
95 |
27 |
|
|
12 |
90 |
04 |
58 |
54 |
97 |
51 |
98 |
15 |
06 |
54 |
|
|
13 |
73 |
18 |
95 |
02 |
07 |
47 |
67 |
72 |
52 |
69 |
|
|
14 |
75 |
76 |
87 |
64 |
90 |
220 |
97 |
18 |
17 |
49 |
|
|
15 |
67 |
35 |
86 |
33 |
26 |
50 |
10 |
39 |
42 |
61 |
Во-первых, нужно получить полный список
членов генеральной совокупности и
пронумеровать этот список. Такой список,
напомним, называется основой выборки.
Во-вторых, следует определить предполагаемый
объем выборки,т. е. ожидаемое
число опрошенных.
В-третьих,нужно извлечь изтаблицы
случайных чисел(см.табл.
7.7)столько чисел, сколько нам
требуется выборочных единиц. Если в
выборке должно оказаться
100человек, из таблицы берут
100случайных чисел.
В-четвертых,нужно выбрать из
списка-основы (см. выше) те наблюдения,
номера которых соответствуют
выписанным случайным числам8.
Прежде чем мы перейдем к обсуждению
возникающих на этом пути практических
затруднений, рассмотрим упрощенный
пример реализации описанной процедуры.
Пусть нам предстоит построить случайную
выборку объемом в 12человек
из совокупности, содержащей
60членов. Можно предположить, что
мы хотим оценить калорийность ежедневного
рациона питания 60студентов-социологов, обучающихся на
втором курсе университета, чтобы
исследовать возможное влияние
энергетической ценности рациона на
академическую успеваемость. Для этого
можно пронаблюдать за питанием небольшой
выборки, состоящей из двенадцати
студентов. В качестве основы выборки
мы используем список всех60студентов. Присвоим всем студентам в
списке двузначные номера—от
«01»
7 Составлено
на основе
таблицы: Appendix С:
Random Numbers // Zeiler R. A., Carmines
E. G. Statistical Analysis of Social
Data. Chicago: Rand McNally, 1978.
P. 364—367.
8Здесь и далее речь
идет о случайнойбезвозвратнойвыборке, так как выборка свозвращениемотобранной единицы в совокупность на
каждом шаге отбора не очень удобна
практически (хотя и обладает рядом
статистических преимуществ).
до «60» (если бы максимальный номер в
списке был трехзначным, мы бы присваивали
трехзначные номера, используя нули в
отсутствующих разрядах—
например, «067», «003»). Далее нам
предстоит последовательно выписать
двенадцать двузначных чисел из
таблицы случайных чисел (см.табл.
7.7).Отметим, что таблицы случайных
чисел фактически состоят изслучайных
цифр, которые обычно сгруппированы
для удобства в блоки, состоящие из
двузначных либо пятизначных чисел.
Объединение цифр в последовательности
и блоки условно и не имеет особого
статистического смысла. Поэтому в
случаях, когда нужны, например трехзначные
числа, а таблица состоит из пятизначных,
пользуются каким-то несложным правилом,
скажем, используют только три первые
цифры каждого пятизначного числа, а
оставшиеся две игнорируют. Соответственно
двузначные числа можно объединять.
Чтобы решить, с какого места в таблице
начинать отсчет номеров, достаточно
задаться произвольными номерами строки
и столбца. В нашем примере мы начнем
с пересечения второй строки и третьего
столбца. Первым номером в нашем списке
окажется 51.Далее можно
двигаться по любому правилу: подряд,
через строку, через два столбца и т. п.
Мы будем выписывать нужные нам двенадцать
двузначных номеров подряд по строке,
двигаясь по горизонтали и переходя при
необходимости на следующую строку.
Если при этом будут попадаться числа,
превосходящие по величине самый большой
номер в нашем списке (60),мы будем их пропускать. То же относится
и к повторяющимся числам. В результате
мы получим последовательность:
51, 32, 41, 15, 09, 49, 10, 04, 06, 38, 27, 07.
Нам остается выписать из списка-основы
фамилии, стоящие под этими номерами.
Если вы располагаете персональным
компьютером, то вместо таблицы можно
воспользоваться «генератором случайных
чисел», имеющимся в большинстве
статистических программ.
Простая случайная выборка —это не только наглядное воплощение идеи
случайного отбора, но и своего родаэталон,с которым сравниваются
другие вероятностные процедуры.
Здесь необходимо заметить, что вопреки
часто высказываемому и неверному
мнению простую случайную выборку не
следует рассматривать как самую
примитивную форму вероятностного
отбора. Напротив, более сложные модели
случайных выборок используют в тех
случаях, когда простую нельзя применить
из-за практических или финансовых
ограничений. О качестве этих более
сложных процедур отбора также судят
посредством сравнения с простой случайной
выборкой.
Самые очевидные ограничения для
использования простой выборки возникают
в случае большого объема генеральной
совокупности. Прежде всего исследователь
сталкивается с проблемами поиска полной
и несмещенной основы выборки.При обследованиях небольших групп и
первичных коллективов эти проблемы
обычно легко решаются: достаточно
воспользоваться членскими списками,
списками личного состава и т. п., внеся
в них необходимые уточнения. В
широкомасштабных опросах общественного
мнения и социологических обследованиях
чаще применяют другие основы:
переписные листы, списки избирателей,
домовые книги, карточки паспортных
столов милиции (а также картотеки РЭУ,
ДЭЗ и т. п.), нехозяйственные книги
сельских советов. Все эти «готовые»
основы выборки обладают определенными
преимуществами и не-
достатками9. Решая практическую
задачу планирования выборочного
исследования, социолог обычно
оценивает возможные основы по нескольким
параметрам.
Во-первых,списки, пригодные для
составления основы выборки, могут
храниться либо централизованно, либо
децентрализованно, «вразброс», в
различных территориальных органах
власти, статистических учреждениях и
т. п. Естественно, что в первом случае
затраты на получение доступа к основе
будут значительно ниже, чем во втором.
Фактически при децентрализованном
хранении исследователь должен
самостоятельно составить единый
список-основу, собрав необходимые данные
в результате обхода (или объезда) всех
соответствующих институций.
Во-вторых,используемые в качестве
основы выборки списки могут обладать
различной степенью точности. Точность
списка, в свою очередь, зависит от его
полноты, частоты его обновления. Эти
качества (полнота списка и высокая
частота его пересмотра) редко
встречаются одновременно. Как правило,самыми полными оказываются именно те
основы, которые реже всего обновляются.
Таковы, конечно, данные переписей или
эпизодически составляемые именные
распределительные списки (типа списков
на получение приватизационных чеков).
К сожалению, чем больше времени отделяет
планируемое вами исследование от
последней переписи, тем больше вероятность
возникновения ошибок и смещений в основе
выборки.
Очень существенными достоинствами
обладают списки паспортных столов
милиции, жилищно-эксплуатационных
контор и других местных административных
органов.
Качество основы выборки оценивают уже
на стадии планирования исследования.
Особое внимание уделяют таким потенциальным
угрозам валидности, как неполнота
выборочной основы, «склеивание» единиц
отбора, «пустые» элементы в списке.
Онеполноте говорят в тех случаях,
когда список, используемый для
построения выборки, не содержит в себе
некоторые единицы, безусловно
относящиеся к целевой совокупности.
Например, списки жильцов могут не
содержать сведений о тех жильцах, которые
еще не зарегистрировались по новому
месту жительства. В некоторых случаях
проблему неполной основы можно решить
за счет использованиядополнительных
основ.В нашем примере со списками
жильцов такой дополнительной основой
могут стать «листки при-бытия-убытия»,
которые хранятся в паспортных столах
отделений милиции (с помощью последних
ведется учет прописки граждан). Примером
«склеивания» может служить ситуация,
когда генеральная совокупность,
определяемая объектом исследования,
состоит из индивидов, а реальной основой
отбора служит список квартир или
домовладений, содержащий лишь сведения
об ответственных квартиросъемщиках
либо о собственниках недвижимости.
«Пустые» элементы в основе выборки
встречаются в тех случаях, когда исходный
список содержит имена или адреса, за
которыми не стоят реально существующие
(или практически доступные) выборочные
единицы. Эта проблема часто возникает
9В отечественной
литературе сравнительный анализ разных
основ и их применения в конкретных
исследованиях осуществлен, например,
в книге:Арутюнян Ю. В., Дроби-жева Л.
М., Кондратьев В. С., Сусоколов А. А.Этносоциология: цели, методы и некоторые
результаты исследования. М.: Наука,
1984.Гл. IV.
при использовании устаревших списков,
содержащих информацию о временно
уехавших, выбывших, умерших и т. п.10
Описанные выше трудности составления
валидной,т. е. соответствующей
объекту исследования (целевой
совокупности), основы выборки носят и
статистический, и «экономический»
характер. Довольно часто исследователь
сталкивается с ситуацией, когда
временные и финансовые затраты на
осуществление простой случайной выборки
становятся неприемлемо высокими.
Наиболее разумным выходом здесь
является использование других,
«компромиссных», процедур случайного
отбора.
Систематическаявыборка по качеству
часто приближается к простой случайной.
Систематическая выборка, как и простая
случайная, требует полного списка или
заданного упорядочения совокупности
(см. ниже). Техника осуществления
систематического отбора элементарна:
сначала случайным образом отбирается
первая единица, затем отбору подлежит
каждыйk-й.элемент.
Числоkв данном случае
называютшагом отбора.Можно,
например, отбирать каждый 25-й или каждый
200-й элемент. Чтобы определить шаг отбора,
нужно поделить известный объем
генеральной совокупности(N)на предполагаемый объем выборки(п).
Пусть, например, нужно отобрать
200человек из 20000владельцев телефонов:
1)определим шаг отбора:N/n
= 20000 : 200 = 100;
2)с помощью таблицы
случайных чисел найдем первую выборочную
единицу. Если, скажем, выпал номер
«053», то из списка владельцев телефонов
выпишем того, кто значится под этим
номером;
3)с установленным шагом
отбираем номера: 153, 253, 353, 453и т. д. до исчерпания списка.
Иногда генеральная совокупность (и
соответственно основа выборки) слишком
велика либо исследователю известен не
полный список, а лишь правило упорядочения
элементовв генеральной совокупности.
Предположим, что мы хотим составить
представление о весе и формате книг,
содержащихся в некой библиотеке, при
том, что мы не располагаем полным
каталогом, а лишь видим, как книги
расставлены на стеллажах. При условии,
что объем библиотечного собрания нам
приблизительно известен, мы можем
воспользоваться процедурой
систематического отбора и отобрать,
скажем, каждую 55-ю книгу. Очень важно
отобрать «стартовую» единицу сугубо
случайным образом. Именно в этом пункте
кроется основная слабость систематического
отбора. Если в способе упорядочения
единиц совокупности имеет место некая
цикличность, т. е.неизвестная нам
«система»(систематический паттерн),
а случайность в выборе «старта» должным
образом не обеспечена, то полученная
выборка может также оказатьсясмещенной(если о систематическом
паттерне мы знаем заранее, то он не
представляет собой угрозы валидности
и может быть учтен в ходе отбора). Если
воспользоваться примером с отбором
книг в библиотеке, то легко представить
себе такую гипотетическую ситуацию:
исследователь выбирает в качестве
стартовой первуюкнигу на нижней
полке ближайшего стеллажа и далее
двигается с шагом 250единиц. Если на каждом стеллаже размещается
около 500книг, то
приблизительно половина его выборки
будет взята с нижних
10Подробнее об
источниках смещений в основе выборки
и некоторых способах борьбы со смещениями
см.:Kish L.Surveysampling.
N. Y.: J. Wiley,
1965. P. 53—59.
полок. Однако известно, что на нижних
полках многих библиотек нередко
размещают книги больших форматов
—художественные альбомы, атласы
и т. п. Если в нашем примере это правило
упорядочения будет соблюдено хотя бы
в половине случаев (т. е. половина нижних
полок будет отведена под «неформатные»
издания, под так называемые фолио), любые
выборочные оценки «направленности»
библиотечного собрания или формата
представленных в нем книг окажутся
невалидными.Аналогией примеру с
библиотечными книгами может служить
случай систематической выборки городских
квартир. Если в результате осуществляемого
непосредственно «в поле» интервьюерами
систематического отбора в выборке
будут сверхпредставлены квартиры,
расположенные на первых и последних
этажах, возникнет систематическая
выборочная ошибка. На первых и последних
этажах в российских городах часто живут
люди из групп, имеющих более низкий
социально-экономический статус и
соответственно ограниченные финансовые
ресурсы: квартиры, расположенные на
«крайних» этажах и соприкасающиеся с
системами коммунального водо- и
теплоснабжения, обычно стоят дешевле,
так как названные системы в России
традиционно являются источником
неприятностей и дисфункций в структуре
жизнеобеспечения.
Стратифицированный отбори
соответственно стратифицированная
выборка используются в тех случаях,
когда из каких-то содержательных
соображений важно обеспечить
представительность вероятностной
выборки по каким-то конкретнымважным
для исследовательских целей критериям.В литературе существует определенная
путаница вокруг проблемы стратификации
(«стра-та» —это социальная,
возрастная или иная группа, буквально
«слой»).
Применительно к стратифицированному
отбору часто высказывают все те неверные
и предрассудочные мнения, которые в
начале XXвека высказывались
относительно квотной выборки (см. ниже)
и ее воображаемых преимуществ перед
случайным отбором. В действительности
стратифицированный отбор имеет
определенные практические преимущества
до тех пор, пока сохраняется его
вероятностный, случайный характер. Как
только стратифицированная выборка
превращается в более или менее специально
отобранную квотную выборку, воспроизводящую
некоторые известные пропорции генеральной
совокупности (например, 51%женщин, 30%горожан и т.
п.), любые статистические, т. е. строгие,
оценки параметров генеральной совокупности
становятся невозможными.
Стратификацией, строго говоря, называют
процедуру, при которой отбор осуществляют
как бы из нескольких «параллельных»
подсовокупностей,заданных на одной
и той же генеральной совокупности. Это
абстрактное определение можно прояснить
с помощью примера. Пусть у нас есть
генеральная совокупность взрослых
горожан, относительно которой мы
располагаем какой-то существенной
с точки зрения исследовательских гипотез
информацией. Наличие такойпредварительной
информации —необходимое условие стратифицированного
отбора. Предположим, мы знаем, что в
генеральной совокупности60%рабочих и 40%служащих. Это
соотношение может оказаться весьма
существенным с точки зрения наших
исследовательских гипотез, если оно
задает одну изнезависимых переменных,как, например, при изучении влияния рода
занятий на частоту посещения футбольных
матчей. Даже при отсутствии значительной
систематической погрешности небольшие
смещения в реализации случайной
выборочной процедуры могут привести к
ситуации, когда в нашей конкретной
выборке соотношение рабочих и служащих
будет существенно
(на
5—7%)
отклоняться от ожидаемой «правильной»
пропорции, имеющей место в генеральной
совокупности (см. обсуждение нормальной
кривой и индуктивного статистического
вывода в гл.
8).
Соответственно под угрозой окажется
точность наших оценок взаимосвязи между
главной независимой переменной
(профессиональным статусом) и интересом
к футболу. Такого рода неточность может
быть устранена при использовании еще
одной случайной выборки из генеральной
совокупности, но здесь вступают в силу
экономические соображения, так как
исследовательский бюджет обычно
ограничен. В описанной ситуации
желательно заранее обеспечить
представленность обеих интересующих
нас групп, т. е. страт,
сохранив вероятностный характер отбора.
Этого можно добиться, если осуществить
некую независимую процедуру случайного
отбора для каждой социальной группы в
отдельности (в нашем примере для рабочих
и служащих) и затем
объединить
полученные случайные подвыборки в одну
(заметьте, что для нашего примера
объем подвыборки рабочих, в согласии с
заранее известной пропорцией, будет
в
1,5 раза
больше объема подвыборки служащих).
Полученная в результате выборка будет
и стратифицированной
(по профессиональному статусу), и
вероятностной.
На практике две
случайные процедуры отбора в
подвыборки-страты можно технически
объединить в одну, если мы располагаем
априорной информацией о принадлежности
каждой выборочной единицы к той или
иной страте. Для этого достаточно
вести параллельный отбор из списка-основы
в несколько подвы-борок (по числу страт).
Собственно выборочная процедура может
быть и простой
случайной,
и систематической
(соответственно мы получим либо простую,
либо систематическую стратифицированную
выборку).
Рассмотрим эту
процедуру на примере составления
систематической выборки населения,
стратифицированной по этнической
принадлежности. Пусть мы осуществляем
выборку взрослых жителей небольшого
промышленного центра, при этом
полученная выборка должна отражать
существующую этнодемографическую
ситуацию:
80% русских,
10% украинцев
и 10%
представителей других национальностей.
Основываясь на информации, хранящейся
в паспортных столах милиции (или на
избирательных списках), мы в идеальном
случае можем составить полный
список-основу, включающий
100000 известных
административным органам постоянных
жителей. Если предварительно мы
предполагаем включить в нашу выборку
около
1000 человек,
нам нужно отобрать из картотек паспортных
столов (или избирательных списков)
каждого сотого. То есть доля генеральной
совокупности f,
включенная в выборку, составит 1/100:
f =
объем выборки (n)
/ объем
целевой совокупности (N).
Выборка объемом в
1000 человек
будет включать в себя
800 русских,
100 украинцев
и
100
представителей других национальностей.
Причем шаг систематического отбора (К)
для всех трех подсовокупностей будет
равен 100.
