3.1. В зависимости
от способа представления продукции на
контроль применяются следующие методы
отбора единиц продукции в выборку:
отбор с применением
случайных чисел;
многоступенчатый
отбор;
отбор «вслепую»;
систематический
отбор.
3.2. Отбор
с применением случайных чисел
3.2.1. Данный метод
применяется для однородной продукции,
представленной на контроль способом
«ряд».
3.2.2. Метод отбора
с применением случайных чисел используется
и при всех остальных способах представления
однородной продукции (если это не ведет
к большим трудностям экономического
или технического порядка).
3.2.3. Метод предполагает
предварительную сплошную нумерацию
единиц продукции. Все номера должны
иметь одно и то же количество цифр.
Существующие номера с разным количеством
цифр следует в начале дополнять слева
нулями.
3.2.4. При методе
отбора единиц продукции в выборку с
применением случайных чисел используют:
таблицы случайных
чисел по СТ СЭВ 546-77;
карточки (числа в
урне) (справочное
приложение 1, пример 6).
3.3. Многоступенчатый
отбор
3.3.1. Метод
многоступенчатого отбора единиц
продукции применяют для однородной
продукции, представленной на контроль
в упаковке, т.е. в упаковочных единицах,
содержащих одинаковое количество единиц
продукции.
3.3.2. При многоступенчатом
отборе выборку образуют по ступеням и
единицы продукции в каждой ступени
отбирают случайным образом из единиц,
отобранных в предыдущей ступени.
3.3.3. Кроме объема
выборки, следует предварительно указывать
и количество упаковочных единиц
(первичных, вторичных и т.д.), выбранных
для составления выборки. Из этих
отобранных упаковочных единиц отбирается
выборка.
3.3.4. Выборку
составляют из примерно одинаковых
объемов продукции, взятых из отобранных
упаковочных единиц.
3.3.5. Если первичные
упаковочные единицы содержат вторичные
и т.д. упаковочные единицы, то сначала
отбирают первичную, затем вторичную и
т.д. упаковочные единицы. Допускается
единицы продукции паковать в первую
(вторую и т.д.) упаковочную единицу
россыпью.
3.3.6. Для упаковочных
единиц следует применять метод отбора
с применением случайных чисел. Если
продукция находится в «россыпи», то
следует применять метод «вслепую»
(справочное
приложение 1, пример 5).
3.4. Отбор
«вслепую» (метод наибольшей объективности)
3.4.1. Метод «вслепую»
применяется для продукции, представленной
на контроль россыпью, а также в том
случае, когда применение метода отбора
с применением случайных чисел технически
затруднительно или экономически
невыгодно.
3.4.2. Метод «вслепую»
не следует применять в тех случаях,
когда бракованные единицы продукции
можно определить органолептически.
3.4.3. В выборку
должны быть включены единицы продукции
из разных частей контролируемой партии.
3.4.4. Единицы
продукции следует отбирать независимо
от субъективных предположений контролера
относительно качества отбираемой
единицы продукции (справочное
приложение 1, пример 7).
3.5. Систематический
отбор
3.5.1. Метод
систематического отбора применяется
для продукции, представленной на контроль
в виде потока (справочное
приложение 1, пример 8).
3.5.2. Единицы
продукции следует отбирать через
определенный интервал времени или
количество единиц продукции. Например,
если выборка должна составить 5% от
контролируемой партии, то отбирают
каждую двадцатую единицу продукции.
Начало отсчета определяется случайным
образом, например с помощью таблиц
случайных чисел по СТ СЭВ 546-77.
3.5.3. Данным методом
можно образовать выборку, если имеется
определенный порядок следования единиц
продукции. При этом необходимо учитывать,
что в следующих одна за другой единицах
продукции значение контролируемого
параметра не должно меняться с той же
периодичностью, что и периодичность
отбора единиц в выборку.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Бизнес зачастую выпускает или продает множество видов продукции. Номенклатура может включать десятки, сотни и даже тысячи позиций.
Из месяца в месяц повторяется ситуация: склад заполнен. Но начальник отдела продаж докладывает, что нужных клиентам позиций недостаточно, хотя в прошлый раз пришлось списать просроченные товары. Получается, что компания заполняет склад излишками, которые не продаются, а того, что пользуется спросом, постоянно не хватает.
Эти проблемы знакомы многим бизнесменам. Руководители компаний часто не понимают, на какие товары или продукцию нужно обратить особое внимание.
Разобраться и понять, что приносит бизнесу основной доход, а от чего лучше отказаться, поможет ABC-XYZ-анализ.
Из этой статьи вы узнаете:
- ABC-анализ выделяет товары, которые приносят основной доход
- XYZ-анализ распределяет товары в зависимости от стабильности спроса
- Объединенный ABC-XYZ-анализ: как работать с каждой группой
- ABC-XYZ-анализ нужен практически любому бизнесу. Но у метода есть ограничения
ABC-анализ выделяет товары, которые приносят основной доход
Больше века назад итальянский экономист Вильфредо Парето сформулировал свой принцип: «20% усилий дают 80% результата». Это значит, что 20% товаров приносят 80% дохода. Бизнесу нужно провести анализ и найти эти 20%.
Для анализа удобно использовать Excel. Это универсальная программа — каждый руководитель может составить таблицы для расчета так, как ему удобно с учетом особенностей своего предприятия.
Чтобы найти ключевые товары, нужно следующее.
Во-первых, определить процент от выручки, который приносит каждая позиция. Для этого нужно разделить выручку по товару на общую выручку компании и умножить на 100%.
Например, ООО «Идея», небольшой мебельный магазин, продает шкафы, кровати, столы, стулья, полки и тумбочки. За месяц компания получает выручку в 33 687 рублей.
При этом шкаф для одежды приносит выручку в 7 368 рублей. Получается, что от общей выручки:
7 368 / 33 687 х 100% = 21,9%
Товарных позиций могут быть сотни и даже тысячи. Чтобы упростить анализ, можно рассчитывать процент не по каждой позиции отдельно, а по группам. Например, если бизнесмен торгует стройматериалами, то считать за одну позицию всю краску, все гвозди и т. п.
Вместо выручки можно взять и другие показатели. Это может быть, например, маржинальность каждого товара, т. е. разность между его продажной и закупочной ценой. Но в примере будем рассматривать выручку, так как данные по ней проще получить.
Во-вторых, распределить все товары по убыванию этого процента.
В-третьих, рассчитать по каждой строке долю выручки нарастающим итогом, начиная с тех товаров, которые дают самый существенный вклад.
В колонке «Доля в общей выручке нарастающим итогом» последовательно прибавляйте итог по каждой строке к итогу следующей.
Например, для кухонного стола показатель будет 63,0%. Он складывается из доли самого кухонного стола (20,2%) и предыдущего итога (42,8%). Для шкафа-купе показатель равен 80% (63% + 17%) и т. д.
В-четвертых, разбить все товары на три группы:
- А — дают 80% выручки;
- В — формируют 15% выручки;
- С — дополняют оставшиеся 5%.
В основную группу А далеко не всегда попадут ровно 20% товаров. Чем больше объем товаров, тем ближе к этому значению будут данные, — таковы закономерности статистики.
Например, если компания производит или продает 10 товаров, то необязательно, что 80% выручки дадут именно 2 из них. Если речь идет о тысячах позиций, то в большинстве случаев группу A составят примерно 20% товаров.
Номенклатура товаров магазина «Идея» состоит из 10 позиций. В группы A и B попали по 4 вида мебели, оставшиеся 2 составили группу C.
Однако ABC-анализ не может полностью показать ценность того или иного товара для компании.
Важно не только то, какой объем выручки приносит конкретный товар, но и регулярность продаж. Чтобы понять, насколько стабильно клиенты покупают те или иные товары, используют XYZ-анализ.
XYZ-анализ распределяет товары в зависимости от стабильности спроса
Сначала нужно разбить выручку на несколько периодов. Обычно берут данные за год и делят их по месяцам. Если использовать сведения за более короткое время, например квартал или полугодие, то результат будет менее точным.
Дело в том, что для многих бизнесов характерна сезонность продаж, и чтобы учесть ее, нужно видеть показатели за весь год.
Например, для кухонного стола разбивка по месяцам будет выглядеть так.
После разбивки данных по месяцам нужно для каждого вида товара провести следующие расчеты.
Определить среднемесячную выручку и занести ее в колонку «Среднее». Для этого итоговую сумму за год нужно разделить на 12.
Для кухонного стола 6 802 / 12 = 567 рублей.
Рассчитать стандартное отклонение с помощью функции Excel СТАНДОТКЛОН() и занести ее в колонку СТДО.
В скобках нужно указать диапазон значений выручки по товару. Если взяты данные за год, то будет 12 ячеек с показателями с января по декабрь.
Рассчитать коэффициент вариации (КВ). Чем меньше коэффициент вариации, тем стабильнее спрос на товар.
Например, для кухонной мебели КВ будет меньше, чем для школьных парт: кухни стабильно покупают в течение всего года, а школьную мебель обычно обновляют летом или в начале осени.
Для расчета КВ нужно разделить стандартное отклонение на среднюю выручку.
КВ = СТДО / СВ
Например, для кухонного стола:
КВ = 31 / 567 = 0,05
Если товарных позиций много, неудобно вручную вводить функцию для расчета по каждой позиции. Но работу можно ускорить, используя возможности Excel.
Зная коэффициент вариации по каждому товару, можно разбить их на группы:
- Группа Х — стабильный спрос, объем продаж от месяца к месяцу почти не изменяются: КВ < 0,1.
- Группа Y — условно стабильный спрос, т. е. объемы продаж меняются, но без резких скачков: 0,25 > КВ > 0,1.
- Группа Z — спрос нестабилен, покупатели приобретают товар от случая к случаю: КВ > 0,25.
Этот пример показывает, что наиболее стабильно продаются двуспальные кровати, кухонные столы и диваны-книжки.
Продажи таких позиций, как тахта, тумбочка и набор стульев спрогнозировать очень сложно, выручка по ним отличается в несколько раз от месяца к месяцу.
Спрос на письменные столы, полки, шкафы для одежды и шкафы-купе можно считать условно стабильным: отклонения между месяцами есть, но они сравнительно невелики.
Объединенный ABC-XYZ-анализ: как работать с каждой группой
Итак, мы разбили товары на три группы по выручке и на три по стабильности спроса. Теперь объединим результаты. Каждый из товаров попадет в одну из 9 групп.
Самый высокий ряд — это категория A, самый нижний — категория C. Чем правее находится товар, тем нестабильнее на него спрос. Левый ряд — это категория X, правый — Z. То есть самые непопулярные товары будут в нижнем правом квадрате, а самые популярные — в верхнем левом.
- Товары из групп AX и BX обеспечивают основной доход и при этом стабильно продаются. Они всегда должны быть на складе. Необходимый запас легко спрогнозировать, так как объемы продаж почти не меняются от месяца к месяцу. В нашем примере это двуспальная кровать, кухонный стол и диван-книжка.
- Группы АY и BY — это тоже высокий доход, но стабильность продаж уже ниже. По этим товарам на складе необходимо создать дополнительные резервы, на случай роста спроса в отдельные периоды. Резерв нужен обязательно, это важные для компании группы, которые приносят значительную часть дохода. В примере это шкаф для одежды, шкаф-купе и письменный стол.
- Группы AZ и BZ тоже приносят существенный доход. Но спрос на них почти невозможно спрогнозировать. Если создавать запасы на складе, исходя из максимально возможной месячной выручки, то значительная часть товара может остаться непроданной. Поэтому лучше использовать другие способы, которые обеспечат нужное количество товара. Например, заключить договоры с поставщиками, которые находятся максимально близко от магазина и могут в любой момент привезти нужную партию. В примере такие товары — это тахта и набор стульев.
- Группа CX продается стабильно, но в небольших объемах. По этой позиции нужно создать постоянный запас, исходя из среднего объема продаж.
- Группа CY — небольшие объемы продаж и невысокая стабильность. Запасы этой группы нужно создавать по остаточному принципу, т. е. после того, как выделены деньги на закупки товаров из более выгодных групп. Даже если в какой-то момент товара из этой группы не окажется на складе, потери компании будут невелики. В примере это полка.
- Группа CZ — самые низкие объемы выручки, при этом спрос невозможно спрогнозировать. Сюда относятся товары, которые уже перестали пользоваться спросом. Запасы по этой категории обычно не создают, работают под заказ. В нашем примере это тумбочка. Но! В эту группу могут попасть и новинки. Они не пользуются спросом потому, что клиенты пока о них не знают. Эти товары еще не привезли в магазины, не выставили на витринах, не запустили маркетинговую кампанию и пр. Учитывайте этот момент при анализе.
ABC-XYZ-анализ нужен практически любому бизнесу. Но у метода есть ограничения
ABC-XYZ-анализ позволяет разбить все товары или продукцию на 9 групп в зависимости от объемов продаж и стабильности спроса.
Однако не следует полностью полагаться на результаты ABC-XYZ-анализа — нужно учитывать и другие факторы. Не нужно сразу отказываться от товаров, которые попали в невыгодные группы. Сначала стоит проанализировать все причины, по которым они туда попали, и только потом принимать решение об изменении ассортимента.
Например, новый товар на начальном этапе его продвижения может довольно долго находиться в группе «аутсайдеров». Но это не значит, что ими не следует заниматься. Возможно, они поднимутся до категории тех, что приносят самую большую прибыль.
Также спад продаж может быть связан с форс-мажорными обстоятельствами, которые носят временный характер. Например, аномально теплая зима 2019–2020 года в европейской части России привела к существенному снижению спроса на зимнюю одежду. Но это не значит, что дальше заниматься продажей зимних товаров невыгодно. При возврате климатической нормы в следующем году восстановится и спрос на эти товары.
Не подойдет ABC-XYZ-анализ компаниям, которые продают один товар или услугу. Но таких очень мало.
Этот анализ полезен для всех бизнесменов, которые работают с несколькими видами товаров или продукции. Чтобы нужные запасы всегда были на складе, но не оставалось непроданных излишков, с каждой из групп необходимо работать по своему алгоритму.
ПРИМЕРЫ СПОСОБОВ ПРЕДСТАВЛЕНИЯ ПАРТИЙ И МЕТОДОВ ОТБОРА
ЕДИНИЦ ПРОДУКЦИИ В ВЫБОРКУ
А.1 Пример 1. Представление продукции на контроль способом “ряд”
К продукции, поступающей на контроль способом “ряд”, можно отнести электродвигатели, пакеты химикатов, бутылки растительного масла и т.п. (рисунок А.1).
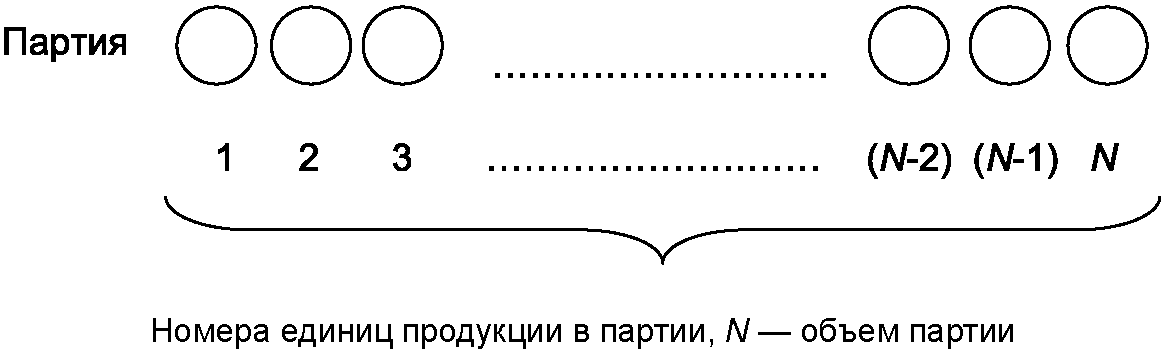
Рисунок А.1 – Представление продукции на контроль
способом “ряд”
А.2 Пример 2. Представление продукции на контроль способом “поток”
Примером продукции, представляемой на контроль способом “поток”, может служить продукция, поступающая с конвейера. На рисунке А.2 схематично показано представление продукции на контроль способом “поток” с отбором в выборку каждой пятой единицы продукции. Единицы продукции, отбираемые в выборку, выделены на рисунке А.2 с помощью жирной линии окружности.
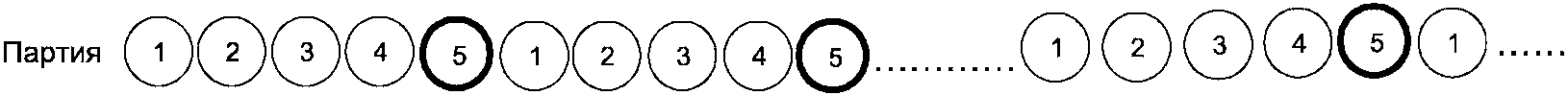
Рисунок А.2 – Представление продукции на контроль способом
“поток” с отбором в выборку каждой пятой единицы продукции
А.3 Пример 3. Представление продукции на контроль способом “ряд” в упаковке (рисунок А.3)
Партия

Объем партии – 80 шт.; количество упаковочных
единиц – 5 шт.; количество единиц продукции
в упаковочной единице – 16 шт.
Рисунок А.3 – Представление продукции способом “ряд”
в упаковке
А.4 Пример 4. Отбор продукции, представленной на контроль способом “ряд” в упаковке
Продукция, представленная на контроль способом “ряд”, состоит из 4000 единиц продукции, расположенных в 80 рядах и 50 колонках. Требуется случайным образом отобрать для контроля 8 единиц продукции.
Каждой строке присваивают порядковый номер от 01 до 80, а каждой колонке – номер от 01 до 50.
Каждой единице продукции соответствует четырехзначный номер, состоящий из номера строки и колонки. В данном случае первые две цифры номера меньше или равны 80, а вторые две цифры номера – меньше или равны 50. Случайным образом установлено начало отсчета в таблице равномерно распределенных случайных чисел: 1-я строка, 1-я колонка таблицы Б.2. В соответствии с таблицей получены следующие цифры: 5132, 6916, (4488), (9710), (0664), (1077), 6908, (8897), (1070), 0930, (8743), (8237), 1433, (2467), 2109, (9682), 1436, 4741. Цифры в скобках следует исключить, так как они выходят за пределы интервалов изменения номера строки и номера колонки.
В условиях данного примера следует использовать числа 0930, 1433, 1436, 2109, 4741, 5132, 6908, 6916 (числа расположены в порядке возрастания). Таким образом, необходимо отобрать в выборку единицы продукции из:
– ряда N 09, колонки N 30;
– ряда N 14, колонки N 33;
– ряда N 14, колонки N 36;
– ряда N 21, колонки N 09;
– ряда N 47, колонки N 41;
– ряда N 51, колонки N 32;
– ряда N 69, колонки N 08;
– ряда N 69, колонки N 16.
А.5 Пример 5. Отбор выборки из партии болтов, упакованной в ящики
При приемке партии болтов контролируют внешний вид, размеры, механические свойства и покрытие.
Установленное в документации на контроль количество ящиков (первичных упаковочных единиц), подлежащих отбору из партии, приведено в таблице А.1, объем выборки приведен в таблице А.2.
Таблица А.1
Количество ящиков (первичных упаковочных единиц),
подлежащих отбору из партии
|
Количество ящиков в партии |
Количество ящиков, подлежащих отбору |
|
1 – 5 |
Все |
|
6 – 99 |
5 |
|
100 – 399 |
1/20 часть (5%) |
|
400 и более |
20 |
Таблица А.2
Объем выборки в зависимости от объема партии
|
Объем партии, шт. |
Объем выборки (шт.) для контроля |
||
|
внешнего вида и размеров |
механических свойств |
||
|
без разрушения |
с разрушением |
||
|
До 1200 |
32 |
13 |
5 |
|
1201 – 3200 |
50 |
||
|
3201 – 10000 |
80 |
20 |
|
|
10001 – 35000 |
125 |
Образцы для контроля механических свойств отбирают из выборки для контроля внешнего вида и размеров.
Партия включает 20000 штук, упакованных в 100 ящиках по 200 штук в каждом. Внутри ящиков болты находятся в россыпи. В данном случае отбирают 5 ящиков с использованием таблицы случайных чисел. Затем из ящиков болты отбирают методом “вслепую”, так как нумерация отдельных болтов технически затруднительна.
Случайным образом определено начало отсчета, в данном случае это строка 15, колонка 4 в таблице Б.1. Числа выбирались последовательно. Получены числа 60, 01, 59, 56, 48. Таким образом, для контроля необходимо взять ящики с номерами 1, 48, 56, 59, 60.
В соответствии с таблицей А.2 объем выборки для контроля внешнего вида и размеров составляет 125 штук. Из каждого ящика отбирают методом “вслепую” 125/5 = 25 штук. Порядок штук следует сохранять, не допуская перемешивания образцов из различных ящиков.
Для контроля механических свойств без разрушения в соответствии с таблицей А.2 объем выборки составляет 20 штук. Выборочные единицы отбирают методом “вслепую”, 4 штуки из каждого ящика, т.е. из ранее отобранных из ящика 25 штук. Всего отбирают 5 x 4 = 20 штук.
Для контроля механических свойств с разрушением аналогично отбирают по 1 штуке из каждого ящика, т.е. по 1 штуке из отобранных 25 штук (всего 5 штук).
Если партия имела бы 200 ящиков, содержащих каждый 100 штук, то следовало бы открыть 10 ящиков и отобрать из них 125/10, т.е. 12 или 13, всего 125 штук, как раньше. Далее – как указано выше.
А.6 Пример 6. Отбор выборки из партии продукции, представленной способом “россыпь”
Количество единиц продукции 1000, для контроля необходимо отобрать в выборку 100 единиц. Единицы продукции уложены в 10 ящиков по 100 единиц в каждом. Внутри ящиков единицы продукции находятся в россыпи. Из каждого ящика “вслепую” отбирают для контроля по 10 единиц продукции.
А.7 Пример 7. Отбор выборки с конвейера
Необходимо проконтролировать продукцию, поступающую с конвейера за первые пять смен месяца. Выборка должна составить 10% продукции, изготовленной за смену. За смену изготавливают 100 единиц продукции. Для отбора единиц в выборку применен метод систематического отбора. Случайным образом выбирают начало отсчета для первых пяти смен, например строка 21 и колонка 4 таблицы Б.1. В строке 21 и колонках 4, 5, 6, таблицы Б.1 приведены числа 1, 8, 9. Так как выборка составляет 10%, то отбирают каждую десятую единицу продукции, поступающую с конвейера. Для первой смены в выборку попадут единицы 1, 11, 21, 31 и т.д. Для второй смены в выборку попадут единицы 8, 18, 28, 38 и т.д.
Приложение Б
(обязательное)
Скачать документ целиком в формате PDF
В зависимости от способа представления продукции на контроль применяются следующие методы отбора единиц продукции в пробу или выборку:
- отбор с применением случайных чисел;
- многоступенчатый отбор;
- отбор “вслепую”;
- систематический отбор.
Отбор с применением случайных чисел используется в основном для продукции, представленной на контроль способом “ряд”. Метод отбора с применением случайных чисел используется при всех остальных способах представления однородной продукции, если его применение не ведет к большим трудностям экономического или технического порядка. При методе отбора единиц продукции в выборку с применением случайных чисел используют таблицы случайных чисел по СТ СЭВ 546-77, карточки (числа в урне).
Для осуществления наиболее правильного случайного отбора и получения репрезентативной выборки первоначально проводят предварительную нумерацию единиц продукции. Все номера должны иметь одно и то же количество цифр.
Существующие номера с разным количеством цифр следует вначале дополнять слева нулями. Затем отбирают в выборку те единицы продукции, номера которых выбирают подряд из любых строк или колонок таблицы случайных чисел или по карточкам.
Например, необходимо проконтролировать 8 000 ящиков с лампами бегущей волны.
Известно, что в каждом ящике лежат по две лампы. Объем выборки равен 320 лампам (160 ящиков). Ящики уложены в четыре штабеля по 2 000 штук в каждом. В каждом штабеле ящики плотно уложены в четыре этапа по 500 штук (20 × 25) в каждом этапе. Доступ к каждому штабелю одинаково свободен с любой стороны.
Для обеспечения репрезентативности формируется расслоенная выборка, т. е. каждый штабель представляет собой выборочный слой. Объем выборки из каждого слоя пропорционален количеству ящиков в штабеле и составляет 40 ящиков. В связи с тем, что доступ к центру штабеля затруднителен, а по верхней и боковым поверхностям находится значительная часть ящиков, выборку формируют следующим образом: из одного штабеля, например второго, выбранного методом случайного отбора по карточкам, производят выборку из всего объема.
Из остальных трех штабелей (1, 3 и 4-го) производят выборку по верхней и боковым поверхностям. Для отбора ящиков второго штабеля применяют таблицу случайных чисел. Ящики второго штабеля нумеруют от 0000 до 1999. Если за начало отсчета взять строку 16 колонки 9 по табл. 2 стандарта СТ СЭВ 546-77, то, отбрасывая числа больше 1999, получим числа 1858, 1961, 0061, 1270, 0076, 1860, 1392, 1743, 1838, 0716, 1167,1028, 1099, 0267, 1675, 0221, 0709, 1577, 1781, 0891, 1953, и т. д. до тех пор, пока не будут набраны 40 чисел. Следовательно, для контроля необходимо взять: 61, 76, 221, 267, 709,716, 891, 1028, 1167, 1270, 1392, 1577, 1675, 1743, 1781, 1838, 1860, 1953, 1961 и т. д. ящики.
Ящики 1, 3 и 4-го штабелей, контролируемых по верхней и боковым поверхностям, нумеруют от 000 по 514 каждый. Выбрав случайным образом для каждого штабеля начало отсчета по таблицам случайных чисел СТ СЭВ 546-77, определяют номера тех 40 ящиков по штабелям, которые необходимо включить в выборку. Полученная таким образом выборка будет представительной и характеризовать свойства всей партии, представленной для контроля.
Метод многоступенчатого отбора применяют для однородной продукции, представленной на контроль в упаковке, т. е. в упаковочных единицах, содержащих одинаковое количество единиц продукции. При многоступенчатом отборе выборку образуют по ступеням и единицы продукции в каждой ступени отбирают случайным образом из единиц, отобранных в предыдущей ступени. Выборка составляется из примерно одинаковых объемов продукции, взятых из отобранных упаковочных единиц.
Если первичные упаковочные единицы содержат вторичные и т. д. упаковочные единицы, то сначала отбирают первичную, затем вторичную и т. д. упаковочные единицы. Допускается единицы продукции паковать в первую (вторую и т. д.) упаковочную единицу россыпью. Для упаковочных единиц применяют метод отбора с применением случайных чисел. Если продукция находится в “россыпи”, то следует применять метод “вслепую”.
В зависимости от количества ступеней многоступенчатый отбор может быть одноступенчатым, двухступенчатым, трехступенчатым и т. п.
Одноступенчатые методы предусматривают отбор пробы из всей генеральной совокупности без предварительного деления ее на части. Так, одноступенчатой является выборка пары обуви из партии обуви. При одноступенчатом методе чаще используют случайный отбор, при котором объекты отбирают из разных частей партии с одинаковой долей вероятности и независимо от субъективной оценки качества отбираемых объектов. Если при этом можно визуально выявлять дефектные объекты или отличающиеся по другим признакам, то данный метод применять нельзя.
Двухступенчатые методы отбора применяют при разделении генеральной совокупности (партии продукции) на отдельные примерно равные части и фиксации этого разделения в выборке, а также при обработке результатов испытаний. При двухступенчатом отборе вначале отбирают упаковочные единицы или единицы продукции, а потом на второй ступени от каждой упаковочной единицы или единицы продукции отбирают пробу (выборку). Например, партия тканей состоит из нескольких кусков (рулонов), от каждого куска отбирают пробу ткани.
Однако если партия продукции разделена на части, но отобранные из разных ее частей объекты потом объединяют в одну общую выборку, то такая выборка является одноступенчатой. Она будет такой же и при объединении всех результатов испытаний, без подразделения их соответственно отдельным частям совокупности.
Трехступенчатые методы отбора используют, когда генеральная совокупность разделена примерно на равные части, а каждая часть — на серии из приблизительно одинакового количества единиц продукции. Из нескольких частей продукции отбирают по одинаковому числу серий, а из каждой отобранной серии испытывают по одинаковому числу единиц продукции.
В качестве примера можно привести партию нитей из нескольких ящиков (групп), содержащих примерно одинаковое количество паковок (серий); по каждой паковке можно провести примерно одинаковое число измерений свойств нити, определяемое ее длиной в паковке и длиной испытываемых образцов (отрезков) нитей.
Метод отбора “вслепую” (метод наибольшей объективности) применяется для продукции, представленной на контроль россыпью, а также в том случае, когда применение метода отбора с применением случайных чисел технически затруднительно или экономически невыгодно.
Метод “вслепую” не следует применять в тех случаях, когда бракованные единицы продукции можно определить органолептически. В выборку должны быть включены единицы продукции из разных частей контролируемой партии. Единицы продукции следует отбирать независимо от субъективных предположений контролера относительно качества отбираемой единицы продукции.
Например, продукция представлена на контроль россыпью, количество единиц продукции 1000, необходимо проконтролировать 100 единиц. Единицы продукции уложены в 10 ящиков по 100 единиц в каждом. Из каждого ящика “вслепую” отбирают для контроля по 10 любых единиц продукции.
Метод “вслепую” обеспечивает независимость попадания единиц продукции в выборку, но не обеспечивает равную вероятность попадания единиц продукции в выборку.
Метод систематического отбора применяется для продукции, представленной на контроль в виде потока. Единицы продукции отбирают через определенный интервал времени или количество единиц продукции. Например, если выборка должна составить 5% от контролируемой партии, то отбирают каждую двадцатую единицу продукции. Начало отсчета определяется случайным образом, например с помощью таблиц случайных чисел по СТ СЭВ 546-77.
Данным методом можно образовывать выборку, если имеется определенный порядок следования единиц продукции. При этом необходимо учитывать, что в следующих одна за другой единицах продукции значение контролируемого параметра не должно меняться с той же периодичностью, что и периодичность отбора единиц в выборку.
Например, необходимо проконтролировать продукцию, поступающую с конвейера за первые пять смен месяца. Выборка должна составить 10% от продукции, изготовляемой за смену. За смену изготовляют 100 единиц продукции. Для отбора единиц в выборку применяется метод систематического контроля. Случайным образом выбирают начало отсчета для первых пяти смен.
Если возьмем 21 строку 4, 5, 6, 7 и 8 колонок в табл. 3 случайных чисел СТ СЭВ 546-77, то получим числа 8, 5, 1, 9, 4. Так как выборка в 10%, то отбираем каждую десятую единицу. Для первой смены в выборку попадут единицы 8, 18, 28, 38, 48, 58, 68, 78, 88, 98. Для второй смены в выборку попадут единицы 5, 15, 25, 35, 45, 55, 65, 75, 85, 95 и т. д.
Метод систематического отбора обеспечивает независимость попадания единиц продукции при случайном смещении начала отсчета, но не обеспечивает равную вероятность попадания единиц продукции в выборку. Если продукция однородна и поступает на контроль в хорошо перемешанном виде, все методы приводят к одинаковым результатам, такт как представительность обеспечивается однородностью продукции, а случайность — ее предварительным перемешиванием (случайность попадания на каждое определенное место).
В настоящее время имеется множество компьютерных программ по контролю, которые избавляют от необходимости утомительных подсчетов. Например, стандартные программы позволяют составить планы отбора образцов, ведут статистику по образцам, выбирают наугад изделия, составляют графики показателей качества, строят гистограммы и определяют границы точности.

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:
 (в данной формуле не используется показатель объема генеральной совокупности N)
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p – ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p – ∆; p + ∆) = (20% – 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ – ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ – ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
