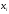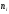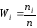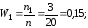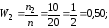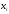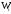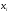Как составить выборочное распределение

Как составить выборочное распределение

Представьте, что существует популяция из 10 000 дельфинов, и средний вес дельфина в этой популяции составляет 300 фунтов.

Если мы возьмем простую случайную выборку из 50 дельфинов из этой популяции, мы можем обнаружить, что средний вес дельфинов в этой выборке составляет 305 фунтов.

Затем, если мы возьмем еще одну простую случайную выборку из 50 дельфинов, мы можем обнаружить, что средний вес дельфинов в этой выборке составляет 295 фунтов.

Каждый раз, когда мы берем простую случайную выборку из 50 дельфинов, вполне вероятно, что средний вес дельфинов в выборке будет близок к среднему значению популяции в 300 фунтов, но не точно 300 фунтам.

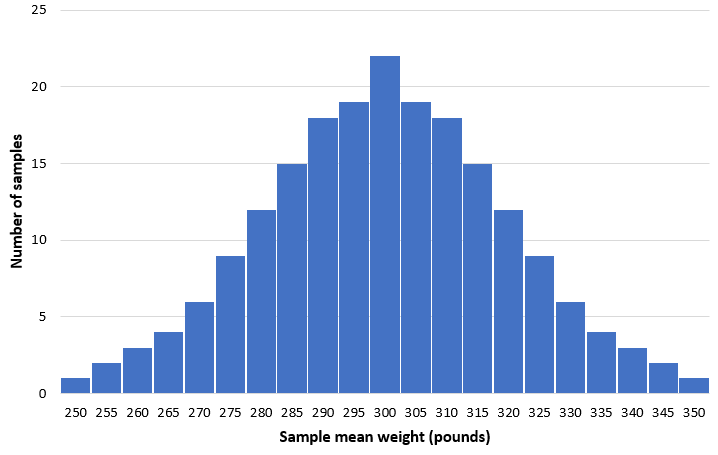
Представьте, что мы берем 200 простых случайных выборок из 50 дельфинов из этой популяции и строим гистограмму среднего веса в каждой выборке:

В большинстве образцов средний вес будет близок к 300 фунтам. В редких случаях может случиться так, что мы выберем образец, полный маленьких дельфинов, средний вес которых составляет всего 250 фунтов. Или мы можем случайно выбрать образец, полный крупных дельфинов, средний вес которых составляет 350 фунтов. В целом распределение выборочных средних будет приблизительно нормальным, а центр распределения будет находиться в истинном центре генеральной совокупности.

Это распределение выборочных средних известно как выборочное распределение среднего и обладает следующими свойствами:

м х = м

где μx — выборочное среднее, а μ — среднее значение генеральной совокупности.

σ х = σ/ √n

где σ x — стандартное отклонение выборки, σ — стандартное отклонение генеральной совокупности, а n — размер выборки.

Например, в этой популяции дельфинов мы знаем, что средний вес равен μ = 300. Таким образом, среднее значение выборочного распределения равно μ x = 300 .

Предположим, мы также знаем, что стандартное отклонение населения составляет 18 фунтов. Таким образом, стандартное отклонение выборки равно σ x = 18/√50 = 2,546 .

Выборочное распределение доли

Рассмотрим ту же популяцию из 10 000 дельфинов. Предположим, что 10% дельфинов черные, а остальные серые. Предположим, мы берем простую случайную выборку из 50 дельфинов и обнаруживаем, что 14% дельфинов в этой выборке — черные. Затем мы берем еще одну простую случайную выборку из 50 дельфинов и обнаруживаем, что 8% дельфинов в этой выборке черные.

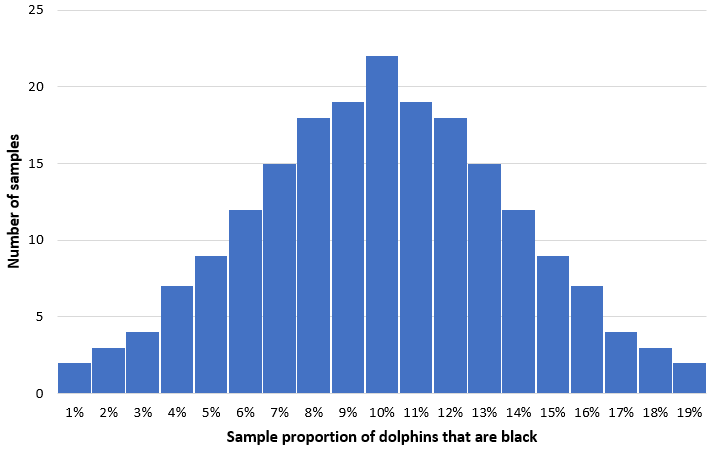
Представьте, что мы берем 200 простых случайных выборок из 50 дельфинов из этой популяции и строим гистограмму доли черных дельфинов в каждой выборке:

В большинстве выборок доля черных дельфинов будет близка к истинной популяции в 10%. Распределение выборочной доли черных дельфинов будет приблизительно нормальным, а центр распределения будет находиться в истинном центре популяции.

Это распределение выборочных долей известно как выборочное распределение доли и обладает следующими свойствами:

μ р = P

где p — доля выборки, а P — доля совокупности.

σ p = √ (P) (1-P) / n

где P — доля населения, а n — размер выборки.

Например, в этой популяции дельфинов мы знаем, что истинная доля черных дельфинов составляет 10% = 0,1. Таким образом, среднее значение выборочного распределения доли составляет μ p = 0,1 .

Предположим, мы также знаем, что стандартное отклонение населения составляет 18 фунтов. Таким образом, стандартное отклонение выборки равно σ p = √ (P)(1-P) / n = √ (0,1)(1-0,1) / 50 = 0,042 .

Установление нормальности

Чтобы использовать приведенные выше формулы, распределение выборки должно быть нормальным.

Согласно центральной предельной теореме , выборочное распределение среднего значения выборки приблизительно нормально, если размер выборки достаточно велик, даже если распределение генеральной совокупности не является нормальным.В большинстве случаев мы считаем, что размер выборки в 30 или более человек является достаточно большим.

Выборочное распределение доли выборки является приблизительно нормальным, если ожидаемое количество успешных и неудачных попыток равно как минимум 10.

Примеры

Мы можем использовать выборочные распределения для расчета вероятностей.

Пример 1: Определенная машина создает файлы cookie. Распределение веса этих печенек смещено вправо со средним значением 10 унций и стандартным отклонением 2 унции. Если мы возьмем простую случайную выборку из 100 печений, произведенных этой машиной, какова вероятность того, что средний вес печенья в этой выборке будет меньше 9,8 унций?

Шаг 1: Установите нормальность.

Нам нужно убедиться, что выборочное распределение среднего значения выборки является нормальным. Поскольку размер нашей выборки больше или равен 30, в соответствии с центральной предельной теоремой мы можем предположить, что выборочное распределение выборочного среднего является нормальным.

Шаг 2: Найдите среднее значение и стандартное отклонение выборочного распределения.

м х = м

σ х = σ/ √n

мкх = 10 унций

σ x = 2/√100 = 2/10 = 0,2 унции

Шаг 3: Используйте калькулятор площади Z Score, чтобы найти вероятность того, что средний вес печенья в этом образце меньше 9,8 унций.

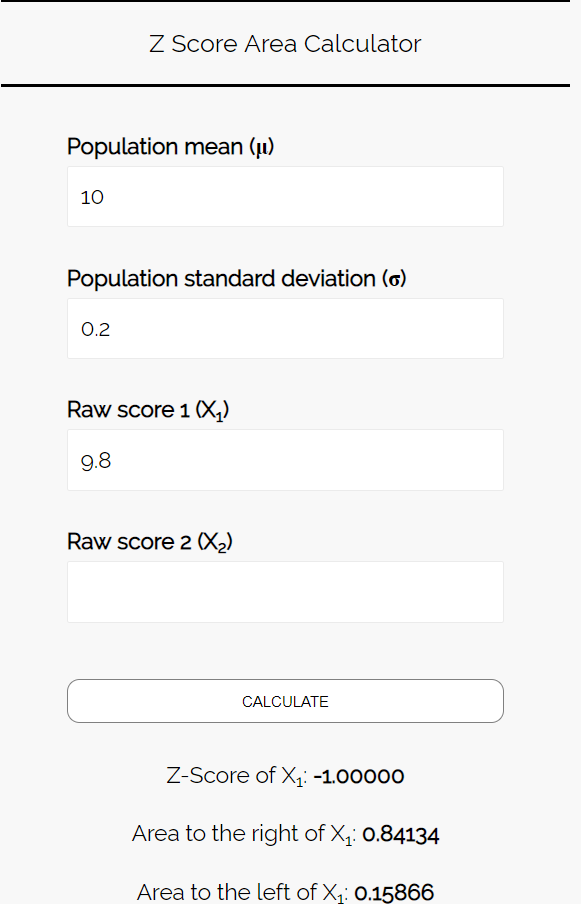
Введите следующие числа в Калькулятор площади Z Score.Вы можете оставить «Исходный балл 2» пустым, так как в этом примере мы находим только одно число.

Поскольку мы хотим узнать вероятность того, что средний вес печенья в этой выборке меньше 9,8 унций, нас интересует площадь слева от 9,8. Калькулятор говорит нам, что эта вероятность равна 0,15866 .

Пример 2. Согласно общешкольному исследованию, 87% учащихся в определенной школе предпочитают пиццу мороженому. Предположим, мы берем простую случайную выборку из 200 студентов. Какова вероятность того, что доля студентов, предпочитающих пиццу, меньше 85 %?

Шаг 1: Установите нормальность.

Напомним, что выборочное распределение доли выборки является приблизительно нормальным, если ожидаемое количество «успехов» и «неуспехов» равно как минимум 10.

В этом случае ожидаемое количество студентов, которые предпочтут пиццу, составляет 87% * 200 студентов = 174 студента. Ожидаемое количество студентов, которые не предпочтут пиццу, составляет 13% * 200 студентов = 26 студентов. Поскольку оба эти числа не меньше 10, можно предположить, что выборочное распределение выборочной доли студентов, предпочитающих пиццу, примерно нормальное.

Шаг 2: Найдите среднее значение и стандартное отклонение выборочного распределения.

μ р = P

σ p = √ (P) (1-P) / n

мк р = 0,87

σ p = √ (0,87) (1–0,87) / 200 = 0,024

Шаг 3: Используйте Калькулятор Z Score Area Calculator , чтобы определить вероятность того, что доля учащихся, предпочитающих пиццу, составляет менее 85 %.

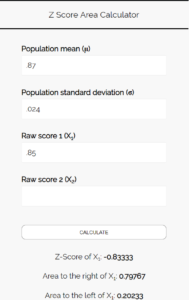
Введите следующие числа в Калькулятор площади Z Score.Вы можете оставить «Исходный балл 2» пустым, так как в этом примере мы находим только одно число.

Поскольку мы хотим узнать вероятность того, что доля студентов, предпочитающих пиццу, составляет менее 85 %, нас интересует область слева от 0,85. Калькулятор говорит нам, что эта вероятность равна 0,20233 .

Бонус: видео-объяснение распределений выборки

Источник

Пусть
для изучения количественного (дискретного
или непрерывного) признака Х из генеральной
совокупности извлечена выборка, причем
значение x1
наблюдалось n1
раз, значение x2
наблюдалось n2
раз, …, значение xk
наблюдалось nk
раз.

Наблюдаемые
значения xi
(i
= 1, 2, …, n)
признака Х называют вариантами, а
последовательность всех вариант,
записанных в возрастающем порядке, –
вариационным
рядом.
Числа наблюдений ni
называют частотами,
их сумма
─объем
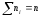
выборки.
Отношения частот к объему выборки
─относительными
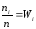
частотами.

Статистическим
распределением выборки
называют перечень вариант xi
вариационного ряда и соответствующих
им частот ni
(сумма всех частот равна объему выборки
n)
или относительных частот Wi
(сумма всех относительных частот равна
единице). Статистическое распределение
можно задать также в виде последовательности
интервалов и соответствующих им частот
(в качестве частоты, соответствующей
интервалу, принимают сумму частот,
попавших в этот интервал).

Заметим,
что в теории вероятностей под распределением
понимают соответствие между возможными
значениями случайной величины и их
вероятностями, а в математической
статистике – соответствие между
наблюдаемыми вариантами и их частотами
(или относительными частотами).

Пример.
Задано распределение частот выборки
объема n
= 20:

2

6

12

3

10

7

В
данной выборке получены следующие
варианты x1
= 2; x2
= 6; x3
= 12,

соответствующие
частоты n1
= 3; n2
= 10; n3
= 7.

Напишем
распределение относительных частот.

Решение.
Найдем относительные частоты, для чего
разделим частоты на объем выборки
= 3 + 10 + 7 = 20.


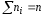
─ относительные
частоты:


Напишем распределение
относительных частот:

2

6

12

0,15

0,50

0,35

Контроль:
сумма всех относительных частот
равна единице:

.

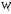
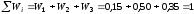
§14. Эмпирическая функция распределения

Пусть
известно статистическое распределение
частот количественного признака Х.
Введем обозначения:
─
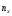
число наблюдений, при которых наблюдалось
значение признака, меньше х; n
– общее число наблюдений (объем выборки).
Ясно, что относительная частота события
Х<х равна
.
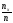
Если х изменяется, то, вообще говоря,
изменится и относительная частота, то
есть относительная частота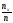есть функция от х. Так как эта функция
находится эмпирическим (опытным) путем,
то ее называют эмпирической.

Определение.
Эмпирическая
функция распределения
(функция распределения выборки) –
функция F*(x),
определяющая для каждого значения х
относительную частоту события X<x.

,

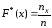
где
─ число вариант, меньших х;n
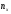
– объем выборки.

Например,
для того чтобы найти F*(x2),
надо число вариант, меньших x2,
разделить на объем выборки:

.

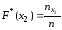
В
отличие от эмпирической функции
распределения выборки функцию
распределения F(x)
генеральной совокупности называют
теоретической
функцией распределения.
Различие между эмпирической и теоретической
функциями состоит в том, что теоретическая
функция F(x)
определяет вероятность события X<x,
а эмпирическая функция F*(x)
определяет относительную частоту этого
же события.

Из
теоремы Бернулли следует, что относительная
частота события X<x,
то есть F*(x),
стремится по вероятности к вероятности
этого события, то есть к значению F(x).
Другими словами, при больших значениях
n
числа F*(x)
и F(x)
мало отличаются одно от другого в том
смысле, что
.
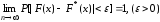
Уже отсюда следует целесообразность
использования эмпирической функции
распределения выборки для приближенного
представления теоретической (интегральной)
функции распределения генеральной
совокупности. Такое заключение
подтверждается и тем, что F*(x)
обладает всеми свойствами F(x).

Из
определения функции F*(x)
вытекают следующие ее свойства:

  1. Значения
    эмпирической функции принадлежит
    отрезку [0; 1];

  2. F*(x)
    – неубывающая функция;

  3. Если
    x1
    ─ наименьшая варианта, то F*(x)
    = 0 при х < х1;

если
хk
─ наибольшая варианта, то F*(x)
= 1 при х > xk.

Итак,
эмпирическая функция распределения
выборки служит для оценки теоретической
функции распределения генеральной
совокупности.

Пример.
Построить эмпирическую функцию по
данному распределению выборки:

Варианты

2

6

10

Частоты

12

18

30

Решение.
Найдем объем выборки (сумма всех частот
ni):

n
= n1
+ n1
+ n1
= 12 + 18 + 30 = 60.

Наименьшая
варианта равна 2 (x1
= 2), следовательно, F*(x)
= 0 при х ≤ 2 (по свойству 3 функции F*(x));

значения,
меньшие 6 (х<6), а именно x1
= 2, наблюдались n1
= 12 раз, следовательно,
при 2<x≤6;

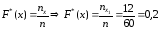
значения
х<10, а именно x1
= 2, x1
= 2 наблюдались n1
+ n2
= 12 + 18 = 30 раз, следовательно
при 6<х≤10.

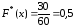
Так
как х =10 – наибольшая варианта, то F*(x)
= 1 при х>10 (по свойству 4 функции F*(x)).

Искомая
эмпирическая функция имеет вид:

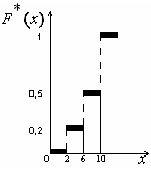
Ниже приведен график
полученной эмпирической функции.

На графике на
соответствующих осях откладывают
значения функции F*(x)
и интервалы вариант

Рис.
5. График эмпирической функции.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Основной целью анализа данных являются статистические выводы, т.е. применение выборочных показателей для оценки параметров генеральной совокупности. Статистические выводы относятся к генеральным совокупностям, а не к выборкам из них. Например, социологи изучают результаты выборочных обследований только для того, чтобы оценить шансы кандидатов получить голоса из всей генеральной совокупности избирателей в целом. Выборочное среднее, полученное при обследовании конкретной выборки, само по себе интереса не представляет. [1]

На практике из генеральной совокупности извлекается выборка заранее установленного объема. Элементы, принадлежащие данной выборке, выбираются случайным образом, например, с помощью датчика случайных чисел. Распределения выборочных параметров называют выборочными.

Выборочное распределение средних значений

Ранее мы рассмотрели несколько оценок математического ожидания распределения. Чаще всего для этого используется арифметическое среднее. Это наилучшая оценка математического ожидания, если распределение является нормальным.

Арифметическое среднее называется несмещенным, поскольку среднее значение всех выборочных средних (при заданном объеме выборки n) равно математическому ожиданию генеральной совокупности. Продемонстрируем это свойство на примере. Предположим, что генеральная совокупность машинисток в секретариате компании состоит из четырех сотрудниц. Каждую из них попросили напечатать один и тот же текст. Количество опечаток, сделанных каждой машинисткой: Энн – Х1 = 3, Кэт – Х2 = 2, Карла – Х3 = 1, Ширли – Х4 = 4. Распределение ошибок приведено на рис. 1.

Рис. 1. Количество опечаток, сделанных четырьмя машинистками

Скачать заметку в формате Word или pdf, примеры в формате Excel2013

Математическим ожиданием генеральной совокупности называется сумма всех значений совокупности, деленная на ее объем:

где μ – математическое ожидание генеральной совокупности, N – объем генеральной совокупности, Xi— i-й элемент генеральной совокупности.

Стандартным отклонением генеральной совокупности называется корень квадратный из ее дисперсии:

Таким образом, в нашем примере:

Если из этой генеральной совокупности необходимо извлечь с возвращением выборку, состоящую из двух машинисток, возникает 16 вариантов выбора (Nm= 42=16, подробнее см. Первое правило счета в заметке Основные понятия теории вероятностей). Эти варианты приведены в таблице (рис. 2). Если усреднить все 16 средних значений, мы получим величину , равную математическому ожиданию генеральной совокупности μ, т.е. числу 2,5.

Рис. 2. Все возможные варианты выбора двух машинисток из четырех

Итак, среднее значение всех выборочных средних равно математическому ожиданию генеральной совокупности. Следовательно, хотя нам неизвестно, насколько хорошо конкретное выборочное среднее аппроксимирует математическое ожидание генеральной совокупности, среднее значение всех выборочных средних совпадает с математическим ожиданием генеральной совокупности.

Стандартная ошибка среднего. На рис. 3 приведено выборочное распределение среднего количества ошибок, сделанных машинистками, образующих все 16 возможных выборок, полученных путем случайного выбора с возвращением. Как видим, колебание выборочных средних вокруг математического ожидания генеральной совокупности меньше, чем колебание исходных данных. Этот факт непосредственно следует из закона больших чисел. Исходная генеральная совокупность может содержать числа, которые являются как очень большими, так и очень маленькими. Однако, если экстремальное значение попадет в выборку, ее влияние на среднее значение будет ослаблено, поскольку оно будет просуммировано со всеми остальными элементами выборки. При увеличении объема выборки влияние экстремальных значений ослабевает, поскольку в усреднении принимает участие все большее количество элементов.

Рис. 3. Распределение выборочных средних из таблицы (рис. 2); по оси абсцисс отложены значения выборочных средних Хi, по оси ординат – частота встречаемости этих значений; например, на рис. 2 среднее значение Хi = 2,5 встретилось 4 раза, т.е. точке с абсциссой 2,5 соответствует ордината 4

Диапазон изменения выборочных средних описывается их стандартным отклонением. Эта величина называется стандартной ошибкой среднего и обозначается как . Стандартная ошибка среднего равна стандартному отклонению генеральной совокупности σ, деленному на квадратный корень из объема выборки n:

Следовательно, при возрастании объема выборки n стандартная ошибка среднего уменьшается со скоростью, пропорциональной квадратному корню из n. Эту формулу можно применять для аппроксимации стандартной ошибки среднего, если выборки извлекаются из генеральной совокупности без возвращения при условии, что каждая выборка содержит не более 5% элементов всей генеральной совокупности. Проиллюстрируем это свойство следующим примером. Если из нескольких тысяч коробок случайным образом извлекается без возвращения выборка из 25 коробок, в нее попадет не более 5% элементов всей генеральной совокупности. Вычислите стандартную ошибку среднего, если стандартное отклонение веса коробки равно 15 г. Подставим в формулу значения n = 25 и σ =15, получаем стандартную ошибку среднего:

Обратите внимание на то, что изменчивость выборочных средних намного меньше, чем изменчивость исходных данных (т.е. = 3 намного меньше, чем σ = 15).

Выборки из нормально распределенных генеральных совокупностей. Введя понятие выборочных распределений и дав определение стандартной ошибки среднего, мы можем ответить на вопрос, как распределены выборочные средние . Можно доказать, что если выборки извлекаются с возвращением из нормально распределенной генеральной совокупности, математическое ожидание которого равно μ, а стандартное отклонение — σ, то выборочное распределение средних также является нормальным при любом объеме выборок n, причем = μ, а стандартная ошибка — .

В наиболее простом варианте, когда объем каждой выборки равен единице, каждое выборочное среднее равно единственному элементу выборки:

Следовательно, если генеральная совокупность является нормально распределенной, причем ее математическое ожидание равно μ, а стандартное отклонение — σ, то выборочное распределение средних также является нормальным при n = 1, причем = μ, а стандартная ошибка = σ/√1 = σ. Обратите внимание на то, что при увеличении объема выборок выборочное распределение средних остается нормальным, причем = μ. Однако увеличение объема выборки приводит к уменьшению стандартной ошибки среднего, поэтому чем больше становится выборка, тем ближе становятся выборочные средние к математическому ожиданию генеральной совокупности.

В этом можно убедиться, проанализировав рис. 4. На нем изображены выборочные распределения среднего, построенные по 500 выборкам с объемами n = 1, 2, 4, 8, 16 и 32, случайным образом извлеченным из нормально распределенной генеральной совокупности. Полигоны, изображенные на рис. 4, свидетельствуют от том, что выборочное распределение средних является лишь приближенно нормальным. Однако по мере возрастания объема выборок выборочные средние становятся ближе к математическому ожиданию генеральной совокупности.

Рис. 4. Выборочные распределения средних, построенные по 500 выборкам с объемами n = 1, 2, 4, 8, 16 и 32, извлеченным из нормально распределенной генеральной совокупности

Чтобы глубже разобраться в понятии выборочного распределения, вернемся к примеру с коробками. Предположим, что упаковочная машина, заполняющая 368-граммовые коробки, настроена так, что количество кукурузных хлопьев, засыпанных в мешки, распределено нормально, причем среднее значение распределения равно 368 г. Измерения показали, что стандартное отклонение веса коробок равно 15 г. Допустим, что из многих тысяч коробок, заполненных за день, наугад выбираются 25 коробок и вычисляется их средний вес. Следует ли ожидать, что выборочный средний вес окажется равным 368 г? А может быть, он будет равен 200 г или 365 г?

Выборка является миниатюрной моделью генеральной совокупности, поэтому если исходная генеральная совокупность распределена нормально, выборка из нее должна быть приближенно нормальной. Следовательно, если мат. ожидание генеральной совокупности равно 368 г, выборочное среднее также должно быть близким к 368 г. Продолжая наши рассуждения, зададимся вопросом, как вычислить вероятность того, что выборочное среднее, полученное для выборки объемом n = 25, окажется меньше 365 г. Из свойств нормального распределения следует, что площадь, отсекаемая каждым значением случайной величины X от фигуры, ограниченной гауссовой кривой, можно вычислить, преобразовав стандартизованную нормальную случайную величину Z:

Z = (Х – μ)/σ

Для расчетов в Excel преобразование не требуется. Просто воспользуйтесь функцией =НОРМ.РАСП() (рис. 5).

Рис. 5. Нормальная функция распределения; параметры: х – нормальная случайная величина, μ – среднее, σ – стандартное_откл, интегральная = ИСТИНА

Подставляя в приведенную выше формулу величину вместо X, величину вместо μ и величину вместо σ, получаем:

Обратите внимание на то, что благодаря несмещенности величина μХ̅ всегда равна μ. Таким образом, значение величины Z, соответствующее вероятности того, что выборочное среднее, полученное для выборки объемом n = 25, окажется меньше 365 г, равна:

а вероятность, соответствующая значению Z = –1, равна Р(Z=–1) = 0,1587

Следовательно, выборочное среднее 15,87% всех возможных выборок, имеющих объем n = 25, не превосходит 365 г. Это не значит, что вес 15,87% элементов выборок не превосходит 365 г. Долю таких элементов можно вычислить по следующей формуле:

а вероятность, соответствующая значению Z = –0,2, равна Р(Z=–0,2) = 0,4207

Следовательно, в каждой выборке, имеющей объем n = 25, вес 42,07% коробок не превосходит 365 г. Это можно объяснить тем, что каждая выборка состоит из 25 разных значений, некоторые из которых велики, а некоторые — малы. Процедура усреднения ослабляет влияние отдельных элементов, особенно при увеличении объема выборки. Таким образом, вероятность того, что выборочное среднее, вычисленное по выборке, состоящей из 25 коробок, будет значительно отличаться от математического ожидания генеральной совокупности, меньше вероятности, что вес отдельных элементов значительно отличается от этого значения.

В Excel задачу можно решить с помощью одной формулы (рис. 6).

Рис. 6. Вероятность того, что выборочное среднее, полученное для выборки объемом n = 25, окажется меньше 365 г.

Иногда необходимо найти интервал, в котором лежит фиксированная часть элементов выборки или выборочных средних. В этом случае необходимо вычислить расстояние от математического ожидания генеральной совокупности, которому соответствует заданная площадь фигуры, ограниченной гауссовой кривой. Воспользуемся формулой

Преобразовав ее получим, что величину можно вычислить по формуле:

Рассмотрим несколько примеров.

Пример 1. Влияние объема выборки n на стандартное отклонение выборочного среднего. Увеличим объем выборки с 25 до 100. Как изменится стандартное отклонение выборочного среднего? Решение. Если n = 100, то

Обратите внимание на то, что четырехкратное увеличение объема выборки приводит к уменьшению стандартного отклонения выборочного среднего вдвое — с 3 г до 1,5 г. Это значит, что, извлекая из генеральной совокупности выборки большего объема, мы обнаружим меньшую изменчивость выборочного среднего.

Пример 2. Влияние объема выборки n на концентрацию средних значений в выборочном распределении. Увеличим объем выборки с 25 до 100. Как изменится вероятность того, что выборочное среднее, полученное для выборки объемом n = 25, окажется меньше 365 г? Решение. Используя функцию =НОРМ.РАСП() получаем: Р(n = 100) = 2,28% (рис. 7). Следовательно, в каждой выборке, имеющей объем n = 100, вес 2,28% коробок не превосходит 365 г. Напомним, что для выборок, имеющих объем n = 25, эта вероятность была равна 15,87%.

Рис. 7. Вероятность того, что выборочное среднее, полученное для выборки объемом n = 100, окажется меньше 365 г.

Пример 3. Определение интервала, содержащего заданную часть выборочных средних. Найдите интервал, в котором лежат 95% всех выборочных средних, вычисленных по выборкам, состоящим из 25 коробок с кукурузными хлопьями. Решение. Интервал, содержащий 95% всех выборочных средних, вычисленных по выборкам, имеющим объем n = 25, делится на две равные части. Первая часть лежит слева от математического ожидания генеральной совокупности, а вторая — справа. Для расчета нижней L и верхней U границ интервалов воспользуемся функцией =НОРМ.ОБР(), возвращающая обратное нормальное распределение (рис. 8).

Рис. 8. Функция =НОРМ.ОБР(), возвращающая обратное нормальное распределение

Следовательно, 95% всех выборочных средних, вычисленных по выборкам, имеющим объем n = 25, лежат в интервале от 362,1 г до 373,9 г.

Выборки из генеральных совокупностей, распределения которых отличаются от нормального. До сих пор мы рассматривали выборочное распределение средних для нормально распределенной генеральной совокупности. Однако во многих ситуациях распределение генеральной совокупности либо неизвестно, либо заведомо отличается от нормального. Таким образом, следует рассмотреть выборочное распределение средних для генеральной совокупности, распределение которой отличается от нормального. Этот анализ приводит нас к основной теореме статистики:

Центральная предельная теорема утверждает, что при достаточно большом объеме выборок выборочное распределение средних можно аппроксимировать нормальным распределением. Это свойство не зависит от вида распределения генеральной совокупности.

Какой объем выборок следует считать «достаточно большим»? Этот вопрос изучался во многих статистических исследованиях. Как правило, для подавляющего большинства генеральных совокупностей выборочное распределение средних становится приближенно нормальным при n = 30. Однако, если известно, что распределение генеральной совокупности является колоколообразным, эту теорему можно применять и для меньшего объема выборок. Если же распределение генеральной совокупности обладает сильной асимметрией или имеет несколько мод, объем выборок следует увеличить.

Применение центральной предельной теоремы к различным генеральным совокупностям проиллюстрировано на рис. 9.

Рис. 9. Выборочное распределение средних для разных генеральных совокупностей при объемах выборок n = 2, 5 и 30

Панель А: выборочное распределение средних, построенное для генеральной совокупности, имеющей нормальное распределение. Как указывалось выше, если генеральная совокупность является нормально распределенной, выборочное распределение средних также является нормальным, независимо от объема выборок. При увеличении объема выборок изменчивость выборочных средних уменьшается. Панель Б: выборочное распределение средних, построенное для генеральной совокупности, имеющей равномерное распределение. При n = 5 выборочное распределение средних является приближенно нормальным. При n = 30 выборочное распределение средних становится практически нормальным. Панель В: выборочное распределение средних, построенное для генеральной совокупности, имеющей экспоненциальное распределение. Это распределение имеет ярко выраженную положительную асимметрию. При n = 2 асимметрия выборочного распределения средних сохраняется, но выражена слабее. При n = 5 выборочное распределение средних становится почти симметричным со слабой положительной асимметрией. При n = 30 выборочное распределение средних становится приближенно нормальным. В любом случае среднее выборочных средних всегда совпадает с математическим ожиданием генеральной совокупности, а его изменчивость при увеличении объема выборок уменьшается.

Свойства выборочного распределения средних:

  • Если объем выборок превышает 30, выборочное распределение средних для большинства генеральных совокупностей является приближенно нормальным.
  • Если генеральная совокупность распределена симметрично, выборочное распределение средних становится приближенно нормальным уже при n = 15.
  • Если генеральная совокупность является нормально распределенной, выборочное распределение средних является нормальным при любом объеме выборок.

Генерирование выборок в Excel

Чтобы создать массив случайных нормально распределенных чисел (например, стандартизованных, т.е. имеющих μ = 0 и σ = 1), подставим в функцию =НОРМ.СТ.ОБР(вероятность) в качестве параметра вероятность генератор случайных чисел СЛЧИС() (рис. 10). Этот генератор создает случайные числа в диапазоне от 0 (включая) до 1 (не включая). Случайные числа расположились в столбце А. Чтобы совокупность была «внушительной» формулой заполнены 1000 строк (при каждом изменении на листе формулы пересчитываются; кроме того, можно принудительно пересчитать формулы, нажав F9). Глядя на числа в столбце А трудно определить, что они нормально распределены. Чтобы эта закономерность стала видна, я создал сводную таблицу, а затем сгруппировал данные в столбце С по диапазонам, от –3 до 3 с шагом 0,4. В столбце D я отразил количество чисел, попадающих в диапазон (если ранее вы не сталкивались с такими настройками сводной таблицы, рекомендую почитать Изменение настраиваемого вычисления для поля в отчете сводных таблиц).

Рис. 10. Сгенерированный массив случайных нормально распределенных чисел (μ = 0 и σ = 1)

Аналогичного результата можно добиться, с помощью надстройки Пакет анализа. Выберите закладку Данные → область Анализ → Анализ данных → Генератор случайных чисел. (Если у вас не установлена надстройка Пакет анализа см. описание после рис. 5 заметки Представление числовых данных в виде таблиц и диаграмм.) Параметры открывшегося окна Генератор случайных чисел изменяются в зависимости от выбранного типа распределения. В поле Число переменных указывается необходимое количество столбцов, а в ноле Число случайных чисел — необходимое количество строк. Например, если нужно получить 200 случайных чисел, расположенных в 10 столбцах и 20 строках, введите в эти поля соответственно числа 10 и 20.

Рис. 11. Генерирование случайных чисел с помощью надстройки Пакет анализа

Поле Случайное рассеивание позволяет задать начальное значение, которое будет использовано программой в алгоритме генерации случайных чисел. Обычно это поле оставляют пустым. Однако, если необходимо генерировать одинаковые последовательности случайных чисел, задайте рассеивание в диапазоне от 1 до 32 767 (допускаются только целые числа). Из раскрывающегося списка Распределение можно выбрать одну из перечисленных ниже опций.

  • Равномерное. Генерируется последовательность равномерно распределенных случайных чисел в заданном интервале. Необходимо указать верхнюю и нижнюю границы интервала.
  • Нормальное. Генерируется последовательность случайных чисел, соответствующих нормальному распределению. Задается среднее значение и стандартное отклонение.
  • Бернулли. Генерируется последовательность случайных чисел, принимающих только значение 0 или 1, в зависимости от заданной вероятности успеха.
  • Биномиальное. Генерируется последовательность случайных чисел, соответствующих распределению Бернулли для некоторого числа попыток, с заданной вероятностью успеха.
  • Пуассона. Генерируется последовательность случайных чисел, соответствующих распределению Пуассона. Это распределение характеризует дискретные события, произошедшие в интервале времени, где вероятность одного события пропорциональна размеру интервала. Параметр Лямбда — это ожидаемое количество событий в интервале. В распределении Пуассона Лямбда равняется среднему, которое совпадает с дисперсией. Подробнее см. Распределение Пуассона
  • Модельное. Эта опция на самом деле не генерирует случайных чисел. Вместо этого она повторяет последовательность чисел в заданном порядке.
  • Дискретное. Эта опция позволяет определить вероятность, характеризующую выбираемые значения. Для нее требуется входной диапазон, состоящий из двух столбцов: в первом столбце содержатся значения, а во втором — вероятности каждого значения. Сумма вероятностей во втором столбце должна равняться 1.

Полученное в результате работы Пакета анализа случайные числа в диапазоне А2:А1001, я проанализировал также как и выше с помощью сводной таблицы и гистограммы. Надо отметить, что качество сгененрированных чисел мне не понравилось. В частности, за пределами диапазона ±3σ наблюдалось 6 чисел (теоретически их должно быть порядка трех), а одно даже приняло значение
–9,5, что уж совсем невероятно…

Выборочное распределение долей

При анализе категорийных данных, принимающих одно из двух значений — мужчина или женщина, любит / не любит и т.д., — результаты часто обозначают единицами (да) и нулями (нет). Среднее значение, вычисленное по выборке, состоящей из n таких элементов, равно количеству единиц, деленному на n. Например, из пяти респондентов три человека предпочитают торговую марку А, а двое — торговую марку Б. Следовательно, выборка состоит из трех единиц и двух нулей. Суммируя элементы выборки и деля сумму на пять, получаем, что доля поклонников торговой марки А в данной выборке равна 0,6. Таким образом, для категорийных данных выборочное среднее нулей и единиц представляет собой выборочную долю рS некоторой характеристики, которой обладают элементы выборки.

Выборочная доля признака:

pS = X / n = количество объектов, имеющих указанную характеристику / размер выборки

Выборочная доля признака pS имеет особое свойство: она принимает значения от 0 до 1. Если все элементы выборки обладают одинаковыми характеристиками, то каждому из них присваивается единица, а выборочная доля признака также становится равной единице. Если только половина элементов выборки обладает интересующим нас свойством, им приписываются единицы, а остальные обозначаются нулями. В этом случае выборочная доля признака pS равна 0,5. Если ни один элемент выборки не обладает интересующим нас свойством, им приписываются нули. В этом случае выборочная доля признака pS равна нулю.

В то время как выборочное среднее является несмещенной оценкой математического ожидания генеральной совокупности статистика pS является несмещенной оценкой доли признака р в генеральной совокупности. По аналогии с распределением выборочных средних можно ввести стандартную ошибку доли признака:

Если выборка извлекается из конечной генеральной совокупности без возвращения, выборочное распределение доли признака подчиняется биномиальному закону (см. Биномиальное распределение). Однако, если значения nр и n(1 – р) больше 4, это распределение можно аппроксимировать нормальным. При статистическом анализе долей признака объем выборки играет очень важную роль. Следовательно, во многих ситуациях для оценки выборочного распределения доли признака можно использовать нормальное распределение. Таким образом, в формуле

величину можно заменить величиной pS, величину μ — величиной р, а величину σ/√n – величиной

Разность между выборочной долей признака и долей признака в генеральной совокупности:

Проиллюстрируем выборочное распределение доли признака следующим примером. Предположим, что менеджер местного отделения банка выяснил, что 40% всех вкладчиков имеют в банке несколько счетов. Если создать выборку из 200 вкладчиков, то можно вычислить вероятность того, что выборочная доля вкладчиков, имеющих несколько счетов, не превосходит 0,3. Поскольку np = 200*0,4 = 80 > 5 и n(1 – р) = 200×0,6 = 120 > 5, выборочное распределение доли вкладчиков практически совпадает с нормальным. Применим только что полученную формулу:

Значению Z = –2,89 соответствует р(Z) = 0,0019. Следовательно, вероятность того, что доля вкладчиков, имеющих несколько счетов, не превосходит 0,3, равна 0,19%, т.е. крайне мала.

Выборки из конечных генеральных совокупностей

Центральная предельная теорема, а также формулы для вычисления стандартной ошибки среднего и стандартной ошибки доли признака основаны на предположении, что выборки извлекаются из генеральной совокупности с возвращением. Однако практически во всех статистических исследованиях выборки извлекаются из генеральных совокупностей конечного объема N без возвращения. Если объем выборок n достаточно велик по сравнению с объемом генеральной совокупности N (т.е. выборка содержит более 5% элементов генеральной совокупности), так что n/N > 0,05, то при вычислении стандартной ошибки среднего и стандартной ошибки доли признака следует учитывать поправочный коэффициент для конечной генеральной совокупности (fpc — finite population correction factor). Эта поправка вычисляется по формуле:

где n — объем выборки, а N — объем генеральной совокупности.

Таким образом, формулы для вычисления стандартной ошибки среднего и стандартной ошибки доли признака принимают следующий вид:

Анализ формулы для вычисления поправочного коэффициента для конечной генеральной совокупности (6.19) показывает, что ее числитель всегда меньше знаменателя, поскольку число n всегда больше единицы. Следовательно, поправочный коэффициент для конечной генеральной совокупности меньше единицы. Поскольку этот коэффициент умножается на стандартную ошибку, скорректированная стандартная ошибка уменьшается. Таким образом, с учетом поправочного коэффициента для конечной генеральной совокупности мы получаем более точные оценки.

Например, предположим, что банк обслуживает 1000 клиентов, причем 400 из них имеют больше одного счета. Используя поправочный коэффициент для конечной генеральной совокупности, определите вероятность извлечь выборку, состоящую из 200 клиентов, в которой доля клиентов, имеющих несколько банковских счетов меньше 0,30.

Решение. Разность между выборочной долей признака и долей признака в генеральной совокупности (при n = 200):

Значению Z = –3,23 соответствует вероятность р(Z) = 0,00062. Следовательно, вероятность того, что доля вкладчиков, имеющих несколько счетов, не превосходит 0,3, равна 0,06%. Учет поправочного коэффициента для конечной генеральной совокупности втрое уменьшил вероятность (см. аналогичный пример выше, где p(Z) = 0,19%).

Предыдущая заметка Равномерное и экспоненциальное распределения

Следующая заметка Построение доверительного интервала для математического ожидания генеральной совокупности

К оглавлению Статистика для менеджеров с использованием Microsoft Excel

[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 385–415

Источник

From Wikipedia, the free encyclopedia

In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given random-sample-based statistic. If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value of a statistic (such as, for example, the sample mean or sample variance) for each sample, then the sampling distribution is the probability distribution of the values that the statistic takes on. In many contexts, only one sample is observed, but the sampling distribution can be found theoretically.

Sampling distributions are important in statistics because they provide a major simplification en route to statistical inference. More specifically, they allow analytical considerations to be based on the probability distribution of a statistic, rather than on the joint probability distribution of all the individual sample values.

Introduction[edit]

The sampling distribution of a statistic is the distribution of that statistic, considered as a random variable, when derived from a random sample of size n. It may be considered as the distribution of the statistic for all possible samples from the same population of a given sample size. The sampling distribution depends on the underlying distribution of the population, the statistic being considered, the sampling procedure employed, and the sample size used. There is often considerable interest in whether the sampling distribution can be approximated by an asymptotic distribution, which corresponds to the limiting case either as the number of random samples of finite size, taken from an infinite population and used to produce the distribution, tends to infinity, or when just one equally-infinite-size “sample” is taken of that same population.

For example, consider a normal population with mean mu and variance sigma ^{2}. Assume we repeatedly take samples of a given size from this population and calculate the arithmetic mean {displaystyle {bar {x}}} for each sample – this statistic is called the sample mean. The distribution of these means, or averages, is called the “sampling distribution of the sample mean”. This distribution is normal {displaystyle {mathcal {N}}(mu ,sigma ^{2}/n)} (n is the sample size) since the underlying population is normal, although sampling distributions may also often be close to normal even when the population distribution is not (see central limit theorem). An alternative to the sample mean is the sample median. When calculated from the same population, it has a different sampling distribution to that of the mean and is generally not normal (but it may be close for large sample sizes).

The mean of a sample from a population having a normal distribution is an example of a simple statistic taken from one of the simplest statistical populations. For other statistics and other populations the formulas are more complicated, and often they do not exist in closed-form. In such cases the sampling distributions may be approximated through Monte-Carlo simulations,[1] bootstrap methods, or asymptotic distribution theory.

Standard error[edit]

The standard deviation of the sampling distribution of a statistic is referred to as the
standard error of that quantity. For the case where the statistic is the sample mean, and samples are uncorrelated, the standard error is:

{displaystyle sigma _{bar {x}}={frac {sigma }{sqrt {n}}}}

where sigma is the standard deviation of the population distribution of that quantity and n is the sample size (number of items in the sample).

An important implication of this formula is that the sample size must be quadrupled (multiplied by 4) to achieve half (1/2) the measurement error. When designing statistical studies where cost is a factor, this may have a role in understanding cost–benefit tradeoffs.

For the case where the statistic is the sample total, and samples are uncorrelated, the standard error is:

{displaystyle sigma _{Sigma x}=sigma {sqrt {n}}}

where, again, sigma is the standard deviation of the population distribution of that quantity and n is the sample size (number of items in the sample).

Examples[edit]

Population Statistic Sampling distribution
Normal: {mathcal {N}}(mu ,sigma ^{2}) Sample mean {bar {X}} from samples of size n {bar X}sim {mathcal {N}}{Big (}mu ,,{frac {sigma ^{2}}{n}}{Big )}.

If the standard deviation sigma is not known, one can consider {displaystyle T=left({bar {X}}-mu right){frac {sqrt {n}}{S}}}, which follows the Student’s t-distribution with nu = n - 1 degrees of freedom. Here S^{2} is the sample variance, and T is a pivotal quantity, whose distribution does not depend on sigma .

Bernoulli: operatorname {Bernoulli}(p) Sample proportion of “successful trials” {bar {X}} n{bar X}sim operatorname {Binomial}(n,p)
Two independent normal populations:

{mathcal {N}}(mu _{1},sigma _{1}^{2})  and  {mathcal {N}}(mu _{2},sigma _{2}^{2})

Difference between sample means, {bar X}_{1}-{bar X}_{2} {bar X}_{1}-{bar X}_{2}sim {mathcal {N}}!left(mu _{1}-mu _{2},,{frac {sigma _{1}^{2}}{n_{1}}}+{frac {sigma _{2}^{2}}{n_{2}}}right)
Any absolutely continuous distribution F with density f Median X_{{(k)}} from a sample of size n = 2k − 1, where sample is ordered X_{{(1)}} to X_{{(n)}} f_{{X_{{(k)}}}}(x)={frac {(2k-1)!}{(k-1)!^{2}}}f(x){Big (}F(x)(1-F(x)){Big )}^{{k-1}}
Any distribution with distribution function F Maximum M=max X_{k} from a random sample of size n F_{M}(x)=P(Mleq x)=prod P(X_{k}leq x)=left(F(x)right)^{n}

References[edit]

  1. ^ Mooney, Christopher Z. (1999). Monte Carlo simulation. Thousand Oaks, Calif.: Sage. p. 2. ISBN 9780803959439.
  • Merberg, A. and S.J. Miller (2008). “The Sample Distribution of the Median”. Course Notes for Math 162: Mathematical Statistics, pgs 1–9.

External links[edit]

  • Mathematica demonstration showing the sampling distribution of various statistics (e.g. Σx²) for a normal population
Источник

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость

Статистическое распределение выборки

Содержание:

  • Примеры использования формул и таблиц для решения практических задач
  • Статистический интервальный ряд распределения

Предположим случай, когда из генеральной совокупности извлекается некоторая выборка, при этом каждому значению соответствует некоторый параметр, означающий количество раз, когда появлялось данное значение. Здесь $x_1$ было зафиксировано $n_1$ раз, $x_2$ было обнаружено $n_2$$x_k$ выявлено $n_k$. При этом

$sum_{i=1}^{k}n_i=n$

Где n — объём рассматриваемой выборки.

Определение 1

Используется следующая терминология: $x_k$ носят наименование вариантов, а последовательность таких вариантов, зафиксированный по возрастанию именуется вариационным рядом. Количество наблюдений каждого из вариантов носят название частот. При этом частное частот и выборки называют относительными частотами.

Определение 2

Статистическое распределение —это название всего набора вариантов и частот, которые с ними соотносятся. Чаще всего задаётся с помощью специальной таблицы, где представлены частоты, а также интервалы им соответствующие.

$x_1$ $x_2$ … $x_k$
$n_1$ $n_2$ … $n_k$
$frac{n_1}{n}$ $frac{n_2}{n}$ $frac{n_k}{n}$

Здесь в первой строке представлены варианты, во второй частоты, в третьеq взяты относительные частоты.

Для определения размера интервала используется следующее выражение:

$d=frac{x_{max}- x_{min}}{1+3,332cdot lg n}$

Здесь $x_{max}$, $x_{min}$ наибольшее и наименьшее значения ряда вариантов, а n характеризуем объём выборки.

Примеры использования формул и таблиц для решения практических задач

Пример 1

В ходе проведения измерений в однородных группах, были определены следующие значения выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74. Необходимо использовать данные значения, что определить ряд распределения частот и ряд распределения относительных частот.

Решение.

1) Составим статистический ряд распределения частот:

xi 70 71 72 73 74
ni 2 4 8 2 4

2) Рассчитаем суммарный размер выборки: n=2+4+8+2+4=20. Определим относительные частоты, для этого используем формулы: ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Теперь зафиксируем в таблице распределение относительных частот:

xi 70 71 72 73 74
wi 0.1 0.2 0.4 0.1 0.2

Контрольная сумма должна равняться единице: 0,1+0,2+0,4+0,1+0,2=1.

Полигон частот

Название «полигоном частот» применяют для обозначения ломаной линии, каждый отрезок, которой соединяют точки $(х_1,n_1),(х_2,n_2),…,(х_k,n_k)$. Для построения на графике полигона частот по оси абсцисс отмечают варианты $х_2$, при этом на оси ординат отсчитывают– соответствующие частоты $n_i$. Когда полученные точки $(х_i,n_i)$ соединяются с помощью отрезков, то автоматически получают полигон частот.

Статистический интервальный ряд распределения.

Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются, если число различающихся вариант в полученной выборке не слишком большое. Также применение возможно, когда дискретность имеет важное значение для экспериментатора. В тех случаях, когда важный для задачи признак генеральной совокупности Х распределяется непрерывным образом, либо его дискретность нет возможности учесть, то варианты предпочтительнее всего группировать, чтобы получить интервалы.

Статистическое распределение допустимо задавать в том числе в качестве последовательности интервалов и частот, соответствующих этим интервалам. При это за частоту какого-либо интервала принимается сумма всех частот, вошедших в данный интервал.

Особенно следует отметить ,что $h_i-h_{i-1}=h$ при всех i, т.е. группировка проводится с равным шагом h. Также в вопросе группировки можно ориентироваться на ряд полученных опытным путём рекомендацийу, касающихся таких параметров, как а, k и $h_i$:

1. $Rраз_{мах}=X_{max}-X_{min}$

2. $h=R/k$; k-число групп

3.$ kgeq 1+3.321lgn$ (формула Стерджеса)

4. $a=x_{min}, b=x_{max}$

5.$ h=a+h_i, i=0,1…k$

Определённую в ходе решения задачи группировку удобнее всего скомпоновать и перевести в вид специальной таблицы, которая также может именоваться — «статистический интервальный ряд распределения»:

Интервалы группировки [h0;h1) [h1;h2) … [hk-2;hk-1) [hk-1;hk)
Частоты n1 n2 … nk-1 nk

Таблицу подобного вида можно сделать, поменяв частоты $n_i$ на относительные частоты:

Интервалы группировки [h0;h1) [h1;h2) … [hk-2;hk-1) [hk-1;hk)
Отн. частоты w1 w2 … wk-1 wk

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример 2

На склад пришла крупная партия деталей. Из них методом случайного отбора взято 50 экземпляров. Рассматривая изделия по одному, особенно интересующему признаку — размеру, определённому с точностью до 1 см, получим следующий вариационный ряд: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Требуется произвести расчёт и определить статистический интервальный ряд распределения.

Решение

Найдём параметры выборки используя сведения из условия задачи.

$k geq1+3,321cdot lg50=1+3.32lg(5cdot10)=1+3.32(lg5+lg10)=6.6$

Получили a=22, k=7, h=(50-22)/7=4, hi=22+4i, i=0,1,…,7.

Интервалы группировки 22-26 26-30 30-34 34-38 38-42 42-46 46-50
Частоты 1 4 10 18 9 5 3
Отн. частоты 0.02 0.08 0.2 0.36 0.18 0.1 0.06

Десятичные логарифмы от 1 до 10

n 1 2 3 4 5 6 7 8 9 10
lnn≈ 0 0.3 0.48 0.6 0.7 0.78 0.85 0.9 0.95 1

Не получается написать работу самому?

Доверь это кандидату наук!

Источник

Добавить комментарий