Слайд 1
3.10 Классная работа
Слайд 2
Проверка домашнего задания № 307 I – а лет II – ?, на b лет старше а + b (лет) – другому брату а) если а =14; b = 13, то 14 + 13 = 27 б) если а =6; b = 8, то 6 + 8 = 14 Ответ: другому брату 27 лет; 14 лет
Слайд 3
№ 312 б) Р = 13 + с + d если с = 5 и d = 12, то Р = 13 + 5 + 12 = 30 (см) Ответ: Р = 30 (см) № 336 в) в) ( а + b ) – 674 если а = 830; b = 243, то (830 + 243) – 674 = 399 если а = 1712; b = 805, то (1712 + 805) – 674 = 1843
Слайд 4
Тест Выражение (234 + b ) · 63 называется: а) буквенным ; б) числовым ; в) простым 3) У Маши 7 карандашей, а у Саши на к больше . Сколько карандашей у Саши и Маши вместе ? а)7 + а; б) 7 + (7 + а); в) (7 + а) · 7 2) Прочитай (24 + р) – 63. Определи – это а) сумма ; б)разность; в) уменьшаемое
Слайд 5
Задача Папа на рыбалке поймал 13 рыб, а Женя на m рыб меньше . Сколько рыб поймали папа и Женя вместе ? Составь выражение для решения задачи П. – 13 р. Ж. – ?, на m р. м. ? 13 13 – m 13 + (13 – m )
Слайд 6
Решите самостоятельно Масса одного арбуза 6 кг, а масса другого на n кг меньше. Какова общая масса двух арбузов? Составьте выражение и найдите его значение при n = 2; 3; 4 Подсказка 1 1арб. – 6 кг 2арб. – ?, на n кг м. ? 6 6 – n Подсказка 2 6 + ( 6 – n )
Слайд 7
Задача Пусть цена футболки а рублей, а цена трусов b рублей. Какой смысл имеет выражение: а + b а – b 340 – (а + b )
Слайд 8
Ёжик нашёл в лесу а грибов, а белочка – b грибов. Какой смысл имеют следующие выражения? а – b а + b b – a
Слайд 9
Решите самостоятельно I вариант – №305а), 335в) II вариант – №305б), 335б)
Слайд 10
Домашнее задание № 329, 334, 335г), 321 (устно)
Составьте выражение для решения задачи и найдите его значение:
а) В одном мешке было 46 кг зерна, что на 18 кг меньше, чем во втором мешке. Сколько килограммов зерна было в обоих мешках вместе?
б) Площадь одной теплицы 234
м
2
, что на 108
м
2
больше площади другой. Какова площадь двух теплиц вместе?

reshalka.com
Математика 5 класс Виленкин. Номер №305
Решение а
Во втором мешке: (46 + 18) кг зерна, а в обоих мешках: 46 + (46 + 18) = 46 + 64 = 110 кг зерна.
Решение б
Площадь другой теплицы равна (234 − 108)
м
2
.
Площадь обеих теплиц равна 234 + (234 − 108) = 234 + 126 = 360
м
2
.
Натуральные числа
Сложение и вычитание натуральных чисел
Буквенная запись свойств сложения и вычитания
Ответы к стр. 56
345. Из свойств вычитания следует:
(154 + b) – 24 = (154 – 24) + b = 130 + b;
α – 10 + 15 = (α – 10) + 15 = (α + 15) – 10 = α + (15 – 10) = α + 5.
Какое свойство вычитания применяется в этом примере? Используя это свойство, упростите выражение:
а) (248 + m) – 24; в) b + 127 – 84; д) (12 – k) + 24;
б) 189 + n – 36; г) α – 30 + 55; е) х – 18 + 25.
Свойство вычитания числа из суммы.
а) (248 + m) – 24 = (248 – 24) + m = 224 + m;
б) 189 + n – 36 = (189 – 36) + n = 153 + n;
в) b + 127 – 84 = b + (127 – 84) = b + 43;
г) α – 30 + 55 = α + (55 – 30) = α + 25;
д) (12 – k) + 24 = (12 + 24) – k = 36 – k;
е) х – 18 + 25 = x + (25 – 18) = x + 7.
346. Найдите значение выражения, предварительно упростив его:
а) α – 28 – 37 при α = 265; в) 237 + с + 163 при с = 194; 188;
б) 149 + b – 99 при b = 77; г) d – 135 + 165 при d = 239; 198.
а) α – 28 – 37 = α – (28 + 37) = α – 65,
при α = 265: 265 – 65 = 200;
б) 149 + b – 99 = b + 149 – 99 = b + (149 – 99) = b + 50,
при b = 77: 77 + 50 = 127;
в) 237 + с + 163 = с + 237 + 163 = с + (237 + 163) = с + 400,
при с = 194: 194 + 400 = 594;
при с = 188: 188 + 400 = 588;
г) d – 135 + 165 = d + (165 – 135) = d + 30,
при d = 239: 239 + 30 = 269;
при d = 198: 198 + 30 = 228.
347. На отрезке АВ отмечены точки С и D, причём точка С лежит между точками А и D. Составьте выражение для длины отрезка:
а) АВ, если АС = 453 мм, CD = х мм и DB = 65 мм. Найдите значение получившегося выражения при х = 315; 283.
б) АС, если АВ = 214 мм, CD = 84 мм и DB = у мм. Найдите значение получившегося выражения при у = 28; 95.
![]()
а) АВ = АС + CD + DB = 453 + х + 65 = 453 + 65 + х = 518 + х (мм),
при х = 315: АВ = 518 + 315 = 833 (мм),
при х = 283: АВ = 518 + 283 = 801 (мм);
б) АС = АВ – CD – DB = 214 – 84 – у = 130 – у (мм),
при у = 28: АС = 130 – 28 = 102 (мм),
при у = 95: АС = 130 – 95 = 35 (мм).
348. Токарь выполнил заказ на изготовление одинаковых деталей за три дня. В первый день он изготовил 23 детали, во второй день – на b деталей больше, чем в первый день, а в третий день – на четыре детали меньше, чем в первый день. Сколько деталей изготовил токарь за эти три дня? Составьте выражение для решения задачи и найдите его значение при b = 7 и b = 9.
23 + (23 + b) + (23 – 4) = 23 + 23 + 23 – 4 + b = 65 + b (д.) – изготовил за 3 дня
при b = 7: 65 + 7 = 72 (д.)
при b = 9: 65 + 9 = 74 (д.)
О т в е т: 72 детали, 74 детали.
349. Вычислите устно:
а) 50 + 40 в) 100 – 70 д) 67 – 23
90 : 30 30 • 3 44 : 11
3 • 50 90 – 18 4 • 25
150 – 100 72 : 36 100 – 19
50 2 81
б) 30 + 70 г) 100 – 80
100 : 10 20 : 4
10 • 15 5 • 14
150 – 150 70 – 67
0 3
350. Найдите половину, четверть и треть каждого из чисел: 12; 36; 60; 84; 120.
| Число | 12 | 36 | 60 | 84 | 120 |
| Половина | 6 (12 : 2) |
18 (36 : 2) |
30 (60 : 2) |
42 (84 : 2) |
60 (120 : 2) |
| Четверть | 3 (12 : 4) |
9 (36 : 4) |
15 (60 : 4) |
21 (84 : 4) |
30 (120 : 4) |
| Треть | 4 (12 : 3) |
12 (36 : 3) |
20 (60 : 3) |
28 (84 : 3) |
40 (120 : 3) |
351. Придумайте задачу, решением которой является выражение:
а) (47 – 15) + (62 – 12); б) х + (39 – 14); в) 81 – (х + у).
а) Вика купила 47 конфент и съела 15 из них, а Катя купила 62 конфеты и съела 12 из них. Сколько всего конфет осталось у девочек?
(47 – 15) + (62 – 12) = 32 + 50 = 82 (к.) – осталось
О т в е т: у девочек осталось 82 конфеты.
б) В автобусе ехало несколько пассажиров. На остановке вышло 14 человек и вошло 39 человек. Сколько человек стало в автобусе после остановки?
х + (39 – 14) = х + 25 (п.) – стало в автобусе
О т в е т: в автобусе остал х + 25 пассажиров.
в) На отрезке АВ отмечены точки С и D, причём точка С лежит между точками А и D. Найдите длину отрезка АС, если АВ = 81 мм, CD = х мм и DB = у мм.
81 – (х + у) (мм)- длина отрезка АС
О т в е т: длина отрезка АС 81 – (х + у) мм.
Ответы по математике. 5 класс. Учебник. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И
Математика. 5 класс
5 класс. Математика. Виленкин. Учебник. Ответы к стр. 56
1.5 (29.7%) от 33 голосующих
Урок математики в 5 классе «Решение задач с помощью уравнений»

Цель урока:
- ознакомиться с примером одного из типов задач на составление уравнения; тренировать способность к построению моделей текстовых задач на основе использования таблиц и способность к решению усложненных уравнений; повторить и закрепить зависимости между компонентами в уравнениях.
- формирование алгоритма рефлексивного мышления.
Просмотр содержимого документа
«Урок математики в 5 классе «Решение задач с помощью уравнений»»
Урок математики в 5 классе «Решение задач с помощью уравнений»
ознакомиться с примером одного из типов задач на составление уравнения; тренировать способность к построению моделей текстовых задач на основе использования таблиц и способность к решению усложненных уравнений; повторить и закрепить зависимости между компонентами в уравнениях.
формирование алгоритма рефлексивного мышления.
Обучающие:
•формирование представлений о решении задач с помощью уравнений;
•приобретение опыта применения уравнения для решения текстовых задач.
Развивающие:
•умение определять понятия, создавать обобщения, устанавливать причинно-следственные связи, строить логические рассуждения и делать выводы;
•умение создавать, применять и преобразовывать математические модели для решения учебных и познавательных задач;
•умение оценивать правильность выполнения учебной задачи, собственные возможности ее решения.
Воспитательные:
•формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
•формирование целостного мировоззрения;
•формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками
Тип урока: изучение нового материала.
Формы работы учащихся: фронтальная, индивидуальная
Оборудование, демонстрационный материал: компьютер, мультимедиа проектор, презентация, таблицы для самостоятельной работы.
I. Проверка д/з (крылья доски)
Конспект урока по математике по теме :”Решение задач при помощи уравнений”
план-конспект урока по алгебре (5 класс) на тему
Конспект урока по математике по теме :”Решение задач при помощи уравнений” 5 класс Виленкин Фгос
Скачать:
| Вложение | Размер |
|---|---|
| Конспект урока по теме “Решение задач при помощи уравнений” | 57.5 КБ |
| reshenie_zadach_pri_pomoshchi_uravneniy.ppt | 2.28 МБ |
Предварительный просмотр:
1. Организационный момент (1-2)
Решение задач при помощи уравнений.
стр. 63 № 382 (а, б, в)
В книжном магазине на двух полках 73 книги. На второй полке 54 книги. Сколько книг на первой полке?
Здравствуйте! Присаживайтесь! Мы начинаем урок!
Ребята, откройте тетради, запишите число (на полях) и классная работа.
Записывают число и классная работа.
2. Актуализация опорных знаний (5-7 мин)
Откройте учебник на
стр. 63 № 382 (а, б, в)
Мы начинаем математическую разминку.
Начинаем устный счет.
Ребята, мы провели математическую разминку в форме устного счета. Для чего нам нужен устный счет?
Ребята, мы переходим на следующий этап нашего урока.
Устный счет нам нужен для того, чтобы отработать вычислительные навыки.
3. Изучение нового материала (15-20 мин)
Ребята, чего нам не хватает, чтобы начать урок?
Посмотрите на доску, на доске записана задача.
Решив данную задачу, мы узнаем тему нашего сегодняшнего урока.
Итак, ребята, что необходимо, чтобы приступить к решению задачи? Верно! Давайте запишем условие данной задачи.
Какой следующий этап после записи условия задачи?
Давайте обратимся еще раз к условию задачи, что нам необходимо найти?
По условию задачи, сможем мы найти количество книг на первой полке.
Ребята, давайте обратимся к тексту задачи, мы ответили на вопрос задачи?
Ребята, при помощи чего мы решили данную задачу?
Этот метод называют арифметический (по действиям).
Ребята, а можно ли как – то еще решить эту задачу? Мы с вами на прошлых уроках изучали равенства? Как они называются?
А что мы называем уравнением?
Можем ли мы применить уравнение, чтобы решить нашу задачу?
Верно, давайте составим уравнение.
Ребята, мы нашли х, а что мы обозначали за х? Правильно! Мы ответили на вопрос задачи?
Значит, какой можно сделать вывод?
Ребята, как вы думаете, какая тема нашего сегодняшнего урока?
Верно! Ребята, данный метод еще называют алгебраический.
А какую цель урока мы поставим перед собой?
Молодцы! Ребята, но прежде чем мы приступим к выполнению упражнений, я вам покажу, то, как мы будем оформлять задачи, которые можно решать при помощи уравнений.
Итак, посмотрите на доску.
У нас с вами была задача. Решение задачи любой задачи начинается с чего? Верно, записали условие и слово решение, а после слово решения, задачи, которые решаются при помощи уравнений начинаются с:
Что мы обозначаем за х?
Пусть х книг на первой полке.
Какую следующую величину мы можем составить?
На двух полках (х+54) книги,
А по условию задачи нам известно чему равно значение этого выражения?
На двух полках (х+54) книги, а по условию задачи на двух полках 73 книги .
Составим и решим уравнение.
Вернемся к условию задачи! Что мы обозначали за неизвестное х?
19 книг на первой полке.
Ответ: 19 книг на первой полке.
Ребята, какие вопросы по решению задачи при помощи уравнений у вас есть?
Давайте еще раз посмотрим на доску, с чего мы начинаем решение задачи при помощи уравнений?
Верно, а через нее выражаем остальные величины.
Записать условие.
1 полка -? книг
2 полка – 54 книги
Нам необходимо найти количество книг на первой полке.
- 73-54=19 (книг) – на первой полке
Ответ: 19 книг на первой полке
При помощи арифметического действия – вычитания.
Уравнение – равенство, содержащее букву, значение которой надо найти.
Обозначить количество книг на первой полке и составить уравнение.
Х- неизвестное слагаемое, чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Количество книг на первой полке.
Мы решили задачу при помощи уравнения.
Решение задач при помощи уравнений.
Научиться решать задачи при помощи уравнений.
Решение задач уравнением. Задачи по математике для 5 класса.
Задача 1
Лена загадала некоторое число. Если это число уменьшить на 12, то получится 5. Какое число загадала Лена?
-
Решение
- Пусть число, которое задумала Лена x. Тогда:
- x – 12 = 5,
- x = 12 + 5,
- x = 17.
- Ответ: Лена загадала число 17.
Задача 2
Некоторое число увеличили в 7 раз, после чего получили 119. Что это за число?
-
Решение
- Пусть y неизвестное число. Тогда:
- 7y = 119,
- y = 119 : 7,
- y = 17.
- Ответ: это число 17.
Задача 3
Найдите числа, следующие друг за другом, если их сумма равна 159.
-
Решение
- Пусть первое число равно x. Тогда:
- x + x + 1 = 159,
- 2x + 1 = 159,
- 2x = 159 – 1 = 158,
- x = 158 : 2,
- x = 79,
- x + 1 = 79 + 1 = 80.
- Ответ: 79, 80.
Задача 4
Одно число больше другого на 38. Чему равны эти числа, если их сумма равна 184.
-
Решение
- Пусть меньшее число равно y. Тогда:
- y + y + 38 = 184
- 2y + 38 = 184,
- 2y = 184 – 38 = 146,
- y = 146 : 2 = 73,
- y + 38 = 73 + 38 = 111.
- Ответ: 111, 73.
Задача 5
За три дня турист преодолел 105 км. Сколько километров турист преодолел в первый день, если в каждый последующий день он преодолевал на 3 км больше, чем в предыдущий?
-
Решение
- Пусть в первый день турист преодолел x км. Тогда:
- x + x + 3 + x + 3 + 3 = 105,
- 3x + 9 = 105,
- 3x = 105 – 9 = 96,
- x = 96 : 3 = 32 (км).
- Ответ: в первый день турист преодолел 32 км.
Задача 6
Сколько лет маме, если она старше дочери на 24 года, а дочь моложе матери в 7 раз?
-
Решение
- Пусть дочери x лет. Тогда:
- x + 24 = 7x,
- 24 = 7x – x,
- 6x = 24,
- x = 24 : 6 = 4,
- x + 24 = 4 + 24 = 28.
- Ответ: маме 28 лет.
Задача 7
На рисунке изображены треугольники и четырехугольники. Сколько тех и других изображено на рисунке, если у всех фигур вместе 69 углов, а всего фигур – 18?
-
Решение
- Пусть на рисунке изображено x четырехугольников. Тогда:
- 4x + (18 – x) * 3 = 69,
- 4x + 54 – 3x = 69,
- x = 69 – 54 = 15,
- 18 – x = 18 – 15 = 3.
- Ответ: на рисунке было изображено 15 четырехугольников и 3 треугольников.
Задача 8
Швейная мастерская закупила 2 сорта ткани всего 49 метров. Стоимость одного 110 рублей за 1 метр, стоимость другого 100 рублей за 1 метр. Сколько метров каждого сорта было куплено, если всего потратили 5150 рублей?
-
Решение
- Пусть первого сорта ткани было закуплено x метров. Тогда:
- 110x + (49 – x) * 100 = 5150,
- 110x + 4900 – 100x = 5150,
- 10x = 5150 – 4900 = 250,
- x = 250 : 10 = 25,
- x – 25 = 49 – 25 = 24.
- Ответ: первого сорта ткани было куплено 25 метров, второго 24 метра.
Задача 9
Мама покупала в магазине овощи и фрукты. За овощи она заплатила на 90 рублей меньше чем за фрукты, а за фрукты заплатили в 2 раза больше, чем за овощи. Сколько мама заплатила за овощи и за фрукты по отдельности?
-
Решение
- Пусть за овощи мама заплатила x рублей. Тогда:
- x + 90 = 2x,
- x = 90,
- 2x = 2 * 90 = 180 (рублей).
- Ответ: за фрукты мама заплатила 180 рублей, за овощи 90 рублей.
Задача 10
Стоимость фломастеров и тетрадей вместе составляет 276 рублей, стоимость фломастеров составляет 0,6 стоимости книги, а тетради на 60 рублей дороже книги. Сколько стоят тетради?
-
Решение
- Пусть тетради стоят x рублей. Тогда:
- (276 – x) : 0,6 – x = 60,
- 276 – x = (60 + x) * 0,6,
- 276 – x = 36 + 0,6x,
- 1,6x = 276 – 36 = 240,
- x = 240 : 1,6 = 150 (рублей).
- Ответ: тетради стоят 150 рублей.
Задача 11
Саша задумал 3 натуральных числа. Первое из чисел наибольшее двузначное число, второе в 4 раза больше третьего. Что за числа задумал Саша, если сумма этих чисел равна 934?
-
Решение
- Наибольшее двузначное число – 99. Пусть третье число равно x. Тогда:
- x + 4x + 99 = 934,
- 5x = 934 – 99 = 835,
- x = 835 : 5 = 167;
- 4x = 4 * 167 = 668,
- Ответ: Саша задумал числа 99, 167, 668.
Задача 12
На трех книжных полках стояли книги. На первой полке книг стояло в 2 раза меньше, чем на второй, а на третьей на 4 меньше чем на первой. Сколько книг стояло на каждой из полок, если всего в шкафу было 88 книг?
-
Решение
- Пусть на первой полке стояло x книг. Тогда:
- x + 2x + x – 4 = 88,
- 4x = 88 + 4 = 92,
- x = 92 : 4 = 23 (книги) на первой полке;
- 2x = 2 * 23 =46 (книг) на второй полке;
- x – 4 = 23 – 4 = 19 (книг) на третьей.
- Ответ: на первой полке стояло 23 книг, на второй 46, на третьей 19.
[spoiler title=”источники:”]
http://nsportal.ru/shkola/algebra/library/2014/06/16/konspekt-uroka-po-matematike-po-teme-reshenie-zadach-pri-pomoshchi
http://mat-zadachi.ru/5-class/zadachi/zadachi-uravneniyem.php
[/spoiler]
 2013г.ВыбранВыбрать
2013г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №329 по учебнику Математика. 5 класс : учебник для учащихся общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. – 31 издание 2013г.
 2019г.ВыбранВыбрать
2019г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №329 по учебнику Математика. 5 класс : учебник для учащихся общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. – 37 издание 2019г.
Условие
20132019г.
Составьте выражение для решения задачи и найдите его значение:
«В треугольнике ABC длина стороны АВ равна 5 см, сторона ВС длиннее стороны АВ на 8 см, а длина стороны АС меньше суммы длин сторон АВ и ВС на 6 см. Найдите периметр треугольника».
Составьте выражение для решения задачи и найдите его значение:
«В треугольнике ABC длина стороны АВ равна 5 см, сторона ВС длиннее стороны АВ на 8 см, а длина стороны АС меньше суммы длин сторон АВ и ВС на 6 см. Найдите периметр треугольника».
Решение 1
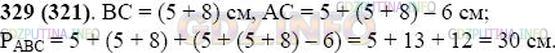
Решение 1
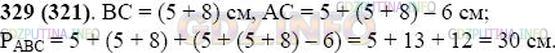
Решение 2
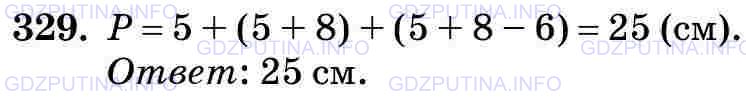
Решение 2
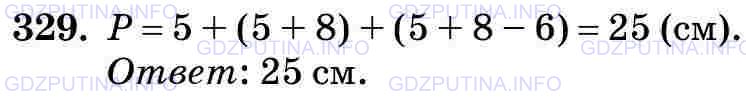
Решение 3
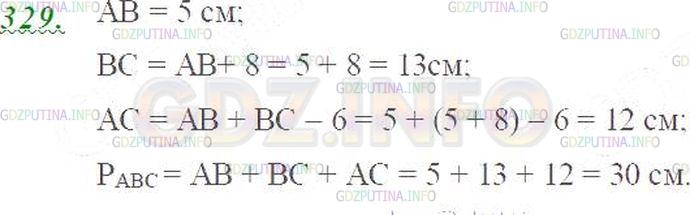
Решение 3
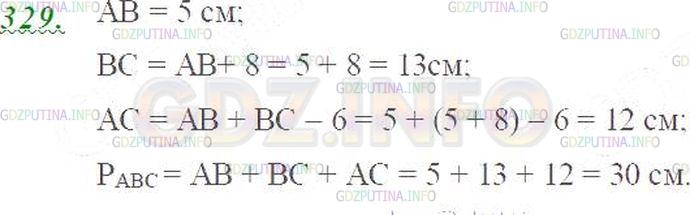
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено


