Найди верный ответ на вопрос ✅ «Преобразуйте выражение в многочлен: 1. (n+6) 2; 2. (13h+1) 2; 3. (4-3y) 2; 4. (2k-8) 2; 5. (3c+7d) 2; 6. (9a+t) 2; 7. (k-8) 2; 8. (5-7m) 2; …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Алгебра » Преобразуйте выражение в многочлен: 1. (n+6) 2; 2. (13h+1) 2; 3. (4-3y) 2; 4. (2k-8) 2; 5. (3c+7d) 2; 6. (9a+t) 2; 7. (k-8) 2; 8. (5-7m) 2; 9. (13p-3) 2; 10. (2f-10a) 2; 11. (-3h+7) 2; 12. (-10x-y) 2; 13. (с-10) 2; 14. (11 х+4) 2; 15. (6+2y) 2; 16.
Упростить выражение
Онлайн калькулятор для упрощения математических выражений. В выражении можно использовать одну переменные, целые и дробные константы, алгебраические действия, математические, прямые и обратные тригонометрические и гиперболические функции. Введите свое выражение в специально предназначенное для этого поле и калькулятор автоматически упростит выражение.
Калькулятор способен упрощать алгебраические выражения, тригонометрических выражений, выражения с корнями и другими степенями, сокращение дробей, раскрывать скобки, приводить к общему знаменателю также упрощает сложные буквенные выражения.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Чтобы составить задачу, которая приведёт к этим выражениям, например, с двумя неизвестными, нужно сначала поиграться с числами.
Берём две машины. Одна движется со скоростью 60 км/час, а вторая на 20 быстрее 80 км/час. У этих скоростей оптимальный общий множитель 48. Увеличиваем его в 10 раз получится 480 км.
Первой машине потребуется 8 часов, для преодоления этого расстояния, а второй 6 на 2 часа меньше. 480 км – это известное расстояние. Неизвестные величины — это скорость и время.
Напускаем туману. Определяемся, что скорость 1-й машины на 20 км/час меньше второй машины. Но вторая выехала на 2 часа позже и догнала первую на расстоянии 480 км. Задача готова. Нужно хитро задать вопрос. Например: Через какое время 2-я машина будет на расстоянии в 100 км от первой после из встречи.
Чтобы решить такую задачу потребуется составлять выражение. Принимать за “х” скорость первой или второй машины до встречи. За “у” время первой или второй машины также до встречи. Или обходиться одним “х”, а можно и просто обойтись числами. Но это не для составителя. Составитель оперирует известными ему числами, а “решала” составляет выражения.
Конечно это интересно. Составить хитрую математическую задачку, и чтобы её не быстро решили. А выдёргивать с интернета любой может. Я составляю сама. Бывает до взрыва мозга, а не такую легкотню, как написала выше. Например вот эта: про курагу, чернослив и инжир.
Содержание
- Числовые и буквенные выражения
- Числовые выражения
- Чтение числовых выражений
- Решение числовых выражений
- Сравнение значений числовых выражений
- Буквенные выражения
- Алгоритм решения буквенного выражения
- Переменные
- Чтение математических выражений учебно-методический материал по математике (1, 2 класс) на тему
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Развитие математической речи в начальных классах
Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.
Например, 44 + 32
Значение выражения — это результат выполненных действий.
Например, в записи 44 + 32 = 76, значение выражения — это 76.
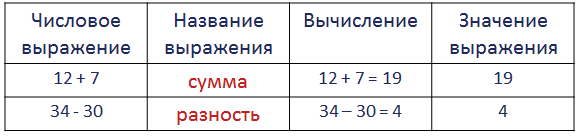
Чтение числовых выражений
49 — 20 — разность
34 — (8 + 21) — из 34 вычесть сумму чисел 8 и 21
13 + (26 — 8) — к 13 прибавить разность чисел 26 и 8
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Давай сравним значения двух выражений: 14 — 6 и 18 — 9.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением .
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
Алгоритм — значит, порядок, план выполнения команд.
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Источник
Чтение математических выражений
учебно-методический материал по математике (1, 2 класс) на тему

Памятка «Чтение математических выражений» во 2 классе
Скачать:
| Вложение | Размер |
|---|---|
| Памятка «Чтение математических выражений» во 2 классе | 14.95 КБ |
Предварительный просмотр:
5- первое слагаемое
2 – второе слагаемое
Чтобы найти первое слагаемое, надо из суммы вычесть второе слагаемое.
Чтобы найти второе слагаемое, надо из суммы вычесть первое слагаемое.
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти вычитаемое , надо из уменьшаемого вычесть вычитаемое
— к десяти прибавить разность чисел пяти и двух
— десять увеличить на разность чисел пяти и двух
— первое слагаемое 10, второе представлено разностью чисел пяти и двух
— из десяти отнять сумму чисел пяти и двух
— десять уменьшить на сумму чисел пяти и двух
— уменьшаемое 10, вычитаемое представлено суммой чисел пяти и двух
— к десяти прибавить разность чисел пяти и двух
— десять увеличить на разность чисел пяти и двух
— первое слагаемое 10, второе представлено разностью чисел пяти и двух
— из десяти отнять сумму чисел пяти и двух
— десять уменьшить на сумму чисел пяти и двух
— уменьшаемое 10, вычитаемое представлено суммой чисел пяти и двух
5-= первое слагаемое
2 – второе слагаемое
Чтобы найти первое слагаемое, надо из суммы вычесть второе слагаемое.
Чтобы найти второе слагаемое, надо из суммы вычесть первое слагаемое.
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти вычитаемое , надо из уменьшаемого вычесть вычитаемое
— к десяти прибавить разность чисел пяти и двух
— десять увеличить на разность чисел пяти и двух
— первое слагаемое 10, второе представлено разностью чисел пяти и двух
— из десяти отнять сумму чисел пяти и двух
— десять уменьшить на сумму чисел пяти и двух
— уменьшаемое 10, вычитаемое представлено суммой чисел пяти и двух
— к десяти прибавить разность чисел пяти и двух
— десять увеличить на разность чисел пяти и двух
— первое слагаемое 10, второе представлено разностью чисел пяти и двух
— из десяти отнять сумму чисел пяти и двух
— десять уменьшить на сумму чисел пяти и двух
— уменьшаемое 10, вычитаемое представлено суммой чисел пяти и двух
По теме: методические разработки, презентации и конспекты

Урок математики «Математические выражения».3 класc. Образовательная программа «Начальная школа XXIвека»
Урок математики в 3 классе. Тема урока : «Математические выражения». Закрепление умений читать выражения разными способами, устанавливать порядок действий, находить значения выражений, составлят.
Урок математики в 4 классе по теме «Решение математических выражений, уравнений».
Данный урок включает в себя нестандартный подход к решению математических выражений, учит сравнивать и анализировать разные типы уравнений.
Урок математики в 4 классе по теме «Решение математических выражений, уравнений».
Данный урок предполагает нестандартный подход к решению математических выражений.

Конспект урока математики в 3 классе по теме «Решение математических выражений на порядок действий.»
Конспект урока математики в 3 классе по теме «Решение математических выражений на порядок действий.» Цели: 1. Совершенствовать вычислительные навыки выполнения арифметичес.
Методическая разработка урока математики в 1 классе по теме «Составление математических выражений и их сравнение.».
По данной презентацииможно построить урок в 1 классе.

Проверочная работа по математике 1 класс 4 четверть. Контроль формирования навыков решения задач, математических выражений в одно и два действия, неравенств.
Проверочная работа по математике 1 класс 4 четверть направлена на проверку навыков решения задач, математических выражений в одно и два действия. При решении неравенств дети применяют знан.

Конспект урока «Всегда ли математическое выражение является числовым?» (4 класс, УМК «Перспективная начальная школа»)
Цель: познакомить с новым типом математического выражения — буквенным.Планируемые результаты:Личностные:Формировать интерес к познанию, к новому учебному материалу, к овладению новыми способами .
Источник
Развитие математической речи в начальных классах
Способность чётко и ясно излагать свои мысли в настоящее время требуется каждому. В этом качестве нуждаются руководитель предприятия и рабочий, учёный и инженер, педагог и экономист, врач и агроном. Поэтому вопрос о развитии речи является одним из основных в жизни всей школы. Им должны заниматься все преподаватели, внося в это общее дело каждый своё, присущее его специальности: математик должен приучить к краткому и логически полноценному изложению, литератор – к выразительной и эмоционально насыщенной речи, историк – к последовательному изложению и умению приводить отдельные факты в систему и т.д.
Забота о чистоте, правильности, выразительности речи учащихся всегда была общим делом школьных учителей всех предметов. Ведь именно учителя – начиная с первой учительницы, встретившей ребят на пороге школы, на протяжении всех школьных лет оказывают определяющее влияние на речевую культуру детей.
В обучении математики младших школьников используется как естественный, разговорный язык, так и специальный язык науки математики – математический. Под математическим языком понимается совокупность всех средств, с помощью которых можно выразить математическое содержание. К таким средствам относятся математические термины, символы, схемы, графики, диаграммы и т.д.
Изучение математического языка, знакомство с его компонентами – неотъемлемая часть начального обучения математике. Именно в начальной школе учащиеся впервые знакомятся с искусственным языком математики, где так же существуют определённые правила синтаксиса и семантики. Синтаксис устанавливает правила использования математических знаков в выражениях, равенствах, неравенствах, других предложениях математического языка. Семантика определяет смысловое значение каждого математического знака.
Основываясь на методику русского языка, можно выделить следующие направления по работе над математической речью на уроках математики:
- Работа над звуковой стороной речи.
- Словарная работа с математическими терминами.
- Формирование культуры математической речи.
- Развитие связной математической речи.
Работа над звуковой стороной речи сводится к формированию правильного произношения и употребления математических терминов.
При введении новых терминов нужно прикреплять к доске таблички (карточки) с этими словами, обращая внимания учащихся на их произношение и написание. Ежедневно в ходе устного опроса давать детям упражнения, содержащие в себе задания на употребление математических терминов, что способствует формированию потребности в их использовании.
Например, следующие упражнения:
1. Прочитайте слова, соблюдая ударения: километр, килограмм, вычислить, сложить, наименование, миллиметр, выражение, количество, дециметр и т.п.
2. Прочитайте выражения, используя математические термины:
(83-47):4; 69-42:6; 35+9х(24-14)
3. Прочитайте выражения разными способами:
36+18, 72:12, 59-7, 17х3
4. Прочитайте: прибавить к числу 86, вычесть из числа 347, к числу 473 прибавить число 441и т.п.
5. Прочитайте: прибавить к 86, вычесть из 347, к 473 прибавить 441 и т.п.
6. Пример 25-12 Коля прочитал так: «Из двадцать пять вычесть двенадцать». Прав ли он?
Если учащиеся употребляют падеж неправильно, учитель помогает им, читает сам, а затем просит повторить кого-нибудь из учеников. Таким образом, из урока в урок дети учатся читать выражения, используя математические термины.
Словарная работадолжна проводиться в разных направлениях: понимание и умение объяснять значение математических терминов, усвоение их правильного написания и формирование умений составлять связное высказывание.
1. Упражнения на объяснение значений математических терминов:
— объясните значение слов и выражений: уменьшаемое, сложение, разрядное число, разрядные слагаемые, произведение чисел, делимое и т.д.
— математическое выражение 18х3 Серёжа прочитал так: «18 взять 4». Как надо прочитать это выражение? (рассматриваются различные способы прочтения)
2. Следующие упражнения требуют включения зданий на применение терминов (правильное и неправильное).
— выполнив действие 18+2, Наташа ответила: «У меня получилось 20, я сосчитала правильно». Правильно ли она сказала?
— Определите верно или неверно данное высказывание:
- Произведение 8 и 3 равно 21.
- Первый множитель равен 6, второй множитель равен 3. Тогда произведение равно 18.
- Произведение 5 и 3 меньше произведения 7и 2.
- Сумму 6 и 9 уменьшили на 7, получили 3.
— В каком из уравнений правильно названо неизвестное число «с»?
а) 32 : с = 8, частное;
б) 9 х с = 45, множитель;
в) с : 6 = 12, делитель;
г) 19 – с = 15, вычитаемое.
3. Упражнения на правильное написание терминов:
— запишите слова, вставив пропущенные буквы: нум..рация, выч..таемое, ед..ница, кил..грамм, сл..жение, сл..гаемое, д..литель, д..лимое, ч..стное, к..личество, сто..мость, ра..тояние, пр..изведение, ра..ность и т.п.
— исправить ошибку в записи слов: «слажить», «дилить», «вычеслить» и т.п.
4. Упражнения на составление правильных связных высказываний:
— прочитайте предложения, вставив пропущенные слова: «Если соединить два числа … знаком, то получится числовое …».
— используя данные слова и выражения, составьте известное вам правило, определение: «число, это, неизвестное, которое, равенство, содержащее, уравнение, найти, надо».
— Какое из предложений соответствует выражению 18+16:2?
а) сумму 18и 16 уменьшили на 2.
б) к 18 прибавили частное 16 и 2.
в) сумму 18 и 16 уменьшили в 2 раза.
Упражнения этого вида направлены на усвоение правильной и точной формулировки правил и определений.
5.Упражнения на умение записывать математические выражения по названиям компонентов арифметических действий:
1) Запишите с помощью цифр и знаков действий выражения:
а) сумма двадцати девяти и тридцати семи;
б) разность шестидесяти четырёх и девятнадцати;
в) произведение восьмидесяти пяти и четырнадцати;
г) частное пятидесяти двух и четырёх;
2) Запиши выражение и найди его значение:
а) из суммы двадцати и семи вычесть число девятнадцать
б) к числу тридцать восемь прибавить разность восьмидесяти шести и пятидесяти девяти.
в) сложите разность чисел 51 из 8 с суммой чисел 24 и 9
г) из разности чисел 70 и 22 вычесть сумму чисел 6 и 35.
3) Составить более сложные выражения:
а) из числа 75, разности 81-63 и знака +;
б) из суммы 54+8, числа 36 и знака — ;
в) из числа 36, произведения 8х7 и знака «минус»;
г) из частного 72:6, числа 28 и знака =;
4) Определите, что больше:
а) сумма 30 и 10 или разность 40и 10;
б) разность 26 и 16 или сумма 4и 8,
в) сумма 5 и 9 или сумма 6 и 7;
г) разность 32 и 12 или разность 19 и 8.
Следующее направление работы – формирование культуры математической речи сводится к устранению ошибок, речевых недостатков, таких как неточность и бедность речи, употребление лишних слов, неправильный порядок слов в предложении и т.п.
1. Упражнения на устранение грамматических и математических ошибок:
— устраните математические ошибки в тексте: «Чтобы найти неизвестное число в выражении …+2=8, надо к 8 прибавить 2»;
— на вопрос учителя Коля ответил так: «При прибавлении к цифре 5 числа 4 будет 9». Какие ошибки допустил Коля? Как следовало ответить Коле?.
— Сережа, решая уравнение 8-х=3, рассуждал так: «Чтобы найти неизвестное число х , надо из большего числа (8) вычесть меньшее (3) и получим х: х=8-3, х=5». Правильно ли рассуждал Серёжа? Каким правилом ему следовало воспользоваться?
2. Упражнения на устранение речевых недостатков подбираются в основном такие же, как на уроках чтения, только используется математический материал:
— устраните недостатки в объяснении ученика, если его ответ на вопрос «Как сложить числа 25 и 8?» был таким: «К 25 надо прибавить сумму чисел 5 и 3. Заменим второе число 8 суммой удобных слагаемых 5 и 3. Удобнее к 25 прибавить первое слагаемое 5, получим 30. К полученной сумме прибавим второе слагаемое 3, т.е. 25+(5+3)=(25+5)+3=33»;
— пример 295+12=307 Коля прочитал так: «К двести девяносто пять прибавим 12 и получим триста семь». Правильно ли он прочитал? Как ещё можно прочитать эту запись?
Работа по развитию связной математической речи:
1.Составьте текст, используя набор карточек со словами:
— чтобы, на, произведение, двух чисел, это, умножить, число, можно, умножить, первый, число, на, множитель, число, на второй, и, полученное, умножить, множитель;
— 4х(2х3), тогда (4х2)х3, 24, =, 8х3, = .
2. Прочитайте данные предложения в таком порядке, чтобы получилось связное объяснение:
«Значит, 48:12=4. Это число 4. Разделить 48 на 12 значит найти такое число, которое при умножении на 12 даёт 48».
Развитие математической речи будет происходить эффективно при определённой последовательной педагогической работы, в основе которой лежит логика усвоения речевого материала, его неоднократностью восприятие, многократное воспроизведение, самостоятельное использование усвоенного материала в речевых ситуациях.
Хочется отметить, что успех в овладении речью – это залог успеха во всём школьном обучении и развитии детей, т.к. через язык, через речь школьник открывает широкий мир науки и жизни.
Источник
Онлайн калькулятор. Упрощение выражений.
Онлайн-калькулятор позволяет решать математические выражения любой сложности с выводом подробного результата решения по шагам. 
Также универсальный калькулятор умеет производить действия по разложению, упрощению выражений, раскрывать скобки и пр.
Онлайн калькулятор упрощения выражений
Перенос?
frac{6x^3-24x^2}{6x^3}
$$textbf{Упрощение/раскрытие скобок/} newlinetextbf{разложение на множители выражения: }newline {{x-4}over{x}} =newline 1-{{4}over{x}}$$
Пояснения к калькулятору
- Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵.
- Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и →.
- ⌫ – удалить в поле ввода символ слева от курсора.
- C – очистить поле ввода.
- При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
- Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½, ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби. Для ввода целой части смешанного числа необходимо установить курсор перед дробью с помощью клавиши ← и ввести число.
- Ввод числа в n-ой степени и квадратного корня прозводится кнопками ab и √ соответственно. Завершить ввод значения в степени или в корне можно клавишей →.
Упрощение выражений, раскрытие скобок, разложение многочленов на множители
Калькулятор позволяет произвести некоторые алгебраические преобразования с выражениями. Результат выводится в нескольких вариантах упрощения/разложения/раскрытия скобок и пр.
$$frac{left(frac{2a}{2a+b}-frac{4a^2}{4a^2+4ab+b^2}right)}{left(frac{2a}{4a^2-b^2}+frac{1}{b-2a}right)}+frac{8a^2}{2a+b}$$ (упростить выражение)
$$frac{1-sin ^4left(xright)-cos ^4left(xright)}{2sin ^4left(xright)}+1$$ (упростить выражение)
$$left(sqrt{a}-frac{a}{sqrt{a}+1}right)cdot frac{a-1}{sqrt{a}}$$ (упростить выражение)

