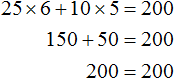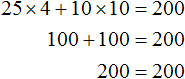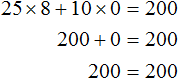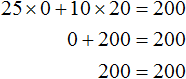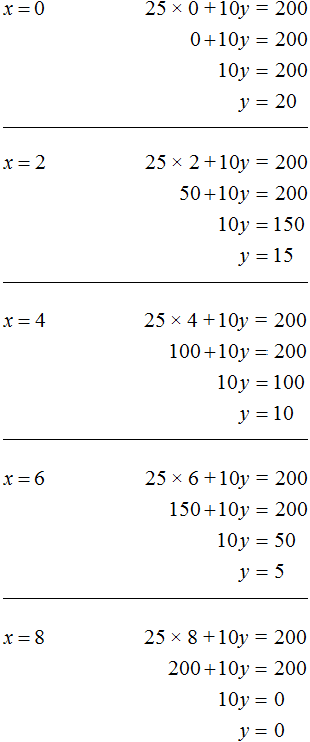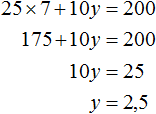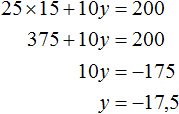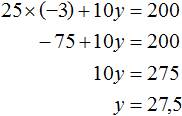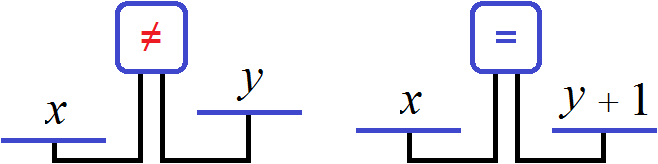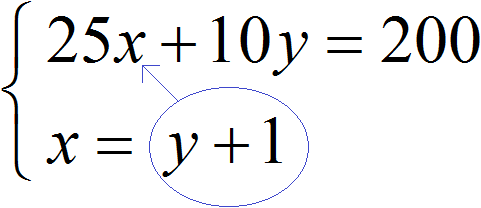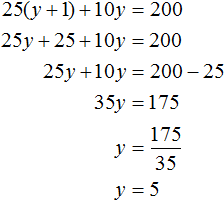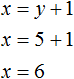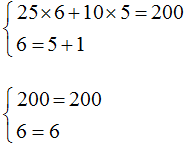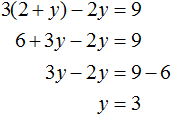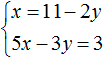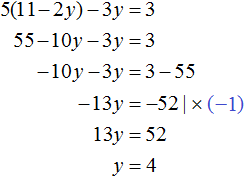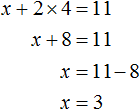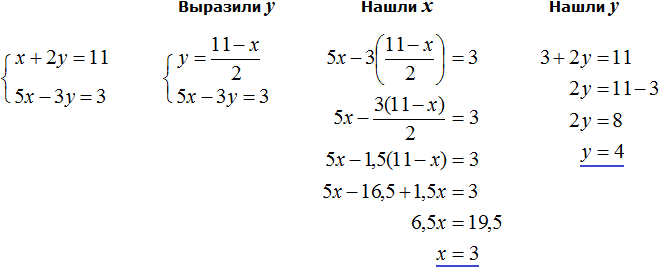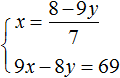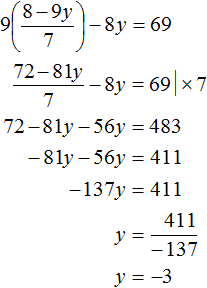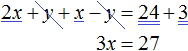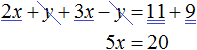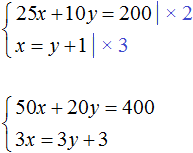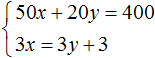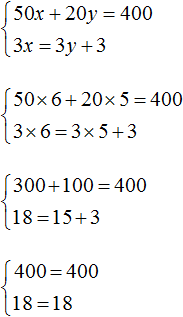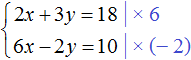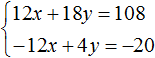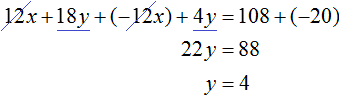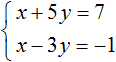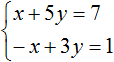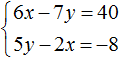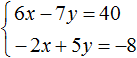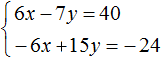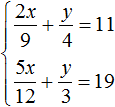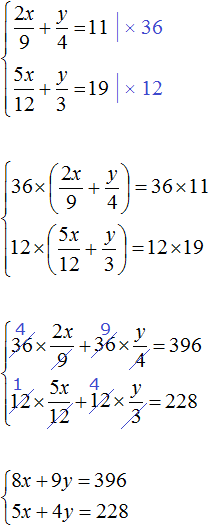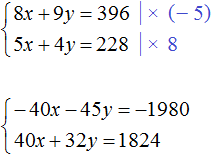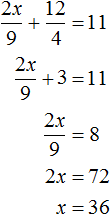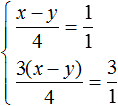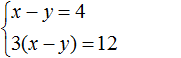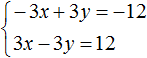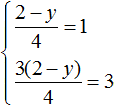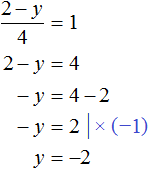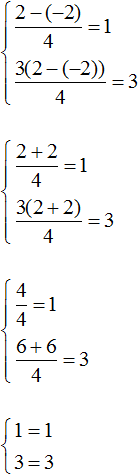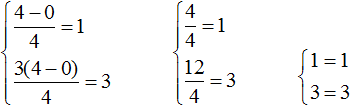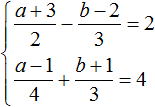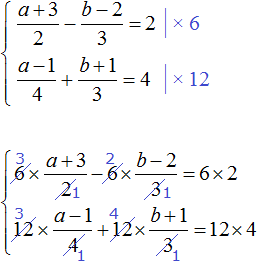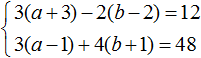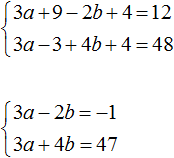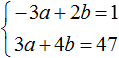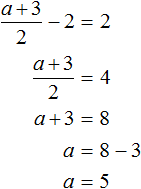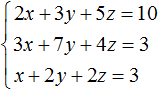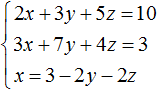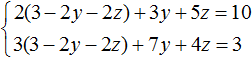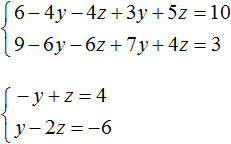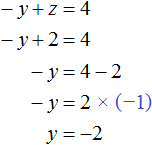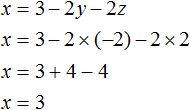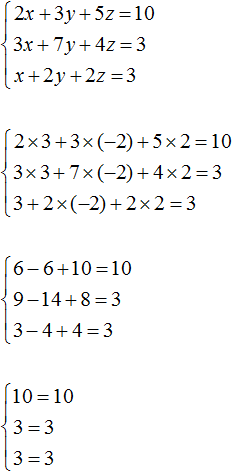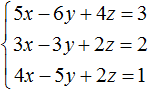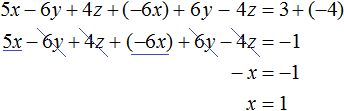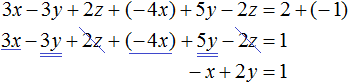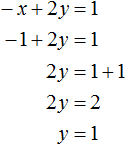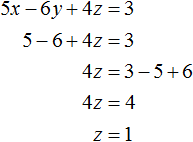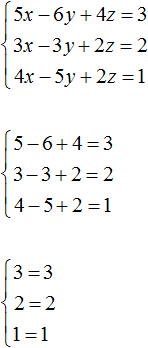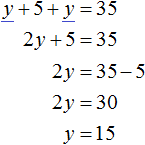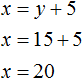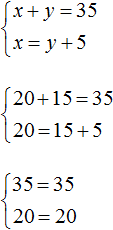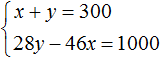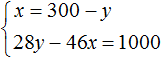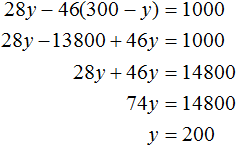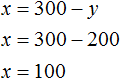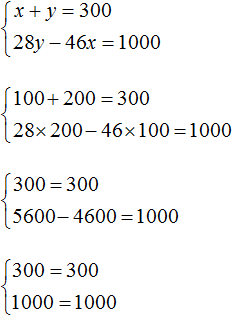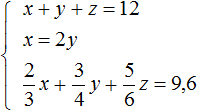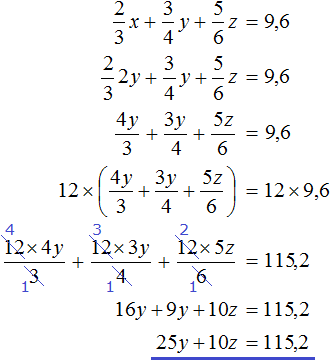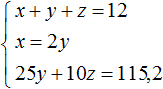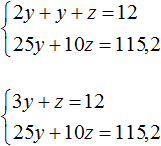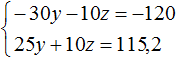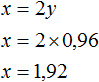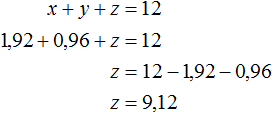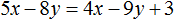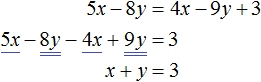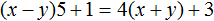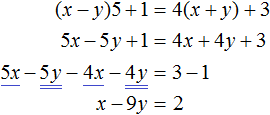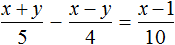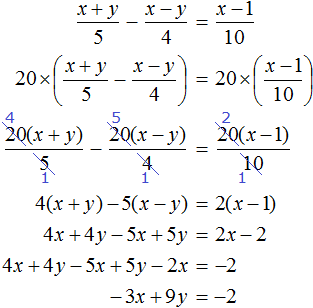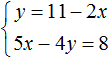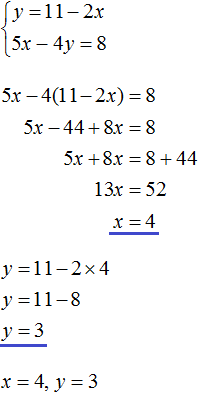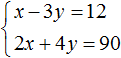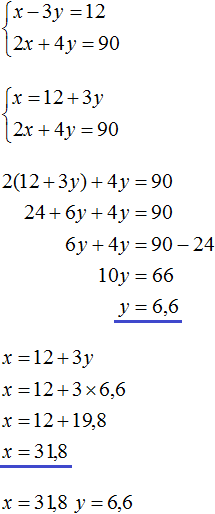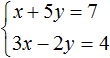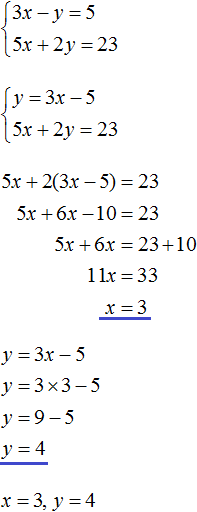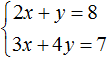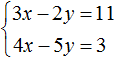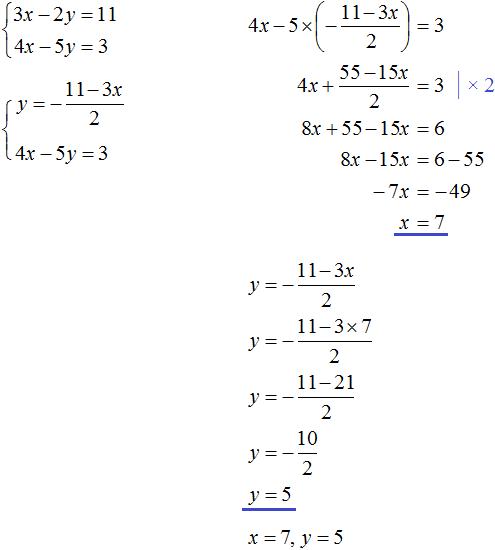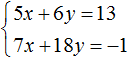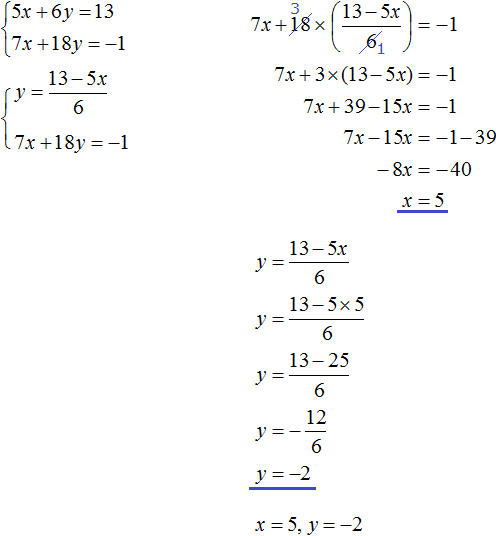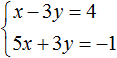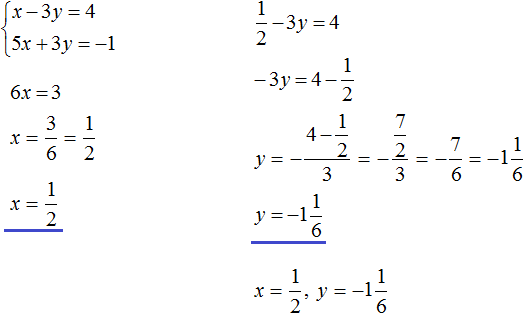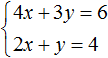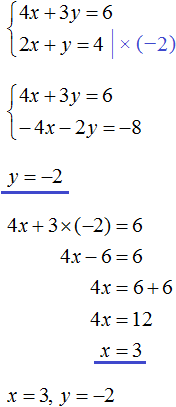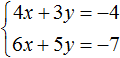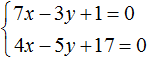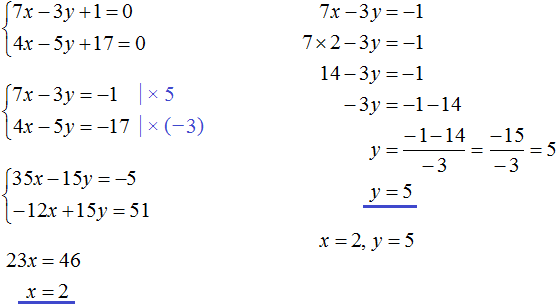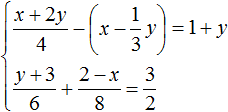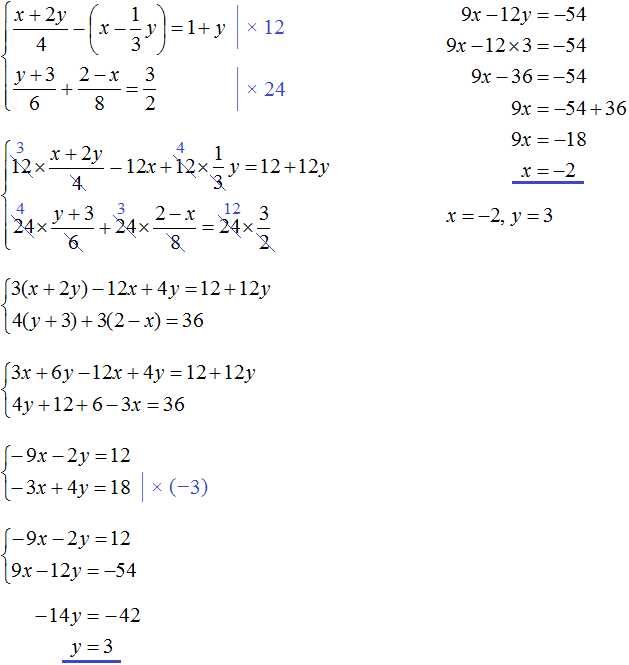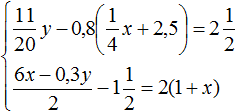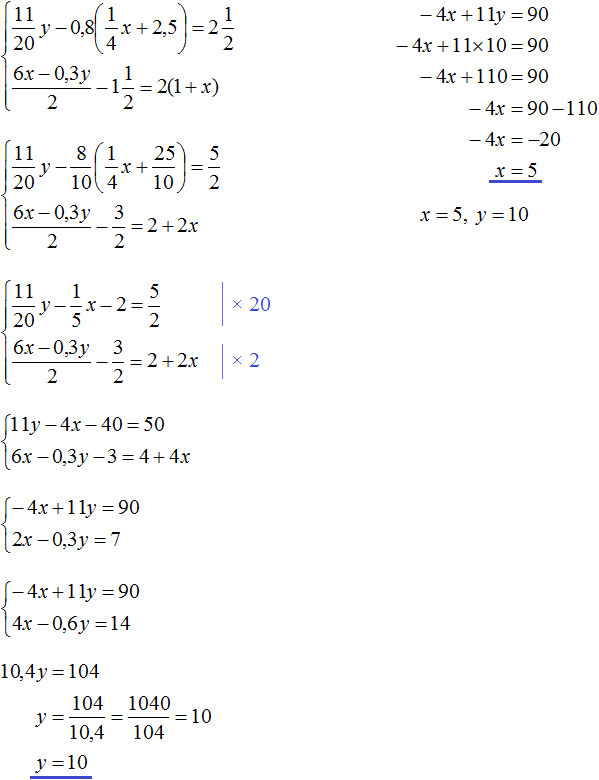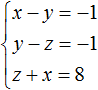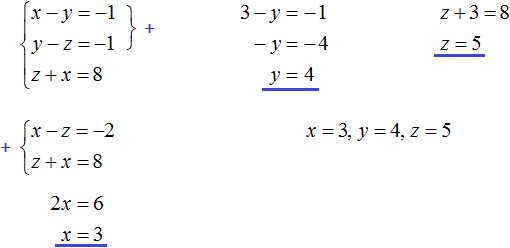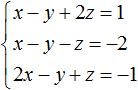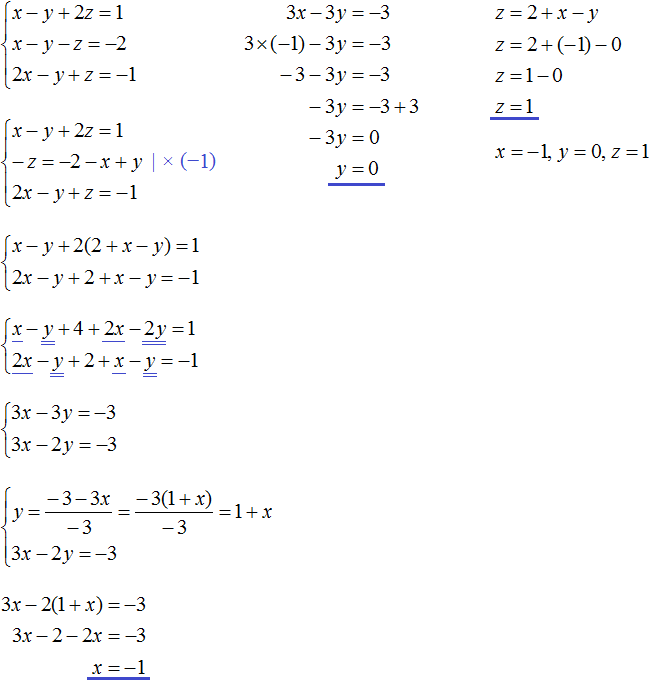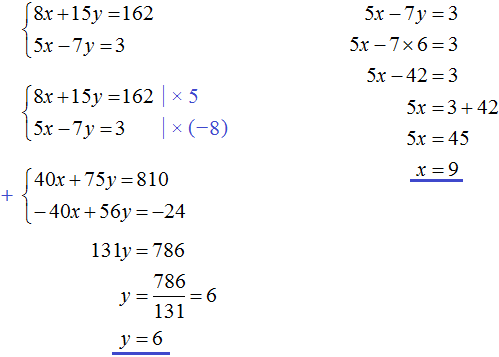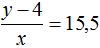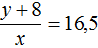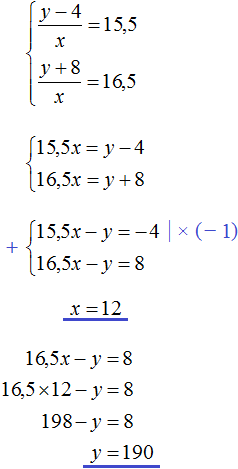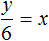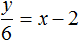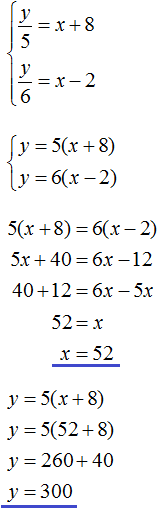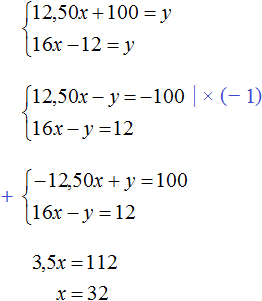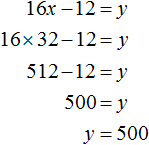В математике большая часть задач ориентирована на решение стандартных уравнений, в которых представлена одна переменная. Однако, некоторые из них, помимо числовых выражений, содержат одновременно две неизвестные. Перед тем как приступить к решению такого уравнения, стоит изучить его определение.
Содержание:
- Определение
- Решение задач
- Система уравнений с двумя неизвестными
- Метод подстановки
- Метод сложения
- Графический метод
- Видео
Определение
Итак, уравнением с двумя неизвестными называют любое равенство следующего типа:
a*x + b*y =с, где a, b, c — числа, x, y — неизвестные переменные.
Ниже приведены несколько примеров:
- 10x + 25y = 180.
- x — y = 6.
- -6x + y = 7.
Уравнение с двумя неизвестными точно так же, как и с одной, имеет решение. Однако такие выражения, как правило, имеют бесконечное множество разных решений, поэтому в алгебре их принято называть неопределенными.
Решение задач
Чтобы решить подобные задачи, необходимо отыскать любую пару значений x и y, которая удовлетворяла бы его, другими словами, обращала бы уравнение с неизвестными x и y в правильное числовое равенство. Найти удовлетворяющую пару чисел можно при помощи метода подбора.
Для наглядности объяснений подберем корни для выражения: y-x = 6.
При y=5 и x=-1 равенство становится верным тождеством 5- (-1) = 6. Поэтому пару чисел (-1; 5) можно считать корнями выражения y-x = 6. Ответ: (-1; 5).
Необходимо отметить, что записывать полученный ответ по правилам необходимо в скобках через точку с запятой. Первым указывается значение х, вторым — значение y.
У равенств такого вида может и не быть корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9
Приведем исходное равенство к следующему виду:
- x+y-x-y-9 = 0;
- 9 = 0.
В результате мы видим ошибочное равенство, следовательно, это выражение не имеет корней.
При решении уравнений можно пользоваться его свойствами. Первое их них: каждое слагаемое можно вынести в другую часть выражения. Вместе с этим обязательно нужно поменять знак на обратный. Получившееся равенство будет равнозначно исходному.
Например, из выражения 20y — 3x = 16 перенесем неизвестное y в другую его часть.
- 20y — 3x = 16;
- -3x = 16−20y.
Оба равенства равносильны.
Второе свойство: допустимо умножать или делить части выражения на одинаковое число, не равное нолю. В итоге получившиеся равенства будут равнозначны.
Пример:
- y — x = 6*2;
- 2y — 2x = 12.
Оба уравнения также равносильны.
Система уравнений с двумя неизвестными
Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.
Для решения системы уравнений необходимо найти пару чисел, обращающих оба уравнения системы в правильное равенство. Решением может служить одна пара чисел, несколько пар чисел или вовсе их отсутствие.
Решить подобные системы уравнений можно, применяя следующие методы.
Метод подстановки
Последовательность действий:
- Выражаем неизвестное из любого равенства через вторую переменную.
- Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
- Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.
Метод сложения
Этапы решения:
- Приводим к равенству модули чисел при каком-либо неизвестном.
- Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
- Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.
Графический метод
- Выражаем в каждом равенстве одну переменную через другую.
- Строим графики двух имеющихся уравнений в одной координатной плоскости.
- Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
- Делаем проверку, подставив полученные значения в исходную систему равенств.
При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.
В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.
Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!
Видео
Из этого видео вы узнаете, как решать уравнения с двумя неизвестными.
Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений
с двумя неизвестными.
Запомните!
Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют
«x» и «y»),
которые объединены в общую систему фигурной скобкой.
Например, система уравнений может быть задана следующим образом.
Чтобы решить систему уравнений, нужно найти и «x», и «y».
Как решить систему уравнений
Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.
Способ подстановки
или
«железобетонный» метод
Первый способ решения системы уравнений называют способом подстановки или «железобетонным».
Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно
решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений,
всегда пробуйте решить её методом подстановки.
Разберем способ подстановки на примере.
Выразим из первого уравнения «x + 5y = 7»
неизвестное «x».
Важно!
Чтобы выразить неизвестное, нужно выполнить два условия:
- перенести неизвестное, которое хотим выразить, в левую часть уравнения;
- разделить и левую и правую часть уравнения на нужное число так,
чтобы коэффициент при неизвестном стал равным единице.
Перенесём в первом уравнении «x + 5 y = 7» всё что
содержит «x» в левую часть,
а остальное в правую часть по
правилу переносу.
При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение
на число не требуется.
Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.
| x = 7 − 5y | |
| 3(7 − 5y) − 2y = 4 |
Подставив вместо «x» выражение «(7 − 5y)»
во второе уравнение,
мы получили обычное линейное уравнение с одним неизвестным «y».
Решим его по правилам
решения линейных уравнений.
Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение
«3(7 − 5y) − 2y = 4» отдельно.
Вынесем его решение отдельно с помощью
обозначения звездочка (*).
| x = 7 − 5y | |
| 3(7 − 5y) − 2y = 4 (*) |
(*) 3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
− 17y = − 17 | :(−17)
y = 1
Мы нашли, что «y = 1».
Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение.
Таким образом можно найти «x».
Запишем в ответ оба полученных значения.
Ответ: x = 2; y = 1
Способ сложения
Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения.
Вернемся к нашей системе уравнений еще раз.
По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные
уравнения, получить такое уравнение, в котором останется только одно неизвестное.
Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.
Запомните!
При сложения уравнений системы
левая часть первого уравнения полностью складывается
с левой частью второго уравнения,
а правая часть полностью складывается с
правой частью.
| x + 5y = 7 | (x + 5y) + (3x − 2y) = 7 + 4 | ||
| + => |
x + 5y + 3x − 2y = 11 |
||
| 3x − 2y = 4 | 4x + 3y = 11 |
При сложении уравнений мы получили уравнение «4x + 3y = 11».
По сути, сложение уравнений в исходном виде нам ничего
не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.
Вернемся снова к исходной системе уравнений.
Чтобы при сложении неизвестное «x» взаимноуничтожилось,
нужно сделать так, чтобы в первом уравнении при «x» стоял коэффициент
«−3».
Для этого умножим первое уравнение на «−3».
Важно!
При умножении уравнения на число, на это число умножается каждый член уравнения.
| x + 5y = 7 | ·(−3) | |
| 3x − 2y = 4 |
| x ·(−3) + 5y · (−3) = 7 · (−3) |
|
| 3x − 2y = 4 |
| −3x −15y = −21 | |
| 3x − 2y = 4 |
Теперь сложим уравнения.
| −3x −15y = −21 | (−3x −15y ) + (3x − 2y) = −21 + 4 | ||
| + => |
−3x −15y + 3x − 2y = −21 + 4 |
||
| 3x − 2y = 4 | −17y = −17 |:(−17) | ||
| y = 1 |
Мы нашли «y = 1».
Вернемся к первому уравнению и подставим вместо «y» полученное числовое
значение и найдем «x».
Ответ: x = 2; y = 1
Пример решения системы уравнения
способом подстановки
Выразим из первого уравнения «x».
Подставим вместо «x» во второе уравнение полученное выражение.
| x = 17 + 3y | |
| (17 + 3y) − 2y = −13 (*) |
(*) (17 + 3y) − 2y = −13
17 + 3y − 2y = −13
17 + y = −13
y = −13 − 17
y = −30
Подставим в первое уравнение полученное числовое значение «y = −30» и
найдем «x».
| x = 17 + 3 · (−30) | |
| y = −30 |
Ответ: x = −73; y = −30
Пример решения системы уравнения
способом сложения
Рассмотрим систему уравнений.
| 3(x − y) + 5x = 2(3x − 2) | |
| 4x − 2(x + y) = 4 − 3y |
Раскроем скобки и упростим выражения в обоих уравнениях.
| 3x − 3y + 5x = 6x − 4 | |
| 4x − 2x − 2y = 4 − 3y |
| 8x − 3y = 6x − 4 | |
| 2x −2y = 4 − 3y |
| 8x − 3y − 6x = −4 | |
| 2x −2y + 3y = 4 |
Мы видим, что в обоих уравнениях есть «2x».
Наша задача, чтобы при сложении уравнений «2x» взаимноуничтожились и в
полученном уравнении осталось только «y».
Для этого достаточно умножить первое уравнение на «−1».
| 2x − 3y = −4 |·(−1) | |
| 2x + y = 4 |
|
2x · (−1) − 3y · (−1) = −4 · (−1) |
|
| 2x + y = 4 |
Теперь при сложении уравнений у нас останется только «y» в уравнении.
| −2x + 3y = 4 | (−2x + 3y ) + (2x + y) = 4 + 4 | ||
| + => |
−2x + 3y + 2x + y = 4 + 4 |
||
| 2x + y = 4 | 4y = 8 | :4 | ||
| y = 2 |
Подставим в первое уравнение полученное числовое значение «y = 2» и
найдем «x».
Ответ: x = 1; y = 2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
8 мая 2020 в 16:20
Алина Козлова
Профиль
Благодарили: 0
Сообщений: 1
Алина Козлова
Профиль
Благодарили: 0
Сообщений: 1
у-2х=-3
х+у=3
0
Спасибо
Ответить
9 мая 2020 в 21:50
Ответ для Алина Козлова
Evgeny Bayron
Профиль
Благодарили: 0
Сообщений: 1
Evgeny Bayron
Профиль
Благодарили: 0
Сообщений: 1
y=3-x
3-x-2x=-3
x=2
y-2*2=-3
y=1
0
Спасибо
Ответить
15 мая 2019 в 13:21
Марина Чернявская
Профиль
Благодарили: 0
Сообщений: 1
Марина Чернявская
Профиль
Благодарили: 0
Сообщений: 1
Решительно систему уравнений.
4x+3y =22.
-x+7y =10.
a)графическим способом.
б)способом подстановки
в)способом сложения
0
Спасибо
Ответить
15 мая 2019 в 22:31
Ответ для Марина Чернявская
Лёха Чешуйка
Профиль
Благодарили: 0
Сообщений: 2
Лёха Чешуйка
Профиль
Благодарили: 0
Сообщений: 2
в): Домножаем первое на 1, второе на 4:
4x+3y=22
-4x+28y=40
Складываем:
4x+(-4x)+3y+28y=22+40
31y=62
y=62/31
y=2
Подставляем y в первое:
4x+3 · 2=22
4x=22-6
4x=16
x=4
0
Спасибо
Ответить
15 мая 2019 в 22:41
Ответ для Марина Чернявская
Лёха Чешуйка
Профиль
Благодарили: 0
Сообщений: 2
Лёха Чешуйка
Профиль
Благодарили: 0
Сообщений: 2
б): Выражаем из второго x:
-x=10-7y
x=7y-10
Подставляем x в первое:
4(7y-10)+3y=22
28y-40+3y=22
31y=22+40
31y=62
y=2
Подставляем y в первое:
4x+3 · 2=22
4x=22-6
4x=16
x=4
0
Спасибо
Ответить
20 октября 2015 в 13:24
Елена Тутуликова
Профиль
Благодарили: 0
Сообщений: 1
Елена Тутуликова
Профиль
Благодарили: 0
Сообщений: 1
Помогите, пожалуйста, решить систему уравнений.{y + sinx = 5; {4y + 2 sinx = 19
Спасибо!
0
Спасибо
Ответить
23 октября 2015 в 21:25
Ответ для Елена Тутуликова
Елизавета Яременко
Профиль
Благодарили: 0
Сообщений: 5
Елизавета Яременко
Профиль
Благодарили: 0
Сообщений: 5
Я думаю{y + sinx =5; {4y + 2 sinx =19
0
Спасибо
Ответить
9 июня 2016 в 14:19
Ответ для Елена Тутуликова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
sinx = 1/2
y = 9/2
0
Спасибо
Ответить
Линейные уравнения с двумя переменными
У школьника имеется 200 рублей, чтобы пообедать в школе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе можно накупить на 200 рублей?
Обозначим количество пирожных через x, а количество чашек кофе через y. Тогда стоимость пирожных будет обозначаться через выражение 25x, а стоимость чашек кофе через 10y.
25x — стоимость x пирожных
10y — стоимость y чашек кофе
Итоговая сумма должна равняться 200 рублей. Тогда получится уравнение с двумя переменными x и y
25x + 10y = 200
Сколько корней имеет данное уравнение?
Всё зависит от аппетита школьника. Если он купит 6 пирожных и 5 чашек кофе, то корнями уравнения будут числа 6 и 5.
Говорят, что пара значений 6 и 5 являются корнями уравнения 25x + 10y = 200. Записывается как (6; 5), при этом первое число является значением переменной x, а второе — значением переменной y.
6 и 5 не единственные корни, которые обращают уравнение 25x + 10y = 200 в тождество. При желании на те же 200 рублей школьник может купить 4 пирожных и 10 чашек кофе:
В этом случае корнями уравнения 25x + 10y = 200 является пара значений (4; 10).
Более того, школьник может вообще не покупать кофе, а купить пирожные на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 8 и 0
Или наоборот, не покупать пирожные, а купить кофе на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 0 и 20
Попробуем перечислить все возможные корни уравнения 25x + 10y = 200. Условимся, что значения x и y принадлежат множеству целых чисел. И пусть эти значения будут бóльшими или равными нулю:
x ∈ Z, y ∈ Z;
x ≥ 0, y ≥ 0
Так будет удобно и самому школьнику. Пирожные удобнее покупать целыми, чем к примеру несколько целых пирожных и половину пирожного. Кофе также удобнее брать целыми чашками, чем к примеру несколько целых чашек и половину чашки.
Заметим, что при нечетном x невозможно достичь равенства ни при каком y. Тогда значениями x будут следующие числа 0, 2, 4, 6, 8. А зная x можно без труда определить y
Таким образом, мы получили следующие пары значений (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Эти пары являются решениями или корнями уравнения 25x + 10y = 200. Они обращают данное уравнение в тождество.
Уравнение вида ax + by = c называют линейным уравнением с двумя переменными. Решением или корнями этого уравнения называют пару значений (x; y), которая обращает его в тождество.
Отметим также, что если линейное уравнение с двумя переменными записано в виде ax + by = c, то говорят, что оно записано в каноническом (нормальном) виде.
Некоторые линейные уравнения с двумя переменными могут быть приведены к каноническому виду.
Например, уравнение 2(16x + 3y − 4) = 2(12 + 8x − y) можно привести к виду ax + by = c. Раскроем скобки в обеих частях этого уравнения, получим 32x + 6y − 8 = 24 + 16x − 2y. Слагаемые, содержащие неизвестные сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой. Тогда получим 32x − 16x + 6y + 2y = 24 + 8. Приведём подобные слагаемые в обеих частях, получим уравнение 16x + 8y = 32. Это уравнение приведено к виду ax + by = c и является каноническим.
Рассмотренное ранее уравнение 25x + 10y = 200 также является линейным уравнением с двумя переменными в каноническом виде. В этом уравнении параметры a, b и c равны значениям 25, 10 и 200 соответственно.
На самом деле уравнение ax + by = c имеет бесчисленное множество решений. Решая уравнение 25x + 10y = 200, мы искали его корни только на множестве целых чисел. В результате получили несколько пар значений, которые обращали данное уравнение в тождество. Но на множестве рациональных чисел уравнение 25x + 10y = 200 будет иметь бесчисленное множество решений.
Для получения новых пар значений, нужно взять произвольное значение для x, затем выразить y. К примеру, возьмем для переменной x значение 7. Тогда получим уравнение с одной переменной 25 × 7 + 10y = 200 в котором можно выразить y
Пусть x = 15. Тогда уравнение 25x + 10y = 200 примет вид 25 × 15 + 10y = 200. Отсюда находим, что y = −17,5
Пусть x = −3. Тогда уравнение 25x + 10y = 200 примет вид 25 × (−3) + 10y = 200. Отсюда находим, что y = 27,5
Система двух линейных уравнений с двумя переменными
Для уравнения ax + by = c можно сколько угодно раз брать произвольные значение для x и находить значения для y. Отдельно взятое такое уравнение будет иметь бесчисленное множество решений.
Но бывает и так, что переменные x и y связаны не одним, а двумя уравнениями. В этом случае они образуют так называемую систему линейных уравнений с двумя переменными. Такая система уравнений может иметь одну пару значений (или по-другому: «одно решение»).
Может случиться и так, что система вовсе не имеет решений. Бесчисленное множество решений система линейных уравнений может иметь в редких и в исключительных случаях.
Два линейных уравнения образуют систему тогда, когда значения x и y входят в каждое из этих уравнений.
Вернемся к самому первому уравнению 25x + 10y = 200. Одной из пар значений для этого уравнения была пара (6; 5). Это случай, когда на 200 рублей можно можно было купить 6 пирожных и 5 чашек кофе.
Составим задачу так, чтобы пара (6; 5) стала единственным решением для уравнения 25x + 10y = 200. Для этого составим ещё одно уравнение, которое связывало бы те же x пирожных и y чашечек кофе.
Поставим текст задачи следующим образом:
«Школьник купил на 200 рублей несколько пирожных и несколько чашек кофе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе купил школьник, если известно что количество пирожных на одну единицу больше количества чашек кофе?»
Первое уравнение у нас уже есть. Это уравнение 25x + 10y = 200. Теперь составим уравнение к условию «количество пирожных на одну единицу больше количества чашек кофе».
Количество пирожных это x, а количество чашек кофе это y. Можно записать эту фразу с помощью уравнения x − y = 1. Это уравнение будет означать, что разница между пирожными и кофе составляет 1.
Либо второе уравнение можно записать как x = y + 1. Это уравнение означает, что количество пирожных на единицу больше, чем количество чашек кофе. Поэтому для получения равенства, к количеству чашек кофе прибавлена единица. Это легко можно понять, если воспользоваться моделью весов, которые мы рассматривали при изучении простейших задач:
Получили два уравнения: 25x + 10y = 200 и x = y + 1. Поскольку значения x и y, а именно 6 и 5 входят в каждое из этих уравнений, то вместе они образуют систему. Запишем эту систему. Если уравнения образуют систему, то они обрамляются знаком системы. Знак системы это фигурная скобка:
Давайте решим данную систему. Это позволит увидеть, как мы придём к значениям 6 и 5. Существует много методов решения таких систем. Рассмотрим наиболее популярные из них.
Метод подстановки
Название этого метода говорит само за себя. Суть его заключается в том, чтобы одно уравнение подставить в другое, предварительно выразив одну из переменных.
В нашей системе ничего выражать не нужно. Во втором уравнении x = y + 1 переменная x уже выражена. Эта переменная равна выражению y + 1. Тогда можно подставить это выражение в первое уравнение вместо переменной x
После подстановки выражения y + 1 в первое уравнение вместо x, получим уравнение 25(y + 1) + 10y = 200. Это линейное уравнение с одной переменной. Такое уравнение решить довольно просто:
Мы нашли значение переменной y. Теперь подставим это значение в одно из уравнений и найдём значение x. Для этого удобно использовать второе уравнение x = y + 1. В него и подставим значение y
Значит пара (6; 5) является решением системы уравнений, как мы и задумывали. Выполняем проверку и убеждаемся, что пара (6; 5) удовлетворяет системе:
Пример 2. Решить методом подстановки следующую систему уравнений:
Подставим первое уравнение x = 2 + y во второе уравнение 3x − 2y = 9. В первом уравнении переменная x равна выражению 2 + y. Это выражение и подставим во второе уравнение вместо x
Теперь найдём значение x. Для этого подставим значение y в первое уравнение x = 2 + y
Значит решением системы 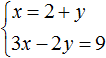
Пример 3. Решить методом подстановки следующую систему уравнений:
Здесь в отличие от предыдущих примеров, одна из переменных не выражена явно.
Чтобы подставить одно уравнение в другое, сначала нужно выразить одну из переменных.
Выражать желательно ту переменную, которая имеет коэффициент единицу. Коэффициент единицу имеет переменная x, которая содержится в первом уравнении x + 2y = 11. Эту переменную и выразим.
После выражения переменной x, наша система примет следующий вид:
Теперь подставим первое уравнение во второе и найдем значение y
Подставим y в первое уравнение и найдём x
Значит решением системы 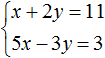
Конечно, выражать можно и переменную y. Корни от этого не изменятся. Но если выразить y, получится не очень-то и простое уравнение, на решение которого уйдет больше времени. Выглядеть это будет следующим образом:
Видим, что в данном примере выражать x намного удобнее, чем выражать y.
Пример 4. Решить методом подстановки следующую систему уравнений:
Выразим в первом уравнении x. Тогда система примет вид:
Подставим первое уравнение во второе и найдём y
Подставим y в первое уравнение и найдём x. Можно воспользоваться изначальным уравнением 7x + 9y = 8, либо воспользоваться уравнением , в котором выражена переменная x. Этим уравнением и воспользуемся, поскольку это удобно:
Значит решением системы 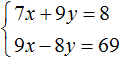
Метод сложения
Метод сложения заключается в том, чтобы почленно сложить уравнения, входящие в систему. Это сложение приводит к тому, что образуется новое уравнение с одной переменной. А решить такое уравнение довольно просто.
Решим следующую систему уравнений:
Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. Получим следующее равенство:
Приведем подобные слагаемые:
В результате получили простейшее уравнение 3x = 27 корень которого равен 9. Зная значение x можно найти значение y. Подставим значение x во второе уравнение x − y = 3. Получим 9 − y = 3. Отсюда y = 6.
Значит решением системы 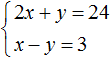
Пример 2. Решить следующую систему уравнений методом сложения:
Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. В получившемся равенстве приведем подобные слагаемые:
В результате получили простейшее уравнение 5x = 20, корень которого равен 4. Зная значение x можно найти значение y. Подставим значение x в первое уравнение 2x + y = 11. Получим 8 + y = 11. Отсюда y = 3.
Значит решением системы 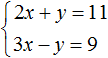
Процесс сложения подробно не расписывают. Его нужно выполнять в уме. При сложении оба уравнения должны быть приведены к каноническому виду. То есть к виду ax + by = c.
Из рассмотренных примеров видно, что основная цель сложения уравнений это избавление от одной из переменных. Но не всегда удаётся сразу решить систему уравнений методом сложения. Чаще всего систему предварительно приводят к виду, при котором можно сложить уравнения, входящие в эту систему.
Например, систему 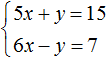
А систему уравнений 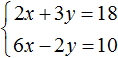
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному. Это правило справедливо и для системы линейных уравнений с двумя переменными. Одно из уравнений (или оба уравнения) можно умножить на какое-нибудь число. В результате получится равносильная система, корни которой будут совпадать с предыдущей.
Вернемся к самой первой системе 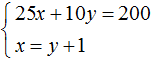
Умножим оба уравнения, входящие в эту систему на какие-нибудь числа. Скажем первое уравнение умножим на 2, а второе на 3
В результате получили систему
Решением этой системы по-прежнему является пара значений (6; 5)
Это значит, что уравнения входящие в систему можно привести к виду, пригодному для применения метода сложения.
Вернемся к системе 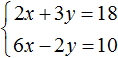
Умножим первое уравнение на 6, а второе на −2
Тогда получим следующую систему:
Сложим уравнения, входящие в эту систему. Сложение компонентов 12x и −12x даст в результате 0, сложение 18y и 4y даст 22y, а сложение 108 и −20 даст 88. Тогда получится уравнение 22y = 88, отсюда y = 4.
Если первое время тяжело складывать уравнения в уме, то можно записывать как складывается левая часть первого уравнения с левой частью второго уравнения, а правая часть первого уравнения с правой частью второго уравнения:
Зная, что значение переменной y равно 4, можно найти значение x. Подставим y в одно из уравнений, например в первое уравнение 2x + 3y = 18. Тогда получим уравнение с одной переменной 2x + 12 = 18. Перенесем 12 в правую часть, изменив знак, получим 2x = 6, отсюда x = 3.
Пример 4. Решить следующую систему уравнений методом сложения:
Умножим второе уравнение на −1. Тогда система примет следующий вид:
Сложим оба уравнения. Сложение компонентов x и −x даст в результате 0, сложение 5y и 3y даст 8y, а сложение 7 и 1 даст 8. В результате получится уравнение 8y = 8, корень которого равен 1. Зная, что значение y равно 1, можно найти значение x.
Подставим y в первое уравнение, получим x + 5 = 7, отсюда x = 2
Пример 5. Решить следующую систему уравнений методом сложения:
Желательно, чтобы слагаемые содержащие одинаковые переменные, располагались друг под другом. Поэтому во втором уравнении слагаемые 5y и −2x поменяем местами. В результате система примет вид:
Умножим второе уравнение на 3. Тогда система примет вид:
Теперь сложим оба уравнения. В результате сложения получим уравнение 8y = 16, корень которого равен 2.
Подставим y в первое уравнение, получим 6x − 14 = 40. Перенесем слагаемое −14 в правую часть, изменив знак, получим 6x = 54. Отсюда x = 9.
Пример 6. Решить следующую систему уравнений методом сложения:
Избавимся от дробей. Умножим первое уравнение на 36, а второе на 12
В получившейся системе 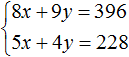
Сложим уравнения в получившейся системе. Тогда получим простейшее уравнение −13y = −156. Отсюда y = 12. Подставим y в первое уравнение и найдем x
Пример 7. Решить следующую систему уравнений методом сложения:
Приведем оба уравнения к нормальному виду. Здесь удобно применить правило пропорции в обоих уравнениях. Если в первом уравнении правую часть представить как , а правую часть второго уравнения как
, то система примет вид:
У нас получилась пропорция. Перемножим её крайние и средние члены. Тогда система примет вид:
Первое уравнение умножим на −3, а во втором раскроем скобки:
Теперь сложим оба уравнения. В результате сложения этих уравнений, мы получим равенство, в обеих частях которого будет ноль:
Получается, что система 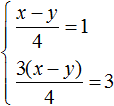
Но мы не можем просто так взять с неба произвольные значения для x и y. Мы можем указать одно из значений, а другое определится в зависимости от значения, указанного нами. Например, пусть x = 2. Подставим это значение в систему:
В результате решения одного из уравнений, определится значение для y, которое будет удовлетворять обоим уравнениям:
Получившаяся пара значений (2; −2) будет удовлетворять системе:
Найдём еще одну пару значений. Пусть x = 4. Подставим это значение в систему:
На глаз можно определить, что значение y равно нулю. Тогда получим пару значений (4; 0), которая удовлетворяет нашей системе:
Пример 8. Решить следующую систему уравнений методом сложения:
Умножим первое уравнение на 6, а второе на 12
Перепишем то, что осталось:
Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:
Первое уравнение умножим на −1. Тогда система примет вид:
Теперь сложим оба уравнения. В результате сложения образуется уравнение 6b = 48, корень которого равен 8. Подставим b в первое уравнение и найдём a
Система линейных уравнений с тремя переменными
В линейное уравнение с тремя переменными входит три переменные с коэффициентами, а также свободный член. В каноническом виде его можно записать следующим образом:
ax + by + cz = d
Данное уравнение имеет бесчисленное множество решений. Придавая двум переменным различные значения, можно найти третье значение. Решением в этом случае является тройка значений (x; y; z) которая обращает уравнение в тождество.
Если переменные x, y, z связаны между собой тремя уравнениями, то образуется система трех линейных уравнений с тремя переменными. Для решения такой системы можно применять те же методы, которые применяются к линейным уравнениям с двумя переменными: метод подстановки и метод сложения.
Пример 1. Решить следующую систему уравнений методом подстановки:
Выразим в третьем уравнении x. Тогда система примет вид:
Теперь выполним подстановку. Переменная x равна выражению 3 − 2y − 2z. Подставим это выражение в первое и второе уравнение:
Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:
Мы пришли к системе линейных уравнений с двумя переменными. В данном случае удобно применить метод сложения. В результате переменная y исчезнет, и мы сможем найти значение переменной z
Теперь найдём значение y. Для этого удобно воспользоваться уравнением −y + z = 4. Подставим в него значение z
Теперь найдём значение x. Для этого удобно воспользоваться уравнением x = 3 − 2y − 2z. Подставим в него значения y и z
Таким образом, тройка значений (3; −2; 2) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:
Пример 2. Решить систему методом сложения
Сложим первое уравнение со вторым, умноженным на −2.
Если второе уравнение умножить на −2, то оно примет вид −6x + 6y − 4z = −4. Теперь сложим его с первым уравнением:
Видим, что в результате элементарных преобразований, определилось значение переменной x. Оно равно единице.
Вернемся к главной системе. Сложим второе уравнение с третьим, умноженным на −1. Если третье уравнение умножить на −1, то оно примет вид −4x + 5y − 2z = −1. Теперь сложим его со вторым уравнением:
Получили уравнение x − 2y = −1. Подставим в него значение x, которое мы находили ранее. Тогда мы сможем определить значение y
Теперь нам известны значения x и y. Это позволяет определить значение z. Воспользуемся одним из уравнений, входящим в систему:
Таким образом, тройка значений (1; 1; 1) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:
Задачи на составление систем линейных уравнений
Задача на составление систем уравнений решается путем ввода нескольких переменных. Далее составляются уравнения на основании условий задачи. Из составленных уравнений образуют систему и решают её. Решив систему, необходимо выполнить проверку на то, удовлетворяет ли её решение условиям задачи.
Задача 1. Из города в колхоз выехала машина «Волга». Обратно она возвращалась по другой дороге, которая была на 5 км короче первой. Всего в оба конца машина проехала 35 км. Сколько километров составляет длина каждой дороги?
Решение
Пусть x — длина первой дороги, y — длина второй. Если в оба конца машина проехала 35 км, то первое уравнение можно записать как x + y = 35. Это уравнение описывает сумму длин обеих дорог.
Сказано, что обратно машина возвращалась по дороге которая была короче первой на 5 км. Тогда второе уравнение можно записать как x − y = 5. Это уравнение показывает, что разница между длинами дорог составляет 5 км.
Либо второе уравнение можно записать как x = y + 5. Этим уравнением и воспользуемся.
Поскольку переменные x и y в обоих уравнениях обозначают одно и то же число, то мы можем образовать из них систему:
Решим эту систему каким-нибудь из изученных ранее методов. В данном случае удобно воспользоваться методом подстановки, поскольку во втором уравнении переменная x уже выражена.
Подставим второе уравнение в первое и найдём y
Подставим найденное значение y в во второе уравнение x = y + 5 и найдём x
Длина первой дороги была обозначена через переменную x. Теперь мы нашли её значение. Переменная x равна 20. Значит длина первой дороги составляет 20 км.
А длина второй дороги была обозначена через y. Значение этой переменной равно 15. Значит длина второй дороги составляет 15 км.
Выполним проверку. Для начала убедимся, что система решена правильно:
Теперь проверим удовлетворяет ли решение (20; 15) условиям задачи.
Было сказано, что всего в оба конца машина проехала 35 км. Складываем длины обеих дорог и убеждаемся, что решение (20; 15) удовлетворяет данному условию: 20 км + 15 км = 35 км
Следующее условие: обратно машина возвращалась по другой дороге, которая была на 5 км короче первой. Видим, что решение (20; 15) удовлетворяет и этому условию, поскольку 15 км короче, чем 20 км на 5 км: 20 км − 15 км = 5 км
При составлении системы важно, чтобы переменные обозначали одни и те же числа во всех уравнениях, входящих в эту систему.
Так наша система 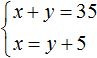
Задача 2. На платформу были погружены дубовые и сосновые шпалы, всего 300 шпал. Известно, что все дубовые шпалы весили на 1 т меньше, чем все сосновые. Определить, сколько было дубовых и сосновых шпал отдельно, если каждая дубовая шпала весила 46 кг, а каждая сосновая 28 кг.
Решение
Пусть x дубовых и y сосновых шпал было погружено на платформу. Если всего шпал было 300, то первое уравнение можно записать как x + y = 300.
Все дубовые шпалы весили 46x кг, а сосновые весили 28y кг. Поскольку дубовые шпалы весили на 1 т меньше, чем сосновые, то второе уравнение можно записать, как 28y − 46x = 1000. Это уравнение показывает, что разница масс между дубовыми и сосновыми шпалами, составляет 1000 кг.
Тонны были переведены в килограммы, поскольку масса дубовых и сосновых шпал измерена в килограммах.
В результате получаем два уравнения, которые образуют систему
Решим данную систему. Выразим в первом уравнении x. Тогда система примет вид:
Подставим первое уравнение во второе и найдём y
Подставим y в уравнение x = 300 − y и узнаем чему равно x
Значит на платформу было погружено 100 дубовых и 200 сосновых шпал.
Проверим удовлетворяет ли решение (100; 200) условиям задачи. Для начала убедимся, что система решена правильно:
Было сказано, что всего было 300 шпал. Складываем количество дубовых и сосновых шпал и убеждаемся, что решение (100; 200) удовлетворяет данному условию: 100 + 200 = 300.
Следующее условие: все дубовые шпалы весили на 1 т меньше, чем все сосновые. Видим, что решение (100; 200) удовлетворяет и этому условию, поскольку 46 × 100 кг дубовых шпал легче, чем 28 × 200 кг сосновых шпал: 5600 кг − 4600 кг = 1000 кг.
Задача 3. Взяли три куска сплава меди с никелем в отношениях 2 : 1, 3 : 1 и 5 : 1 по массе. Из них сплавлен кусок массой 12 кг с отношением содержания меди и никеля 4 : 1. Найдите массу каждого исходного куска, если масса первого из них вдвое больше массы второго.
Решение
Пусть x — масса первого куска, y — масса второго куска, z — масса третьего куска. Если из этих кусков сплавлен кусок массой 12 кг, то первое уравнение можно записать как x + y + z = 12.
Масса первого куска вдвое больше массы второго куска. Тогда второе уравнение можно записать как x = 2y.
Полученных двух уравнений недостаточно для решения данной задачи. Если второе уравнение подставить в первое, то мы получим уравнение 2y + y + z = 12, откуда 3y + z = 12. Это уравнение имеет бесчисленное множество решений.
Составим ещё одно уравнение. Пусть это уравнение будет описывать количество меди, взятого с каждого сплава и сколько меди оказалось в получившемся сплаве.
Если первый сплав имеет массу x, а медь и никель находится нём в отношении 2 : 1, то можно записать, что в новом сплаве содержится меди от первого куска.
Если второй сплав имеет массу y, а медь и никель находится в нём в отношении 3 : 1, то можно записать, что в новом сплаве содержится меди от второго куска.
Если третий сплав имеет массу z, а медь и никель находится в отношении 5 : 1, то можно записать, что в новом сплаве содержится меди от третьего куска.
Полученный сплав имеет имеет массу 12 кг, а медь и никель находится в нём в отношении 4 : 1. Тогда можно записать, что в полученном сплаве содержится меди.
Сложим ,
,
и приравняем эту сумму к 9,6. Это и будет нашим третьим уравнением:
Попробуем решить данную систему.
Для начала упростим третье уравнение. Подставим в него второе уравнение и посмотрим, что из этого выйдет:
Теперь в главной системе вместо уравнения запишем уравнение, которое мы сейчас получили, а именно уравнение 25y + 10z = 115,2
Подставим второе уравнение в первое:
Умножим первое уравнение на −10. Тогда система примет вид:
Сложим оба уравнения. Тогда получим простейшее уравнение −5y = −4,8 откуда найдём y равный 0,96. Значит масса второго сплава составляет 0,96 кг.
Теперь найдём x. Для этого удобно воспользоваться уравнением x = 2y. Значение y уже известно. Осталось только подставить его:
Значит масса первого сплава составляет 1,92 кг.
Теперь найдём z. Для этого удобно воспользоваться уравнением x + y + z = 12. Значения x и y уже известны. Подставим их куда нужно:
Значит масса третьего сплава составляет 9,12 кг.
Задания для самостоятельного решения
Задание 1. Приведите следующее уравнение к каноническому (нормальному) виду:
Решение
Задание 2. Приведите следующее уравнение к каноническому (нормальному) виду:
Решение
Задание 3. Приведите следующее уравнение к каноническому (нормальному) виду:
Решение
Задание 4. Приведите следующее уравнение к каноническому (нормальному) виду:
Решение
Задание 5. Решите следующую систему уравнений методом подстановки:
Решение
Задание 6. Решите следующую систему уравнений методом подстановки:
Решение
Задание 7. Решите следующую систему уравнений методом подстановки:
Решение
Задание 8. Решите следующую систему уравнений методом подстановки:
Решение
Задание 9. Решите следующую систему уравнений методом подстановки:
Решение
Задание 10. Решите следующую систему уравнений методом подстановки:
Решение
Задание 11. Решите следующую систему уравнений методом подстановки:
Решение
Задание 12. Решите следующую систему уравнений методом подстановки:
Решение
Задание 13. Решите следующую систему уравнений методом подстановки:
Решение
Задание 14. Решите следующую систему уравнений методом подстановки:
Решение
Задание 15. Решите следующую систему уравнений методом сложения:
Решение
Задание 16. Решите следующую систему уравнений методом сложения:
Решение
Задание 17. Решите следующую систему уравнений методом сложения:
Решение
Задание 18. Решите следующую систему уравнений методом сложения:
Решение
Задание 19. Решите следующую систему уравнений методом сложения:
Решение
Задание 20. Решите следующую систему уравнений методом сложения:
Решение
Задание 21. Решите следующую систему уравнений методом сложения:
Решение
Задание 22. Решите следующую систему уравнений методом сложения:
Решение
Задание 23. Решите следующую систему уравнений методом подстановки:
Решение
Задача 24. На прокормление 8 лошадей и 15 коров отпускали ежедневно 162 кг сéна. Сколько сéна ежедневно выдавали каждой лошади и каждой корове, если известно, что 5 лошадей получали сéна на 3 кг больше, чем 7 коров?
Решение
Пусть x кг сена выдавали каждой лошади, и y кг каждой корове. Лошадей было 8, а коров 15. Это значит, что сена всем лошадям выдавали 8x кг, а всем коровам 15y кг. Вместе лошадям и коровам сена выдавали 162 кг. Тогда первое уравнение можно записать как 8x + 15y = 162
Известно, что 5 лошадей получали 5x кг сена, а 7 коров 7y кг. Если 5 лошадей получали на 3 кг больше сена, чем 7 коров, то второе уравнение можно записать как 5x − 7y = 3.
Поскольку в обоих уравнениях переменные x и y обозначают одно и то же число, то можно образовать из них систему и решить её
Ответ: ежедневно сена каждой лошади выдавали 9 кг, а каждой корове 6 кг.
Задача 25. Для отправки груза было подано несколько вагонов. Если грузить по 15,5 т в вагон, то 4 т груза останутся непогруженными; если же грузить по 16,5 т в вагон, то для полной загрузки вагонов не хватит 8 т груза. Сколько было подано вагонов и сколько тонн было груза?
Решение
Пусть x вагонов было подано для отправки y тонн груза. Погрузку груза в вагоны можно описать с помощью отношения 
В первом случае в каждый вагон грузится 15,5 т. Тогда первое уравнение можно записать как 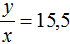
Во втором случае в каждый вагон грузится 16,5 т. Тогда второе уравнение можно записать как 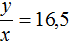
Поскольку в обоих уравнениях переменные x и y обозначают одно и то же число, то можно образовать из них систему и решить её:
Ответ: вагонов было 12, а груза 190 тонн.
Задача 26. В школьном зале поставлены скамейки. Если на каждую скамью посадить по 5 учеников, то не хватит 8 скамеек; если же на каждую скамью посадить по 6 учеников, то 2 скамьи останутся свободными. Сколько скамеек было поставлено в зале и сколько было учеников?
Решение
Пусть x скамеек было поставлено в зале, а учеников было y.
В первом случае на каждую скамейку сажается 5 учеников. Разделим y учеников по 5 человек и посадим их на x скамеек:
Но в условии сказано, что если посадить по 5 учеников на скамейку, то не хватит 8 скамеек. У нас имеется только x скамеек. Чтобы все y учеников смогли сесть на скамейки, добавим к x скамейкам ещё 8 скамеек
Во втором случае на каждую скамейку сажается 6 учеников. Разделим y учеников по 6 человек и посадим их на x скамеек:
Но в условии сказано, что если посадить по 6 учеников на скамейку, то 2 скамейки останутся свободными. В этом случае ученики сядут не на x, а на x − 2 скамейки. Перепишем второе уравнение в следующем виде:
Поскольку в обоих уравнениях переменные x и y обозначают одно и то же число, то можно образовать из них систему и решить её:
Ответ: скамеек было 52, а учеников 300.
Задача 27. Несколько человек отправляются на экскурсию. Если при этом каждый внесёт на расходы по 12 руб. 50 коп., то для оплаты расходов не хватит 100 руб.; если же каждый внесёт по 16 руб., то останется излишек 12 руб. Сколько человек участвует в экскурсии?
Решение
Пусть x человек участвует в экскурсии, а расходы на эту экскурсию составляют y рублей.
Если каждый участник экскурсии внесет по 12 руб. 50 коп., то расходы составят 12,50x руб. При этом сказано, что в таком случае для покрытия расходов не хватит 100 руб. Чтобы покрыть расходы прибавим к расходам 12,50x еще 100 рублей
12,50x + 100
Выражение 12,50x + 100, как и переменная y описывает одну и ту же величину — расходы на экскурсию. Поэтому можно соединить эти два выражения знаком равенства, образуя тем самым первое уравнение для системы:
12,50x + 100 = y
Далее в задаче сказано, что если каждый участник внесёт по 16 руб., то останется излишек 12 руб. Поскольку количество участников это x, то расходы при таком раскладе составят 16x. Расходы в 16x рублей больше планируемых y рублей на 12 руб. Чтобы получить второе уравнение вычтем из 16x руб излишек 12 руб.
16x − 12
Как и предыдущее выражение 12,50x + 100, выражение 16x − 12 описывает расходы на экскурсию и его можно приравнять к переменной y. Это будет вторым уравнением для системы:
16x − 12 = y
Получили два уравнения: 12,50x + 100 = y и 16x − 12 = y. Переменные x и y обозначают одно и то же число, поэтому можно образовать из них систему и решить её:
Значит в экскурсии участвует 32 человека.
В данной задаче не стоял вопрос какими будут расходы на экскурсию. Но для интереса можно вычислить и их:
Ответ: в экскурсии участвует 32 человека.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Системы уравнений
Система уравнений — это группа уравнений, в которых одни и те же неизвестные обозначают одни те же числа. Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:
 |
x — 4y = 2 |
| 3x — 2y = 16 |
Решить систему уравнений — это значит, найти общие решения для всех уравнений системы или убедиться, что решения нет.
Чтобы решить систему уравнений, нужно исключить одно неизвестное, то есть из двух уравнений с двумя неизвестными составить одно уравнение с одним неизвестным. Исключить одно из неизвестных можно тремя способами: подстановкой, сравнением, сложением или вычитанием.
Способ подстановки
Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное. Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.
Рассмотрим решение системы уравнений:
 |
x — 4y = 2 |
| 3x — 2y = 16 |
Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:
Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:
| 3x | — 2y = 16; |
| 3( 2 + 4y ) | — 2y = 16. |
Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.
| 3(2 + 4y) — 2y = 16; |
| 6 + 12y — 2y = 16; |
| 6 + 10y = 16; |
| 10y = 16 — 6; |
| 10y = 10; |
| y = 10 : 10; |
| y = 1. |
Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:
x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6.
Способ сравнения
Способ сравнения — это частный случай подстановки. Чтобы решить систему уравнений способом сравнения, нужно в обоих уравнениях найти, какому выражению будет равно одно и то же неизвестное и приравнять полученные выражения друг к другу. Получившееся в результате уравнение позволяет узнать значение одного неизвестного. С помощью этого значения затем вычисляется значение второго неизвестного.
Например, для решение системы:
 |
x — 4y = 2 |
| 3x — 2y = 16 |
найдём в обоих уравнениях, чему равен y (можно сделать и наоборот — найти, чему равен x):
| x — 4y = 2 | 3x — 2y = 16 |
| -4y = 2 — x | -2y = 16 — 3x |
| y = (2 — x) : — 4 | y = (16 — 3x) : -2 |
Составляем из полученных выражений уравнение:
Решаем уравнение, чтобы узнать значение x:
|
||||||
| 2 — x = 32 — 6x | ||||||
| —x + 6x = 32 — 2 | ||||||
| 5x = 30 | ||||||
| x = 30 : 5 | ||||||
| x = 6 |
Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:
| x — 4y = 2 | 3x — 2y = 16 |
| 6 — 4y = 2 | 3 · 6 — 2y = 16 |
| -4y = 2 — 6 | -2y = 16 — 18 |
| -4y = -4 | -2y = -2 |
| y = 1 | y = 1 |
Способ сложения или вычитания
Чтобы решить систему уравнений способом сложения, нужно составить из двух уравнений одно, сложив левые и правые части, при этом одно из неизвестных должно быть исключено из полученного уравнения. Неизвестное можно исключить, уравняв при нём коэффициенты в обоих уравнениях.
 |
x — 4y = 2 |
| 3x — 2y = 16 |
Уравняем коэффициенты при неизвестном y, умножив все члены второго уравнения на -2:
 |
x — 4y = 2 |
| -6x + 4y = -32 |
Теперь сложим по частям оба уравнения, чтобы получить уравнение с одним неизвестным:
| + | x — 4y = 2 |
| -6x + 4y = -32 | |
| -5x = -30 |
Находим значение x (x = 6). Теперь, подставив значение x в любое уравнение системы, найдём y = 1.
Если уравнять коэффициенты у x, то, для исключения этого неизвестного, нужно было бы вычесть одно уравнение из другого.
Уравняем коэффициенты при неизвестном x, умножив все члены первого уравнения на 3:
(x — 4y) · 3 = 2 · 3
 |
3x — 12y = 6 |
| 3x — 2y = 16 |
Теперь вычтем по частям второе уравнение из первого, чтобы получить уравнение с одним неизвестным:
| — | 3x — 12y = 6 |
| 3x — 2y = 16 | |
| -10y = -10 |
Находим значение y (y = 1). Теперь, подставив значение y в любое уравнение системы, найдём x = 6:
| 3x — 2y = 16 |
| 3x — 2 · 1 = 16 |
| 3x — 2 = 16 |
| 3x = 16 + 2 |
| 3x = 18 |
| x = 18 : 3 |
| x = 6 |
Для решения системы уравнений, рассмотренной выше, был использован способ сложения, который основан на следующем свойстве:
Любое уравнение системы можно заменить на уравнение, получаемое путём сложения (или вычитания) уравнений, входящих в систему. При этом получается система уравнений, имеющая те же решения, что и исходная.
Как решать систему уравнений
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Основные понятия
Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.
Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.
Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.
Линейное уравнение с двумя переменными
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.
Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.
Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:
Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.
Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).
Провести прямую через эти две точки и вуаля — график готов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Метод подстановки
Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:
Выразить одну переменную через другую из более простого уравнения системы.
Подставить то, что получилось на место этой переменной в другое уравнение системы.
Решить полученное уравнение, найти одну из переменных.
Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.
Записать ответ. Ответ принято записывать в виде пар значений (x; y).
Потренируемся решать системы линейных уравнений методом подстановки.
Пример 1
Решите систему уравнений:
x − y = 4
x + 2y = 10
Выразим x из первого уравнения:
x − y = 4
x = 4 + y
Подставим получившееся выражение во второе уравнение вместо x:
x + 2y = 10
4 + y + 2y = 10
Решим второе уравнение относительно переменной y:
4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2
Полученное значение подставим в первое уравнение вместо y и решим уравнение:
x − y = 4
x − 2 = 4
x = 4 + 2
x = 6
Ответ: (6; 2).
Пример 2
Решите систему линейных уравнений:
x + 5y = 7
3x = 4 + 2y
Сначала выразим переменную x из первого уравнения:
x + 5y = 7
x = 7 − 5y
Выражение 7 − 5y подставим вместо переменной x во второе уравнение:
3x = 4 + 2y
3 (7 − 5y) = 4 + 2y
Решим второе линейное уравнение в системе:
3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1
Подставим значение y в первое уравнение и найдем значение x:
x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2
Ответ: (2; 1).
Пример 3
Решите систему линейных уравнений:
x − 2y = 3
5x + y = 4
Из первого уравнения выразим x:
x − 2y = 3
x = 3 + 2y
Подставим 3 + 2y во второе уравнение системы и решим его:
5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1
Подставим получившееся значение в первое уравнение и решим его:
x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1
Ответ: (1; −1).
Метод сложения
Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:
При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.
Складываем почленно левые и правые части уравнений системы.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Запишем ответ в в виде пар значений (x; y).
Система линейных уравнений с тремя переменными
Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:
Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).
Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Решение задач
Разберем примеры решения систем уравнений.
Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?
5x − 8y = 4x − 9y + 3
5x − 8y = 4x − 9y + 3
5x − 8y − 4x + 9y = 3
Задание 2. Как решать систему уравнений способом подстановки
Выразить у из первого уравнения:
Подставить полученное выражение во второе уравнение:
Найти соответствующие значения у:
Задание 3. Как решать систему уравнений методом сложения
- Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
- Решаем полученное квадратное уравнение любым способом. Находим его корни:
- Найти у, подставив найденное значение в любое уравнение:
- Ответ: (1; 1), (1; -1).
Задание 4. Решить систему уравнений
Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.
Задание 5. Как решить систему уравнений с двумя неизвестными
При у = -2 первое уравнение не имеет решений, при у = 2 получается:
Решение уравнений с двумя неизвестными
В математике большая часть задач ориентирована на решение стандартных уравнений, в которых представлена одна переменная. Однако, некоторые из них, помимо числовых выражений, содержат одновременно две неизвестные. Перед тем как приступить к решению такого уравнения, стоит изучить его определение.
Определение
Итак, уравнением с двумя неизвестными называют любое равенство следующего типа:
a*x + b*y =с, где a, b, c — числа, x, y — неизвестные переменные.
Ниже приведены несколько примеров:
Уравнение с двумя неизвестными точно так же, как и с одной, имеет решение. Однако такие выражения, как правило, имеют бесконечное множество разных решений, поэтому в алгебре их принято называть неопределенными.
Решение задач
Чтобы решить подобные задачи, необходимо отыскать любую пару значений x и y, которая удовлетворяла бы его, другими словами, обращала бы уравнение с неизвестными x и y в правильное числовое равенство. Найти удовлетворяющую пару чисел можно при помощи метода подбора.
Для наглядности объяснений подберем корни для выражения: y-x = 6.
При y=5 и x=-1 равенство становится верным тождеством 5- (-1) = 6. Поэтому пару чисел (-1; 5) можно считать корнями выражения y-x = 6. Ответ: (-1; 5).
Необходимо отметить, что записывать полученный ответ по правилам необходимо в скобках через точку с запятой. Первым указывается значение х, вторым — значение y.
У равенств такого вида может и не быть корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9
Приведем исходное равенство к следующему виду:
В результате мы видим ошибочное равенство, следовательно, это выражение не имеет корней.
При решении уравнений можно пользоваться его свойствами. Первое их них: каждое слагаемое можно вынести в другую часть выражения. Вместе с этим обязательно нужно поменять знак на обратный. Получившееся равенство будет равнозначно исходному.
Например, из выражения 20y — 3x = 16 перенесем неизвестное y в другую его часть.
Оба равенства равносильны.
Второе свойство: допустимо умножать или делить части выражения на одинаковое число, не равное нолю. В итоге получившиеся равенства будут равнозначны.
Оба уравнения также равносильны.
Система уравнений с двумя неизвестными
Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.
Для решения системы уравнений необходимо найти пару чисел, обращающих оба уравнения системы в правильное равенство. Решением может служить одна пара чисел, несколько пар чисел или вовсе их отсутствие.
Решить подобные системы уравнений можно, применяя следующие методы.
Метод подстановки
- Выражаем неизвестное из любого равенства через вторую переменную.
- Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
- Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.
Метод сложения
- Приводим к равенству модули чисел при каком-либо неизвестном.
- Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
- Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.
Графический метод
- Выражаем в каждом равенстве одну переменную через другую.
- Строим графики двух имеющихся уравнений в одной координатной плоскости.
- Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
- Делаем проверку, подставив полученные значения в исходную систему равенств.
При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.
В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.
Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!
Видео
Из этого видео вы узнаете, как решать уравнения с двумя неизвестными.
источники:
http://skysmart.ru/articles/mathematic/reshenie-sistem-uravnenij
http://liveposts.ru/articles/education-articles/matematika/reshenie-uravnenij-s-dvumya-neizvestnymi
Решение уравнений с двумя неизвестными
В математике большая часть задач ориентирована на решение стандартных уравнений, в которых представлена одна переменная. Однако, некоторые из них, помимо числовых выражений, содержат одновременно две неизвестные. Перед тем как приступить к решению такого уравнения, стоит изучить его определение.
Определение
Итак, уравнением с двумя неизвестными называют любое равенство следующего типа:
a*x + b*y =с, где a, b, c — числа, x, y — неизвестные переменные.
Ниже приведены несколько примеров:
Уравнение с двумя неизвестными точно так же, как и с одной, имеет решение. Однако такие выражения, как правило, имеют бесконечное множество разных решений, поэтому в алгебре их принято называть неопределенными.
Решение задач
Чтобы решить подобные задачи, необходимо отыскать любую пару значений x и y, которая удовлетворяла бы его, другими словами, обращала бы уравнение с неизвестными x и y в правильное числовое равенство. Найти удовлетворяющую пару чисел можно при помощи метода подбора.
Для наглядности объяснений подберем корни для выражения: y-x = 6.
При y=5 и x=-1 равенство становится верным тождеством 5- (-1) = 6. Поэтому пару чисел (-1; 5) можно считать корнями выражения y-x = 6. Ответ: (-1; 5).
Необходимо отметить, что записывать полученный ответ по правилам необходимо в скобках через точку с запятой. Первым указывается значение х, вторым — значение y.
У равенств такого вида может и не быть корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9
Приведем исходное равенство к следующему виду:
В результате мы видим ошибочное равенство, следовательно, это выражение не имеет корней.
При решении уравнений можно пользоваться его свойствами. Первое их них: каждое слагаемое можно вынести в другую часть выражения. Вместе с этим обязательно нужно поменять знак на обратный. Получившееся равенство будет равнозначно исходному.
Например, из выражения 20y — 3x = 16 перенесем неизвестное y в другую его часть.
Оба равенства равносильны.
Второе свойство: допустимо умножать или делить части выражения на одинаковое число, не равное нолю. В итоге получившиеся равенства будут равнозначны.
Оба уравнения также равносильны.
Система уравнений с двумя неизвестными
Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.
Для решения системы уравнений необходимо найти пару чисел, обращающих оба уравнения системы в правильное равенство. Решением может служить одна пара чисел, несколько пар чисел или вовсе их отсутствие.
Решить подобные системы уравнений можно, применяя следующие методы.
Метод подстановки
- Выражаем неизвестное из любого равенства через вторую переменную.
- Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
- Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.
Метод сложения
- Приводим к равенству модули чисел при каком-либо неизвестном.
- Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
- Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.
Графический метод
- Выражаем в каждом равенстве одну переменную через другую.
- Строим графики двух имеющихся уравнений в одной координатной плоскости.
- Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
- Делаем проверку, подставив полученные значения в исходную систему равенств.
При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.
В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.
Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!
Видео
Из этого видео вы узнаете, как решать уравнения с двумя неизвестными.
Решить систему из 2-х уравнений с 2-мя неизвестными онлайн
Онлайн калькулятор для решения систем из двух уравнений с двумя неизвестными. Во многих примерах калькулятор показывает решение на графике.
Калькулятор
Инструкция
Примечание: π записывается как pi; корень квадратный как sqrt().
Шаг 1. Введите заданные уравнение в поля калькулятора.
Шаг 2. Нажмите кнопку “Решить систему”.
Шаг 3. Получите развёрнутый результат.
В калькулятор можно вводить любые буквы, но только на латинском языке. Кроме того, калькулятор считает десятичные и обыкновенные дроби так же хорошо, как и целые числа. Переходить с одного поля на другое можно при помощи клавиши “Tab”
Каким путём решать систему из двух уравнений с двумя неизвестными
Система с двумя уравнениями с двумя неизвестными можно решать, как методом Крамера, так и методом Гаусса. Всё зависит от определённых чисел. Например, правило Крамера можно применять в том случае, если определитель основной матрицы не равен нулю. Если же методом Крамера не получается решить систему, тогда можно использовать метод Гаусса, который решается путём последовательного исключения неизвестных.
Уравнения с двумя переменными (неопределенные уравнения)
Разделы: Математика
Обращение автора к данной теме не является случайным. Уравнения с двумя переменными впервые встречаются в курсе 7-го класса. Одно уравнение с двумя переменными имеет бесконечное множество решений. Это наглядно демонстрирует график линейной функции, заданный в виде ax + by=c. В школьном курсе учащиеся изучают системы двух уравнений с двумя переменными. В результате из поля зрения учителя и, поэтому ученика, выпадает целый ряд задач, с ограниченными условиями на коэффициент уравнения, а также методы их решения.
Речь идет о решении уравнения с двумя неизвестными в целых или натуральных числах.
В школе натуральные и целые числа изучаются в 4-6-х классах. К моменту окончания школы не все ученики помнят различия между множествами этих чисел.
Однако задача типа “решить уравнение вида ax + by=c в целых числах” все чаще встречается на вступительных экзаменах в ВУЗы и в материалах ЕГЭ.
Решение неопределенных уравнений развивает логическое мышление, сообразительность, внимание анализировать.
Я предлагаю разработку нескольких уроков по данной теме. У меня нет однозначных рекомендаций по срокам проведения этих уроков. Отдельные элементы можно использовать и в 7-м классе (для сильного класса). Данные уроки можно взять за основу и разработать небольшой элективный курс по предпрофильной подготовке в 9-м классе. И, конечно, этот материал можно использовать в 10-11 классах для подготовки к экзаменам.
Цель урока:
-
повторение и обобщение знаний по теме “Уравнения первого и второго порядка”
- воспитание познавательного интереса к учебному предмету
- формирование умений анализировать, проводить обобщения, переносить знания в новую ситуацию
Урок 1.
Ход урока.
1) Орг. момент.
2) Актуализация опорных знаний.
Определение. Линейным уравнением с двумя переменными называется уравнение вида
mx + ny = k, где m, n, k – числа, x, y – переменные.
Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Уравнения с двумя переменными, имеющими одни и те же решения, называются равносильными.
1. 5x+2y=12 
Данное уравнение может иметь сколько угодно решений. Для этого достаточно взять любое значение x и найти соответствующее ему значение y.
Пусть x = 2, y = -2.5•2+6 = 1
x = 4, y = -2.5•4+6 =- 4
Пары чисел (2;1); (4;-4) – решения уравнения (1).
Данное уравнение имеет бесконечно много решений.
3) Историческая справка
Неопределенные (диофантовы) уравнения – это уравнения, содержащие более одной переменной.
В III в. н.э. – Диофант Александрийский написал “Арифметику”, в которой расширил множество чисел до рациональных, ввел алгебраическую символику.
Так же Диофант рассмотрел проблемы решения неопределенных уравнений и им даны методы решения неопределенных уравнений второй и третьей степени.
4) Изучение нового материала.
Определение: Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = k, где m, n, k, x, y 

Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.
Пример: 34x – 17y = 3.
НОД (34; 17) = 17, 3 не делится нацело на 17, в целых числах решения нет.
Пусть k делится на НОД (m, n). Делением всех коэффициентов можно добиться, что m и n станут взаимно простыми.
Если m и n уравнения (1) взаимно простые числа, то это уравнение имеет по крайней мере одно решение.
Если коэффициенты m и n уравнения (1) являются взаимно простыми числами, то это уравнение имеет бесконечно много решений:




Определение. Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = 0, где (2)
m, n, x, y 
Если m и n – взаимно простые числа, то всякое решение уравнения (2) имеет вид
5) Домашнее задание. Решить уравнение в целых числах:
Замечание. На данном уроке не представлены примеры решения уравнений в целых числах. Поэтому домашнее задание дети решают исходя из утверждения 1 и подбором.
Урок 2.
1) Организационный момент
2) Проверка домашнего задания
5 не делится нацело на 9, в целых числах решений нет.
Методом подбора можно найти решение
3) Составим уравнение:
Пусть мальчиков x, x 

Многие учащиеся, составив уравнение, не смогут его решить.
Ответ: мальчиков 4, девочек 6.
3) Изучение нового материала
Столкнувшись с трудностями при выполнении домашнего задания, учащиеся убедились в необходимости изучения их методов решений неопределенных уравнений. Рассмотрим некоторые из них.
I. Метод рассмотрения остатков от деления.
Пример. Решить уравнение в целых числах 3x – 4y = 1.
Левая часть уравнения делится на 3, следовательно, должна делиться и правая часть. Рассмотрим три случая.
- Если y = 3m, m
Z, то 4y + 1= 4•3m + 1 = 12m + 1 не делится на 3.
- Если y = 3 m + 1, то 4y +1 = 4• (3m + 1)+1 = 12m + 5 не делится на 3.
- Если y = 3 m + 2, то 4y +1 = 4• (3m + 2)+1 = 12m + 9 делится на 3, поэтому 3x = 12m + 9, следовательно, x = 4m + 3, а y = 3m + 2.
Ответ: 

Описанный метод удобно применять в случае, если числа m и n не малы, но зато разлагаются на простые сомножители.
Пример: Решить уравнения в целых числах.
Пусть y = 4n, тогда 16 – 7y = 16 – 7•4n = 16 – 28n = 4*(4-7n) делится на 4.
y = 4n+1, тогда 16 – 7y = 16 – 7• (4n + 1) = 16 – 28n – 7 = 9 – 28n не делится на 4.
y = 4n+2, тогда 16 – 7y = 16 – 7• (4n + 2) = 16 – 28n – 14 = 2 – 28n не делится на 4.
y = 4n+3, тогда 16 – 7y = 16 – 7• (4n + 3) = 16 – 28n – 21 = -5 – 28n не делится на 4.
Следовательно, y = 4n, тогда
4x = 16 – 7•4n = 16 – 28n, x = 4 – 7n
Ответ: 

II. Неопределенные уравнения 2-ой степени
Сегодня на уроке мы лишь коснемся решения диофантовых уравнений второго порядка.
И из всех типов уравнений рассмотрим случай, когда можно применить формулу разности квадратов или другой способ разложения на множители.
Пример: Решить уравнение в целых числах.
13 – простое число, поэтому оно может быть разложено на множители лишь четырьмя способами: 13 = 13•1 = 1•13 = (-1)(-13) = (-13)(-1)
Рассмотрим эти случаи
а) 
б) 
в) 
г) 
4) Домашнее задание.
Примеры. Решить уравнение в целых числах:
а)
 |
 |
 |
| 2x = 4 | 2x = 5 | 2x = 5 |
| x = 2 | x = 5/2 | x = 5/2 |
| y = 0 | не подходит | не подходит |
 |
 |
 |
| 2x = -4 | не подходит | не подходит |
| x = -2 | ||
| y = 0 |
б)
в)
Итоги. Что значит решить уравнение в целых числах?
Какие методы решения неопределенных уравнений вы знаете?
Упражнения для тренировки.
1) Решите в целых числах.
| а) 8x + 12y = 32 | x = 1 + 3n, y = 2 – 2n, n  Z Z |
| б) 7x + 5y = 29 | x = 2 + 5n, y = 3 – 7n, n  Z Z |
| в) 4x + 7y = 75 | x = 3 + 7n, y = 9 – 4n, n  Z Z |
| г) 9x – 2y = 1 | x = 1 – 2m, y = 4 + 9m, m  Z Z |
| д) 9x – 11y = 36 | x = 4 + 11n, y = 9n, n  Z Z |
| е) 7x – 4y = 29 | x = 3 + 4n, y = -2 + 7n, n  Z Z |
| ж) 19x – 5y = 119 | x = 1 + 5p, y = -20 + 19p, p  Z Z |
| з) 28x – 40y = 60 | x = 45 + 10t, y = 30 + 7t, t  Z Z |
2) Найти целые неотрицательные решения уравнения:
| а) 8x + 65y = 81 | x = 2, y = 1 |
| б) 17x + 23y = 183 | x = 4, y = 5 |
3) Найти все пары целых чисел (x; y), удовлетворяющие следующим условиям
| а) x + y = xy | (0;0), (2;2) |
б)  |
(1;2), (5;2), (-1;-1), (-5;-2) |
Число 3 можно разложить на множители:
в)  |
(11;12), (-11;-12), (-11;12), (11;-12) |
г)  |
(24;23), (24;-23), (-24;-23), (-24;23) |
д)  |
(48;0), (24;1), (24;-1) |
е)  |
x = 3m; y = 2m, m Z Z |
| ж) y = 2x – 1 | x = m: y = 2m – 1, m  Z Z |
з)  |
x = 2m; y = m; x = 2m; y = -m, m  Z Z |
и) |
решений нет |
4) Решить уравнения в целых числах
 |
(-3;-2), (-1;1), (0;4), (2;-2), (3;1), (5;4) |
| (x – 3)(xy + 5) = 5 | (-2;3), (2;-5), (4;0) |
| (y + 1)(xy – 1)=3 | (0;-4), (1;-2), (1;2) |
 |
(-4;-1), (-2;1), (2;-1), (4;1) |
 |
(-11;-12), (-11;12), (11;-12), (11;12) |
 |
(-24;23), (-24;23), (24;-23), (24;23) |
5) Решить уравнения в целых числах.
[spoiler title=”источники:”]
http://nauchniestati.ru/kalkulatory/reshit-sistemu-iz-2-h-uravnenij-s-2-mja-neizvestnymi-onlajn/
http://urok.1sept.ru/articles/417558
[/spoiler]