Выражение константы равновесия
Для реакции:
SO2Cl2(г) = SO2(г) + Cl2(г) ∆H0х.р. > 0.
1) Написать математические выражения константы равновесия Кс и Кр и установить взаимосвязь между ними;
2) В сторону расходования или образования хлора сдвигается равновесие при: а) увеличении концентрации диоксида серы; б) увеличении температуры; в) введении катализатора.
Решение задачи
1)
Константой химического равновесия (Kр) отношение констант скоростей прямой и обратной реакций.
![]()
Уравнение константы равновесия показывает, что в условиях равновесия концентрации всех веществ (исходных и продуктов), участвующих в реакции, связаны между собой. Изменение концентрации любого из них влечет за собой изменения концентрации всех остальных веществ. Концентрации веществ при установившемся равновесии называются равновесными концентрациями.
Константу равновесия можно выразить через молярные концентрации веществ, участвующих в реакции. В этом случае она обозначается Кс. Константа равновесия данной реакции выражается уравнением. Запишем выражение константы равновесия:
![]()
Если же выразить константу равновесия через парциальные давления газообразных веществ, участвующих в реакции, то её обозначают Кр и она будет равна для приведенной формальной реакции:
![]()
Константы Кс и Кр связаны между собой соотношением:
![]()
Где:
∆n – изменение числа молей реагирующих веществ и продуктов в результате реакции.
Если ∆n = 0, то есть реакция не сопровождается изменением числа молей компонентов, то
Кр = Кс.
2) Если увеличить концентрацию диоксида серы (SO2) равновесие сместится в сторону обратной реакции (в сторону расходования хлора (Cl2)).
Увеличение температуры влечет смещение равновесия в в сторону прямой реакции (в сторону образования хлора (Cl2)).
Введение катализатора одинаково ускоряет и прямую и обратную реакции и поэтому не происходит смещение химического равновесия. Катализатор только способствует более быстрому достижению состояния равновесия.
Константа
равновесия может быть выражена различными
способами. Если концентрации веществ,
участвующих в реакции, выражены в
молярных единицах молярности , т.е. в
моль/л, то она обычно обозначается Кс и
для равновесия обратимой реакции
аА
+ bB
dD
+ rR
записывается в
виде:
 (2.4)
(2.4)
Для
гомогенной газовой реакции константу
равновесия удобнее выразить через
парциальные давления веществ:
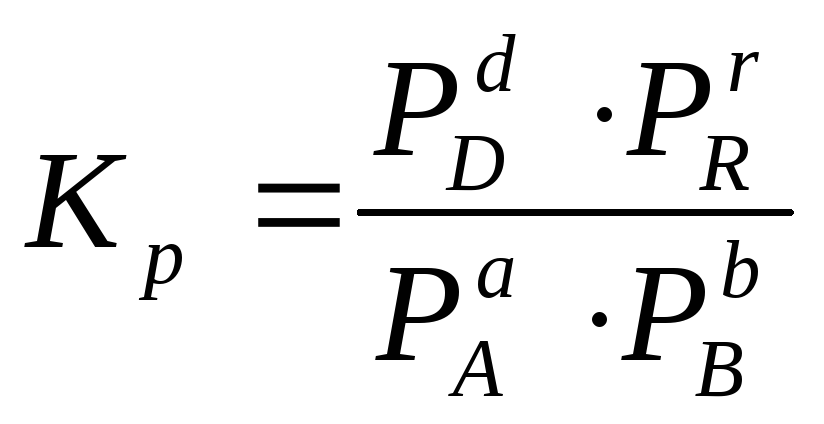 (2.5)
(2.5)
Иногда
константу равновесия удобно выразить
не через парциальные давления и
концентрации, а через количества
веществ:
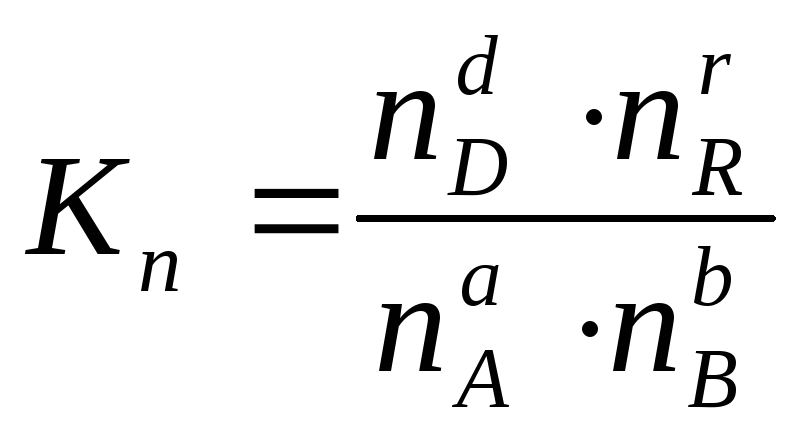 (2.6)
(2.6)
или через
соответствующие мольные доли:
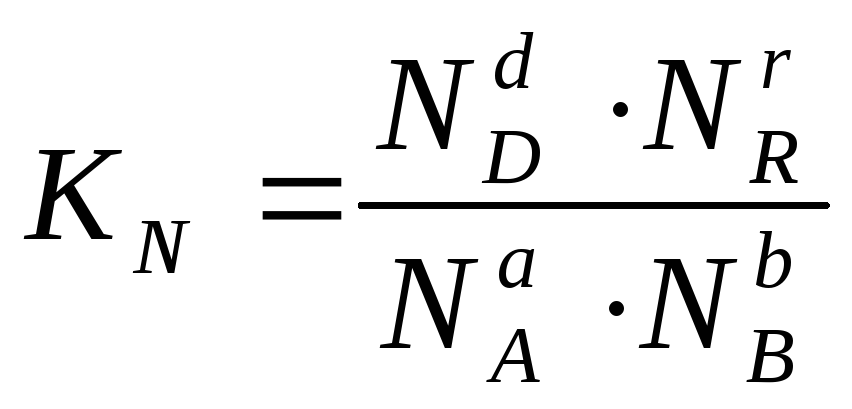 (2.7)
(2.7)
В
общем случае константы равновесия Кс,
Кр, Кn
и КN
различны по значениям. Установим связь
между ними.
В
газовых системах, для характеристики
которых применимо уравнение состояния
идеальных газов Менделеева – Клайперона,
значение парциального давления любого
компонента можно вычислить следующим
образом:
![]()
откуда
![]()
![]() (2.8)
(2.8)
где
C
– концентрация i-го
компонента, выраженная в моль/л. Подставим
значение р из уравнения (2.8) в уравнение
(2.5) и получим соотношение, которым
определяется связь Кс и Кр:
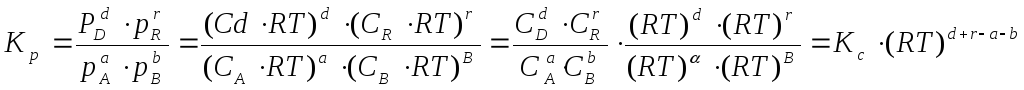
или
![]() ,
,
(2.9)
где
![]() –
–
изменение числа моль в результате
реакции.
Для
идеальных газов парциальные давления
связаны с общим давлением Робщ
и мольной долей Ni
данного компонента в смеси согласно
законам Дальтона следующим равенством:
pi
= NiPобщ
(2.10),
где
рi
– парциальное давление компонента; Ni
– мольная доля этого компонента в смеси;
Робщ
– общее давление.
Подставим
значение рi
в уравнение (2.5), получим:
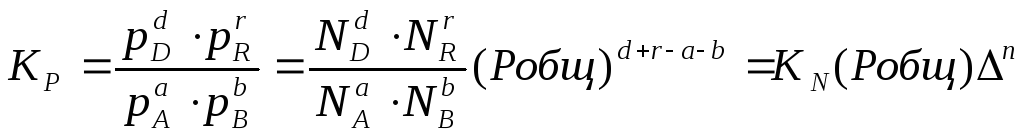
или
Кр
= К∙ (Робщ)∆n
(2.11).
Воспользовавшись
соотношением Pi
= Ni∙
Робщ
=![]() общ)∆n,
общ)∆n,
где
ni
– число моль компонента i
в смеси, а ni
– число моль всех компонентов в смеси,
получаем:
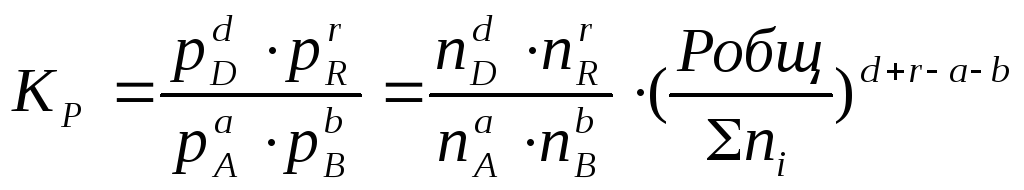 или
или
![]()
Таким
образом, если n≠
0, т.е. если
реакция сопровождается изменением
числа моль, то имеет место соотношение:
![]() (2.12).
(2.12).
Если
же ∆n=0
(реакция не сопровождается изменением
числа моль), то Кр
= Кс
= Кn
= KN
, т.е. значения
всех видов констант равновесия совпадают.
Кр
и Кс
для реакции идеальных газов не зависят
от давления.
КN
и Кn
от давления зависят в случае ∆n≠0.
2.4. Смещение химического равновесия
При
постоянных условиях химическое равновесие
сохраняется как угодно долго. Однако
внешние условия не могут бесконечно
оставаться неизменными, а изменение
хотя бы одного из них нарушает состояние
равновесия, т.е. скорос-
ти
прямой и обратной реакций не будут равны
между собой (v1
v2).
Но, так как все физико-химические системы
самопроизвольно стремятся к состоянию
равновесия, то с течением времени оно
вновь установится. Однако, это будет
новое равновесие, с другими значениями
равновесных концентраций, отвечающими
другим, изменившимся условиям.
В
каком направлении сместится равновесие
при том или ином внешнем воздействии?
Ответ на этот вопрос дает принцип
Ле-Шателье
Брауна, который можно сформулировать
следующим образом: если
на систему, находящуюся в состоянии
равновесия, оказывается какое – либо
внешнее воздействие, то система отвечает
таким образом, чтобы это воздействие
ослабить.
При этом, если в результате нарушения
равновесия скорость прямой реакции
будет больше скорости обратной реакции,
то говорят, что равновесие смещено
вправо (v1
v2),
и соответственно, если преобладает
скорость обратной реакции, говорят, что
равновесие смещено влево (v1
v2
).
Важнейшими
условиями, определяющими состояние
химического равновесия, являются:
1) концентрация
реагирующих веществ
2) температура
3)
давление (для реакций, протекающих с
изменением давления).
Изменение
хотя бы одного из них приведет к нарушению
равновесия.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как правильно рассчитывать равновесные концентрации веществ. Смещение равновесия реакции
Задача 249.
Для предложенной обратимой реакции напишите математическое выражение константы химического равновесия и укажите направление смещения равновесия при изменении условий:
а) уменьшении концентрации одного из газообразных продуктов;
б) понижении давления в системе;
в) повышении температуры в системе.
2Н2(г) + О2(г) ⇔ 2Н2O(г); ∆Hx.p. = -484кДж.
Решение:
Кр можно выразить через соотношение констант прямой и обратной реакций, получим:
Кр = [Н2О]/[Н2]2 . [O2].
а) Понижение концентрации продукта реакции (отведение из системы Н2О) будет увеличивать скорость прямой реакции, поэтому согласно принципа Ле-Шателье при понижениии концентрации Н2О равновесие сместится в сторону прямой реакции, т. е. в сторону увеличения образования Н2О.
б) При понижении давления смещение равновесия будет наблюдаться в сторону прямой реакции, так как объм газообразного реагента в полтора раза больше объема продукта реакции системы:
2V(Н2) + 1VO2 > 2V(H2O).
в) При повышении температуры равновесие сместится в сторону обратной реакции, так как прямая реакция – экзотермическая (∆Hx.p. = -484кДж). Согласно принципу Ле-Шателье равновесие реакции смещается в сторону уменьшения оказываемого на систему действия. Данная реакция протекает с выделением тепла (∆H < 0), то, естественно, что при повышении температуры равновесие экзотермической реакции сместится в сторону уменьшения тепловой энергии реакции, т.е. в сторону обратной реакции.
Задача 250.
Дано уравнение реакции: N2 + 3H2 = 2NH3
1) Укажите в какую сторону сместится равновесие системы при повышении и уменьшения давления. 2) Напишите выражение константы равновесия данной системы.
Решение:
1. При воздействии на систему равновесие смещается в сторону уменьшения этого воздействия. Так в системе N2 + 3H2 = 2NH3 из 4 объемов газообразных исходных веществ образуется 2 объема газообразного продукта, значит, при обычных условиях система протекает с уменьшением объема в 2 раза [4V(исх.в-ва)/2V(пр.) = 2]. Поэтому при повышении давления равновесие системы сместится в сторну прямой реакции, т.е. в сторону уменьшения воздействия на систему (уменьшения объема), на образование NH3, а при уменьшении давления – равновесие сместится в сторону увеличения воздействия на систему (увеличение объема), в сторону образовани исходных продуктов реакции (N2 и H2).
2. Выражение константы равновесия системы N2 + 3H2 = 2NH3 будет иметь вид:
[NH3]2/[N2].[H2]3.
Отсюда находим константу равновесия реакции, получим:
Кр = [NH3]2/[N2].[H2]3 = (4)2/3 . (9)3 = 16/2187 = 0,0073 или 7,3 . 10-3.
Задача 251.
Константа равновесия реакции А + В = С + D равна 1. Начальная конццентрация [А] = 0,01 моль/л, [В ]= 0,1 моль/л. Какая доля (в %) исходного количества вещества А подвергнется превращению при равновесии? Каковы равновесные концентрации веществ?
Решение:
Уравнение реакции имеет вид:
А + В = С + D
Из уравнения следует, что из 1 моля А и 1 моля В образуется по 1 молю С и D т.е. по 0,01 молю С и D.
Обозначим равновесную концентрацию С и D через х, тогда [С] = [D].
Таким образом, равновесные концентрации A и B будут составлять, соответственно, (0,01 – х) и (0,1 – х) моль/л, а С и D – по х моль/л. Подставим эти значения в выражение константы равновесия реакции:
К = [C][D]/[A][B];
1 = (х . х)/[(0,01 – х)(0,1 – х)];
x2 = 0,001 – 0,1x – 0,01x – x2;
0,001 = 0,11x;
x = 0,0091.
Отсюда равновесные концентрации (моль/л):
[C]p = [D]p = х = 0,0091 моль/л;
[A]p = 0,01 – х = 0,01 – 0,0091 = 0,0009 моль/л;
[B]p = 0,1 – х = 0,1 – 0,0091 = 0,0909 моль/л.
Значит, 91% вещества А подвергнется превращению при равновесии.
0,01 — 100%
0,0091 — х
х = (0,0091 . 100%)/0,01 = 91%.
Задача 252.
В какую сторону сместится равновесие системы – PCl5(г) = PCl2(г) + Cl2(г), Н > 0:
а) при увеличении температуры;
б) при увеличении давления;
в) при увеличении концентрации хлора?
Решение:
а) прямая реакция эндотермическая (с поглощением тепла). Чтобы компенсировать увеличение температуры – должна пойти реакция с поглощением тепла. Смещение в сторону образования продуктов.
б) При увеличении давления равновесие смещается в сторону меньших газов, при уменьшении давления – в сторону больших газов.
Прямая реакция идет с увеличением числа молей газообразных веществ (увеличение давления). Обратная реакция с понижением давления. При увеличении давления пойдет реакция, уменьшающая его (обратная). Равновесие сместится влево.
в) При вводе в систему продукта реакции пойдет реакция, способствующая его расходу. Это обратная реакция. Равновесие сместится влево.
Задача 253.
При нагревании смеси углекислого газа и водорода образуется угарный газ и вода, а также устанавливаетася равновесие. При температуре 1123 К и константе скорости Кр = 1. Сколько молей углекислого газа необходимо на 1 моль водорода, чтобы 70% его превратилось в воду.
Решение:
Уравнение реакции имеет вид:
СО2(г.) + Н2(г.) ⇔ СО(г.) + +Н2О(г.).
Из уравнения следует, что из 1 моля СО2 и 1 моля Н2 образуется по 1 молю СО и Н2О.
Находим количество Н2, которое вступило в реакцию: 1 . 0,7 = 0,7 моль/л. Остаток количества СО2 и Н2 одинаков и будет составлять 0,3 моль/л (1 – 0,7 = 0,3). Следовательно, из взятых веществ остаются непрореагировавшими 0,3 моля углекислого газа и 0,3 моля водорода:
Первоначальные количества реагирующих веществ (в молях)…. 1(СО2) : 1(Н2) = 0(СО) : 0(Н2О).
Количества веществ по достижении предела реакции 1123 К (в молях)…. 0,3(СО2) : 0,3(Н2) = 0,7(СО) : 0,7(Н2О)
Значит, причиной «остановки» разбираемой нами реакции является наличие обратной реакции.
После смешения углекислого газа с водородом между ними начинается взаимодействие, в результате которого образуются молекулы окиси углерода и воды. По мере течения этой реакции концентрации взятых веществ уменьшаются и скорость реакции становится все меньше и меньше. В то же время возникает возможность обратной реакции. Молекулы окиси углерода и воды, сталкиваясь между собой, могут снова превращаться в молекулы углекислого газа и водорода. Вначале, пока молекул окиси углерода и воды еще мало, их столкновения происходят довольно редко. Однако по мере накопления молекул этих веществ столкновения становятся все чаще, в результате чего скорость обратной реакции постепенно увеличивается. Наконец, наступает момент, когда скорости прямой и обратной реакций уравниваются, т. е. в каждую единицу времени исчезает столько же молекул углекислого газа и водорода, сколько их появляется вновь вследствие обратной реакции. С этого момента концентрации всех четырех газов перестают изменяться, несмотря на то, что первоначально взятые углекислый газ и водород целиком не прореагировали.
Таким образом, при температуре 1123 К в данной системе наступает равновесие когда на 1 моль водорода и на 1 моль углекислого газа прореагируют по о,7 моль этих веществ и образуется такое же количество угарного газа и воды, и в системе наступит равновесие при концентрациях веществ (в молях)….
0,3(СО2) : 0,3(Н2) = 0,7(СО) : 0,7(Н2О).
Ответ: СО2 = 0,7 моль.
Тогда объёмные соотношения СО2 и Н2, к моменту наступления равновесия, составляют:
V(H2) : V(CO2) = 0,7 : 0,3 = 2,33 : 1. Значит, на 1 моль водорода необходимо 0,43 моль СО2 (1/2,33 = 0,429).
Константа равновесия химической реакции


4.8
Средняя оценка: 4.8
Всего получено оценок: 164.
4.8
Средняя оценка: 4.8
Всего получено оценок: 164.
Количественная характеристика, показывающая направление реакции и смещение концентрации веществ, называется константой равновесия химической реакции. Константа равновесия зависит от температуры и природы реагентов.
Обратимые и необратимые реакции
Все реакции можно разделить на два типа:
- обратимые, одновременно протекающие в двух взаимно противоположных направлениях;
- необратимые, протекающие в одном направлении с полным расходом хотя бы одного исходного вещества.
При необратимых реакциях обычно образуются нерастворимые вещества в виде осадка или газа. К таким реакциям относятся:
- горение:
C2H5OH + 3O2 → 2CO2 + H2O;
- разложение:
2KMnO4 → K2MnO4 + MnO2 + H2O;
- присоединение с образованием осадка или газа:
BaCl2 + Na2SO4 → BaSO4↓ + 2NaCl.
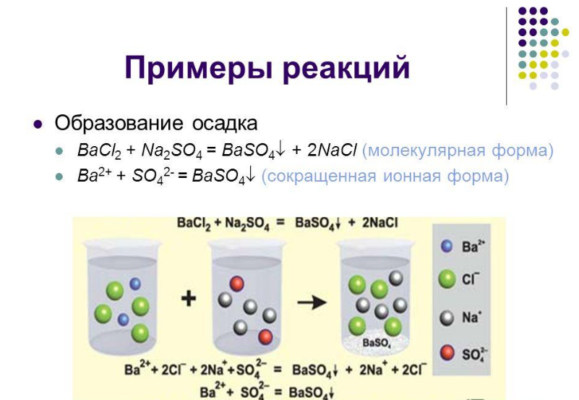
Обратимые реакции возможны только в определённых неизменных условиях. Исходные вещества дают новое вещество, которое тут же распадается на составные части и собирается вновь. Например, в результате реакции 2NO + O2 ↔ 2NO2 оксид азота (IV) легко разлагается на оксид азота (II) и кислород.
Равновесие
Через определённое время скорость обратимой реакции замедляется. Достигается химическое равновесие – состояние, при котором не происходит изменения концентрации исходных веществ и продуктов реакции с течением времени, так как скорость прямой и обратной реакций уравниваются. Равновесие возможно только в гомогенных системах, то есть все реагирующие вещества являются либо жидкостями, либо газами.
Рассмотрим химическое равновесие на примере реакции взаимодействия водорода с йодом:
- прямая реакция –
H2 + I2 ↔ 2HI;
- обратная реакция –
2HI ↔ H2 + I2.
Как только смешиваются два реагента – водород и йод – йодоводорода ещё не существует, так как простые вещества только вступают в реакцию. Большое количество исходных веществ активно реагируют друг с другом, поэтому скорость прямой реакции будет максимальной. При этом обратная реакция не протекает, и скорость её равна нулю.
Скорость прямой реакции можно выразить графически:
νпр = kпр ∙ [H2] ∙ [I2],
где kпр – константа скорости прямой реакции.
Со временем реагенты расходуются, их концентрация снижается. Соответственно, скорость прямой реакции уменьшается. Одновременно с этим увеличивается концентрация нового вещества – йодоводорода. При накоплении он начинает разлагаться, и скорость обратной реакции повышается. Её можно выразить как
νобр = kобр ∙ [HI]2.
Йодоводород в квадрате, так как коэффициент молекулы равен двум.
В определённый момент скорости прямой и обратной реакции уравниваются. Наступает состояние химического равновесия.
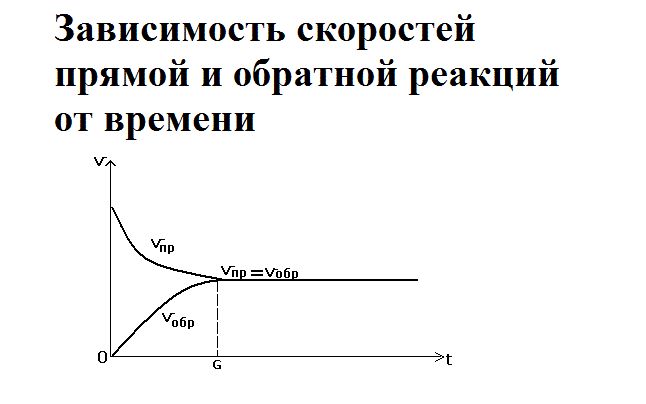
Равновесие можно сместить либо в сторону исходных веществ, либо в сторону продуктов реакции. Смещение под воздействием внешних факторов называется принципом Ле Шателье. На равновесие влияют температура, давление, концентрация одного из веществ.
Расчёт константы
В состоянии равновесия обе реакции идут, но при этом концентрации веществ находятся в равновесии (образуются равновесные концентрации), так как уравновешенны скорости (νпр = νобр).
Химическое равновесие характеризуется константой химического равновесия, которая выражается сводной формулой:
Kp = kпр / kобр = const.
Константы скорости реакции можно выразить через соотношение скорости реакции. Возьмём условное уравнение обратной реакции:
aA + bB ↔ cC + dD.
Тогда скорости прямой и обратной реакции будут равны:
- νпр = kпр ∙ [A]pa ∙ [B]pb
- νобр = kобр ∙ [C]pc ∙ [D]pd.
Соответственно, если
νпр = νобр,
то
kпр ∙ [A]pa ∙ [B]pb = kобр ∙ [C]pc ∙ [D]pd.
Отсюда можно выразить соотношение констант:
kобр / kпр = [C]pc ∙ [D]pd / [A]pa ∙ [B]pb.
Это соотношение равно константе равновесия:
Kp = [C]pc ∙ [D]pd / [A]pa ∙ [B]pb.
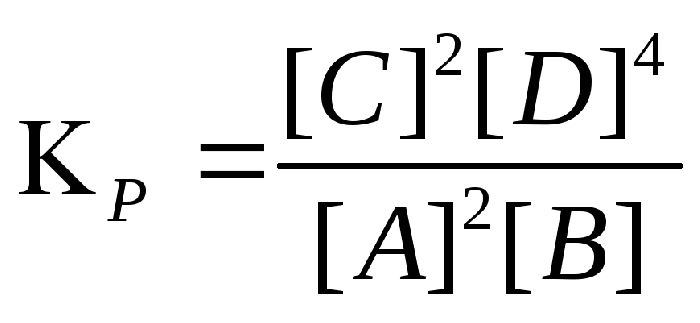
Величина показывает, во сколько раз скорость прямой реакции больше скорости обратной реакции.

Что мы узнали?
Реакции в зависимости от конечных продуктов классифицируются на обратимые и необратимые. Обратимые реакции протекают в обе стороны: исходные вещества образуют конечные продукты, которые разлагаются на исходные вещества. В ходе реакции скорости прямой и обратной реакций уравновешиваются. Такое состояние называется химическим равновесием. Оно может быть выражено как соотношение произведения равновесных концентраций продуктов реакции к произведению разновесных концентраций исходных веществ.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Усмон Бозоров
4/5
Оценка доклада
4.8
Средняя оценка: 4.8
Всего получено оценок: 164.
А какая ваша оценка?
У этого термина существуют и другие значения, см. Константа.
Конста́нта равнове́сия — величина, определяющая для данной химической реакции соотношение между термодинамическими активностями (либо, в зависимости от условий протекания реакции, парциальными давлениями, концентрациями или фугитивностями) исходных веществ и продуктов в состоянии химического равновесия (в соответствии с законом действующих масс). Зная константу равновесия реакции, можно рассчитать равновесный состав реагирующей смеси, предельный выход продуктов, определить направление протекания реакции.
Способы выражения константы равновесия[править | править код]
Для реакции в смеси идеальных газов константа равновесия может быть выражена через равновесные парциальные давления компонентов 
где 

Например, для реакции окисления монооксида углерода:
константа равновесия может быть рассчитана по уравнению:
Если реакция протекает в идеальном растворе и концентрация компонентов выражена через молярность 
Для реакций в смеси реальных газов или в реальном растворе вместо парциального давления и концентрации используют соответственно фугитивность 

В некоторых случаях (в зависимости от способа выражения) константа равновесия может являться функцией не только температуры, но и давления. Так, для реакции в смеси идеальных газов парциальное давление компонента может быть выражено по закону Дальтона через суммарное давление и мольную долю компонента (
где 



Часто вместо самой константы равновесия 


Стандартная константа равновесия[править | править код]
Стандартная константа равновесия реакции в смеси идеальных газов (когда начальные парциальные давления участников реакции равны их значениям в стандартном состоянии 
где 

Стандартная константа равновесия — безразмерная величина. Она связана с 
Видно, что если 


Для реакции в смеси реальных газов в стандартном начальном состоянии парциальные фугитивности газов принимаются равными их парциальным давлениям 


где 

Константа равновесия реакций в гетерогенных системах[править | править код]
Для гетерогенной химической реакции, например, между компонентами реального газа и реального раствора, константа равновесия в общем случае может быть выражена уравнением:
где 

Если конденсированные фазы (твёрдые или жидкие) представляют собой практически чистые вещества, их активности постоянны и могут быть включены в константу равновесия (то есть в левую часть выражения выше). Условно можно принять их равными единице и, таким образом, исключить из выражения.
Например, для реакции твёрдофазного восстановления оксида железа:
константа равновесия (при условии, что газовая фаза идеальна) имеет вид:
Термодинамическое описание равновесия[править | править код]
Наряду с обозначением 

- (обозначения для приведённой ниже реакции; последнее равенство написано в обозначении, что стехиометрические коэффициент берутся со знаком «+» для продуктов и со знаком «−» для исходных веществ)
в химической термодинамике используется обозначение 
- (то есть соотношения активностей в момент
, в момент равновесия). Далее приведено термодинамическое описание химического равновесия и описана связь
со стандартной энергией Гиббса процесса.
В системе, где протекает химическая реакция
равновесие может быть описано условием
где 
или, то же самое условие равновесия может быть записано с использованием химических потенциалов как
где химические потенциалы
здесь 
Выражение для энергии Гиббса принимает вид
а так как 
При равновесии (иначе говоря, при условии что время 
Записав теперь условие равновесия 

Равновесный состав смеси и направление реакции[править | править код]
Упомянутый выше «коэффициент реакции» 


отражает соотношение текущих активностей всех участников реакции и может быть использован для определения направления реакции в момент, для которого известен 
- Если в момент
коэффициент
, то текущие активности продуктов больше равновесных, и значит они должны уменьшиться к тому моменту, когда установится равновесие, то есть в данный момент протекает обратная реакция;
- Если
, то равновесное состояние достигнуто и скорости прямой и обратной реакций равны;
- Если
, то
С использованием величины 
где 



а стандартная энергия Гиббса и стандартная константа суть
где 
Уравнение изотермы показывает, как величина 
- при
для прямой реакции
, то есть
для продуктов прямой реакции больше, чем для исходных веществ — это означает, что прямая реакция запрещена (значит, не запрещена обратная);
- при
для прямой реакции
, то есть реакция достигла равновесного состояния;
- при
для прямой реакции
, то есть эта самопроизвольное протекание этой реакции разрешено
Величина 



- Если
, то в системе преобладают продукты (прямой) реакции.
- Если
, то в системе преобладают исходные вещества (продукты обратной реакции)[5].
Стандартные состояния[править | править код]
Стандартная энергия Гиббса реакции в газовой смеси — энергия Гиббса реакции при стандартных парциальных давлениях всех компонентов, равных 0,1013 МПа (1 атм).
Стандартная энергия Гиббса реакции в растворе — энергия Гиббса при стандартном состоянии раствора, за которое принимают гипотетический раствор со свойствами предельно разбавленного раствора, но с концентрацией всех реагентов, равной единице.
Для чистого вещества и жидкости стандартная энергия Гиббса совпадает с энергией Гиббса образования этих веществ.
Величина стандартной энергии Гиббса реакции может быть использована для приближенной оценки термодинамической возможности протекания реакции в данном направлении, если начальные условия не сильно отличаются от стандартных. Кроме того, сравнивая величины стандартной энергии Гиббса нескольких реакций, можно выбрать наиболее предпочтительные, для которых 
Кинетическое описание[править | править код]
Для обратимой химической реакции константа равновесия 
Рассмотрим элементарную обратимую химическую реакцию первого порядка
По определению, равновесие задаётся условием 
В соответствии с законом действующих масс
где 

можно записать условие равновесия в виде
То есть
(см. термодинамическое описание константы равновесия), что возможно только если
Это важное соотношение даёт одну из «точек соприкосновения» химической кинетики и химической термодинамики[4][6].
Множественные равновесия[править | править код]
В случае, когда в системе устанавливается сразу несколько равновесий (то есть одновременного или последовательного протекает нескольких процессов), каждый из них может быть охарактеризован своей константой равновесия, из которых можно выразить общую константу равновесия для всей совокупности процессов. Можно рассмотреть такую ситуацию на примере ступенчатой диссоциации двухосновной кислоты 






Другой пример множественного равновесия — анализ системы осадок/растворимое комплексное соединение.
Допустим, имеется равновесие
Реакцию можно представить в виде двух последовательных равновесий — равновесия разложения комплексного иона на составляющие его ионы, которое характеризуется «константой нестойкости» (величина, обратная «константе устойчивости» 
и равновесия перехода ионов из объёма растворителя в кристаллическую решётку
с учётом того, что для твёрдых веществ активность принимается равной 1, а в разбавленных растворах активности могут быть заменены на молярные концентрации, получаем
где 
Тогда суммарное равновесие будет описываться константой
И значение этой константы будет условием преобладания в равновесной смеси комплексного соединения или твёрдой соли: как и выше, если 

Зависимость константы равновесия от температуры[править | править код]
Зависимость константы равновесия реакции от температуры может быть описана уравнением изобары химической реакции (изобары Вант-Гоффа):
и изохоры химической реакции (изохоры Вант-Гоффа):
Здесь 



Методы расчета константы равновесия[править | править код]
Расчётные методы определения константы равновесия реакции обычно сводятся к вычислению тем или иным способом стандартного изменения энергии Гиббса в ходе реакции (
, где
— универсальная газовая постоянная.
При этом следует помнить, что энергия Гиббса — функция состояния системы, то есть она не зависит от пути процесса, от механизма реакции, а определяется лишь
начальным и конечным состояниями системы. Следовательно, если непосредственное определение или расчёт 

Энтропийный расчёт изменения энергии Гиббса и константы равновесия реакции[править | править код]
Энтропийный метод расчёта 
или, соответственно, для стандартного изменения энергии Гиббса:
Здесь 
Необходимо получить изменение энтропии в ходе реакции. Эта задача может быть решена несколькими способами, например:
- По термическим данным — с опорой на тепловую теорему Нернста и с использованием сведений о температурной зависимости теплоёмкости участников реакции. Например, для веществ, при нормальных условиях находящихся в твёрдом состоянии:
где 
-
.
- (здесь индекс sol — от англ. solid, «твердый»). При некоторой заданной температуре
:
- Для жидких или газообразных при нормальной температуре веществ, или, в более общем случае, для веществ, в интервале температур от 0 (или 298) и до
претерпевающих фазовый переход, следует учитывать изменение энтропии, связанное с этим фазовым переходом.
- Для идеальных газов — методами квантовой статистики.
- Различными эмпирическими и полуэмпирическими методами, для этого часто достаточно небольшого объёма исходных данных. Например, для твёрдых неорганических веществ оценить энтропию можно по формуле[7]:
- где
и
— табличные константы, зависящие от типа рассматриваемого соединения,
— молекулярная масса.
Итак, если известны 


Несколько упрощённый вариант этой формулы получают, считая сумму теплоёмкостей веществ не зависящей от температуры и равной сумме теплоёмкостей при 298 K:
И ещё более упрощённый расчёт проводят, приравнивая сумму теплоёмкостей к нулю:
Переход от 
Расчёт константы равновесия методами статистической термодинамики[править | править код]
|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016) |
Экспериментальное определение константы равновесия[править | править код]
|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (30 июня 2016) |
См. также[править | править код]
- Константа диссоциации
- Константа автопротолиза
- Константа гидролиза
- Константа устойчивости
- Константа Михаэлиса
- Энергия Гиббса
Примечания[править | править код]
- ↑ 1 2 Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим.-технол. спец. вузов / Под ред. А. Г. Стромберга. — 2-е изд. — М.: Высш. шк., 1988. — 496 с.
- ↑ 1 2 3 Патров Б. В., Сладков И. Б. Физическая химия. Ч. 1 : учеб. пособие. — СПб.: Изд-во Политехн. ун-та, 2009. — 127 с. — ISBN 978-5-7422-2206-4.
- ↑ Эткинс П. Физическая химия в 2 т., том 1. — М.: Мир, 1980. — 580 с.
- ↑ 1 2 3 Жмурко Г. П., Казаков Е. Ф., Кузнецова В. Н., Яценко А. В. Общая химия. — М.: Академия, 2012. — ISBN 978-5-7695-9188-4. — 512 с.
- ↑ 1 2 Неорганическая химия в 3 т. /Под редакцией Третьякова Ю. Д. — Том 1: Физико-химические основы неорганической химии. — М.: Академия, 2004. — 240 с.
- ↑ Эткинс П. Физическая химия в 2 т., том 2. — М.: Мир, 1980. — 584 с.
- ↑ Физическая химия. Теоретическое и практическое руководство. Учеб. пособие для вузов / Под ред. акад. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987. — 880 с.
Литература[править | править код]
- Киреев В. А. Методы практических расчётов в термодинамике химических реакций. — 2-е изд. — М., 1975.
- Жоров Ю. М. Термодинамика химических процессов. — М., 1985.















![{displaystyle K_{mathrm {eq} }={frac {[C]^{sigma }[D]^{tau }}{[A]^{alpha }[B]^{beta }}}={frac {prod a_{j(t=infty )}^{nu _{j}}}{prod a_{i(t=infty )}^{nu _{i}}}}=prod a_{n(t=infty )}^{nu _{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc5a2f2f80438a4b8a7072323eeedbaa7bab18ae)


















![{displaystyle mathrm {H} _{2}mathrm {A} rightleftharpoons mathrm {HA} ^{-}+mathrm {H} ^{+}:K_{1}={frac {[mathrm {HA} ^{-}][mathrm {H} ^{+}]}{[mathrm {H} _{2}mathrm {A} ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/143e0b7ec27f2411ba87210539820c138128cb0b)
![{displaystyle mathrm {HA} ^{-}rightleftharpoons mathrm {A} ^{2-}+mathrm {H} ^{+}:K_{2}={frac {[mathrm {A} ^{2-}][mathrm {H} ^{+}]}{[mathrm {HA} ^{-}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2111b38183d19279cd9090c7793ffd68ce588f74)
![{displaystyle mathrm {H} _{2}mathrm {A} rightleftharpoons mathrm {A} ^{2-}+2mathrm {H} ^{+}:K_{1+2}={frac {[mathrm {A} ^{2-}][mathrm {H} ^{+}]^{2}}{[mathrm {H} _{2}mathrm {A} ]}}=K_{1}K_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98c0dfdacfd5dda0925e8f0ddcc7965d7424997f)



![{displaystyle K_{2}={frac {alpha _{mathrm {AgI} }}{alpha _{mathrm {Ag} ^{+}}alpha _{mathrm {I} ^{-}}}}={frac {1}{[mathrm {Ag} ^{+}][mathrm {I} ^{-}]}}={frac {1}{K_{mathrm {sp} }}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b49f9de23845acc735a4c02c2fc69aa94341943c)












