Содержание
- 1 Строим таблицу для анализа
- 2 Пример выводов к данной таблице по экономике
- 3 Разбавляйте выводы рисунками. Пример
Строим таблицу для анализа
В таблице 1 представлены основные экономические показатели деятельности ООО «СХО «Заречье» за 2017-2019 гг.
Таблица 1 — Основные экономические показатели деятельности ООО «СХО «Заречье» за 2017-2019 гг.
| Показатели | 2017 г. | 2018 г. | 2019 г. | 2018 г. к 2017 г. | 2019 г. к 2018 г. |
| Выручка от реализации с/х продукции, тыс.руб. | 71511 | 76731 | 65462 | 5220 | -11269 |
| Себестоимость, тыс.руб. | 129282 | 126771 | 109343 | -2511 | -17428 |
| Прибыль (убыток) от продаж, тыс.руб. | -74294 | -64029 | -56575 | 10265 | 7454 |
| Дебиторская задолженность, тыс.руб. | 1535 | 1645 | 1178 | 110 | -467 |
| Кредиторская задолженность тыс.руб. | 331150 | 245071 | 331736 | -86079 | 86665 |
| Прочие доходы, тыс.руб. | 111192 | 129065 | 77624 | 17873 | -51441 |
| Прочие расходы, тыс.руб | 129065 | 58805 | 94106 | -70260 | 35301 |
| Чистая прибыль (непокрытый убыток), тыс.руб. | 24542 | 6231 | -73057 | -18311 | -79288 |
| Численность работников, чел. | 170 | 168 | 146 | -2 | -22 |
| Производительность труда, тыс.руб. / чел. | 420,7 | 456,7 | 448,4 | 36,08 | -8,36 |
| Среднегодовая стоимость ОПФ, тыс.руб. | 528434,5 | 474125 | 447043 | -54309,5 | -27082 |
| Фондоотдача ОПФ, руб./руб. | 0,14 | 0,16 | 0,15 | 0,02 | -0,01 |
| Средняя заработная плата работников, тыс.руб. / мес. | 19,78 | 19,83 | 19,71 | 0,05 | -0,12 |
| Среднегодовая стоимость оборотных активов, тыс.руб. | 127270 | 124974 | 111049 | -2296 | -13925 |
| Оборачиваемость оборотных активов, об. | 0,56 | 0,61 | 0,59 | 0,05 | -0,02 |
| Рентабельность (убыточность) продаж, % | -103,89 | -83,45 | -86,42 | 20,45 | -2,98 |
| Рентабельность (убыточность) производства с/х продукции, % | -57,47 | -50,51 | -51,74 | 6,96 | -1,23 |
Пример выводов к данной таблице по экономике
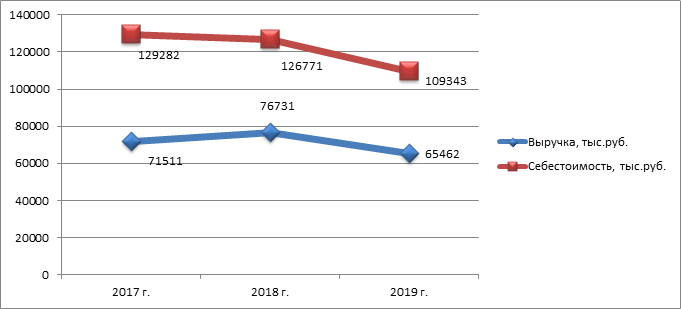
Как можно пронаблюдать из данных, представленных в таблице 6, в СХО «Заречье» в 2017-2019 году, наблюдается нестабильная динамика показателей выручки и себестоимости продаж сельскохозяйственной продукции. Так, в 2018 году рост выручки от продаж составлял 7,3% по сравнению с 2017 годом, а уже в 2019 году данный показатель снизился на 14,69% по сравнению с 2018 годом. Себестоимость же продаж имеет отрицательную динамику на протяжении всего анализируемого периода.
В связи с тем, что на протяжении 2017-2019 года, как можно заметить из данных представленных в таблице 6 и на рисунке 3, величина себестоимости превышала величину выручки от продаж, в СХО «Заречье» был сформирован убыток от реализации сельскохозяйственной продукции в существенном размере. Так, в 2017 году убыток от продаж составил 74294 тыс.руб., что превышало величину общей выручки от продаж. В 2018 году величина убытка от продажи составила 64029 тыс.руб., а в 2019 году данный показатель возрос до 56575 тыс.руб. Примечательно то, что при таком уровне убытка от продаж, в 2017-2018 году СХО «Заречье» по итогам отчетного периода был получен положительный финансовый результата.
В 2019 году величина непокрытого убытка превысила величину убытка от продаж. В 2017 и 2018 году величина чистой прибыли была сформирована за счет превышения прочих доходов над прочими расходами. В состав же прочих доходов в 2017 – 2018 году в основном входили государственные бюджетные субсидии и дотации.
В связи с тем, что на протяжении 2017-2019 года предприятием был получен убыток от продаж сельскохозяйственной продукции, уровень рентабельности производства и продаж находился в отрицательной зоне.
Среднесписочная численность работников предприятия в 2019 году составила 146 чел., что меньше аналогичного периода 2018 года на 22 человека и меньше 2017 года на 24 человека. Средняя заработная плата работников составляла на протяжении исследуемого периода чуть менее 20 тыс.руб.
Рост производительности труда в 2018 году был обусловлен, прежде всего, повышением выручки от продаж, при этом даже существенное снижение численности работников в 2019 году, не смогло стать фактором за счет снижения выручки, роста производительности труда.
Рост фондоотдачи на 0,02 руб. в 2018 году относительно 2017 года был вызван общим сокращением среднегодовой стоимости основных производственных фондов сельскохозяйственного предприятия и положительной динамикой выручки от продаж. В 2019 году фондоотдача ОПФ снизилась, что было определено только общим снижением выручки от продаж сельскохозяйственной продукции.
Оборачиваемость оборотных активов повышается за счет роста выручки в 2018 году относительно 2017 года, в данный период повышение оборачиваемости составило 0,05 оборота. В 2019 же году снижение выручки от продаж способствовало снижению оборачиваемости оборотных активов в СХО «Заречье» на 0,02 оборота.
Разбавляйте выводы рисунками. Пример
Основные показатели предприятия
Просмотров 17 672
До сих пор мы исходили из того, что наши данные, например, о росте тысячи мужчин-респондентов в России полностью отражают реальные показатели роста всех россиян. На самом деле мы не знаем, так это или нет.
Мы сможем об этом говорить только, если получим измерения каждого человека. Эта задача представляется нереализуемой.
Те же, кого нам всё-таки удалось измерить, называются выборкой (sample). А вот все мужчины в России — это генеральная совокупность (population).
Существует ли вообще возможность сказать что-либо определенное про генеральную совокупность по ограниченному набору данных?
На самом деле существует. Теоретическое обоснование этой возможности называется Центральной предельной теоремой.
Центральная предельная теорема (Central Limit Theorem) гласит, что если мы будем много раз выборочно собирать данные, то среднее средних всех выборок (распределение средних) будет стремится к среднему генеральной совокупности. Рассмотрим этот процесс подробнее.
Для начала возьмем несколько выборок из одной генеральной совокупности и выясним среднее каждой выборки.
Затем посчитаем среднее арифметическое средних этих выборок. Это новое среднее будет стремиться к среднему генеральной совокупности (обозначается греческой буквой μ, мю).
Этот вывод чрезвычайно важен, потому что мы наконец-то получаем инструменты, позволяющие сказать что-то определенное про величину, которую мы в принципе не можем охватить измерением.
Теперь рассмотрим статистический вывод на практике. Центральная предельная теорема является обоснованием для двух важных инструментов изучения генеральной совокупности.
С одной стороны, даже предполагая, что выборочное среднее стремится к истинному среднему, мы не можем быть на 100 процентов уверены, что знаем этот параметр генеральной совокупности. С другой, теорема позволяет задать доверительный интервал (Confidence Interval) для среднего (и на самом деле любого другого параметра, например, пропорции).
Другими словами, мы можем утверждать, что, например, в 90 процентах случаев, наш доверительный интервал будет включать истинный параметр генеральной совокупности.
На графике греческой буквой μ (мю) как раз обозначено среднее генеральной совокупности, которое попадает в наш доверительный интервал только в 9 случаях из 10 (то есть в 90 процентах случаев).
Например, мы можем найти доверительный интервал для среднего роста всех мужчин в России. Сделаем это с помощью Питона.
|
# вначале вновь подгрузим данные [185.0, 179.0, 186.0, 195.0, 178.0, 178.0, 196.0, 188.0, 175.0, 185.0, 175.0, 175.0, 182.0, 161.0, 163.0, 174.0, 170.0, 183.0, 171.0, 166.0, 195.0, 178.0, 181.0, 166.0, 175.0, 181.0, 168.0, 184.0, 174.0, 177.0, 174.0, 199.0, 180.0, 169.0, 188.0, 168.0, 182.0, 160.0, 167.0, 182.0, 187.0, 182.0, 179.0, 177.0, 165.0, 173.0, 175.0, 191.0, 183.0, 162.0, 183.0, 176.0, 173.0, 186.0, 190.0, 189.0, 172.0, 177.0, 183.0, 190.0, 175.0, 178.0, 169.0, 168.0, 188.0, 194.0, 179.0, 190.0, 184.0, 174.0, 184.0, 195.0, 180.0, 196.0, 154.0, 188.0, 181.0, 177.0, 181.0, 160.0, 178.0, 184.0, 195.0, 175.0, 172.0, 175.0, 189.0, 183.0, 175.0, 185.0, 181.0, 190.0, 173.0, 177.0, 176.0, 165.0, 183.0, 183.0, 180.0, 178.0, 166.0, 176.0, 177.0, 172.0, 178.0, 184.0, 199.0, 182.0, 183.0, 179.0, 161.0, 180.0, 181.0, 205.0, 178.0, 183.0, 180.0, 168.0, 191.0, 188.0, 188.0, 171.0, 194.0, 166.0, 186.0, 202.0, 170.0, 174.0, 181.0, 175.0, 164.0, 181.0, 169.0, 185.0, 171.0, 195.0, 172.0, 177.0, 188.0, 168.0, 182.0, 193.0, 164.0, 182.0, 183.0, 188.0, 168.0, 167.0, 185.0, 183.0, 183.0, 183.0, 173.0, 182.0, 183.0, 173.0, 199.0, 185.0, 168.0, 187.0, 170.0, 188.0, 192.0, 172.0, 190.0, 184.0, 188.0, 199.0, 178.0, 172.0, 171.0, 172.0, 179.0, 183.0, 183.0, 188.0, 180.0, 195.0, 177.0, 207.0, 186.0, 171.0, 169.0, 185.0, 178.0, 187.0, 185.0, 179.0, 172.0, 165.0, 176.0, 189.0, 182.0, 168.0, 182.0, 184.0, 171.0, 182.0, 181.0, 169.0, 184.0, 186.0, 191.0, 191.0, 166.0, 171.0, 185.0, 185.0, 185.0, 219.0, 186.0, 191.0, 190.0, 187.0, 177.0, 188.0, 172.0, 178.0, 175.0, 181.0, 203.0, 161.0, 187.0, 164.0, 175.0, 191.0, 181.0, 169.0, 173.0, 187.0, 173.0, 182.0, 180.0, 173.0, 201.0, 186.0, 160.0, 182.0, 173.0, 189.0, 172.0, 179.0, 185.0, 189.0, 168.0, 177.0, 175.0, 173.0, 198.0, 184.0, 167.0, 189.0, 201.0, 190.0, 165.0, 175.0, 193.0, 173.0, 184.0, 188.0, 171.0, 179.0, 148.0, 170.0, 177.0, 168.0, 196.0, 166.0, 176.0, 181.0, 194.0, 166.0, 192.0, 180.0, 170.0, 185.0, 182.0, 174.0, 181.0, 176.0, 181.0, 187.0, 196.0, 168.0, 201.0, 160.0, 178.0, 186.0, 183.0, 174.0, 178.0, 175.0, 174.0, 188.0, 184.0, 173.0, 189.0, 183.0, 188.0, 186.0, 172.0, 174.0, 187.0, 186.0, 180.0, 181.0, 193.0, 174.0, 185.0, 178.0, 178.0, 191.0, 188.0, 188.0, 193.0, 180.0, 187.0, 177.0, 183.0, 179.0, 181.0, 186.0, 172.0, 201.0, 170.0, 168.0, 192.0, 188.0, 186.0, 186.0, 180.0, 171.0, 181.0, 173.0, 190.0, 179.0, 172.0, 177.0, 184.0, 174.0, 172.0, 182.0, 182.0, 175.0, 175.0, 182.0, 166.0, 166.0, 173.0, 178.0, 183.0, 195.0, 189.0, 178.0, 180.0, 170.0, 180.0, 177.0, 183.0, 172.0, 185.0, 195.0, 179.0, 184.0, 187.0, 176.0, 182.0, 180.0, 181.0, 172.0, 180.0, 185.0, 195.0, 190.0, 202.0, 172.0, 189.0, 182.0, 202.0, 172.0, 172.0, 174.0, 159.0, 175.0, 172.0, 182.0, 183.0, 199.0, 190.0, 174.0, 171.0, 185.0, 167.0, 198.0, 192.0, 175.0, 163.0, 194.0, 179.0, 192.0, 164.0, 174.0, 180.0, 180.0, 175.0, 186.0, 169.0, 179.0, 181.0, 185.0, 187.0, 169.0, 165.0, 193.0, 183.0, 173.0, 196.0, 181.0, 192.0, 181.0, 201.0, 198.0, 178.0, 190.0, 186.0, 194.0, 170.0, 187.0, 191.0, 162.0, 168.0, 160.0, 177.0, 187.0, 195.0, 181.0, 196.0, 166.0, 163.0, 179.0, 184.0, 180.0, 159.0, 179.0, 167.0, 187.0, 184.0, 171.0, 175.0, 169.0, 179.0, 190.0, 170.0, 185.0, 175.0, 172.0, 179.0, 170.0, 174.0, 168.0, 200.0, 180.0, 173.0, 182.0, 179.0, 178.0, 186.0, 188.0, 175.0, 174.0, 177.0, 157.0, 165.0, 194.0, 196.0, 178.0, 186.0, 183.0, 211.0, 191.0, 179.0, 170.0, 164.0, 182.0, 172.0, 166.0, 174.0, 169.0, 197.0, 189.0, 180.0, 195.0, 181.0, 171.0, 195.0, 185.0, 170.0, 178.0, 171.0, 166.0, 189.0, 199.0, 166.0, 186.0, 173.0, 175.0, 174.0, 171.0, 180.0, 172.0, 183.0, 179.0, 178.0, 171.0, 174.0, 188.0, 185.0, 170.0, 181.0, 188.0, 163.0, 185.0, 173.0, 186.0, 172.0, 162.0, 164.0, 180.0, 183.0, 171.0, 186.0, 163.0, 179.0, 168.0, 173.0, 180.0, 171.0, 176.0, 190.0, 174.0, 188.0, 169.0, 185.0, 194.0, 155.0, 172.0, 186.0, 178.0, 184.0, 174.0, 181.0, 178.0, 192.0, 183.0, 183.0, 176.0, 175.0, 176.0, 184.0, 176.0, 183.0, 201.0, 189.0, 177.0, 192.0, 176.0, 160.0, 170.0, 161.0, 176.0, 180.0, 197.0, 183.0, 178.0, 188.0, 158.0, 182.0, 188.0, 165.0, 191.0, 183.0, 176.0, 186.0, 203.0, 182.0, 182.0, 175.0, 172.0, 188.0, 171.0, 181.0, 175.0, 185.0, 183.0, 190.0, 175.0, 177.0, 170.0, 176.0, 184.0, 188.0, 171.0, 189.0, 194.0, 184.0, 199.0, 172.0, 168.0, 162.0, 195.0, 187.0, 179.0, 183.0, 169.0, 204.0, 181.0, 181.0, 187.0, 185.0, 182.0, 172.0, 185.0, 199.0, 193.0, 196.0, 175.0, 170.0, 179.0, 181.0, 191.0, 163.0, 195.0, 178.0, 176.0, 170.0, 163.0, 188.0, 181.0, 167.0, 167.0, 177.0, 197.0, 177.0, 165.0, 178.0, 177.0, 153.0, 179.0, 178.0, 187.0, 198.0, 191.0, 177.0, 169.0, 206.0, 181.0, 180.0, 180.0, 182.0, 179.0, 174.0, 175.0, 180.0, 175.0, 173.0, 181.0, 177.0, 195.0, 153.0, 191.0, 192.0, 159.0, 177.0, 176.0, 166.0, 172.0, 169.0, 198.0, 189.0, 193.0, 187.0, 169.0, 175.0, 185.0, 168.0, 187.0, 178.0, 176.0, 187.0, 184.0, 176.0, 192.0, 169.0, 186.0, 186.0, 177.0, 183.0, 167.0, 189.0, 178.0, 175.0, 190.0, 173.0, 166.0, 164.0, 186.0, 167.0, 198.0, 159.0, 197.0, 182.0, 179.0, 175.0, 184.0, 180.0, 191.0, 181.0, 182.0, 176.0, 179.0, 183.0, 163.0, 167.0, 187.0, 182.0, 178.0, 180.0, 183.0, 175.0, 172.0, 182.0, 170.0, 184.0, 163.0, 190.0, 185.0, 183.0, 190.0, 197.0, 190.0, 162.0, 167.0, 174.0, 180.0, 185.0, 173.0, 182.0, 172.0, 174.0, 166.0, 171.0, 166.0, 170.0, 191.0, 171.0, 206.0, 185.0, 182.0, 171.0, 187.0, 174.0, 181.0, 206.0, 179.0, 191.0, 173.0, 180.0, 198.0, 174.0, 198.0, 187.0, 174.0, 186.0, 190.0, 186.0, 164.0, 173.0, 178.0, 179.0, 186.0, 182.0, 167.0, 184.0, 186.0, 186.0, 191.0, 188.0, 185.0, 179.0, 163.0, 184.0, 182.0, 183.0, 167.0, 169.0, 191.0, 180.0, 187.0, 180.0, 180.0, 189.0, 175.0, 181.0, 175.0, 176.0, 177.0, 182.0, 175.0, 193.0, 171.0, 178.0, 176.0, 194.0, 182.0, 190.0, 165.0, 183.0, 189.0, 181.0, 191.0, 175.0, 194.0, 203.0, 176.0, 176.0, 195.0, 196.0, 175.0, 176.0, 177.0, 167.0, 171.0, 170.0, 172.0, 180.0, 182.0, 196.0, 170.0, 190.0, 178.0, 180.0, 187.0, 169.0, 184.0, 182.0, 185.0, 183.0, 205.0, 174.0, 175.0, 174.0, 174.0, 174.0, 192.0, 194.0, 174.0, 172.0, 185.0, 174.0, 186.0, 182.0, 165.0, 195.0, 198.0, 174.0, 176.0, 183.0, 183.0, 187.0, 200.0, 178.0, 172.0, 166.0, 173.0, 180.0, 198.0, 175.0, 182.0, 180.0, 192.0, 205.0, 175.0, 175.0, 190.0, 187.0, 198.0, 186.0, 176.0, 186.0, 191.0, 188.0, 185.0, 191.0, 192.0, 194.0, 186.0, 178.0, 181.0, 192.0, 172.0, 184.0, 176.0, 180.0, 193.0, 182.0, 180.0, 166.0, 187.0, 186.0, 202.0, 177.0, 182.0, 182.0, 196.0, 179.0, 183.0, 186.0, 182.0, 176.0, 182.0, 191.0, 170.0, 181.0, 173.0, 192.0, 165.0, 174.0, 184.0, 196.0, 179.0, 174.0, 199.0, 166.0, 158.0, 184.0, 175.0, 170.0, 187.0, 182.0, 174.0, 167.0, 189.0, 187.0, 179.0, 198.0, 169.0, 165.0, 173.0, 180.0, 182.0, 178.0, 184.0, 167.0, 194.0, 179.0, 191.0, 183.0, 185.0, 186.0, 184.0, 186.0, 193.0, 182.0, 187.0, 179.0, 194.0, 173.0, 198.0, 180.0, 166.0, 181.0, 173.0, 188.0, 173.0, 176.0, 161.0, 175.0, 156.0, 164.0, 188.0, 188.0, 184.0, 170.0, 180.0, 180.0, 168.0, 195.0, 189.0, 178.0, 180.0, 182.0, 160.0, 178.0, 173.0, 170.0, 177.0, 198.0, 186.0, 174.0, 186.0] |
Теперь импортируем новый для нас модуль stats библиотеки SciPy (Scientific Python) и построим доверительный интервал.
В данном случае мы передаем функции interval три параметра: уровень точности alpha, среднее выборки mean (используем библиотеку numpy для расчета) и стандартную ошибку среднего (пока отложим объяснение этого параметра).
Уже не так плохо, мы стали хоть что-то знать про реальную картину мира. Но какие еще применения можно найти для Центральной предельной теоремы?
Вторым применением статистического вывода является построение гипотез и их проверка.
Например, мы можем попытаться понять на основе выборки, правда ли, что средний рост всех мужчин в России составляет 182 см (предположим, так утверждает Минздрав).
По сути нам нужно ответить на вопрос, какова вероятность получить среднее выборки 180.2 см (мы его рассчитали на прошлом занятии), если истинное среднее генеральной совокупности действительно равно 182 см.
Если вероятность (probability value или p-value) окажется ниже определенного порога, мы отвергнем нашу нулевую гипотезу и скажем, что для альтернативной гипотезы есть основания. Если выше, мы будем считать нулевую гипотезу обоснованной.
Пороговое значение часто выбирают на уровне одного, пяти или десяти процентов.
Проверим наше гипотезу с помощью Питона. Для этого снова воспользуемся библиотекой SciPy.
Получилась крошечная вероятность. Около 0.000000009. Она гораздо меньше порога в пять и даже один процент, поэтому мы можем отвергнуть нашу нулевую гипотезу о том, что истинное среднее равно 182 сантиметрам.
Может показаться, что достижения не слишком велики. Мы ведь так и не выяснили, каким является среднее генеральной совокупности. Но взгляните на это иначе. Что если речь идет о невиновности человека или безвредности медицинского препарата? Проверка нулевой гипотезы уже будет иметь важные последствия.
Вы собрали данные по 1000 пациентов для того, чтобы оценить эффективность нового лекарства. Это выборка или генеральная совокупность?
Посмотреть правильный ответ
Ответ: выборка
Посмотреть правильный ответ
Ответ: доверительный интервал и проверка гипотезы
Итак, мы изучили описательную статистику и познакомились со статистическим выводом. На следующем занятии, вооружившись этими знаниями, мы перейдем к вопросу взаимосвязи переменных и построению первой модели.
Вопрос. Никак не могу понять разницу между правильной и неправильной интерпретацией:
Буду благодарен, если поясните этот момент.
Ответ. Начну немного издалека. Смотрите, когда мы не можем (но очень хотим) измерить какой-либо истинный параметр генеральной совокупности, то возникает неопределенность.
Для оценки истинного параметра и степени неопределенности можно использовать два подхода:
На занятии в примере с ростом мужчин в России мы использовали первый, частотный подход. Давайте еще раз повторим его основные тезисы.
У нас есть генеральная совокупность — все мужчины в России. У этой генеральной совокупности есть неизвестный нам параметр — средний рост (истинное среднее). Провести измерения этого параметра не представляется возможным.
При этом мы можем делать выборки из генеральной совокупности (например, опрашивать людей на улице) и без особых усилий вычислять средний рост внутри каждой выборки (выборочное среднее).
К сожалению, мы не можем быть уверены, что выборочное среднее адекватно отражает истинное среднее. Однако, полагаясь на Центральную предельную теорему, для каждой выборки мы можем построить доверительный интервал (confidence interval), который очень важно правильно интерпретировать.
Предположим, мы провели десять опросов, собрали десять выборок и для каждой выборки мы рассчитали 90-процентные интервалы. У нас получилось десять доверительных интервалов.
Так вот, следуя частотному подходу, девять из этих десяти интервалов будут включать истинное среднее, а один — нет. Приведу картинку с занятия еще раз.
Каждая черная горизонтальная черта — это выборка, кружок — выборочное среднее, а вертикальная пунктирная линия — истинное среднее. Третья сверху (и одна из 10) выборка не включает истинное значение генеральной совокупности.
Повторю сделанный вывод, но немного другими словами. Мы по-прежнему ничего не знаем о значении истинного среднего, однако в 90% случаев наш доверительный интервал его «захватит».
Это та самая «правильная» интерпретация, о которой я говорил.
Байесовский метод в корне отличается от частотного. В не слишком формальном ключе его можно выразить следующим образом.
У нас есть некоторое изначальное представление о мире и его свойствах. Например, о среднем росте мужчин в России, мы можем достаточно уверенно сказать, что человека с ростом 180 см встретить довольно легко, а человека с ростом 210 см — гораздо сложнее.
Предположим, что 180 см и есть наш изначальный средний рост.
Далее, получая данные (опрашивая людей на улице), мы будем модифицировать наше изначальное представление, исходя из того, кто нам встретится. Если вдруг окажется, что людей с ростом 210 см очень много, мы скорректируем наше изначальное представление о среднем росте в сторону повышения. Например, со 180 до 190 см.
При этом, мы разумеется понимаем, что в таких расчетах также присутствует неопределенность, поэтому мы не будем говорить, что средний рост мужчин в России составляет ровно 190 см. Мы скажем, например, что с вероятностью 90% он находится в диапазоне от 187 до 193 см (цифры, конечно, приведены для примера).
Такой интервал по-английски называется credible interval. По-русски его называют байесовским доверительным интервалом, хотя, наверное, credible можно перевести как достоверный интервал, что лучше отразит его суть.
Это та «неправильная интерпретация», про которую я говорил. Конечно, неправильной я назвал ее только потому, что она относится к байесовскому методу, который на занятии рассмотрен не был.
Еще одна причина, почему я решил заострить на этом внимание, байесовской интерпретацией интервала часто подменяют частотную.
Это связано с тем, что интерпретация байесовского доверительного интервала (credible interval) более интуитивно понятна, здесь мы напрямую делаем предположение о значении истинного параметра.
Интерпретация частотного доверительного интервала (confidence interval) лишь указывает, как часто мы «захватим» истинный параметр, но ничего не говорит о его значении.
Вопрос.
(1) Поясните пожалуйста, как из вот этой цифры 9.035492171563733e−09 получилась вот такая вероятность 0.000000009?
(2) В строчке кода
t_statistic, p_value = st.ttest_1samp(height, 182). Что это за переменная t_statistic? Хотелось бы понять откуда она взялась. Я прорешал в Google Colab, t_statistic равен -5.797229652505048. Но что это за цифра и откуда берется абсолютно не ясно.
(3) И еще одно. Загнал данные в словарь, просто посчитать количество разных значений.
Получил, что 182 встречается аж 50 раз, в то время как 180 только 45 раз. Я правильно понял, что чем объем выборки больше, тем пиковые значения в выборке меньше влияют на все средние величины?
Ответ.
1) 9.035492171563733e-09 — это так называемая экспоненциальная запись (scientific notation). С ее помощью удобно записывать очень большие и очень малые числа. Для того чтобы преобразовать экспоненциальную запись в обычную, вы умножаете число до буквы e на 10 в степени числа после буквы e.
В данном случае $9.035492171563733 times 10^{-9}$. Так как число и так чрезвычайно мало, цифры после девяти можно отбросить. Получается 0.000000009.
2) Про t-statistic я планировал подробно рассказать на курсе по статистике вывода, так как тема довольно обширная, но попробую в общих чертах объяснить суть этого показателя.
Когда мы проводим статистический тест, нам нужно выбрать критерий (распределение), относительно которого мы будем тестировать нашу гипотезу. Опуская некоторые детали, скажу, что в данном случае мы выбрали распределение Стьюдента (его еще называют t-распределением). Это распределение в целом похоже на нормальное распределение Гаусса. Ниже привожу график функции плотности (probability density function) этого распределения. Обратите внимание, оно стандартизировано, чтобы иметь среднее арифметическое 0 и СКО 1.
Значения по оси x — t-критерий (t-statistic), площадь под кривой слева (или справа) от t-statistic — вероятность (p-value).
Так вот, проводя тест (в данном случае с помощью функции ttest_1samp()), мы получаем два значения, t-statistic и p-value, которые и показывают насколько на стандартизированном t-распределении встретившееся нам среднее значение выборки 180,2 см отличается от предполагаемого истинного среднего в 182 см.
Получившийся t-критерий равен −5.797229652505048. Отложите его по оси x. Как вы видите, показатель находится очень далеко от среднего и площадь под кривой слева от этого значения чрезвычайно мала. Отсюда и такое крошечное значение p-value.
Дополню, что так как в данном случае нулевая гипотеза утверждает, что рост составляет именно 182 см (а не меньше или больше 182 см), то нам нужно посчитать площадь слева от −5.797229652505048 и справа от 5.797229652505048 (то есть как бы два хвоста по краям симметричного распределения). Такой тест называется двусторонним (two-sided).
Для наглядности можно взять функцию распределения cdf() объекта t (t-распределение) библиотеки scipy (см. в конце ноутбука), которой мы передадим наше значение t-statistic и степени свободы (рассчитываются как количество наблюдений − 1). Эта функция посчитает площадь слева от −5.797229652505048. Умножив на два (чтобы учесть оба хвоста), мы как раз получим площадь (p-value) 9.035492171563733e-09.
Возможно, если вы в первый раз сталкиваетесь с частотной статистикой вывода (frequentist inferencial statistics), тема может показаться сложной. На самом деле все довольно интуитивно и логично. Опять же постараюсь пошагово разобрать это на курсе по статистике вывода.
3) Не уверен, что до конца понял ваши вопросы. Отвечу на них в соответствии со своим пониманием того, что вы спрашиваете.
Когда вы считаете количество каждого из значений распределения, то по большому счету ищете моду (наиболее часто встречающееся значение). И мода в выборке действительно равна 182 см. Она отличается от среднего арифметического (180,2 см), потому что распределение сгенерировано псевдослучайным образом, и это расхождение — элемент случайности. В теоретическом нормальном несмещенном распределении мода, медиана и среднее арифметическое конечно совпадают.
В том что касается размера выборки и выбросов, если вы спрашиваете в целом, то конечно, по мере того как размер выборки стремится к размеру генсовокупности, показатели выборки стремятся к истинным показателям. Сложность в том, что в большинстве случаев собрать выборку больше определенного размера не представляется возможным, и насколько репрезентативны имеющиеся данные наверняка мы не знаем.
Для того чтобы преодолеть это ограничение и нужна Центральная предельная теорема. Она утверждает, что если брать выборки из одной и той же генеральной совокупности, то показатели этих выборок (например, выборочные средние) будут нормально распределены и их среднее (то есть среднее средних) будет приближаться к истинному среднему показателю генеральной совокупности. В этом смысле, действительно, мы будем получать все менее смещенную оценку истинного показателя.
При этом опять же, и это важно, мы продолжаем оставаться в неведении относительно истинного распределения (то есть генеральной совокупности).
P.S. Помимо метода .get() для подсчета частоты элементов может быть удобно использовать модуль collections, привел пример в конце ноутбука.
На
практике часто приходится делать
некоторые выводы по имеющемуся у нас
небольшому объему данных (выборки) о
свойствах всей генеральной совокупности.
Эти выводы осуществляются с помощью
определенных статистик и поэтому
называются статистическими. Теория
статистического вывода занимает
центральное место в статистике. Основным
способом, с помощью которого делаются
статистические выводы, является проверка
гипотез.
Существует
два вида гипотез: 1) научные 2) статистические.
Научная гипотеза – это предполагаемое
решение некоторой проблемы. Она обычно
формулируется в виде теоремы.
Статистическая гипотеза – некоторое
утверждение относительно неизвестного
параметра или какой-либо характеристики.
Например, среднее значение генеральной
совокупности равно 125 х=125 или
коэффициент корреляции равен 0 =0. Для
проверки статистических гипотез
используются статистические критерии,
которые представляют собой некоторое
правило, по которому мы делаем вывод о
правильности или неправильности
рассматриваемой статистической
гипотезы.
2. Общая схема проверки статистической гипотезы
Она
состоит из пяти этапов:
1 этап – выдвигаются
две статистические гипотезы: 1) основная
нулевая Н0 и 2) альтернативная
(конкурирующая) Н1.
Например, Н0 среднее
значение ГС = 125.
Н1 среднее
значение ГС = 125. Математически это можно
записать: Н0: х = 125
Н1: х =
125 ( х < 125 : x > 125).
2 этап – задаемся
уровнем значимости . Статистический
вывод никогда не может быть сделан со
стопроцентной уверенностью. Всегда
допускается риск принятия неправильного
решения. При проверке статистических
гипотез мерой такого риска и выступает
уровень значимости, который обычно
обозначается . Фактически уровень
значимости представляет собой долю и
процент ошибок, которые мы можем себе
позволить при статистических выводах.
Чаще всего используют следующие три
значения уровня значимости. = 0,1 или
10%; = 0,05 или 5%; = 0,01 или 1%. Наиболее
популярным из них является = 0,05 или
5% (допускается 5% ошибок, если всего 100
выборок).
3 этап – по исходным
данным, т.е. по выборке вычисляется
наблюдаемое значение статистики
критерия. В общем случае будем ее
обозначать gнабл. Для этого используются
статистические таблицы. Выбор необходимой
статистической таблицы осуществляется
в зависимости от распределения статистики
критерия. При проверке статистических
гипотез статистика критерия выбирается
(статистиками) таким образом, чтобы она
имела одну из рассмотренных в параграфе
11 распределений.
5 этап – путем
сравнения найденных наблюдаемых
критических значений делаем вывод о
правильности этой или иной гипотезы.
3.
СРАВНЕНИЕ
СРЕДНИХ ЗНАЧЕНИЙ КОЛИЧЕСТВЕННЫХ
ПРИЗНАКОВ ДВУХ НЕЗАВИСИМЫХ ВЫБОРОК
Часто на
практике возникает задача сравнения
средних значений исследуемого показателя,
признака для двух разных генеральных
совокупностей. Например, одинаков ли
средний уровень коэффициента IQ для
мальчиков и девочек одного и того же
возраста. При решении такой задачи
необходимо, чтобы исследуемый признак
был измерен в количественной шкале.
Таким образом, будем считать, что в
результате эксперимента в качестве
исходных данных у нас имеются две
выборки необязательно одинакового
объема: х1, х2, …, хn и y1, y2, …, ym, где n = m.
Необходимо обращать внимание на то,
чтобы эти две выборки были независимыми,
т.е. чтобы элементы 1 выборки не влияли
на значения элементов 2 выборки. Для
решения поставленной задачи воспользуемся
общей схемой проверки статистической
гипотезы.
1 этап. Выдвигаются
две гипотезы: основная нулевая о том,
что средние значения исследуемого
признака двух рассматриваемых ГС
статистически одинаковы и альтернативная
гипотеза о том, что эти средние значения
статистически различны.
Н0 : х = у, где
х – среднее значение 1 ГС
Н1 : х = у, где
х – среднее значение 2 ГС
2 этап. Задаемся
уровнем значимости .
3 этап. Вычисляется
наблюдаемое значение статистики
критерия. Для этого сначала по исходным
выборкам вычисляется среднее значение
х и у
2
2
(см. меры центральной
тенденции), а также дисперсии Sх Sy .
Тогда наблюдаемое значение статистического
критерия вычисляется по следующей
формуле: 2
2
tнабл. = (х – у)
: ((n – 1) Sx + (m – 1) Sy ) : (n + m – 2) ( 1/n + 1/m)
4 этап. Находим
критическое значение статистики
критерия. В нашем случае статистика
критерия имеет t-распределение Стьюдента
с числом степеней свободы
= n + m – 2
Поэтому для
нахождения критического значения
необходимо воспользоваться статистической
таблицей распределения Стьюдента. В
этой таблице находим столбец,
соответствующий величине 1 – /2, если
таблица называется квантили распределения
или величине /2, если таблица называется
верхние процентные точки распределения.
В этой же таблице находим строку,
соответствующую числу степеней свободы
= n + m – 2, на пересечении выбранных
строки и столбца и находится требуемое
нам критическое значение tкр.
5 этап. Делаем вывод
о правильности той или иной гипотезы
по следующему правилу:
1) если – tкр<
tнабл. < tкр, то принимается нулевая
гипотеза Н0, т.е.на основе имеющихся
данных мы делаем вывод о том, что средние
значения двух рассматриваемых генеральных
совокупностей статистически одинаковы
на уровне значимости .
2) если же tнабл.<
– tкр или tнабл. > tкр, то принимается
альтернативная гипотеза Н1, т.е. делается
вывод о том, что средние значения двух
рассматриваемых ГС статистически
различны на уровне значимости .
Пример: был проведен
эксперимент по исследованию влияния
усовершенствованного пособия (вводный
материал, подготавливаемый к восприятию
изучаемого предмета) на успеваемость
по определенному разделу математики.
50 учащихся были разбиты случайным
образом на две группы: 25 (1 группа)
знакомились с усовершенствованным
пособием, а 25 (2 группа) не знакомились,
в конце эксперимента всем учащимся был
предложен тест на усвоение понятий
определенного раздела математики. В
качестве измеряемых признаков
рассматривалось количество правильных
ответов. Проверить гипотезу о наличии
или отсутствии влияния усовершенствованного
пособия на успеваемость по математике.
В нашем случае в
качестве измеряемой переменной
рассматривалось количество правильных
ответов, поэтому она измерена в
количественной шкале. Так как учащиеся
разбивались на 2 группы случайно, то в
результате эксперимента мы получили
две независимых выборки. х1, х2, …, х25 и
у1, у2, …, у25. По полученным выборкам
были найдены средние значения х=7,65;
2 2
у=6,0
и дисперсии Sx=6,5 Sy=5,9 n=25 m=25 =0,05
t = (7,65 – 6,0) : (((25
– 1) 6,5 + (25 – 1) 5,9) : (25+25 – 2) (1/25 +1/25)) = 2,34.
Найдем в статистической таблице tкр.
/2 = 0,05/2 = 0,025. = 25 – 25 – 2 = 48
(часть таблицы)
tкр = 2, 01 tнабл.
> tкр., то мы должны принимать
альтернативную гипотезу Н1 о статистическом
различии средних значений. Имеется
влияние усовершенствованного пособия
на среднюю успеваемость по математике
на уровне значимости 0,05 (5% ошибок
допускается). Глядя на соотношение
между х и у (в нашем случае х>у), делаем
вывод, что усовершенствованное пособие
повышает среднюю успеваемость по
математике.
Примечания.
1. Рассмотренный
в этом параграфе критерий должен
применяться для выборок, извлеченных
из ГС и имеющих нормальное распределение
с одинаковыми дисперсиями.
2. Если исходные
выборки извлечены не из нормальной ГС,
то необходимо воспользоваться критерием,
рассмотренным далее в параграфе 17 или
критерием этого параграфа, но при этом
помнить, что полученные выводы будут
приближенными, т.е. могут оказаться
неправильными.
3. Предположение
о равенстве дисперсий может легко, если
брать обе выборки одинакового объема.
4. Рассмотренный
в этом параграфе критерий в литературе
обычно называется t-критерий Стьюдента.
4
СРАВНЕНИЕ СРЕДНИХ ЗНАЧЕНИЙ КОЛИЧЕСТВЕННЫХ
ПРИЗНАКОВ ДВУХ ЗАВИСИМЫХ (СВЯЗАННЫХ)
ВЫБОРОКИногда
нам приходится измерять один и тот же
признак (показатель) для одной и той же
группы лиц, но в различные моменты
времени. Например, до проведения
эксперимента и после эксперимента. В
результате в качестве исходных данных
мы получаем две выборки одинакового
объема х1, х2, …, хn и у1, у2, …, уn (одни и
те же люди). Причем элементы выборки,
стоящие на одном и том же месте в каждой
из выборок должны соответствовать
измененному показателю для одного и
того же лица. Поэтому такие выборки
часто называются связанными. Они
являются зависимыми, т.к. значения
элементов второй выборки зависят от
значений элементов первой выборки.
Исходные данные в рассматриваемом
примере называются типа «до – после».
Связанными выборками могут рассматриваться
также данные типа «брат – сестра» (в 1
выборке показываем мальчиков, во второй
– девочек), «муж – жена». Для таких
данных можно рассмотреть задачу
сравнения средних значений двух выборок,
для решения которой применяется общая
схема проверки статистической гипотезы.
1 и 2 этапы – см.
15.
3 этап – вычисляем
наблюдаемое значение статистики
критерия. Для этого сначала из двух
исходных выборок получаем одну выборку
разностей, которую будем обозначать
d1, d2, …, dn, где di = xi – yi. По полученной
n
выборке разностей
вычисляем среднее значение d = di : n, а
также
n
2 i=1
стандартное
отклонение Sd = (di – d) : (n – 1), тогда
наблюдаемое
i=1
значение статистики
критерия вычисляется по следующей
формуле:
tнабл. = n
d/Sd
4 этап – находим
критическое значение статистики
критерия. В нашем случае статистика
критерия имеет t-распределение Стьюдента
с числом степеней свободы = n – 1,
поэтому для нахождения t-критического
необходимо воспользоваться статистической
таблицей распределения Стьюдента (см
4 этап 15 параграфа).
5 этап – делаем
вывод о правильности той или иной
гипотезы по следующему правилу:
1) если –tкр <
tнабл. < tкр, то принимается нулевая
гипотеза, т.е. делаем вывод о том, что
средние значения ГС статистически
одинаковы или, другими словами,
проведенный эксперимент не оказал
влияния на средние значения изучаемого
показателя.
2) если tнабл. < –
tкр или tнабл. > tкр, то принимается
альтернативная гипотеза, т.е. мы делаем
вывод о том, что средние значения
рассматриваемых ГС статистически
различны или, другими словами, эксперимент
привел к изменению среднего значения
изучаемого показателя. Для того, чтобы
выяснить, в какую сторону произошло
изменение среднего значения (стало
больше или меньше), необходимо сравнить
среднее значение двух исходных выборок
х и у (арифметически). Примечание.
1) рассмотренный критерий должен
применяться для выборок, извлеченных
из ГС, имеющих нормальное распределение
с одинаковыми дисперсиями. 2) если эти
условия не выполняются, то необходимо
воспользоваться критерием, рассмотренным
далее в параграфе 18. 3) рассмотренный в
данном параграфе критерий в литературе
обычно называется парным t-критерием.
Пример: Был проведен
эксперимент по исследованию влияния
процесса обучения на уровень знаний
студентов колледжа. 100 первокурсникам
был предложен тест из 60 вопросов, этот
же тест был предложен этим же студентам,
но уже выпускникам (когда они уже
отучились). В качестве измеряемого
показателя рассматривалось количество
правильных ответов. Проверить гипотезу
о наличии либо отсутствии влияния
процесса обучения в колледже на уровень
знаний. Решение. В нашем эксперименте
исходные данные представляют собой
100 пар значений типа «до – после», т.е.
две связанные выборки х1, х2, …, х100 и
у1, у2, …, у100. Выбираем уровень значимости
= 0,01. По исходным выборкам была вычислена
выборка разности, по которой было
найдено d = – 7,02 Sd = 8,02 (стандартное
отклонение) n = 100 tнабл. = 100 (- 7,02:8,02) = –
8,75. Будем искать по таблице tкр. /2 =
0,01:2 = 0,005 = n – 1 = 100 – 1 = 99. Выбираем
из таблицы
Т.е. мы делаем
вывод, что процесс обучения в колледже
приводит к изменению среднего уровня
знаний. d = – 7,02 < 0 d = х – у < 0 = х <
у. Таким образом, средний уровень знаний
за время обучения в колледже повысился.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Суть статистического вывода при тестировании исследовательских гипотез
Статистический вывод (statistical inference) представляет собой процесс получения логических вывовод о статистической совокупности на основании случайно извлеченных выборок. Логика статистического вывода не зависит от конкретной проблемы и используемых статистических методов. На основании выборки исследователь тестирует те или иные гипотезы, часто:
- о различии статистических совокупностей,
- наличии закономерностей,
- отсутствии случайностей.
Проверка этиз статистических гипотез может быть уложена в следующую последовательность этапов статистического вывода:
- Формируется нулевая и альтернативную гипотезы.
Например, нулевая гипотеза (Ho): параметр совокупности равен какому-то определённому значению, альтернативная теория (Ha): не равен. Обычно исследовательская теория является альтернативной к уже существующей парадигме. Чаще всего мы хотим указать на имеющую место новую закономерность (альтернативная гипотеза) и соотнести ее с консервативной нулевой гипотезой (которая часто говорит о случайной природе находок и об отсутствии закономерностей в реальности). - Формируется случайная выборка элементов совокупности и определяются параметры выборки.
- Преобразуется параметр выборки в статистический критерий.
- Находим p-значение для полученного статистического критерия.
- Сравниваем с критическим значением статистического критерия.
- Делаем выводы о сохранении нулевой гипотезы или о подтверждении альтернативной.
Нулевая гипотеза сохраняется или отвергается исходя из того, насколько вероятным оказывается наблюдаемый результат. Для оценки выборочных статистик в отношении изменчивости используются статистически статистических критериев для которых имеются рассчитанные распределения и по которым эти самые вероятности можно посчитать (z-, хи-квадрат-, t-, и прочие виды распределений).
Если пазличие между исследуемыми группами (выборками) заметно выражено относительно величины изменчивости данных, исследователь отвергает нулевую гипотезу и делает вывод, что случайное появление такого результата маловероятно: полученный результат статистически значим. В медицине традиционно принято отвергать нулевую гипотезу на уровне близкому к краю распределения (случайной величины), которая моглы бы проявиться случайно с вероятностью менее 5% (p<0,05).
Поскольку статистический вывод основывается на оценках вероятности, возможны два основных вида ошибочных решений: Ошибка первого (I) рода (alpha, уровень достоверности, отвергается истинная нулевая гипотеза), и ошибки II рода (при которой сохраняется ложная нулевая гипотеза. Первые имеют следствием ошибочное подтверждение гипотезы исследования (ложноположительные результаты), а последние — неспособность распознать статистически значимый результат (ложно отрицательные результаты).
Автор: Кирилл Мильчаков
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:
Выводы и рекомендации к курсовой работе по статистике
Проанализировав результаты проведенных исследований, можно сделать следующие выводы и рекомендации:
1) На основе анализа тенденции развития фирмы можно сделать вывод, что товарооборот рассматриваемой фирмы был более-менее стабилен в течение 1996 и 1997 гг., разве что наблюдался небольшой спад в течение 1-го полугодия и 4-го квартала 1996 года. После снижения в 1996 году товарооборот остался на таком же уровне в течение всего 1997 года. В 3-м же квартале 1996 года и особенно в 1995 году наблюдался рост товарооборота, обусловленный тем, что фирма наиболее оптимально проводила товарно-ценовую политику в данных периодах.
2) С учётом динамики развития деятельности фирмы можно порекомендовать фирме изменить существующую политику, направить больше сил и средств на стимулирование покупательского спроса (повышение качества продукции, более эффективная реклама, поддержание марки, имиджа, престижа фирмы, снижение цены, дополнительные условия, облегчающие покупку потребителя, сервисное обслуживание и т.д.).
3) Учитывая тот факт, что товарооборот подвержен сезонным колебаниям, фирме необходимо уделить особое внимание сезонной политике. Стабилизация работы в течение сезона позволит повысить эффективность деятельности фирмы, т.к. любые, даже предусмотренные колебания, являются негативным фактором, отрицательно влияющем на работоспособность персонала, на мнение клиентов и партнёров о деятельности фирмы. В этом аспекте, как ранее было отмечено, предлагаются 2 пути: стимулирование путём увеличения затрат на рекламу, предоставление скидок и различных льгот или же минимизация издержек фирмы путём уменьшения числа рабочих в периоды низкой покупательской активности, сдачи в аренду площадей и т.д.
4) Можно отметить, что товарооборот в 1997 году по сравнению с 1995 годом увеличился в 1,0304 раз, т.е. на 337 млн. руб. (соответственно индекс товарооборота и в фактических ценах и прирост товарооборота за счет всех факторов), но из показателя общего индекса цен и из его сравнения с индексом фактического товарооборота (соответственно 0,9095 против 1,1329) видно, что повышение товарооборота вызвано в подавляющей степени увеличением объёма продаж. Таким образом, товарооборот фирмы возрос на 337 млн. руб., что вызвано изменением объёма продаж (увеличение товарооборота на 1475 млн. руб.) изменение цены продаж (уменьшение товарооборота на 1138 млн. руб.). Цены понижаются, а товарооборот растёт. Это может свидетельствовать о том, что:
· улучшилась маркетинговая политика (больше потратили на рекламу, чтобы увеличить рынок сбыта);
· ожесточилась конкуренция, и фирма была вынуждена понизить цену, чтобы не потерять рынок сбыта;
· в 1995 году фирма внедрила новый товар (телевизор) на рынок, а теперь он находиться в стадии роста за счет снижения издержек, планирования, ноу-хау и т.д.;
· фирма использовала стратегию ” снятия сливок ”- внедрение на рынок товара либо очень хорошего качества, либо какую- нибудь диковинку, доступную определенным соям общества, а когда происходит насыщение данного общества этим товаром, тогда фирма снижает цену на товар, чтобы он был доступен и другим потребителям;
· фирма, возможно, нашла более дешёвого поставщика сырья;
· фирма получила бюджетное ассигнование в поддержку российского производителя и т.д.
В этих условиях руководство фирмы должно обратить больше внимание на стимулирование спроса на свою продукцию, наладить ценовую политику, задействовать более квалифицированную рабочую силу, улучшить организацию производства, а также постараться внедриться в другие области теле рынка: например, начать продавать другими марками телевизоров и т.д. Рассматриваемые меры в комплексе позволят расширить уже завоеванный рынок сбыта, а также найти новые категории покупателей. Это дает увеличение фактического объёма товарооборота, фирма сможет получать большую прибыль и вести более эффективную борьбу на рынке.
5)Рекомендуется планировать рекламную кампанию в следующей последовательности:
· определить «портрет» покупателя. Рекламная кампания должна быть рассчитана на разные демографические характеристики населения (возраст, пол, социальный статус, место жительства и т.д.). Наиболее полно составить «портрет» потенциального покупателя должны помочь маркетинговые исследования.
· определить цели рекламной кампании;
· определить основную идею рекламной кампании. Идея – это тот стержень, на котором должна строиться вся рекламная кампания. Разработав идею, следует проверить на сколько соответствует ей имидж фирмы, её логотип, слоган и т.д.;
· выбрать формы размещения рекламы;
· определить наиболее оптимальные сроки размещение рекламных мероприятий относительно друг друга во времени. Рекламную кампанию можно разделить на 4 этапа:
первый этап – выброс, рассчитан на 3 мес.
В это время заявляется о фирме как таковой и качестве её продукции.
второй этап – поддерживающая реклама – 4мес.
В этот период идёт закрепление полученной информации среди потенциальных покупателей, поддержание имиджа и акцентирование на высокое качество товара и его отличительные черты от других. Идёт накопление средств на следующий этап.
третий этап – повторный выброс – 1,5 мес.
Основная задача – занять на рынке максимальную долю, выработать предпочтительное отношение при выборе по отношению к другим производителям за счёт качества продукции. Направленность на повышение престижа марки. Цель данного выброса – повышение цены продукции.
четвертый этап – поддерживающая реклама – 4 мес.
Создаётся рекламная кампания, которая позволяет поддерживать имидж торговой марки до следующего выброса.
· подсчитать возможные расходы на рекламную кампанию. Процент необходимый для отчисления от прибыли на рекламу зависит в основном от стабильности производства и ввода на рынок новых товаров. При условии, что фирма и товар хорошо известны потребителям, фирма может позволить тратить на рекламу
· 2 – 3% от прибыли. При введении новых товаров или новых направлений, фирме придётся отчислить на рекламу 10 или даже более процентов;
· составить план рекламной кампании;
· организовать работу фирмы во время рекламной кампании;
· подвести итоги рекламной кампании.