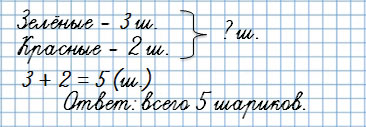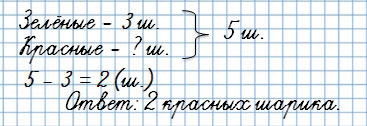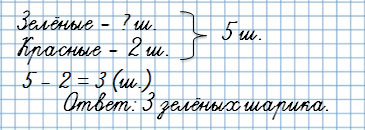|
Что значит “обратная задача” в математике (1, 2, 3, 4 класс)? Как записать и решить обратную задачу, пример? В математике обратная задача составляется на основании какой-либо имеющейся задачи. В обратных задачах искомые данные уже известны. Требуется найти одну из величин, которые были даны в условии исходной задачи. Пример 1 Исходная задача. В магазине яблоки стоят 120 рублей за 1 килограмм, а груши стоят 150 рублей за 1 килограмм. Требуется узнать, на сколько груши дороже яблок. Для решения этой задачи нужно найти разницу между 2 числами – стоимостью груш и стоимостью яблок. 150 – 120 = 30 (руб.) Таким образом, груши дороже яблок на 30 рублей. _ Обратная задача. Здесь нам будет известна разница в стоимости фруктов, то есть 30 рублей. Будем находить либо стоимость яблок, либо стоимость груш – то есть можно составить 2 разных обратных задачи. 1) Яблоки стоят 120 рублей, а груши на 30 рублей дороже. Сколько стоят груши? Решение: 120 + 30 = 150 (руб.) 2) Груши стоят 150 рублей, а яблоки на 30 рублей дешевле. Сколько стоят яблоки? Решение: 150 – 30 = 120 (руб.) Пример 2 Исходная задача. Покупатель хочет купить 500 грамм говядины, которая стоит 200 рублей за 1 килограмм. Сколько он должен заплатить? Для решения данной задачи нужно вспомнить соотношение между граммами и килограммами. 1 килограмм = 1000 грамм. 500 грамм – это ровно половина от 1000 грамм (или 1 килограмма): 500 / 1000 = 1/2. Таким образом, покупатель заплатит не 200 рублей, а только половину: 200 / 2 = 100 (руб.) _ Обратная задача. Здесь нам будет известна цена покупки, то есть 100 рублей. Можно найти, например, стоимость за 1 килограмм. Вот формулировка подобной задачи: Покупатель купил 500 грамм говядины за 100 рублей. Сколько стоит 1 килограмм говядины? Решение: 1) 1 килограмм – это 1000 грамм. 1000 / 500 = 2, то есть 1 килограмм будет в 2 раза больше, чем 500 грамм. 2) Стоимость 1 килограмма составляет 100 * 2 = 200 (руб.) модератор выбрал этот ответ лучшим Математический термин “обратная задача” включает два слова. С существительным задача все понятно. Возникает вопрос: что значит обратная. Данное прилагательное по отношению к задаче можно определить как противоположная или ведущая назад, к исходному состоянию. Для того, чтобы составить обратную задачу, нужно иметь задачу исходную. И исходную задачу необходимо решить. Это нужно для того, чтобы использовать полученный результат в качестве исходных данных для обратной задачи. Если сказать еще проще, то то, что дано ( известно ) в исходной задача, в обратной ей нужно будет искать. А решение исходной задачи станет тем, что известно по условию обратной задачи. Это мое определение термину “обратная задача”, простого определения для начальной школы я не нашла. Проще пояснить на примерах. Исходная задача: Мама купила 5 пирожных и 7 кексов к чаю. Сколько всего кексов и пирожных купила мама? Решение 5+7=12 (шт.) выпечки купила мама. Обратная ей задача: Обратных задач можно в этом случае составить две: 1) Мама всего купила 12 пирожных и кексов к чаю, из них 5 пирожных. Сколько кексов купила мама? Решение 12-5=7 (к.) купила мама. 2) Мама всего купила 12 пирожных и кексов к чаю, из них 7 кексов. Сколько пирожных купила мама? Решение 12-7=5 (п.) купила мама. Марина Вологда 3 года назад Обратная задача – это такая задача, в которой все искомые величины уже известны. Из этих известных величин и составляем обратную задачу. Например, нам дана задача: В автопарк заехало три красных машины и пять белых. Сколько всего машин заехало в автопарк? Решение: 3+5 = 8 машин. Составляем обратную задачу: 1) Сколько машин заехало в автопарк красного цвета, если известно, что всего машин было 8. А белых машин было 5. Решение: 8-5 = 3 машины красного цвета. 2) Известно, что в автопарк заехало 8 машин. Из них три были красного цвета. Остальные машины были белые. Сколько машин белого цвета? Решение: 8-3 = 5 машин белого цвета. Алиса в Стране 3 года назад Многие из нас, наверное, уже забыли, что такое обратная задача, но на самом деле ничего сложного в ней нет. Приведу пример. Допустим, у нас есть расстояние (путь) и время, за которое человек его прошел, все мы знаем, как просто определить скорость, нужно расстояние (путь) разделить на время. Так вот к этой элементарной задачке можно составить две обратные задачи: на определение пути (расстояния), если известна скорость и время (чтобы решить эту задачу, нужно скорость умножить на время): Второй обратной задачей будет задача на определение времени, если известно расстояние (путь) и скорость (нужно путь поделить на скорость): Не знаю, кто их назвал “обратными” потому что задача это всегда, как минимум, поиск третьего неизвестного по двум известным, и какая разница какое из них будет неизвестным. Составить их проще простого, просто поменять неизвестное с известным, ну и вероятно математическое действие будет другое – вместо сложения – вычитание, вместо деления – умножение (как и наоборот) Вот пример. У Васи было две конфеты, Валя дала Васе еще три конфеты, сколько у Васи конфет теперь? Ответ – пять. Якобы обратная задача. У Васи было пять конфет, две из которых были его, сколько конфет ему дала Валя что бы у него получилось пять? Ответ – три. Zummy out off 3 года назад Обратная задача в математике – это такая задача, которая составляется по исходной задаче, но ответ исходной задачи включается в условие обратной задачи, а требуется найти то, что было одним из условий исходной задачи. Составление обратных задач тренирует «мозги» для решения задач в математике. Пример составления обратной задачи. Исходная задача. У Маши было 20 рублей, она купила тетрадь за 12 рублей. Сколько денег осталось у Маши? Решение: 20-12=8. Ответ: 8 рублей осталось у Маши. Обратная задача. В условие задачи надо включить сумму сдачи 8 руб. Составляем задачу: Маша купила тетрадь за 12 руб и у неё осталась сдача 8 руб. Сколько денег было у Маши до покупки тетради? Решение: 12+8=20. Ответ: 20 рублей было у Маши. Бархатные лапки 3 года назад Обратная задача составляется на основе уже имеющейся решенной задачи. В обратной задаче требуется узнать то, что было известно в нашей задаче. Объясним, что такое обратная задача, на примере простейшей задачки для начальных классов. У Иры 10 яблок, у Маши 5 яблок. Нужно найти, сколько яблок у обоих девочек вместе. Это наша задача, решается она так: общее количество яблок равно: яблоки Иры плюс яблоки Маши = 5 + 10 + 15 Обратная задача к этой задаче: у двух девочек, Иры и Маши 15 яблок, сколько яблок у Иры, если у Маши 5 яблок. Решение: 15 – 5 = 10 яблок у Иры. Также обратную задачу можно составить и так: у Иры и Маши 15 яблок, сколько яблок у Маши, если у Иры 10 яблок. Решение: 15 – 10 = 5, у Маши 5 яблок. KritikSPb 4 года назад Обратная задача в математике требует найти то, что было известно в первоначальной задаче. То есть обязательным условием составления обратной задачи является наличие прямо задачи, от которой и отталкиваются для составления обратной. Например, первоначально известно, что человеку нужно дойти из дома до магазина. Расстояние 10 км. Идёт он со скоростью 5 км в час. Через сколько времени он будет на месте? Решение: 10 / 5 = 2 часа. А теперь обратная задача: За два часа человек дошёл от дома до магазина. Определите расстояние, если известно, что скорость человека 5 км в час. Решение: 2 * 5 = 10 км. Для составления обратной задачи необходимо решить исходную. Бекки Шарп 3 года назад Обратные задачи бывают в разных науках и в математике тоже. Обратная составляется на основании уже полученных данных. Когда то что требовалось найти уже известно. Например. У Миши было 7 яблок, а у Васи 8 яблок. Сколько всего было яблок у мальчиков. Решение: 7+8=15 (яблок) Обратная задача к нашей будет такая. Всего у Миши и Васи 15 яблок. У Миши – 7 яблок. Сколько у Васи яблок? Решение: 15-7=8 (яблок) Еще одна обратная задача к нашей. У Миши и Васи 15 яблок, у Васи – 8. Сколько яблок у Миши? Решение: 15-8=7 (яблок) Val111111 4 года назад Обратная задача- это когда то, что требовалось найти, теперь известно, а то, что было в дано нужно найти. Пример, есть три яблока. Два забрали. Сколько осталось? Обратная задачка: Забрали два яблока, осталось одно, сколько было? TheSun 3 года назад В обратной задаче неизвестным является дано, именно его и нужно найти. Но, при этом известен результат. Рассмотрим на примере. У Маши было 4 синих мяча и 3 зелёных мяча. Сколько всего у Маши мячей? 4+3=7 (шт.) мячей у Маши. Теперь обратная задача. У Маши всего 7 мячей. Из них синих мячей 4, а остальные мячи зелёного цвета. Сколько у Маши зелёных мячей? 7-4=3 (шт.) зелёных мяча у Маши. Знаете ответ? |
ХОД УРОКА
1. Введение.
Перед нашей школой всегда стояла задача
построения такой методической системы, которая
обеспечивала бы резкое повышение качества
знаний при значительной экономии времени,
расходуемого на изучение материала. В наше время
при все возрастающем потоке информации эта
проблема стоит особенно остро.
Еще в 60-е годы Комиссией по определению
содержания обучения математике, работающей в АПН
СССР, был разработан проект программы по
математике. Авторы проекта одним из главных
средств ускоренного и сознательного изучения
материала в школе считали изменение структуры
существующих программ, осуществление более
целесообразной группировки вопросов,
рациональной группировки вопросов, рациональной
последовательности разделов, то есть применение
метода противопоставления на уроках
математики.
Общепринятая традиционная система обучения
математике соблюдает принцип раздельного
изучения взаимосвязанных понятий или
преобразований. При одновременном изучении
взаимосвязанных вопросов в пределах одних и тех
же уроков дидактической единицей усвоения
становится более крупная единица знаний, чем в
случае раздельного изучения их. Переход в
обучении к более крупным дидактическим единицам
усвоения знаний дает экономию сил и времени.
При изучении задач в курсе математики, как
простых, так и сложных, как обычных
арифметических, так и типовых оказывается высоко
эффективным систематическое применение так
называемого метода обратных задач.
Успех обучения решению задач посредством
преобразования прямой задачи в обратные задачи
объясняется как первопричиной тем, что такой
путь заставляет поднимать из сферы подсознания
наибольшее разнообразие связей, заключенных в
содержании задачи. Это и обеспечивает – на языке
дидактики – глубокое и прочное усвоение
материала.
На составление и решение обратной задачи
уходит несравненно меньше времени, чем на
решение новой задачи, так как числовые данные и
сюжет остаются прежними; производится здесь лишь
логическая операция по переосмыслению ролей
чисел; неизвестное в прямой задаче становится
известным и наоборот.
Поэтому я взяла для изучения и последующей
работы тему “Решение взаимно обратных задач в
начальной школе”.
На мой взгляд, самое трудное в начальной школе
– научить ребенка грамотно писать, а самое
трудное в математике – научить решать задачи.
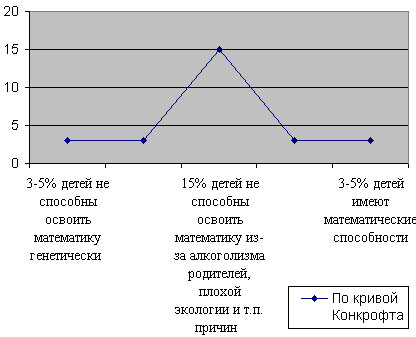
В процессе работы мне хотелось повысить
процент способных детей и уменьшить процент
слабых.
Кроме того, в своей работе я стремлюсь к тому,
чтобы как можно больший процент детей имел качественный
показатель знаний по математике. Далее я опишу,
как я этого добиваюсь и каковы результаты молей
работы.
Я ознакомилась с мнением различных
ученых-методистов (смотреть список литературы)
по вопросу классификации задач и решению взаимно
обратных задач, как по традиционной, так и по
развивающей методике.
Работа со взаимно обратными задачами
просматривается у Аритской Н.И., у Свечникова А.А.,
но у Аритской И.И. нет четкой классификации задач,
также, как у Истоминой Н.Б.
Классификация сложных задач в принципе сходна
у Эрдниева П.М., Свечникова А.А., Баитовой М.А. но
простые задачи Свечников А.А. и Баитова М.А.
классифицируют несколько иначе, чем Эрдниев П.М.
За основу я взяла работу над задачами по
Эрдниеву П.М., так как на сегодняшний день более
четкой классификации задач и методики работы над
взаимно обратными задачами я пока не вижу.
Следует отметить существенно важные дидактические
достоинства метода обратных задач.
Во время преобразования задачи учащийся
выявляет и использует взаимно обратные связи
между величинами задачи:
| Прямая задача |
Ц. |
К. |
С. |
|
30 р. |
6 к. |
? р. |
|
| Обратная задача |
Ц. |
К. |
С. |
|
30 р. |
? к. |
180 р. |
Во время преобразования учащийся практически
познает связи между действиями. Полезно,
например, обратить внимание учащихся на то, что
количество действий при решении прямой и
обратной задач совпадает (это правило нарушается
крайне редко). Кроме того, полезно знать учащимся
следующее явление: каждому действию прямой
задачи соответствует действие той же ступени в
обратной задаче.
Количество комбинаций при составлении
обратной задачи ограниченно: оно равно
количеству данных в задаче.
Решая обратную задачу, учащийся перестраивает
суждения и умозаключения, использованные при
решении прямой задачи, преодолевая при этом в
мышлении инерцию действий, выполненных при
решении прямой задачи.
Решение обратной задачи представляет проверку
решения прямой задачи, то есть при этом возникают
благоприятные условия для потоков информации по
целям обратных связей в мыслительных процессах
(систематическое сочетание прямых и обратных
задач вырабатывает важное качество личности –
чувство самоконтроля).
Учащиеся, составляя обратные задачи,
знакомятся со значительно большим разнообразием
задач, чем в традиционных задачниках.
При составлении и решении обратных задач
выдвигается на первый план анализ и
видоизменение математических зависимостей.
Итак, для развития мышления ценны не столько
прямые и обратные задачи, взятые вне времени сами
по себе, а наиболее важный познавательный
элемент заключается в процессе преобразования
одной задачи в другую, в сравнении условий,
решений, ответов задач, то есть тех “невидимых”,
трудно уловимых и трудно изобразимых при
логическом анализе элементов мысли, которые
связывают решения обеих задач (прямой и
обратной).
Однако нельзя забывать, что переходы эти
осуществляются во времени: чем меньше интервал
времени между противоположными процессами
решения взаимно обратных задач, тем быстрее и
чаще будут совершаться эти переходы и тем
прочнее будут сохраняться в памяти следы этих
переходов, то есть тем более глубокими и
основательными окажутся осваиваемые знания.
2. Решение простых задач на сложение и
вычитание.
Разновидности задач на сложение и вычитание в
учебниках математики по традиционной системе
как бы перетасованы, что затрудняет
возникновение циклических связей мысли.
Задачи на сложение и вычитание целесообразно
рассматривать следующими циклами:
- задачи на нахождение суммы и неизвестного
слагаемого; - задачи на нахождение разности, уменьшаемого,
вычитаемого; - задачи на увеличение и уменьшение числа на
несколько единиц; - задачи на разностное сравнение величин.
2.1. Задачи на нахождение суммы и неизвестного
слагаемого.
Прямая задача
Катя купила 9 открыток, а Надя 8 открыток.
Сколько всего открыток купили девочки?
Краткая запись:
К. Н. Всего 9 от. 8 от. ? от.
Решение: 9 + 8 = 17 (от.)
Ответ: девочки купили 17 открыток.
Дается название вида задачи, вводится таблица
видов простых задач.
Обратная задача.
Какие числа были даны в задаче?
Какие числа мы нашли, решая задачу?
Составим новую задачу, для чего неизвестным
числом сделаем одно из двух других чисел,
например, 9 открыток. Сформулируйте эту задачу.
Катя купила несколько открыток, а Надя 8
открыток. Всего девочки купили 17 открыток.
Сколько открыток купила Катя?
Краткая запись:
К. Н. Всего ? от. 8 от. 17 от.
Решение: 17 – 8 = 9 (от.)
Ответ: Катя купила 9 открыток.
Сравните решения задач:
- Обе задачи решаются одним действием.
- Прямая задача – действием сложения, обратная –
действием вычитания.
Вводится термин – обратная задача.
Определяется вид задачи – нахождение
неизвестного слагаемого.
Аналогично вводится вторая обратная задача.
Введение обратных задач не изолированно от
прямой, а через нее имеет следующие
положительные стороны.
- Достигается ознакомление не только с новой
задачей, но и повторение старой. - Учащиеся усваивают связи между задачами,
умозаключения здесь возникают в цикле, во
взаимопревращениях друг в друге. - На следующем этапе мы учимся делать обратные
преобразования: дается одна обратная задача,
решается, а к ней составляется прямая и другая
обратная. Причем, здесь уместно ввести решение
задачи уравнением.
Саша купил несколько тетрадей в линейку и 7
тетрадей в клетку. Всего он купил 13 тетрадей.
Сколько тетрадей в линейку купил Саша?
- Читаем условие: “Саша купил несколько тетрадей
в линейку”. Сколько было – неизвестно,
обозначаем “окошечком”. - Читаем дальше: “и 7 тетрадей в клетку”. Пишем: 7 .
- Всего у него было 13 тетрадей. Пишем: 13 (? 7 13)
- При каком действии получается 13? (? + 7 = 13)
Вместо “окошечка” обозначаем неизвестное
число буквой Х. Получается уравнение: Х + 7 = 13
Как решить задачу? (Найти неизвестное
слагаемое)
Решение:
Х = 13 – 7
Х = 6
6 + 7 = 13
13 = 13
Эта задача преобразуется в прямую и во вторую обратную.
Совершенно аналогично проводим обучение
решению задач на нахождение третьего
(четвертого) слагаемого.
В одном ящике 23 кг яблок, во втором – 20 кг, а в
третьем 18 кг яблок. Сколько кг яблок в трех
ящиках?
Решение: 23 + 20 + 18 = 61 (кг)
Составим обратную задачу:
| 1 ящ. | 2 ящ. | 3 ящ. | Всего |
| ? кг | 20 кг | 18 кг. | 61 кг |
Как найти неизвестное слагаемое? (Из суммы
вычесть известное слагаемое)
Как это можно сделать?
1 способ: 61 – (20 + 18) = 23 (кг)
2 способ: (61 – 18) – 20 = 23 (кг)
3 способ: (61 – 20) – 18 = 23 (кг)
Таким образом. При решении задач на нахождение
неизвестного слагаемого появляется возможность
ознакомления с несколькими способами решения
одной и той же задачи.
Сколько еще обратных задач можно составить?
(Еще 2 задачи, каждую решить разными способами)
Часто учителя начальных классов выбирают из
нескольких способов простейший и им
ограничиваются. Но нужно помнить старое
дидактическое правило: иногда полезнее одну
задачу решить разными способами, чем несколько
задач одним и тем же способом.
Естественно, не всегда задачи на уроке мы
решаем с преобразованием в обратные. Можно
обратную задачу сформулировать и р6ешить устно,
сформулировать условие без ее решения, выяснив,
какие числа даны, что надо найти и т.д.
2.2. Задачи на нахождение разности, уменьшаемого
и вычитаемого.
Прямая задача.
У Веры было 87 рублей. Она купила книгу за 37
рублей. Сколько денег у нее осталось?
Краткая запись:
| Было | Израсходовано | Осталось |
| 87 р. | 37 р. | ? р. |
Решение: 87 – 37 = 50 (р.)
Какие числа были даны в задаче?
Что мы узнали после решения? (50 р. – сколько
осталось, разницу между числами)
Определяем вид задачи: нахождение остатка
(разности).
Составим обратную задачу,
сделав известным число 50 р., а неизвестным то, что
было.
У веры было несколько рублей. Она купила книгу
за 37 рублей, после этого у нее осталось 50 рублей.
Сколько денег было у Веры до покупки?
Эту задачу уместно решить уравнением.
- Сколько денег было у Веры? (Неизвестно – Х)
- Сколько денег она израсходовала?
- Сколько у нее осталось?
- Вопрос задачи?
Запись на доске: Х 37 50
- Чтобы получилось уравнение, нужно эти числа
связать знаками. Если человек уплатил (истратил,
израсходовал) деньги. То у него их стало больше
или меньше? - Какое действие надо выполнить? (Х – 37 = 50)
- У веры осталось 50 р., да она израсходовала 37 р.
Сколько денег у нее было вначале: больше, чем 50,
или меньше? - Почему больше?
- На сколько больше?
- Как узнать, сколько денег было вначале?
Х – 37 = 50
Х = 37 + 50
Х = 87
87 – 37 = 50
50 = 50
Ответ: у Веры было 87 р.
Какой компонент находили?
Каким действием?
Вид задачи: нахождение уменьшаемого.
Сравнение прямой и обратной задач:
Решены одним действием, прямая задача –
вычитанием, обратная – сложением.
На последующих уроках решаются задачи в иной
последовательности: сначала на нахождение
уменьшаемого, затем она преобразуется в задачу
на нахождение разности.
Затем мы решаем задачи на нахождение разности,
когда вычитаемых несколько.
Прямая задача.
В магазине было 90 коробок конфет. В первый день
продали 30 коробок, во второй день – 32 коробки.
Сколько коробок конфет продали в третий день?
К этому времени мы изучили следующие свойства:
- прибавление суммы к числу,
- прибавление числа к сумме,
- вычитание суммы из числа,
- вычитание числа из суммы.
Поэтому решение подобных задач разными
способами не вызывает особых затруднений у
детей.
Краткая запись:
| Было | Израсходовано | Осталось |
| 90 к. | 30 к. и 32 к. | ? р. |
Решение: 1 способ – 90 – (30 + 32) = 28 (к.)
2 способ – (90 – 30) – 32 = 28 (к.)
3 способ – (90 – 32) – 30 = 28 (к.)
Что мы находим в этой задаче?
Составьте обратную задачу на нахождение
уменьшаемого.
В магазине было несколько коробок конфет. В
первый день продали 30 коробок, во второй – 32
коробки, в третий – оставшиеся 28 коробок. Сколько
коробок конфет было в магазине первоначально?
Краткая запись: ? к. 30 к. и 32 к. 28 к.
Решение:
1 способ – (30 + 32) + 28 = 90 (к.)
2 способ – (30 + 28) + 32 = 90 (к.)
3 способ – (32 + 28) + 30 = 90 (к.)
Вслед за задачей на нахождение уменьшаемого
вводится задача на нахождение вычитаемого.
Прямая задача.
К обеду в столовой сделали 70 бутербродов. За
обедом съели 62 бутерброда. Сколько бутербродов
осталось в столовой?
Краткая запись:
| Было | Израсходовано | Осталось |
| 70 б. | 62 б. | ? р. |
Решение: 70 – 62 = 8 (б.)
Изменим краткую запись: 70 б. ? б. 8б.
Составьте по ней обратную задачу. К
обеду в столовой сделали 70 бутербродов. После
обеда осталось 8 бутербродов. Сколько
бутербродов съели за обедом?
Эту задачу удобнее решить уравнением.
Сколько было сделано бутербродов?
Сколько съели?
Сколько осталось? 70 Х 8
Как связать эти три числа?
70 – Х = 8
Х = 70 – 8
Х = 62
70 – 62 = 8
8 = 8
Какой компонент находили?
Определите вид задачи. (Нахождение вычитаемого)
Далее решаются задачи на преобразование задач
на нахождение вычитаемого в задачи на нахождение
разности.
В конце изучения данной темы необходимо решать
изолированные задачи без составления к ним
обратных, а иногда решать все три задачи по одной
и той же ситуации.
2.3. Задачи на уменьшение и увеличение числа на
несколько единиц и задачи на разностное
сравнение величин.
К введению понятия разностного сравнения мы
находим через прямую задачу на увеличение и
уменьшение числа на несколько единиц.
Прямая задача.
Набор цветных карандашей стоит 16 рублей, а
набор фломастеров на 12 рублей дороже. Сколько
стоит набор фломастеров?
Краткая запись:
| К. | Ф. | |
| 16 р. | на 12 р. дороже | ? р. |
Решение: 16 + 12 = 28 (р.)
Обратная задача: ? р. на 12 р. дороже 28 р.
Набор карандашей стоит несколько рублей. Набор
фломастеров на 12 рублей дороже. Он стоит 28 рублей.
Сколько стоит набор карандашей?
Производим рассуждения и преобразования:
Набор фломастеров на 12 р. дороже, значит, набор
карандашей на 12 р. дешевле. Поэтому получаем
следующую задачу:
Набор фломастеров стоит 28 руб., набор
карандашей на 12 руб. дешевле. Сколько стоит набор
карандашей?
Краткая запись:
| К. | Ф. |
| ? р. на 12 р. дешевле | 28 р. |
Решение: 28 – 12 = 16 (р.)
Преобразовываю схему:
на ? р. дешевле
Составьте обратную задачу:
Набор карандашей стоит 16 рублей, а набор
фломастеров 28 рублей. На сколько рублей
фломастеры дороже карандашей? (На сколько рублей
карандаши дешевле фломастеров?)
Решение: 28 – 16 = 12 (р.)
Обязательно сравниваем решение прямой и
обратных задач.
На следующих уроках сначала решается задача на
разностное сравнение, которая преобразуется в
две другие задачи. После этого решаем задачи на
сложение и вычитание, выраженные в косвенной
форме.
Таким образом, взаимосвязь между задачами на
сложение и вычитание укладывается в таблицу
(прилагается). В ней обозначены три вида задач
на сложение и шесть видов задач на вычитание.
Чтобы обобщить эти задачи и подготовить почву
для свернутого решения этих задач, полезно
упражнять учащихся по мере изучения материала в
составлении нескольких видов задач к одному
выражению, например, 15 + 3.
Составьте три задачи, чтобы в них
использовались слова:
“больше на…”
“сколько вместе”
“сколько было вначале”
Например:
- В одном ящике было 15 кг яблок, в другом на 3 кг
больше. Сколько килограмм яблок во втором ящике? - В одной коробке 15 кг конфет, в другой – 3 кг.
Сколько конфет в двух коробках. - За обедом съели 3 яблока, после чего в вазе
осталось 15 яблок. Сколько яблок было в вазе
вначале? - Эти упражнения содействуют развитию
множественных связей (ассоциаций). В данном
случае множественная связь имеет следующее
строение:
Сложение –
“увеличить на”
“сколько вместе”
“сколько всего”
“сколько было вначале”.
– Составьте четыре задачи на вычитание: 70 – 30.
- У мамы было 70 рублей. Она купила апельсинов на 30
рублей. Сколько денег у ней осталось? - У мамы было 70 рублей. Она истратила несколько
рублей на покупку апельсинов, после чего у нее
осталось 30 рублей. Сколько денег мама истратила
на апельсины? - У Коли 70 марок, у Пети на 30 марок меньше. Сколько
марок у Пети? - Зеленая лента 70 см, белая – 30 см. на сколько см
зеленая лента длиннее белой?
Здесь формируется следующий пучок ассоциаций:
Вычитание –
“сколько осталось”
“сколько истратили”
“меньше на”
“на сколько меньше (больше)”.
3. Литература.
|
№ п/п |
Автор |
Издание |
Выходные данные |
|
1. |
Моро М.И. | Математика, 1 класс
Математика, 2 Математика, 3 класс |
М., Просвещение, 2001.
М., М., Просвещение, 2003. |
|
2. |
Аритская И.И. | Математика, 1 класс
Математика, 2 Математика, 3 класс Математика, 4 класс |
М., Просвещение, 2000.
М., М., Просвещение, 2002. М., Просвещение, 2003. |
|
3. |
Истомина Н.Б. | Математика, 1 класс
Математика, 2 Математика, 3 класс Математика, 4 класс |
С., Асс XXI век, 2002.
С., Асс XXI век, С., Асс XXI век, 2004. С., Асс XXI век, 2005. |
|
4. |
Аритская И.И. | Обучаем по системе Занкова 1 кл., 2 кл., 3 кл. |
М., Новая школа, 1993, 1994. |
|
5. |
Эрдниев П.М. | Взаимно обратные действия в арифметике 2–4 классы |
М., Просвещение, 1969. |
|
6. |
Рудницкая В.Н. | Тематические и итоговые контрольные работы по математике. |
М., Дрофа, 1996. |
|
7. |
Холомкина А.И. | Решение задач на движение | М., Просвещение, 1982. |
|
8. |
Уткина Н.Г. | Составные задачи в 1 классе | М., Просвещение, 1982. |
|
9. |
Кондратьева Д.Ф. | Составные задачи небольшой сложности в 1 классе |
М., Просвещение, 1982. |
|
10. |
Гусева Т.В. | Обучение решению простых задач в 1 классе |
М., Просвещение, 1982. |
|
11. |
Свечников А.А. | Решение математических задач в 1 классе |
М., Просвещение, 1982. |
|
12. |
Баитова М.А., Бельтюкова Г.В. |
Обучение решению арифметических задач |
М., Просвещение, 1984. |
|
13. |
Шамсутдинова Г.С. | Преемственность в обучении математике |
М., Просвещение, 1978. |
|
14. |
Истомина Н.Б. | Активизация учащихся на уроках математики в нач. классах |
М., Просвещение, 1985. |
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Обратные задачи
В обратной задаче одна из искомых величин становится известной, а одна из данных величин становится неизвестной.
Прямая задача:
У Тани было 3 зелёных шарика и 2 красных. Сколько всего шариков было у Тани?
Первая обратная задача:
У Тани было 5 шариков, 3 шарика были зелёными, а остальные красные. Сколько красных шариков было у Тани?
Ты видишь, что известная величина – красные шарики – стала неизвестной.
А неизвестная величина – общее количество шариков – стало известной.
Вторая обратная задача:
У Тани было 5 шариков, 2 шарика были красными, а остальные зелёные. Сколько зелёных шариков было у Тани?
Ты видишь, что известная величина – зелёные шарики – стала неизвестной.
А неизвестная величина – общее количество шариков – стало известной.
ТАКИЕ ЗАДАЧИ НАЗЫВАЮТСЯ ОБРАТНЫМИ.
Советуем посмотреть:
Образцы оформления задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 48. Урок 25,
Петерсон, Учебник, часть 2
Страница 50. Урок 26,
Петерсон, Учебник, часть 2
Страница 53. Урок 27,
Петерсон, Учебник, часть 2
Страница 60. Урок 31,
Петерсон, Учебник, часть 2
Страница 63. Урок 32,
Петерсон, Учебник, часть 2
Страница 8. Урок 5,
Петерсон, Учебник, часть 3
Страница 25. Урок 13,
Петерсон, Учебник, часть 3
Страница 33. Урок 17,
Петерсон, Учебник, часть 3
Страница 65. Урок 33,
Петерсон, Учебник, часть 3
Страница 91. Повторение,
Петерсон, Учебник, часть 3
2 класс
Страница 57,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 88,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 36,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 68,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 9. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 52,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 14,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 38,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 71,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 21,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 35. Урок 13,
Петерсон, Учебник, часть 1
Страница 40. Урок 15,
Петерсон, Учебник, часть 1
Страница 74. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 11,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 87,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 68,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 44,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 2
Математика, 2 класс
Урок № 10. Задачи, обратные данной
Перечень вопросов, рассматриваемых в теме:
- Что такое задачи, обратные данной?
- Как составлять и решать обратные задачи?
Глоссарий по теме:
Задачи, обратные данной – считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.26, 27
2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 16, 17
3. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.-с.31
Теоретический материал для самостоятельного изучения
Решим три задачи.
Составим по рисунку первую задачу.
В классе 10 девочек и 8 мальчиков. Сколько всего детей в классе?
Составим схематический рисунок.
Решим задачу:
10 + 8 = 18 (д.)
Ответ: 18 детей в классе.
Составим вторую задачу.
В классе 18 детей. Девочек 10, остальные-мальчики. Сколько мальчиков в классе?
Решим задачу:
18 – 10 = 8 (м.)
Ответ: 8 мальчиков в классе.
Составим третью задачу.
В классе 18 детей. Мальчиков 8, остальные – девочки. Сколько девочек в классе?
Решим задачу:
18 – 8 = 10 (д.)
Ответ: 10 девочек в классе.
Посмотрим еще раз на схемы к каждой задаче. Обратим внимание на то, что во всех задачах одинаковый сюжет, но то, о чем спрашивается в первой задаче стало известным во второй и третьей задачах, а узнать во второй задаче, сколько мальчиков и в третьей задаче сколько девочек в классе надо то, что известно в первой задаче.
Задачи, в которых известно то, о чем спрашивается в первой задаче и надо узнать то, что в первой задаче известно, называют обратными первой.
Сделаем вывод: задачи, обратные данной – считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Тренировочные задания.
1. Решите задачу. Выберите задачи, обратные данной.
Кате подарили 8 воздушных шариков красного и синего цвета. Красных шариков было 5. Сколько синих шариков у Кати?
Варианты ответов:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
2. У Кати было 8 шариков. 3 шарика она подарила. Сколько шариков осталось у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
Правильные варианты:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
2 . Восстановите пропуски в задачах.
1.В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в ________?
2. В июне ____ дней. Из них 10 дней были пасмурными. Сколько______ дней было в июне?
3. В июне 30 дней. Ясными были ____ дней. Сколько ____ дней было в июне?
Варианты ответов:
30, 20, ясных, пасмурных, июне
Правильный вариант:
1. В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в июне?
2. В июне 30 дней. Из них 10 дней были пасмурными. Сколько ясных дней было в июне?
3. В июне 30 дней. Ясными были 20 дней. Сколько пасмурных дней было в июне?
|
Обратные задачи – это задачи, в которых то, что было неизвестно, становится известно. Задача: На тарелке было 6 яблок, а в корзине 10 яблок. Сколько всего яблок? На тарелке – 6 ябл. В корзине – 10 ябл. ? ябл. 6+10=16 ( ябл.) Ответ: 16 яблок всего. Обратные задачи На тарелке – 6 ябл. В корзине – ? ябл. 16 ябл. 16-6=10 (ябл.) Ответ: 10 яблок в корзине. На тарелке – ? ябл. В корзине – 10 ябл. 16 ябл. 16-10=6 (ябл.) Ответ: 6 яблок на тарелке. |
Обратные задачи – это задачи, в которых то, что было неизвестно, становится известно. Задача: На тарелке было 6 яблок, а в корзине 10 яблок. Сколько всего яблок? На тарелке – 6 ябл. В корзине – 10 ябл. ? ябл. 6+10=16 ( ябл.) Ответ: 16 яблок всего. Обратные задачи На тарелке – 6 ябл. В корзине – ? ябл. 16 ябл. 16-6=10 (ябл.) Ответ: 10 яблок в корзине. На тарелке – ? ябл. В корзине – 10 ябл. 16 ябл. 16-10=6 (ябл.) Ответ: 6 яблок на тарелке. |
|
Обратные задачи – это задачи, в которых то, что было неизвестно, становится известно. Задача: На тарелке было 6 яблок, а в корзине 10 яблок. Сколько всего яблок? На тарелке – 6 ябл. В корзине – 10 ябл. ? ябл. 6+10=16 ( ябл.) Ответ: 16 яблок всего. Обратные задачи На тарелке – 6 ябл. В корзине – ? ябл. 16 ябл. 16-6=10 (ябл.) Ответ: 10 яблок в корзине. На тарелке – ? ябл. В корзине – 10 ябл. 16 ябл. 16-10=6 (ябл.) Ответ: 6 яблок на тарелке. |
Обратные задачи – это задачи, в которых то, что было неизвестно, становится известно. Задача: На тарелке было 6 яблок, а в корзине 10 яблок. Сколько всего яблок? На тарелке – 6 ябл. В корзине – 10 ябл. ? ябл. 6+10=16 ( ябл.) Ответ: 16 яблок всего. Обратные задачи На тарелке – 6 ябл. В корзине – ? ябл. 16 ябл. 16-6=10 (ябл.) Ответ: 10 яблок в корзине. На тарелке – ? ябл. В корзине – 10 ябл. 16 ябл. 16-10=6 (ябл.) Ответ: 6 яблок на тарелке. |