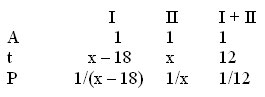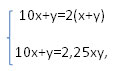Цели урока.
Образовательные:
систематизировать знания и умения учащихся
решать текстовые задачи.
Развивающие:
совершенствование, развитие, углубление
знаний, умений, навыков по решения текстовых
задач;
развитие мыслительной деятельности: умение
анализировать, обобщать, сравнивать;
развитие творческой деятельности: смекалки;
развитие математической речи и графической
культуры, памяти
Воспитательные:
формирование мировоззрения с помощью
взаимосвязанной системы знаний по данной теме;
формирование обще учебных навыков:
вычислительных, эстетических навыков при
оформлении записей;
формирование качеств личности: трудолюбия,
самостоятельности, стремления к самореализации.
Ожидаемые результаты обучения:
В результате повторения данных тем учащиеся:
• закрепляют знания о рациональных уравнениях,
понятие “решение уравнения”, понятие “решение
системы уравнений”,
• развивают способности к анализу и синтезу
изучаемого материала, умение выделять главное в
тексте учебника,
• воспитывают волю и настойчивость при
решении, желание добиться результата.
Тип урока: урок комплексного применения ЗУН.
Форма организации урока: урок-практикум.
Структура урока.
- Актуализация ЗУН, необходимых для творческого
применения. - Обобщение и систематизация знаний и способов
деятельности. - Усвоение образца комплексного применения ЗУН.
- Творческое применение ЗУН.
- Контроль и самоконтроль.
- Подведение итогов урока.
- Информация по домашнему заданию.
Ход урока
I. Устный счёт
Фронтальная работа.
Решаем устно задания из бока “Реальная
математика”
Найдите 30% от 27. (0,9)
Какое число получится, если 140 увеличить на 60%?
(224)
Кафельная плитка продается коробками по 6 м2.
Сколько коробок плитки нужно купить, чтобы
хватило на облицовку стен площадью 35 м2? (6)
Билеты в ботанический сад стоит 50 рублей.
Сколько рублей сдачи нужно получить с 2000 рублей,
заплаченных за проход 36 человек? (200)
Горные лыжи стоят 16 000 рублей. Сколько рублей
будут стоить горные лыжи во время сезонной
распродажи, когда на них объявлена скидка 20%? (12800)
II. Решение задач.
1. Задачи на движение.
В настоящее время на экзамене по математике в
блоке “алгебра” предлагаются задачи, решение
которых требует составления уравнения, а также
их систем на основании условия задачи.
Указания к задачам:
1.Основными компонентами этого типа являются:
а) пройденный путь (S);
б) скорость (v);
в) время (t).
2. Зависимость между величинами выражается
известными формулами:
S=v/t; v=S/t; t=S/v.(Указанные величины должны быть в
одной системе единиц, например: путь в км, время в
часах, то скорость в км/час.)
Задача 1.
Из А в В по течению реки отправился плот. А через
час вслед за ним отправилась яхта, которая,
прибыв в пункт В тотчас повернула обратно и
возвратилась в А. К этому времени плот
удалился от А на расстояние 24 км. Пристань А
расположена в 120 км от пристани В. Найдите
скорость яхты в неподвижной воде, если скорость
течения реки равна 2 км/ч. Ответ дайте в км/ч.
1. Заполните таблицу.
| S (км) | v (км/ч) | t (ч) | |
| Плот | |||
| Яхта (по течению) | |||
| Яхта (против течения) |
Учитель математики. Анализируя текст с
позиций русского языка, мы определили
последовательность действий, а также сделали
акценты в следующих аспектах:
- время движения плота (“к этому времени”),
- путь, который прошла яхта по течению и против
течения (основа предложения “пристань
расположена”), - характер движения по (против) течения
(придаточное условия), - объект, который двигался в обе стороны
(относительное местоимение “которая”), - направление, в котором двигалась яхта,
достигнув пункта В (слово “обратно”).
| S (км) | v (км/ч) | t (ч) | |
| Плот | 120 | 2 | 60 |
| Яхта (по течению) | 120 | Х+2 | 120/х+2 |
| Яхта (против течения) | 120 | Х-2 | 120/х-2 |
2. Составим и решим уравнение:
120/х+2+120/х-2=11 /*(х2-4)
11х2-240х-44=0
Д=240*240-4*11*(-44)=59536
Х1= (240+244)/22=22; х2 = (240-244)/22=-4/22 – не
удовлетворяет условию задачи.
Ответ: 22 км/час.
Задача 2.
Пристани А и В расположены на реке, скорость
течения которой на этом участке равна 4 км/ч.
Лодка проходит от А до В и обратно без остановок
со средней скоростью 6 км/ч. Найти собственную
скорость лодки.
Решение:
Пусть х км/ч – собственная скорость лодки.
| Лодка | V км/ч | tчас | Sкм |
| Из А в В | x-4 | S/x-4 | S |
| Из В в А | X+4 | S/x+4 | S |
Составим уравнение:
(S/x-4 + S/x+4)*6=2 S.
Получим х=8 км/ч или х=-2(не удовлетворяет условию
задачи)
Ответ: 8 км/час.
2. Задачи на совместную работу.
Алгоритм решения задач на совместную работу
Принимаем всю работу, которую необходимо
выполнить за 1.
Находим производительность труда каждого
рабочего в отдельности, т.е., где t – время, за
которое этот рабочий может выполнить всю работу,
работая отдельно.
Находим ту часть всей работы, которую выполняет
каждый рабочий отдельно за то время, которое он
работал.
Составляем уравнение, приравнивая объем всей
работы к сумме слагаемых, каждое из которых есть
часть всей работы, выполненная отдельно каждым
из рабочих.
Задача 1.
Первая бригада может выполнить задание за 20
часов, а вторая – за 30 часов. Сначала бригады
выполнили при совместной работе 3/4 задания, а
остальную часть задания выполнила одна первая
бригада. За сколько часов было выполнено задание?
Решение:
- 1:20=1/20 (задания) – выполняет первая бригада за 1
час; - 1:30=1/30 (задания) – выполняет вторая бригада за 1
час; - 1/20+1/30=1/12 (задания) – выполняют две бригады за 1
час совместной работы; - ?:1/12=9 (ч) – две бригады работали совместно;
- 1 -3/4=1/4 (задания) – выполнила одна первая бригада;
- 20*1/4=5 (ч) – время работы одной первой бригады;
- 9+5=14 (ч) – время выполнения всей работы.
Ответ: за 14 часов.
Задача №2
Две трубы, работая вместе, наполнили бассейн за
12 часов. Первая труба, работая отдельно,
наполняет бассейн на 18 часов быстрее, чем вторая.
За сколько часов наполняет бассейн вторая труба.
Решение:
1/12 = 1/(x – 18) + 1/x
Х2 -42Х +216=0
Х1=36; Х2 =6 (не удовлетворяет условию
задачи)
Ответ: 36 часов.
3. Задачи с использованием формул двузначного
числа
Алгоритм решения задач, в которых используется
формула двузначного числа.
Вводится обозначение:
х – цифра десятков
у – цифра единиц
Искомое двузначное число 10х + у
Составить систему уравнений.
Задача 1
Двузначное число в четыре раза больше суммы его
цифр. Если к этому числу прибавить произведение
его цифр, то получится 32. Найдите это двузначное
число.
Х – цифра десятков. У – цифра единиц. 10х + у –
искомое число.
2х2 + 12х – 32 =0
х2 +6х – 16 =0
х1 =-8 (посторонний корень)
х2 =2, тогда у =4.
Ответ: 24.
Задача 2
Найти двузначное число, которое в 2 раза больше
суммы его цифр и в 2,25 раза больше произведения
его цифр.
Решение:
Пусть число ху =10х+у, тогда составим
систему:
10х+у=2х+2у, 8х=у
10х+8х=2.25х*8х
18х=18х2
18х(х-1)=0, х1=0 (не удовлетворяет условию
задачи).
и х2 =1, у=8, искомое число 18.
Ответ: 18.
4. Задачи на смеси и растворы.
Алгоритм решения задач на смеси.
х – масса первого раствора, у – масса второго
раствора, (х + у) – масса полученной смеси.
Найти содержание растворенного вещества в
растворах, т.е.
а % от х, в % от у, с % от (х+у)
Составить систему уравнений.
Задача 1
Смешали 30%-й раствор соляной кислоты с 10%-м и
получили 600 г 15%-го раствора. Сколько граммов
каждого раствора было взято?
Решение:
Введем обозначение. Пусть взяли х г первого
раствора, у г – второго раствора, тогда масса
третьего раствора – (х+у).
Определим количество растворенного вещества в
первом, втором, третьем растворах, т.е. найдем 30%
от х, 10% от у, 15% от 600.
15% от 600=90
Составим систему уравнений:
0,3х + 60 – 0,1х = 90
0,2х = 30
х = 30:0,2
х = 150, у = 600 – 150 = 450
Ответ: взяли 150 г первого раствора и 450 г второго
раствора.
III. Подведение итогов урока (4 минуты)
Ребята вы сегодня от души потрудились,
порадовали меня своими знаниями. У кого 4 и более
жетончиков подойдите с дневниками. Проставляю
оценки в журнал:
4-5 ж – “4”,
5 и более жетонов – “5”.
IV. Домашнее задание
1. Моторная лодка прошла 48 км по течению реки, и
вернулся обратно, потратив на весь путь 7 часов.
Скорость течения реки равна 2 км/час. Скорость
течения реки равна 2 км/час. Найдите скорость
лодки в неподвижной воде.
2. Две машины, работая вместе, могут расчистить
каток за 20 минут. Если первая машина будет
работать 25 минут, а затем её сменит вторая, то она
закончит расчистку катка через 16 минут. За
сколько времени может расчистить каток каждая из
машин, работая отдельно?
В результате изучения учащиеся должны уметь:
- определять тип текстовой задачи, знать
особенности методики её решения, использовать
при решении различные способы; - применять полученные математические знания при
решении задач; - применять полученные математические знания в
решении жизненных задач; - использовать дополнительную математическую
литературу с целью углубления материала
основного курса.
В обучении математике текстовые задачи всегда
занимали особое место. Пока мы будем учить детей
на русском языке – не только великом и могучем,
но и достаточно трудном, пока мы хотим учить их
сравнивать, выбирать наиболее простой путь
достижения поставленной цели, пока мы не
отказались от воспитания гибкости и критичности
мышления, пока мы стараемся увязывать обучение
математике с жизнью, нам будет трудно обойтись
без текстовых задач.
Рефлексия.
Продолжи фразу:
Сегодня на уроке …
Теперь я знаю …
Мне на уроке …
Релаксация.
Активно на уроке работали …
Старались …
Жду большей активности от …
Литература для учителя
- Лурье М.В., Александров Б.И. Задачи на
составление уравнений. – М.; Наука, 1990. - Перельман Я.И. Занимательная алгебра. – М.:
АСТ-Астрель, 2002. - Прокофьев А., Соколова Т., Бардушкин В., Фадеичева
Т. Текстовые задачи. Материалы вступительных
экзаменов в МИЭТ. // Математика, 2005, № 9. - Сканави М.Н., Егерев В.К., Зайцев В.В. и др., 2500
задач по математике с решениями для поступающих
в вузы. – М. “ОНИКС 21 век”, “Мир и образование”,
2002. - Тоом А. Как я учу решать текстовые задачи. //
Математика, 2004, № 46, № 47. - Черкасов О.Ю., Якушев А.Г. Математика.
Справочник для старшеклассников, поступающих в
вузы. – М. “АСТ-ПРЕСС”, 2001. - Шевкин А.В. Текстовые задачи в школьном курсе
математики (5-9-е классы). – М.: Педагогический
университет “Первое сентября”, 2006.
Текстовые задачи в курсе алгебры основной щколы
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Давиденко В.И. 1
1МКОУ СОШ №8
Никитина Н.С. 1Варченко О.А. 1
1МКОУ СОШ №8
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
ВВЕДЕНИЕ
Для формирования математической культуры школьников чрезвычайно важно глубокое и прочное усвоение основ курса математики. Принципиально иную организацию собственной познавательной деятельности школьников предполагает формирование высокой математической культуры выпускников современной школы, в ходе которой у них определяются умения изучать математику самостоятельно и творчески, а значит, создаются основания к активному использованию математических знаний в будущем.
Эффективному использованию учебных задач способствует активизация самостоятельно-познавательной деятельности школьников при изучении курса математики, которые являются первостепенным средством зарождения у школьников системы базовых математических знаний, умений и навыков, ведущей формой учебной деятельности в процессе изучения математики, средством их математического развития.
Уровень подготовленности учащихся к следующей за обучением практической деятельности в любой сфере производства, культуры, в чем-то зависит от продуктивности использования задач в обучении математике.
Действительно, в современном мире все в большей степени необходимы не только базовые общие и специальные знания, но и способность трудится оригинально и творчески, проявлять деловую инициативу, способность к постоянному самообучению и самообразованию. Все перечисленные качества человека характеризуют эффективность его приспособления к разнообразию и изменчивости современного производства. Решая математические текстовые задачи, представленные в обдуманной математической системе, школьники не только динамично овладевают содержанием курса математики, но и обретают умения мыслить не стандартно. Все это проявляется в умении трансформировать задачную ситуацию с целью создать условия использования того или иного метода, приема; в умении создавать новые приемы для решения задач; в умении выделять и накапливать вероятно полезную информацию; в умении конструировать и моделировать потенциально важную информацию; в умении создавать на базе данной задачи новые; в умении осуществлять самоконтроль, исследовать результаты решения.
Без решения задачи очень трудно овладеть теорией, так как конкретно в процессе решения задач взаимосвязи базовых математических понятий и свойств между собой и окружающим миром становятся понятнее и очевиднее.
Как показывает практика и анализ математической подготовки учащихся, текстовые задачи вызывают затруднения. Поэтому рационализация умений решать текстовые алгебраические задачи — актуальная проблема методики преподавания математики.
Цель исследования:
– разработать приемы, способствующие совершенствованию умения решать текстовые задачи.
Для достижения цели было необходимо:
-проанализировать литературу по теме исследования;
-выявить затруднения, которые испытывают учащиеся в ходе решения текстовых задач;
– проанализировать методы обучения решению текстовых задач;
– разработать методические приемы, способствующие совершенствованию умения учащихся решать текстовые математические задачи.
Объект исследования: процесс обучения алгебре в 7-9 классах основной школы.
Предмет исследования: процесс обучения решению текстовых задач в курсе алгебры основной школы.
Гипотеза: мы исходили из предложения, что целенаправленная работа не над всей задачей, а над отдельными компонентами, входящими в структуру ее решения, будет способствовать совершенствованию умения учащихся решать текстовые задачи.
Работа состоит из введения, двух глав, заключения и списка литературы. В первой главе изложены теоретические основы решения текстовых задач: понятие «текстовая задача» рассмотрена роль таких задач в обучении математике, их топология, приемы решения и моделирование в процессе решения текстовых задач.
Во второй главе рассмотрены методические особенности формирования умения решать текстовые задачи: подготовленная работа, этапы решения текстовых задач и методические особенности обучения решению текстовых задач по учебникам «Алгебра», 7-9 класс под редакцией А.Г. Мерзляка, В.Б. Полонского, М.С. Якира.
МЕТОДИЧЕСКИЕ АСПЕКТЫ ФОРМИРОВАНИЯ УМЕНИЯ РЕШАТЬ ТЕКСТОВЫЕ ЗАДАЧИ
§1 Пропедевтика обучения решению текстовых задач
Решение задач важный этап в обучении математике школьников, поэтому работать по этому вопросу учитель начинает еще с начальной школы, помогая понять простые виды задач и уметь их классифицировать в зависимости от их сюжетных линий. Чтобы понять суть методов решения различных задач, методически важно начать с приемов помогающих успешному прочтению текста задачи. Затем основываясь на понимании смысла условия помочь учащимся классифицировать задачи, после чего определить вид вспомогательных моделей, которые будут использоваться в той или иной задаче. Далее учитель помогает найти взаимосвязи между условием и требованием задачи, переводя тест задачи на математический язык. Рассмотрим этапы работы над обучением решению таких задач подробнее [1].
Первый этап пропедевтики.
Первый этап очень важен, так как фундаментально готовит детей к пониманию и осмыслению задачи. Выделяют несколько моментов входящих в первый этап. Это понимание текста задачи, способность увидеть условие и вопросы задачи (требования), овладение способами сжатой записи текста задачи и создания вспомогательной модели в виде рисунка (чертежа).
Умения считаются сформированными, если самостоятельно прочитав задачу, возможно сделать краткую запись или построить чертеж. Ежедневная систематическая работа в данном направлении влечет за собой стойкий навык в этом направлении.
Второй этап пропедевтики
Чтобы достичь словесного выражения смены величин необходимо, выполнять соответствующие упражнения. К таким упражнениям можно обращаться на каждом уроке в рамках изучаемой темы или в разделе повторения.
Рассмотрим несколько примеров, в которых требуется задать вопросы после прочтения текста задачи.
Задача 1. Рассмотрим задачу из сборника Шевкина А.: «В бочке было 40 ведер воды. Когда из нее отлили несколько ведер, то воды осталось в 7 раз больше, чем отлили. Сколько ведер отлили?» [19]
Задания:
Определим те величины, которые связаны отношениями:
– количество воды в ведре в 7 раз больше осталось, чем отлили;
– отлили в 7 раз меньше, чем осталось.
2) Как понять составленные выражения: 40-x=7x? 7х?
Задача 2. Рассмотрим задачу из учебника по математике для 7 класса авторов Мерзляк А.Г., Полонский В.Б., Якир М.С.: «Найдите три последовательных натуральных числа, если удвоенный квадрат большего из них на 79 больше суммы двух других» [12].
Подготовиться к осмысленному решению задач методом составления уравнений позволит прочно усвоить методы решения «чисто арифметических» задач [19]. Тем самым, этот вид задач можно рассмотреть в связи прикладной направленностью курса школьной математики.
§2 Этапы решения задачи и приемы их выполнения
Выбирая тот или иной метод решения задачи, необходимо рассматривать этапы работы над задачей. Рассмотрим основные этапы работы над задачей:
анализ содержания задачи;
составления плана решения задачи;
решение задачи, выполнение плана;
проверка полученного решения задачи.
Арифметический метод.
Задача 3. Ученики приобрели одинаковые тетради. Один приобрел 5 штук, второй 3 штуки, третий – 4. Вместе они заплатили 13 р. 56 к. Сколько заплатил каждый ученик?
Решение.
Анализ задачи.
Задача повествует об учениках, купивших тетради. Один купил 5 штук, другой – 3 штуки, а третий – 4. Сказано, что общая стоимость тетрадей 13 р. 56 к. необходимо узнать, сколько потратили ученики по отдельности. Сделаем краткую запись задачи.
1 -й ученик – 5 т., ? р.
2-й ученик – 3 т., ? р. 13р. 56 к.
3-й ученик – 4 т, ? р.
Поиск пути решения задачи и составление алана ее решения.
Сначала надо узнать, сколько стоит одна тетрадь и за сколько заплатит каждый ученик в отдельности, что поможет дать ответ на вопрос задачи. По условию известно количество тетрадей, приобретенных учениками по отдельности. Так же в условии сказано общая стоимость тетрадей, купленных всеми учениками и зная их количество можно узнать, сколько стоит одна тетрадь. Общее количество тетрадей найдем, зная из условия количество тетрадей, купленных каждым учеником.
Составим план для решения данной задачи:
Какое количество тетрадей купили всего?
Какова стоимость одной тетради?
Сумма, заплаченная первым учеником?
Сумма, заплаченная вторым учеником?
Сумма, заплаченная третьим учеником?
Решение задачи по намеченному плану:
5т.+3т.+4т.=12т.;
13 р. 56 к. : 12 = 1 р.13к.;
1р.13 к.*5=5р.65к.;
1р.13к. * 3= 3р.39к.;
1р.13к.*4=4 р.52 к.
Проверка решения задачи.
Суммируем полученные данные и получим: 5р.65к. +3р.39к. +4р.52к. = 13р.56к. Расхождения с условием задачи нет. Следовательно задача имеет верное решение.
Ответ: первый ученик заплатил 5р.65к., второй – 3р.39к., третий – 4 р.52к.
Алгебраический метод
Задача 4. Рассмотрим задачу из учебника по математике для 7 классов авторов Мерзляк А.Г., Полонский В.Б., Якир М.С.: «За первый день Вася прочел 8/15 страниц книги, за второй 5/12 страниц этой книги, а за третий оставшиеся 12 страниц. Сколько страниц в книге?» [12]
Рассмотрим решение данной задачи:
Анализ задачи.
В задаче говорится о книге, которую прочитал Вася. Известно, что книгу он читал три дня, при чем, не известно, сколько страниц в первый и второй день было прочитано. Сказано, что в первый день он прочитал 8/15 страниц книги, во второй 5/12 страниц всей книги. В третий день было прочитано 12 страниц. Требование задачи заключается в том, чтобы узнать количество страниц в книге.
Составим краткую запись задачи:
1 день – ? стр., 8/15
2 день – ? стр., 5/12
3 день – 12 стр.
Всего – ? стр.
Составление плана решения задачи.
Возьмем за х количество страниц в книге, для удобства вычисления, так как эта задача на нахождение части от числа. Далее, зная тип задачи, будем оформлять поиск количества страниц за каждый день. Чтобы найти количество страниц в книге суммируем прочитанные страницы за каждый день.
Решения задачи на основе, составленного плана.
Пусть х – количество страниц в книге. Тогда в первый день Вася прочитал 8/15х, а во второй 5/12х. По условию известно, что в третий день прочитано оставшиеся 12 страниц. Составим и решим уравнение: х-(8/15х+5/12х)=12;
х-(32/60х+25/60х)=12;
х-57/60х=12;
1/20х=12;
х=240. Значит в книге 240 страниц.
Проверка решения задачи.
Проверим полученный результат. Вычислим количество страниц прочитанных в первый день: 8/15х=8/15*240=128 стр. Вычислим количество страниц, прочитанных во второй день: 5/12х=5/12*240=100 стр. Проверим суммарное количество страниц за три дня: 128+100+12=240. Следовательно, задача решена, верно.
Чтобы процесс задачи был целенаправленным и осознанным при решении каждой задачи в обязательном порядке необходимо отражать все этапы, которые при знании приемов решения помогают в успешном решении [18].
2.1. Анализ содержания задачи
Прочитав задачу, осмыслив ее текст, происходит понимание сюжетных линий задачи. При этом полное осознание отдельных объектов задачи, не обязательно наступает сразу. Главным в этом приеме является выявление количественных и качественных характеристик, связывающих отдельные величины.[7].
Однако существует ряд приемов, необходимых для реализации данного этапа. Рассмотрим один из них.
Важным приемом этого этапа является анализ текста задачи, или рассмотрение ее вспомогательной модели. Существует два пути поиск решения задачи аналитический и синтетический, к первому относится поиск от вопроса задачи к данным, а ко второму от данных к вопросу [15].
План решения задачи замыкает поиск пути ее решения. Составить план решения, значит определить порядок, выполнения арифметических действий. Рассмотрим задачу, где поиск решения задачи осуществляется аналитическим путем.
Отметим, что при решении задач разными методами работа на этом этапе имеет свои специфические особенности [17].
2.3. Осуществление плана решения задачи
Суть данного этапа заключается в непосредственном решении задачи и нахождении ответа на поставленные вопросы. В записи решения и ответа в задаче важно опираться на общепринятые математические сокращения, в том числе систему Си и метрические меры. Необходимо помнить, что в этих сокращениях точка не ставится, а если рядом с математическими сокращениями нет чисел, то обозначение пишется полностью. Если в задании числовые значения заменены буквенными, то при работе с ними так же сокращения не используются. Остальные значения не имеют условных обозначений и записываются на усмотрение решающего задачу.
2.4. Проверка решения задачи
Понять, верно ли изучена задача, проверить, не противоречит ли ответ условиям данной задачи и есть назначение данного этапа. При этом надо помнить, что этот этап обязателен при решении текстовых задач. Так, логическое рассуждение, имеет смысл на этапе проверки решения, на других этапах оно не гарантируют верного решения.
Задача 5. Рассмотрим задачу, взятую из сборника задач Виноградовой Е.П.: «Проценты содержания спирта в трех растворах составляют геометрическую прогрессию. Если смешать первый, второй и третий растворы в весовом отношении 2:3:4, то получится раствор, содержащий 32% спирта. Если же смешать их в весовом отношении 3:2:1, то получится раствор, содержащий 22% спирта. Сколько процентов спирта содержит первый раствор?» [5]
Решение. Пусть в первом растворе содержание спирта х%, во втором – у% и в третьем – z% спирта. Это означает, что в 1 г первого раствора содержит г спирта, в 1 г второго раствора – г и в 1 г третьего раствора – г спирта. Если возьмем 2 г первого раствора, 3 г второго и 4 г третьего, то получим 9 г смеси, содержащей (2·+3·+4·) г спирта. По условию задачи полученная смесь содержит 32% спирта, т.е в 9 г. смеси содержит 9·(32/100) г спирта. Из этого условия получаем уравнение =.
Совершенно аналогично получаем еще одно уравнение: =.
Учитывая, что числа х, у, z составляют геометрическую прогрессию, составим третье уравнение у2=хz. Преобразовав первые два уравнения, получим систему уравнений:
2 х+3у+4z=288,
3х+2у+z=132;
y2=хz.
Выражаем у и z через х из первых двух уравнений: у=48-2х, z=36+х.
Подставляя эти выражения в третье уравнение системы, приходим у уравнению х2-76х-768=0, корни которого х1=64 и х2=12. Так как оба корня положительны, можно считать, что они удовлетворяют условию задачи, т.е. задача имеет два решения. Но значение х1=64 не удовлетворяет условию задачи, так как соответствующее значение у1=48-2х1 отрицательно. Таким образом, первый раствор содержит 12% спирта.
Ответ: первый раствор содержит 12% спирта.
Решая задачи, методически правильно, провести проверку, которая покажет, верно ли вы ее решили. Существуют различные приемы проверки: установление соответствия между числами, полученными в результате решения задачи и данными в условии задачи; составление и решение задачи, обратной данной; решение задачи различными способами; решение задачи различными методами; прикидка (грубая проверка).
Алгоритм решения текстовых задач
Изучая данную тему целесообразно повесить в классе алгоритм, помогающий в решении задач данного типа. При ознакомлении с алгоритмом ребята понимают, что он очень полезен при решении сложных задач и служит им помощником.
Алгоритм решения задач:
Обозначить неизвестную величину переменной (при решении задач с помощью системы уравнений вводят несколько переменных);
Выразить через нее другие величины;
Составить уравнение (или систему уравнений), показывающее зависимость неизвестной величины от других величин;
Решить уравнение (или систему уравнений);
Сделать проверку при необходимости;
Выбрать из решений уравнения (или системы уравнений) те, которые подходят по смыслу задачи;
Оформить ответ.
§3. Методические особенности обучения решению текстовых задач по учебникам «Алгебра» для 7-9 классов под редакцией А.Г. Мерзляка, В.Б. Полонского, М.С. Якира
В школе, решая текстовые задачи, как правило, реализуются все выделенные этапы: анализ текста задачи, выбор варианта решения и проработка плана ее решения, проверка полученного ответа. Обучая решению текстовых задач, авторы учебников для 7-9 классов А.Г. Мерзляк, В.Б. Полонский, М.С. Якира уделяют особое внимание каждому этапу решение задач.
Так, в учебнике 7 класс в теме «Текстовые задачи» обособляется в отдельный этап решения перевод словесной формулировки условия на математический язык [12].
Точные математические выражения и предложения, содержащие буквы, используются с целью решения текстовых задач. С их поддержкой требование задачи, записанное в обыкновенном стиле, переходит в общематематический стиль.
Присутствие в постановлении текстовых задач литеры, применяются с целью обозначения названия определенных чисел аналогичных этому, равно тому, как в геометрии буквы используют с целью обозначения точек.
Рассмотрим некоторые примеры перевода русского текста на математический язык.
Задача 6. Задача взята в сборнике задач Шевкина А.: «Когда Маша прочитала несколько страниц, то ей осталось прочитать на 40 страниц больше, чем она уже прочитала. Сколько страниц она прочитала сначала, если в книге 90 страниц?» [19]
Обозначим за х – количество страниц, которые уже прочитала Маша, тогда ей осталось прочитать (х+40) страниц, на 40 страниц больше. х+(х+40) – количество страниц в книге, которое по условию составляет 90 страниц. Составим уравнение: х+(х+40)=90.
Задача 7. Партию и 35 ящиков бананов нужно было развести по нескольким магазинам, заказавшим по одинаковому числу ящиков. Однако два магазина отказались от заказа, и поэтому каждый магазин получил на 2 ящика больше, чем предполагалось вначале. Сколько было магазинов [3]?
Обозначим искомое число буквой х. Тогда каждый магазин должен был получить 35/х ящиков, а поскольку число магазинов, получивших бананы, равно х-2, то фактически каждый из них получил 35/(х-2) ящиков. По условию, это число на 2 больше, чем 35/х, так что выполняется равенство
=
То есть по этому учебнику на первых порах учат составлять уравнения с одним или несколькими неизвестными, оперируя различными действиями. Чтобы анализировать взаимосвязь между объектом и составлять уравнения.
Упражнения так же направлены на составление уравнений, без их решения.
В предыдущем пункте мы переводили тексты задач на математический язык. Однако эти задачи не были решены – неизвестные числа мы не нашли. Здесь мы доведем решения задач до конца. При этом будут применяться разнообразные рассуждения, и прежде всего – основные свойства числовых равенств.
Например, если к двум равным числам прибавить третье число, то получатся равные числа, если первое равно второму, то и второе равно первому и т.п. Можно сказать иначе: если к обеим частям верного равенства прибавить одно и то же число, то получится также верное числовое равенство; если левую и правую часть верного равенства поменять местами, то получится также верное равенство [10].
Ясно, кроме того, что равенство не нарушается, если его левую и правую часть мы заменим на равное выражение.
Таким образом, решение текстовой задачи ограничивается составлением уравнения, которое рассматривается как математическая модель условия задачи. Представляется, что отделение этапа составления уравнения из всего процесса решения целесообразно с методической точки зрения. С одной стороны важно научить школьников составлению уравнений. С другой стороны, обособление такого этапа как средства формулирования умения решать текстовые задачи, упрощает работу, так как освобождает ученика от полного решения задачи [14]. В дальнейшем в учебнике 8-9 классов решение текстовых задач является как бы закреплением изучения различных видов уравнений.
То есть сначала изучается новая тема, например, «Квадратные уравнения», которая включает в себя: понятие квадратного уравнения, целые корни квадратных уравнений, теорему Виета, дробные корни квадратных уравнений, выделение полного квадрата, решение произвольных квадратных уравнений, примеры решения квадратных уравнений, частные случаи квадратных уравнений. И только после того, как они основательно изучили тему «Квадратные уравнения», решаются задачи приводящие к решению квадратных уравнений. Особое внимание при решении задач следует уделять самому переводу их текста на математический язык.
Таким образом, в учебнике А.Г. Мерзляка, В.Б. Полонского, М.С. Якира при изучении различных видов уравнений, сначала изучается новый вид уравнений, со всеми его особенностями, а долее решаются текстовые задачи на составление уравнений этого вида [14].
Большое разнообразие разно уровневых задач, вошедших в учебники, поможет заинтересовать учеников математикой, осуществить дифференциацию и индивидуальный подход. Сочетание традиционных и современных методов обучения, логичность и доступность подачи материала дают возможность достичь высокого уровня математической подготовки.
ЗАКЛЮЧЕНИЕ
Приведем основные результаты проделанной работы.
Анализ алгебраической подготовки школьников позволяет выявить необходимость совершенствования умения решать текстовые задачи.
В выпускной квалификационной работе рассматриваются теоретические основы решения текстовых задач: исследуется понятие текстовой задачи и их роль в обучении математике, представлены классификация задач, методы их решения, отдельное внимание уделено моделированию в процессе решения текстовых задач.
Методические особенности формирования умения решать текстовые задачи рассматриваются в процессе подготовительной работы и на отдельных этапах решения задачи, таких как анализ содержания, поиск пути решения и составления плана решения, реализация плана решения и проверка правильности решения.
Следует отметить, что в практике обучения решению текстовых задач алгебраическим методом сложилась традиция реализация всех этих этапов решения. Однако проведенное исследование показывает целесообразность изолированной работы над отдельными этапами решения. «Поэтапное» формирование умения решать текстовые задачи составляет методическую основу представленной работы.
СПИСОК ЛИТЕРАТУРЫ
Блажина Е.В. Текстовые задачи в школьном курсе математики / Е.В. Блажина // Открытый урок. Первое сентября [Электронный ресурс]. – Режим доступа: http://festival.1september.ru/articles/604951 (дата обращения 21.02.2017).
Буцко Е.В., Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7 класс. Методическое пособие.- М.: Вената – Граф, 2018.
Буцко Е.В., Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 8 класс. Методическое пособие.- М.: Вената – Граф, 2018.
Буцко Е.В., Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 9 класс. Методическое пособие.- М.: Вената – Граф, 2018.
Виноградова Е. П. Математика: текстовые задачи и методы их решения: учебно-методическое пособие / Е. П. Виноградова. – Орск : Издательство ОГТИ, 2008.
Информационный образовательный портал ЕГЭ и ГИА [Электронный ресурс]. – Электрон. дан. – URL: http://egeigia.ru (дата обращения: 21.12.2016).
Мерзляк А.Г, Полонский В.Б., Якир М.С. Алгебра 7-й класс.- М.: Вената – Граф, 2018.
Мерзляк А.Г, Полонский В.Б., Якир М.С. Алгебра 8-й класс.- М.: Вената – Граф, 2018.
Мерзляк А.Г, Полонский В.Б., Якир М.С. Алгебра 9-й класс.- М.: Вената – Граф, 2018.
Овечкина А.В. Обучение учащихся решению задач реальной математики в средней школе / А.В. Овечкина //Информационно-коммуникационные технологии в педагогическом образовании. КГПА, 2017.- №4.
Попов Н.И. Использование специальной методики при обучении решению математических задач / Н.И. Попов, А.Н. Марасанов // Вестник МГОУ. Серия: Педагогика. – 2014. – № 1. – С. 86 89.
Шевкин А.В. Текстовые задачи по математике: 511 / А.В. Шевкин – М. : ИЛЕКСА, 2018.
Шевкин, А.В. Роль текстовых задач в школьном курсе математики / А.В. Шевкин // Математика. 2005. – № 17.
Просмотров работы: 443
ФГАОУ ВПО «Казанский (Приволжский) федеральный университет»
Институт педагогики и психологии
Приволжский межрегиональный центр повышения квалификации
и профессиональной переподготовки работников образования
Проектная работа
«Текстовые задачи и систематизация методов их решения »
Выполнила: Елена Павловна Егорова
Слушатель курсов повышения
квалификации учителей математики
по проблеме «Современные технологии, формы и методы подготовки к итоговой аттестации в формате ГИА и ЕГЭ»
Должность: учитель математики
Место работы: МБОУ «Гимназия №3 ЗМР РТ»
Проектная работа допущена к защите
Руководитель проектной работы: Гульсия Хабриевна Ахметшина
«11 апреля» 2014г.
г. Казань – 2014г
Оглавление.
|
№ |
Содержание |
Стр. |
|
Постановка проблемы. Цель проекта. Задачи проекта. |
3 |
|
|
1 |
Введение. |
4 |
|
2.1 |
Текстовые задачи и способы их решения |
|
|
2.1.1 |
Структура процесса решения задач |
5-6 |
|
2.1.2 |
Способы решения текстовых задач. |
7 |
|
2.1.3 |
Виды текстовых задач |
7-8 |
|
2.2 |
Решение текстовых задач арифметическим и алгебраическим способами |
|
|
2.2.1 |
Задачи на движение |
8-14 |
|
2.2.2 |
Задачи на проценты |
14-16 |
|
2.2.3 |
2.2.3. Задачи на работу |
16-19 |
|
2.2.4. |
Задачи на концентрацию. |
19-20 |
|
2.2.4. |
Примеры задач ОГЭ и ЕГЭ |
21-24 |
|
3 |
Сложности при решении текстовых задач и пути их решения. |
25-26 |
|
4 |
Заключение |
26 |
|
5 |
Литература |
27 |
Постановка проблемы
Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Поэтому любой экзамен, проверка знаний содержит текстовую задачу. Но довольно часто встречаются случаи, когда учащиеся показывают, казалось бы, хорошие знания в области теории, знают все требуемые определения и теоремы, но запутываются при решении весьма несложных задач. Причин, конечно много. Встает вопрос, а можно ли научиться решать любые задачи? Конечно любые задачи научиться решать невозможно. Но если говорить о задачах, которые предлагаются в школьном курсе и на ЕГЭ и ОГЭ, то наверное каждый в принципе может научиться их решать. Для этого надо научиться такому подходу к задаче, при котором задача выступает как объект тщательного изучения, а ее решение – как объект конструирования и изобретения.
Цель проекта
изучить и обобщить различные способы решения текстовых задач алгебраическим и арифметическим способами по определенному алгоритму.
Задачи проекта
- Рассмотреть основные типы задач, которые наиболее часто встречаются в ГИА 9-ых классов и ЕГЭ в 11-ых классов.
- Рассмотреть разнообразные задачи по мере увеличения их сложности, представить оформленное решение, необходимое при подготовке к экзаменам.
- Рассмотреть способы решения текстовых задач и составить алгоритм для их решения.
Введение
Решение задач – это работа несколько необычная, а именно умственная работа. Чтобы научиться какой – либо работе, нужно предварительно хорошо изучить тот материал, над которым придется работать, те инструменты, с помощью которых выполняется эта работа.
Значит, чтобы хорошо решать задачи, надо разобраться в том, что они собой представляют, как устроены, из каких составных частей состоят, каковы инструменты, с помощью которых производится решение задач.
Решение любой текстовой задачи состоит из двух совершенно различных частей: логической и математической. В разных задачах на первый план выходит или первая или вторая часть, гораздо реже – обе. Наибольшую трудность для учащихся составляет первая часть, так как надо представить, что происходит и как это сформулировать на языке математики. Для этого необходим житейский опыт, умение логически мыслить, рассуждать, умение перевести происходящее на язык уравнений и неравенств. А это под силу не каждому. Иногда задачи вызывают практически непреодолимые трудности, которые к математике не имеют никакого отношения, после преодоления которых они не кажутся неразрешимыми.
Вторая часть текстовых задач более понятна учащимся – это чисто математическая задача: решить полученные уравнения или неравенства. Затруднения здесь чаще всего возникают, если эта математическая задача им практически не встречалась в школьном учебнике. Это ситуация, когда число уравнений меньше числа неизвестных. Такие задачи делятся на два больших класса. В одних на «лишнее» неизвестное просто можно сократить или в задаче просят найти какое – то отношение, поэтому, если ввести это отношение в качестве переменной, то задача легко решится. Но не всякий школьник это сразу сообразит и будет решать дальше. В задачах второго класса, как правило, надо из условий задачи найти какие – то дополнительные ограничения, которые сформулированы «не очень ясно». Это прежде всего задачи. В которых решение уравнения надо искать в целых или натуральных числах, что в обычной школе не изучается.
2.1. Текстовые задачи и способы их решения.
2.1.1. Структура процесса решения задач
Внимание текстовым задачам уделяется в основном только до 9 класса, затем экзамен – на этом работа в школе с ними заканчивается. Поэтому все методические пособия, содержащие решение текстовых задач, адресуются учащимся 5 – 9 классов. И к 11 классу «хватка» уже потеряна. Поэтому, когда выпускников спрашивают, какие задачи вызывают у них затруднения, они единогласно отвечают, что текстовые и задачи с параметром. Для решения текстовых задач применяются три основных метода: арифметический, алгебраический и комбинированный. Рассмотрим каждый из этих методов.
Прежде выясним, в чем заключается процесс решения задачи.
Формулировка любой задачи состоит из нескольких утверждений и требований. Утверждения задачи называются условиями задачи. Первое что нужно сделать – это провести анализ задачи (это расчленить формулировку задачи на условия и требования). Результаты предварительного анализа задач надо зафиксировать, записать, т.е. сделать схематическую запись задачи. Анализ задачи и построение ее схематической записи (первый и второй этап процесса решения задачи) необходимо сделать для того, чтобы найти способ ее решения. Когда способ решения задачи найден (третий этап), его нужно осуществить, – это будет уже четвертый этап процесса решения – этап осуществления (изложения) решения. После того как решение осуществлено и изложено, необходимо убедиться, что это решение правильное, что оно удовлетворяет всем требованиям задачи. Для этого производят проверку решения, что составляет пятый этап процесса решения. При решении многих задач, кроме проверки, необходимо еще произвести исследование задачи, а именно установить, при каких условиях задача имеет решение и при этом сколько различных решений в каждом отдельном случае. Все это составляет шестой этап процесса решения.
Убедившись в правильности решения и, если нужно, произведя исследование задачи, необходимо сформулировать ответ задачи, – это будет седьмой этап процесса решения. Также полезно произвести анализ выполненного решения, в частности установить, нет ли другого, более рационального способа решения, нельзя ли задачу обобщить, какие выводы можно сделать из этого решения и т.д. все это составляет последний, но необязательный, восьмой этап решения.
И так процесс решения задачи можно разделить на восемь этапов:
- Анализ задачи;
- Схематическая запись;
- Поиск способа решения задачи;
- Осуществление решения задачи;
- Проверка решения задачи;
- Исследование задачи;
- Формулирование ответа задачи;
- Анализ решения задачи.
2.1.2 Способы решения текстовых задач.
В качестве основных в математике различают арифметические и алгебраические способы решения задач.
При арифметическом способе ответ на вопрос задачи находится в результате выполнения арифметических действий над числами. Решение текстовой задачи арифметическим способом – это сложная деятельность.
При алгебраическом способе ответ на вопрос задачи находится в результате составления и решения уравнения. В зависимости от выбора неизвестного для обозначения буквой, от хода рассуждений можно составить различные уравнения по одной и той же задаче. В этом случае можно говорить о различных алгебраических решениях этой задачи. Решение задач алгебраическим методом не подчиняется какой-либо единой, достаточно универсальной схеме. Поэтому всякое указание, относящееся ко всем задачам, носит самый общий характер. Задачи, которые возникают при решении практических и теоретических вопросов, имеют свои индивидуальные особенности. Поэтому их исследование и решение носят самый разнообразный характер.
2.1.3 Виды текстовых задач
Все арифметические задачи по числу действий, выполняемых для их решения, делятся на простые и составные.
Задача, для решения которой надо выполнить один раз арифметическое действие, называется простой.
Задача, для решения которой надо выполнить несколько действий называется составной. Составная задача включает в себя ряд простых задач, связанных между собой так, что искомые одних простых задач служат данными других. Решение составной задачи сводится к расчленению её на ряд простых задач и к последовательному их решению. Таким образом, для решения составной задачи надо установить систему связей между данными и искомыми, в соответствии с которой выбрать, а затем выполнить арифметические действия. Запись решения составной задачи с помощью составления по ней выражения позволяет сосредоточиться на логической стороне работы над задачей, видеть ход решения её в целом.
Среди всего многообразия задач можно выделить четыре большие группы
1. Задачи на движение.
2. Задачи на работу (на совместную работу).
3. Задачи на проценты и концентрацию.
4. Остальные…
2.2 Решение текстовых задач арифметическими и алгебраическими способами
2.2.1 Задачи на движение
Для успешного решения задач на движение нужно твёрдо держать в голове:
– формулу – ключ: s = v t;
– рисовать картинки и составлять таблицы,
Полезно напоминать учащимся, что: при одновременном движении пройденные расстояния прямо пропорциональны скоростям: s 1 / s 2 = v 1 / v 2; при движении на одно расстояние – времена обратно пропорциональны скоростям: , t 1/ t 2 = v 2 / v 1
При анализе условия задач на «движение» необходимо сразу выделять такие стандартные ситуации, как
- одновременное движение (встречное и в одном направлении);
- движение на одно расстояние;
- движение по течению или против течения реки;
- Задачи на движение протяженных тел;
- Задачи на движение по замкнутой трассе;
- Задачи на определение средней скорости движения.
Рассматривая классификацию задач на движение, необходимо отметить следующее. Различают простые и составные задачи на движение. Составные задачи на движение подразделяют на задачи на движение в одном направлении, задачи на сближение объектов, задачи на удаление объектов, задачи на движение по реке. В виду специфичности задач на движение для их решения удобно записывать данные условия в виде таблицы (скорость – время – расстояние) и использовать схемы, которые отражают процесс движения, а не отношения между величинами.
Отдельное внимание уделим решению составных задач на встречное движение и на противоположное движение.
После наглядного представления каждого из случаев необходимо использовать иллюстрации в виде чертежа, так как чертеж помогает правильно использовать, определять и представлять жизненную ситуацию, отраженную в задаче. При решении задач на встречное движение очень важно понимать, что если два тела вышли одновременно навстречу друг другу, то до встречи они будут в пути одинаковое время и пройдут все расстояние.
При решении задач на движение в противоположных направлениях необходимо помнить, что при таком движении расстояние между движущимися телами увеличивается.
Задачи на встречное движение двух тел.
Пусть движение первого тела характеризуется величинами s1, v1, t1; движение второго – s2, v2, t2.
Формулы: t1= t2= t встр., v сбл.= v1+ v2 , S= v сбл * tсбл..
Задачи на движение двух тел в одном направлении.
Среди них следует различать два типа задач:
1) движение начинается одновременно из разных пунктов;
2) движение начинается в разное время из одного пункта.
Формулы: v1 > v2, v сбл.= v1– v2, S = s1 – s2 и S = v сбл * tвстр.
Задачи на движение двух тел в противоположных направлениях.
В таких задачах два тела могут начинать движение в противоположных направлениях из одной точки:
1) одновременно;
2) в разное время.
А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время. Формулы: v удал. = v1+ v2,
Задачи на движение протяженных тел
В задачах на движение протяжных тел требуется определить длину одного из них. Наиболее типичные ситуации: определение длины поезда проезжающего мимо
- придорожного столба
- идущего параллельно путям пешехода
- лесополосы определенной длины
- другого двигающегося поезда
Если поезд движется мимо столба, то он проходит расстояние равное его длине.
Если поезд движется мимо протяженной лесополосы, то он проходит расстояние равное сумме длины самого поезда и лесополосы.
Задача 1 Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найти длину поезда в метрах.
Решение:
Зная скорость движения v = 60 км/ч = 1000 м/мин и время, за которое он проезжает мимо столба t = 30 сек. = 1/2 мин, можно найти длину поезда как пройденное расстояние s=v t=1000 * 1/2=500.
Ответ: 500м
Задача 2 Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо лесополосы, длина которого 800 метрам, за 1 минуту. Найти длину поезда в метрах.
Решение:
Зная скорость движения v = 90 км/ч = 1500 м/мин и время, за которое он проезжает мимо лесополосы длиной 800 метров за t = 1мин, можно найти длину поезда как пройденное расстояние s=v t=1500*1=1500 плюс длина лесополосы 800 метров и получим длину поезда равную 2300 метра.
Ответ: 2300 м
Задачи на движение по замкнутой трассе
Движение по замкнутой трассе (допустим по стадиону) похоже на движение вдогонку: если два бегуна начинают двигаться по окружности одновременно с разными скоростями v1, v2(v1 > v2 ), то первый бегун приближается ко второму бегуну со скоростью v1 − v2 и в момент, когда первый бегун догоняет второго бегуна, то первый бегун как раз проходит на один круг больше второго. И поэтому время считается так: t = S : (v1– v2 )
Задача Из одной точки круговой трассы, длина которой равна 16 км, в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч и через 40 минут после старта, он опережает второй автомобиль ровно на один круг. Найдите скорость второго автомобиля.
Решение:
Примем скорость второго автомобиля за x км/ч и учтем, что 40 минут составляют 2/3 часа, тогда 16 : ( 80−x )= 2/3 , 160−2x = 48, x=56.
Ответ: 56 км/ч.
Задачи на движение по воде.
Формулы: vпо т.= vс + vт. , vпрот. т.= vс – vт , vт.= vс – vпрот. т. , v т.= vпо т. – vс ,
vт.= (vпо т – vпрот. т. ) : 2 , vс.= vпо т – vт. , vс.= vпрот. т + vт, vс.= (vпо т. + v прот. т) ) : 2
Задача. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч.
Решение:
Х км/ч – скорость течения реки
|
Скорость, v Км/ч |
Время, t ч |
расстояние, s км |
|
|
По течению |
11 + Х |
112 / (11 + Х) |
112 |
|
Противтечения |
11 – Х |
112 / (11 – Х) |
112 |
Задачи на определение средней скорости движения.
Средняя скорость. Если S – путь пройденный телом, а t – время за которое этот путь пройден, то средняя скорость вычисляется по формуле: v = s : t.
Если путь состоит из нескольких участков, то для нахождения средней скорости на всем пути, надо весь пройденный путь разделить на сумму времени, затраченного на каждый участок пути.
Задача. Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути.
Решение:
Пусть весь путь равен 3S, тогда первую треть трассы велосипедист проехал за время –2s:12, вторую треть за время – s :16, последнюю треть за время – s:24. Значит время потраченное на весь путь находится так t=t1+t2+t3=s:12+s:16+s:24=9s :48,и поэтому средняя скорость вычисляется так v=3s:9s48 = 16 км/ч Ответ: 16 км/ч
1.Задача
Если Аня идёт в школу пешком, а обратно едет на автобусе, то всего на дорогу она тратит 1,5 ч. Если же она едет на автобусе в оба конца, то весь путь у неё занимает 30 мин. Сколько времени потратит Аня на дорогу, если и в школу и из школы она будет идти пешком?
Решение:
Путь в оба конца на автобусе занимает 30 мин, следовательно, путь в один конец на автобусе займёт 15 мин. На дорогу в один конец пешком понадобится 1,5 ч – 15 мин, т.е. 1 ч 15 мин. Значит, на дорогу пешком в оба конца Аня тратит 2, 5 ч.
2. Задача. Три бегуна — Антон, Серёжа и Толя — участвуют в беге на 100 м. Когда Антон финишировал, Серёжа находился в десяти метрах позади него, а когда финишировал Серёжа — Толя находился позади него в десяти метрах. На каком расстоянии друг от друга находились Толя и Антон, когда Антон финишировал? (Предполагается, что все мальчики бегут с постоянными, но, конечно, не равными скоростями.)
Решение:
Поскольку скорость Толи составляет 9/10 от скорости Серёжи, то к моменту, когда финишировал Антон, Толя пробежал 9/10 расстояния, преодолённого Серёжей, т.е. 90* 9/10 = 81 м. Значит, к этому моменту Толя отставал от Антона на (100 – 81) = 19 м.
Ответ: 19 м
4. Задача. Буратино сел в поезд. Проехав половину всего пути, он лёг спать и спал до тех пор, пока не осталось проехать половину того пути, который он проспал. Какую часть всего пути Буратино проехал бодрствующим?
Решение:
Обозначим через s отрезок пути, который Буратино проехал от того момента, как проснулся, до конца. Тогда путь, который Буратино проспал, составит 2s. Всего же от момента, как Буратино заснул, он проехал путь 2s + s = 3s. Но известно, что это — половина всего пути. Значит, длина всего пути 6s. Поскольку же бодрствующим Буратино проехал путь 4s, то по отношению ко всему пути эта часть составит 4 s/ 6s = 2/3.
Ответ: 2/3 пути.
5. Задача. Расстояние между Атосом и Арамисом, скачущими по одной дороге, равно 20 лье. За час Атос покрывает 4 лье, а Арамис — 5 лье. Какое расстояние будет между ними через час?
Решение:
Эта задача допускает четыре разных ответа, которые зависят от расположения всадников в первый момент. Мушкетёры могли ехать: а) в разные стороны, навстречу друг другу; б) в разные стороны, удаляясь друг от друга; в) в одну сторону — Атос за Арамисом; г) в одну сторону — Арамис за Атосом. Соответственно и ответы: а) 11 лье; б) 29 лье; в) 21 лье; г) 19 лье.
Ответ: а) 11 лье; б) 29 лье; в) 21 лье; г) 19 лье.
Варианты решения типовых задач повышенной трудности.
1. Задача. Из пункта А по реке отправился плот. Одновременно навстречу ему из пункта В, расположенного ниже по течению относительно пункта А, отправляется катер. Встретив плот, катер сразу поворачивает и идет вниз по течению. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде в 4 раза больше скорости течения реки?
Решение:
1 способ. Очевидно v 2 / v 1 = (4 v – v) / v = 3. К моменту встречи плот пройдет ¼ часть пути от А до В. Обратный путь катер пройдет быстрее в отношении
(4 v + v) / (4 v – v) = 5/3. А плот проплывет за это же время 3/5 первоначального пути:
3/5 * ¼ * АВ = 3/20 * АВ. Всего плот пройдет расстояние: 1/4АВ + 3/20АВ = 2/5АВ,т.е. 2/5 всего пути от А до В.
2 способ. Пусть время, необходимое плоту на весь путь от А до В равен 1. Тогда катеру, на путь от В до А потребуется 1/3, а обратно уже 1/5, в сумме 1/3 + 1/5 = 8/15 всего времени плота. Катер за все время проплыл ¾ всего пути туда и обратно между А и В, значит катер затратит 8/15 * ¾ = 2/5полного времени плота из А в В. Так как движение было одновременным, то плот за то же время проплыл 2/5 всего пути.
Ответ: 2/5.
2.2.2 Задачи на проценты
Задачи на проценты решаются путём составления пропорции. Напомним, что пропорция — это равенство двух отношений:
это разная форма записи.
Основное правило пропорции: произведение крайних членов равно произведению средних:
то есть a*b=c*d
Если какая-либо величина в пропорции неизвестна, ее можно найти именно по этому правилу. например, из пропорции:
Для кого-то будет удобным следующее правило. Его ещё называют «правило креста». Название этого правила исходит от пересечения диагоналей, они образуют крест:
Кроме того, можно обойтись без этого правила, и решать пропорцию как простое линейное уравнение:
Как видим результат тот же. Или такую пропорцию:
Для решения используйте тот способ, который вам удобен. Чтобы составить пропорцию при решении задач на проценты, необходимо установить некоторое соответствие между процентами и количеством чего-либо. По приведенным ниже примерам вы поймёте, что это значит.
Задача на проценты и покупки. До распродажи брюки стоили дешевле пиджака на 60% и дороже рубашки на 300%. В период распродажи цена пиджака снизилась на 20%, а цена брюк – на 25%. Витя купил пиджак и брюки во время распродажи. Сколько рубашек он мог купить на ту же сумму, если цена рубашки не изменилась?
|
Рубашка |
Брюки |
Пиджак |
|
|
Было |
x руб |
3x руб |
4.8x руб |
|
Стало |
x руб |
2.25x руб |
3.84x руб |
Брюки+пиджак= ? рубашек
Составим уравнение:
2,25x+3,84x=nx, n – количество рубашек
6,09x=nx
N = 6 то есть 6 рубашек.
Задача на проценты и покупки. Яблоки подешевели на 20%. Сколько яблок можно теперь купить на те же деньги, на которые раньше покупали 2,8 кг?
|
Цена за кг |
Масса |
Вся цена |
|
|
Было |
X руб |
2,8 кг |
2,8X руб |
|
Стало |
0,8X руб |
? кг |
2,8X руб |
Составим уравнение и решим его:
X=3,5 кг
Для решения задач базового уровня можно применять пропорцию для быстрого и более простого решения.
2.2.3. Задачи на работу
В задачах на работу речь идёт о какой-то деятельности. Трубы заполняют бассейн, комбайнёры убирают урожай, строители строят дом и так далее. В таких задачах всегда обыгрывается один и тот же набор величин. Величины связаны между собой и образуют формулу-ключ.
Первая величина в задачах на работу – время. Параметр простой и привычный. Это время, за которое выполняется та или иная работа.
Вторая величина – объём работы. Параметр, описывающий, сколько сделано деталей, налито воды, вспахано полей и так далее. Измеряется, соответственно, в тех единицах, о которых идёт речь в задаче. В деталях, литрах, полях и т.д.
Третья величина – производительность. По сути, это просто скорость работы.
Скорость любой работы (т.е. производительность) можно определить, как объём работы, сделанной за какое-то время. За единицу времени. (например: литры за час, табуретки за день, пирожки за минуту… )
Тогда получается формула для производительности:
Это и есть формула-ключ для решения любых задач на работу. Она очень похожа на формулу скорости в задачах на движение. В простых задачах на работу необходимо начинать с определения величин, входящих в формулу-ключ. Надо попытаться из условия задачи найти производительность, объём, время. Обычно этот первый шаг проясняет весь ход решения. В задачах “на совместный труд”, также используются величины: объём работы (если он неизвестен и не является искомым, то принимается за 1); время выполнения работы; скорость выполнения работы (производительность труда, т.е. объём работы, выполняемый за единицу времени).
Для решения таких задач необходимо:
1) Определить скорость работы (производительность труда) каждого объекта v1; v2; v3 …
2) Определить общую скорость выполнения работы vобщ.= v1 + v2 +…
3) Найти общее время совместной работы.
В задачах на совместный труд объём работы может быть известен, а может быть и нет. При составлении графических схем приходим к выводу, что схемы задач на производительность труда похожи на схемы задач на движение, в которых также участвуют три величины: υ; t; S. Таким образом, задачи на производительность труда и задачи на движение укладываются в одну схему:
ЦЕЛОЕ = МЕРКА КОЛИЧЕСТВО МЕРОК
В роли целого может выступать объём работы или расстояние. В качестве мерки – скорость движения или скорость работы (производительность труда). Третьим составляющим является время – количество мерок.
Задача на совместную работу. Четыре бригады должны разгрузить вагон с продуктами. Вторая, третья и четвертая бригады вместе могут выполнить эту работу за 4 час, первая, третья и четвертая – за 3 часа. Если же будут работать только первая и вторая бригады, то вагон будет разгружен за 6 часов. За какое время могут разгрузить вагон все четыре бригады, работая вместе?
Составим краткое условие:
|
U (производительность) |
t (время работы) |
V (объем) |
|
|
1 бригада |
1/X |
X часов |
1 |
|
2 бригада |
1/Y |
Y часов |
1 |
|
3 бригада |
1/Z |
Z часов |
1 |
|
4 бригада |
1/T |
T часов |
1 |
|
2 , 3 и 4 |
1/Y+1/Z+1/T |
4 часа |
1 |
|
1 ,3 и 4 |
1/X+1/Z+1/T |
3 часа |
1 |
|
1 и 2 |
1/X+1/Y |
6 часов |
1 |
|
1, 2 ,3 и 4 |
1/X+1/Y+1/Z+1/T |
а часов |
1 |
Составим систему уравнений:
Ответ: Все четыре бригады выполнят работу за 2 час и 40 минут.
Для решения задач на совместную работу необходимо знать производительность каждого участника задачи и уметь находить эту производительность.
2.2.4. Задачи на концентрацию.
Достаточно часто на экзамене предлагаются задачи на концентрацию, смеси, сплавы. Эти задачи вызывают трудности, связанные с нечетким пониманием химических процессов. Необходимо иметь в виду, что в задачах такого рода, предлагаемых на ОГЭ и ЕГЭ по математике, никаких химических процессов, влияющих на количественные соотношения задачи, не происходит.
Решать их можно разными способами. При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешении. При расчетах записывают одну над другой массовые доли растворенного вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
Задача на растворы: Один раствор содержит 20% кислот, а второй – 70% кислот. Сколько литров первого и второго раствора нужно взять, чтобы получить 100 л раствора с 50%-ным содержанием кислот?
Составим краткую запись:
Было:
20-ти % раствор – ? литров
70-ти % раствор – ?литров
Получили:
50-ти % раствор – 100 литров
Первый способ (алгебраический):
Решение: Пусть объем 20-ти % раствора V=X литров,
тогда объем 70-ти % раствора V =(100-X) литров
Составим уравнение и решим его:
0,2X+0,7(100-X)=0.5*100
X=40 (литров) первого раствора
100-40=60(литров) второго раствора
Используем условие и краткую запись предыдущей задачи
Второй способ (арифметический):
Используем метод креста из курса химии.
70 20
50
30 20
Объемы искомых веществ относятся как 2 к 3
Объем всего полученного раствора = 100 литров, который составляет 5 частей
Следовательно, V первого =40 литров ,а
Vвторого=60литров.
Таким образом текстовые задачи можно решать как алгебраическим, так и арифметическим способом. Каждый ученик должен выбрать самостоятельно тот способ, который более близок и понятен ему или который дает более рациональное решение.
2.2.4. Примеры задач ОГЭ и ЕГЭ
Задачи В1.
1. Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды? 2. Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
3. Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?
4. Налог на доходы составляет 13% от заработной платы. После удержания налога на доходы Марья Константиновна получила 9570 рублей. Сколько рублей составляет заработная плата Марьи Константиновны?
5. В городе N живет 200000 жителей. Среди них 15% детей и подростков. Среди взрослых 45% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?
Задачи В13 (на движение)
- Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 4 часа позже автомобилиста. Ответ дайте в км/ч.
- Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 70 км. На следующий день он отправился обратно со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
- Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
- Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.
- Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.
- Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, баржа отправилась назад и вернулась в пункт А в 16:00. Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.
- Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
- Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой? Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
- Поезд, двигаясь равномерно со скоростью 65 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 5 км/ч пешехода за 30 секунд. Найдите длину поезда в метрах.
Задачи В13 (на работу)
- Резервуар наполняется двумя насосами за 7,5 часов. Если включить только первый насос, то бассейн наполнится на 8 часов быстрее, чем при включении только второго насоса. За сколько часов заполняет резервуар второй насос?
- Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
- Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?
- Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров?
Задача В13. (на проценты, сплавы, растворы)
- В 2008 году в городском квартале проживало 40000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 8%, а в 2010 году — на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
- В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4 % дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
- Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20000 рублей, через два года был продан за 15842 рублей.
- Четыре рубашки дешевле куртки на 8%. На сколько процентов пять рубашек дороже куртки?
- Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
- В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
- Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
- Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
- Имеется два сплава. Первый сплав содержит 105 % никеля, второй —
30 % никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
3.Сложности при решении текстовых задач и пути их решения.
|
1.Составление математической модели |
|
|
непонимание физических, химических, экономических терминов, законов, зависимости |
Тщательно изучить и правильно истолковать содержание задачи, выразив искомые величины через известные величины и введенные переменные. Не зацикливаться на периодичности маршрута при движении по окружности, а мыслить только в категориях время, путь, скорость. |
|
непонимание связи между расстоянием, скоростью и временем при равномерном движении или между работой, производительностью труда и временем и т.п. |
|
|
затруднения в определении скорости сближения объектов при движении навстречу, в одном направлении или при движении по окружности |
|
|
2. Составление уравнений и неравенств, связывающих данные величины и переменные, которые вводят учащиеся |
|
|
неправильный выбор величин, относительно которых составляется уравнение |
Важно правильно выбрать величины, относительно которых будет составлено уравнение. Неправильный выбор делает процесс составления уравнения более сложным. |
|
усложнение процесса составления уравнения из-за неправильного выбора величин |
|
|
3. Нахождение соответствия между различными величинами, применительно к которым формулируется вопрос задачи. |
|
|
невозможность нахождения значения переменных, которые в уравнениях присутствуют и не являются необходимыми |
Держать в поле зрения основную цель, не боясь вводить столько вспомогательных переменных, сколько их понадобится по ходу решения. Совсем необязательно ставить в качестве непременного условия сведение числа неизвестных к минимуму. |
|
большое количество неизвестных, нахождение значения которых не являются необходимыми |
|
|
4. Решение уравнений, системы уравнений или невозможность решения уравнения, неравенства. |
|
|
Невозможно решения уравнения, неравенства или их системы |
Решение полученной системы уравнений или неравенств желательно наиболее рациональным методом. |
Заключение
В результате проведенных исследований удалось доказать правдивость гипотезы, что текстовые задачи можно решить алгебраическими и арифметическими способами по определенному алгоритму. Для того чтобы научиться решать задачи, надо приобрести опыт их решения путем многократного повторения операций, действий, составляющих предмет изучения. Редкие ученики самостоятельно приобретают такой опыт. Долг учителя – помочь учащимся приобрести опыт решения задач, научить их решать задачи. Помощь учителя не должна быть чрезмерной, но и не быть слишком малой. Причем для решения задач базового уровня необходимо применять простейшие пропорции, а для решения более сложных задач необходимо использовать уравнения, а также в задачах повышенного уровня сложности необходимо использовать смешенное решение с применением, как уравнения, так и пропорции. Материалы работы могут быть использованы для подготовки к государственной итоговой аттестации как выпускниками 9-х, 11-х классов, так и учителями на уроках, факультативах, индивидуальных консультациях.
Литература
- Бунимович Е.А., Кузнецова Л.В. и др. Экзамен в новой форме. Математика 2013: тренировочные варианты экзаменационных работ для проведения государственной итоговой аттестации в новой форме.-М.:АСТ:Астрель,2013.-94с.
- Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи, Москва «Просвящение» 1984. – 175.,ил.
- Лаппо Л.Д., Попов М.А. ГИА, 9 класс. Математика. Тематические тестовые задания. -М.: Издательство «Экзамен», 2013.-80с.
- Семенов А.В., Трепалин А.С. и др. Государственная итоговая аттестация выпускников 9 классов в новой форме: математика 2013.-М.:Интеллект-Центр, 2013.-88с.
- Шевкин А.В. Материалы курса «Обучение решению текстовых задач в 5-6 классах»: Методическое пособие для учителя. – 3-е изд., дораб. – М.: ООО «ТИД «Русское слово»-РС,2001.-208с.: ил.
- Ресурсы Internet: http://www.art-con.ru/node/3649. Методика решения задач на растворы с применением правила креста; http://www.bibliofond.ru/view.aspx?id=6032; Схематическое моделирование при обучении решению задач на движение; http://www.6yket.ru/index.html. Методика обучения школьников приемам решения текстовых арифметических задач; http://www.egesdam.ru/page242.php. Задачи на работу
Задачи по алгебре
Рассмотрим задачи на концентрацию, в которых речь идет о процентном содержании вещества в сплаве или растворе. В этом случае
Задачи на цену, количество, стоимость начинают изучать еще в курсе математики начальной школы. В курсе алгебры решение задач на цену, как правило, проводится с помощью систем уравнений. Рассмотрим, как решать задачи на цену, количество, стоимость, на конкретном примере.
Задачи на движение — один из самых распространенных видов задач алгебры. Простейшие задачи на движение изучаются еще в начальной школе. В 6-7 классах решение задач на движение сводится к линейному уравнению либо системе линейных уравнений. Здесь мы рассмотрим задачи на движение, которые можно решить с помощью дробного рационального уравнения.
Задачи на состав числа решают, как правило, с помощью системы уравнений. Если речь идет о двузначном числе, за x принимают количество десятков, за y — количество единиц числа. Тогда двузначное число равно 10x+y.
Рассмотрим типичные задачи на совместную работу из курса алгебры 8-9 классов. Решение таких задач начинается с того, что принимаем всю работу за единицу.
Задачи на работу связывают производительность труда, время работы и объем работы соотношением Рассмотрим типичные задачи на работу из курса алгебры 8-9 классов. Как и в задачах на планирование и грузоперевозки, условие многих задач на работу удобно оформлять с помощью таблицы, а решение — через систему уравнений. В этом случае решение сводится к квадратному уравнению, решить […]
Следующая страница »
УДК
51-3
Задачи на составление
уравнений с помощью таблиц
Оплачко О.В.
Муниципальное казенное
общеобразовательное учреждение средняя общеобразовательная школа №2
Аннотация. В
статье представлены различные типы решения задач на составление уравнений с
помощью таблиц, а именно, задачи на работу, на сплавы, на движение.
Ключевые слова:
математика, задачи через пусть х, табличный способ.
Tasks for composing equations using
tables
Oplachko O. V.
Municipal state educational
institution secondary school №2
Annotation.
The
article presents various types of solving problems for drawing up equations
using tables, namely, tasks for work, for alloys, for movement.
Keywords: mathematics,
problems through let x, tabular way.
Задачи
на составление уравнений встречаются в кимах ОГЭ, ЕГЭ, ВПР как по математике,
так и по другим предметам. Но многие из обучающихся не приступают к выполнению
данных заданий. Возникает вопрос, что вызывает трудность? Почему ребята не
решают такие задания и теряют баллы при поступлении? Каждому учителю
математики очень интересна данная проблема и пути её решения.
В
результате опроса среди обучающихся 5-11 классов были получены следующие
данные: более 30% учеников не могут перевести текст задачи на математический
язык, 53 % – не знают формул, которые помогают решить задачи на работу,
концентрацию и движение, 68% – не понимают, какое выражение больше, из какого выражения
нужно вычитать другое.
Таким
образом, целью исследования является выявление наиболее эффективного способа
решения задач на составление уравнений, который смогут освоить не только
отличники.
Рассмотрим
некоторые понятия, которыми будем пользоваться, при решении таких задач.
Уравнение
– это равенство, которое содержит в себе
переменную (переменные), значения которых требуется найти.
Корень
уравнения – это значение переменной, при
подстановке которого уравнение обращается в верное числовое равенство.
Решить
уравнение – значит найти все значения переменных,
входящих в него, которые обращают это уравнение в верное числовое равенство,
или установить, что данное уравнение решений не имеет.
Система
уравнений – это несколько уравнений, объединенных
фигурной скобкой, в которых одни и те же переменные обозначают одни и те же
числа.
Решением
системы уравнений является набор значений всех входящих
в него переменных, который обращает каждое уравнение системы в верное числовое
равенство.
Решить
систему уравнений – значит найти все её решения или
установить, что таких решений не существует.
Табличный
способ решения задач – это способ, который
заключается в построении таблицы, строки которой соответствуют элементам одного из рассматриваемых в
условии задачи множеств, столбцы — элементам другого, пересечение
строки и столбца — комбинации двух элементов разных множеств.
Решить
задачу – значит найти последовательность
понятий, формул, правил, которая приводит к ответу.
На
уроках алгебры, факультативах, внеурочных занятиях ребятам восьмых классов были
предложены различные способы решения данных задач. Лучше всех справились с
контрольной работой ученики того класса, с которыми был отработан табличный
метод. Более 73 % из тех, кто писал контрольную работу, смогли решить задачи.
85 % обучающихся этого класса правильно составили уравнение к условию задачи
(на ОГЭ заработали бы один из двух баллов). Среди этих 85 % были и те ученики,
у которых в четверти стоит тройка. Кроме того, как только с ребятами другого
класса был отработан этот же метод решения задач, качество знаний при написании
аналогичных вариантов контрольной работы выросло на 61 %.
Рассмотрим
некоторые примеры задач ОГЭ и ЕГЭ на составления уравнений, которые решим
табличным способом. При заполнении таблицы к каждой задаче нужно задавать
наводящие вопросы.
Задача
1. Катер прошёл 16 км по течению реки
и 30 км против течения, затратив на весь путь 1 час 30 мин.
Найдите собственную скорость катера, если скорость течения реки составляет
1км/ч [3, с. 198].
Перед
тем, как заполнить таблицу, ученикам было предложено решить данную задачу. С
данным заданием справились только 36 %. После одного разобранного примера
следующую задачу табличным методом решало 93% и справились с ней 68%
обучающихся.
Ученикам
задаются следующие наводящие вопросы: что нам известно? Что нужно найти? Что
обозначим за х? Каким выражением будем обозначать скорость по течению и против
течения? Чему равен путь по течению и против течения? Как выразить время через
скорость и путь? Какую вы знаете формулу? Как только ребята отвечают на
вопросы, параллельно заполняется таблица. С помощью такого метода обучающиеся
начинают рассуждать и понимают принцип решения задач.
Решение:
пусть х км/ч – собственная скорость
катера
|
v |
s |
t |
|
|
по течению |
х+1 |
16 |
|
|
против течения |
х-1 |
30 |
|
При решении данных задач нужно пояснять, что при нахождении
скорости против течения, необходимо из скорости катера вычитать скорость
течения реки.
Составим
и решим уравнение
Перенесем
из левой части уравнения
в правую с противоположным знаком, приведем дроби к общему знаменателю и
выполним арифметические действия.
Дробь
равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель
отличен от нуля
Умножим
первое уравнение на минус один, получим следующую систему:
не
удовлетворяет условию задачи, так как скорость не может быть отрицательным
числом.
Ответ:
31км/ч – собственная скорость катера.
Задача
2. Во дворе Николая Павловича расположен
бассейн, подача воды обеспечивается двумя насосами. Один из них, работая
самостоятельно, наполняет бассейн за 30 минут, а другой – за 20 минут. За
сколько минут оба насоса наполнят бассейн, работая одновременно [2, с. 53].
Решение:
в задачах на работу часто объём работы обозначают за
единицу, В – время, П – производительность, Р – работа.
В=Р:П,
Р=П*В, П=Р:В (1)
Перед
тем, как заполнить таблицу, ученикам было предложено решить данную задачу. С
данным заданием справились только 29 %. После одного разобранного примера
следующую задачу табличным методом решало 78% и справились с ней 52%
обучающихся.
Ученикам
задаются следующие наводящие вопросы: что нам известно? Что нужно найти? Какие
величины будем обозначать переменными? Чему равна в данном случае работа? Как
выразить время наполнения бассейна первого насоса, второго насоса, время их
совместной работы? Как только ребята отвечают на вопросы, параллельно
заполняется таблица.
|
П |
Р |
В |
|
|
Первый насос |
х |
1 |
30 |
|
Второй насос |
у |
1 |
20 |
|
Первый насос + второй |
х |
1 |
? |
Пользуясь формулами (1), выразим время работы первого, второго
насоса и их совместное время.
В
выражение вместо х и у подставим
выражения, полученные на предыдущем шаге
приведем дроби к общему
знаменателю, сложим их и выполним деление
Ответ:
за 12 минут оба насоса наполнят бассейн, работая
одновременно.
Задача
3. Имеются два сосуда, содержащие 25
кг и 21 кг раствора кислоты различной концентрации. Если их слить вместе, то
получим раствор, содержащий 39 % кислоты. Если же слить равные массы этих
растворов, то полученный раствор будет содержать 42 % кислоты. Сколько кг
кислоты содержится в первом растворе? [1, с. 88]
Решение:
Перед тем, как заполнить таблицу, ученикам было
предложено решить данную задачу. С данным заданием справились только 17 %.
После одного разобранного примера следующую задачу табличным методом решало 62%
и справились с ней 41% обучающихся.
Ученикам
задаются следующие наводящие вопросы: что нам известно? Что нужно найти? Какие
величины будем обозначать переменными? Чему равны массы первого, второго
раствора, их совместная масса? Как найти массу кислоты для каждого из данных
случаев? Как только ребята отвечают на вопросы, параллельно заполняется
таблица.
|
mр-ра |
% |
mкислоты |
|
|
1 |
25 |
а |
25а*0,01 |
|
2 |
21 |
в |
21в*0,01 |
|
1 |
25+21=46 |
39 |
0,39*46 |
|
Равные |
|||
|
1 раствор |
1 |
а |
1*а*0,01 |
|
2 |
1 |
в |
1*в*0,01 |
|
1 |
1+1 |
42 |
0,42*2 |
Составим и решим систему уравнений
Умножим
оба уравнения системы на 100, чтобы избавиться от десятичных дробей
Выразим из второго
уравнения системы переменную а через переменную в и подставим во второе
уравнение
Раскроем скобки во втором
уравнении системы, приведем подобные слагаемые, найдем значения переменных и а
(кг) кислоты в 1
растворе.
Ответ:
1,875 кг
В
заключение следует отметить, что табличный способ решения задач позволяет
структурировать текстовую информацию, является более наглядным и понятным для
многих учеников, позволяет оформить задачу более компактно, не требует
написания большого текста и экономит время, что является немаловажным фактом на
экзаменах. Кроме того, исследование показало, что табличный метод позволил
повысить процент правильности выполнения данных задач, а именно, задачи на
движение – на 32 % , задачи на работу – на 23 % , задачи на смеси и сплавы –
на 24%.
Список
литературу
1)
Лысенко Ф.Ф. Математика. 9-й класс.
Подготовка к ОГЭ – 2021. 40 тренировочных вариантов по демоверсии 2021 года:
учебно-методическое пособие / под ред. Ф.Ф. Лысенко, С.О. Иванова. – Ростов н /Д.:Легион,2020.-384
с.
2)
Лысенко Ф.Ф. Математика. Подготовка к ЕГЭ
– 2021. 40 тренировочных вариантов по демоверсии 2021 года: учебно-методическое
пособие / под ред. Ф.Ф. Лысенко, С.О. Иванова. – Ростов н /Д.:Легион,2020.-400
с.
3)
Мерзляк А.Г. Алгебра: 8 класс: учебник для
учащихся общеобразовательных учреждений / А.Г. Мерзляк, В..Полонский, М.С.
Якир. – М:Вентана –Граф, 2013. – 256 с.
|
ФИО |
Оплачко |
|
Ученая |
Нет |
|
Должность |
Учитель |
|
Муниципальное |
Город |
|
|
olia.tsimbalova@yandex.ru |
|
Телефон |
8-952-559-60-33 |
|
Адрес |
397853, |