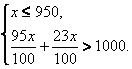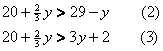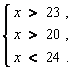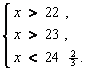Как составить задачи на неравенства

1. Неравенства первой степени с одним
неизвестным

Решим задачу.

Задача 1. От деревни до
железнодорожной станции 20 км. Поезд уходит со
станции в 11 часов. В каком часу человеку, живущему
в деревне, надо выйти из дома, чтобы успеть на
поезд, если он будет идти со скоростью 5 км/ч?

Решение. Если пешеход выйдет из дома в х
ч. Утра, то до 11 ч. он шёл бы (11 – х) ч. За это
время он прошёл бы 5(11 – х) км. Чтобы он успел
на поезд, надо, чтобы это расстояние было не
меньше 20 км, т. е. должно выполняться неравенство
5(11 – х) > 20. Рассуждаем так. Найдём, в
каком часу человек должен выйти, чтобы в точности
успеть на поезд. Для этого должно выполняться
равенство 5(11 – х) = 20. Решая это уравнение,
получаем (11 – х) = 4 и потому х = 7. Значит,
выйдя из дома в 7 часов утра, пешеход успеет на
поезд. Тем более он успеет на него, выйдя из дома
ещё раньше. А если он выйдет из дома позднее, то
опоздает на поезд. Значит, чтобы успеть на поезд
нужно выйти не позднее чем в 7 часов утра. На языке
математики это значит, что решение неравенства
5(11 – х) > 20 имеет вид х < 7.

Задача 2. В одном бассейне налито 100
литров воды, а во втором – 150 литров воды. Каждый
час в первый бассейн вливается 15 литров воды, а во
второй – 5 литров. В какие моменты времени в
первом бассейне будет больше воды, чем во втором?

Решение: За х часов в первый бассейн
вольётся 15х л. воды и в нём станет (100 + 15х)
л. воды. Так же находим, что через х ч. во
втором бассейне будет (150 + 5х)л. воды. Надо
найти такие значения х, для которого
выполняется неравенство (100 + 15х) > (150 + 5х),
т.е. решить неравенство с переменной х.
Это неравенство решается так (15х – 5х)
> (150 – 100), Т.е. 10х > 50. Но если 10х > 50,
то х > 5. Итак в первом бассейне окажется
больше воды, чем во втором, при х > 5, т.е.
после 5 ч. с начала вливания воды.

2. Системы неравенств с одним
неизвестным

Решим следующую задачу.

Задача 3. Человек выехал в 6 ч. утра на
автомашине из города А в город В, через
город С. В городе С он должен взять по
дороге пакет, привезённый на поезде, проходящем
через город С в 10 ч, и отвезти его в город В,
чтобы успеть на поезд, отходящий в 17 часов. С
какой скоростью он должен ехать, если расстояние
от А до С равно 400 КМ., а от С до В
– 480 км?

Решение. Т.к. в город С автомобилист
должен приехать не ранее 10 часов (до этого
времени пакет ещё не привезён в С), а 10 – 6 = 4,
то скорость х км/ч должна быть такой,
что 4х < 400. С другой стороны, за 17 – 6 = 11
ч, он должен приехать в В, т.е. покрыть путь в
400 + 480 = 880 (км). Поэтому должно выполняться
неравенство 11х > 880. Итак надо найти
значение х, для которого выполняются оба
неравенства 4х < 400 и 11х > 880.
Эту задачу записывают в виде системы неравенств:

Из первого неравенства находим, что х <
100, а из второго, что х > 80. Значит, должно
выполнятся двойное неравенство 80 < х <
100.

Ответ: 80 < х < 100, т.е. х
принадлежит отрезку [80;100].

Задача 4. Производительность первого
автомобильного завода не превышает 950 машин в
сутки. Производительность второго завода
первоначально составляла 95% от
производительности первого завода. После ввода
дополнительной линии второй завод увеличил
производство машин в сутки на 23% от числа машин,
выпускаемых в сутки на первом заводе, и стал их
выпускать более 1000 штук в сутки. Сколько
автомобилей за сутки выпускал каждый завод до
реконструкции второго завода? Предполагается,
что каждый завод в сутки выпускает целое число
машин.

Решение: Обозначим через х количество
машин, производимых в сутки первым заводом. Тогда
второй завод до реконструкции производил в сутки
 машин, а после
ввода дополнительной линии стал выпускать машин. Из условия
задачи следует система неравенств:

Множество решений этой системы есть промежуток
, т. к. числа и должны быть
целыми, то х должно делиться на 100 и быть из
указанного промежутка, поэтому х = 900.
Следовательно I завод выпускает в сутки 900
автомобилей, а II завод до реконструкции выпускал автомобилей.

Ответ: 900 и 885.

Задача 5. Партию деталей решили
поровну разложить по ящикам, сначала в каждый
ящик положили по 12 деталей, но при этом осталась
одна деталь. Тогда из одного ящика вынули все
детали, и в оставшиеся ящики удалось разложить
все детали поровну. Сколько деталей было в
партии, если в каждый ящик помещается не более 20
деталей.
Решение. Пусть n – число ящиков, в
каждый из которых первоначально положили по 12
деталей. Тогда общее число деталей равно (12n +
1). Так как из одного ящика все детали изъяли, а
затем поровну разложили их в оставшиеся (n –
1) ящики, то в каждый ящик было положено (12n + 1)
/ (n – 1) деталей. Отношение (12n + 1) / (n
– 1) должно удовлетворять двум условиям:

1) оно должно быть целым положительным числом,
2) оно не должно превосходить 20.
Поскольку ,
последнее выражение может быть натуральным при n
 = 2 и n = 14.Но при , и это значение не является подходящим.
При n = 14 условия 1) и 2) выполняются. Таким
образом, в партии было 12•14 + 1 = 169 деталей.

Ответ: 169.

3. Неравенства и системы неравенств с
двумя неизвестными

Решим следующую задачу.

Задача 6. Цена 1 м сатина 2000р., а цена 1 м
капрона 4000 р. Сколько метров сатина и сколько
метров капрона можно купить, чтобы общая цена
покупки была не более 20000 рублей?

Решение. Обозначим число метров сатина
через х, а число метров капрона через у,
тогда общая стоимость покупки равна (2000х + 4000у)
рублей. По условию задачи должно выполняться
неравенство  2000х + 4000у = 20000.  При
этом числа х и у должны быть
неотрицательными. Обе части данного неравенства
можно разделить на 2000. Таким образом, чтобы
решить задачу, нужно сначала решить неравенство х
+ 2у < 10, а потом отобрать из этих решений
неотрицательное. Неравенство х + 2у <
10 имеет бесконечно много решение. Например, можно
взять х = 0, у = 0, или х = 1, у = 2,
или х = 5, у = 2 и, конечно,   х = 6, у
= –9. При всех этих значениях х и у
выполняется неравенство х + 2у < 10.
Итак, из неравенства двумя неизвестными (как и из
одного уравнения с двумя неизвестными) нельзя
найти значения этих неизвестных. Можно только
дать наглядное представление о совокупности
всех решений этого неравенства. С этой целью
заметим, что неравенства х + 2у < 10
имеет те же решения, что и неравенство у <
5 – 0,5х (перенесли х в правую часть с
переменной знака и разделили обе части
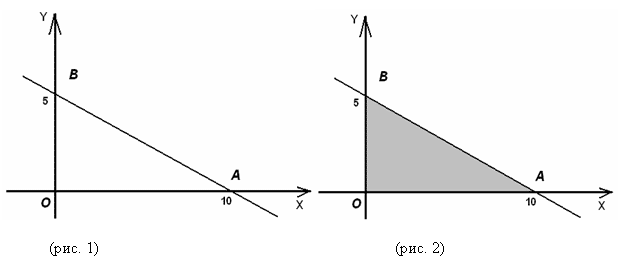
неравенства на 2). Уравнение у = 5 – 0,5х задаёт
прямую АВ (рис. 1). Выше этой прямой выполняется
неравенство у < 5 – 0,5х, поэтому нестрогое
неравенство у < 5 – 0,5х
изображается множеством, состоящим из всех точек
прямой АВ и всех точек, лежащих ниже этой прямой.
Это множество на рисунке 1 заштриховано.
Мы отмечали, что числа х и у должны быть
неотрицательными. Но неотрицательные координаты
имеют точки первой четверти, поэтому решение
задач изображается найденного множества и
первой четверти, т.е. треугольником АОВ (рис. 2).
Вообще, чтобы изобразить наглядно решение
какого-нибудь неравенства знаком равенства и
начертить линию, имеющую полученное уравнение.
Эта линия делит плоскость. С каждой части следует
выбрать пробную точку и подставить её координаты
в неравенство. Если получится верное числовое
неравенство, то вся часть, содержащая данную
точку, принадлежит решению (граница части – лишь
в случае, когда неравенство нестрогое!).
Объединяя все такие части, получаем наглядное
изображение решения неравенства.

 Задача 7. (МИФИ, 1976 г.). Найдите все
двузначные числа, удовлетворяющие следующим
условиям: сумма цифр числа не менее 7; сумма
квадратов цифр не более 30; число, записанное теми
же цифрами, но в обратном порядке, по крайней
мере, вдвое меньше данного.
Решение. Запишем искомое число в виде 10х +
у, где х – цифра в разряде десятков, у
– цифра в разряде единиц. По условию задачи

х + y > 7,      
                                           (1)
х² + у² < 30,
                                            (2)
10х + y > 2(10у + х). или 8х
> 19у.        (3)

Из (3) следует, что у может принимать
значения 0, 1, 2, 3 (так как х < 9).Если у =
0, то из (1) следует, что х > 7. Эти числа не
удовлетворяют неравенству (2). Если у =  l,
то из (1) следует, что х > 6. Эти числа не
удовлетворяют неравенству (2). Если у = 2, то х
> 5. Числа х = 5, у = 2 удовлетворяют
всем неравенствам. При у = 2, х > 5
неравенство (2) не выполняется. Пусть у = 3. Из
(3) следует х > 8, такие числа не удовлетворяют
неравенству (2). Таким образом, больше решений нет.

Ответ: 52.

Задача 8. В двух ящиках находится более
29 одинаковых деталей. Число деталей в первом
ящике, уменьшенное на 2, более чем в три раза
превышает число деталей во втором ящике.
Утроенное число деталей в первом ящике превышает
удвоенное число деталей во втором ящике менее
чем на 60. Сколько деталей в каждом ящике?

Решение: Обозначим через х число
деталей в первом ящике, а через у число
деталей во втором ящике. Тогда согласно условию
имеет место система неравенств:

 

Перепишем эту систему в виде

Отсюда следуют, справедливые неравенства:

Неравенство (2) можно переписать в виде , а неравенство (3) в
виде

Т. к. и у –
натуральное число, то у может быть равен
либо 6, либо 7.

Если у равен 6, то система неравенств (1)
перепишется в виде

Ясно, что нет натуральных чисел х,
удовлетворяющих ей. Пусть у = 7, тогда система
(1) примет вид:

Откуда следует, что существует единственное
натуральное число х = 24, удовлетворяющее ей.
Следовательно, в первом ящике 24 детали, а во
втором ящике 7 деталей.
Ответ: в I ящике 24 детали, а во II – 7 деталей.

Задача 9. Пункты А и В
расположены на одному реке так, что плот плывущий
от А до В со скоростью течения реки,
проходит путь от А до В за 24 часа. Весь
путь от А до В и обратно катер проходит
не менее чем за 10 часов. Если бы собственная
скорость (скорость в стоячей воде) катера
увеличилась на 40 %, то тот же путь (от А до В
и обратно) занял у катера не более 7 часов. Найдите
время, за которое катер проходит путь из В в А,
когда его собственная скорость не увеличена.

Решение. Пусть s – расстояние между
пунктами А и В, u – собственная
скорость катера, v – скорость течения. Имеем
следующую систему уравнений и неравенств:

Надо определить  и полагая (по смыслу задачи, х > 1),
преобразуем неравенства:

 

Так как и х
> 1, то после преобразования получим систему
неравенств, эквивалентную исходной: 5х²
– 24х – 5 < 0, 1,96х² – 9,6х –
1 > 0. Эта система совместна при х = 5.
Далее, получаем:

Ответ: 6.

Общие задачи:

Задача 10. Груз вначале погрузили в
вагоны вместимостью по 80 тонн, но один вагон
оказался загружен не полностью. Тогда весь груз
переложили в вагоны вместимостью 60 тонн, однако
понадобилось на восемь вагонов больше, и при этом
всё равно один вагон остался не полностью
загруженным. Наконец, груз переложили в вагоны
вместимостью по 50 тонн, однако понадобилось ещё
на пять вагонов больше, при этом все такие вагоны
были загружены полностью. Сколько тонн груза
было?

Решение. Обозначим через n количество
вагонов вместимостью 50 тонн, в которые был
загружен весь груз, тогда вес груза = 50п тонн.
Вагонов вместимостью 60 тонн было использовано (n
– 5). Так как в них был помещён весь груз и один
вагон оказался не полностью загруженным, то 60 • (п
– 5) > 50п и 60 • (п – 6) < 50п. Из этих
неравенств следует, что 300 < 10п < 360 или 30 <
n < 36. Поскольку n – целое число, то 31 <
n < 35. Вагонов вместимостью 80 тонн при
погрузке было использовано(n – 13) . Подобно
предыдущему получаем, что 80 • (п – 13) > 50п
и 80 • (п – 14) < 50n или . Так как , а n – целое число, то 35 <
n < 37. Из 31 < n < 35 и 35 <
n < 37 следует, что n = 35. Значит, вес
груза = 50 • 35 = 1750 тонн.

Ответ: 1750 тонн.

Задача 11. В школьной газете
сообщается, что процент учеников некоторого
класса, повысивших успеваемость во II полугодии,
заключён в пределах от 2.9% до 3.1%. Определить
минимальное число учеников в таком классе.

Решение. Пусть n – число учеников в
таком классе, о котором сообщают в газете, m – число
учеников этого класса, повысивших успеваемость,
тогда про цент учеников, повысивших
успеваемость, равен 100. По условию задачи (1)

Из равенства (1) следует, что т m =/= 0 (т.е. m
> 1) и.
Поскольку очевидно, что , то n > 33. Итак, в классе о
котором сообщается в газете, учеников не меньше,
чем 33. Теперь надо выяснить, какое минимальное
количество учеников всё-таки может быть в классе.
Легко видеть, что если в классе будет 33 ученика и
один из них повысит успеваемость, т.е. если n =
33 и m = 1, то такая пара чисел удовлетворяет
неравенство (1). Значит, в классе, о котором
сообщается в газете, минимально возможное число
учеников 33.

Ответ: 33 учеников.

Задача 12. Все коробки какие есть на
базе, имеют одинаковые площади оснований.
Грузчики хотят поместить в один контейнер с той
же площадью основания 20 коробок. Какой высоты
должен быть контейнер. Если высоты коробок
оцениваются неравенствами 29 см < h < 32
см?

Решение. 29 • 20 < 20h < 31 • 20, т. е. 580 <
20h < 620.
Допустим, все плоские коробки имеют минимальную
высоту 29 мм. Тогда все они поместятся в коробке
высотой 580 см. но если найдётся хоть одна коробка
большей высоты, то затея грузчиков провалится. В
реальности очень часто бывает, что минимальный и
максимальный размеры колеблются в заданных
допусках. А если мы хотим быть уверенным, что 20
коробок действительно всегда поместятся в
контейнер, то надо считать, будто все коробки
имеют максимальную высоту, т. е. выбрать
контейнер высотой 620 см. Это и будет убедительным
доводом в пользу затеи грузчиков.

Ответ: 620 см.

Литература.

1. Говоров В.М., Дыбов П.Т., Мирошин Н.В.,
Смирнова С.Ф. Сборник конкурсных задач по
математике (с методическими указаниями и
решениями). – М.: Наука, Главная редакция Физико-математической
литературы, 1983. с 8–9.
2. Дорофеев Г.В. Потапов Н.К. Розов Н.Х. Пособие
по математике для поступающих ВУЗы. Издательство
«Наука» главная редакция Физико-математической
литературы 1976. с 146–150.
3. Савин А.П. Энциклопедический словарь юного
математика – 3-е издание, испр. и доп. Москва:
Педагогика-Пресс, 1999. с 213–214.
4. Фролова ИЛ. Методика изучения приложений
неравенств в курсе математики средней школы.
Автореферат канд. дис .. М., 1982.
5. Фирсов В.В. О прикладной ориентации курса
математики. В кн.: Углубленное изучение алгебры и
анализа: Пособие для учителей/ Составитель. С.И.Шварцбурд,
О.А.Боковнев.-М.: Просвещение, 1977.
6. Потапов М.К. Олехник С.Н., Нестеренко Ю.В.
Конкурсные задачи по математике: Справочное
пособие – М.: Наука. Гл. ред. физ.-мат. лит., 1992. – 480
с.

Решение задач при помощи неравенств

Категория: Математика.

Задачи на составление уравнений и неравенств занимают важное место в школьном курсе математики. Решение их способствует развитию логического мышления, сообразительности и наблюдательности, развивает умение самостоятельно осуществлять небольшие исследования. Задачи, связанные с неравенствами, бывают двух видов:

• задачи на сравнение двух выражений;
• задачи, которые решаются с помощью неравенств, систем неравенств, систем неравенств и уравнений.

Эти задачи необходимо начинать решать уже в восьмом классе. Предлагаемые примеры задач собраны из разных источников и предназначены для школьников и педагогов, любящих решать задачи вообще, и для использования на уроках и факультативных занятиях.

Задачи с решением

Задача 1.

Самолет пролетел путь от А до В по ветру и путь от В до А против ветра, причем скорость ветра не менялась. В другой раз самолет совершил рейс по тому же маршруту в безветренную погоду. В обоих случаях моторы самолета развивали одинаковую мощность. В каком случае на весь полет ушло меньше времени?

Решение.

Ответ. В безветренную погоду.

Задача 2.

Два туриста вышли из пункта А в пункт В. Первый турист половину затраченного времени от начала движения шел со скоростью V₁, затем со скоростью V₂. Второй же турист первую половину пути шел со скоростью V₁, а вторую половину со скоростью V₂. Кто из них затратил меньше времени на прохождение пути от А до В?

Решение.

Ответ. Первый турист затратил времени меньше.

Задача 3.

Туристы отправились на моторной лодке по течению реки и должны вернуться обратно к стоянке не позднее чем через 3 часа. На какое расстояние могут отъехать туристы, если скорость течения реки 2 км/ч, а скорость в стоячей воде 18 км/ч?

Решение.

Ответ. Не больше чем на 26 и две третьих км.

Задача 4.

На соревнованиях каждый стрелок делал 10 выстрелов. За каждое попадание он получал 5 очков, за каждый промах с него снимали одно очко. Успешным считалось выступление, при котором стрелок получал не менее 30 очков. Сколько раз стрелок должен попасть в мишень, чтобы его выступление было сочтено успешным?

Решение.

Ответ. 7, 8, 9 или 10 раз.

Задача 5.

Со склада вывозят железные болванки массой по 500 кг и медные массой 200 кг. На грузовик, который может везти не более 4 тонн, погрузили 12 болванок. Сколько среди них может быть железных болванок?

Решение.

Ответ. Не более 5 болванок.

Задача 6.

Турист на байдарке проплыл по течению реки 6 км, тут же повернул обратно и проплыл против течения реки 4 км. С какой собственной скоростью должен плыть турист, чтобы на все путешествие затратить не более часа, если скорость реки равна 2 км/ч?

Решение.

Ответ. Не менее 10 км/ч

Задача 7.

Около дома посажены липы и березы, причем общее их количество более 14. если увеличить вдвое количество лип, а количество берез на 18, то берез станет больше. Если увеличить вдвое количество берез, не меняя количество лип, то лип все равно будет больше. Сколько лип и сколько берез было посажено?

Решение.

Ответ. 11 лип, 5 берез.

Задача 8.

Группа студентов решила купить цветок ценой от 170 до 195 рублей. Однако в последний момент двое отказались участвовать в покупке, поэтому каждому из оставшихся пришлось внести на 1 руб. больше. Сколько стоил цветок?

Решение.

Ответ. 180 рублей.

Задача 9.

Лодка спускается по течению реки на расстояние 10 км, а затем поднимается против течения на расстояние 6 км. Скорость течения реки равна 1 км/ч. В каких пределах должна быть собственная скорость лодки, чтобы вся поездка заняла от 3 до 4 часов.

Решение.

Ответ: 

Задача 10.

Школьник переклеивает все свои марки в новый альбом. Если он наклеит по 20 марок на один лист, то ему не хватит альбома, а если по 23 марки на лист, то по крайней мере один лист окажется пустым. Если школьнику подарить такой же альбом, на каждом листе которого наклеено по 21 марке, то всего у него станет 500 марок. Сколько листов в альбоме?

Решение.

Ответ. 12 листов.

Задача 11.

Пункты А и В расположены на одной реке так, что плот, плывущий из А в В со скоростью течения реки, проходит от А до В за 24 часа. Весь путь от А до В и обратно катер проходит не менее чем за 10 часов. Если бы собственная скорость катера увеличилась на 40%, то тот же путь (от А до В и обратно) занял бы у катера не более 7 часов. Найдите время, за которое катер проходит путь от В в А, когда его собственная скорость не увеличена.

Решение.

Ответ: 6 часов.

Задачи для самостоятельного решения с ответами

Задача 1.

Расстояние между станциями А и В равно 360 км. В одно и то же время из А и В навстречу друг другу выходят два поезда. Поезд, отправившийся из А, прибывает на станцию В не ранее чем через 5 часов. Если бы его скорость была в 1,5 раза больше, чем на самом деле, то он встретил бы второй поезд раньше, чем через два часа после своего выхода из А. Скорость какого поезда больше?

Ответ. Скорость поезда, вышедшего из В, больше.

Задача 2.

Из пункта А в пункт С в 9 часов утра отправился скорый поезд. В это же время из пункта В, расположенного между пунктами А и С, выходят два пассажирских поезда, первый из которых следует в пункт А, а второй – в пункт С. Причем, скорости пассажирских поездов равны. Скорый поезд встречает первый пассажирский поезд не позже чем через 3 часа после его отправления, потом приходит в пункт В не ранее 14 часов того же дня и, наконец, прибывает в пункт С одновременно с первым пассажирским поездом. Найти время прибытия в пункт А первого пассажирского поезда.

Ответ. 16 ч 30 мин.

Задача 3.

Из А в В по течению реки плывет плот. Одновременно с тем, когда плот начал путь из А в В, из В в А навстречу ему поплыла лодка, которая встречает плот не ранее чем через 2 ч и затем прибывает в А, затратив на весь путь менее 3 ч 20 мин. Успеет ли плот преодолеть путь из А в В за 5 ч, если расстояние между А и В равно 20 км?

Ответ. Не успеет.

Задача 4.

Квартал застроен пятиэтажными и девятиэтажными домами, причем девятиэтажных домов меньше, чем пятиэтажных. Если число девятиэтажных домов увеличить вдвое, то общее число домов станет более 24, а если увеличить вдвое число пятиэтажных домов, то общее число домов станет менее 27. сколько построено пятиэтажных домов и сколько девятиэтажных?

Ответ. 9 пятиэтажных и 8 девятиэтажных.

Задача 5.

Пункты А и В расположены на одной реке так, что плот, плывущий из А в В со скоростью течения реки, проходит путь от А до В за 24 часа. Весь путь от А до В и обратно моторная лодка проходит не менее чем за 10 ч. если бы собственная скорость моторной лодки увеличилась на 40% , то тот же путь (т.е. путь от А до В и обратно) занял бы у лодки не более 7 ч. Найти время, за которое моторная лодка проходит путь от А до В в случае, когда ее собственная скорость не увеличена.

Ответ. За 4 ч.

Задача 6.

В 9 ч утра из пункта А выезжает велосипедист, который едет до пункта В. Через 2 ч после выезда велосипедиста из А в В выезжает автомобилист, который догоняет велосипедиста не позже 12 ч дня. Продолжая движение, автомобилист прибывает в пункт В, мгновенно поворачивает и едет из В в А. На этом пути автомобилист встречает велосипедиста и потом прибывает в пункт А в 17 ч того же дня. Найти время прибытия велосипедиста в пункт В , если известно, что между двумя встречами велосипедиста и автомобилиста прошло не более 3 ч.

Ответ. 18 ч.

Задача 7.

От пристани А вниз по реке, скорость течения которой равна V км/ч, отходит плот. Через час вслед за ним выходит катер, скорость которого в стоячей воде равна 10 км/ч. догнав плот, катер возвращается обратно. Определить все те значения V ,при которых к моменту возвращения катера в А плот проходит более 15 км.

Ответ. 5 < V< 10

Задача 8.

Расстояние между А и В равно7 км. Два пешехода одновременно вышли навстречу друг другу и встретились раньше чем через 1 час, если бы первый шел вдвое быстрее, чем он шел на самом деле, а скорость движения второго была бы на 2 км/ч больше его фактической скорости, то к моменту встречи второй прошел бы большую часть пути. Скорость какого пешехода больше?

Ответ. Скорость второго пешехода больше.

Задача 9.

Из пунктов А и В, расстояние между которыми 120 км, одновременно друг другу навстречу выезжают два велосипедиста и встречаются позже, чем через 5 ч после выезда. На следующий день они выезжают навстречу одновременно в одну и ту же сторону из пунктов С и D, расстояние между которыми 36 км, причем велосипедист, едущий впереди, движется со скоростью, на 6 км/ч больше, чем накануне, а велосипедист, едущий сзади, движется с той же скоростью, что и накануне. Хватит ли второму велосипедисту двух часов, чтобы догнать первого?

Ответ. Не хватит.

Задача 10.

Из города А в город В, находящийся на расстоянии 105 км от А, с постоянной скоростью V км/ч выходит автобус. Через 30 мин вслед за ним из А со скоростью 40 км/ч выезжает автомобиль, который, догнав в пути автобус, поворачивает обратно и движется с прежней скоростью. Определить все те значения V, при которых автомобиль возвращается в город А позже, чем автобус приходит в город В.

Ответ. 30 < V < 33,6

Метки: Математика

Для многих математических вычислений, как в математическом анализе, так и в дискретной математике полезно знать ограничения, накладываемые на некоторые функции и величины. Например, для программистов полезно разбираться в алгоритмах. А значит нужно определять верхние и нижние границы поведения каких-либо выражений. В этой заметке поговорим о неравенствах, которые встречаются в школьной математике.

Ох уж эти странные средние…

Задача 0. Среднее арифметическое двух положительных чисел всегда больше либо равно их среднему геометрическому (простейшая форма неравенства Коши)

Проще всего будет рассмотреть случай для двух переменных. Для наглядности нужно начинать с простого. Это можно доказать аналитически. Представим, что есть два неотрицательных числа a и b, обоснуем, что их среднее арифметическое всегда больше их среднего геометрического.

Данное неравенство можно доказать и геометрически. Получается довольно красиво. Если построить окружность диаметром a + b, тогда радиус R будет как раз совпадать со средним арифметическим чисел. Если же взять на окружности любую точку и построить к ней высоту h, а также учесть подобие треугольников (розового и желтого по рисунку), то данная высота будет средним геометрическим. А по рисунку видно, что для любой точки высота h не сможет превысить радиус R. Что и требовалось доказать.

Конечно же одним частным случаем нельзя ограничиваться. Наше неравенство о среднем арифметическом и среднем геометрическом принадлежит к целому блоку, который называется…

Неравенства о средних или неравенства Коши

Допустим, все числа отсортированы по возрастанию, тогда получается, что: x₁ = min(x₁, x₂, …, xₙ) и xₙ = max(x₁, x₂, …, xₙ)

Доказательство того, что среднее арифметическое больше либо равно среднего геометрического для чисел, количество которых является степенью 2

Доказательство можно провести также через индукцию

Доказательство с шагом индукции -1 (индуктивное доказательство вниз)

Мы доказали, что если наше наше неравенство верно для n = k, то неравество также выполняется для всех четных значениях n = 2k и для всех предыдущих значениях n = k – 1. А это значит, что неравенство Коши соотношение среднего арифметического и среднего геометрического верно для всех n. Аналогично (по индукции) можно доказать и другие соотношения.

Практика решения задач

Теперь давайте порешаем задачи с интересными школьными неравенствами.

Задача 1. Простейшее, но популярное соотношение

Доказать, что t + 1/t ⩾ 2 для любого положительного t > 0

Задача 2. Интересное практическое задание из учебника по алгебре для 8 класса:

Доказать справедливость неравенства (a + b)(b + c)(a + c) ⩾ 8•a•b•c

Данное неравенство можно также доказать, используя неравенство Коши:

Задача 3. Неравенство на базе геометрии треугольника

Докажите нервенство P/a + P/b + P/c ⩾ 9, где a, b, c – стороны и P – периметр треугольника.

Решение:

Задача 4. Еще одна задачка, использующая доказанное нами ранее неравенство

Доказать, что a⋅b⋅(a + b – 2⋅c) + b⋅c⋅(b + c – 2⋅a) + a⋅c⋅(a + c – 2⋅b) > 0, где a>0, b>0, c>0.

Задача 5. Надо что-нибудь поинтереснее, например, со степенями..

Доказать, что если a + b = 1, то имеет место неравенство a⁸ + b⁸ ⩾ 1/128

Задача 6. Что больше exp(e)×π^π или exp(2π) ? Хороший вопрос, не правда ли? Так сразу и не скажешь 🙂

Задача 7. А что если у нас будут логарифмы и суммы с неизвестным количеством слагаемых? Это вас напугает? 🙂

Доказать, что lg(n+1) > (lg1 + lg2 + … +lgn) / n

Задача 8. Еще немного сумм и факториалов в неравенствах…

Докажите, что для любого натурального числа n выполняется неравенство: 1/1! + 1/2! + 1/3! +…+ 1/n! ≤ (2n-1)/n

Задача 9.

Пусть a₁² , a₂² , a₃² ,…, an² — квадраты n различных натуральных чисел. Докажите, что (1-a₁²)⋅(1- a₂²)⋅(1 – a₃²)⋅…⋅(1 – an²) > 1/2

Задача 10. Типичная олимпиадная задача, когда числа совпадают с годом олимпиады…

Доказать, что 2013^2015 ⋅ 2015^2013 < 2014^(2⋅2014)

Задача 11. Рассмотрим кое-что посложнее?

Даны положительные числа a₁ , a₂ , a₃ ,…, an. Известно, что их сумма меньше либо равна 1/2. Докажите, что (1+a₁)⋅(1+a₂)⋅(1+a₃)⋅…⋅(1+an)<2

Заметим, что данную задачу можно решить методом математической индукции (попробуйте сделать это самостоятельно, можете написать в комментариях решение). А еще стоит обратить внимание на то, как часто используется геометрическая прогрессия для анализа рядов, неравенств, последовательностей, а следовательно и алгоритмов дискретной математики. Кто-то еще сомневается, что школьная математика не нужна программистам? 🙂 Разве что тем программистам, которые старательно избегают собственной реализации алгоритмов и не хотят исследовать теорию.

Задача 12. И последняя задача по неравенствам на сегодня. Доказать неравенство Бернулли:
( 1 + a )ⁿ ⩾ 1 + n⋅a , где a > -1 , n – натуральное число.

Задачи для самостоятельного решения

На этом закончу данную статью. Надеюсь, что Вам было интересно! Если да, то проявите активность комментариях!

Понравилась заметка ? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram

автор: Лобанова Людмила Викторовна

учитель математики МБОУ СОШ №2 Барабинского района Новосибирской области

«Текстовые задачи на решение неравенств и их систем в целых числах»

Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа №2 Барабинского района Новосибирской области

Исследовательская работа по математике

«Текстовые задачи на решение неравенств

 и их систем в целых числах»

Выполнила:

ученица 8 «б» класса

Семениченко Алина

Руководитель:

учитель математики 

высшей квалификационной категории

Лобанова Людмила Викторовна

                     Содержание:

1. Цель и задачи……………………………………………..стр. 3
2. Введение…………………………………………………..стр. 4
3. Виды и методы решения задач…………………………..стр. 5-8
4. Практическая часть………………………………………..стр. 9-11
5. Примеры задач из сборника по подготовке к ЕГЭ………стр. 12
6. Заключение…………………………………………………стр. 13
7. Литература…………………………………………………стр. 14

Цель и задачи:

Цель:  рассмотреть решение текстовых задач с помощью неравенств в целых числах.

Задачи:

– закрепить умения и навыки решать неравенства и системы неравенств;

– разобрать некоторые нестандартные приемы решения задач;

– научиться различать, видеть основные приемы, подходы решения неравенств и систем и применять их в традиционных и нетрадиционных примерах и задачах;

– воспитывать чувство уверенности в себе, своих силах.

Введение.

В задачах на составление уравнений и неравенств,  их называют ещё текстовыми задачами, как правило, речь идёт о конкретных ситуациях из практической деятельности. Известно, что исторически долгое время математические знания передавались из поколения в поколение в виде списка задач практического содержания вместе с их решениями. При  решении задач выписываются соотношения, представляющие собой математическую модель описанной в задаче практической ситуации. Таким образом, текстовые задачи позволяют проверить не только навыки в решении уравнений и неравенств, но и умение описывать с помощью математических соотношений реальные события. Решение таких задач способствует развитию логического мышления, умению самостоятельно проводить небольшие исследования. Этим и объясняется тот факт, что задачи на составление уравнений и неравенств являются непременным элементом вариантов вступительных экзаменов.

Виды и методы решения задач

Текстовая задача — это описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения.

Текстовые задачи отличаются большим разнообразием содержания и могут существенно различаться по уровню сложности. Стандартные текстовые задачи, в которых условия записываются в виде уравнений, число которых равно числу неизвестных, обычно не вызывают особых затруднений, хотя и здесь могут встретиться непредвиденные сложности. Что же касается «нестандартных» по содержанию задач, то при их решении часто возникают трудности, объяснимые именно их непривычностью, необходимостью анализировать, рассуждать, а не просто формально решать системы уравнений или неравенств.

Все текстовые задачи по методике решения можно подразделить на основные виды:

– текстовые задачи группы vts (задачи на движение, на производительность, на цену – количество, стоимость, на перевозку груза и заполнение ёмкостей);

– процентносодержащие текстовые задачи и задачи на доли (задачи на проценты и доли, задачи с экономическим содержанием);

– текстовые задачи на прогрессии (применение формул арифметической и геометрической прогрессий и свойств этих последовательностей);

– текстовые задачи на целые числа (использование кратности чисел и запись чисел через сумму поразрядных произведений и через неполное частное и остаток);

– текстовые задачи на оптимизацию (решение задач с помощью неравенств и элементов математического анализа).

Методика алгебраического способа решения текстовых задач (с помощью уравнений и неравенств).  

 Основные моменты:

Этап	Цель	Форма записи
1.Арифметическая краткая запись условий задачи.	Осмысление задачи.	Схематический чертёж или таблица всех известных и неизвестных данных задачи
2. Алгебраическая краткая запись условий задачи.	Удачно выбрать переменную и выразить все неизвестные величины задачи через неё.	такая, как и на 1этапе, но только вместо знаков “?” везде записать выражения с переменной.
3.Составление и решение уравнения или неравенства (системы уравнений или неравенств).	Опираясь на условия задачи составить уравнение или неравенство ( систему уравнений или неравенств ) и найти его (её) решение.	Уравнение или неравенство, система уравнений или неравенств.
4.Анализ решения уравнения или неравенства (системы уравнений или неравенств).	Из всех найденных решений уравнений или неравенств (систем уравнений или неравенств) выбрать те, которые подходят по смыслу задачи и, по мере необходимости, довычислить искомую величину.	Провести проверку  решения, причём проверять нужно соответствие полученного ответа условию задачи, а не составленным уравнениям.
5.Ответ.	Записать правильный ответ, удовлетворяющий всем описанным условиям задачи и отвечающий на её “главный вопрос”.

Немного остановлюсь подробнее на этапах:

1 этап. Арифметическая краткая запись условий задачи.

Важно помнить: этот этап может отсутствовать, если решение задачи элементарно или она не особо усложнена условиями. На этом этапе решения задачи происходит понимание или осмысление её текста. Намного облегчает этот процесс умение правильно “увязать” все известные и неизвестные величины в таблицу данных задачи или составить чертёж. Неизвестные величины удобно обозначать знаком “?”, а “главный вопрос” задачи для того, чтобы потом на последних этапах не запутаться и правильно найти “Ответ”, так как в некоторых задачах, содержащих неявный вопрос искомую величину приходится довычислять.

Значительно облегчает решение и делает задачу более понятной введение обозначений, общепринятых в физике, химии, геометрии, алгебре, экономике и так далее. Например: V,t,s-скорость, время, расстояние (длина пути или отрезка); р,V,m-плотность вещества, объём тела, масса тела; W,t,V–производительность, время работы, объём работы; a,b,P,S–две стороны прямоугольника, его периметр, его площадь; А0,р,n,An-первоначальная величина, процент её увеличения, количество увеличений, конечная величина после увеличения А0 на р процентов n раз; MА,СА,M–масса вещества А в растворе или в смеси, концентрация вещества А в растворе или смеси (доля), масса раствора или смеси; mn=10m+n–запись двузначного числа, где m,n–цифры.

Схематический чертёж оказывает большую помощь в задачах “на движение”. Он позволяет увидеть динамику движения, а также учесть все характерные ситуации–встречи, остановки, повороты и тому подобное.

2 этап. Алгебраическая краткая запись условий задачи.

Обычно, этот этап в оформлении задачи начинается с фразы “Пусть х ед.-…,тогда…”,

не следует пытаться обойтись небольшим числом неизвестных. Наоборот, чем больше неизвестных, тем легче составлять уравнения или неравенства.

Выбирая неизвестные, мы создаём математическую модель ситуации, описанной в условии задачи, точнее, набор переменных представляет собой список параметров, определяющих эту модель, поэтому все они должны быть независимы, и все соотношения должны следовать лишь из конкретных условий задачи.

При введении переменных, следует руководствоваться принципом наибольшего удобства математической записи условий задачи, при этом искомая величина может не входить в их число. Часто имеет место ситуация, когда составленная по условию задачи система уравнений не позволяет однозначно определить неизвестные, однако, искомая величина, являющаяся некоторой комбинацией введенных неизвестных, находится однозначно. В большинстве задач “главный вопрос” подсказывает выбор переменной.

3 этап. Составление и решение уравнения или неравенства (системы уравнений или неравенств).

Обычно этот этап в оформлении задачи начинается словами “По условию задачи (выписать условия из текста задачи), значит,…(запись уравнения или неравенства).”

 При составлении математической модели необходимо учитывать ОДЗ переменной (переменных) помня условия существования уравнения или неравенства (системы уравнений или неравенств). Для составления уравнения или неравенства (системы уравнений или неравенств) из текста задачи выбираем условие (условия), которое позволяет увязать известные и неизвестные данные задачи в формулы: S=vt-вычисление длины пути, пройденного телом; m=pV-вычисление массы тела; V=Wt-вычисление объёма работы; S=ab–вычисление площади прямоугольника.

В простейших ситуациях мы получаем уравнение (неравенство) с одной переменной или систему уравнений (неравенств), в которой число уравнений (неравенств) совпадает с числом неизвестных. Но, если число уравнений (неравенств) оказалось меньше числа неизвестных и при этом использованы все условия задачи, то надо попытаться выразить то, что нужно найти, через введенные неизвестные. В корректной задаче, если все условия использованы, то нужное неизвестное или нужная комбинация неизвестных обязательно найдётся.

4 этап. Анализ решения уравнения или неравенства (системы уравнений или неравенств).

Обычно этот этап в оформлении задачи начинается фразой “По смыслу задачи х, должна быть величиной… (натуральной, положительной, целой, принадлежащей промежутку и так далее), (проверка на выполнение условий задачи по смыслу найденного значения переменной)=>(значение х) –постороннее решение ( если смысловое условие не выполнено) или (значение х)–(записать пояснение к найденной величине, если смысловое условие выполнено).”

Не каждое решение уравнения может являться решением задачи. Для любой текстовой задачи полезно провести проверку её решения, причём проверять нужно соответствие полученного ответа условию задачи, а не составленным уравнениям.

Практическая часть.

ЗАДАЧА 1.

Прибывших на парад солдат планировали построить так, чтобы в каждом ряду стояло по 24 человека. Но в действительности не все прибывшие смогли участвовать в параде, и их перестроили так, что число рядов стало на 2 меньше, а число человек в ряду на 26 больше нового числа рядов. Если бы все солдаты участвовали в параде, то их можно было бы построить так, чтобы число рядов было равно числу человек в ряду. Сколько солдат прибыло на парад?

РЕШЕНИЕ:

Пусть первоначально предполагаемое число рядов- n, тогда число прибывших солдат равно 24n. После перестроения число рядов стало равным n-2, а число человек в ряду – соответственно n+24. Очевидно, что число солдат после перестроения явно меньше числа прибывших первоначально. Итак, число прибывших: 24n; число солдат после перестроения (n-2)*(n+24). Составим неравенство: 24n >(n-2)*(n+24)

 Получили: n2 – 2n – 48< 0

D=196, n1=8; n2= -6, n ϵ (0;8), n=1;2;3;4;5;6;7

Решая его, получаем, что число рядов лежит в интервале (-6;8). Число рядов может быть целым и положительным. Следовательно, круг решений ограничен от 1 до 7. Учитывая, что число человек в ряду, после перестроения, рано числу рядов,

 т.е. x2=24n,x= 2. Единственное число, удовлетворяющее этому условию  n=6, а соответствующее число солдат равно 144.

Ответ: 144

ЗАДАЧА 2.

Бригады рабочих получали спецодежду со склада по 2 комплекта на каждого человека. Каждая бригада получала на 20 комплектов больше, чем было бригад. Если бы бригад было на 4 больше и каждой выдавали по 12 комплектов, то одежды на всех не хватило бы. Сколько комплектов спецодежды было на складе?

РЕШЕНИЕ: Пусть было x бригад и n рабочих в каждой бригаде. Тогда число комплектов на каждую бригаду будет 2n, что на 20 больше, чем число бригад, т.е. 2n=x+20.

Если бы бригад было x+4, и каждая получила по 12 комплектов, то общее количество спецодежды было бы 12(x+4) и превысило бы их количество на складе: 12*(x+4) > 2nx . 

Это равносильно неравенству: 12*(x+4)>x*(x+20) 

X2+8x-48<0

D=256, x1=-12, x2=4, x ϵ (-12;4)

Условию задачи удовлетворяют лишь три числа: 1,2,3.

Далее из 2n=x+20 получаем, что x= 2n – 20, т.е. x – четное число, т.е. бригад 2 штуки. Итак, 2n – 20 =2, n=11, а число комплектов спецодежды будет равно 2nx= 2*11*2 = 44.

Ответ: 44.

ЗАДАЧА 3.

Токарю необходимо сделать 90 деталей, а ученику – 35. Первые 30 деталей токарь делал с производительностью, вдвое большей, производительности ученика. Остальные 60 деталей он делал, повысив производительность ещё на 2 детали. Токарь свою работу закончит не раньше ученика, чем на 1 час. Однако, если бы токарь и первые 30 деталей делал с такой же производительностью, как оставшиеся 60, то он закончил бы работу не раньше чем через 30 минут после ученика. Какова производительность ученика?

РЕШЕНИЕ:

 За x дет/ч примем производительность ученика. Тогда ученик затратил времени ч.  Первые 30 деталей токарь делал с производительностью 2x , а остальные 60 с производительностью (2x+2),т.е. он затратил времени + ч. По условию, токарь свою работу закончит не раньше ученика, чем на 1 час. Известно, что при производительности (2x+2) на 90 деталей токарь закончит работу не раньше, чем через 30 минут после ученика.   Получим систему неравенств:

  + – ≥ 1 ;

     – ≥

Условию удовлетворяет единственное значение x = 5.           Ответ: 5.

ЗАДАЧА 4.

Планы выплат. За выполнение малярных работ, Эрику может быть выплачена заработная плата одним из двух способов:

План A: $250 плюс $10 в час; 

План B: $20 в час.

В каком из случаев выгоднее воспользоваться планом выплат A или B.

РЕШЕНИЕ:

Предположим, что работа занимает n часов. Для каких значений n план B лучше для Эрика?  Предположим, что работа отнимет 20 часов. Тогда n = 20, и согласно плану A, Эрик заработает $250 + $10.20, или $250 + $200, или $450. Его заработок согласно плану B составит $20.20, или $400. Это показывает, что план A лучше для Эрика, если он будет работать 20 часов. Подобным образом, если он будет работать 30 часов, тогда n= 30, и согласно плану A, Эрик заработает $250 + $10.30, или $250 + $300, или $550. При плане B, он заработает $20.30, или $600, поэтому план B лучше в этом смысле.

 Чтобы определить все значения n, для которых план B является лучшим для Эрика, составим и решим неравенство. 

20n > 250 + 10n

10n > 250

n > 25

 Проверка. 

Для n = 25 выплаты согласно плану A составят: $250 + $10.25, или $250 + $250, или $500, и выплаты согласно плану B составят $20.25, или $500. То есть, для работы длительностью менее 25 часов, доход одинаков для каждого плана в разделе Понимание задачи мы видели, что согласно плану B выплаты больше для работы, которая занимает больше 30-и часов. Так как 30 > 25, это обеспечивает частичную проверку результата, но мы не можем проверить все значения n.

 Вывод: 

Для значений n, больше чем 25 часов, план B является лучшим.

Примеры задач из сборника по подготовке к ЕГЭ.

ЗАДАЧА 1.

Высота над землей подброшенного вверх мяча меняется по закону h(t)=1+11t-5t2 ,

где h- высота в метрах, t- время в секундах, прошедшее с момента броска.

Сколько секунд мяч будет находиться на высоте не менее 3 метров?

РЕШЕНИЕ:

Составим и решим неравенство:

1+11t-5t2 ≥3

-5t2+11t+1-3≥0

-5t2+11t -2≥0

-5t2+11t -2=0

D=81, D>0, 2 действительных корня: t1=0,2 ; t2 =2; tϵ [0,2;2].  Для ответа на вопрос необходимо найти ∆t.  ∆t=2-0,2=1,8

Ответ: 1,8

ЗАДАЧА 2.

Зависимость объема спроса q (тыс. руб.) на продукцию предприятия-монополиста от цены p (тыс.руб.) задается формулой q=85-5p . Выручка предприятия за месяц r (в тыс.руб.) вычисляется по формуле r(p) = q*p. Определите наибольшую цену p , при которой месячная выручка r(p) составит не менее 300 тыс.руб. Ответ приведите в тыс.рублей.

РЕШЕНИЕ:

Составим и решим неравенство: (85-5p)p≥300

-5p2 +85p-300≥0

-5p2 +85p-300=0

D=49, D>0, 2 действительных корня:p1 =5; p2 =12; pϵ [5;12]. Наибольшая цена p=12.

Ответ: 12

Заключение:

Решение задач занимает в математическом образовании огромное место. Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала.

Задачи выполняют очень важную функцию в курсе математики — они являются полезным средством развития  логического мышления, умения проводить анализ и синтез, обобщать, абстрагировать и конкретизировать, раскрывать связи, существующие между рассматриваемыми явлениями.

Считаю, что поставленной цели: рассмотреть решения текстовых задач с помощью неравенств, добилась.

В ходе работы закрепила умения и навыки решать неравенства и системы неравенств, разобрала некоторые нестандартные приемы решения задач. Убедилась, что решение задач способствует воспитанию терпения, настойчивости, воли. В процессе работы я расширила рамки школьной программы и испытала чувство удовлетворенности от приложенного труда.

Литература:

1. Бродский И.Л., Видус А.М. , Коротаев А.Б. Сборник текстовых задач по математике для профильных классов.- М.: АРКТИ, 2004
2. Иванов М.А. Математика без репетитора. 800 задач с ответами и решениями для абитуриентов Учебное пособие. – М.: Издательский центр «Вентана – Граф», 2002г.
3. Лурье М.В., Александров Б.И.  Задачи на составление уравнений. Учебное руководство. – М.: Наука. Главная редакция физико-математической литературы, 1990г.
4. Садовничий Ю.В. Математика. Конкурсные задачи по алгебре с решениями. Часть 6. Решение текстовых задач. (серия < В помощь абитуриенту>). Учебное пособие.- 3-е изд., стер. – М.: Издательский отдел УНЦ ДО, 2003г. 
5. Семёнов А.Л., Ященко И.В. Математика: типовые экзаменационные варианты. М .-Издательство «Национальное образование», 2013.

Тезисы к работе «Текстовые задачи на решение неравенств и их систем в целых числах».

Цель:  рассмотреть решение текстовых задач с помощью неравенств в целых числах. Задачи: закрепить умения и навыки решать неравенства и системы неравенств;  разобрать некоторые нестандартные приемы решения задач; научиться различать, видеть основные приемы, подходы решения неравенств и систем и применять их в традиционных и нетрадиционных примерах и задачах; воспитывать чувство уверенности в себе, своих силах.

В задачах на составление уравнений и неравенств,  как правило, речь идёт о конкретных ситуациях из практической деятельности. Известно, что исторически долгое время математические знания передавались из поколения в поколение в виде списка задач практического содержания вместе с их решениями. 

Решение таких задач способствует развитию логического мышления, умению самостоятельно проводить небольшие исследования. Этим и объясняется тот факт, что задачи на составление уравнений и неравенств являются непременным элементом вариантов вступительных экзаменов.

Текстовая задача — это описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения.

Текстовые задачи отличаются большим разнообразием содержания и могут существенно различаться по уровню сложности. 

Решение задач занимает в математическом образовании огромное место. Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала.

Для успешной сдачи ГИА и ЕГЭ необходимо внимательно разобрать и глубоко усвоить теоретический материал, получить твердые и прочные навыки в решении задач. Залог успеха на экзаменах – систематическая самостоятельная работа в течение всего оставшегося до экзаменов времени. Математику нельзя выучить за день или за неделю – только планомерные длительные занятия сделают экзаменационные задачи и вопросы простыми и легкими. И хотя предлагаемая вашему вниманию статья не может заменить учебник, она должна помочь устранить некоторые пробелы в знаниях и предостережет вас от возможных ошибок.

1. При решении задач, в которых используются процентные соотношения, важно правильно определить количество, принимаемое за 100%.

Пример 1.

За смену двое рабочих изготовили вместе 72 детали. После того, как первый рабочий повысил производительность труда на 15%, а второй – на 25%, они вдвоем изготовили 86 деталей. Сколько деталей за смену стал изготавливать каждый рабочий после повышения производительности труда?

Неправильное решение.

Введем обозначения. Пусть x – число деталей, изготавливаемых за смену первым рабочим после повышения производительности труда, а y – число деталей, изготавливаемых за смену вторым рабочим после повышения производительности труда.

Тогда (x – 0,15x) – число деталей, изготавливаемых за смену первым рабочим до повышения производительности труда; (y – 0,25y) – число деталей, изготавливаемых за смену вторым рабочим до повышения производительности труда.

Решаем систему уравнений:

{x + y = 86,
{0,85x + 0,75y = 72. 

Имеем:

{x = 75,
{y = 11.

Неправильный ответ: (75; 11).

Правильное решение.

Введем обозначения: x – число деталей, изготавливаемых за смену первым рабочим до повышения производительности труда; y – число деталей, изготавливаемых за смену вторым рабочим до повышения производительности труда.

Тогда: (x + 0,15x) – число деталей, изготавливаемых за смену первым рабочим после повышения производительности труда; (y + 0,25y) – число деталей, изготавливаемых за смену вторым рабочим после повышения производительности труда.

Решаем систему уравнений:

{x + y = 72,
{1,15x + 1,25y = 86.

Имеем:

{x = 40,
{y = 32.

Следовательно,

{1,15x = 46.
{1,25y = 40.

Правильный ответ: (46; 40).

2. При решении задач, в которых используются отношения частей, важно правильно определить количество, принимаемое за единицу.

Пример 2.

Имеется два сплава золота и серебра. В первом сплаве количество этих металлов находится в отношении 2 : 3, а во втором – 3 : 7. В каком отношении нужно взять указанные сплавы, чтобы получить новый сплав, в котором золото и серебро были бы в отношении 5 : 11?

Правильное решение.

Введем обозначения:

x – необходимое количество первого сплава;

y – необходимое количество второго сплава.

Из условия следует, что в первом сплаве 2/5 части золота и 3/5 части серебра, а во втором сплаве – 3/10 части золота и 7/10 части серебра. Тогда в новом сплаве будет (2/5 x + 3/10 y) золота и (3/5 x + 7/10 y) серебра. Следовательно,

(2/5 x + 3/10 y) : (3/5 x + 7/10 y) = 5 : 11.

После упрощения получим, что 7x = y или x/y = 1/7.

Правильный ответ: 1/7.

3.

Пример 3.

Расстояние между городами А и В равно 100 км. Из А в В отправляются одновременно два автомобиля. Скорость первого автомобиля на 10 км/ч больше скорости второго, и в пути он делает остановку на 50 мин. В каких пределах может меняться скорость первого автомобиля при условии, что он прибывает в город В не позже второго автомобиля?

Правильное решение.

Введем обозначения:

x км/ч – скорость первого автомобиля, тогда (x – 10) км/ч – скорость второго автомобиля.

100/(x – 10) ч – время, в течение которого второй автомобиль находится в пути, а (100/x + 5/6) ч – время, в течение которого первый автомобиль находится в пути.

Из условия следует, что

(100/x + 5/6) ≤ 100/(x – 10). После упрощения получим:

(x² – 10x – 1200) / (x(x – 10)) ≤ 0.

В итоге имеем: x > 0 и 10 < x ≤ 40.

Правильный ответ: (10; 40].

4.

Пример 4.

По двум улицам к перекрестку движутся две машины с постоянными скоростями 50 км/ч и 60 км/ч. Считая, что улицы пересекаются под прямым углом, и зная, что в некоторый момент времени машины находятся на расстоянии соответственно 2 км и 3 км от перекрестка, установите, через какое время расстояние между ними будет наименьшим.

Правильное решение.

Через x часов расстояние между машинами будет  S = √((3 – 60x²) + (2 – 50x²)) (рис. 1). Требуется найти x, при котором данное выражение достигает минимума. Так как то же самое x  доставляет минимум выражению

S₁(x) = (3 – 60x²) + (2 – 50x²), найдем его минимум из уравнения

S₁‘(x) = 0 или ((3 – 60x²) + (2 – 50x²))’ = 0, откуда

610x = 28, x = 14/305.

Правильный ответ: x = 14/305 ч.

5.

Пример 5.

Сумма цифр двузначного числа равна 12. Если к искомому числу прибавить 36, то получим число, записанное с помощью тех же цифр, но расположенных уже в обратном порядку. Найдите это число.

Правильное решение.

Пусть xy – искомое число (x – первая цифра, y – вторая цифра). Тогда xy  = 10x + y.

Согласно условию, x + y = 12 и xy + 36 = 10x + y + 36 = yx = 10y + x.

Таким образом, получили систему уравнений:

{ x + y = 12,
{ 9x – 9y = -36.

Решая данную систему, получим, что x = 4 и y = 8.

Правильный ответ: Исходное число 48.

Запомните, самостоятельное решение даже одной задачи принесет гораздо больше пользы, чем разбор готовых решений пусть и нескольких задач. Поэтому всегда пытайтесь решить пример самостоятельно, а только потом, в случае необходимости, воспользуйтесь указанием или разберите правильное решение задачи, если оно у вас имеется.

Остались вопросы? Не знаете, как решать задачи?
Чтобы получить помощь репетитора – зарегистрируйтесь.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.