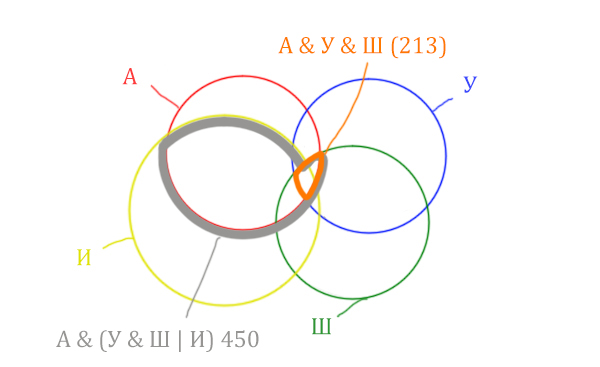Пояснительная записка
Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.
В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.
Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.
Основные понятия
Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.
Пересечение множеств в теории множеств – это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.
Круги Эйлера – геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.
2. Решение задач с помощью кругов Эйлера
2.1. “Обитаемый остров” и “Стиляги”
Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Решение:
Чертим два множества таким образом:
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.
1. 15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров»,
2. 11- 6 = 5 – человек, которые смотрели только «Стиляги».
Получаем:
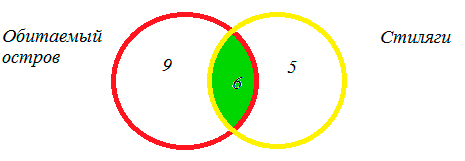
Ответ: 5 человек.
2.2. Задача про библиотеки
Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.
Сколько шестиклассников:
- Являются читателями обеих библиотек;
- Не являются читателями районной библиотеки;
- Не являются читателями школьной библиотеки;
- Являются читателями только районной библиотеки;
- Являются читателями только школьной библиотеки?
Решение:
Чертим два множества таким образом:
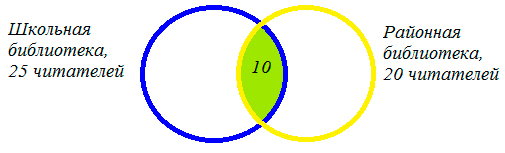
1) 20+ 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
2) 35 – 20 = 15 (человек) – не являются читателями районной библиотеки,
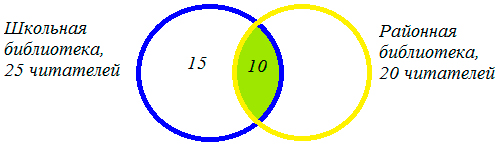
3) 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки,
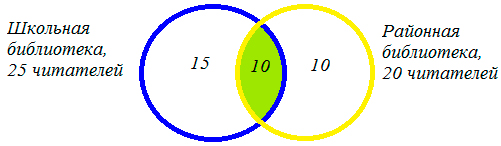
4) 35- 20 = 10 (человек) – являются читателями только районной библиотеки,
5) 35- 20 = 15 (человек) – являются читателями только школьной библиотеки.
Очевидно, что вопросы 2 и 5, а также 3 и 4 – равнозначны и ответы на них совпадают.
Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.
2.3. Гарри Поттер, Рон и Гермиона
На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
Решение:
Учитывая условия задачи, сделаем чертеж:
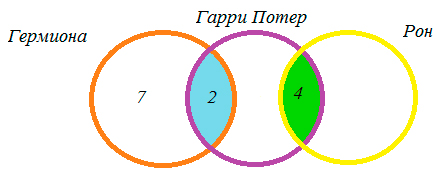
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри.
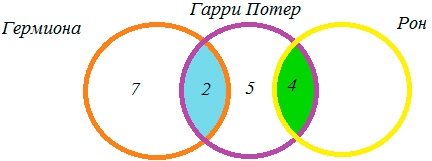
Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон.

Ответ: 8 книг.
2.4. Задача про любимые мультфильмы
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым – «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Решение:
Чертим три круга, таким образом:
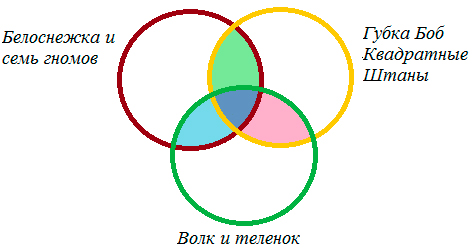
Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым – «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.
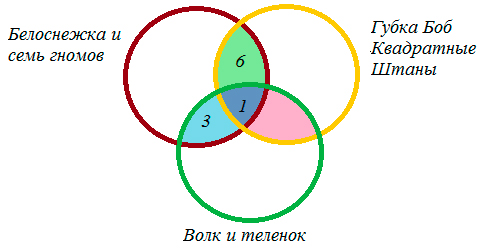
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 – 3 = 2 – ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».
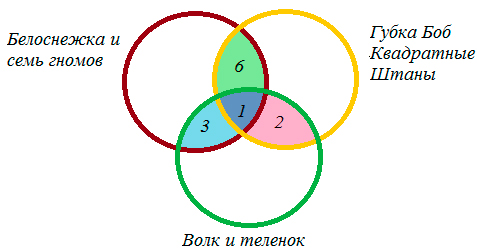
1) 21 – 3 – 1 – 6 = 11 – учеников выбрали только «Белоснежка и семь гномов»,
2) 13 – 3 – 1 – 2 = 7 – учеников выбрали – «Волк и теленок»,
3) 38 – (11 + 3 + 1 + 2 + 6 + 7) = 8 – ребят выбрали «Губка Боб Квадратные Штаны».
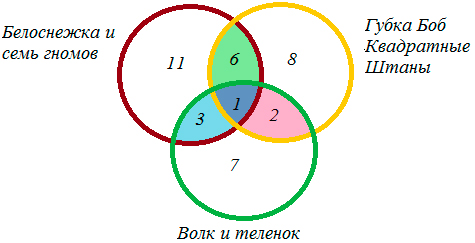
4) 8 + 2 + 1 + 6 = 17 – человек выбрали мультик «Губка Боб Квадратные Штаны».
Ответ: 17 учеников.
2.5. Задача про Крейсер и Линкор
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.
|
Запрос |
Найдено страниц, тыс. |
|
Крейсер и Линкор |
7000 |
|
Крейсер |
4800 |
|
Линкор |
4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.)
Решение:
При помощи кругов Эйлера изобразим условия задачи.
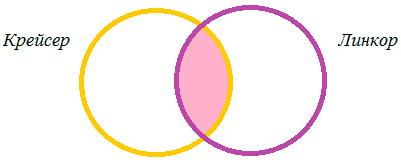
1) 4800 + 4500 – 7000 = 2300 (тыс. страниц) – найдено по запросу Крейсер и Линкор,
2) 4800 – 2300 = 2500 (тыс. страниц) – найдено по запросу Крейсер,
3) 4500 – 2300 = 2200 (тыс. страниц) – найдено по запросу Линкор.
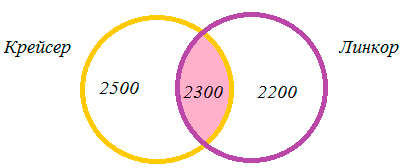
Ответ: 2300 тыс. страниц.
2.6. Задача про блондинок
Каждый ученик класса – либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика – блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?
Решение:
Изобразим с помощью кругов Эйлера данные из задачи:
1) 12 – 1 = 11 (учеников) – девочек блондинок,
2) 12 – 1 = 11 (учеников) – блондины и любят математику,
3) 6 – 1 = 5 (учеников) – девочек, которые любят математику,
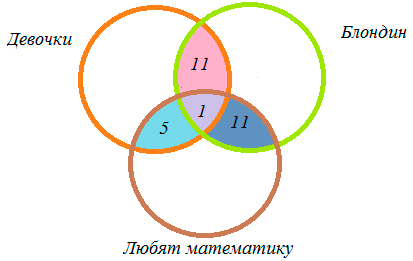
4) 20 – 11 – 1 – 5 = 3 (ученика) – девочки,
5) 24 – 11 – 1 – 11 = 1 (ученик) – блондин,
6) 17- 5 – 1 – 11 = 0 (учеников) – любят математику,
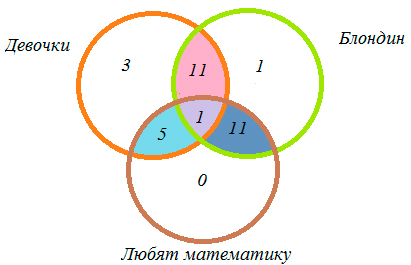
7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) – всего в классе.
Ответ: 32 ученика.
2.7. Задача про кружки
В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение:
Учитывая условия задачи, сделаем чертеж:
1) 10 – 3 = 7 (ребят) – посещают драмкружок и хор,
2) 6 – 3 = 3 (ребят) – поют в хоре и занимаются спортом,
3) 8 – 3 = 5 (ребят) – занимаются спортом и посещают драмкружок,
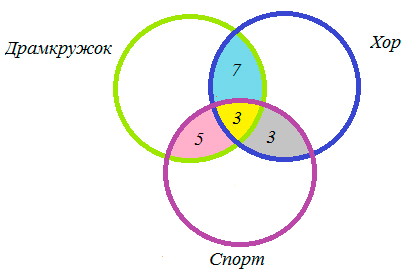
4) 27 – 7 – 3 – 5 = 12 (ребят) – посещают драмкружок,
5) 32 – 7 3 – 3 = 19 (ребят) – поют в хоре,
6) 22 – 5 – 3 – 3 = 11 (ребят) – увлекаются спортом,
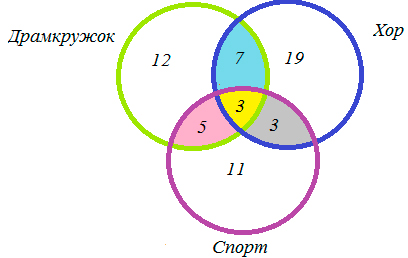
7) 70 – (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) – не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.
Ответ: 10 человек и 11 человек.
Задачи для самостоятельного решения
1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 – немецкий язык, а 23 – оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?
2. Из 40 учащихся нашего класса 32 любят молоко, 21 – лимонад, а 15 – и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
3. 12 моих одноклассников любят читать детективы, 18 – фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?
5. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом – 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
6. В одном классе 25 учеников. Из них 7 любят груши, 11 – черешню. Двое любят груши и черешню; 6 – груши и яблоки; 5 – яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 – умных и 9 – добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?
8. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике – 12; по истории – 23. По русскому и математике – 4; по математике и истории – 9; по русскому языку и истории – 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?
9. Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?
10. Из сотрудников фирмы 16 побывали во Франции, 10 – в Италии, 6 – в Англии; в Англии и Италии – 5; в Англии и Франции – 6; во всех трех странах – 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
Список использованных источников
1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.
2. Марков И.С. Новые олимпиады по математике – Ростов н/Д: Феникс, 2005.
3. https://ru.wikipedia.org/wiki/
4. http://logika.vobrazovanie.ru
5. http://www.otvet-prost.ru/load/diskretnaja_matematika/na_krugi_ehjlera/zadacha_na_krugi_ehjlera/18-1-0-22
6. http://urok.1sept.ru/articles/550092/
7. http://www.tutoronline.ru/blog/reshit-zadachu-pomogut-krugi-jejlera
Здравствуйте, уважаемые гости и подписчики моего канала. Знаете ли, вы,что многие задачи можно решить с помощью геометрических схем?
Сегодня я представлю вашему вниманию 3 задачи с подробным решением. Воспользуемся для этого кругами Эйлера.
Круги Эйлера – схема, в которой, решением является пересечение или объединение множеств и которая существенным образом упрощает рассуждения и безусловно помогает решить логические задачи. Но прежде чем приступить к решению, нужно обязательно проанализировать условия задачи.
Задача №1
В классе 35 учеников. Из них 20 человек занимаются в математическом кружке, 11 – в биологическом , 10 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?
Решение:
Всего 35 ребят, внутри двух меньших кругов 35-10=25 ребят, 20 из них увлекаются математикой.
Теперь 25-20=5 биологов – не посещают математический кружок.
Всего биологов – 11, значит 11 – 5 = 6 биологов, увлекающихся математикой. Это как раз те, ребята, которые находятся в общей части кругов МБ.
Ответ: 6 биологов увлекаются математикой.
Буду рада вашим лайкам👍, комментариям и подписке✍✍✍))
Задача №2
В классе 38 человек. Из них 16 играют в баскетбол, 17 – в хоккей, 18 – в футбол. Увлекаются двумя видами спорта – баскетболом и хоккеем – четверо, баскетболом и футболом – трое, футболом и хоккеем – пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом.
Сколько ребят увлекаются одновременно тремя видами спорта?
Сколько ребят увлекаются лишь одним из этих видов спорта?
Воспользуемся кругами Эйлера:
Найдём ребят, увлекающихся только баскетболом: Б: 16- (4+Z+3)=9-Z;
Аналогичным образом поступаем для Х: 17-(4+Z+5)=8-Z ;
Ф: 18- (3+Z+5)=10-Z.
Составим уравнение:
38 – (4+3+5+3)-(9-Z)-(10-Z)-(8-Z)=Z,
Раскрываем скобки и приводим слагаемые, получаем простейшее уравнение: 2Z=4, откуда Z=2.
Мы получили ответ на первый вопрос задачи – 2 человека увлекаются одновременно тремя видами спорта.
Найдём ответ на второй вопрос. Для этого необходимо подставить число 2 в выражения 9-Z, 8-Z, 10-Z.
Получаем: 9-Z=9-2=7? 8-Z=8-2=6, 10-Z= 10-2=8, складываем полученные числа 7+6+8 = 21 человек – увлекаются одним из этих видов спорта.
Ответ: 2 человека увлекаются одновременно тремя видами спорта.
21 человек – увлекаются одним из этих видов спорта.
Задача №3
Из 100 коллекционеров 70 собирают старинные монеты, 75 – значки, 80 – этикетки со спичечных коробков и 85 – марки.
Сколько их них увлекаются всеми четырьмя видами коллекционирования сразу?
Решение:
Из 100 коллекционеров 100-85 = 15 – не собирают марки, 100-80=20 – этикетки, 100-70=30 – старинные монеты, и 100-75=25 – не коллекционируют значки.
А теперь опираясь на решение предыдущих задач, найдём ответ на вопрос задачи:
100- (15+25+20+30)= 100-90=10 коллекционеров увлекаются всеми четырьмя видами коллекционирования.
Ответ: 10 коллекционеров увлекаются всеми четырьмя видами коллекционирования.
Буду рада вашим лайкам👍, комментариям и подписке✍✍✍))
СОДЕРЖАНИЕ:
ВВЕДЕНИЕ …………………………………………………………… 3
ГЛАВА 1. Немного из истории………………………………….5
ГЛАВА 2. Из
теории множеств……………………………………….7
2.1. Понятие множества.……………………………………..8
2.2. Операции над множествами. …………………………..9
ГЛАВА 3. Решение задач с помощью
кругов Эйлера ………………..10
ЗАКЛЮЧЕНИЕ…………………………………………………………..22
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
………………….23
ВВЕДЕНИЕ
Ничто так не способствует
формированию
мыслительной культуры,
как
решение логических задач. Математика-
не
сухая и скучная наука, а полная
необычных
и интересных открытий
Решать логические
задачи очень увлекательно. Есть люди, для которых решение логической задачи –
увлекательная, но несложная задача. Их мозг как луч прожектора сразу освещает
все хитроумные построения, и к правильному ответу они приходят необычайно
быстро. Замечательно, что при этом не могут объяснить, как пришли к решению.
Логические задачи составляют
обширный класс нестандартных задач. Сюда относятся, прежде, всего, текстовые
задачи, в которых требуется распознать объекты или расположить их в
определенном порядке по имеющимся свойствам.
Существует
множество приемов, которые используются при решении текстовых логических задач.
Очень часто решение помогает найти рисунок. Использование рисунка делает
решение задачи простым и наглядным. Изображение
условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к
её решению.
Актуальность состоит
в том, что задачи имеют практический характер, что немаловажно в современной
жизни. Задачи заставляют задумываться, подходить к решению какой-либо проблемы
с другой стороны, уметь выбирать из множества способов решения, наиболее
простой, легкий путь.
Цель работы:
– познакомится с кругами Эйлера –
Венна;
-научиться применять способ решения
задач с помощью кругов Эйлера;
-составлять задачи практического
содержания.
Глава 1. Немного из истории

г. по приглашению Петербургской академии наук он приехал в Россию. В
Петербурге Эйлер попал в круг выдающихся ученых: математиков, физиков,
астрономов, получил большие возможности для создания и издания своих трудов. Он
работал с увлечением и вскоре стал, по единодушному признанию современников,
первым математиком мира. Научное наследие Эйлера поражает своим объемом и
разносторонностью. В списке его трудов более 800 названий. Полное собрание
сочинений ученого занимает 72 тома. Среди его работ – первые учебники по
дифференциальному и интегральному исчислению. В теории чисел Эйлер продолжил
деятельность французского математика П. Ферма.
Эйлер много работает в области
математического анализа. Ученый впервые разработал общее учение о
логарифмической функции. В геометрии Эйлер положил начало совершенно новой
области исследований, выросшей впоследствии в самостоятельную науку-топологию.
Имя Эйлера носит формула,
связывающая число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В
-Р + Г = 2. Даже основные результаты научной деятельности Эйлера трудно
перечислить. Здесь и геометрия кривых и поверхностей, и первое изложение
вариационного исчисления с многочисленными новыми конкретными результатами. У
него были труды по гидравлике, кораблестроению, артиллерии, геометрической
оптике и даже по теории музыки. Он впервые дает аналитическое изложение
механики вместо геометрического изложения Ньютона, строит механику твердого
тела, а не только материальной точки или твердой пластины. Одно из самых
замечательных достижений Эйлера связано с астрономией и небесной механикой. Он
построил точную теорию движения Луны с учетом притяжения не только Земли, но и
Солнца. Это пример решения очень трудной задачи.
Последние 17 лет жизни Эйлера
были омрачены почти полной потерей зрения. Но он продолжал творить так же
интенсивно, как в молодые годы. Только теперь он уже не писал сам, а диктовал
ученикам, которые проводили за него наиболее громоздкие вычисления.
С1761 по 1768 год
им были написаны знаменитые «Письма к немецкой принцессе», где Эйлер как раз и
рассказывал о своем методе, об изображении множеств в виде кругов. Именно
поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал,
что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить
наши рассуждения».
После Эйлера этот же метод
разрабатывал чешский математик Бернард Больцано (1781 – 1848). Только в отличие
от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера
пользовался и немецкий математик Эрнст Шредер (1841 – 1902). Этот метод широко
используется в его книге «Алгебра логика». Но наибольшего расцвета графические
методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С
наибольшей полнотой этот метод изложен им в книге «Символическая логика»,
изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера
соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах
их называют также диаграммами (или кругами) Эйлера – Венна.
Глава 2. Из теории множеств
2.1. Понятие множества.
Одним из основных понятий, которые
используются в математике, является понятие множества. Для него не дается
определения. Можно пояснить, что множеством называют произвольную совокупность
объектов, а сами объекты – элементами данного множества. Так, можно говорить о
множестве учеников в классе (элементы – ученики ),множестве дней недели (элементы
– дни недели ), множестве натуральных делителей числа 6 (элементы – числа 1, 2,
3, 6 ) и т. д.
В курсах алгебры и алгебры
начало анализа чаще всего рассматривают множества, элементами которых являются
числа, и поэтому их называют числовыми множествами.
Как правило, множества
обозначают прописными буквами латинского алфавита. Например, если множество M состоит из чисел 1; 2; 3, то его
обозначают так: M = {1; 2; 3}. Тот факт, что
число 2 входит в это множество
( является элементом данного
множества M) записывается с помощью
специального значка следующим образом: 2
M; а то что число 5 не
входит в это множество ( не является элементом данного множества M ), записывается так: 5 M.
Можно рассматривать
также множество, не содержащее ни одного элемента, – пустое множество.
Например: множество простых делителей числа 1 – пустое множество.
Для некоторых
множеств существуют специальные обозначения. Так, пустое множество обозначается
символом , множество всех натуральных чисел –
буквой N, множество всех
целых чисел – буквой Z, множество всех рациональных чисел – буквой Q, а множество всех
действительных чисел буквой R. С помощью кругов Эйлера – Венна это можно изобразить так:
Рис.1
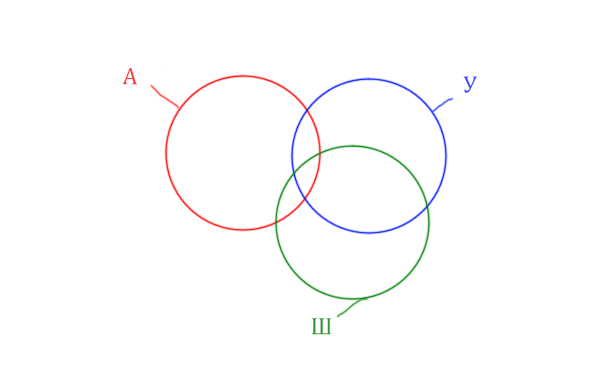
Если каждый элемент
множества A является
элементом множества B, то говорят, что множество A является подмножеством множества B.
Это записывают следующим
образом: A B.

Рис.2
2.2. Операции над
множествами.
Над множествами можно
выполнять определенные действия: находить их пересечение, объединение. Дадим
определение этих операций и проиллюстрируем их с помощью кругов.
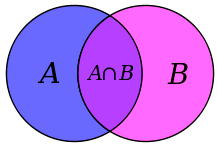
Пересечением
множеств A и B называют их общую часть, то есть множество C всех элементов,
принадлежащих как множеству A, так и множеству B
Пересечение множеств
обозначают знаком ∩ и записывают A ∩ B
.
Рис.3
Объединением
множеств A и B называют множество C, состоящее из всех элементов, принадлежащих хотя
бы одному из этих множеств (A или B). Объединение множеств обозначают знаком и записывают A
B

Глава3.
Решение задач с помощью Кругов Эйлера
Задача № 1.
Из 52 школьников 23 собирают значки, 35 собирают
марки, а 16 – и значки, и марки.
Остальные не увлекаются коллекционированием. Сколько школьников
не увлекаются коллекционированием.
Решение.
В условии этой задачи не так легко разобраться. Если
сложить 23 и 35, то получится больше 52. Это объясняется тем, что некоторых
школьников мы здесь учли дважды, а именно тех, которые собирают и значки, и
марки.
чтобы легче решать задачу, представим ее данные на
следующей схеме

На этой схеме большой круг означает всех школьников, о
которых идёт речь. Круг З изображает школьников, собирающих значки
(всего их 23), а круг М – школьников, собирающих марки (всего их 35). В
пересечении кругов З и М стоит число 16 – это те, кто собирает и
значки, и марки. Значит, только значки собирает 23 – 16 = 7 человек, только
марки собирает 35 – 16 = 19 человек. Всего марки и значкисобирает19 + 7 + 16 =
42 человека. Остаётся 52 – 42 = 10 человек, не увлечённых коллекционированием.
Это число можно вписать в свободное поле круга. Ответ: 10 человек.
Задача 2.
В классе 15 мальчиков. Из них 10 человек занимается
волейболом и 9 баскетболом. Сколько мальчиков занимается и тем, и другим?
Решение.
Изобразим условие с помощью кругов Эйлера . Этот
рисунок подсказывает нам рассуждения. Разберём это рассуждение и впишем нужное
число в каждую из образовавшихся на диаграмме частей .
Пусть всеми видами спорта занимаются х мальчиков.
Тогда только волейболом занимаются (10-х) мальчиков, а только баскетболом
(9-х) мальчиков. Составим уравнение: 10-х + х+ 9-х=15, откуда х=4

В
10-х
Б
х
9-х
Рис.6
Ответ: 4 человека.
Задача № 3.
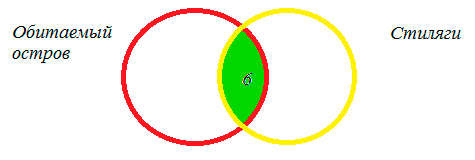
Некоторые ребята из нашего класса
любят ходить в кино. Известно, что 15 ребят смотрели фильм «Чучело», 11 человек
– фильм «Выше неба», из них 6 смотрели и «Чучело», и «Выше неба». Сколько
человек смотрели только фильм «Выше неба»?
Решение: Чертим два множества
таким образом: 6 человек, которые смотрели фильмы «Чучело» и «Выше неба»,
помещаем в пересечение множеств.
15 – 6 = 9 – человек,
которые смотрели только «Чучело».
11 – 6 = 5 – человек, которые смотрели только «Выше неба».
Получаем:
Рис.7
Ответ. 5 человек
смотрели только «Выше неба».
Задача № 4.
В группе из 80 туристов, приехавших на экскурсию в
Москву, 52 хотят посетить Большой театр, 30 – Художественный театр, 12 хотят
посетить оба театра, остальные в театры ходить не хотят. Сколько человек не
собирается идти в театр?
Решение.
Только большой театр посетят: 52-12=40 туристов;
только художественный театр посетят
30-12=18 туристов;

собираются идти в театр.
Рис.8
Ответ: 10 человек.
Задача № 5.
На полке стояло 26
волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон.
Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две
книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько
книг прочитал Рон?
Решение.
Учитывая условия задачи,
чертеж будет таков:
Рис.9
Так как Гарри Поттер
всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 –
4 – 2 = 5 – книг прочитал только Гарри.
Следовательно, 26 – 7 – 2
– 5 – 4 = 8 – книг прочитал Рон. Ответ.
8 книг прочитал Рон.
Задача№6.
В туристической группе из 100
человек 75 человек знают немецкий язык, 65 человек – английский язык, а 10
человек – не знают ни немецкого, ни английского языка. Сколько туристов знают
два языка? Решение.
Изобразим условие задачи в виде
кругов Эйлера.

Легко видеть, что
90 туристов (100-10) знают хотя бы один язык; Пусть х туристов знают и
английский , и немецкий языки. Тогда (65-х) туристов знают только английскй, а
(75-х) человек только немецкий. Получим уравнение 65-х+75-х+х=90, откуда х=50 –
туристов знают оба языка. Ответ:
50 туристов.
Задача№7.
Сколько человек участвует в прогулке, если известно, что 16
из них взяли бутерброд с ветчиной, 24 – с колбасой, 15 – с сыром, 11 и с
ветчиной, и с колбасой, 8 и с ветчиной, и с сыром, 12 и с колбасой, и с
сыром, 6-бутерброды всех видов, а 5- взяли
пирожки?
Решение: Изобразим множества
следующим образом: 
16+24+15-11-8-12+6=30(чел)
– участвовали в прогулке и с собой брали бутерброды или
3+2+6+5+7+6+1=30(чел)
30+5=35(чел) – участвовали в прогулке
Ответ. 35 человек
Задача №8
В 5 классе нашей
школы 22, в 6 классе – 16, в 7 классе – 23 ребят. Известно, что кружки по
лыжам, шахматам и спортивным играм ходят 4 человека. Каждые две секции
посещают 9 человек. Сколько человек ходит из каждого класса на секции? Сколько
учеников не ходит ни на какой спортивный кружок?
Решение. Если на все три
кружка ходят 4 ученика, а на каждые два – 9 человек, то две секции с 5 и 6
класса, с 6 и 7 класса, с 5 и 7 класса посещают по 5
человек.
Рис.12
Получаем 5+5+4=14 пятиклассников
посещают кружки, 22-14=8 человек не ходят ни на какой кружков. Рассуждая
также, из шестиклассников 16-14=2 ученика никуда не ходя, а из семиклассников
– 23-14=9 человек.
Ответ: 14 учеников с каждого
класса посещают кружки, не ходят ни на какой из 5-ого – 7, из 6-ого – 2, из
7-ого – 9 учеников.
Задача № 9.
Из 100 ребят,
отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30
ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют
кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах –
5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на
скейтборде, ни на роликах?
Решение: Воспользуемся
кругами Эйлера.

Рис.13
Всеми тремя спортивными
снарядами владеют три человека, значит, в общей части кругов вписываем число 3.
На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и
на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют
10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде
умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека.
Внесем эти данные в соответствующие части. Определим теперь, сколько человек
умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют
30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно,
только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на
скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию
задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на
одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на
одном спортивном снаряде.
Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.
Задача
№ 10.
В трёх седьмых классах 70 ребят. Из
них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В
драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов;
3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не
увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только
спортом?
Решение. Д – драмкружок; Х – хор; С – спорт.
В круге Д – 27 ребят, в круге Х – 32 человека, в круге С – 22 ученика. Те 10 ребят из драмкружка, которые
поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены,
они окажутся в общей части всех трёх кругов. Остальные семеро спортом не
увлекаются. Аналогично, 8-3=5
спортсменов, не поющих в хоре и
6-3=3, не посещающих драмкружок. Легко видеть, что 5+3+3=11 спортсменов
посещают хор или драмкружок, 22-(5+3+3)=11 заняты только спортом;
70-(11+12+19+7+3+3+5)=10 – не поют в хоре, не занимаются в драмкружке, не
увлекаются спортом.
Рис.14
Ответ: 10 человек.
Задача№11. В классе 30
человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 —
троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и
троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя
видами транспорта?
Решение.

Рис.15
Пусть х человек
пользуется всеми тремя видами транспорта. Тогда пользуются только метро и
троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х)
человек, только метро и автобусом —(12 − х) человек. Найдем, сколько человек
пользуется одним только метро:
20 − (12 − х) − (10 − х)
− х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только
троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 − х) + (9 − х) +
(10 − х) + (х + 4) + (х − 2) + (х − 6) = 30.
отсюда х = 3.
Ответ: 3 человека.
Задача № 12.
Из сотрудников фирмы 16
побывали во Франции,10-в Италии,6-в Англии; в Англии и Италии-5; в Англии и
Франции -6; во всех трех странах – 5 сотрудников. Сколько человек посетили и
Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них
побывал хотя бы в одной из названных стран?
Решение:
Нам известно, что во всех
трех странах было 5 сотрудников. В Англии и Италии тоже 5, значит эти же
сотрудники были и во Франции и поэтому в пересечении кругов А и И ставим 0. В
Франции и Италии нам неизвестно поэтому пишем х-5 в пересечении кругов А и Ф.
Т.к. в Англии было 6 человек, то 6-5-1=0 пишем 0,во Франции 16-х+5-6 и Италии
10-х+5-5 и всего в фирме 19 сотрудников, то остается составить и решить
уравнение: 1+16-х+5-6+5+х-5+10-х+5-5=19, отсюда х=7, значит в Италии и Франции
побывало 7-5=2 сотрудника фирмы.

Рис.16
Ответ: 2 сотрудника.
Задача № 13.
Ребят, которые хотят обмениваться
различного рода журналами, собралось 10 человек. Среди них выписывают К – 6
человек, Т – 5 человек, Ю – 5 человек, К и Т – 3 человека, Т и Ю -2 человека, К
и Ю – 3 человека., а один человек не выписывает ни одного журнала., но читает
все эти журналы в библиотеке. Надо узнать, сколько человек выписывают все три
журнала, сколько – два, а сколько – только один журнал.
Решение. Пусть большой круг,
состоящий из 10 человек, – это множество всех ребят, обменивающихся журналами.
Внутри большого круга нарисуем три меньших круга: К, Т, Ю, которые изображают
ребят, подписавшихся на соответствующие журналы.. Известно, что один человек не
выписывает ни одного журнала.
Пусть х ребят выписывают все три
журнала, тогда (3-х)ребят выписывают только К и Т, (2-х) –только Т и Ю, (3-х)-
только К и Ю. Значит, только журнал К выписывают 6-(3-х+х+3-х)=х человек,
журнал Т 5-(3-х+х+2-х)=х, журнал Ю 5-(3-х+х+2-х)=х.

Составим
уравнение: х+3-х+3-х+х+х+х+х+2-х=9, 8+х=9,х=1
Итак, 3 – это число ребят,
подписавшихся только на один журнал, 5 – это число ребят, подписавшихся на два
журнала, а 1 – число ребят, подписавшихся на все три журнала.
ЗАКЛЮЧЕНИЕ
Предмет
математики настолько серьезен,
что нельзя упускать случая сделать
его немного занимательным.
Б. Паскаль
Среди
математических задач логические задачи занимают особое место Решение таких
задач способствует развитию математического мышления. Они отличаются от
большинства математических задач тем, что для их решения часто не требуется
запас каких-то специальных знаний, а нужна, как правило, сообразительность. Одна
из характерных черт любой логики состоит в том, что она позволяет, получив
некоторую информацию, извлечь (выявить) содержащиеся в ней новые знания.
Оказывается приемов, с помощью которых можно решать текстовые
логические задачи, несколько. Они разнообразны и каждый из них имеет свою
область применения.
В моей работе рассмотрены
задачи, которые состоят из множества данных. Найденные решения
подчиняются одному и тому же способу: составляем рисунок; заносим
первоначальные данные в круги; анализируя и рассуждая, записываем результаты в
части кругов; ищем и записываем ответ. Изображение условий задачи в виде
кругов Эйлера, как правило, упрощает и облегчает путь к её решению. Кроме того с
их помощью можно ответить на множество вопросов, поставленных к одному
условию задачи.
Данная тема расширила
мой математический кругозор, обогатила арсенал средств, используемых в решении
разнообразных задач.
Список используемых источников:
1. Гаврилова
Т. Д..Занимательная математика. 5 – 11 классы. Волгоград: Учитель, 2005.-96 с.
2. Германович П.Ю. «Сборник задач по
математике на сообразительность».
3. Гетманова
А. Д. Логические основы математики 10 – 11 класс: учебное пособие.
– М.: Дрофа, 2005.
4. Глейзер Г. И. История математики в школе. — М.: Просвещение,
1964. — С. 232.
5. Гусев В.А., Орлов А.И.,
Розенталь А.Л. «Внеклассная работа по
математике». М.:
Просвещение, 1984.
6. Нелин Е.П., Долгова О.Е.. Учебник
алгебра и начала анализа 11 класс.
Тезисы
к работе
Тема моей
исследовательской работы «Решение задач с помощью кругов Эйлера ». При
подготовке к олимпиаде я столкнулась с задачами, в которых большое количество
данных. Оказывается, упростить решение таких задач помогают так называемые
круги Эйлера, с помощью которых можно изобразить множество элементов,
обладающих определённым свойством. Целью данной работы является изучение
этого способа и умение применять его для решения задач.
В работе
рассмотрены задачи, решение которых подчиняются одному алгоритму: составляем
рисунок; заносим первоначальные данные в круги, начиная с условия которое
содержит больше свойств; анализируя и рассуждая записываем результаты в части
круга; записываем ответ.
Актуальность
состоит в том, что задачи имеют практический характер, что немаловажно в
современной жизни. Задачи заставляют задумываться, подходить к решению
какой-либо проблемы с другой стороны, уметь выбирать из множества способов
решения, наиболее простой, легкий путь. Способ, рассмотренный в работе доступен и легок в
понимании, что позволяет расширить круг его применения. Круги Эйлера можно
встретить и в истории, и в биологии, и при изучении других предметов.
Материал,который был исследован в
работе ,а также практическая часть, могут быть применены на дополнительных занятиях, при подготовке к математическим
олимпиадам .
Сегодня разберём задачи на круги Эйлера в информатике.
Леонард Эйлер – швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
Задача (Простая)
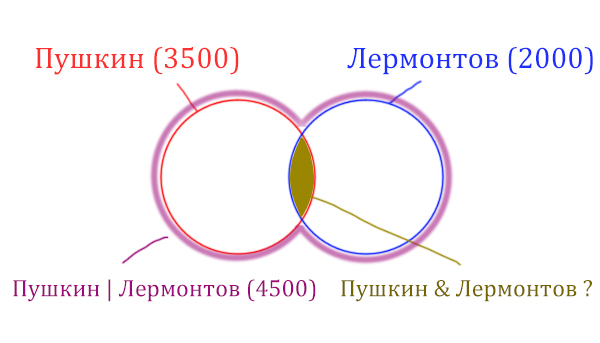
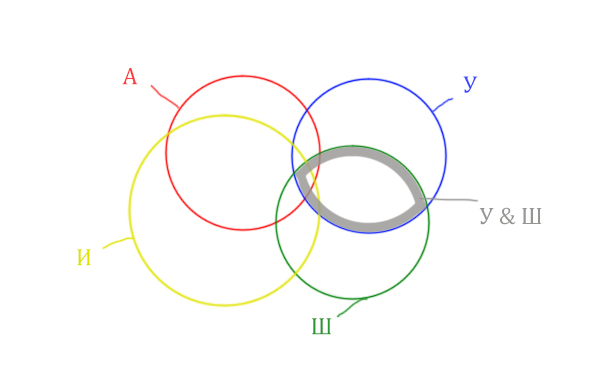
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин | Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Видим, что по запросу “Пушкин” в поисковике нашлось 3500 страниц. По запросу “Лермонтов” – 2000 страниц.
Запрос “Пушкин | Лермонтов” обозначает, что поисковик выдаст страницы, где есть слова про “Пушкина”, и страницы, где есть слова про “Лермонтова”, а так же могут быть страницы, где написано и про “Пушкина”, и про “Лермонтова” одновременно.
Если сложить страницы, в которых написано про “Пушкина” и про “Лермонтова” получается 3500 + 2000 = 5500 страниц. Но почему же при запросе “Пушкин | Лермонтов” получается меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про “Пушкина” (3500 страниц), мы подсчитали и те страницы, где было написано и про “Пушкина”, и про “Лермонтова” одновременно.
Тоже самое и для количества страниц, где написано про “Лермонтова” (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про “Пушкина”, и про “Лермонтова”.
В вопросе спрашивается, сколько страниц будет по запросу “Пушкин & Лермонтов“. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про “Пушкина”, и про “Лермонтова”.
Отсюда получается:
Пушкин & Лермонтов = (3500 + 2000) – 4500 = 5500 – 4500 = 1000 страниц.
Это и будет ответ!
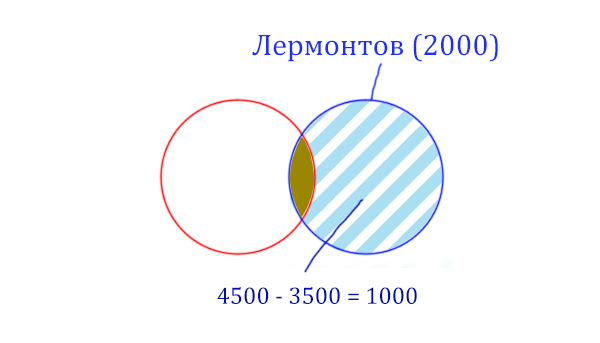
Теперь решим эту задачу с помощью Кругов Эйлера!
У нас всего есть две сущности: “Пушкин” и “Лермонтов”. Поэтому рисуем два пересекающихся круга, желательно разными цветами.
Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию “Пушкин | Лермонтов”. Эта операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» “Пушкин | Лермонтов” (4500).
Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц) = 2000 – 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.
Ответ: 1000
Рассмотрим ещё одну не сложную разминочную задачу.
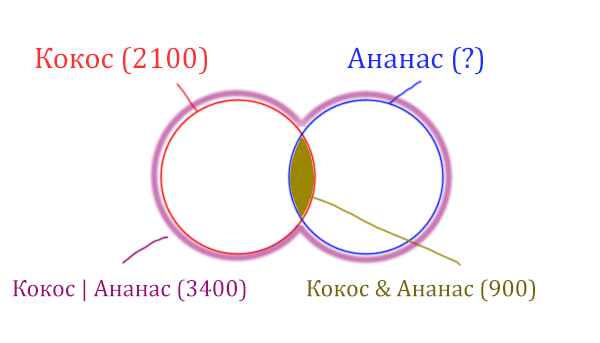
Задача (Разминочная)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Кокос | Ананас | 3400 |
| Кокос & Ананас | 900 |
| Кокос | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Ананас?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.
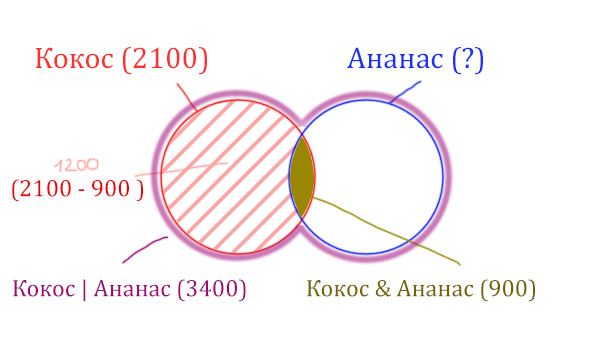
Найдём заштрихованную часть красного круга.
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 – 900 = 1200.
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 – 1200 = 2200
Ответ: 2200
Разберём классическую задачу из информатики по кругам Эйлера.
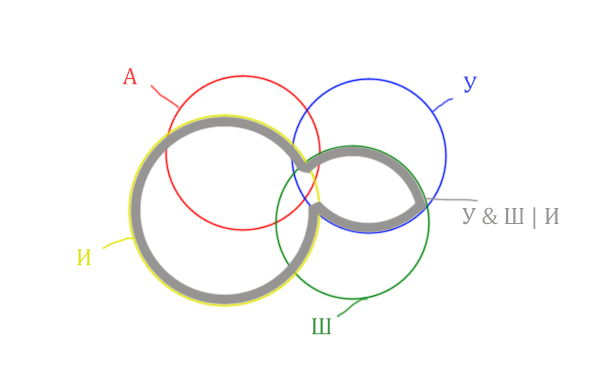
Задача (Классическая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
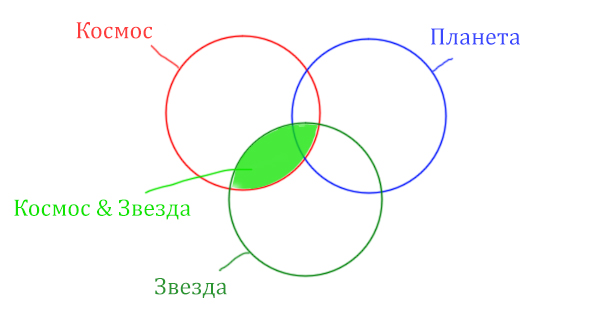
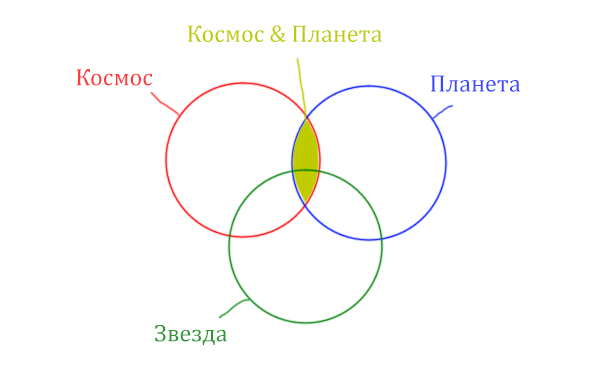
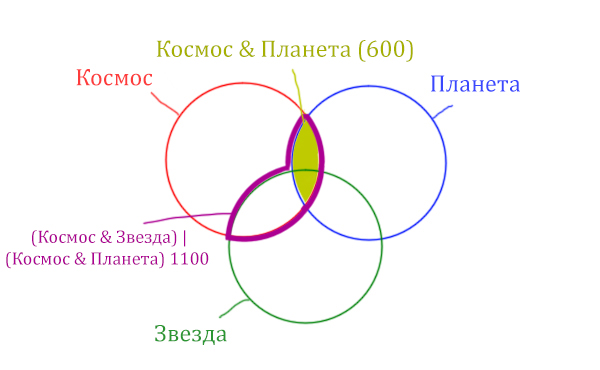
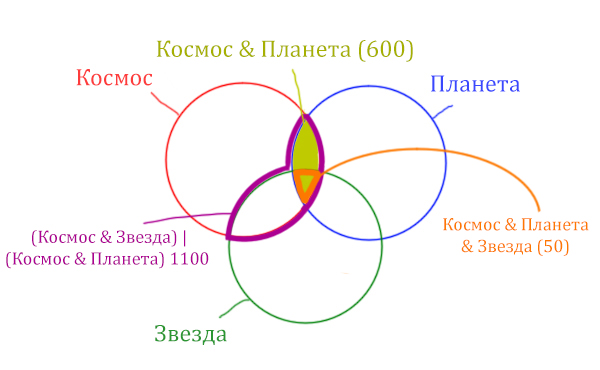
| (Космос & Звезда) | (Космос & Планета) | 1100 |
| Космос & Планета | 600 |
| Космос & Планета & Звезда | 50 |
Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
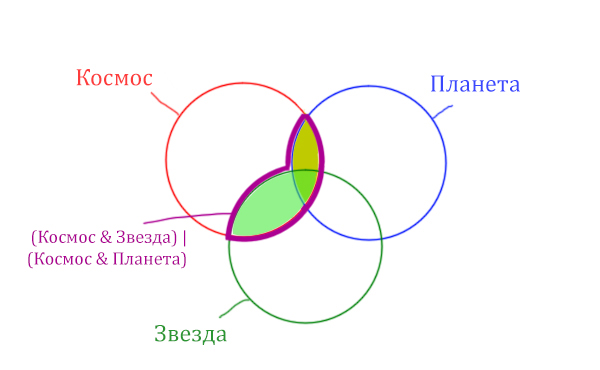
Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического “ИЛИ”.
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда
Теперь отметим вторую скобку Космос & Планета.
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического “ИЛИ”. Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!
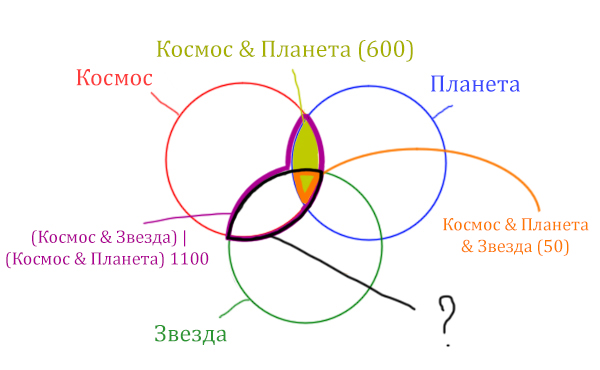
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.
Теперь у нас есть все компоненты, чтобы решить эту задачу.
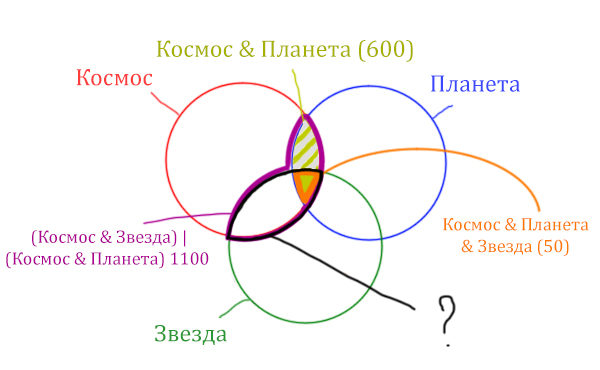
Найдём заштрихованную область.
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).
Количество страниц в заштрихованной части = 600 – 50 = 550
Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).
Количество страниц (при запросе Космос & Звезда) = 1100 – 550 = 550
Ответ: 550
Закрепляем материал по задачам на Круги Эйлера.
Задача (На закрепление)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Море & Солнце | 290 |
| Море & Пляж | 355 |
| Море & (Пляж | Солнце) | 465 |
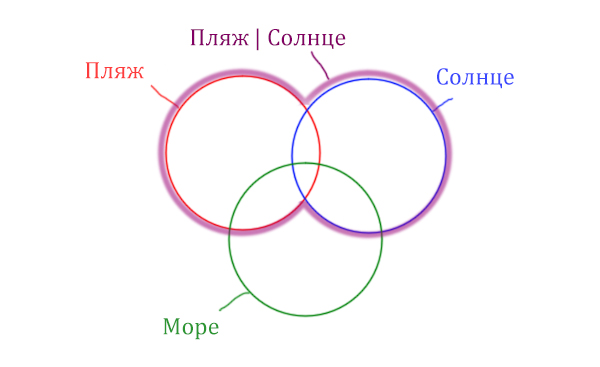
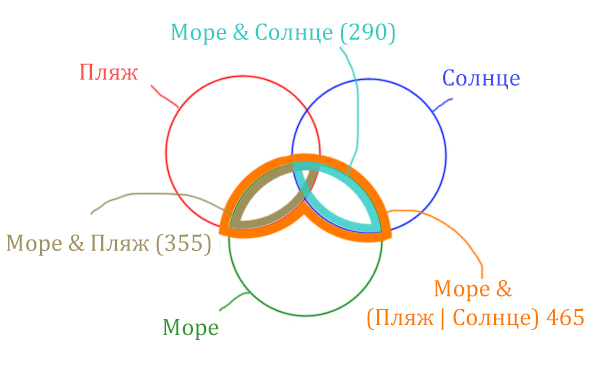
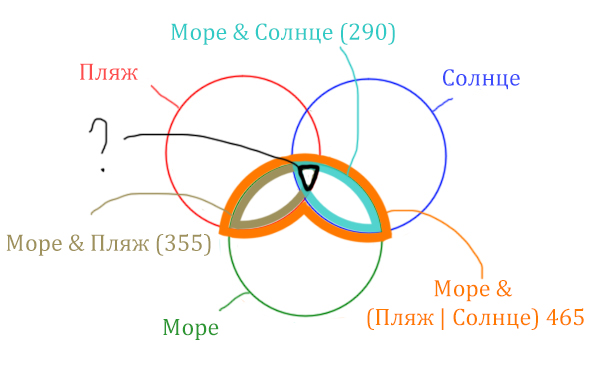
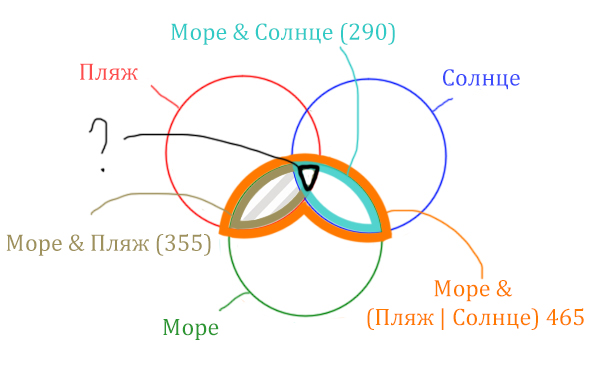
Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.
Отметим все области для которых нам даны количество страниц.
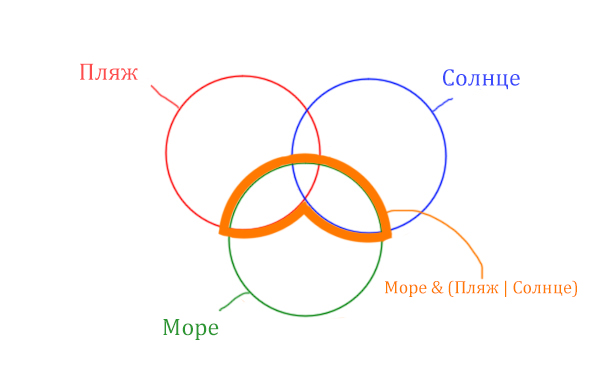
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.
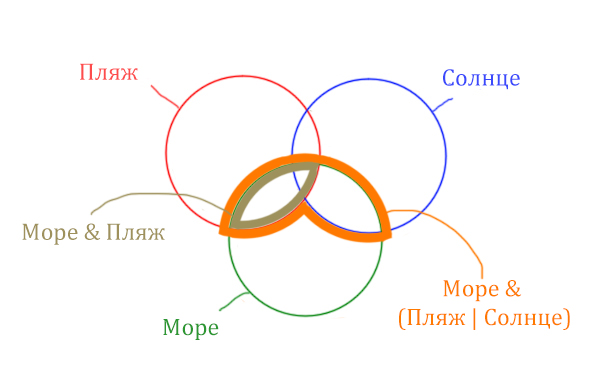
Теперь отметим Море & Пляж.
Теперь отметим Море & Солнце.
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
Найдём заштрихованную область!
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) – Море & Солнце =
= 465 – 290 = 175
Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) – Количество страниц (в заштрихованной области) 175 =
= 355 – 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.
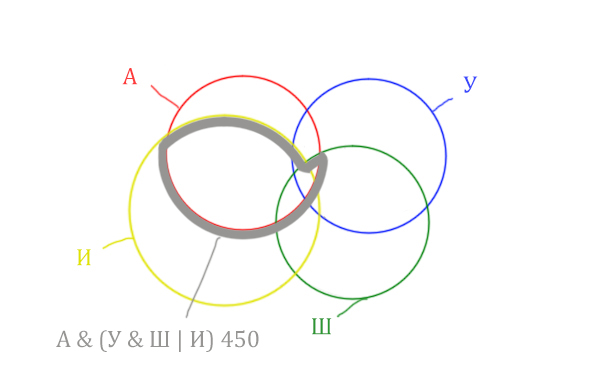
Задача (с 4 сущностями)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
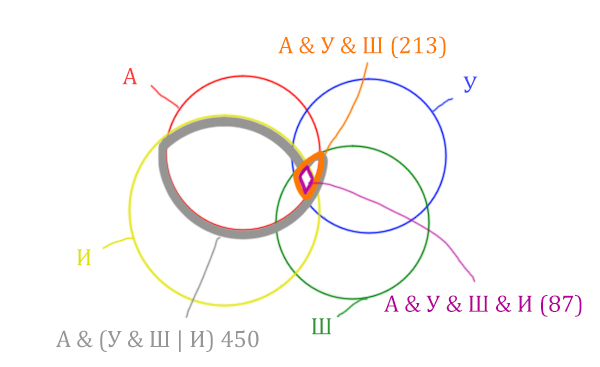
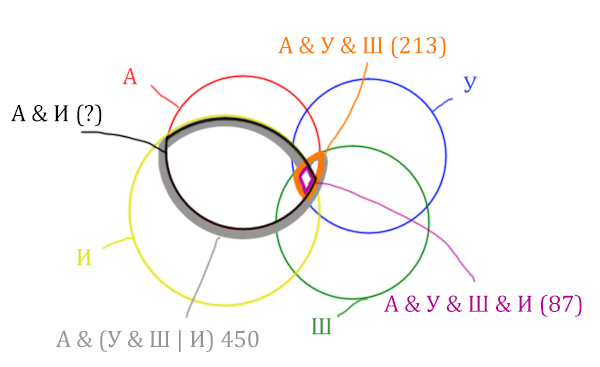
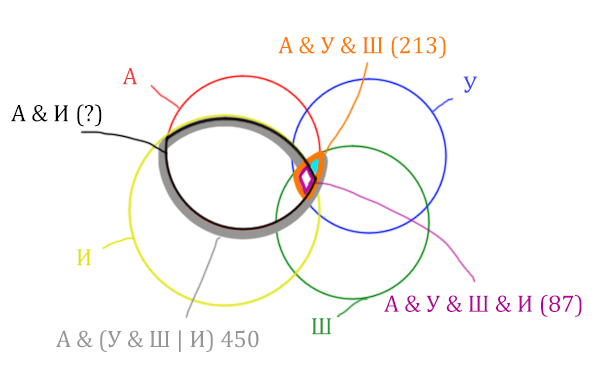
| Запрос | Найдено страниц (в тысячах) |
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Англия & Ирландия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
Область Уэльс & Шотландия выглядит так:
Добавим к этой области Ирландию через логическое “ИЛИ”. Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!
Теперь нужно сделать операцию логического “И” получившийся области с “Англией”. Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:
Т.е. это общее между предыдущем серым контуром и красным кругом!
Отметим Англия & Уэльс & Шотландия – это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.
Отметим Англия & Уэльс & Шотландия & Ирландия – это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) – Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 – 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) – Количество (для бирюзового кусочка) =
450 – 126 = 324
Это и будет ответ!
Ответ: 324.
Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)
Задача (ЕГЭ по информатике, 2019, Москва)
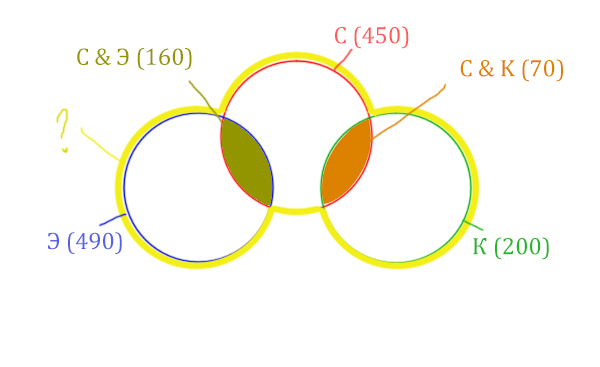
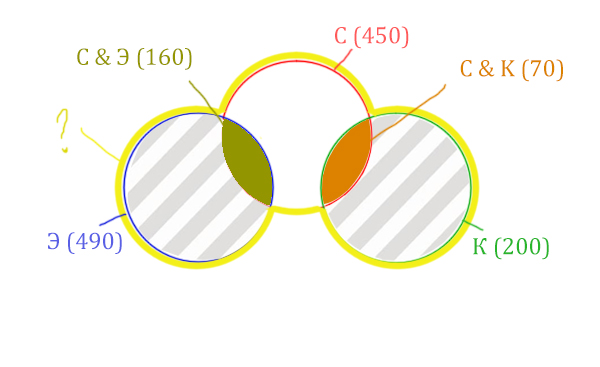
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Суфле | Корзина | Эклер
Решение:
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!
Так же видим, что логическое “И” между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического “ИЛИ” совпадала бы с суммой этих кругов.
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.
Отметим всё, что нам дано в условии.
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область) =
= Эклер (490) – Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область) =
= Корзина (200) – Суфле & Корзина (70) = 130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Ответ: 910
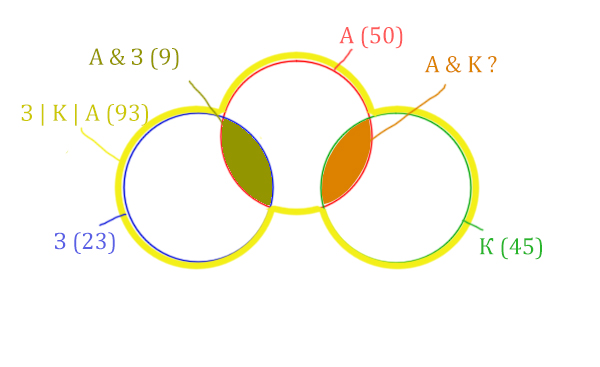
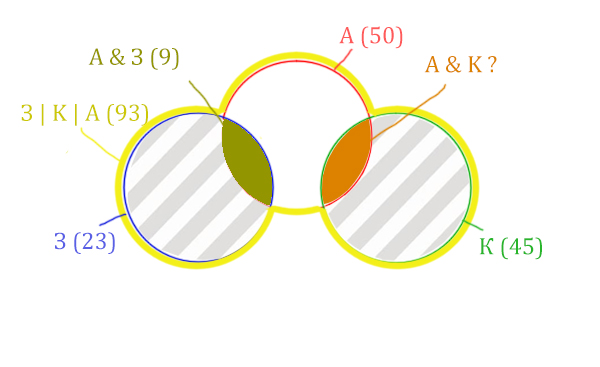
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
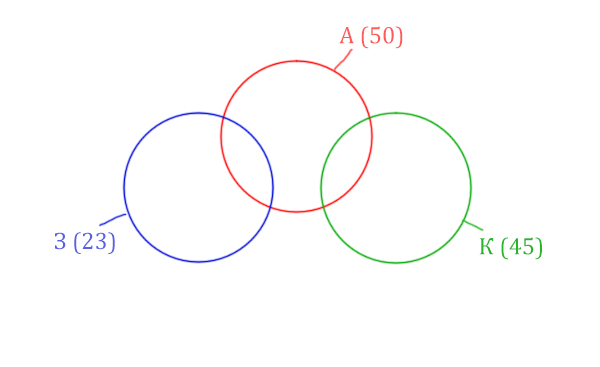
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу
Аврора & Крейсер
Решение:
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.
Нарисуем все данные на рисунке.
Нужно найти для начала заштрихованную правую часть.
Количество страниц (для двух заштрих. частей) =
З | К | А (93) – Красный круг (50) = 43
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих. части) =
Синий круг (23) – А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) – Колич. страниц (для лев. заштрих. части) (14) =
= 43 – 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) – Колич. страниц (для правой заштрих. части) (29) =
45 – 29 = 16
Ответ: 16
На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.
Интересно…
как быть , когда идет произведение3 предметов + произведниее 3 педметов..
ОГРОМНОЕ СПАСИБО за Ваш труд!!! Всё очень понятно и доходчиво. +++++++++++++++
Решение задач с помощью кругов Эйлера
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Давыдова В.А. 1
1ГБОУ СОШ № 5 «ОЦ «Лидер» г. о. Кинель
Маеренкова В.В. 1
1ГБОУ СОШ № 5 «ОЦ «Лидер» г. о. Кинель
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
1. Введение
Во все времена представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов.
Комбинаторика – раздел математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из данных объектов.
Выбор объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например, конструктору, разрабатывающему новую модель механизма, учёному-агроному, планирующему распределение сельскохозяйственных культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав [3].
Гипотеза: показать, что решение комбинаторных задач с помощью кругов Эйлера имеет практическое применение.
Проблема: как решение комбинаторных задач с помощью кругов Эйлера помогают в изучении математики и в жизни.
Цель работы: показать широту применения решений комбинаторных задач с помощью кругов Эйлера для привития интереса учащихся к математике.
Задачи:
Познакомиться с историей возникновения науки комбинаторики;
Научиться составлять и решать задачи с помощью кругов Эйлера;
Применять полученные знания в дальнейшем обучении;
Расширить и углубить представление о практическом значении математики в жизни;
Работать с научно-познавательной литературой, анализировать, делать выводы;
Создать собственный банк задач.
Актуальность выбранной темы заключается в необходимости решения комбинаторных задач на уроках математики, применении их в жизни, т.к. они имеют социальную значимость, помогают разобраться в новых веяниях жизни. Основа хорошего понимания комбинаторики – умение считать, думать, рассуждать, находить удачные решения задач.
2. Основная часть
2.1 Решение задач с помощью кругов Эйлера
Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью [4].
Круги Эйлера – это тот метод, который наглядно демонстри-рует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.
Метод Эйлера является незаменимым при решении некоторых задач.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы [3].
Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна [2].
Задача №1
В классе учатся 40 человек. Из них по русскому имеют «тройки» 19 человек, по математике – 17 человек и по физике – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека и по физике – 11 человек. Семь человек имеют «тройки» и по математике, и по физике, из них пятеро имеют «тройки и по русскому языку. Сколько людей учатся без «троек»? Сколько людей имеют «тройки» по двум из трёх предметов? [1] Приложение1, Рис. 1
Дальнейшие расчёты не составляют труда.
40-(4+4+11+4+6+2+5)=4 человек учатся без «троек»
6+4+2=12 человек имеют «тройки» по двум предметам
Ответ: 4 человек учатся без «троек», человек имеют «тройки» по двум предметам.
Задача №2
В небольшом городке NN живут 10000 человек. Недавно среди них был проведён опрос «какие машины вам нравятся больше всего?». Результат был таким: 5 000 людям нравятся отечественные машины, 6 000 людям иностранные машины, а 7 тысяч довольны и общественным транспортом. 2000 людям нравятся отечественные машины, но при этом готовы поездить на автобусах. 4000 предпочитаю иностранные машины и автобусы. 2500 людей любят и отечественные и иностранные машины. И только 1000 человек всем довольны. Сколько человек участвовало в опросе? [1]
Решение:
2000 – 1000 = 1000 людей любят только отечественные машины и автобусы
4000 – 1000 = 3000 людей любят только иностранные машины и автобусы
2500 – 1000 = 1500 людей любят и отечественные, и иностранные машины
5 000 людям нравятся отечественные машины, но при этом 1000+1500+1000=3500 людей предпочитают и другие машины, следовательно только отечественные авто любят 500 человек. Также иностранные машины предпочитают 500 людей, а автобусы – 2000 человек. Теперь находим общее количество людей.
3000+1000+500+2000+1000+500+1000=9000 человек
Ответ: 9000 человек участвовали в опросе.
Приложение 1, РИС. 2
Задача №3
На стройке работают 30 рабочих. 17 рабочих строят обувной магазин, 20 рабочих строят парикмахерскую. Сколько рабочих работают на обоих объектах?
Решение:30 – 17= 13 людей строят только обувной магазин. Теперь от 20 отнимем 13 и найдём, что и там, и тут работают только 7 человек. [1] Приложение 1, Рис.3
Задача № 4
Часть туристов разговаривает на английском, а часть на немецком. Английский – 90%, немецкий – 60%. Сколько учеников в классе изучают сразу два языка.
Решение: от всего класса (100%) отнимем английских туристов (90%), получим туристов говорящих только по-английски (10%). А теперь от всех, изучающих немецких (60%), отнимем эти 10%. Получим говорящих на обоих языках (50%).[1] Приложение 2, Рис.4
Задача №5
В классе 30 человек.19-ходят на кружок по математике, 10-на кружок по русскому языку, 1-человек ходит на русский и на математику.
Сколько человек не посещают кружки?
Решение:
19-1=18
10-1=9
30-(18+9+1)=2 человека не посещают ни математику, ни русский.
Приложение 2, Рис.5
Задача № 6
Из 90 детей на футбол ходят 35 детей, на волейбол 28 и на баскетбол 27 детей. На футбол и волейбол ходят одновременно 10 детей, на футбол и баскетбол – 8 детей, на волейбол и баскетбол – 5, на все три – 4. Сколько детей никуда не ходят? [1]
Решение:
10-4=6 ходят на футбол и волейбол
8-4=4 ходят на футбол и баскетбол
5-4=1 ходят на волейбол и баскетбол
На футбол ходят 35 детей, но 4+4+6=14 из них ходят и на другие секции, следовательно, только на футбол ходят 21 ребёнок. Аналогично получаем, что на волейбол ходят 17, а на баскетбол 18. По условию задачи всего 90 детей. 21+17+18+1+4+6+4=71 детей ходят хотя бы на одну секцию, следовательно, 19 детей никуда не ходят.
Приложение 2, Рис. 6
Задача № 7
100 шестиклассников участвовали в опросе, в ходе которого выяснялось, какие пирожки нравятся им нравятся больше: с мясом, с капустой и картошкой. В результате 20 опрошенных выбрали с мясом, 28-с капустой, 12 с картошкой. Выяснилось, что 13 школьников отдают одинаковое предпочтение пирожкам с мясом и капустой, 6-учеников-с мясом и картошкой, 4 ученика с капустой и картошкой, а 9 ребят совершенно равнодушны к пирожкам. Некоторые из школьников ответили, что одинаково любят и мясом, и картошкой, и капустой. Сколько таких ребят? [1]
Решение:
Пусть X – искомое число учеников, любящие все виду пирожков. Тогда: 20+28+12+13+6+4+9+Х=100 Х=6 Приложение 3, Рис. 7
Задача №8
Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной. [1]
Приложение 3, Рис. 8
Сколько шестиклассников:
1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?
Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.
Решение.
1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
2. 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга)
3. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки. (На схеме правая часть правого круга)
4. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга)
5. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга).
Очевидно, что 2 и 5, а также 3 и 4– равнозначны и ответы на них совпадают.
Задача №9.
Часть жителей нашего дома выписывают только газету «Комсомольская правда», часть – только газету «Известия», а часть – и ту, и другую газету. Сколько процентов жителей дома выписывают обе газеты, если на газету «Комсомольская правда» из них подписаны 85%, а на «Известия» – 75%? [1]
Решение.
Здесь нет принципиального отличия от решения предыдущей. На готовом рисунке заменим данные: 25 на 85% и 20 на 75%. Учитывая, что все жители дома составляют 100%, заменяем 35 на 100% и получаем готовое решение: 85% + 75% – 100% = 60%.
Ответ: обе газеты выписывают 60% жителей.
Чем более сложная и запутанная логическая задача, связанная с множествами, тем более очевиден эффект от применения кругов Эйлера. Только после составления рисунка их решение становится достаточно очевидным.
Задача №10.
В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом? [1] Приложение 3, Рис. 9
Решение.
Д – драмкружок,
Х – хор,
С – спорт.
в круге Д – 27 ребят,
в круге Х – 32 человека,
в круге С – 22 ученика.
Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8 – 3 = 5 спортсменов, не поющих в хоре и 6 – 3 = 3, не посещающих драмкружок.
Легко видеть, что 5 + 3 + 3 = 11 спортсменов посещают хор или драмкружок,
22 – (5 + 3 + 3) = 11 занимаются только спортом;
70 – (11 + 12 + 19 + 7 + 3 + 3 + 5) = 10 – не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.
Ответ: 10 человек и 11 человек.
Задача №11.
В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта? [1]
Решение.
1 способ. Для решения опять воспользуемся кругами Эйлера. Приложение 4, Рис. 10
Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом – (10 – х) человек, только автобусом и троллейбусом – (9 – х) человек, только метро и автобусом – (12 – х) человек.
Найдем, сколько человек пользуется одним только метро:
20 – (12 – х) – (10 – х) – х = х – 2.
Аналогично получаем: х – 6 – только автобусом и х + 4 – только троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30,
отсюда х = 3.
2 способ. А можно эту задачу решить задачу другим способом: 20 + 15 + 23 – 10 – 12 – 9 + х = 30, 27 + х = 30, х = 3. Здесь сложили количество учеников, которые пользуются хотя бы одним видом транспорта и из полученной суммы вычли количество тех, кто пользуется двумя или тремя видами и, поэтому, вошли в сумму 2-3 раза. Таким образом, получили количество всех учеников в классе.
Ответ. 3 человека ежедневно пользуются всеми тремя видами транспорта.
2.2 Практическая часть
Я проводила опрос среди учащихся 7-х классов. В опросе принимали участие 87 человек.
Результаты социологического опроса представлены на диаграмме. Приложение 5.
Из результатов диаграммы видно, что хотели научиться решать задачи с помощью кругов Эйлера около 80 % учащихся.
2.3 Сборник задач по комбинаторике
Жена попросила своего мужа купить лук, капусту и морковь. Какими различными способами муж мог совершить покупку?
Записанный номер телефона из пяти цифр (5, 3, 4, 7, 2) оказался неверным. Необходимо определить варианты номера телефона.
Сколько трехзначных чисел можно составить из цифр 2,4,6,8 используя в записи числа каждую из них не более одного раза?
Сколько всевозможных вариантов pin-кода надо перебрать, чтобы среди них наверняка был и забытый?
Из группы теннисистов, в которую входят четыре человека – Иванов, Петров, Сидоров и Федоров, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?
Составьте все возможные трёхзначные числа из указанных цифр,
используя в записи числа каждую из них не более одного раза:
1, 3, 6, 8.
У Арины пять подруг: Катя, Юля, Лиза, Алёна и Таня. Она решила пригласить двух из них в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов?
Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?
В школьных кружках занимаются 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?
Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 — в районной. Сколько учеников не являются читателями школьной библиотеки?
В классе 35 учеников. 24 из них играют в футбол, 18 — в волейбол, 12 — в баскетбол. 10 учеников одновременно играют в футбол и волейбол, 8 — в футбол и баскетбол, а 5 — в волейбол и баскетбол. Сколько учеников играют и в футбол, и в волейбол, и в баскетбол одновременно?
58 человек ежедневно добираются на работу общественным транспортом: на автобусе, на трамвае или на метро. Каждый пользуется хотя бы одним из видов транспорта. 42 человека из них используют метро, 32 – трамвай, 44 – автобус. 21 человек из них используют метро и трамвай, 31 – метро и автобус, 22 – трамвай и автобус. Сколько среди них человек, которые используют все три вида транспорта, чтобы добраться на работу?
В 6 А классе 15 человек. В кружок «Эрудит» ходят 5 человек, в кружок «Путь к слову» 13 человек, спортивную секцию посещают 3 человека. Причем 2 человека посещают кружок «Эрудит» и кружок «Путь к слову», «Эрудит» и спортивную секцию, спортивную секцию и «Путь к слову». Сколько человек посещают все три кружка?
В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 – и микроволновку, и телевизор, 15- холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
В детском саду 52 ребенка. Каждый из них любит либо пирожное, либо мороженое, либо и то, и другое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?
В поход ходили 80 % учеников класса, а на экскурсии было 60 %, причем каждый был в походе или на экскурсии. Сколько процентов класса были и там, и там?
В нашем классе 24 ученика. Все они хорошо провели зимние каникулы.10 человек катались на лыжах, 16 ездили на каток, а 12 — лепили снеговиков. Сколько учеников смогли покататься и на лыжах, и на коньках, и слепить снеговика?
9 моих друзей любят бананы, 8 – апельсины, а 7 – сливы, 5 – бананы и апельсины, 3 – бананы и сливы, 4 – апельсины и сливы, 2 – бананы, апельсины и сливы. Сколько у меня друзей?
В пионерском лагере «Дубки» в смене актива отдыхали: 30 отличников, 28 победителей олимпиад и 42 спортсмена. 10 человек были и отличниками и победителями олимпиад, 5 — отличниками и спортсменами, 8 — спортсменами и победителями олимпиад, 3 — и отличники, и спортсмены, и победители олимпиад. Сколько ребят отдыхали в лагере?
У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро – собак. И только у двоих есть и те и другте. Угадайте, сколько у меня подруг?
В кондитерском отделе супермаркета посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет. В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет?
Во дворе стоят машины. Некоторые из них — москвичи, а остальные — жигули. Некоторые из машин красные, а остальные белые. Некоторые из машин новые, а остальные — старые. Известно, что красных москвичей — 3, новых москвичей — 4, а новых красных машин — 5. При этом старых белых москвичей — 2, новых белых жигулей — 1, а старых красных москвичей вообще ни одного. Сколько во дворе новых красных москвичей, если всего машин 21, а старых белых жигулей — 6.
В результате выполнения проектной работы был создан задачник, который состоит из 23 задач и по теории вероятности, и по комбинаторике.
Как видно из моей исследовательской работы, задачи состоят из множества данных. Выстроив данные в единую цепочку, можно увидеть, что решение задач подчиняется одному и тому же способу. Для решения задач, решаемых с помощью кругов Эйлера, был составлен алгоритм, состоящий из следующих этапов:
• Записываем краткое условие задачи.
• Выполняем рисунок.
• Записываем данные в круги (или в диаграмму Эйлера).
• Выбираем условие, которое содержит больше свойств.
• Анализируем, рассуждаем, не забывая записывать результаты в части круга (диаграммы).
• Записываем ответ.
Логические задачи заставляют думать, рассуждать, составлять цепочку действий, последовательность, учат алгоритмизации, что немаловажно в современной жизни. А исследовательские работы учат искать информацию из различных источников (включая и интернет) и обрабатывать её, учат находить из большого материала лишь тот, который необходим.
На уроках математики мы решали эти задачи, некоторые из них вызывали у нас затруднение.
3. Заключение
Диаграммы Эйлера — это общее название целого ряда способов графической иллюстрации, широко используемых в различных областях математики: теория множеств, теория вероятностей, логика, статистика, компьютерные науки, и др. Применение кругов Эйлера позволяет даже пятикласснику легко решать задачи, которые обычным путем решаются только в старших классах.
Моя работа заключалась в том, чтобы узнать подробнее об одном из разделов математики – комбинаторике. Я постаралась выяснить, какие комбинаторные методы применяются в наше время. Научилась составлять и решать задачи с помощью кругов Эйлера. В школьных учебниках мало комбинаторных задач. А ведь они включены в олимпиадные задания, ОГЭ и ЕГЭ. Поэтому мне захотелось помочь учителям и ребятам в изучении данной темы. Я надеюсь продолжить работу над этой темой, разработать уже задачи для учащихся старших классов. Самое главное я считаю, что своей работой я заинтересовала и учащихся нашей школы, и учителей. Ведь придумывая самостоятельно задачи, ребята будут развивать в себе еще логическое мышление и творческие способности.
Список использованной литературы
Гусев В. А., Орлов А. И., Розенталь А. Л. Внеклассная работа по математике в 6-8 классах: книга для учителя. М.: Просвещение, 1984– 286с
Савин А. П. Энциклопедический словарь юного математика – М.: Педагогика, 1989. – 352с.
http://ru.wikipedia.org
ПРИЛОЖЕНИЕ 1. Задачи № 1, № 2, № 3
Рис. 1
Рис. 2
Рис. 3
ПРИЛОЖЕНИЕ 2. Задачи № 5, № 6
Рис. 4
Рис. 5
Рис. 6
ПРИЛОЖЕНИЕ 3. Задачи № 7, № 8, № 10
Рис. 7
Рис. 8
Рис. 9
ПРИЛОЖЕНИЕ 4. Задача № 11
Рис. 10
ПРИЛОЖЕНИЕ 5. Результаты социологического опроса
Просмотров работы: 21069