Как составить задачу геометрические фигуры

Содержание:

Логическое построение геометрии

Геометрия – это наука о пространственной форме и количественных характеристиках предметов реального мира. Прочие свойства предметов изучают другие дисциплины. Если при изучении предмета учитывать только пространственную форму и размеры, то получим абстрактный объект, называемый геометрической фигурой.

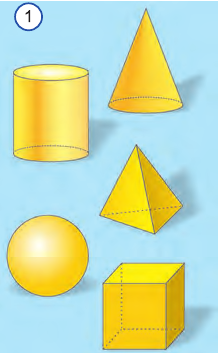
Слово “геометрия” – греческого происхождения и в переводе означает землеизмерение. Геометрию, изучаемую в школе, называют евклидовой по имени древнегреческого ученого Евклида. Геометрия состоит из двух частей: планиметрии и стереометрии. Планиметрия изучает свойства фигур на плоскости, а стереометрия – в пространстве (рис. 1).

Чтобы отличать геометрические фигуры друг от друга, их свойства описывают в виде утверждения, которое называют определением. Однако, определить вес геометрические фигуры невозможно. Некоторые из них, первоначальные, вынуждены принять без определения. Принимаем их за неопределяемые, начальные (основные) геометрические фигуры. Логическое построение геометрии осуществляют в следующем порядке: 1. Вначале принимают основные (начальные) геометрические фигуры без определения; 2. Принимают основные свойства этих фигур без доказательств;

3. Определяют другие геометрические фигуры через основные фигуры и их свойства, а затем доказывают свойства этих фигур и утверждений, истинность которых устанавливается путем доказательств, опираясь на известные.

Такое построение науки называют аксиоматическим построением. Свойства фигур, принятые без доказательства, называют аксиомами.

В планиметрии, которую мы изучали до сих пор основными геометрическими фигурами были точка и прямая. Их приняли без определения. Но определили отрезок, луч, треугольник и другие геометрические фигуры. Точно так же следующие свойства (утверждения) мы принимаем без доказательств в качестве аксиом:

I. Аксиомы принадлежности

1.1. Какова бы ни была прямая на плоскости, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

1.2. Через любые две точки можно провести прямую, и притом только одну.

II. Аксиомы расположения

2.1. Из трех точек, лежащих на прямой, одна и только одна лежит между двумя другими.

2.2. Любая прямая делит плоскость на две части: на две полуплоскости.

III. Аксиомы измерения

3.1. Любой отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

3.2. Любой угол имеет определенную градусную меру, большую нуля. Градусная мера развернутого угла равна 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

IV. Аксиомы откладывания

4.1. На любом луче от его начальной точки можно отложить единственный отрезок, равный данному.

4.2. От любого луча в определенную полуплоскость можно отложить единственный угол, равный данному, не развернутому углу.

4.3. Для любого треугольника существует единственный равный ему треугольник в заданном расположении относительно данного луча.

V. Аксиома параллельности

5.1. На плоскости через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

Вывод некоторого утверждения с помощью логических размышлений называют доказательством. Утверждение, верность которого установлена с помощью доказательства, называют теоремой. Обычно теорема состоит из условия и заключения. В первой части теоремы – условии объясняют что задано. А во второй части – заключении формулируют что требуется доказать.

Доказать теорему – эго значит, используя ее условие, опираясь на принятые и доказанные ранее свойства, рассуждая, привести к правильности предложения, сформулированного в заключении.

Уточнение условия и заключения теоремы – разъясняет ее, облегчает понимание и доказательство теоремы.

Древнегреческий ученый Платон отмстил удивительную закономерность в геометрии: из свойств, изученных и доказанных ранее, логически размышляя и обдумывая, можно получить новые свойства. Следовательно, используя эти удивительные возможности, можно формулировать остальные свойства в виде теорем, которые доказывают с помощью логических размышлений, аксиом, а также свойств, доказанных до этого.

В процессе размышления запрещается использование недоказанных свойств, даже если их правильность очевидна.

Таким образом, если рассматривать геометрию как одно здание, начальные понятия и аксиомы составляют его фундамент. Кирпичи, уложенные на этом фундаменте – это новые определяемые понятия и свойства, доказанные в виде теорем.

В формировании геометрии в качестве самостоятельной науки большой вклад внесли древнегреческие ученые. Например, Гиппократ Хиосский дал разъяснения о первых геометрических понятиях. Наибольший вклад в этой области принадлежит великому древнегречеcкому ученому Евклиду (356-300 годы до нашей эры). Его основной труд “Начала” содержит планиметрию, стереометрию и некоторые вопросы теории вероятностей, кроме того, алгебру, основы теории отношений, способы вычисления площадей и объемов и также элементы теории пределов. Евклид в “Началах” собрал все достижения древнегреческих математиков того времени и создал основу для дальнейшего развития математики.

“Начала” состоят из 13 книг и содержат переработанные труды древнегреческих ученых V – IV веков до нашей эры. В нем приведены 23 определения, 5 постулатов и 9 аксиом. В этом труде даны правильные определения прямоугольника, квадрата и окружности. Для точки и прямой приведены следующие определения: “Точка-это то, что не имеет частей”, “Линия-это длина без ширины”.

В “Началах” приведены 9 аксиом – высказывания, принятые без доказательства. Также приведены следующие 5 математических умозаключений (постулатов), позволяющие осуществлять геометрические построения:

I. Через любые две точки можно провести только одну прямую.

II. Отрезок прямой можно бесконечно продолжить.

III. Из любой точки можно построить окружность произвольныго радиуса.

IV. Все прямые углы равны между собой.

V. Если две прямые, лежащие в одной плоскости, пересеченные третьей, образуют внутренние углы, сумма которых меньше двух прямых углов, то при продолжении вышеупомянутых прямых они пересекутся с той стороны, где сумма углов меньше двух прямых углов.

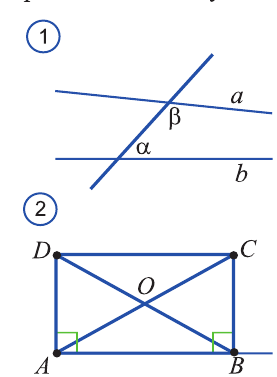
Упомянутый труд получил огромную славу и признание. Особенно V постулат стал причиной большой научной дискуссии. Если обозначить внутренние углы в V постулате а и (3 (рис. 1), а прямые а и b, то по смыслу этого постулата а+(3 <180°, и прямые аи b пересекаются.

Многие ученые, пытаясь доказать постулат V, заменяли его другими равносильными умозаключениями. Например, аксиома параллельных английского математика Яна Плейфер (1748-1819) звучит так: На плоскости из точки, расположенной вне прямой, можно провести только одну прямую, параллельную этой прямой.

Математик, поэт, астроном и философ Омар Гиясаддин Лбул Фахт ибн Ибрахим Хайям также занимался этой задачей. Хайям в своем сочинении “Комментарии к сложностям в вводной части книги Евклида” остановился на V постулате. Он, пытаясь доказать постулат Евклида как теорему, рассмотрел прямоугольник с двумя прямыми углами в основании и сделал вывод, что, если два угла при нижнем основании прямые, то и углы при верхнем основании должны быть прямыми (рис.2). Хайям говорит:

“Две прямые, перпендикулярные одной и той же прямой, не могут пересечься”. Итальянский математик Д. Саккери (1667-1733), не знакомый с работой Омара Хайяма, занимаясь V постулатом, также обратился к прямоугольнику. Данный прямоугольник вошел в основания геометрии под названием “Прямоугольник Хайяма-Саккери”.

Эту проблему решил великий русский математик Николай Иванович Лобачевский, построив неевклидовую геометрию. Лобачевский впервые доказал, что пятый постулат Евклидовой геометрии не связан с другими аксиомами. Эта геометрия полностью отличалась от Евклидовой геометрии. Однако, ни к каким логическим противоречиям это не привело, несмотря на то, что две геометрии не могли существовать одновременно. Несмотря на это, Лобачевский сделал новые результаты, которые также не имели логических противоречий. Новая геометрия и геометрия Евклида полностью совпадали по первым четырем аксиомам. Эта группа аксиом и их следствия назвали абсолютной геометрией.

Однако, неевклидовая геометрия (геометрия Лобачевского) серьезно отличалась от геометрии Евклида. Например, в геометрии Лобачевского сумма внутренних углов треугольника может быть меньше л, подобных, но неравных треугольников не существует, множество точек, равноудаленных от данной прямой, являются не прямой, а кривой линией и так далее.

В создание неевклидовой геометрии внесли большой вклад венгерский математик Янош Бойяи (1802-1860) и немецкий математик Карл Фридрих Гаусс (1777-1855). Также большую работу по описанию новой геометрии проделали итальянский ученый Эудженио Бельтрами (1835-1900) и немецкий математик Бернхард Риман (1826-1866).

Начатая Евклидом аксиоматика в некотором смысле получила завершение в работах немецкого математика Давида Гильберта (1862-1943) и русского математика Вениамина Федоровича Кагана (1869-1953).

• Заказать решение задач по высшей математике

Геометрические задачи и методы их решения

Как было отмечено ранее, одно из самых замечательных свойств геометрии заключается в возможности создания новых утверждений на основе ранее изученных, доказанных предложений, с помощью рассуждений и логического мышления. С помощью этой замечательной возможности доказываются и оставшиеся утверждения, выраженные в виде теорем или задач, основываясь на аксиомах и ранее доказанных свойствах. На основе этого и появлялись математические или геометрические задачи.

В математической задаче приводятся данные (условия). Используя их, требуется что-то найти (вычислить), или доказать, или построить. Выполнение поставленных требований и является решением задачи.

Геометрические задачи в соответствии с поставленным требованием делятся на вычислительные задачи, на задачи, требующие доказательства, исследовательские задачи и задачи на построение.

Для решения математической задачи знание условия недостаточно. Предполагается также наличие навыков и опыта решения задач. Чтобы добиться таких навыков нужно начать с решения простых задач и последовательно переходить к решению болсс сложных. Точно также нужно рассматривать различные методы решения и для их успешного усвоения решать много задач. Каждый метод применяется для определенной группы задач. Чем больше методов вы будете применять, тем больше получите навыков решения задач.

Ниже мы остановимся на некоторых наиболее важных методах решения геометрических задач. Методы решения задач по структуре делятся на синтетический, аналитический, доказательства от противного и другие. А но применению аппарата математики делятся на методы: алгебраический, векторный, координатный, вычисления площадей, подобия, геометрического преобразования.

Синтетический метод

Синтетический метод: используя данные условия задачи строят цепочку логических рассуждений. Цепочку продолжают до тех пор, пока ее последнее звено не совпадет с требованием задачи.

Пример:

Биссектриса прямоугольника делит его сторону на отрезки длиной 7 см и 9 см (рис. 1). Найдите периметр прямоугольника.

Решение:

Пусть ABCD- прямоугольник, А К -биссектриса,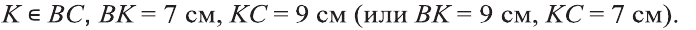

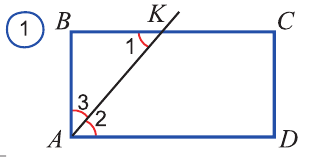
Эта задача входит в число опорных задач, так как многие задачи составляют на основании аналогичной идеи. Биссектрисы параллелограмма и трапеции отсекают от плоскости этих фигур равнобедренные треугольники. О таких важных фактах нужно помнить всегда. Они очень помогают при решении других задач.

Аналитический метод

Аналитический метод заключается в том, что, исходя из требования (вывода) утверждения (теоремы или задачи) и опираясь на известное утверждение, строится цепочка логических рассуждений, которая показывает, что требование является следствием условия.

Пример:

Докажите, что середины сторон любого четырехугольника являются вершинами параллелограмма.

Доказательство:

Пусть ABCD – четырехугольник (рис. 2), АК — КВ, BL = LC, CQ = QD, АР = PD. Проведем диагонали АС и BD четырехугольника.

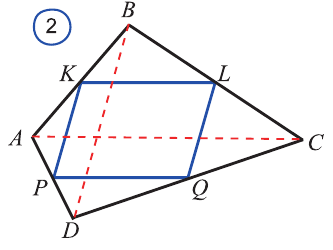
5. Из (3) и (4) имеем: KLQP – параллелограмм.

Рассмотренные выше синтетический и аналитический методы также называются прямыми методами. При решении задач прямыми способами сначала анализируется условие задачи. По результатам анализа выбирается метод, после этого строится и разбирается модель (чертеж) задачи в виде рисунка. В таком русле ведется обсуждение и переход от условия задачи к ее решению.

Есть и обратный метод решения задачи. С ним мы часто сталкивались. Называется этот метод “методом доказательства от противного“. Приведем алгоритм использования этого метода.

Алгоритм применения метода доказательства от противного.

Пример:

Если каждая из двух прямых параллельна третьей, то они параллельны между собой.

Пусть заданы прямые а и b, и пусть каждая из них параллельна третьей прямой с. Докажем теорему методом доказательства от противного.

Доказательство: Предположим противное:

Пусть каждая из прямых а и Ъ параллельна третьей прямой с, но сами прямые не параллельны друг лругу, то есть они пересекаются в некоторой точке А (рис. 3). Тогда через точку А прямой с проходят две прямые а и Ъ, параллельные ей. Это противоречит аксиоме параллельности. Следовательно, предположение было неверным. Значит, если каждая из двух прямых а и b параллельна третьей прямой с, то эти прямые параллельны между собой.

Вышеприведенный метод основан на следующем логическом законе: из двух противоречащих друг другу утверждений только одно верно, а другое ложно, третьего не дано.

Теперь рассмотрим другие методы решения геометрических задач.

Алгебраический метод

При решении геометрических задач алгебраическим методом целесообразно пользоваться следующим алгоритмом:

1. проанализировать содержание задачи и построить модель его чертежа;
2. обозначить неизвестные буквами;
3. по условию задачи составить уравнение или систему уравнений;
4. решить составленные уравнения или системы уравнений;
5. проанализировать полученное решение;
6. написать ответ.

Пример:

Периметр прямоугольного треугольника равен 36 см. Отношение гипотенузы к катету равно 5 : 3. Найдите стороны треугольника.

Пусть задан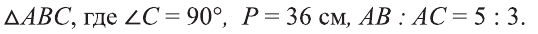

Решение:

Обозначим коэффициент пропорциональности буквой к.

Тогда АВ = 5к, АС = 3к.

По теореме Пифагора: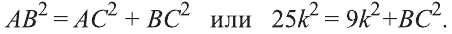

Откуда,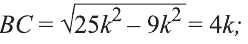

По условию задачи: Р = 36 см, Р = АВ + АС + ВС.

Следовательно, 5к + 3к + 4к = 36. Откуда, к- 3;

Тогда, АВ = 5к = 15 (см), АС =3к=9 (см), ВС = 4к=12 (см).

Ответ: 15 см, 9 см, 12 см.

Метод площадей

При решении некоторых геометрических задач применение формул вычисления площадей быстро приводит к ожидаемому результату. В этом случае требуемые в задаче неизвестные находят из уравнения, полученного в результате уравнивания площадей вспомогательных фигур. В этом случае требуемые в задаче неизвестные находят из уравнения, полученного в результате уравнивания площадей вспомогательных фигур. Продемонстрируем это на следующем примере.

Пример:

Стороны треугольника 13 см, 14 см и 15 см. Найдите высоту, которая опущена на сторону, равную 14 см.

Решение.

Пусть задан треугольник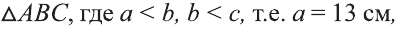

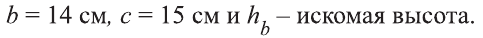
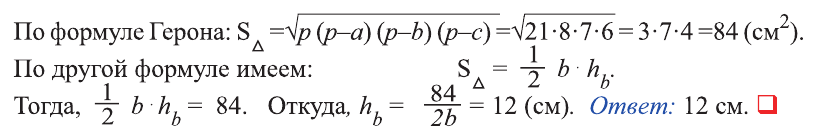
Векторный метод

При решении геометрических задач векторным методом целесообразно пользоваться следующим алгоритмом:

1. перевести задачу на язык векторов, то есть рассмотреть некоторые величины (отрезки), заданные в задаче как векторы, составить векторное равенство;
2. используя свойства действий над векторами преобразовать векторные равенства и найти неизвестное;
3. вернуть с векторного языка на геометрический;
4. записать ответ.

Метод векторов используется при решении задач, в которых требуется:

• доказать параллельность прямых (отрезков);
• поделить отрезки в заданном отношении;
• показать, что три точки лежат на одной прямой;
• показать, что четырехугольник является параллелограммом (ромбом, трапецией, квадратом, прямоугольником).

Пример:

Докажите, что середины сторон выпуклого четырехугольника являются вершинами параллелограмма.

Решение:

Пусть ABCD заданный четырехугольник, где АК – КВ, BL – LC, CQ = QD, АР = PD (рис. 4).

Доказательство:

1. Заменив отрезки соответствующими векторами

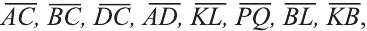, запишем задачу векторным языком;

2. Используем для сложения векторов правилом треугольника:

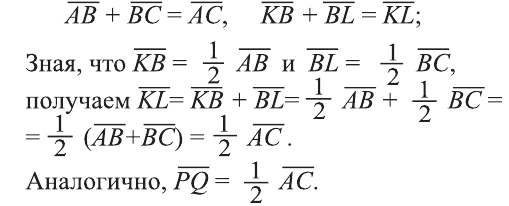
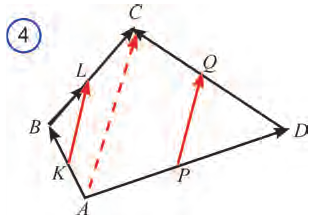
3. 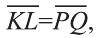то есть эти векторы одинаково направлены и их длины равны. Следовательно, по признаку параллелограмма четырехугольник KLQP является параллелограммом.

Метод координат

При решении геометрических задач методом координат целесообразно пользоваться следующим алгоритмом:

1. проанализировать содержание задачи и записать геометрическую задачу на языке координат;
2. преобразовать выражение и вычислить его значение;
3. перевести результат на геометрический язык и записать ответ.

Методом координат чаще всего решают следующие задачи: а) на нахождение геометрических мест точек; б) на доказательство зависимости между линейными элементами геометрических фигур.

При решении задач методом координат важно рационально выбрать систему координат. Данную фигуру следует разместить относительно осей координат таким образом, чтобы как можно больше координат нужных точек равнялись нулю или одному и тому числу.

Пример:

Докажи те, что параллелограмм, диагонали которого равны, является прямоугольником.

Доказательство:

Выберем систему координат так, чтобы вершины параллелограмма имели следующие координаты (рис. 5):

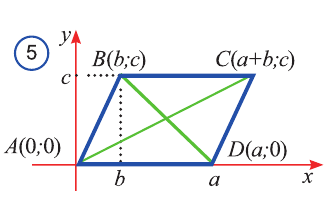
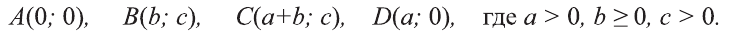
Выразим расстояния между точками А, В, С, D через их координаты: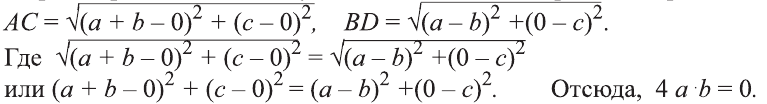

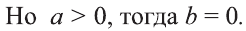
Это, в свою очередь, означает, что точка В (b; с) лежит на оси Оу. Поэтому АBСD прямоугольный.

Отсюда следует, что параллелограмм ABCD является прямоугольником.

Метод геометрических преобразований

Метод геометрических преобразований: метод поворота, метод симметрии, метод параллельного переноса и метод гомотетии. При решении задач методом геометрических преобразований наряду с данными геометрическими фигурами рассматриваются и фигуры, полученные в результате определенного преобразования. Определяются свойства новых фигур и переносятся на данную фигуру. Затем выбирается способ решения задачи.

Все приведенные выше методы, где используется больше свойств геометрических фигур, называются геометрическими методами.

                                                                               
Охрименко Елена Викторовна,

учитель
начальных классов

высшей
квалификационной категории

                                                     
МБОУ «Средняя общеобразовательная

школа № 43
им. Г.К.Жукова» города Курска

Урок
математики. 1класс

Решение
задач. Геометрические фигуры.

Пояснительная
записка

Автор материала (ФИО)	Охрименко Елена Викторовна
Должность (с указанием преподаваемого предмета)	Учитель начальных классов, МБОУ «Средняя общеобразовательная школа № 43 им. Г.К.Жукова» города  Курска
Название материала	Урок по теме «Решение задач. Геометрические фигуры.»
Класс (возраст)	1 класс  (7 – 8 лет)
Учебный предмет	Математика
Название учебного пособия, образовательной программы (УМК) с указанием авторов, к которому относится ресурс	УМК «Школа России» Учебник: Моро, М. И. Математика. 1 класс : учеб. Для общеобразоват. Учреждений : в 2 ч. / М. И. Моро, С. И. Волкова, С. В. Степанова. – М. : Просвещение, 2013. Моро, М. И. Математика. 1 класс : рабочая тетрадь для обучающихся общеобразоват. Учреждений : в 2 ч. / М. И. Моро, С. И. Волкова. – М. : Просвещение, 2013.
Вид ресурса (презентация, видео, текстовый документ и другие)	Презентация, текстовый документ.
Техническое оснащение Оборудование	Ноутбук, экран, проектор, презентация, конверт с письмом, картинки,   музыка из кинофильма «Золушка», наборы счетного материала (геометрические фигуры), цветочки, три цветных карандаша : желтый, зеленый, красный.
	Планируемые результаты (предметные): – уметь находить в тексте задачи условие и вопрос; – анализировать готовую схему, выбирать нужную, заполнять схему самостоятельно; – устанавливать зависимость между величинами, объяснять выбор действий; – решать простые задачи: раскрывающие смысл действий сложения и вычитания, «увеличить (уменьшить) на …»; Универсальные учебные действия (метапредметные): Регулятивные: уметь самостоятельно ставить цель предстоящей  практической работы. Коммуникативные: уметь слушать и вступать в диалог, участвовать в коллективном обсуждении. Познавательные: уметь осуществлять анализ объектов с выделением существенных и несущественных признаков, синтез как составление целого из частей. Личностные: проявлять познавательный интерес, положительное отношение к школе, одноклассникам.
Краткое описание работы с ресурсом (на каком этапе предполагается применение, форма использования: индивидуальная, групповая и другое, на усмотрение автора)	Данный урок   продолжает изучение раздела « Числа от 1 до 10 и число 0. Сложение и вычитание». Так как данный материал содержит большой объём   информации, был выбран такой тип урока  – комбинированный.             Урок составлен с опорой на психолого-педагогическую характеристику класса с учетом возрастных особенностей обучающихся. По наполняемости обучающимися класс средний, поэтому на уроке использовался дифференцированный подход –  работа в  парах велась по принципу «сильный помогает слабому», деление класса на  2 группы (по вариантам ) было осуществлено таким образом, что в них вошли  ученики  разного уровня обучаемости.           Для активизации изучения   достаточно серьезного и объемного материала на уроке были использованы различные методы: словесные, наглядные, частично-поисковый метод,  исследовательский метод, метод прогнозирования.  Также были использованы различные формы работы: игровая работа с текстом  тетради и  учебника, работа с  математическими  терминами, работа со наглядным материалом, с счетным геометрическим материалом  и прочее. Все виды работ на уроке организовывались на базе  математического  учебного материала .            Работа на уроке активизирована, еще и тем, что перед обучающимися поставлена конкретная типовая задача,      и они видят конечную цель.    Обучающиеся  сами себя оценивали поэтапно (расскрашивали  лепестки в цветочке.)            На уроке идет  сочетание различных форм работы. Каждый новый вид занятий включает отработку и закрепление разнообразных  УУД .           Каждый этап урока сопровождается контролем учителя и самоконтролем обучающихся для выявления степени усвоения  материала.           Обучающимся   предлагаются :    работа в парах и самостоятельная работа.          Содержание урока полностью соответствуют требованиям программы.
Список используемой литературы. Ссылки на Интернет -источники.	http://www.zavuch.info/uploads/methodlib/2012/3/9/ http://nsportal.ru/ http://www.zavuch.info/methodlib/305/ http://www.zavuch.info/methodlib/305/58537/ http://www.zavuch.info/methodlib/68/ http://www.rusedu.ru/detail_23182.html http://n-shkola.ru/files/repos_2/163_4

Этап урока, время	Деятельность учителя	Деятельность обучающихся	Задачи этапа. УУД
1.Органи-зационное начало урока. Эмоцио- нальный настрой. (1 мин.)	-Начинаем урок математики. Проверьте свою  готовность к уроку. Давайте улыбнемся друг другу, постараемся доставить себе радость и положительные эмоции. Обнимите себя крепко, настройтесь на работу на уроке.	1.Встают из-за парт. 2.Проверяют школьные принадлежности. 3.Улыбаются друг другу. 4.Крепко обнимают себя руками. 5. Организация внутренней речи.	Способствует созданию состояния психо-эмоциональной стабильности, внешней мотивации. УУД (личностные): – внутренняя позиция обучающегося на уровне положительного отношения к процессу обучения; –мотивационная основа учебной деятельности
2. Мобилизу- ющий этап  (7-8 мин)	Стук в дверь .. Учитель вносит письмо в класс. Читает на конверте : « Ученикам 1 В класса от Феи ». -Вам интересно, что там написано ? -Прочитаем? -И..так … Жил-был вдовец, у которого была прелестная добрая дочка. Однажды он решил жениться вновь и взял в жены злую, эгоистичную женщину. У нее были две дочери, которые по характеру были как две капли воды похожи на свою мать. После свадьбы мачеха сразу же показала свой злой нрав. Она прекрасно понимала, что рядом с красивой добросердечной падчерицей ее родные дочки выглядят еще грязнее и уродливее. Поэтому она возненавидела падчерицу и заставляла ее делать всю самую грязную работу по дому. Бедная девочка готовила и стирала, убирала комнаты сестер и мыла лестницы. Сама же она жила в маленькой тесной каморке на чердаке…По вечерам она часто сидела на теплой золе у самого очага, поэтому ее прозвали ….  -Вы догадались, как звали эту сказочную героиню? -Кто автор? -Кто из вас знает, как называется это произведение? – Золушка пришла к нам на урок, и с ней мы отправимся в путешествие  по сказочному  Царству -государству . -Куда хотела попасть Золушка в сказке? -Для  чего? -Но так просто ей туда  не попасть. -На ее пути будет много препятсвий. – Давайте поможем Золушке их преодолеть.  Пусть  она попадёт на бал и встретится с принцем . -Помогите продолжить Золушке числовую дорожку, по которой  пройдет ее путь. -Прочитайте ряд чисел. -Найдите закономерность. -Докажите её. -Вспомните, в какое время начинала работать наша героиня? -Выполните задания устного счета, и помогите Золушке преодолеть еще одно препятствие. -Что нужно сделать?  -Прочитайте примеры по-разному, найдите их значение. -Ребята, Золушка представила замок, в котором она встретится с принцем. -Откройте учебник на странице 97 и рассмотрите его.  -Какие геометрические фигуры вы видите на рисунке? -Назовите фигуры, похожие на круг? -Назовите фигуры похожие на треугольник? -Назовите фигуры, похожие  на четырехугольник? -Назовите фигуры, похожие  на шестиугольник?	Примерные ответы (ПО) -Да -Да ПО:  -Звали эту сказочную героиню – Золушка -Ш.Перро -Сказка «Золушка» -Золушка хотела попасть на бал -Она хотела встретится с принцем ПО: -Каждое следующее число уменьшается на 2, увеличивается  на 2 -9-2, получится,7; -из 7 вычесть 2 ,получится 5, -5 минус 2, равно 3, вставим – 3, –из 3 вычесть 2, получится 1, вставляем 1 (аналогичная работа проводится с другим рядом чисел ) -Очень рано, солнце еще не взошло ПО: -К числам на конце лучиков прибавить  2 ПО: -К 6 прибавить 2,получится 8; – 3 да 2 это 5; -Первое слагаемое – 7, второе – 2, сумма чисел равна 9; -2 плюс 2, равно 4; -Сумма чисел 5-и  и 2-ух равна 7; -6 и 2 это 8; -4 увеличить на 2, получится 6; ПО:  -Круг, треугольник, четырехугольник,шестиугольник, ломаная линия, луч и т.д. -Солнце, колеса кареты, окно в карете, окна в башне. -Крыши башен, флаги на башнях. -Окна , двери в башне, дорожка в замке, коврик в карете, окно в двери кареты. -Изразец около окна .	Обеспечивает высокий уровень вовлеченности обучающихся в учебную деятельность и развитие их интеллектуальных качеств. УУД (познаватель- ные, регулятивные): – выбор оснований для классификации; –самостоятель- ное формулирова- ние познавательной цели данного  этапа урока; – сохранение учебной задачи; –осуществлять пошаговый контроль.
3. Определение темы и цели урока (2-3мин.)	-Как вы думаете, чем мы будем заниматься на уроке математики? -А как мы будем с этим справляться? – Нам помогут  цветочки, с помощью которых вы будете оценивать каждый этап своей работы. -Они лежат у вас на парте. -Напомните, что еще нужно Золушке, чтобы отправиться на бал?  -Сверим свои ответы с учебником  –На чем собиралась отправиться   на бал героиня? – Чтобы появилась карета у Золушки, добрая фея  предлагает вам прочитать первое задание в учебнике на странице 96 .	-Устанавливать закономерность. -Складывать и вычитать числа. -Находить геометрические фигуры. -Отличать текст от задачи; решать задачи; составлять модели задач. -Карета, лошади, кучер, новое платье,  туфельки. -На карете	Активизация терменологической речи. УУД (познавательные): -выделение опоры, значимой для построения цепочки мыслительных операций; -формирование решать учебнуюзадачу, опираясь на математическое чутьё; -постановка и формулировка темы и цели урока.
4. Работа с информацион ным полем (5-7 мин)	-Что вы прочитали? -Докажите, что это задача. –Вычитайте условие задачи. -Что мы должны составить к задаче? -Чтобы решить задачу, сколько чисел должно быть в ней? -Назовите эти числа?  -Какой вопрос задачи? -Вычитайте  его. -Давайте поработаем со счетным материалом  -Используя геометрические фигуры – квадраты, выложите решение задачи. -Чего не хватает в записи? -Чтобы назвать ответ, надо вспомнить  вопрос задачи. -Вычитайте вопрос.  -Дайте ответ. -И вот фея дарит нашей героине карету.  -Закройте учебники, сложите счетный материал, возьмите цветные карандаши и оцените свою работу. -Как вы справились с ней? -Если вы считаете, что работу выполнили без ошибок – желтый карашдаш, зеленый – маленькие недочеты, красный, если вы испытываете трудности в выполнении этого задания. -Раскрасьте  один лепесток у цветка.	ПО:  -Задачу. -Есть условие и вопрос. – У Люси было 4 тетради. Стало на 2 больше. -Решение -Хотя бы 2 числа – 4 и 2 -Сколько тетрадей стало у Люси? Конструирование схемы к задаче, запись её. ПО: -В задаче говорится о 4 тетрадях -Обозначу 4 тетради – 4-мя квадратами, -4 квадрата обозначу цифрой 4 (работа с наборным полотном);  -В условии сказано , что  стала на 2 больше, это столько же , да еще 2 -Показывает указкой на счетном материале;  – Добавлю еще 2 квадрата – 2 квадрата обозначу цифрой 2 -В условии сказано, что тетрадей стало больше, выберу знак «плюс» -В запись добавлю знак «=», получится 6 -Решение задачи (4 + 2 = 6) ПО: -Ответа -Сколько тетрадей стало у Люси? -6 тетрадей При необходимости организация диалога.	Разграничение области знания и незнания по данной теме. УУД ; (познавательные, регулятивные, личностные): -формирование умения рациональной работы с текстом; -формирование самооценки, уровня собственных знаний; -осуществление пошагового контроля; -развитие умения корректоровать информацию; -учебно-познавательный интерес к учебному материалу; -создание ситуации речевого высказывания,  участие в диалоге; -формирование умения доказывать свою точку зрения;
5.Физкульт-минутка (1-2 мин)	Пока мы с вами преодолевали препятствия, Золушка много работала, она устала и  просит помочь ей   постирать белье. -Поможем нашей героине? (Дети повторяют движения под музыку из кинофильма «Золушка») -Постираем белье вместе с Золушкой ( потерли кулачки). -Прополоскали белье  ( полощат белье). -Выжимаем белье (скручиваем). -Стряхнули белье. -Повесили на веревочку. –Расправили белье. -Прищепками закололи белье. -Вытерли пот с лица…  -Перевели дух, и ..вновь за работу..		Способствует снятию эмоционального и статического физического напряжения. Способствует поддержанию активной мыслительной деятельности. УУД (коммуни-кативные): -формирование умения пользоваться средствами невербального общения.
6.Стадия практического осмысления (5-7 мин.)	– Вспомните, кто нужен, чтобы карета двигалась? -Правильно, вот и еще  одно задание от доброй феи. -Откройте тетради на странице  37. -Работаем в парах, сядьте поближе друг к другу. -Прочитайте «базарчиком» задание от доброй феи.  -Обсудите  его. -Напоминаю вам, что надо найти 2 задачи, обвести их номера, записать решение и ответ. -На выполнение задания дается 5 минут. Та пара, которая быстрее всех выполнит задание, подаст знак. -Первая пара. -Записывает на крыльях доски решение и ответ задач,объясняя их. -Ребята, сверьте свои записи с записями своих товарищей ( открываются крылья доски) -Фея дарит вам по лошадке, за быструю и отличную работу (вручаются подарки). И добрая фея для Золушки дарит лошадок. -Вы вновь возьмите три цветных карандаша (желтый, зеленый, красный) и оцените свою работу -Раскрасьте  следующий  лепесток у цветка –  Золушка устала, она перебирала крупы у нее  устали глаза. Давайте отдохнем.	-Лошади ПО: 5 + 2 = 7 (ш.) Ответ: 7 шариков. 10 – 2 = 8 (м.) Ответ: 8 мячей.	УУД (познаватель ные): -формирование  умения работать с  информацион ным текстом; (регуля- тивные) : -формирование  умения предвидеть трудности, осознание их причин и способов избегания.
7.Физкульт минутка (1-2 мин)	-Расслабьтесь, примите удобное положение и повторяйте движения для глаз за нашими помощниками:стрелкой, звездочкой, точкой		Способствует снятию эмоционального и статического физического напряжения. Способствует поддержанию активной мыслительной деятельности. УУД  (комму-никативные): -формирование умения пользоваться средствами невербального общения.
8.Работа с информацион-ным полем (3-5 мин.)	–Продолжаем нашу работу. -Вспомните,  что еще подарила добрая фея Золушке? – Правильно. – Это роскошное платье, расшитое золотом и серебром и хрустальные туфельки. -А как назвать все это одним словом? –  Наряд появится только тогда, когда вы поработаете самостоятельно в тетради. -Рассмотрите следующее  задание на странице 37. -Что вы видите на рисунке? -Из скольких звеньев состоит ломаная? -Какое задание вам предстоит  выполнить? Это задание вы будете выполнять по вариантам: -Слева-работа для 1 варианта, справа – для 2-ого. -Когда вы выполните задание, отложите ручки в сторону и поднимите на меня глаза, тогда я буду знать кто из вас готов к дальнейшей работе.  -На выполнение этой работы вам 3 минуты, приступайте. -Сверьте правильность выполнения своей работы  с образцом на слайде . И вновь возьмите цветные карандаши и оцените свою работу. -Как вы справились с ней? -Раскрасьте   последний   лепесток у цветка.	ПО: -Добрая фея подарила Золушке платье и хрустальные туфельки.  -Наряд ПО: -Ломаную -Из двух звеньев -Измерить длины ломаных, сравнить длины  звеньев  ломаных	Активизация имеющихся знаний. УУД (познавательные, регулятивные, личностные): -развитие распределения внимания; -сохранение учебной задачи; -способность к снижению состояния дискомфорта. УУД (познавательные, регулятивные, личностные): -развитие аналитическо-синтетической операции мышления; – умение обосновывать свою точку зрения;
9. Рефлексия (2-3 мин.)	– Фея благодарит вас за помощь Золушке и дарит ей роскошный наряд с хрустальными туфельками, в котором она и отправится на бал к своему принцу   –Ребята, Фея предлагает  украсить это платье цветочками, которые вы расскрашивали. (Звучит музыка из кинофильма «Золушка») – Скажите, какой цвет преобладает? – О чем это говорит? -Ребята, я тоже  украшу наряд Золушки своим цветком, потому что мне понравилась ваша работа на уроке, – Вы   с легкостью преодолевали  все препятствия. Молодцы! -В каком царстве – государстве мы побывали?  -Какие сказочные герои нас сопровождали? -Чему вы учились на уроке, преодолевая препятствия? – Спасибо за работу. – Урок окончен.	выходят  и крепят цветочки к наряду ПО: -Желтый -Мы справились со  всеми заданиями и препятствими, на уроке было очень интересно -В сказочном, математическом -Золушка, Фея -Устанавливать закономерность. -Складывать и вычитать числа. -Находить геомерические фигуры. -Отличать текст от задачи. -Вспоминали из каких частей состоит задача. -Задача имеет условие, вопрос.  -Решение и ответ. -В задаче должно быть хотя бы 2 числа. -В задаче говорится об одних и тех же предметах.	Определение психо-эмоционального состояния обучающихся к концу урока. УУД (комму-никативые, личностные): -адекватно использовать речевые  средствадля решения заданной задачи; -формулировать собственное мнение; -выявлять  учебно- познавательный интерес.

Цели:

• формировать умение применять полученные на
  уроках знания в новой ситуации;
• учить составлять геометрические задачи;
• развивать умение оценивать факты;
• развивать творческие способности и навыки
  исследовательской деятельности;
• формировать и развивать умение мыслить по
  аналогии, умение обобщать, анализировать,
  наблюдать и делать выводы;
• воспитывать творческий подход к решению
  математических задач.

Задача урока: создание ситуации на
уроке, в которой учащийся проявит себя и сам
проанализирует уровень сложности, на котором он
может работать

Оборудование: презентация,
раздаточный материал: каждому ученику карточки
“Секреты мастерства”, набор заказов для
умельца, для подмастерья, для мастера.

Для создания соответствующей атмосферы:

• “Вещь, созданная руками Мастера, радует
  окружающих и приносит уважение своему
  создателю” Н. Конышева
• “Кто красотой гордиться, кто славой, кто
  уменьем:
  Да здравствует Мастер, гордящийся уменьем!” Н.
  Матвеева
• “Для подмастерья выше счастья нет,
  чем гнаться с тонкой кисточкой учёбы
  За смелой кистью Мастера вослед!”

Тип урока: комбинированный.

Вид урока: урок-мастерская.

Формы работы на уроке: фронтальная,
индивидуальная, работа в парах.

На уроке использована методика обратного
поэтапного формирования способа действий.

План урока.

1. Организационный момент.
2. Сообщение темы и цели урока.
3. Актуализация знаний учащихся Повторение
   изученного.
4. Отработка приёмов составления геометрических
   задач.
5. Творческая самостоятельная работа.
6. Презентация работ. Подведение итогов.
7. Задание на дом.

Ход урока

1. Организационный момент. Приём
отсроченной мотивации.

Я приглашаю Вас на урок геометрии, в мастерскую.

Скажите, а чем занимаются в мастерской?

А что можно мастерить на уроке геометрии?

2. Сообщение темы и цели урока.

Как бы вы сформулировали тему нашего урока?

В мастерской творит Мастер. Мы шагнём по
ступеням мастерства.

“Шагнуть вперёд можно лишь тогда, когда нога
отталкивается от чего-то, движение от ничего или
из ничего невозможно:” Василий Белов (русский
писатель)

Нам есть от чего оттолкнуться – от знаний.

Как настоящим мастерам нам понадобятся
инструменты.

С помощью чего можно составлять задачи?

Какие инструменты нам необходимы?

Теоремы, определения, свойства геометрических
фигур.

Проверим готовность наших инструментов.

3. Повторение изученного.

Приготовьтесь к сборке набора инструментов. На
наборном полотне в ячейках изображены чертежи.
Разложи теоремы, определения в соответствии с
чертежами.

Если вы сложили правильно, то узнаете, что можно
открыть с помощью инструментов. Это “секреты
мастерства”.

Лото “Секреты мастерства” (Приложение 1)

4. Обучение приёмам составления задач.

“Для подмастерья выше счастья нет,
чем гнаться с тонкой кисточкой учёбы
За смелой кистью Мастера вослед!”

Мастерство давало человеку достоинство и
приносило уважение окружающих.

У каждого Мастера есть свои секреты.

Раскроем и мы секреты мастерства составления
геометрических задач.

Приготовьте листы “Секреты мастерства” (Приложение 2)

Как создать геометрическую задачу?

– сконструировать чертёж;

– определить данные;

– получить возможные следствия и их
обоснования;

– на основе полученных следствий выдвинуть
требование к задаче.

Возьмём заготовку – простую задачу и путём
преобразований из простой задачи смастерим
более сложную, то есть с точки зрения геометрии
более красивую задачу. И чем сложнее задачу мы
сможем составить, чем больше знаний мы привлечём,
тем ценнее будет наше изделие.

Мастер-класс. Секрет первый. (Приложение 2)

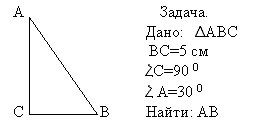
Решение:

1. ВС = 1/2 АВ (свойство катета, лежащего против
угла 30⁰)

АВ = 5 * 2=10 см

Ответ: АВ = 10 см.

Перепрячем в этой задаче условие А=30⁰ следующим образом: пусть
нам известно В=60⁰.

Тогда чтобы решить задачу надо сначала
вычислить угол А. Как это сделать?

На основании какого свойства?

Свойство острых углов прямоугольного
треугольника.

90 ⁰– 60⁰=30⁰.

Теперь наша задача решается в два шага.

Перепрячем ещё раз данное – пусть угол АВД=120⁰.
Этот угол внешний для АВС.
Необходимо применить свойство внешнего угла
треугольника.

Теперь задача решается в 3 шага.

Выглядит она так:

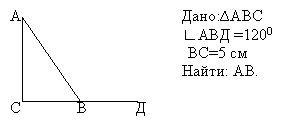
Решение:

1. АВС= 180⁰ – АВД (свойство внешнего угла) АВС= 180⁰-120⁰=60⁰

2. ВАС=90⁰ – АВС

ВАС= 90⁰ – 60⁰=30⁰
(свойство острых углов прямоугольного
треугольника)

3. ВС=1/2 АВ (свойство катета, лежащего против угла
30⁰) АВ=5 * 2=10 см

Ответ: АВ=10 см.

Рецепт

1. Составь простую задачу.
2. Перепрячь одно (несколько) данных с помощью,
   какой-либо теоремы.
3. Сформулируй новую более сложную задачу.

Поиграем в прятки по правилу: данное задачи
прячем с помощью какой-либо теоремы, свойства,
определения.

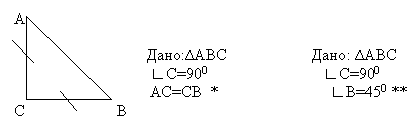
Теперь, чтобы от утверждения **перейти к
утверждению *надо применить

а) свойство острых углов прямоугольного
треугольника;

б) признак равнобедренного треугольника.

Секрет второй “Обработка данных”. (Приложение
2)

Как создать геометрическую задачу?

1. Сконструируй чертёж.
2. Определить данные.
3. Получить возможные следствия и их обоснования.
4. На основе полученных следствий выдвинуть
   требование к задаче.

Задача

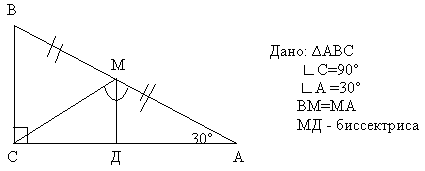
Утверждение обоснование

1. ВС = 1/2 АВ, АВ = 4 * 2 = 8 см Свойство катета,
лежащего против угла в 30^о

2. ВМ = МА по условию

3. СМ – медиана по определению

4. СМ = МА свойство медианы прямоугольного
треугольника

5. СМА – равнобедренный
по определению

6. МД – биссектриса по условию

7. МД – высота свойство биссектрисы
равнобедренного треугольника

8. МДА – прямоугольный
МД СА

9. МД = 1/2 МА , МА= 4 см, МД = 2 см свойство медианы
прямоугольного треугольника.

Это пока ещё не задача- это геометрическая
конструкция.

Для того чтобы получилась задача – выдвинем
требование к её решению.

Если мы потребуем доказать, что СМА – равнобедренный, сколько шагов
будет иметь решение? (5 шагов)

А если мы потребуем найти МД, сколько шагов
придётся выполнить? (9 шагов)

Задача готова!

5. Творческая самостоятельная поуровневая
работа.

Неленивого человека в старину называли
умельцем. Почти каждый умелец становился
подмастерьем, но только самые старательные –
мастерами!

У каждого из вас на столе лежит заказ на
изготовление задачи.

Решите сами, какой заказ вам по силам. (Приложение 3)

• Заказ для умельца – ремонт задачи (вставить
  пропуски);
• заказ для подмастерья – составить задачу по
  готовому чертежу;
• заказ для мастера – сконструировать свою
  задачу.

За выполнение заказа

• умелец может заработать 3 балла,
• подмастерье – 4 балла,
• мастер- 5 баллов.

Настоящий Мастер дарит результаты своего труда
окружающим. По окончанию работы я предлагаю Вам
свою работу поместить на выставку и презентовать
их.

У вас всё получится! Удачи! Приступайте к
работе.

6. Выставка работ. Подведение итогов.

” Кто красотой гордиться, кто славой, кто
уменьем:

Да здравствует Мастер, гордящийся уменьем!” Н.
Матвеева

Будьте

• Мудрыми
• Активными
• Смелыми
• Терпеливыми
• Ещё Решительными

И тогда каждый из Вас станет МАСТЕРОМ!

За работу хотелось бы отметить самых успешных и
старательных!

Им присваивается звание “Мастер задач”.

7. Задание на дом.

Смастерить геометрическую задачу.

Урок окончен!

                         МОУ Гимназия №16, г. Владикавказ

   «Пособие по  оформлению и решению

               геометрических задач».

                                                          Подготовила: Кудряшова Татьяна Александровна,

                                                          учитель начальных классов высшей категории,

                                                          руководитель школьного МО, городского метод.совета

                                                          и член метод.совета учебно-методического кабинета

                                                          начального образования СОРИПКРО

                                                           2010 г.

                            Памятка по решению геометрических задач.

                              Нахождение ПЕРИМЕТРА(Р).

                                                   Правило

Периметр – это сумма длин сторон какой-нибудь геометрической

                      фигуры.

 Кратко будем обозначать геометрические понятия  следующим образом:

 Рпр – это периметр прямоугольника;

 Ркв –  это периметр квадрата;

 а   –  это длина большей стороны  фигуры;

 в   –  это ширина стороны фигуры (иногда буква может меняться на

                                                                           любую другую )

                                                        а

                                                                        в

1. Нахождение периметра прямоугольника (Рпр ) можно находить

3 способами: Рпр = а+в+а+в (этот способ применяется, когда нужно найти

                                                     периметр любой другой геомет. фигуры)

                        Рпр = а ∙ 2+в ∙ 2;

                        Рпр = (а+в) ∙ 2 (этим способом мы будем пользоваться чаще!)

      2. Нахождение сторон прямоугольника (а или в)                            

                              а = Рпр : 2 – в:                                                                

                              в = Рпр : 2 – а

                                                    а

1. Нахождение периметра квадрата (Ркв)  по формуле:                                                                                  

                         Ркв = а ∙ 4

1. Нахождение стороны квадрата (а)

                              а =  Ркв : 4         

                          Оформление задачи в тетради 

Например :

Дано:                          а

а =  5см       

в =  3см                                                       в    

Рпр – ?            

                           (если нужно начертить чертёж, то его нужно чертить на этом месте, а

                               решение начинать с середины листа, а если  не требуется начертить

                            чертёж, то   решение выполнять нужно на этом месте  )  

                                                                       Решение.

      Рпр = (а+в) ∙ 2

      Рпр = (5см +3см) ∙ 2 = 16 (см)

       Ответ: Рпр = 16 см

    (Аналогично выполняются подобные задачи геометрического характера.)

                                    Нахождение ПЛОЩАДИ(S).

                                                  Правило

Площадь – это внутренняя часть какой-нибудь геометрической фигуры.

Кратко будем обозначать геометрические понятия  следующим образом:

 Sпр – это площадь прямоугольника;

 Sкв –  это площадь квадрата;

 а   –  это длина большей стороны  фигуры;

 в   –  это ширина стороны фигуры (иногда буква может меняться на

                                                                           любую другую )

                                                               а

                                                                                 в

1. Нахождение площади  прямоугольника (Sпр )  по формуле:

                                             Sпр = а ∙  в

1. Нахождение сторон прямоугольника (а или в):

                                             а = Sпр: в;                

                                             в = Sпр:а

                                                   а

                                                                а

3.Нахождение площади квадрата (Sкв)  по формуле:

                                                Sкв = а ∙ а                                                                                                                                                                                                

 4.Нахождение стороны квадрата (а)

                                           а =  Sкв : а         

                 Оформление задачи в тетради 

Например: ( данные могут быть разные, но оформление одинаковое)

  Дано:                                        Решение.            

 а =  5см                 Sпр = а ∙  в  

 Sпр = 15см2            в = Sпр: а       

  в – ? см               в = 15см2 : 5 см = (3 см)

  Рпр -?см               Рпр = (а+в) ∙ 2  

                              Рпр = (5см + 3 см) ∙ 2 = 16 (см)  

Ответ: в = 3 см; Рпр = 16 см  

5.Нахождение площади  прямоуг.треугольника (Sтр)  по формуле:

                                                Sтр. = (а ∙ в):2                                                                                                                                                                                                

                                              а

                                                  в                                    

Выполняя
задания на построение геометрических
фигур, учащиеся должны принимать во
внимание не только размеры и ее вид, но
и положение на плоскости относительно
других элементов. Например: «Начерти
два круга. Раздели окружность первого
круга на четыре части, а второго – на
три части. Точки деления соедини
последовательно отрезками. Какие
многоугольники получились внутри
круга?».

В
начальной школе решаются простейшие
конструктивные задачи с использованием
линейки, угольника, циркуля. Эти задачи
способствуют формированию умений и
навыков выполнения элементарных
построений чертежными инструментами.

Существует
ряд простейших геометрических задач
на построение, которые особенно часто
входят в качестве составных частей в
решение более сложных задач. Задачи
такого рода рассматриваются преимущественно
в первых главах школьного курса геометрии.
К таким задачам относятся: деление
отрезка пополам; деление угла пополам;
построение угла, равного данному;
построение треугольника по трем заданным
сторонам; построение треугольника по
стороне и двум прилежащим углам;
построение треугольника по двум сторонам
и углу между ними; построение прямой,
проходящей через данную точку и касающейся
данной окружности; построение
прямоугольного треугольника по гипотенузе
и катету и др.

Обучение
геометрии в начальной школе может
строиться только на интуитивно-содержательной
основе. При этом одной из главных целей
обучения выступает задача развития у
младших школьников образного мышления,
формирование умения воспринимать и
осмысливать графическую информацию.
Это значит, что изучение геометрии
невозможно без овладения определенными
графическими умениями. Решение
геометрических задач требует от учащихся
эстетически привлекательного и точного
выполнения рисунков и чертежей, что
формирует умение пользоваться основными
чертежными инструментами. Первые шаги
в этом направлении естественно начать
с раскрашивания предметных картинок,
в процессе которого они осмысливают
уже знакомые им пространственные
отношения. Постепенное усложнение
графических заданий ведет к формированию
умений построить фигуру с заданными
свойствами с помощью линейки, чертежного
угольника, циркуля [Шадрина, 2002, с. 58].

Существует
условия, которые необходимо соблюдать
при построении фигур с помощью циркуля
и линейки.

Циркуль
– это инструмент, позволяющий построить:

а)
окружность, если построены ее центр и
отрезок, равный радиусу;

б)
любую из двух дополнительных дуг
окружности, если построены ее центр и
концы этих дуг;

Линейка
используется как инструмент, позволяющий
построить:

а)
отрезок, соединяющий две построенные
точки;

б)
прямую, проходящую через 2 построенные
точки;

в)
точку, принадлежащую какой-либо
построенной фигуре.

Учитель
должен систематически проводить работу
по формированию умений и навыков
применения чертежных и измерительных
инструментов, построению изображений
геометрических фигур, умений описывать
словесно процесс работы, выполняемой
учеником, и ее результат, умений применять
усвоенную символику и терминологию.
Важным методическим условием реализации
этой системы является сначала осознание
выполнения действий и лишь за тем
автоматизация этих действий.

Результатом
обучения в 1-3 классах бывает формирование
первоначальных представлений о точности
построений и измерений.

Работа
по формированию навыков проводиться
распределено и постепенно, почти на
каждом уроке (и не только на уроках
математики). Это создает условие для
более частого применения этих навыков
в учебной и практической деятельности,
обеспечивает необходимую их прочность.

Для
построения многоугольников, содержащих
прямые углы, в 1 классе сначала используют
линии клетчатой бумаги, образующие
прямые углы.

Наблюдение
и построение различных многоугольников
наглядно убеждает детей в том, что только
у четырёхугольника все углы могут быть
прямыми. Такие четырёхугольники
называются прямоугольниками.

В
результате измерений сторон прямоугольников
выясняется, что есть прямоугольники, у
которых все стороны равны между собой.

Такие
прямоугольники называют квадратами.
Большое значение при этом имеют
упражнения, в которых по заданным точкам
– вершинам, нужно построить прямоугольник
(квадрат). Вначале задаются все четыре
вершины, затем три – в этих случаях
задача имеет единственное решение.

Учащимся
рассказывают, что кроме многоугольников,
существуют окружности, для их вычерчивания
есть специальный инструмент – циркуль.
В момент показа работы циркуля, когда
ещё не вся окружность начерчена, полезно
заметить, что одна ножка циркуля (с
силой) стоит на одном месте, неподвижна.
Эту точку называют центром окружности.
Другая ножка циркуля движется, и её
конец вычерчивает линию. Эту линию
называют окружность. Полезно показать
учащимся, как можно вычертить окружность
с помощью планки (картонной полоски,
кусочка шпагата). Полоска прибивается
гвоздиком к доске. К другому концу
прикладывается мел. Затем учащиеся
знакомятся с радиусом окружности. Для
этого на окружности отмечают, какую –
ни будь точку, и соединяют эту точку
отрезком с центром. Детям объясняют,
что отрезок, соединяющий точку окружности
с центром, называют радиусом.

Надо
стремиться, чтобы дети сами рассказывали,
какие действия и в каком порядке они
выполняют при построении каждой фигуры,
или какими инструментами они пользуются
на каждом шаге построения. Младших
школьников знакомят с пошаговым
представлением решения задачи на
построение геометрических фигур.
Построение геометрической фигуры можно
пояснить устно, учитывая порядок
выполнения действий.

К
геометрическим задачам на построение
можно отнести задачи на нахождение
периметра треугольника двумя способами.
Они выполняются во 2 классе.

I
способ: периметр треугольника – это
сумма длин всех сторон;

II
способ: на луче откладывают с помощью
циркуля последовательно отрезки (стороны
треугольника), а затем измеряют длину
получившегося в итоге отрезка.

Для
решения задач на построение окружности
необходимо актуализировать знания
младших школьников.

Задавая
им вопросы по чертежу: покажите окружность,
круг, его центр, радиус и т.д., выясняем
что окружность представляет собой
границу круга, а круг – это окружность
вместе с внутренней областью, ограниченной
этой окружностью. В этом и состоит
различие между кругом и окружностью.

Для
примера можно изобразить какой-нибудь
круг и показать, что круг так же имеет
центр и радиус. Однако, в отличие от
окружности, круг можно закрасить.

Особую
важность для достижения указанных целей
при изучении геометрического материала
приобретает использование метода
практической работы. Этот метод обучения
представляет собой осуществление
учащимися предметной деятельности с
целью накопления опыта, использования
уже имеющихся знаний и получения новых,
относящихся к использованию предмета.

Ученики
любят выполнять задания с геометрическим
материалом, потому что на этих занятиях
они удовлетворяют свой познавательный
интерес с помощью таких видов деятельности,
которые соответствуют их возрасту:
рисования, вырезания, рассматривания
иллюстраций, дидактической игры.
Организованная таким образом геометрическая
работа оказывает положительное влияние
на формирование пространственных
представлений обучающихся, совершенствование
их математической речи, развитие интереса
к изучению математики в целом.

Задания
на «геометрию формы» начинают выполнять
с 1-го класса с игр на составление целого
из частей (геометрические фигуры,
изображения) и на воссоздание силуэтов
из наборов геометрических фигур. К ним
относятся игры «Составь картинку»,
геометрические мозаики. Специально
изготовленные наборы геометрических
фигур (квадратов или треугольников)
также являются материалом для таких
игр. Эти игры дают развитие у детей
сенсорных умений и способностей,
аналитического восприятия. Ребята
учатся различать геометрические фигуры,
составлять из них какое-либо изображение,
картинку по образцу, указанию учителя,
по собственному замыслу.

Очень
интересны игровые упражнения «Дорисуй»,
«Дострой». На листах бумаги изображаются
геометрические фигуры, и ребёнок должен
дорисовать, закончить изображение
предмета, имеющего в своей структуре
данную геометрическую форму. Аналогичные
упражнения, состоящие в том, что к взятой
за основу геометрической фигуре,
например, треугольнику, надо присоединить
другие фигуры и получить при этом
какой-либо силуэт: ёлку, домик и др. Во
время игр у детей развивается геометрическое
воображение, пространственное
представление, закрепляются знания о
геометрических фигурах, их свойствах.
Дети привлекаются к оценке работ,
подчёркивается разнообразие работ.

В
качестве дополнительного материала на
уроках математики мы решаем задачи на
смекалку геометрического характера,
т.к. в ходе решения этих задач идёт
трансфигурация, преобразование одних
фигур в другие, а не только изменение
их количества.

Задачи
на смекалку различны по степени сложности,
характеру преобразования (трансфигурации).
Их нельзя решать каким-либо усвоенным
ранее способом. В ходе решения каждой
новой задачи ребёнок включается в
активную умственную деятельность,
стремясь достичь конечной цели –
видоизменить или построить пространственную
фигуру.

Задачи
на смекалку, связанные с построением
геометрических фигур, объединяют в три
группы:

1.
Задачи на составление заданной фигуры
из определенного количества палочек.

2.
Задачи на изменение фигур, для решения
которых надо убрать указанное количество
палочек: две палочки так, чтобы получилось
два прямоугольника.

3.
Задачи на смекалку, решение которых
состоит в перекладывании палочек с
целью видоизменения, преобразования
заданной фигуры.

Выводы
из I
главы.

В
программе традиционной начальной школы
геометрический материал является
составной частью курса математики. Он
не выделяется в самостоятельный раздел,
а включается в программу каждого года
обучения. Но, к сожалению, изучается
геометрический материал в основном на
уровне знания-знакомства.

В
начальных классах кроме знания определений
и свойств, необходимо уметь решать
геометрические задачи с фигурами. Среди
них выделяются задачи на построение
геометрических фигур с помощью циркуля
и линейки. Класс задач на построение
геометрических фигур привлекает не
только строгостью теории, но и изяществом
самого решения и чертежа к нему.

Учитель
должен систематически проводить работу
по формированию умений и навыков
применения чертежных и измерительных
инструментов, построению изображений
геометрических фигур, умений описывать
словесно процесс работы, выполняемой
учеником, и ее результат, умений применять
усвоенную символику и терминологию.
Важным методическим условием реализации
этой системы является сначала осознание
выполнения действий и лишь за тем
автоматизация этих действий.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #