Как составить задачу на движение вдогонку 4 класс

Цель урока:  познакомить учащихся с
новым видом задач на движение (вдогонку).

Задачи:

• обучающие: учиться читать и
  записывать информацию, представленную в виде
  различных математических моделей, строить
  высказывания, продолжать учиться называть цели
  конкретного задания, алгоритм (план работы),
  проверять, исправлять и оценивать результаты
  работы так, как это было описано ранее.
• развивающие: способствовать развитию
  математического мышления, познавательной
  активности обучающихся,  умения пользоваться
  математической терминологией.
• воспитательные: продолжить работу по
  воспитанию взаимопомощи, культуры общения,
  способствующей созданию благоприятного
  психологического климата;
• воспитывать внимание, самостоятельность,
  самоконтроль, аккуратность, прививать интерес к
  предмету.

Тип урока:  Урок изучения и первичного
закрепления новых знаний

Методы и приемы: словесные, наглядные,
частично-поисковые.

Используемые учебники и учебные пособия: Учебник
“Математика” Алматы “Атамра” 2011

Используемое оборудование: 

• интерактивное оборудование (мультимедийный
  проектор), компьютер,
• интер.доска. 

Ход урока

1. Вводно-мотивационная часть

Загадка.

Всем она давно знакома –
Ждёт послушно возле дома,
Только выйдешь из ворот-
Куда хочешь поведёт.

(дорога)

– Какое действие совершают машины по дороге?

– Прочитайте дружно, хором наш девиз:

Смело иди вперед,
Не стой на месте,
Чего не сделает один,
Сделаем вместе!

2. Актуализация знаний. Минутка чистописания

– Запишите формулы нахождения расстояния,
скорости и времени.

S = V x t

V = S : t

t = S : V

– Чем отличаются величины: расстояние и
скорость?

– Расстояние – это путь, пройденный за
несколько единиц времени;

– Cкорость – это путь, пройденный за одну
единицу времени

3. Устный счёт (задачи на движение)

Задача №1

Шофер все сильнее давит на газ
Скорость – сто километров в час.
Тебе нетрудно будет сказать,
Сколько проедет за три часа
Автомобиль со скоростью этой?
Решай поскорее – жду ответа!

Решение:

S = U х t

100 х 3 = 300 (км)

Задача №2

За 5 часов один пешеход
Тридцать пять километров пройдет.
Должен быть ответ поскорее готов:
Сколько пройдет он за восемь часов
Если скорость свою не изменит?
Решай – и учитель ответ оценит!

Решение:

1) 35 : 5 = 7 (км/ч)

2) 7 х 8 = 56 (км)

Задача №3

Возьми-ка ручку,
Открой чистый лист,
Задачу послушай: “Прошел турист
Со скоростью пять километров в час
Сто километров.” Ответ найди:
Сколько часов он был в пути?

Решение: 100 : 5 = 20 (час.)

Задача №4

Лора задачу быстро решила:
“Пятьсот километров проедет машина
За десять часов. Какова же скорость?”
Лора решала, не беспокоясь:
Пятьсот умножает на десять скоро.
Ответ получает. Права ли Лора?

Решение:

Лора не права!

500 : 10 = 50 ( км/ч)

4. Закрепление пройденного.

– С какими видами движения вы знакомы?

– Встречное движение

– Движение в противоположных направлениях.

– Движение с отставанием.

– С какой темой мы познакомились на прошлых
уроках? (- Одновременное движение с отставанием.)

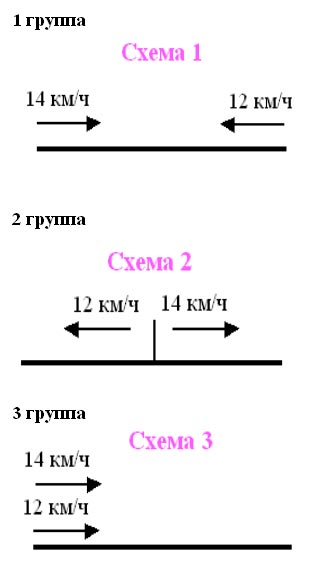
Работа по группам

(Группам раздаются карточки со схемами к
задачам)

Задание: Какое направление движения
соответствует решению?

14 км/ч+12км/ч=26км/ч

14 км/ч-12км/ч=2км/ч

5. Проблемная ситуация. Решите задачи по
схемам.

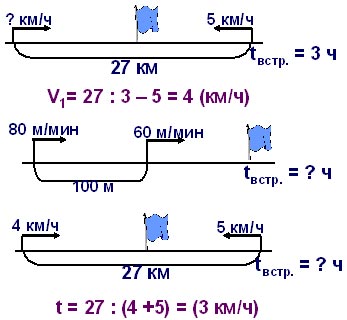
– Почему не удалось решить вторую задачу? – Это
задача на движение вдогонку.

– Не умеем находить скорость сближения при
движении вдогонку.

Постановка учебной задачи.

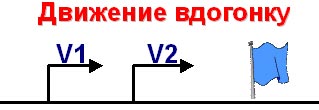
– Какова же тема нашего урока? Задачи на
движение вдогонку.

– Какие цели мы поставим?

• познакомиться со скоростью сближения при
  движении вдогонку;
• научиться решать задачи на движение вдогонку.

7. “Открытие” учащимися нового
знания.

а) Работа над задачей стр. 230 №3

– Вначале понаблюдаем, что происходит с
объектами при движении вдогонку. Заполним
таблицу, чтобы сделать верные выводы.

(Текст задачи на стр.230 №3, чертежи с числовым
лучом, таблица у каждого ученика.)

– Прочитайте условие вслух.

Из городов, длина пути между которыми 240км,
одновременно в одном направлении выехали
автомобиль и автобус. Скорость автомобиля 80 км/ч,
а скорость автобуса 56км/ч. Сколько километров
будет между ними через 2 часа?

Разбор задачи:

– В какой точке находится автомобиль? В точке 0.

– А автобус? В точке 240.

– Какое между ними расстояние до начала
движения? 240 км

– Занесите в таблицу.

– Покажите на числовом луче, где будет
находиться автомобиль через час.

В точке 80.

– И где через час будет находиться автобус. В
точке 296 .

– Как изменилось расстояние между ними?
Расстояние между объектами за каждую единицу
времени будет уменьшаться на одно и то же число.

– Как это записать? (Vб – Vм)

– Составьте выражение и внесите запись в
таблицу. 240 – (80-56) x 1 = 216 км

– Покажите на числовом луче, в каких точках
будут находиться автомобиль и автобус через два
часа. В точках 160 и 352

– Как изменилось расстояние между объектами
через два часа? Уменьшилось еще на (80-56) x 2

Узнайте, какое расстояние стало между ними
через два часа, запишите выражение в таблицу 240
– (80-56) x 2 = 192 км

– Сделайте вывод, с помощью какой формулы мы
узнали, как изменяется расстояние при движении
вдогонку? d = S – (V ₁– V ₂) x t

– Запишите формулы зависимости между
величинами: S, t, V.

Vсбл= (V ₁– V ₂) Sп = Vсбл. x t,

t встр.= S : (V ₁– V ₂), V ₁= S : t – V ₂

d = S – (V ₁– V ₂) x t

8. Для закрепления работа над задачей стр.231 №9

 

9. Рефлексия.

– Что такое скорость сближения.

(- Скорость сближения – расстояние, при котором
объекты сближаются за единицу времени.)

– Как найти скорость сближения при движении
вдогонку?

Vсбл = (Vб – Vм),

– Какие еще знания необходимы, чтобы успешно
решать задачи на движение вдогонку?

Sп = Vсбл. x t,

t встр.= S : (Vб – Vм), V1= S : t – V2

d = S – (Vб – Vм) x t

Презентация.

Тип урока: ОНЗ

Урок составлен по технологии деятельностного метода.

Тема: Решение задач на движение вдогонку.

Автор: Зайцева С. А. (ШЛ № 27 Астана)

Цель: Познакомить с  решением задач на движение вдогонку.

 Задачи:

1. Развивать умение решение задач на движение вдогонку
2. Познакомить с графической моделью движения на числовом луче
3. Тренировать вычислительные навыки  
4. Формировать умение применять формулы для решения задач на движение, способность к исправлению допущенных ошибок на основе рефлексии собственной деятельности
5. Способствовать умению работы в группе и самостоятельной работы с самопроверкой по эталону

Ход урока:

I этап: Мотивация к учебной деятельности.

Математика повсюду.

Глазом только поведёшь

И примеров сразу уйму

Ты вокруг себя найдёшь.

Каждый день, вставая бодро

Начинаешь ты решать:

Идти тихо или быстро,

Чтобы в класс не опоздать.

II этап: Актуализация  знаний

• Работа в группе. Вспомните,  какими правилами мы пользуемся при работе в группе. (Слушай внимательно, говорит только один, говорит по существу, уважай говорящего)
• Сейчас вам дается 2 минуты, чтобы вы выполнили задание, написанное на карточке № 1 (напишите, какие ассоциации у вас возникают при виде данной схемы)
• Проверим. 1-я группа (это задачи на движение в противоположных направлениях, в данных задачах объекты будут удаляться друг от друга за единицу времени, при решении этих задач нужно вспомнить формулы пути s = v * t, v= s : t, t = s : v)
• 2-я группа (это задачи на встречное движение, в данных задачах объекты будут сближаться друг от другом за единицу времени, при решении этих задач нужно вспомнить формулы пути s = v * t, v= s : t, t = s : v)
• 3- я группа. (это задачи на движение) ???

III этап: Выявление места и причины затруднения

• При составлении ассоциаций к этой схеме у вас возникла проблема (мы не решали задачи такого вида, потому что стрелки здесь направлены в одном направлении)
• Что нам необходимо для достижения цели урока (можно проговорить) нам необходимы новые знания, новые понятия?

IV этап: Целеполагание и построение проекта выхода из затруднения.

-Сегодня мы познакомимся с новым видом решения задач на движение: Движение вдогонку.

V этап: Открытие нового знания

   – Откройте учебники на стр. 26 и прочитайте задачу под номером 1.

-Чтение задачи. Расстояние между школой и домом 200 м. Одновременно из школы вышел ученик, а из дома- бабушка. Они пошли в одном направлении. Скорость ученика 110 м/мин, а бабушки- 60 м/мин. На сколько метров уменьшается расстояние каждую минуту? Через какое время ученик догонит бабушку?

Рассмотрим схему и заполним таблицу на карточке № 2.

-На прямой линии отмечены две точки (школа и дом) и обозначено расстояние 200 м. Указана стрелками скорость бабушки и ученика (больше та, стрелка, где скорость больше).

-Давайте проанализируем, как изменяется расстояние при решении задачи на движение вдогонку.

-Если ученик идёт вдогонку, расстояние будет уменьшаться или увеличиваться? (уменьшаться) Значит, они будут сближаться или удаляться? (сближаться)

-Чтобы найти скорость сближения бабушки и ученика за 1 минуту, мы от скорости ученика отнимем скорость бабушки)- это и будет скорость сближения

По формуле v сбл = v 1– v 2         110- 60= 50 (м/мин)

-Давайте заполним таблицу. Чтобы найти расстояние, какую формулу мы используем? (s = v * t)

-На каком расстоянии от школы будет бабушка через 1 минуту? (200 + 60*1 = 260 м-, т. к. расстояние между школой и домом 200 м- отметим на схеме)

-На каком расстоянии от школы будет ученик через 1 минуту? (110 * 1 = 110 м- отметим на схеме)

-На сколько уменьшится расстояние между учеником и бабушкой через 1 минуту? (260 – 110 = 50 (м))

Так же вычитываем за 2, 3, 4 минуты.

t мин	1 мин	2 мин	3 мин	4 мин	t
x б	260	320	380	440	200 + 60 * t
x у	110	220	330	440	110 * t
v сбл	50	100	150	200	v 1 – v 2

        ВЫВОД: ученик и бабушка сближаются на 50 метров в минуту

-Мы рассмотрели, как изменяется расстояние между учеником и бабушкой, через некоторое время.

-Давайте решим задачу. Чтобы узнать скорость сближения ученика и бабушки v сбл = v 1– v 2 110 – 60 = 50 (м/мин)

-Чтобы догнать бабушку, ученику надо преодолеть расстояние 200 м, значит чтобы найти время   t = s : v     200 : 50 = 4 (мин)

-Через какое время ученик догонит бабушку? (через 4 минуты)

VI этап: Первичное закрепление.

Работа по учебнику с. 27 № 3

Расстояние между домами Алибека и Мурата 160 м. Они вышли в школу одновременно. Алибек шёл со скоростью 100 м/мин, а Мурат шёл вдогонку Алибеку со скоростью 120 м/мин. Через сколько минут Мурат догонит Алибека?

Составим алгоритм.

• Определить вид движения.
• Выбрать схему.
• Вспомнить формулы.

1. 120- 100 = 20 (м/мин)- скорость сближения мальчиков
2. 160 : 20 = 8 (мин)- нужно Мурату, чтобы догнать Алибека

Выражение: 160 : (120-100)= 8

VII этап: Самостоятельная работа с самопроверкой по эталону

Разноуровневые  задания:

-Из данных выражений выписать те, которые будут являться решением к данной задаче. Написать пояснения.

1.Миша начал догонять Борю, когда расстояние между ними было 100 м. Миша идёт со скоростью 80 м/мин, а Боря- со скоростью 60 м/мин. Через сколько времени Миша догонит Борю?

80 – 60 = 20                140 – 100 = 40

80 + 60 = 140                100 : 20 = 5

Эталон самопроверки № 1

1)        80 – 60 = 20 (м/мин)- скорость сближения

2)        100 : 20 = 5 (м)- Миша догонит Борю

100 : (80 – 60) = 5

Ответ: через 5 минут Миша догонит Борю

-Составить обратную задачу и решить её

2.Расстояние между посёлками А и Б- 120 км Из посёлка А выехал легковой автомобиль со скоростью 90 км/ч, а из посёлка Б- одновременно грузовой со скоростью 60 км/ч. Через сколько часов легковая машина догонит грузовую?

 Эталон самопроверки № 2

Из посёлка А выехал легковой автомобиль со скоростью 90 км/ч, а из посёлка Б- одновременно грузовой со скоростью 60 км/ч. Через 4 часа легковая машина догнала грузовую. Какое расстояние между посёлками?

1)        90 + 60 = 150 (км/ч)- общая скорость

2)        150 * 4 = 600 (км)- расстояние между ними

(90 + 60) * 4 = 600

Ответ: между посёлками расстояние 600 метров

Расстояние между посёлками А и Б- 120 км Из посёлка А выехал легковой автомобиль со скоростью 90 км/ч, а из посёлка Б- одновременно грузовой автомобиль. С какой скоростью двигался грузовой автомобиль, если через 4 часа его догнал легковой автомобиль?

1)        90 * 4 = 360 (км)- проехал лег автомобиль

2)        360 – 120 = 240 (км)- проехал грузов автомобиль

3)        240 : 4 = 60 (км/ч)- скорость грузового автомоб

Ответ: грузовой автомобиль двигался со скоростью 60 километров в час

-Решить задачу

3.Из одного посёлка одновременно в противоположных направлениях выехали мотоцикл и автобус. Скорость мотоцикла 76 км/ч, автобуса-  44 км/ч. Какой путь проделала каждый, когда расстояние между ними стало 600 км?

Эталон самопроверки  № 3

1)        76 + 44 = 120 (км/ч)- общая скорость

2)        600 : 120 = 5 (ч)- время движения

3)        76 * 5 = 380 (км)- проехал мотоцикл

4)        44 * 5 = 220 (км)- проехал автобус

1)        76 + 44 = 120 (км/ч)- общая скорость

2)        600 : 120 = 5 (ч)- время движения

3)        76 * 5 = 380 (км)- проехал мотоцикл

4)        600 – 380 = 220 (км)- проехал автобус

Ответ: мотоцикл проехал 380 километров, автобус 220 километров

Самопроверка:   Проверьте свою работу.    

                             – Кто допустил ошибку? Почему произошла ошибка?

                             – Кто решил без ошибок?   МОЛОДЦЫ!                                  

VIII этап: Включение в систему знаний и повторение

             1)Расшифруйте, у кого из животных самая большая и самая маленькая скорость передвижения (работа в группах) Записать ответы в порядке возрастания

6009 * 34	К	351456 : 84	И
56 * 1230	Т	72408 : 28	Л
2403 * 93	А	201025 : 85	У

у	л	и	т	к	а

6009 * 34= 204306                2403 * 93= 223479                72408 : 28= 2586

56 * 1230= 68880                351456 : 84= 4184                201025 : 85= 2365

3203 * 32	А	3567 * 75	Д
87 * 1435	Р	188616 : 29	Г
817440 : 16	П	277704 : 38	Е

г	е	п	а	р	д

3203 * 32= 102496                817440 : 16 = 51090                188616 : 29= 6504

87 * 1435 = 124845                3567 * 75 = 267525                277704 : 38 = 7308

Улитка, гепард

Медленнее всех движется улитка. Она проползает 1,5 мм в секунду, а за час всего 5,4 м. Другое медленное животное, но покрупнее улитки — это черепаха; она движется со скоростью 70 м/ч.

Чемпионом мира по бегу является – Гепард. Гепард бегает быстрее всех обитателей нашей планеты. Ему помогают в этом длинные сильные ноги, пружинящая спина и, конечно, когти. Догоняя добычу, он способен развить скорость до 112 км/ч! Почти догоняет его антилопа-гну. Ее скорость равна 100 км/ч.                                      

-А кто же из людей может быстрее всего пробежать стометровку и за сколько? Чемпионы мира в беге на 100 пробегают стометровку за 9,6 секунды.

IX этап: Рефлексия учебной деятельности

• Что нового вы сегодня узнали? (…)
• – Что новое было для вас?
• – Чем вы использовались при открытии нового? (Ранее изученными алгоритмами.)
• – Проанализируйте свою работу на уроке. (…)
• Кто из ваших товарищей показал самые лучшие знания?

Высказывается несколько учеников.

Ответьте на вопросы, подставив «+» или «?».

1) Я знаю, как решить  задачу на движение вдогонку.

2) Я сегодня справился с самостоятельной работой.

3) Я ещё допускаю ошибки при решении задач

Д/З: с 27 № 4 (5, 6), № 6

Литература:

1. «Урок в современной начальной школе» казахский национальный педагогический университет им Абая. Алматы 2012 г.

2. А. Б. Акпаева, Л. А. Лебедева, В. В. Буровова «Математика» методическое пособие. Алматыкітап баспасы 2011 г.

3. А. Б. Акпаева, Л. А. Лебедева, В. В. Буровова «Математика»

Тетрадь для контрольных  работ. Алматыкітап баспасы 2012 г.

4. О.В. Узорова, Е. А. Нефёдова «2500 задач по математике» АСТ 2013

5. А. Б. Акпаева, Л. А. Лебедева, В. В. Буровова «Математика» учебник для 4 класса Алматыкітап баспасы 2011 г.

Интернет ресурсы:

http://www.uchportal.ru/

http://elite-pets.narod.ru/

http://mir-zhivotnux.blogspot.com/2010/02/blog-post_2315.html

http://www.anypics.ru/download/6865/1600×1200/

http://daler.ru/wallpapers/%D0%96%D0%B8%D0%B2%D0%BE%D1%82%D0%BD%D1%8B%D0%B5/1280×960/22.html

http://www.akmar.info/izbrannoe/koshki-takie-koshki/

http://vsplesnuv.ru.com/?c=result&query=%D0%B4%D0%B8%D0%BA%D0%B0%D1%8F+%D0%BF%D1%80%D0%B8%D1%80%D0%BE%D0%B4%D0%B0+%D0%B2%D0%B8%D0%B4%D0%B5%D0%B

Придумай задачи на движение вдогонку, которые решаются так:

Что ты замечаешь?

Слайды и текст этой презентации

Математика. 4 класс.

Дата__________________

Тема: Решение задач на движение вдогонку

Цель: – Познакомить с  решением задач на движение вдогонку.

– Развивать умение решение задач на движение вдогонку

– Познакомить с графической моделью движения вдогонку

– Тренировать вычислительные навыки  

– Формировать умение применять формулы для решения задач на движение, способность к исправлению допущенных ошибок на основе рефлексии собственной деятельности.

Оборудование: Схемы к задачам, формулы, раздаточный материал.

Ход урока:

1.Организационный момент

Математика повсюду.
Глазом только поведёшь
И примеров сразу уйму
Ты вокруг себя найдёшь.
Каждый день, вставая бодро
Начинаешь ты решать:
Идти тихо или быстро,
Чтобы в класс не опоздать.

2.Устный счет

Задача №1

Шофер все сильнее давит на газ 
Скорость – сто километров в час. 
Тебе нетрудно будет сказать, 
Сколько проедет за три часа 
Автомобиль со скоростью этой? 
Решай поскорее – жду ответа!

Решение: 100 · 3 = 300 (км)

Задача №2

За 5 часов один пешеход 
Тридцать пять километров пройдет. 
Должен быть ответ поскорее готов: 
Сколько пройдет он за восемь часов 
Если скорость свою не изменит? 
Решай – и учитель ответ оценит!

Решение: 1) 35 : 5 = 7 (км/ч) 2) 7 · 8 = 56 (км)

Задача №3

Возьми-ка ручку, 
Открой чистый лист, 
Задачу послушай: “Прошел турист 
Со скоростью пять километров в час 
Сто километров.” Ответ найди: 
Сколько часов он был в пути?

Решение:  100 : 5 = 20 (час.)

Задача №4

Лора задачу быстро решила: 
“Пятьсот километров проедет машина 
За десять часов. Какова же скорость?” 
Лора решала, не беспокоясь: 
Пятьсот умножает на десять скоро. 
Ответ получает. Права ли Лора?

Решение: Лора не права! 500 : 10 = 50 ( км/ч)

3. Работа по теме урока.

а) Беседа

– С какими видами задач на движение вы знакомы?

– Встречное движение

– Движение в противоположных направлениях.

– Рассмотрите схемы и назовите виды движения (делают вывод, что с третьим видом задач не встречались)

– А как вы думаете, как будет называться этот вид задач? (движение вдогонку)

– И как вы думаете, будет называться тема нашего урока? (задачи на движение вдогонку.)

– Какие цели мы перед собой поставим? (познакомиться со скоростью сближения при движении вдогонку; научиться решать задачи на движение вдогонку).

б) Работа над задачей (задача на карточке у каждого ребенка)

Из городов, длина пути между которыми 240км, одновременно в одном направлении выехали автомобиль и автобус. Скорость автомобиля 80 км/ч, а скорость автобуса 56км/ч. Сколько километров будет между ними через 2 часа?

– Прочитайте условие задачи.

– Вначале понаблюдаем, что происходит с объектами при движении вдогонку.

Разбор задачи: (работают на карточках)

– В какой точке находится автомобиль? (В точке 0)

– А автобус? (В точке 240)

– Какое между ними расстояние до начала движения? (240 км)

– Занесите в таблицу.

– Покажите на числовом луче, где будет находиться автомобиль через час. (В точке 80)

– И где через час будет находиться автобус. (В точке 296 )

– Как изменилось расстояние между ними? (Расстояние между объектами за каждую единицу времени будет уменьшаться на одно и то же число)

– Как это записать? (Vб – Vм)

– Давайте составим выражение (240 – (80-56) · 1 = 216 км)

– Покажите на рисунке, в каких точках будут находиться автомобиль и автобус через два часа. 

(В точках 160 и 352)

– Как изменилось расстояние между объектами через два часа? Уменьшилось еще на (80-56) x 2

Узнайте, какое расстояние стало между ними через два часа, запишите выражение (240 – (80-56) x 2 = 192 км)

– Сделайте вывод, с помощью какой формулы мы узнали, как изменяется расстояние при движении вдогонку? (d = S – (V ₁– V ₂) · t)

– Запишите формулы зависимости между величинами: S, t, V.

Vсбл= (V ₁– V ₂)

Sп = Vсбл. · t,

t встр.= S : (V ₁– V ₂), V ₁= S : t – V ₂

в) Работа с учебником

стр.26 №1 (рассмотреть задачу устно). Прочитать вывод в синей рамочке.

Стр. 27 №3 (задача)

120м/мин 100м/мин ?

Д Ш

160м

1) 120-100=20(м/мин)

2) 160:20=8(мин)

Ответ: встретятся через 8 минут

Стр. 27 № 2 (устно, таблицу и предполагаемые ответы учитель выносит на доску, ребята решают, подставляют в таблицу, когда повернут карточки с ответами на другую сторону увидят буквы и если решено верно, то сверху вниз прочитают слово «ПЯТЬ»)

Объект	V	t	S
Черепаха	3м/мин	?	18м
Верблюд	16км/ч	3ч	?
Улитка	?	7ч	35м
волк	?	3ч	165 км

18:3=6 мин -П

16·3=48 км – Я

35:7=5м/ч – Т

165:3=55км/ч – Ь

Физминутка

Стр.27 №4 (составить 2 уравнения и решить, 2 ребенка у доски)

7938-14·а=35280:360 Х·32-123=3013

7938-14·а=98 Х·32=3013+123

14·а=7938-98 Х·32=3136

14·а=7840 Х=3136:32

а=7840:14 Х=98

а=560 98·32-123=3013

7938-14·560=35280:360 3013=3013

98=98

Стр.27 №5 (задача)

6 м. по 328ящ. на каждой

?

Ост. – 476ящ.

1. 328·6=1968(ящ.)

2. 1968+476=2444(ящ.)

Ответ: вывезли всего 2444 ящика овощей.

Стр.27 №6 (задача)

Асф. – 60км за 4ч V -?

? на?

Пол. – 60 км за 6ч V -?

1. 60:4=25 (км/ч)

2. 60:6=10(км/ч)

3. 25-10=15(км/ч)

Ответ: на асфальтированной дороге скорость больше на 15 километров в час

4. Домашнее задание.

Учить формулы.

Стр.27 №4 (составить остальные 3 уравнения и решить их)

№8 (решить задачу подбором вариантов)

5. Итог

– Чему учились на уроке?

Что такое скорость сближения? (Скорость сближения – расстояние, при котором объекты сближаются за единицу времени.)

– Как найти скорость сближения при движении вдогонку? (Vсбл= (V ₁– V ₂)

– Что затруднило на уроке?

– Кому необходима помощь подойдите после уроков.

ПРИЛОЖЕНИЕ: домашняя работа

Стр. 27 №4(составить остальные 3 уравнения и решить их)

с·210-900=12750 4860-k·62=2442 91260-320·b=74620

с·210=12750+900 k·62=4860-2442 320·b=91260-74620

с·210=13650 k·62=2418 320·b=16640

с=13650:210 k=2418:62 b=16640:320

с=65 k=39 b=52

65·210-900=12750 4860-39·62=2442 91260-320·52=74620

12750=12750 2442=2442 74620=74620

Стр.27 №4 (задача)

м	м	п	п	к	к
к	п	м	к	м	п
п	к	к	м	п	м

Работа над задачей

Из городов, длина пути между которыми 240км, одновременно в одном направлении выехали автомобиль и автобус. Скорость автомобиля 80 км/ч, а скорость автобуса 56км/ч. Сколько километров будет между ними через 2 часа?

Работа над задачей

Из городов, длина пути между которыми 240км, одновременно в одном направлении выехали автомобиль и автобус. Скорость автомобиля 80 км/ч, а скорость автобуса 56км/ч. Сколько километров будет между ними через 2 часа?

d=S–(V₁–V₂)·t

Vсбл=(V₁–V₂)

Sп=Vсбл·t

tвстр=S:(V₁–V₂) V₁= S : t –V ₂

Объект	V	t	S
Черепаха	3 м/мин	?	18м
Верблюд	16 км/ч	3ч	?
Улитка	?	7ч	35м
волк	?	3ч	165 км

Т

Я

П

Ь

6

48

5

55

V ₁ t V ₂

S

V ₁ V ₂ t

Sсбл.

V ₁ t V ₂