Тема: Решение задач по теме:
«Перпендикулярность прямых и плоскостей»
1. Рассмотрим решение основных задач по тете Параллельность и перпендикулярность в пространстве (все предложенные задачи записать в тетрадь, они являются типовыми задачами для контрольной работы)
Задача№1
Прямая РQ параллельна плоскости α (рис. 1). Через точки Р и Q проведены прямые, перпендикулярные к плоскости α, которые пересекают эту плоскость соответственно в точках Р1 и Q1. Докажите, что PQ = P1Q1.

Дано: 
Доказать:
Доказательство:
1. Две прямые РР1 и QQ1 перпендикулярны к одной и той же плоскости α. Значит, эти прямые параллельны между собой. Пусть через них проходит плоскость β. В плоскости β прямые PQ и P1Q1 параллельны, так как по условию PQ параллельна α.
2. Рассмотрим прямоугольник РР1Q1Q. В прямоугольнике РР1Q1Q противоположные стороны равны, значит, PQ = P1Q1, что и требовалось доказать.
Задача№2
Через точки P и Q прямой PQ проведены прямые, перпендикулярные плоскости α и пересекающие ее соответственно в точках P1 и Q1.
Найдите P1Q1, если PQ = 15см, РР1= 21,5 см, QQ1= 33,5 см

Дано: 


Найти:
Решение:
1. Две прямые РР1 и QQ1 перпендикулярны к одной и той же плоскости α. Значит, прямые РР1 и QQ1 параллельны. Значит, через них проходит единственная плоскость PQQ1P1.
2. Прямая РР1 перпендикулярная плоскости α, а значит и прямой Р1Q1.
3.Так как прямые РР1 и QQ1 параллельны, а угол РР1Q1 прямой, то четырехугольник РР1Q1Q – прямоугольная трапеция.
Рис. 3
4. Проведем прямую РА перпендикулярно прямой QQ1.Отрезки РА и P1Q1 равны.
5. Отрезок Q1A равен отрезку РР1. Найдем QA: QA = QQ1 – АQ1 = QQ1 – РР1 = 33,5 – 21,5 = 12 см.
6. Рассмотрим треугольник АРQ. Он прямоугольный, так как угол QАР прямой. Найдем катет РА.

P1Q1 = РА = 9 см.
Ответ: 9 см.
Задача №3
Четырехугольник АВСD – квадрат. Точка О его центр. Прямая ОМ перпендикулярна к плоскости квадрата.
а) Докажите, что МА = МВ = МС = МD
б) Найдите МА, если АВ = 4 см. ОМ = 1 см.
Напоминание:
Рассмотрим квадрат АВСD (рис. 4). Как известно, точка пересечения диагоналей О равноудалена и от вершин квадрата, и от сторон квадрата. То есть она является центром описанной окружности с радиусом R и центром вписанной окружности с радиусом r. Точка О и называется центром квадрата, т.е. это точка пересечения диагоналей. Если сторона квадрата равна а, то радиус описанной окружности равен:
Радиус вписанной окружности равен:
Рис. 4
Дано:
АВСD – квадрат
О – центр квадрата
АВ = 4 см, ОМ = 1 см.
Доказать: МА = МВ = МС = МD.
Найти: МА
Рис. 5
1. Прямая МО перпендикулярна плоскости АВС, а значит, прямая МО перпендикулярна любой прямой, лежащей в плоскости, в том числе и диагоналям квадрата. Значит, треугольники МОА, МОВ, МОС, МОD прямоугольные.
2. Рассмотрим треугольники МОА, МОВ, МОС, МОD. По свойству квадрата ОА = ОВ = ОС = ОD. Значит, эти стороны треугольников равны друг другу. Катет МО общий. Таким образом, прямоугольные треугольники равны по двум катетам. Из равенства прямоугольных треугольников вытекает равенство его гипотенуз: МА = МВ = МС = МD, что и требовалось доказать.
3.Найдем теперь отрезок МА.Рассмотрим квадрат АВСD. АО – это радиус описанной окружности. Получаем:
Рассмотрим прямоугольный треугольник МОА. С помощью теоремы Пифагора найдем гипотенузу МА:
Ответ: 3 см.
Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 8. Самостоятельная работа № 2 «Перпендикулярные прямые» с ответами и решениями (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 2.
Атанасян 7. Поурочные планы
Самостоятельные работы
Геометрия 7 класс. Урок 8.
Самостоятельная «Перпендикулярные прямые»
I уровень сложности (задания)
II уровень сложности (задания)
III уровень сложности (задания)
Самостоятельная работа № 2
РЕШЕНИЯ и ОТВЕТЫ
I уровень сложности (ответы)
Ответы на Вариант 1 (1-й ур.)
№ 1. Смежные углы относятся как 1 : 2. Найдите эти смежные углы.
ОТВЕТ: Так как ∠1 : ∠2 = 1 : 2, то ∠1 = х, ∠2 = 2х. Но ∠1 + ∠2 = 180°, тогда х + 2х = 180°, x = 60, значит, ∠1 = 60°, ∠2 = 120° (рис. 1.115).
№ 2. Один из углов, образовавшихся при пересечении двух прямых, равен 21°. Найдите остальные углы.
Указание к решению: Пусть ∠1 = 21°, тогда ∠3 = ∠1 как вертикальные и ∠3 = 21°. ∠1 и ∠2 – смежные и ∠1 + ∠2 = 180° (рис. 1.116). Тогда ∠2 = 180° – ∠1 = 159°. Но ∠2 = ∠4 как вертикальные и ∠4 = 159°.
ОТВЕТ: ∠1 = ∠3 = 21°, ∠2 = ∠4 = 159°.
№ 3. Дано: α = 30°, β = 140° (рис. 1.112). Найти: ∠1, ∠2, ∠3, ∠4.
Указание к решению: α = 30°, тогда ∠4 = 30°, так как ∠4 и угол с градусной мерой α – вертикальные,
β = 140°, тогда ∠2 = 140°, так как ∠2 и угол с градусной мерой β – вертикальные.
∠2 + ∠3 + ∠4 = 180°, тогда ∠3 = 180° – (∠2 + ∠4) = 10°.
∠3 и ∠1 – вертикальные, поэтому ∠3 = ∠1, ∠1 = 10°.
ОТВЕТ: ∠3 = ∠1 = 10°, ∠2 = 140°, ∠4 = 30°.
Ответы на Вариант 2 (1-й ур.)
№ 1. Один из смежных углов больше другого на 20°. Найдите эти смежные углы.
ОТВЕТ: ∠2 на 20° больше ∠1, тогда ∠1 = х, ∠2 = х + 20° (рис. 1.117). Но ∠1 + ∠2 = 180°, тогда х + х + 20 = 180, x = 80°, значит, ∠1 = 80°, ∠2 = 100°.
№ 2. Один из углов, образовавшихся при пересечении двух прямых, равен 102°. Найдите остальные углы.
Указание к решению: Пусть ∠1 = 102°, тогда ∠3 = ∠1 как вертикальные и ∠3 = 102° (рис. 1.118). ∠1 и ∠2 – смежные и ∠1 + ∠2 = 180°, тогда ∠2 = 180° – ∠1 = 78°. Но ∠2 = ∠4 как вертикальные и ∠4 = 78°.
ОТВЕТ: ∠1 = ∠3 = 102°, ∠2 = ∠4 = 78°.
№ 3. Дано: α = 20°, β = 130° (рис. 1.113). Найти: ∠1, ∠2, ∠3, ∠4.
Указание к решению: α = 20°, тогда ∠4 = 20°, так как ∠4 и угол с градусной мерой α – вертикальные.
β = 130°, тогда ∠2 = 130°, так как ∠2 и угол с градусной мерой β – вертикальные.
∠2 + ∠3 + ∠4 = 180°, тогда ∠3 = 180° – (∠2 + ∠4) = 30°.
∠3 и ∠1 – вертикальные, поэтому ∠3 = ∠1, ∠1 = 30°.
ОТВЕТ: ∠3 = ∠1 = 30°, ∠2 = 130°, ∠4 = 20°.
Геометрия 7 Атанасян Самостоятельная 2
II уровень сложности (ответы)
Ответы на Вариант 1 (2-й ур.)
№ 1. Один из смежных углов составляет 0,2 другого. Найдите эти смежные углы.
Указание к решению: Пусть ∠1 составляет 0,2∠2, тогда ∠1 = 0,2∠2. Но ∠1 и ∠2 – смежные и ∠1 + ∠2 = 180°, тогда 0,2∠2 + ∠2 = 180°, ∠2 = 150°, a ∠1 = 0,2 • 150° = 30° (рис. 1.119).
ОТВЕТ: 30° и 150°.
№ 2. Сумма трех углов, образовавшихся при пересечении двух прямых, равна 325°. Найдите остальные углы.
Указание к решению: Пусть ∠1 + ∠2 + ∠3 = 325°, тогда ∠4 = 360° – 325° = 35°, ∠4 = ∠2 как вертикальные, тогда ∠2 = 35°.
∠1 + ∠2 = 180°, ∠4 + ∠3 = 180°, тогда ∠1 = ∠3 = 145° (рис. 1.120).
ОТВЕТ: 145°, 35°, 145°.
№ 3. Даны углы α, β и γ. Известно, что α > β, а γ < β. Найдите среди этих углов тот, смежный с которым будет наибольшим.
ОТВЕТ: Так как α > β, γ < β, то γ < β < α, т. е. наименьшим среди углов α, β, γ будет γ, а смежный с ним угол будет наибольшим среди углов, смежных с углами α, β, γ.
Ответы на Вариант 2 (2-й ур.)
№ 1. Один из смежных углов составляет 0,8 другого. Найдите эти смежные углы.
Указание к решению: Пусть ∠1 составляет 0,8∠2, тогда ∠1 = 0,8∠2. Но ∠1 и ∠2 – смежные и ∠1 + ∠2 = 180°, тогда 0,8∠2 + ∠2 = 180°, ∠2 = 100°, a ∠1 = 0,8 • 100° = 80° (рис. 1.121).
ОТВЕТ: 80° и 100°.
№ 2. Сумма двух углов, образовавшихся при пересечении двух прямых, равна 78°. Найдите остальные углы.
Указание к решению: Сумма смежных углов равна 180°, поэтому 78° – это сумма вертикальных углов. Но вертикальные углы равны, и получаем, что ∠1 = ∠2 = 39°. ∠1 + ∠3 = 180°, ∠2 + ∠4 = 180°, тогда ∠2 = ∠4 = 141° (рис. 1.122).
ОТВЕТ: 141°, 141°.
№ 3. Даны углы α, β и γ. Известно, что α > β, а γ < β. Найдите среди углов тот, смежный с которым будет наименьшим.
ОТВЕТ: Так как α > β, γ < β, то γ < β < α, т. е. наименьшим среди углов α, β, γ будет γ, а наименьшим среди смежных с ними углов будет угол, смежный с углом α.
Геометрия 7 Атанасян Самостоятельная 2.
III уровень сложности (ответы)
Ответы на Вариант 1 (3-й ур.)
№ 1. 4/7 одного из смежных углов и 1/4 другого составляют в сумме прямой угол. Найдите эти смежные углы.
Указание к решению: Пусть ∠1 и ∠2 – смежные и 4/7∠1 + 1/4∠2 = 90°.
Так как ∠1 + ∠2 = 180°, то ∠2 = 180° – ∠1, тогда 4/7∠1 + 1/4(180° – ∠1) = 90°, ∠1 = 140°, ∠2 = 40°.
ОТВЕТ: 140° и 40°.
№ 2. Сумма вертикальных углов в 2 раза меньше угла, смежного с каждым из них. Найдите эти вертикальные углы.
Указание к решению: Пусть ∠1 и ∠3 – вертикальные, ∠2 – смежный с каждым из углов ∠1 и ∠3, тогда 2(∠1 + ∠3) = ∠2 (рис. 1.123).
Но ∠1 = ∠3, a ∠2 = 180° – ∠1, тогда 2(∠1 + ∠1) = 180° – ∠1, ∠1 = 36°.
ОТВЕТ: ∠1 = ∠3 = 36°.
№ 3. Один из четырех углов, образовавшихся при пересечении двух прямых, в 11 раз меньше суммы трех остальных углов. Найдите эти четыре угла.
Указание к решению: Пусть данные углы – ∠1, ∠2, ∠3, ∠4.
Тогда ∠4 • 11 = ∠1 + ∠2 + ∠3. ∠1 = ∠3 как вертикальные, ∠2 = ∠4 = 180° – ∠1.
Тогда 11(180° – ∠1) = ∠1 + (180° – ∠1) + ∠1, ∠1 = 150°, ∠2 = 30°, ∠3 = 150°, ∠4 = 30° (рис. 1.124).
ОТВЕТ: 30°, 30°, 150°, 150°.
Ответы на Вариант 2 (3-й ур.)
№ 1. Меньший из смежных углов в 4 раза меньше разности этих смежных углов. Найдите эти смежные углы.
Указание к решению: Пусть ∠1 и ∠2 – смежные и 4∠1 = ∠2 – ∠1.
Так как ∠1 + ∠2 = 180°, то ∠2 = 180° – ∠1, тогда 4∠1 = 180° – ∠1 – ∠1, ∠1 = 30°, ∠2 = 150°.
ОТВЕТ: 30° и 150°.
№ 2. Сумма вертикальных углов на 30° меньше угла, смежного с каждым из них. Найдите эти вертикальные углы.
Указание к решению: Пусть ∠1 и ∠3 – вертикальные, ∠2 – смежный с каждым из углов ∠1 и ∠3.
Тогда ∠1 = ∠3, ∠2 = 180° – ∠1, и ∠1 + ∠3 + 30° = ∠2, т. е. ∠1 + ∠1 + 30° = 180° – ∠1, ∠1 = 50° (рис. 1.125).
ОТВЕТ: ∠1 = ∠3 = 50°.
№ 3. Сумма трех углов, образовавшихся при пересечении двух прямых, на 280° больше четвертого угла. Найдите эти четыре угла.
Указание к решению: Пусть данные углы – ∠1, ∠2, ∠3, ∠4, тогда ∠4 + 280° = ∠1 + ∠2 + ∠3. ∠1 = ∠3 как вертикальные, ∠2 = ∠4 = 180° – ∠1.
Тогда 180° – ∠1 + 280° = ∠1 + (180° – ∠1) + ∠1, ∠1 = 140°, ∠3 = 140°, ∠2 = ∠4 = 40° (рис. 1.126).
ОТВЕТ: 40°, 40°, 140°, 140°.
Вы смотрели: Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 8. Самостоятельная работа № 2 «Перпендикулярные прямые» с ответами и решениями (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 2. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Геометрия 7. Поурочные планы
Геометрия 7. Самостоятельные работы
Описание презентации по отдельным слайдам:
-
1 слайд
Тема урока: Перпендикулярные прямые
Дата проведения: 25.11 -
2 слайд
II. Проверка домашнего задания.
Теоретический опрос
Что такое угол?
Что такое отрезок?
Какие разновидности углов вы знаете?
Какие углы называются смежными?
Чему равна сумма смежных углов?
Какие углы называются вертикальными?
Равны ли между собой вертикальные углы? -
3 слайд
2. Является ли
луч ОС
биссектрисой < АОВ
O
A
B
C -
4 слайд
3. Назовите точки, которые лежат во внутренней области < АОС, и точки, которые лежат во внешней области < АОС
A
O
C
R
B
L
Q
N -
5 слайд
4. Найдите ошибку:
900
700
Данный угол прямой, и он всегда равен 900
За исключение единичных случаев
Данный угол тупой. Он всегда равен 700 . -
6 слайд
5. Назовите смежные углы:
А
О
В
С -
7 слайд
ОТВЕТ: <AOC И <COB – СМЕЖНЫЕ
AO И OB ОБРАЗУЮТ ОДНУ -
8 слайд
6. На каком рисунке изображены вертикальные углы:
1
2
3 -
9 слайд
Ответ: На рисунке 3.
-
10 слайд
7. Решите задачу:
<1 + <2 + <3 = 2200
Найдите <4 и <2 также <1 и <3.2
4
3
1 -
11 слайд
Ответ:
<1 + <2 + <3 = 2200
<4 = 3600 – 2200 = 1400.
< 2 = < 4 = 1400 (вертикальные)
< 1 = <3 = 1800 – 1400 = 400 (< 1 и < 2, < 3 и <4 – смежные) -
12 слайд
8. Решите задачу:
Дано: ОЕ – биссектриса < СOD, < DOE = 320. Найти: < BOC, < AOF.
320
С
В
Е
D
A
F -
13 слайд
ОТВЕТ:
ОТВЕТ: < BOC = 1800 – < COD = 1160.
< AOF = < COE = 320 -
14 слайд
III. Изучение нового материала
Как вы думаете какие прямые называются перпендикулярными?
Две прямые называются перпендикулярными, если при пересечении они образуют четыре прямых угла.
С
А
В
D -
15 слайд
ЗАПИСЫВАЕТСЯ ЭТО ТАК: АВ ┴ СD
< AOC = < BOD = < AOD = 900
Две прямые перпендикулярные третьей, не пересекаются – это свойство перпендикулярных прямых.
Доказательство:
-
16 слайд
AA1 ┴ BB1 .
ОНИ НИКОГДА НЕ ПЕРЕСЕКУТСЯ.А
В
A1
В1 -
17 слайд
Рассмотрим это на рисунке:
Такое быть не может! -
18 слайд
IV. Закрепление изученного материала
Задача № 1
Два тупых угла имеют общую сторону, а две другие стороны взаимно перпендикулярны. Найдите величину тупого угла, если известно, что тупые углы равны.
О
А
В
С
РЕШЕНИЕ: -
19 слайд
РЕШЕНИЕ:
< AOB = < AOC. BO ┴ OC, значит < BOC = 900. < AOB = 3600 – 900 = 2700 -
20 слайд
Задача № 2
Из вершины развернутого угла
проведены два луча, которые делят его на три равные части. Докажем, что биссектриса среднего угла перпендикулярна сторонам развернутого угла.
В
К
С
А
D
О
РЕШЕНИЕ: -
21 слайд
РЕШЕНИЕ:
< AOB = < BOC = < COD = 600. OK – это биссектриса < BOC, тогда < COK = < BOK = 300, следовательно, < DOK = 600 + 300 = 900, т.е. ОК ┴ ОА, ОК ┴ ОD. -
22 слайд
V. Подведение итогов
– УЧИТЕЛЬ ВЫЧТАВЛЯЕТ ОЦЕНКИ ЗА УРОК -
23 слайд
VI. Домашнее задание
№ 66, 70
Дополнительная задача № 1:
Докажите, что сумма каждых трех углов, не прилежащих один к другому и образуемых тремя прямыми, проходящими через одну точку, равна прямым угламДополнительная задача № 2:
Прямые КМ и ВС пересекаются в точке О, < COM = 890 . Перпендикулярны ли прямые КМ и ВС? Объясните ответ.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Построения циркулем и линейкой
- Построение перпендикулярных прямых
Примеры:
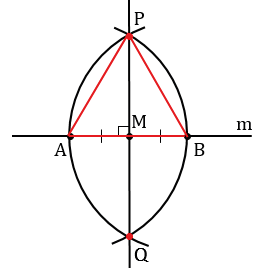
1. Даны прямая и точка на ней. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.
Дано: прямая m, M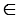
Построить: МP
Решение:
Произвольно строим с помощью линейки прямую m и отмечаем на ней точку М.
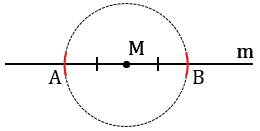
На лучах прямой m, исходящих из точки М, с помощью циркуля откладываем равные отрезки МА и МВ (МА = МВ). Для этого строим окружность с центром в точке М, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки М (смотри выделенное красным).
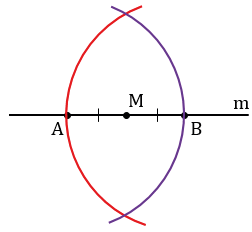
Затем строим две окружности с центрами в точках А и В радиуса АВ (полностью окружности строить необязательно, смотри выделенное фиолетовым и красным цветом).
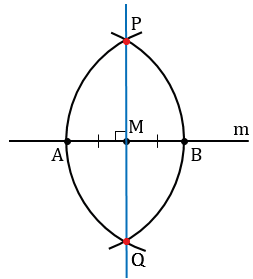
Данные окружности пересекаются в двух точках, обозначим их Р и Q. Проведем с помощью линейки через точку М и одну из точек Р или Q прямую, например, МР.
Докажем, что прямая МР – искомая прямая, т.е. что МP
Рассмотрим треугольник АРВ.
АР = ВР, т.к. по построению это радиусы одинаковых окружностей, следовательно, 

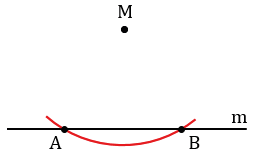
2. Даны прямая и точка не лежащая на этой прямой. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.
Дано: прямая m, M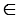
Построить: МN
Решение:
Произвольно строим с помощью линейки прямую m и отмечаем точку М, не лежащую на прямой m.
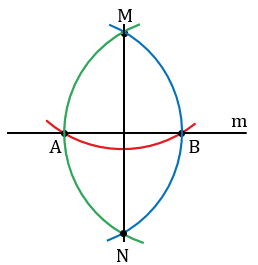
Далее строим окружность с центром в данной точке М, пересекающую прямую m в двух точках, которые обозначим буквами А и В (всю окружность строить необязательно, смотри выделенное красным цветом).
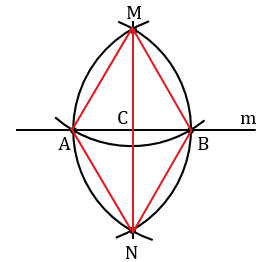
Затем построим две окружности с центрами в точках А и В, проходящие через точку М (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в точке М и еще в одной точке, которую обозначим буквой N. Проведем прямую МN.
Докажем что, прямая МN – искомая, т.е. МN
В 





Советуем посмотреть:
Построение угла, равного данному
Построение биссектрисы угла
Построение середины отрезка
Среднее пропорциональное
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 153,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 316*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 317,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 319*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 356,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 736,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1146,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1147,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1158,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1282,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
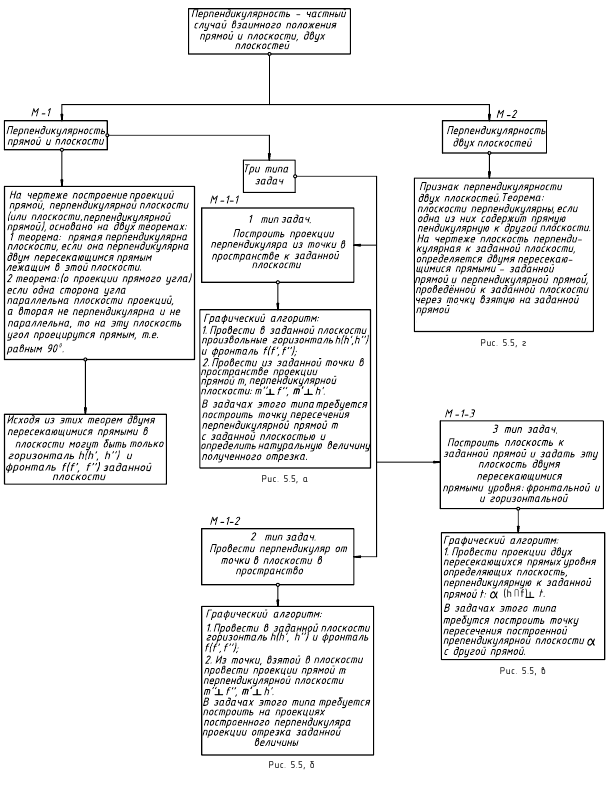
Перпендикулярность:
Решение задач на тему перпендикулярности прямой и плоскости основано на двух теоремах геометрии:
1-я теорема: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
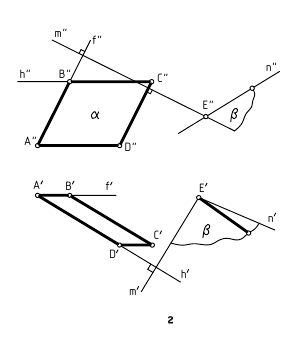
2-я теорема: о проекции прямого угла (изложена выше – см. рис. 2.14, 2.15 и 2.16) – если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то на эту плоскость проекций угол проецируется прямым.
Из этих двух теорем следует, что на чертеже проекции перпендикуляра к плоскости можно провести только к проекциям фронтали и горизонтали, то есть к двум пересекающимся прямым уровня, которые можно провести в плоскости.
!!! Запомните:
- – фронтальная проекция m” прямой, перпендикулярной прямой к плоскости, перпендикулярна к фронтальной проекции f” фронтали этой плоскости (m”
- – горизонтальная проекция m’ прямой, перпендикулярной прямой к плоскости, перпендикулярна к горизонтальной проекции h’ горизонтали этой плоскости (m’
Задачи на тему перпендикулярности прямой и плоскости можно разделить на три группы:
- 1-я группа. Провести от точки, лежащей в плоскости, перпендикуляр в пространство.
- 2-я группа. Провести из точки, не лежащей в плоскости, перпендикуляр к этой плоскости.
- 3-я группа. Построить плоскость, перпендикулярную к прямой общего положения (построить геометрическое место точек – ГМТ).
Первая группа задач требует по условию проведения перпендикуляра от плоскости (восставить перпендикуляр) в пространство (см. рис. 5.1).
В этой группе задач требуется, как правило, построить на проведенном перпендикуляре проекции отрезка заданной величины. Графические действия по построению проекций отрезка заданной величины на проекциях прямой общего положения изложены ранее (см. рис. 2.9).
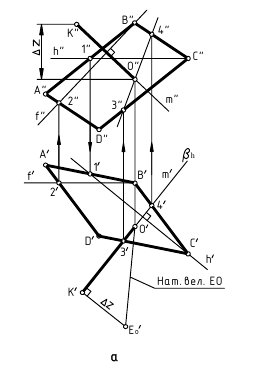
На рисунке 5.1 показано решение примерной задачи первой группы: построить плоскость β, параллельную заданной плоскости α(ABC), на расстоянии 15 мм.
Эта задача относится к первой группе, поскольку для построения параллельной плоскости β нужно предварительно построить произвольную точку на расстоянии 15 мм от заданной плоскости α, то есть из произвольной точки плоскости провести перпендикуляр в пространство.
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Провести в заданной плоскости общего положения ABC проекции фронтали f(f”,f’) и горизонтали h(h’,h’):
- – f’ // x, а f” – построить по вспомогательной точке 1;
- – h” // x, а h’ – построить по вспомогательной точке 2.
2-е действие. Провести от точки плоскости, например, от вершины A в пространство проекции перпендикуляра m(m”,m’):
- – фронтальную проекцию m” перпендикулярно f” (m”
f”);
- – горизонтальную проекцию m’ перпендикулярно h’ (m’
h ‘).
3-е действие. На проекциях перпендикуляра m построить проекции отрезка заданной величины 15 мм, для чего выполнить следующие графические действия:
- Ограничить построенную прямую m(m”, m’) произвольным отрезком AK(AK”, AK’).
- Построить натуральную величину этого отрезка (см. рис. 5.1) способом прямоугольного треугольника – это гипотенуза A’Kо.
- На построенной гипотенузе отложить заданную величину A’Do = 15 мм и построить проекции отрезка AD(A”D”, A’D’) заданной величины (см. построения), то есть проекции точки D(D”, D’), находящейся на расстоянии 15 мм от плоскости α(ABC).
4-е действие. Построить плоскость β, параллельную заданной плоскости ABC, проведя через проекции точки D две пересекающиеся прямые d и n, соответственно параллельные двум пересекающимся прямым AC и AB плоскости ABC:
– d” // A”C”; e” // A”B”; – d’ // A’C’; e’ // A’B’, то есть β(d ∩ e) // α(ABC).
Вторая группа задач требует по условию проведения перпендикуляра из точки в пространстве к плоскости (опустить перпендикуляр). В этой группе задач, как правило, требуется построить точку пересечения построенного перпендикуляра с заданной плоскостью.
Построение точки пересечения прямой общего положения с плоскостью общего положения было рассмотрено выше (см. рис. 4.6).
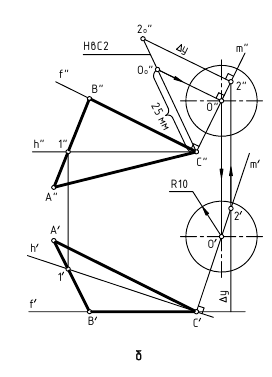
На рис. 5.2 показано решение примерной задачи второй группы: определить расстояние от точки K до заданной плоскости α(∆ABC).
Эта задача относится ко второй группе, так как расстояние от точки K до заданной плоскости α(∆ABC) определяется величиной перпендикуляра, проведенного из точки к плоскости.
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Провести в плоскости фронталь f(f”,f’) и горизонталь h(h”,h’).
2-е действие. Провести через заданную точку K(K”,K’) проекции перпендикуляра m(m”,m’) к плоскости ABC:
- – m” перпендикулярно f” (m”
f”);
- – m’ перпендикулярно h’ (m’
h’).
3-е действие. Построить точку пересечения O(O”,O’) перпендикуляра m с заданной плоскостью общего положения ABC, выполнив промежуточный графический алгоритм:
1. Заключить прямую m во вспомогательную горизонтально-проецирующую плоскость β(βH).
2. Построить вспомогательную линию пересечения 3-4 заданной плоскости α(∆ABC) со вспомогательной плоскостью β:
- – 3′-4′ – определяется на следе βH;
- – 3″-4″ – строится по принадлежности точек 3 и 4 сторонам AC и AB треугольника ABC;
3. Определить проекции искомой точки пересечения O(O”,O’) на пересечении проекций построенной вспомогательной линии пересечения 3-4 с проекциями перпендикуляра m.
4-е действие. Построить натуральную величину отрезка KO способом прямоугольного треугольника, то есть определить расстояние от точки K до плоскости ABC.
Третья группа задач требует по условию построения некоторой вспомогательной плоскости (геометрического места точек), перпендикулярной к прямой общего положения. Эту перпендикулярную плоскость можно задать двумя пересекающимися прямыми, каждая из которых должна быть перпендикулярна прямой общего положения (теорема о перпендикулярности прямой и плоскости, т. е. признак перпендикулярности прямой и плоскости). На чертеже плоскость, перпендикулярную к прямой общего положения, можно задать только проекциями пересекающихся прямых уровня – фронтальной (параллельной плоскости проекций V) и горизонтальной (параллельной плоскости H), что соответствует теореме о проекции прямого угла. В задачах этой группы, как правило, требуется по условию определить точку пересечения заданной прямой со вспомогательной перпендикулярной плоскостью.
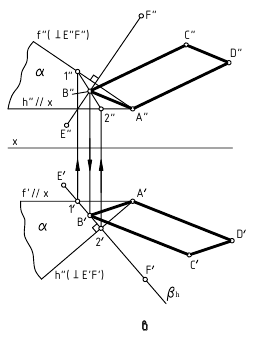
На рис. 5.3 показано решение примерной задачи третьей группы: определить расстояние от точки K до прямой общего положения m.
Эта задача относится к третьей группе, поскольку на чертеже провести перпендикуляр к прямой общего положения, по которому определяется расстояние от точки K до заданной прямой m, нельзя (прямой угол в этом случае не проецируется прямым). Следовательно, для решения нужно построить вспомогательную плоскость β, перпендикулярную к заданной прямой, которая будет геометрическим местом всех перпендикуляров к этой прямой.
Для решения задачи требуется выполнить следующий графический алгоритм:
1-е действие. Построить троим вспомогательную плоскость β, перпендикулярную заданной прямой m, задав ее двумя пересекающимися прямыми уровня a и b:
- – горизонтальной прямой а: a” // x; a’
m’;
- – фронтальной прямой b: b’ // x; b”
m”.
2-е действие. Построить точку О(O’,O”) пересечения заданной прямой m со вспомогательной плоскостью β(a∩b) по алгоритму построения точки пересечения прямой общего положения с плоскостью общего положения (см. рис. 5.3).
3-е действие. Соединить одноименные проекции точек K и O: полученный отрезок общего положения KO(K”O”, K’O’) и есть расстояние от точки до прямой, искаженное на проекциях по величине.
4-е действие. Построить натуральную величину построенного отрезка KO способом прямоугольного треугольника (см. рис. 5.3).
Структуризация материала пятой лекции в рассмотренном объеме схематически представлена на рис. 5.4 (лист 1). На последующем листе 2 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 5.5).
Перпендикулярность:
1 тип задач:
2 тип задач:
3 тип задач:
Перпендикулярность плоскостей:
- Проекции с числовыми отметками
- Перспектива
- Построение окружности
- Цилиндрическая винтовая линия
- Конструктивное отображение пространства
- Чертежи точки, отрезка прямой
- Чертежи плоскости
- Взаимное положение двух плоскостей, прямой линии и плоскости



















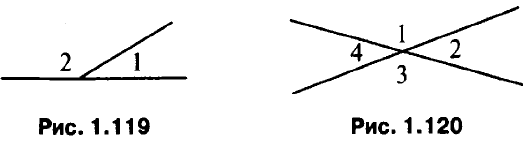


























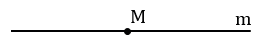

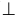
 f”);
f”); h ‘).
h ‘).
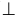 f”);
f”); h’).
h’).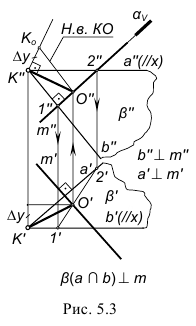
 m’;
m’; m”.
m”.