Как составить задачу на производительность труда

2-й способ решения — без таблицы

Как обойтись без составления таблицы?

Сразу составить уравнение.

Для этого определим, какая величина нам не нужна в уравнении, чтобы затем приравнять.

Производительность? Ее и надо найти. Работа? Она нам дана по условию, поэтому глупо от нее избавляться. Остается время: оно нам и неизвестно, и не нужно.

Слева от знака равно будем писать формулу времени для первого рабочего, а справа – для второго.

А теперь вспомним, что я говорил в сааамом начале: задачи на работу и на движение – это то же самое. Спорное заявление, да? Ну, давай проверим, есть ли аналогия.

Во-первых, сравним формулы:

Движение	Работа
( displaystyle v=frac{S}{t})	( displaystyle P=frac{A}{t})
Скорость движения	Скорость выполнения работы, т.е. производительность
Пройденный путь	Выполненная работа
Потраченное на движение время	Потраченное на работу время

Теперь рассмотрим задачу:

Пример №1

Расстояние ( displaystyle 112) км первый велосипедист проезжает на ( displaystyle 2) часа дольше, чем второй.

Сколько км в час проезжает первый велосипедист, если известно, что второй за час проезжает на один километр больше, чем первый?

Ничего не напоминает? Да я же просто заменил слова: «Заказ» на «расстояние», «деталь» на «километр», «рабочий» на «велосипедист», «выполняет» на «проезжает». Суть осталась той же. Даже решение будет точно таким же (разберу здесь только II способ – без таблицы).

Пусть скорость первого ( displaystyle x), тогда второго ( displaystyle x+1). Сколько времени едет первый? ( displaystyle frac{112}{x}). Сколько времени едет второй? ( displaystyle frac{112}{x+1}). На сколько время первого больше, чем второго? На ( displaystyle 2) часа:

( displaystyle frac{112}{x}=frac{112}{x+1}+2).

То же самое уравнение! Вот и получается, что работа и движение – одно и то же.

Как решать задачи на совместную работу

Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).

Пример №2

Первая труба заполняет бассейн за ( displaystyle 6) часов, а вторая – за ( displaystyle 4).

За какое время они заполнят бассейн, работая вместе?

Решение

Во-первых, давай придумаем аналогию с движением.

Придумал?

Бассейн – это путь. Допустим, из ( displaystyle A) в ( displaystyle B). Итак, первый автомобиль проезжает путь ( displaystyle AB) за ( displaystyle 6) часов, второй – за ( displaystyle 4).

А теперь как сформулировать вопрос? За какое время они проедут весь путь, двигаясь вместе? Бред.

Если двигаться параллельно, то каждый проходит весь путь самостоятельно. А в какой ситуации нам важно, какой путь автомобили проходят в сумме? Все гениальное просто: если они движутся навстречу друг другу!

Тогда что нас просят найти? Время, через которое они встретятся.

Поразмысли немного над этой аналогией. Все понял? Тогда идем дальше.

Какова «скорость» (а по-настоящему, производительность) первого? Путь (работа) деленный на время: ( displaystyle {{P}_{1}}=frac{A}{{{t}_{1}}}=frac{A}{6}). А второго? ( displaystyle {{P}_{2}}=frac{A}{{{t}_{2}}}=frac{A}{4}).

Итак,

( displaystyle P={{P}_{1}}+{{P}_{2}}=frac{A}{6}+frac{A}{4}=frac{5A}{12}).

Тогда время, за которое с такой производительностью будет выполнена работа ( A):

( displaystyle t=frac{A}{P}=frac{A}{frac{5A}{12}}=frac{12}{5}=2,4) (ч)

Итак, правило:

При совместной работе производительности складываются

А теперь давай рассмотрим самый сложный пример, научившись решать который, ты сможешь с легкостью справится с любой задачей на ЕГЭ.

Пример 8

На изготовление ( displaystyle 600) деталей первый рабочий тратит на ( displaystyle 10) часов меньше, чем второй рабочий на изготовление ( displaystyle 500) таких же деталей. За какое время, работая совместно, они изготовят партию в ( displaystyle 1000) деталей, если известно, что за час первый рабочий делает на ( displaystyle 5) деталей больше?

Решение:

Давай определимся, что нам нужно найти? Нам нужно найти время, за которое рабочие изготовят ( displaystyle 1000) деталей, то есть: ( displaystyle frac{1000}{{{P}_{1}}+{{P}_{2}}}).

Значит, нужно найти ( displaystyle {{P}_{1}}) и ( displaystyle {{P}_{2}}).

Первый рабочий за час делает на ( displaystyle 5) деталей больше. Обозначим производительность первого рабочего за х, тогда производительность второго – ( displaystyle x-5).

( displaystyle 600) деталей первый рабочий делает за ( displaystyle {{t}_{1}}) часов, а ( displaystyle 500) таких же деталей второй рабочий делает за ( displaystyle {{t}_{2}}={{t}_{1}}+10) часов.

То есть: ( displaystyle {{t}_{1}}=frac{600}{x}, a {{t}_{2}}={{t}_{1}}+10=frac{500}{x-5}).

Приравняв ( displaystyle {{t}_{1}}), получаем уравнение:

Производительность труда в задаче 17

2 октября 2015

Задачи этого типа появились в ЕГЭ относительно недавно, но застали врасплох как учеников, так и многих учителей. А всё потому что решаются они с помощью производной — инструмента, совершенно непривычного для второй части экзамена.

Задача 17. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно ${{t}^{2}}$часов в неделю, то за эту неделю они производят $3t$единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно ${{t}^{2}}$часов в неделю, то за эту неделю они производят $4t$единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.

В приведённом условии есть важный момент, после осознания которого у вас вообще не будет проблем с решением подобных задач. Дело в том, что величина $t$, указанная для первого завода и для второго — это не одно и то же число! Другими словами, суммарное время рабочих на первом и другом заводе будет разным.

Для решения введём новые переменные: ${{a}^{2}}$ — суммарное время рабочих на первом заводе, ${{b}^{2}}$ — суммарное время на втором. С учётом производительности получим:

$begin{align}& {{a}^{2}}to 3a \& {{b}^{2}}to 4b \end{align}$

Таким образом, затратив суммарно ${{a}^{2}}+{{b}^{2}}$ часов времени, мы получим $3a+4b$ единиц продукции в неделю. Всё остальное — элементарная математика, подробно описанная в видеоуроке:

В прошлый раз мы рассматривали довольно «противные» задачи, связанные с вычислением времени в задачах про кредиты. Но это было очень просто по сравнению с тем, что мы будем рассматривать сегодня, а именно экономическую задачу 17 про производительность труда, в которой требуется применять производную. Эти задачи появились в ЕГЭ по математике относительно недавно, и те, кто уже с ними столкнулся, оценили, что, во-первых, условие таких задач довольно длинное, а, во-вторых, в каждой из таких задач есть неприятная зацепка, на которой «прогорели» очень многие ученики.

Думаю, вы уже догадались, что речь идет о той самой задачи 17, когда у Григория есть два завода, и еще указана производительность труда, и требуется оценить, какое наибольшее количество продукции можно произвести на этих двух заводах, если распределить нагрузку оптимально. Но на самом деле, в этих задачах 17 нет ничего сложного, даже чуть проще, чем многие задачи на кредиты. Поэтому сейчас мы рассмотрим одно из таких заданий, внимательно пробежимся по каждому пункту и посмотрим, как именно должно выглядеть идеальное ее решение.

Задача № 1

Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно ${{t}^{2}}$ часов в неделю, то за эту неделю они производят $3t$ единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно ${{t}^{2}}$ часов в неделю, то за эту неделю они производят $4t$. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.

Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Шаг первый: вводим переменные

Прежде всего, перед тем как переходить к непосредственному решению задачи 17 из ЕГЭ по математике, попытаться что-то посчитать, составить какие-то формулы, поймите одну простую вещь: величина ${{t}^{2}}$, данная и в первом, и во втором предложении, никак не связаны друг с другом. Коэффициент $t$ нам дан исключительно для того, чтобы сравнить производительность на разных заводах при одинаковом расходе времени. Думаю, это сравнение абсолютно очевидно: на первом производительность составляет $3t$, а на втором — $4t$, т.е. чуть побольше. На практике это означает следующее: давайте распишем, что происходит на каждом из них.

На первом заводе у нас расходуется ${{a}^{2}}$ времени (после замены) и производится $3a$ единиц продукции. На втором — ${{b}^{2}}$ времени и $4b$ продукции.

А теперь давайте сложим расходы времени и суммарный выпуск продукта.

Получим, что суммарный расход времени составляет ${{a}^{2}}+{{b}^{2}}$, а суммарный расход продукции — $3a+4b$. При этом еще раз обращаю ваше внимание: никто не говорил, что ${{a}^{2}}$ и ${{b}^{2}}$ должны быть равны. Ключевое слово здесь «если» и в первом, и во втором случае. Именно поэтому мы так смело меняем коэффициенты $t$ на $a$ в первом случае и на $b$ во втором случае.

Шаг второй: составляем и решаем уравнение

Давайте посмотрим, что у нас получилось. ${{a}^{2}}+{{b}^{2}}$ — это суммарный расход времени. Поскольку Григорий платит рабочему 500 рублей за каждый час работы, то всего он сможет заплатить такую сумму:

[500cdot left( {{a}^{2}}+{{b}^{2}} right)=5000000]

Вот и первое уравнение.

На самом деле, основная сложность этой задачи 17 про производительность труда — вовсе не составление уравнения. Она состоит в том, что нужно понять, что на первом и на втором заводе время разное. Именно поэтому для первого мы везде заменили $t$ на $a$, а для второго — $t$ на $b$. В итоге как вы сейчас увидите, мы получим одно уравнение с двумя неизвестными, которое легко упрощается — одна неизвестная легко выражается через другую. И поэтому вся функция, выражающая количество произведенного товара, на самом деле зависит от одной-единственной переменной, в нашем случае это будет переменная $a$.

Далее, я думаю, все понятно: у нас есть функция, отрезок, на котором эта функция рассматривается, а все, что нам требуется найти — это наибольшее значение этой функции на данном отрезке. Вообщем, классическая задача для применения производных, в нашем случае новая задача 17 из ЕГЭ по математике.

Суммарный выпуск продукции ($S$) равен:

[S=3a+4bto max ]

Вот теперь задача и проявилась: имея ограничение на $a$ и $b$, нам нужно добиться того, чтобы $S$ принимала свое максимальное значение. Для начала давайте немножко поработаем с уравнением: $$

[500cdot left( {{a}^{2}}+{{b}^{2}} right)=5000000left| :500 right.]

[{{a}^{2}}+{{b}^{2}}=10000]

Отсюда выразим $b$:

[{{b}^{2}}=10000-{{a}^{2}}]

[b=sqrt{10000-{{a}^{2}}}]

Конечно, тут следовало бы перед выражением поставить $pm $, однако у нас речь идет о времени, а оно не может быть отрицательным, поэтому мы берем положительное значение. Итого суммарный объем выпускаемого товара может быть выписан как функция от одной-единственной переменной $a$:

[S=3a+4sqrt{10000-{{a}^{2}}}]

Шаг третий: находим максимальное значение функции

Теперь нам нужно найти максимальное значение этой функции на всей области определения, а совершенно очевидно, что величину $a$, т.е. количество товара, выпущенного на первом заводе, увеличивать до бесконечности нельзя, просто потому что корень имеет конкретную область определения — величина, стоящая под корнем, не должна быть отрицательной. Давайте запишем это:

[10000-{{a}^{2}}ge 0]

[{{a}^{2}}le 10000]

[left| a right|le 100]

[ain left[ 0;100 right]]

Итого мы получили классическую задачу из первой части ЕГЭ по математике: у нас есть функция, есть интервал, соответственно, нужно найти максимальное значение этой функции на заданном интервале. Давайте считать производную:

[{S}’=3+4cdot frac{1cdot left( 10000-{{a}^{2}} right)}{2sqrt{10000-{{a}^{2}}}}=3+frac{4cdot left( -2a right)}{2sqrt{10000-{{a}^{2}}}}=]

[=3-frac{4a}{sqrt{10000-{{a}^{2}}}}]

[3-frac{4a}{sqrt{10000-{{a}^{2}}}}=0]

Решаем полученное уравнение:

[3=frac{4a}{sqrt{sqrt{10000-{{a}^{2}}}}}]

[3sqrt{10000-{{a}^{2}}}=4a]

[9left( 10000-{{a}^{2}} right)=16{{a}^{2}}]

[90000-9{{a}^{2}}=16{{a}^{2}}]

[25{{a}^{2}}=90000]

[5a=3cdot 100]

[a=frac{3cdot 100}{5}=60]

Теперь, зная, чему равно $a$, легко найти $b$:

[b=sqrt{10000-3600}=sqrt{6400}=80]

Однако для полного и обоснованного решения необходимо понять знак производной. Давайте начертим числовую прямую и отметим на ней $a=60$ и посмотрим, что происходит при $a gt 60$:

Например, если взять $a=99$ мы получим следующее:

[10000-{{99}^{2}}={{100}^{2}}-{{99}^{2}}=left( 100-99 right)left( 100+99 right)=199]

Если посмотрим на исходное выражение, то очевидно, что $sqrt{199} lt 99$, но посчитав его, получаем в ответе отрицательное число.

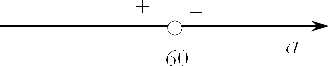
Отсюда следует, что$a=60$является точкой максимума, т.е. именно той, которую мы и хотели найти. Именно в ней наша исходная функция принимает исходное значение. Осталось подставить в $S$ полученное значение $a$ и $b$:

[S=3cdot 60+4cdot 80=180+320=500]

Окончательный ответ: 500 единиц товара.

Нюансы решения

Как видите, все оказалось не так уж и сложно. Единственно, что нам нужно запомнить — это то, что величина ${{t}^{2}}$, когда речь идет о первом заводе дает нам информацию о производительности труда именно на нем, т.е. связывает время, затраченное на производство и количество продукции в рамках только него.

Величина ${{t}^{2}}$, относящаяся ко второму заводу, говорит нам именно о нем и никак не связана с первым.

Более того, считать, что количество времени, затраченного рабочими на первом и на втором заводах, абсолютно одинаково — это вообще глупость, потому что в этом случае полученное уравнение оказалось бы намного проще и решалось бы как элементарное линейное: нам бы не потребовалось никаких производных, никаких доказательств, что мы получили точку максимума — мы просто бы разделили зарплату между рабочими первого и второго производств пополам.

Поэтому запомните: время, потраченное на первом и на втором заводах, разное, поэтому пусть на первом потрачено ${{a}^{2}}$ времени, а на втором — ${{b}^{2}}$. В этом случае задача действительно становится сложнее, при этом интересней и вполне достойной называться задачей 17 из ЕГЭ по математике.

Задача № 2

А в качестве десерта предлагаю решить еще одну такую же задачу 17 из ЕГЭ по математике, однако выкладки в этот раз будут минимальными, по возможности такими, какие и нужно делать на экзамене по математике.

Сергей владеет двумя промышленными заводами, выпускающими одинаковую продукцию. На втором заводе установлено современное оборудование, поэтому на нем может быть выпущено больше единиц продукции. Известно, что если рабочие первого завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $t$ единиц продукции. А если рабочие второго завода суммарно трудятся ${{t}^{2}}$ часов в неделю, то выпускают $2t$ единиц продукции. Ставка заработной платы рабочего составляет 500 рублей в час.

Сергей готов платить рабочим 30 250 000 рублей в неделю. На какое максимальное количество единиц продукции он может рассчитывать?

Шаг первый: вводим переменные

Если рабочие на первом заводе трудятся ${{x}^{2}}$, то это дает нам $x$ единиц товара. На втором ${{y}^{2}}$ времени дает нам $y$ товаров. Вновь складываем расходы времени — ${{x}^{2}}+{{y}^{2}}$ и отдельно складываем объем продукции — $x+2y$. Величина ${{x}^{2}}+{{y}^{2}}$ — это суммарный расход времени за неделю.

Шаг второй: составляем и решаем уравнение

Поскольку за каждый час работы платится 500 рублей, то суммарный расход денег за неделю составит:

[500cdot left( {{x}^{2}}+{{y}^{2}} right)=30250000]

[{{x}^{2}}+{{y}^{2}}=60500]

Таким способом, ограничения на ${{x}^{2}}$ и ${{y}^{2}}$ найдены.

Теперь необходимо записать сумму:

[S=x+2yto max ]

Опять же будем считать производную, но для этого сначала необходимо выразить $y$ через $x$:

[{{y}^{2}}=60500-{{x}^{2}}]

[y=sqrt{60500-{{x}^{2}}}]

Подставляем найденное значение $y$ в нашу формулу и получаем:

[S=x+2cdot sqrt{60500-{{x}^{2}}}]

Находим производную этой конструкции:

[{S}’=1+2frac{1left( -2x right)}{2sqrt{60500-{{x}^{2}}}}=1-frac{2x}{sqrt{60500-{{x}^{2}}}}]

Вновь приравниваем полученное выражение к нулю:

[1-frac{2x}{sqrt{60500-{{x}^{2}}}}=0]

[frac{1}{1}=frac{2x}{sqrt{60500-{{x}^{2}}}}]

[sqrt{60500-{{x}^{2}}}=2x]

[60500-{{x}^{2}}=4{{x}^{2}}]

[60500=5{{x}^{2}}]

[{{x}^{2}}=frac{60500}{5}=121cdot 100]

[x=11cdot 10=110]

Шаг третий: находим максимальное значение функции

Мы получили критическую точку функции $S$. Теперь необходимо доказать, что это точка максимума. Для этого начертим вновь прямую, отметим на ней полученную точку 110 и возьмем любое число, больше чем 110. Однако для упрощения дальнейших выкладок предлагаю взять не рандомное число как в прошлый раз, а посчитать его с помощью следующего метода. Для начала давайте найдем $y$. Запишем такое выражение:

[y=2x=220]

Очевидно, что 220 больше 110, и если мы поставим его в нашу функцию, то получим число на отмеченном интервале:

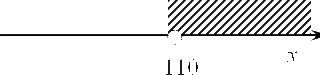
Давайте подставим:

${S}’left( 220 right)=1-frac{2cdot 220}{sqrt{60500-{{220}^{2}}}}=1-frac{440}{sqrt{60500-48400}}=$

$=1-frac{440}{sqrt{12100}}=1-frac{440}{110}=1-4=-3$

Следовательно, справа от числа 110 мы получаем отрицательную производную, а слева, естественно, будет положительная.

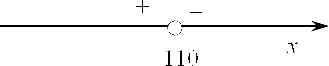
Итого 110 — точка максимума. Это является строгим обоснованием.

Теперь подставляем в выражение $x$ и $y$, которые мы нашли:

[S=110+2cdot 220=110+440=550]

Ответ: 550 единиц товара.

Ключевые моменты решения задач17 на производительность труда из ЕГЭ по математике

Все, что нам нужно знать — это:

1. Правило вычисления производных сложных функций.
2. Правила решения несложных уравнений.

Кроме того, хотел бы отметить, что не надо бояться работать с большими числами. Такие выражения, когда у нас появляются пятизначные и более числа, абсолютно типичны для последних задач 17 из ЕГЭ по математике, потому что они реально трудные. Но на самом деле, в этих задачах из ЕГЭ нет ничего трудного. Вам только нужно знать следующее:

• ${{a}^{2}}to a$ и ${{b}^{2}}to 2b$ — как связано затраченное время с объемом выпущенного товара;
• $S=a+2bto max $ — суммарный объем товара находится по несложной формуле.

Кроме того, необходимо понимать, как связано время, затраченное на первом производстве и на втором, т.е. каковы максимальны ограничения на это время.

А дальше дело техники: считаем производную, решаем уравнение, подставляем в исходное ограничение и получаем окончательный ответ.

Надеюсь, это видео поможет вам построить собственный завод, где вы будете платить рабочим по 30 млн. рублей в неделю, если такой суммы вам окажется недостаточно, заходите на наш сайт, подписывайтесь на паблик ВКонтакте и на канал в YouTube. До новых встреч!

Смотрите также:

1. Задачи на кредит с плавающим платежом
2. Задачи с экономическим содержанием — основные формулы
3. Тест к уроку «Что такое логарифм» (средний)
4. Решение задач B12: №440—447
5. Как решать задачу 18: графический подход
6. Нестандартные задачи B2: кредит в банке

Примеры решения задач.

1. На сколько процентов изменится показатель производительности труда в плановом периоде, если за отчетный период продукции выработано на сумму 2500тыс.руб. Численность работающих составляла 1350 человек, в плановом периоде объем вырабатываемой продукции должен возрасти на 6% численность останется без изменения.

РЕШЕНИЕ.

Расчет можно произвести на основании изменений показателя выработки.

Выработка на одного рабочего за отчетный период составит:

В = Q / N = 2500 / 1350 = 1,85 тыс.руб./ чел.

По условию объем вырабатываемой продукции увеличивается на 6% и будет составлять 2650 тыс.руб.

При сохранении численности в плановом периоде показатель выработки будет составлять: Вп = 2650 / 1350 = 1,96 тыс.руб. /чел.

Рост производительности труда составит:

∆В = 1,96 – 1,85 = 0,11 тыс.руб. или 6%.

ОТВЕТ: Рост производительности труда составит 6%.

2. Определить показатели производительности труда: среднегодовой, среднедневной и среднечасовой, если за год продукции выработано на сумму 10000 тыс.руб., среднесписочная численность рабочих – 380 человек, количество рабочих дней в году 204, эффективная продолжительность рабочего дня – 8 ч.

РЕШЕНИЕ.

Среднегодовая выработка на одного рабочего может быть найдена по формуле: Вг = Q / Nр = 10000 / 380 = 26,3 тыс.руб.

Одним рабочим в течении года произведено продукции на сумму 26,3 тыс.руб., продолжительность года ,по условию 204 дня, следовательно среднедневная выручка на одного рабочего будет составлять: Вдн = 26,3 / 204 = 0,13 тыс.руб..

При продолжительности рабочей смены 8 часов, часовая выработка рабочего составит: Вч = 0,13 / 8 = 0,02тыс.руб..

ОТВЕТ: Вг =26,3 тыс.руб., Вдн = 0,13 тыс. руб., Вч = 0,02 тыс.руб..

3. Общий объем трудозатрат на годовой выпуск продукции (ДСП) – 650000 нормо – часов. Плановый объем выпуска ДСП –220000куб.м. Фактические трудозатраты на выпущенную продукцию – 645000 чел.-ч. Фактически выпущено плит – 195000 куб.м. Определить плановую и фактическую трудоемкость 1 куб.м плит. Сделать вывод.

РЕШЕНИЕ.

Трудоемкость продукции представляет собой затраты живого труда на производство единицы продукции, и может быть найдена по формуле: Тр = Т / Q

Плановая трудоемкость составляет:

Тр п = 650000 / 220000 = 2,95 чел./час

Фактическая трудоемкость равна:

Тр ф = 645000 / 195000 = 3,3 чел./ час.

ОТВЕТ: Фактическая трудоемкость производства ДСП выше плановой, что является причиной невыполнения плана по производству ДСП.

1. Производительность труда

Производительность
(труда)
(productivity)
– соотношение
между выпуском
экономической единицы и использованием
факторов
производства,
которые вовлечены в ее производство.
Производительность обычно измеряется
в единицах выпуска за человеко-час для
выявления различий между фирмами,
отраслями или странами. Увеличение
производительности происходит тогда,
когда выпуск за человеко-час растет.
[28]

Программа

Сущность
и показатели производительности труда.
Понятия «выработка», «трудоемкость»
продукции. Система показателей для
измерения, планирования и учета
производительности труда. Резервы
и факторы
роста производительности труда.
Классификация
резервов роста производительности
труда. Методика расчета роста
производительности труда по факторам.
Соотношение прироста производительности
труда и снижения трудоемкости.

[13, с. 99-102; 15, с.
148-162; 26, с. 328-339; 33, с. 297-308]

Методические
указания к изучению темы

При
изучении данной темы необходимо
разобраться в экономической сущности
понятий «производительность труда»,
показателей, ее характеризующих. Усвоить
виды и методику расчета показателей
производительности труда. Следует четко
представлять, какие факторы влияют на
рост производительности труда, освоить
методику их расчета. Важно понимать
различие между экстенсивными и
интенсивными направлениями повышения
производительности труда, роль
человеческого фактора в этих процессах.
Особое внимание следует уделить роли
и направлениям повышения производительности
труда в современной экономике.

Вопросы для
самопроверки

1. Что понимается
   под «производительностью труда»?

2. Какие
   существуют методы измерения
   производительности труда? Какова сфера
   их применения, точность и достоверность?

3. Чем
   отличается производительность живого
   труда от производительности общественного
   (совокупного) труда?.

4. Какой
   из показателей производительности
   труда является основным плановым и
   учетным показателем для предприятий?

5. Понятие выработки,
   ее разновидности и способы расчета.

6. Перечислите
   резервы роста производительности
   труда.

7. Какие
   показатели характеризуют использование
   рабочего времени?

Методические указания к решению задач

Основным
показателем эффективности
использования
персонала
предприятия является производительность
труда.

Производительность
труда –
результативность полезного, конкретного
труда, определяющего эффективность
целесообразной производительности
деятельности в данный промежуток
времени.

Экономическое
содержание повышения
производительности
труда заключается в увеличении выпуска
продукции или объема выполняемых работ
при одном и том же количестве живого
труда или, что то же самое,
в уменьшении количества труда,
затрачиваемого на единицу
продукции. В
первом случае производительность труда
характеризуется
выработкой
в единицу времени, во втором случае —
трудоемкостью
изготовления
единицы продукции.

1)
Выработка –
показывает количество продукции
производимой в единицу времени одним
работником (рабочим):

или

, (72)

где
V
– объем реализации услуг или продукции,
выполненных предприятиям за определенный
период времени, т. р.; Ч
– среднесписочная численность работников
предприятия за этот период, чел.; Т
– затраты
рабочего времени на производство данного
объема продукции нормо-час (чел.-час).

2)
Трудоемкость
– показывает
затраты труда на единицу произведенной
продукции или выполненной работы:

,
(73)

где
Т
– время, затраченное на производство
всего объема
продукции, нормо-час (чел.-час); V
– объем произведенной продукции или
выполненных работ в натуральных или
условно натуральных единицах.

Между
показателями производительности труда
существует следующая взаимосвязь:

,
(74)

где
∆t
– снижение трудоемкости продукции по
сравнению с базисным уровнем, %; ∆В
– прирост
выработки к базисному уровню, %.

.
(75)

Изменение
производительности труда за определенный
период по показателям выработки или
трудоемкости может быть определена по
формулам (76)
и (77).
Темпы роста производительности труда
рассчитываются как:

или

,
(76)

где
ПТ –
темп роста производительности труда,
%; Впл и
Вб – выработка
на одного работника соответственно в
плановом и базисном периодах; Тпл
и
Тб –
трудоемкость продукции в плановом и
базисном периодах, нормо-час (чел.-час).

Относительный
показатель производительности труда,
определяющий динамику ее роста в
процентах по сравнению с предшествующими
периодами, рассчитывается по формулам
(77):

или

.
(77)

Процент
прироста производительности труда не
совпадает с процентом снижения
трудоемкости: первый всегда больше
второго. Соотношение указанных показателей
может быть определено как:

или

(78)

где
∆ПТ
– темп прироста производительности
труда, %; ∆Т
– процент снижения трудоемкости.

Основными
факторами повышения производительности
труда являются: повышение технического
уровня производства; совершенствование
управления и организации производства
и труда; изменение объема и структуры
производства; снижение доли продукции,
конкурентоспособность которой падает
и повышение удельного веса высокорентабельной
продукции; другие общеэкономические
факторы.

Прирост
производительности труда в целом по
предприятию за счет влияния различных
факторов может быть определен на основе
данных об изменении численности
работников (∆ПТ), %:

∆ПТ
= (Эч ·
100)
/ (Чисх –
Эч) ,
(79)

где
Эч
– возможная экономия (уменьшение) в
планируемом периоде численности
работников по всем факторам, чел.; Чисх
– численность работников предприятия,
рассчитанная на планируемый объем
производства по базовой выработке
продукции на 1 работника, чел., определяется
по формуле (80):

. (80)

Изменение
численности работников под влиянием
различных факторов рассчитывается по
формуле (81):

,
(81)

где
t_1i,
t_2i
– базисная
и планируемая трудоемкость изготовления
единицы i-го
вида продукции, часов; V_i
– объем i-го
вида продукции
в натуральном или стоимостном измерении,
планируемый к выпуску,
штук; У
– удельный вес численности основных
производственных рабочих в численности
всех работающих, в долях единицы; Фпол
– полезный фонд рабочего времени одного
среднесписочного рабочего за год, ч;
Кв.н
– средний процент выполнения норм
выработки основными производственными
рабочими, %.

Общее
уменьшение (увеличение) численности
вычисляется путем суммирования полученных
величин по всем факторам:

,
(82)

где
Эч
– общее уменьшение (увеличение)
численности под влиянием факторов роста
производительности труда, чел.; Эi
– изменение численности под влиянием
i-го
фактора, чел.; п
– количество факторов, оказывающих
воздействие на изменение производительности
труда в плановом периоде.

Прирост
производительности труда за счет
снижения
трудоемкости
(∆ПТ):

∆ПТ
= (100
· ∆ t)
/ (100
– ∆ t),
(83)

где
∆ t
– процент снижения трудоемкости, %
равен:

∆ t
=
((t₁
– t₂)
/ t₁)
·
100,
(84)

тогда

∆ПТ
= ((t₁
– t₂)
/ t₂)
·
100,
(85)

где
t₁,
t₂
– трудоемкость изготовления единицы
изделия до и после проведения мероприятия,
ч.

Прирост
производительности труда (∆ПТ) за счет
улучшения
использования рабочего времени:

∆ПТ=(Фвр.пл.
/ Фвр.о) ·
100
– 100,
(86)

где
Фвр.о,
Фвр.пл.
– полезный фонд рабочего времени 1-го
рабочего в отчетном и плановом периодах
соответственно, ч.

Прирост
производительности труда за счет
снижения потерь рабочего времени:

,
(87)

где
П₁,
П₂
– потери рабочего времени в отчетном
и планируемом периодах, %.

Прирост
производительности труда за счет
увеличения
объема производства
и снижения
численности работников:

∆ПТ=(100
·
(∆V
–
∆Эч)) / (100
–
∆Эч),
(88)

где
∆V
– процент прироста объема выпускаемой
продукции и услуг на предприятии в
данном периоде, %; ∆Эч
– процент относительного сокращения
численности работников предприятия,
%.

Возможное
сокращение (увеличение) численности в
планируемом периоде по суммарному
влиянию факторов можно определить по
следующей формуле (89):

,
(89)

где
∆Эч
– возможное сокращение (увеличение)
численности в планируемом периоде за
счет всех факторов, %.

Абсолютное
сокращение (увеличение) численности
за счет роста
производительности труда
определяется по формуле (90):

Эч =
(∆ПТ ·
Чисх) / (∆ПТ + 100)
,
(90)

где Чисх
– исходная численность работников
предприятия, чел.

Экономия
численности за счет улучшения
использования рабочего времени
рассчитывается по формуле (91):

, ,
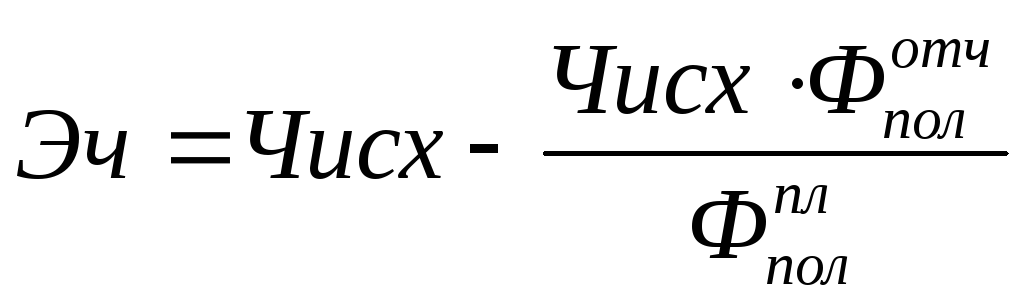
(91)

где
Ф^отч_пол,
Ф^пл_пол
– полезный фонд рабочего времени одного
рабочего в отчетном и последующем
периоде, дней.

ЗАДАЧИ

Задача
1. Определить
выработку продукции на одного рабочего
в натуральном и денежном выражении,
если выпуск изделий в смену – 200 тыс.
шт., среднесписочное число работающих
на предприятии – 500 человек, стоимость
одного изделия – 310 руб.

Задача
2. Плановый
объем реализации продукции по фабрике
за отчетный год составил 15 700 т. р.
Среднесписочная численность работающих
– 345 чел. За год каждый рабочий фабрики
отработал в среднем 1870 часов. Средняя
продолжительность рабочего дня 8 часов.
Определить среднегодовую, среднедневную
и среднечасовую выработку на одного
работающего.

Задача
3. В плановом
году объем производства продукции
предполагается увеличить с 12 млн р. до
12,8 млн. р. При базовой производительности
труда для этого потребовалось бы 1 260
человек. Однако увеличение численности
персонала не входит в планы руководства
предприятия, напротив, она должна
сократиться по сравнению с базовой на
3%. Определить, какими должны быть прирост
производительности труда в этих условиях
и абсолютный уровень плановой выработки.

Задача
4. Определить
трудоемкость единицы продукции по плану
и фактически, а также рост производительности
труда на основе следующих данных:
трудоемкость товарной продукции по
плану –
30 000 нормо-часов; плановый
объем выпуска в натуральном выражении
– 200 шт.; фактическая трудоемкость
товарной продукции –
26 000 нормо-часов;
фактический объем выпуска – 220 шт.

Задача
5. Производительность
труда одного работника в отчетном году
составила 4 250 т. р., потери рабочего
времени – 6%. Из 25 работников цеха 20
являются основными. В результате
улучшения организации труда в планируемом
году потери рабочего времени должны
сократиться до 3%. Определить прирост
производительности труда в процентах
и стоимостном выражении.

Задача
6. Рассчитать
среднегодовую, среднедневную плановую
и фактическую выработку и процент
выполнения плана по выработки при
следующих исходных данных:

Объем реализации
услуг и продукции:

по плану …….. 2
500 т. р.; фактически ……… 2 800 т. р.

Среднесписочная
численность рабочих:

по плану …….. 152
чел.; фактически ………. 150 чел.

Количество
отработанных дней одним рабочим:

по плану …….. 226
дня; фактически ………. 224 дня.

Задача
7. Определить,
на какой процент возрастет производительность
труда всех рабочих, если в результате
внедрения мероприятия 20 человек стали
выполнять объем работ, который раньше
выполняли 25 человек. Всего рабочих 120
человек.

Задача
8. В цехе
намечено сократить потери рабочего
времени с 7 до 3,5%. Численность работников
составляет 50 человек.

Определить
рост производительности труда по
факторам и общий, а также высвобождение
численности.

Задача
9. В результате
внедрения мероприятий объем реализации
составил 230 тыс. руб. Выработка на одного
рабочего в год составила 2870 руб.
Трудоемкость изготовления изделия
после внедрения мероприятия снизится
с 17,2 до 16,5 ч. Определить количество
условно высвободившихся рабочих.

Задача
10. Численность
работающих – 260 человек, в том числе 80%
– основные производственные рабочие.
Фактическая средняя трудоемкость
изготовления одного изделия – 2,3 часа,
количество рабочих дней – 22, средняя
продолжительность рабочего дня – 8
часов. Потери рабочего времени основными
рабочими в смену – 10% от ее продолжительности.
Определите среднемесячную выработку
на одного работающего и рабочего.

Задача
11. Определить
численность рабочих, если выработка
одного рабочего в отчетном году составила
165 т. р., в планируемом году намечается
повысить производительность труда на
8%, а выручка должна составить 2,5 млн р.

Задача
12. Определить
выработку одного рабочего в плановом
периоде, если в результате пересмотра
норм выработки трудоемкость снизилась
на 7%, а в результате мероприятий,
направленных на улучшение качества
услуг, возросла на 4%. Выработка в отчетном
периоде на 1 рабочего составила 130 т. р.

Задача
13. В истекшем
году списочный состав предприятия был
40 человек. На предстоящий год планируется
увеличить объем оказания услуг на 30%,
увеличив производительность труда
работников в среднем по предприятию
лишь на 10%. Определить численность
работников предприятия в планируемом
году с учетом запланированных мероприятий.

Задача
14. В результате
мероприятия трудоемкость пошива изделия
сократилась на 15 мин, объем по плану на
год составил 120 000 единиц. Полезный фонд
рабочего времени на одного среднесписочного
рабочего 1 840 часов. Средний процент
выполнения норм выработки – 105%. Определить
возможное сокращение численности.

Задача
15. Определить
возможное сокращение численности
рабочих и прирост производительности
труда, если объем реализации в отчетном
периоде – 1 300 т. р., численность рабочих
– 45 человек, объем реализации по плану
– 1 500 т. р., число рабочих дней в отчетном
периоде – 256 дней, в плановом периоде –
260 дней.

Задача
16. Определить
выработку в стоимостном и натуральном
выражении по отдельным изделиям и в
целом по всей номенклатуре продукции,
а также отклонение производительности
труда при производстве каждого изделия
от средней производительности труда,
если цена изделия А составляет 150 рублей,
изделия В – 180 рублей, изделия С – 350
рублей. Объем производства изделий А,
В, С составляет соответственно 50 000, 150
000 и 350 000 шт. Численность работающих
составляет 3 400 человек, доля основных
производственных рабочих составляет
75% от общей численности работающих.
Численность рабочих, участвующих в
производстве изделия А – 15%, изделия В
– 45% от общей численности основных
производственных рабочих.

Задача
17. На
предприятии предусматривается внедрить
новую технологию изготовления изделия,
позволяющую снизить трудоемкость
изготовления с 21,5 до 18,3 часов. В течение
года каждый рабочий должен отработать
1 840 часов, нормы выработки выполняются
в среднем на 112%. По плану на год намечено
выпустить 8 500 единиц. Определить процент
снижения трудоемкости, рост
производительности труда, условное
высвобождение численности.

Задача
18. В отчетном
году предприятие оказало услуг на
8
045 т. р., выработка одного рабочего
составила 198 000 руб. Объем реализации в
планируемом году увеличится на 6%. В
течение отчетного года всеми рабочими
отработано 9 394 человеко-дней. По плановому
балансу рабочего времени на одного
среднесписочного рабочего число рабочих
дней составляет 238 дней.

Определить,
имеет ли место улучшение использования
рабочего времени, а также возможное
сокращение численности рабочих и прирост
производительности труда.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #