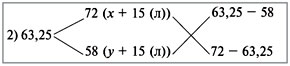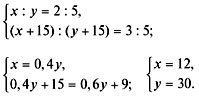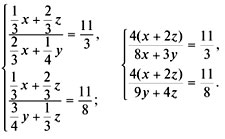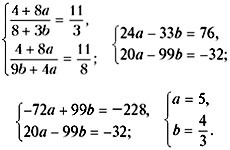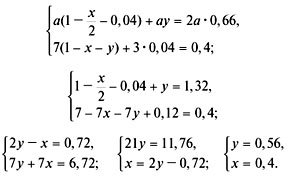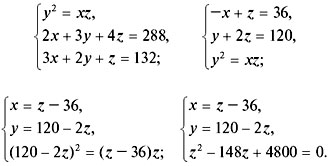Как правило, ученики очень не любят задачи на сплавы и смеси. Для них они являются сложными и непонятными.
Поэтому многие даже время не тратят на попытки решения такой задачи в ЕГЭ, а просто пропускают ее. А зря!
Сейчас покажем, как можно решить такую задачу, выполнив всего три действия.
- Как решить задачу на смеси и сплавы: 3 действия
- Примеры решения задач на смеси: от простого к сложному
- Примеры решения задач на сплавы: от простого к сложному
Как решить задачу на смеси и сплавы: 3 действия
Итак, решение любой задачи на смеси и сплавы сводится к выполнению трех действий:
- Необходимо составить таблицу, в которой указываем общую массу каждого вещества и чистую массу каждого вещества. Эти данные содержатся в условии задачи. Если какие-то данные в условии отсутствуют, то обозначаем их как неизвестные — х, у.
- Составляем систему уравнений, основываясь на том, что при соединении двух смесей (или сплавов) их массы складываются. Т.е. мы складываем как общую массу двух изначальных смесей (или сплавов), так и чистую массу каждого вещества, содержащихся в них. Решаем полученную систему уравнений.
- После решения системы уравнений и нахождения всех неизвестных обязательно возвращаемся к условию задачи и смотрим, что требовалось найти. Многие ученики, решив правильно систему уравнений, неправильно записывают ответ. Ведь решение системы – это еще не ответ к задаче! Вернитесь к условиям задачи, прочитайте, что именно требовалось найти, и запишите ответ.
Примеры решения задач на смеси: от простого к сложному
А теперь разберем на примерах, как с помощью этих трех действий решать задачи на смеси и сплавы.
Задача 1
Смешали 3 литра раствора, содержащего 20% кислоты, и 5 литров раствора, содержащего 40% той же кислоты. Какова концентрация кислоты в полученном растворе.
Решение:
Для решения задачи выполняем три действия, о которых мы говорили выше:
1. Составляем таблицу, в которой указываем общую массу раствора и массу чистого вещества, то есть в нашем случае – кислоты.
Из условий задачи имеем три раствора:
Раствор 1: 3 литра с 20% кислотой, т.е. общая масса = 3 литра, масса чистого вещества = 3 * 20% = 3 * 0,2 = 0,6
Раствор 2: 5 литров с 40% кислотой, т.е. общая масса = 5 литров, масса чистого вещества = 5 * 40% = 5 * 0,4 = 2
Раствор 3: какое-то количество раствора (обозначим его общую массу за х) с какой-то концентрацией кислоты (обозначим ее чистую массу за у), заносим эти данные в таблицу:
2. Составляем уравнения. Вспоминаем, что общая масса раствора 3 является суммой общих масс раствора 1 и раствора 2. А масса чистого вещества в растворе 3 является суммой массы чистового вещества в растворе 1 и массы чистового вещества в растворе 2. Таким образом, получаем:
3 + 5 = х
0,6 + 2 = у
Решаем простейшее уравнение и получаем, что х = 8, а у = 2,6. Таким образом, раствор 3 получился 8 литров, из которых 2,6 литра – это кислота.
Но ответ к задаче записывать рано! Переходим к третьему действию решения нашей задачи.
3. Возвращаемся к условию задачи и вспоминаем, а что же требовалось найти. В нашей задаче требовалось определить концентрацию кислоты в растворе 3. Когда мы решили уравнения, мы нашли общую массу раствора 3 и массу чистого вещества (кислоты), содержащегося в нем.
Чтобы определить концентрацию вещества необходимо разделить массу чистого вещества на общую массу раствора.
Таким образом, концентрация кислоты в растворе 3 равна:
2,6 / 8 = 0,325
Переводим долю вещества в проценты. Для этого умножаем полученный результат на 100:
0,325 * 100 = 32,5%
Ответ: 32,5%
Задача 2
Газ в сосуде А содержал 21% кислорода, а газ в сосуде В содержал 5% кислорода. Масса газа в сосуде А была больше массы газа в сосуде В на 300 г. Когда перегородку между сосудами убрали, газы перемешались, и получился третий газ, который содержит 14,6% кислорода. Найти массу третьего газа.
Решение:
1. Составляем таблицу. Для этого обозначим массу газа в сосуде В – х. Остальные данные берем из условий задачи и формируем таблицу:
(х +300) * 0,21 + х * 0,05 = 0,146 (х + (х +300))
0,21х + 63 + 0,05х = 0,292х + 43,8
0,26х + 63 = 0,292х + 43,8
0,032х = 19,2
х = 600
3. Возвращаемся к условиям задачи и вспоминаем, что нужно было найти. А найти нам нужно было массу третьего газа. Подставляем в уравнение общей массы газа 3 из таблицы и получаем:
600 + 600 + 300 = 1500 г
Ответ: масса третьего газа равна 1500 г.
Задача 3
Смешали 40%ый и 15%ый растворы кислоты, затем добавили 3 кг чистой воды, в результате чего получили 20%ый раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80% раствора той же кислоты, то получили бы 50%ый раствор кислоты. Сколько килограммов 40%го и 15%го растворов кислоты было смешано?
Решение:
1. Составляем таблицу. По условиям задачи мы имеем пять растворов:
Раствор 1: 40%ая кислота. Обозначим ее массу за х, тогда масса чистого вещества = х * 40% = 0,4х
Раствор 2: 15%ая кислота. Обозначим ее массу за у, тогда масса чистого вещества = х * 15% = 0,15х
Вода: вода, масса которой равна 3 кг. Концентрация кислоты в воде равна 0. Таким образом, масса чистого вещества равна 3 * 0 = 0
Раствор 3: 80%ая кислота. Ее масса по условию задачи равна 3 кг, тогда масса чистого вещества равна 3 * 80% = 3 *0,8 = 2,4
Раствор 4: соединение раствора 1, раствора 2 и воды. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 0
Раствор 5: соединение раствора 1, раствора 2 и раствора 3. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 2,4.
Сводим полученные результаты в таблицу:
По условиям задачи раствор 5 имеет концентрацию 50%. Таким образом, чтобы получить массу чистого вещества в растворе 5 нужно его общую массу умножить на концентрацию. Получаем (х + у + 3) * 0,5. Теперь берем массу чистого вещества раствора 5, которую мы выразили в таблице и приравниваем два этих уравнения:
(х + у + 3) * 0,5 = 0,4х + 0,15у + 2,4
Аналогично поступаем с раствором 4. По условиям задачи его концентрация равна 20%. Тогда получаем следующее уравнение:
(х + у + 3) * 0,2 = 0,4х + 0,15у
Объединяем полученные уравнения в систему:
3. Возвращаемся к условиям задачи.
По условиям задачи необходимо было найти, какое количество килограммов 40%го и 15%го растворов кислоты было смешано. Общая масса 40%й кислоты мы обозначали х, а общую массу 15%й кислоты мы обозначили у. Следовательно, масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.
Ответ: масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.
Примеры решения задач на сплавы: от простого к сложному
Задача 1
Бронза является сплавом меди и олова (в разных пропорциях). Кусок бронзы, содержащий 1/12 часть олова, сплавляется с другим куском, содержащим 1/10 часть олова. Полученный сплав содержит 1/11 часть олова. Найдите вес второго куска, если вес первого равен 84 кг
Решение:
1. Составим таблицу. Обозначим массу второго куска – х.
1/12 * 84 + 1/10 * х = 1/11 * (84 + х)
7 + х/10 = 84/11 + х/11
х/10 – х/11 = 7/11
х/110 = 7/11
х/10 = 7
х = 70
3. Возвращаемся к условию задачи. Найти нужно было вес второго куска. Вес второго куска равен 70 кг.
Ответ: 70 кг.
Задача 2
Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Решение.
1. Составим таблицу. Пусть масса первого сплава – х, масса второго сплава – у. Остальные данные берем из решения и составляем таблицу:
х + у = 200
Содержание меди в третьем сплаве по условиям задачи равно 30%, т.е. масса чистого вещества равна 0,3(х + у). Следовательно, берем массу чистого вещества из таблицы и приравниваем:
0,15х + 0,65у = 0,3(х + у)
Получившиеся уравнения сводим в систему и решаем ее:
0,15(200 – у) + 0,65у = 0,3 * 200
30 – 0,15у + 0,65у = 60
0,5у = 30
у = 60
х = 140
3. Возвращаемся к условиям задачи. Необходимо было найти массу первого и второго сплава. Масса первого сплава — 140 г, масса второго сплава -60 г.
Ответ: 140 г и 60 г.
Задача 3
В первом сплаве содержание меди составляет 70%, а во втором – 40%. В каком отношении надо взять эти сплавы, чтобы получить из них новый сплав, который содержит 50% меди?
Решение:
1. Составим таблицу. Обозначим массу первого сплава – х, массу второго сплава – у. Тогда:
0,7х + 0,4у = 0,5 (х + у)
0,7х + 0,4у = 0,5х + 0,5у
0,2х = 0,1у
х/у = ½
3. Возвращаемся к условию задачи. Необходимо было определить отношение первого и второго сплавов в третьем сплаве. Отношение сплавов равно ½.
Ответ: ½
Итак, решение задач на сплавы и смеси можно свести к трем действиям: составление таблицы, составление уравнения (или системы уравнений), возвращение к условиям задачи, чтобы дать ответ на поставленный вопрос. Задание 11 ЕГЭ по математике профильного уровня является одной из самых сложных задач, так как может содержать текстовую задачу любого типа. Это может быть как задача на сплавы и смеси, так и задача на движение, работу, проценты. Как решать все эти задачи вы можете узнать на нашем сайте или
Задачи на смеси и сплавы — подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Почему?
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах «Дроби, и действия с дробями»и «Проценты».
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа № 2»
Решение текстовых задач: задач на смеси, сплавы и растворы при подготовке к ГИА по математике.
( рекомендации учащимся)
Колбасова Л.А., учитель математики высшей категории
1. Теоретические основы решения задач на сплавы и смеси
Решение задач на смеси, сплавы, растворы требует определенной теоретической базы.
Это различные определения, такие как концентрация, процентное содержание и др., а также и всевозможные допущения, например:
1) всё, что мы рассматриваем, считается однородным;
2) все процессы происходят мгновенно;
3) полученное вещество состоит из смешиваемых веществ и равно сумме их объемов;
4) величины, получаемые в результате вычислений, не могут быть со знаком минус.
Существует несколько способов решения задач на слияние растворов. Например, можно воспользоваться расчетной формулой, как это делают на уроках химии. Из области математики можно пользоваться графическим или же алгебраическим методами.
Задачи на смеси и сплавы бывают двух видов:
- Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
- В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
В задачах на смеси и сплавы важно уметь определять концентрацию и массу вещества.
Концентрация вещества – это отношение массы или объема вещества к массе или объему всего раствора. Как правило, концентрация выражается в процентах.
Масса раствора равна сумме масс всех составляющих.
Алгоритм решения задач на смеси и сплавы:
- Определить, какое вещество влияет на концентрацию раствора (главное вещество).
- Следить за весом главного вещества при добавлении других веществ в раствор.
- Исходя из данных об изменениях состояния главного вещества – сделать выводы.
Как правило, концентрация выражается в процентах.
Процент – это сотая доля числа. Она может выражаться либо в виде десятичной дроби (0,11), либо в виде процента (11%).
Важно знать:
1.Масса раствора (смеси, сплава) равна сумме масс всех составляющих.
Если мы смешаем 3 литра апельсинового сока и 77 литров воды, то получим 10
10 литров апельсинового нектара (сделаем предположение, что смешивание происходит в автоматическом режиме, а не вручную).
2.При смешивании нескольких растворов (смесей, сплавов) масса нового раствора становится равной сумме всех смешанных растворов.
Если мы смешаем 6 литров яблочного сока и 66 литров персикового сока – то получится 12 литров яблочно-персикового сока.
И еще одна очевидность (последняя).
3.Масса растворенного вещества при смешивании двух растворов суммируется.
Если мы смешаем 3 литра яблочного сока с 10% мякоти (0,3 л), и 55 литров яблочного сока с 5% мякоти (0,25 л), то получим 88 литров сока с 0,55 л мякоти
(0,3+0,25).
2. Простейшие задачи на смеси и сплавы
Задачи на смеси и сплавы бывают двух основных видов:
- Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
- В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
Строго говоря, подход к решению от этого не меняется. Во втором случае мы тоже смешиваем две смеси, просто в одной концентрация вещества больше 0, а в другой равна 0.
Пример 1.
В 5% раствор кислоты массой 3,8 кг добавили 1,2 кг чистой воды. Чему стала равна концентрация раствора (в процентах)?
Решение:
- Для начала вычислим, сколько кислоты содержится в 5% растворе. Из 3,8 кг 5% – это кислота, а значит в растворе 0,05 * 3,8=0,19 кг кислоты
2. Далее определим массу нового раствора. Как мы уже знаем – масса раствора равна массе его составляющих, т.е. 3,8 кг + 1,2 кг = 5 кг.
3. Поскольку в чистой воде кислоты нет, то в новом растворе количество кислоты не изменилось – 0,19 кг. Таким образом, концентрация кислоты стала равна 0,19:5=0,038
4. Теперь выразим концентрацию в процентах – 0,038⋅100%=3,8%
Ответ: 3,8
Теперь давай попробуем решить задачу посложнее.
Пример 2.
Смешали 3 кг 5%-го водного раствора щелочи и 7 кг 15%-го. Какова концентрация вновь полученного раствора? Ответ дайте в процентах.
Решение:
Давай попробуем визуализировать ситуацию. 3 кг 5% водного раствора. Значит воды в этом растворе 95%.
Нарисуем:
А теперь второй раствор:
После смешивания, вновь получившийся раствор будет весить 3кг + 7 кг = 10 кг. Обозначим количество щелочи в новом растворе за x, а количество воды – (10−x):
Теперь выразим количество щелочи в этих двух растворах в килограммах. В первом растворе –0,05⋅3=0,15 кг щелочи
и 3−0,15=2,85 кг воды,
во втором – 0,15⋅7=1,05 кг щелочи
и 7−1,05=5,95 кг воды:
Из картинки видно, что количество щелочи в новом растворе равно сумме весов кислоты в старых растворах: x=0,15+1,05=1,2 кг кислоты.
Теперь, зная количество щелочи в новом растворе и зная его массу, мы можем легко определить концентрацию:
1,2:10=0,12
Поскольку ответ просят дать в процентах – умножим на 100%
0,12⋅100%=12%.
Ответ: 12.
Эту визуализацию удобно использовать в любых задачах на растворы, смеси и сплавы.
3. Алгебраический метод
Под алгебраическим методом решения задач понимается такой метод решения, когда неизвестные величины находятся в результате решения уравнения или системы уравнений, решения неравенства или систем неравенств, составленных по условию задачи. Иногда алгебраическое решение задачи бывает очень сложным.
Задачи на смешивание растворов решают с помощью составления уравнения или системы уравнений. Главное внимание при обучении учащихся способу решения текстовых задач методом составления уравнений должно быть обращено на сознательную отработку этапности решения.
В процессе решения каждой такой задачи целесообразно действовать по следующей схеме.
1. Изучение условия задачи. Выбор неизвестных величин (их обозначаем буквами х, у и т.д.), относительно которых составляем пропорции. Выбирая неизвестные параметры, мы создаем математическую модель ситуации, описанной в условии задачи.
2. Поиск плана решения. Используя условия задачи, определяем все взаимосвязи между данными величинами.
3. Осуществление плана, т.е. оформление найденного решения – переход от словесной формулировки к составлению математической модели.
4. Изучение полученного решения, критический анализ результата.
При решении большинства задач этого вида, удобнее использовать таблицу, которая нагляднее и короче обычной записи с пояснениями. Зрительное восприятие определенного расположения величин в таблице дает дополнительную информацию, облегчающую процесс решения задачи и её проверки.
Этапы решения задачи:
1. Знакомство с текстом задач и выделение основных компонентов в них. Заполнение таблицы.
Таблица для решения задач имеет следующий вид:
|
Наименование веществ, растворов, смесей, сплавов |
Масса раствора (смеси, сплава) М |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества m |
Или в таком виде:
|
1 – й р-р |
2 – й Р-р |
Смесь 2 растворов |
|
|
Масса растворов |
|||
|
Массовая доля раств-го вещества |
|||
|
Масса вещества в растворе |
2. Составление уравнения и его решение.
3. Анализ полученных данных, ответ на вопрос задачи.
Рассмотрим примеры решения задач с помощью таблицы.
Пример 4. В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20 %. Определите, какое количество железа осталось ещё в руде?
Решение.
Сначала составим таблицу, в которой напишем массу руды, массу железа, концентрацию (долю железа в руде) до и после удаления примесей.
|
Масса руды, кг |
Масса железа, кг |
Концентрация (доля железа в руде) |
|
|
Руда |
500 |
х |
|
|
Руда после удаления примесей |
500-200=300 |
х-0,125⋅200= x-25 |
|
Пусть х кг – масса железа в руде. Так как масса всей руды равна 500 кг, то концентрация железа в ней равна .
Так как масса железа в 200 кг примесей равна 0,125⋅200=25 (кг), то его масса в руде после удаления примесей равна (х-25) кг. Из того, что масса оставшейся руды равна 500-200=300 кг следует, что концентрация железа в ней равна .
По условию, содержание железа в оставшейся руде повысилось на 20%=1/5. Составим уравнение:
Найдём, что 212,5 кг – масса железа в руде. Найдём остаток железа в руде после удаления примесей: 212,5-25=187,5 (кг).
Ответ: 187,5 кг.
Пример 5. Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
|
Наим-е веществ, растворов, смесей, сплавов |
% содержание меди (доля сод-я в-ва) |
Масса раствора (смеси, сплава) |
Масса вещества |
|
Первый сплав |
15%=0,15 |
хг |
0,15х |
|
Второй раствор |
65%=0,65 |
(200 – х)г |
0,65(200–х)=130–0,65х |
|
Получившийся р-р |
30%=0,3 |
200 г |
200 |
Сумма масс меди в двух первых сплавах (то есть в первых двух строчках) равна массе меди в полученном сплаве (третья строка таблицы):
Решив это уравнение, получаем х=140. При этом значении х выражение
200 – х=60. Это означает, что первого сплава надо взять140г, а второго 60г.
Ответ:140г. 60г.
Рассмотрим еще несколько примеров решения задач с помощью таблицы. Как правило обе части уравнения умножают на100, при этом избегают решения уравнения с десятичными дробями.
6. В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
|
Количество раствора |
5 л |
+7 л |
= 12 л |
|
% содержания растворенного вещества |
12 % |
0 % |
х % |
|
Количество растворенного вещества |
|
|
|
|
5 5 х = 5 Ответ: 5. |
7. Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
|
Количество раствора |
4 л |
+ 6 л |
= 10 л |
|
% содержания растворенного вещества |
15 % |
25 % |
х % |
|
4 2 х = 21 Ответ: 21. |
8. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
|
виноград |
изюм |
||
|
Количество раствора |
х кг |
20 кг |
|
|
% содержания растворенного вещества |
100 – 90 = 10 % |
100 – 5 = 95 % |
|
|
10х = 20 х = 190 Ответ: 190. |
9. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
|
Количество раствора |
х кг |
+ (200 – х) кг |
= 200 кг |
|
% содержания растворенного вещества |
10 % |
30 % |
25 % |
|
10х + 30(200 – х) = 200 х + 3(200 – х) = 20 х + 600 – 3х = 500 – 2х = – 100 х = 50 (200 – 50) – 50 = 100 Ответ: 100. |
10. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
|
Количество раствора |
х кг |
+ у кг |
+ 10 кг |
= х + у + 10 |
|
% содержания растворенного вещества |
30 % |
60 % |
0 % |
36 % |
|
Количество раствора |
х кг |
+ у кг |
+ 10 кг |
= х + у + 10 |
|
% содержания растворенного вещества |
30 % |
60 % |
50 % |
41 % |
|
х=4 Ответ: 60. |
Задания для самостоятельного решения:
1. (Типовые тестовые задания ЕГЭ 2012 п/р А.Л.Семенова, И.В.Ященко). Смешав 70%-й и 60%-й растворы кислоты и добавив 2 кг чистой воды, получили 50%-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90%го раствора той же кислоты, то получили бы 70%-й раствор кислоты. Сколько килограммов 70%-го раствора использовали для получения смеси?
2. Первый раствор содержит 40% кислоты, а второй – 60% кислоты. Смешав эти растворы и добавив 5 л воды, получили 20 процентный раствор. Если бы вместо воды добавили 5 л 80 % раствора, то получился бы 70 % раствор. Сколько литров 60 % раствора кислоты было первоначально?
Список использованной литературы.
1. Кузнецова Л.В. Сборник заданий для подготовки к государственной итоговой аттестации в 9 классе. – М.: Просвещение, 2010.
2. Прокопенко Н.И. Задачи на смеси и сплавы.- М. :Чистые пруды, 2010 (Библиотечка «Первого сентября». Выпуск 31 )
3. Лурье М.В., Александров Б.И. Задачи на составление уравнений. Учебное руководство. – М.: Наука. Главная редакция физико-математической литературы, 1990г.
4. Малахова Н. А., Орлов В. В. и др. Методика работы с сюжетными задачами: Учебно-методич. пособие. СПб.: Изд-во РГПУ, 1992. 46 с.
5. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Кн. для учащихся ст. классов сред.школы. – 3-е изд., доработанное. М.: Просвещение, 1989
6. www.mathege.ru
7. www.fipi.ru
8. www. festival.1september.ru
9. http://www.shevkin.ru/
10. http://mat-ege.ru
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на растворы, смеси и сплавы
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 – x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 – x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 – x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 – x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 – x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 – x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
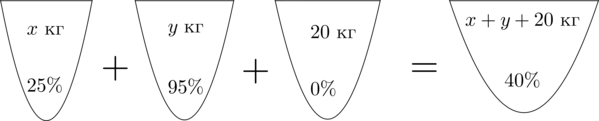
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
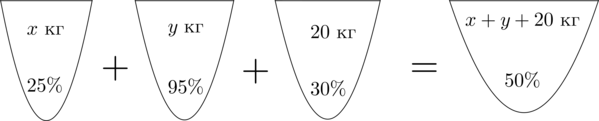
Аналогично составим схему, описывающую получение (50)-процентного раствора:
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20

УСТАЛ? Просто отдохни
ИЗ ОПЫТА РАБОТЫ
Решение задач на смеси и сплавы
с помощью схем и таблиц
Задачи на смеси и сплавы вызывают наибольшие
затруднения у школьников. В процессе решения
каждой такой задачи целесообразно действовать
по следующей схеме.
1. Изучение условия задачи. Выбор неизвестных
величин (их обозначаем буквами х, у и т.д.),
относительно которых составляем пропорции.
Выбирая неизвестные параметры, мы создаем
математическую модель ситуации, описанной в
условии задачи.
2. Поиск плана решения. Используя условия
задачи, определяем все взаимосвязи между данными
величинами.
3. Осуществление плана, т.е. оформление
найденного решения – переход от словесной
формулировки к составлению математической
модели.
4. Изучение полученного решения, критический
анализ результата.
При решении задач на смеси часто путают
проценты и доли, раствор и растворенное вещество.
Необходимо помнить, что массовая доля находится делением
значения процентной концентрации на 100%, а масса
растворенного вещества m(в-ва) равна
произведению массы раствора m(р-ра) на
массовую долю:
m(в-ва) = m(р-ра)•.
В большинстве случаев задачи на смеси и сплавы
становятся нагляднее, если при их решении
использовать схемы, иллюстративные рисунки или
вспомогательные таблицы.
Задача 1. В каких пропорциях нужно смешать а%-й
и b%-й растворы кислоты (a < b), чтобы
получить с%-й раствор?
Возьмем х г а%-го раствора и у г b%-го
раствора кислоты. Составим таблицу:
| Kонцентрация раствора, % |
Масса раствора, г |
Масса кислоты, г |
|---|---|---|
| a | х | 0,01ax |
| b | у | 0,01by |
| c (смесь) | x + y | 0,01c(x + y) |
Составим и решим уравнение:
0,01ах + 0,01by = 0,01c(x + y),
(b – с)у = (с – а)х,
x : у = (b – с) : (с – а).
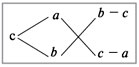
Воспользуемся диагональной схемой*:
В этой схеме а и b – концентрации
исходных растворов, с – требуемая
концентрация кислоты в процентах, а
«крест-накрест» – записаны их разности (b – с)
и (с – а), соответствующие отношению масс
растворов а и b.
Задача 2. Сколько по массе 90%-го и 60%-го
растворов фосфорной кислоты надо взять, чтобы
получить 5,4 кг 80%-го раствора фосфорной кислоты?
Решение
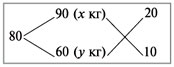
Составим диагональную схему:
Получаем:
х : у = 20 : 10 = 2 : 1.
Значит, 90%-го раствора фосфорной кислоты надо
взять в 2 раза больше, чем 60%-го, т.е. х = 2y.
Составим уравнение: 2y + y = 5,4.
Отсюда y = 1,8 кг.
Ответ. 3,6 кг 90%-го и 1,8 кг 60%-го
растворов фосфорной кислоты.
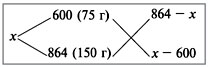
Задача 3. Сплавили два слитка серебра: 75 г
600-й и 150 г 864-й пробы. Определить пробу сплава.
Решение
Пусть проба сплава равна х.
Составим диагональную схему:
Получаем:
(864 – х) : (х – 600) = 75 : 150 = 1 : 2;
1728 – 2х = х – 600; х = 776.
Ответ. Получили сплав 776-й пробы.
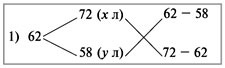
Задача 4. Смешали некоторые количества 72%-го
и 58%-го растворов кислоты, в результате получили
62%-й раствор той же кислоты. Если бы каждого
раствора было взято на 15 л больше, то получился бы
63,25%-й раствор. Сколько литров каждого раствора
было взято первоначально для составления первой
смеси?
Решение
Дважды используем диагональную схему:
Получаем:
х : у = 4 : 10 = 2 : 5.
Получаем:
(х + 15) : (y + 15) = 5,25 : 8,75 = 3 : 5.
Составим систему уравнений и решим ее:
Ответ. В первой смеси было 12 л 72%-го
раствора
и 30 л 58%-го раствора.
Задача 5. Сколько граммов 9%-го раствора
спирта можно получить из 200 г 70%-го раствора
спирта?
Решение
9%-й раствор спирта получают из 70%-го, разбавляя
его водой. В воде 0% спирта. Применим диагональную
схему:
Получаем:
х : у = 63 : 9 = 7 : 1.
Значит, 1 часть 70%-го раствора спирта надо
разбавить 7 частями воды. Поэтому 200 г 70%-го
раствора спирта надо разбавить 200•7 = 1400 г воды.
Всего получим: 200 + 1400 = 1600 г 9%-го раствора спирта.
Ответ. Из 200 г 70%-го раствора спирта
можно
получить 1 кг 600 г 9%-го раствора спирта.
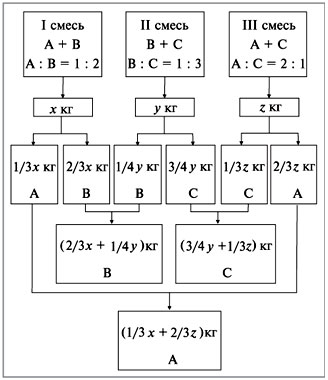
Задача 6. Имеются три смеси (I–III),
составленные из трех элементов А, В и С. В первую
смесь входят только элементы А и В в массовом
отношении 1 : 2, во вторую смесь входят только
элементы В и С в массовом отношении 1 : 3, в третью
смесь входят только элементы А и С в массовом
отношении 2 : 1. В каком соотношении нужно взять
эти смеси, чтобы во вновь полученной смеси
элементы А, В и С содержались в массовом
отношении 11 : 3 : 8?
Решение
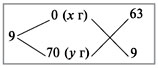
Для решения задачи составим схему 1:
Схема 1
По условию задачи в полученной смеси
соотношение масс А : В : С = 11 : 3 : 8. Поэтому
Составим систему уравнений и решим ее:
Пусть = а,
= b, тогда
система примет вид:
Значит,
х : z = 1 : 5 = 3 : 15, х : у = 3 : 4,
поэтому
х : у : z = 3 : 4 : 15.
Ответ. Чтобы элементы А, В и С
содержались
в массовом отношении 11 : 3 : 8, смеси I, II, III
надо взять в соотношении 3 : 4 : 15 по массе.
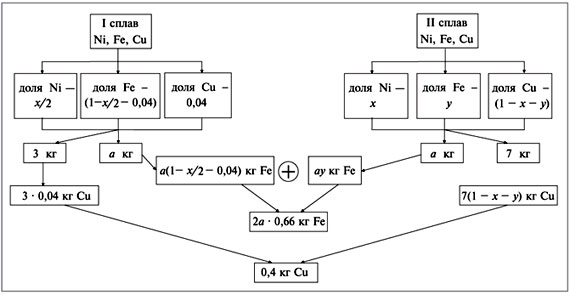
Задача 7. Имеется два сплава меди, никеля и
железа, причем первый из них содержит 4% меди. Если
сплавить их в равных количествах, получится
сплав, содержащий 66% железа, а если взять 3 кг
первого сплава и 7 кг второго, получится сплав,
содержащий 0,4 кг меди. Определить процентное
содержание никеля во втором сплаве, если
известно, что оно в 2 раза выше, чем в первом
сплаве.
Решение
Пусть во втором сплаве массовая доля никеля
равна x, а железа – у. Для решения задачи
составим схему 2.
Исходя из схемы 2, составим и решим систему
уравнений:
Схема 2
Во втором сплаве массовая доля никеля равна 0,4,
т.е. 40%.
Ответ. 40%.
Задача 8. Значения процентного содержания
(по объему) спирта в трех растворах образуют
геометрическую прогрессию. Если смешать первый,
второй и третий растворы в объемном отношении 2 : 3
: 4, то получится 32%-й раствор спирта. Если смешать
их в объемном отношении
3 : 2 : 1, то получится раствор, содержащий 22% спирта.
Сколько процентов спирта содержит каждый
раствор?
Решение
Пусть в первом растворе х% спирта, во втором
– у%, в третьем – z%. Согласно условию
задачи процентное содержание спирта в трех
растворах образует геометрическую прогрессию,
потому справедливо уравнение:
у2 = xz. (1)
На основании данных задачи составим таблицы и
математические выражения.
Таблица 1
Смешивание трех растворов в объемном
отношении 2 : 3 : 4
| Вид раствора | Объем раствора, л | Содержание спирта, % | Объем спирта, л |
|---|---|---|---|
| 1-й раствор | 2 | х | 2х/100 |
| 2-й раствор | 3 | y | 3y/100 |
| 3-й раствор | 4 | z | 4z/100 |
| Cмесь | 9 | 32 | 9•32/100 |
2х/100 + 3y/100 + 4z/100 = 288/100,
2х + 3y + 4z = 288.
(2)
Таблица 2
Смешивание трех растворов в объемном
отношении 3 : 2 : 1
| Вид раствора | Объем раствора, л | Содержание спирта, % | Объем спирта, л |
|---|---|---|---|
| 1-й раствор | 3 | х | 3х/100 |
| 2-й раствор | 2 | y | 2y/100 |
| 3-й раствор | 1 | z | z/100 |
| Cмесь | 6 | 22 | 6•22/100 |
3х/100 + 2y/100 + z/100 = 132/100,
3х + 2y + z = 132.
(3)
Составим и решим систему из трех уравнений (1–3):
При z1 = 48, x = 12, y = 24;
при z2 = 100, x = 64, y = –80, решение не
имеет смысла.
Ответ. В первом растворе 12% спирта,
во втором – 24%, в третьем – 48%.
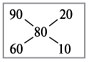
* При решении задач на смешивание
растворов разных концентраций автор использует
диагональные схемы («правило креста»). На
диагональной схеме в точке пересечения двух
прямых обозначают концентрацию смеси. Например,
далее в задаче 2 – это 80%. У концов этих прямых
слева от точки пересечения указывают
концентрации составных частей смеси, а справа –
разности концентраций смеси и ее составных
частей:
Из этой схемы следует, что, например, для
приготовления 30 г 80%-го раствора H3PO4
требуется взять 20 г 90%-го и 10 г 60%-го растворов
кислоты. (Прим. ред.)