Математика, 2 класс
Урок № 10. Задачи, обратные данной
Перечень вопросов, рассматриваемых в теме:
- Что такое задачи, обратные данной?
- Как составлять и решать обратные задачи?
Глоссарий по теме:
Задачи, обратные данной – считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.26, 27
2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 16, 17
3. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.-с.31
Теоретический материал для самостоятельного изучения
Решим три задачи.
Составим по рисунку первую задачу.

В классе 10 девочек и 8 мальчиков. Сколько всего детей в классе?
Составим схематический рисунок.

Решим задачу:
10 + 8 = 18 (д.)
Ответ: 18 детей в классе.
Составим вторую задачу.

В классе 18 детей. Девочек 10, остальные-мальчики. Сколько мальчиков в классе?

Решим задачу:
18 – 10 = 8 (м.)
Ответ: 8 мальчиков в классе.
Составим третью задачу.

В классе 18 детей. Мальчиков 8, остальные – девочки. Сколько девочек в классе?

Решим задачу:
18 – 8 = 10 (д.)
Ответ: 10 девочек в классе.
Посмотрим еще раз на схемы к каждой задаче. Обратим внимание на то, что во всех задачах одинаковый сюжет, но то, о чем спрашивается в первой задаче стало известным во второй и третьей задачах, а узнать во второй задаче, сколько мальчиков и в третьей задаче сколько девочек в классе надо то, что известно в первой задаче.
Задачи, в которых известно то, о чем спрашивается в первой задаче и надо узнать то, что в первой задаче известно, называют обратными первой.
Сделаем вывод: задачи, обратные данной – считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Тренировочные задания.
1. Решите задачу. Выберите задачи, обратные данной.
Кате подарили 8 воздушных шариков красного и синего цвета. Красных шариков было 5. Сколько синих шариков у Кати?
Варианты ответов:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
2. У Кати было 8 шариков. 3 шарика она подарила. Сколько шариков осталось у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
Правильные варианты:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
2 . Восстановите пропуски в задачах.
1.В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в ________?
2. В июне ____ дней. Из них 10 дней были пасмурными. Сколько______ дней было в июне?
3. В июне 30 дней. Ясными были ____ дней. Сколько ____ дней было в июне?
Варианты ответов:
30, 20, ясных, пасмурных, июне
Правильный вариант:
1. В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в июне?
2. В июне 30 дней. Из них 10 дней были пасмурными. Сколько ясных дней было в июне?
3. В июне 30 дней. Ясными были 20 дней. Сколько пасмурных дней было в июне?
1) Составь задачу по краткой записи и реши ее.

2) Составь две задачи, обратные данной. Реши их.

reshalka.com
ГДЗ учебник по математике 2 класс Моро. Часть 2. Страница 81. Номер №3
Решение 1
От шланга отрезали два куска 8 дм и 6 дм, после чего осталось 16 дм шланга. Найди начальную длину шланга?
Решение:
1) 8 + 6 = 14 (дм) − шланга отрезали всего;
2) 14 + 16 = 30 (дм) − шлага было изначально.
Ответ: 30 дм
Решение 2
Обратная задача 1.
От шланга длиной 30 дм отрезали 2 куска длиной 8 дм и 6 дм. Сколько шланга осталось?
Решение:
1) 8 + 6 = 14 (дм) − шланга отрезали всего;
2) 30 − 14 = 16 (дм) − шланга осталось.
Ответ: 16 дм
Обратная задача 2.
От шланга длиной 30 дм отрезали два куска и осталось 16 дм. Найди длину второго куска, если длина первого 8 дм?
Решение:
1) 30 − 16 = 14 (дм) − шланга отрезали всего;
2) 14 − 8 = 6 (дм) − длина второго куска.
Ответ: 6 дм
-
Главная
-
ГДЗ
- 2 класс
- Математика
-
Моро учебник
- Табличное умножение и деление
- Страница 81. Часть 2
Вернуться к содержанию учебника
Табличное умножение и деление
Вопрос
Вычисли и запомни!
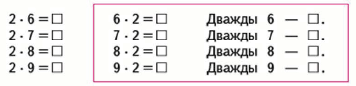
Подсказка
Ответ
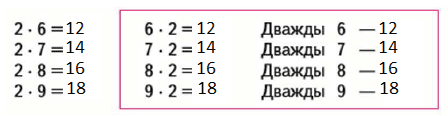
Вопрос
Подсказка
Ответ
Решение
| 2 • 6 + 2 = 2 • 7 | 2 • 8 + 2 = 2 • 9 |
| 2 • 7 + 2 = 2 • 8 | 2 • 9 + 2 = 2 • 10 |
| 2 • 10 – 2 = 2 • 9 | 2 • 5 – 2 = 2 • 4 |
| 2 • 8 – 2 = 2 • 7 | 2 • 9 + 2 = 2 • 10 |
Пояснение
|
2 • 6 + 2 = 2 • 7 12 + 2 = 14 14 = 14 |
2 • 8 + 2 = 2 • 9 16 + 2 = 18 18 = 18 |
|
2 • 7 + 2 = 2 • 8 14 + 2 = 16 16 = 16 |
2 • 9 + 2 = 2 • 10 18 + 2 = 20 |
|
2 • 10 – 2 = 2 • 9 20 – 2 = 18 18 = 18 |
2 • 5 – 2 = 2 • 4 10 – 2 = 8 8 = 8 |
|
2 • 8 – 2 = 2 • 7 16 – 2 = 14 14 = 14 |
2 • 9 + 2 = 2 • 10 18 + 2 = 20 20 = 20 |
Вопрос
2. Составь все, какие сможешь, равенства и неравенства, используя выражения:
| 6 • 2 | 9 • 2 | 2 • 8 + 2 | 7 • 2 – 2 |
Подсказка
Ответ
Решение
6 • 2 = 12 2 • 8 + 2 = 18
9 • 2 = 18 7 • 2 – 2 = 12
| Равенства | Неравенства |
|
6 • 2 = 7 • 2 – 2 9 • 2 = 2 • 8 + 2 |
6 • 2 < 9 • 2 6 • 2 < 2 • 8 + 2 9 • 2 > 6 • 2 2 • 8 + 2 > 6 • 2 |
Пояснение
Чтобы составить равенства и неравенства сначала вычисляем значения данных выражений:
|
6 • 2 = 12 по 6 взять 2 раза |
9 • 2 = 18 по 9 взять 2 раза |
|
2 • 8 + 2 = 18 16 + 2 = 18 |
7 • 2 – 2 = 12 14 – 2 = 12 |
Вопрос
3. 1) Составь задачу по краткой записи и реши ее.
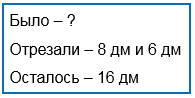
2) Составь две задачи, обратные данной. Реши их.
Подсказка
Ответ
Решение
Задача :
От шёлковой ленты сначала отрезали 8 дм на отделку платья, а потом ещё 6 дм на поясок. В ленте осталось 16 дм. Какова была длина ленты сначала?
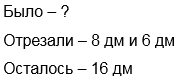
1) 8 + 6 = 14 (дм) – всего отрезали.
2) 16 + 14 = 30 (дм).
Ответ: длина ленты 30 дм.
Обратная задача 1
Длина шёлковой ленты 30 дм. Сначала от неё отрезали 8 дм, а затем еще 6 дм. Сколько ленты осталось?
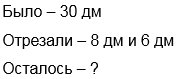
1) 8 + 6 = 14 (дм) – всего отрезали.
2) 30 – 14 = 16 (дм)
Ответ: осталось 16 дм.
Обратная задача 2:
Длина шёлковой ленты 30 дм. Сначала от неё отрезали 8 дм, а затем еще несколько дм. После этого осталось 16 дм. Сколько ленты отрезали во второй раз?
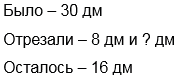
1) 16 + 8 = 24 (дм) – длина ленты, без той части, которую отрезали во второй раз.
2) 30 – 24 = 6 (дм)
Ответ: во второй раз отрезали 6 дм.
Пояснение
Можно составить еще одну задачу обратную данной.
Обратная задача 3:
Длина шёлковой ленты 30 дм. Сначала от неё отрезали несколько дм, а затем еще 6 дм. После этого осталось 16 дм. Сколько ленты отрезали в первый раз?
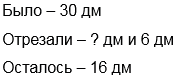
1) 16 + 6 = 22 (дм) – длина ленты, без той части, которую отрезали в первый раз.
2) 30 – 22 = 8 (дм)
Ответ: в первый раз отрезали 8 дм.
Вопрос
4. Реши уравнения:
| х + 27 = 30 | у – 8 = 20 | 64 – х = 64 |
Подсказка
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Ответ
|
х + 27 = 30 х = 30 – 27 х = 3 Проверка 3 + 27 = 30 30 = 30 |
у – 8 = 20 у = 20 + 8 у = 28 Проверка 28 – 8 = 20 20 = 20 |
64 – х = 64 х = 64 – 64 х = 0 Проверка 64 – 0 = 64 64 = 64 |
Вопрос
5.
| 68 + 29 | 72 – 18 | 47 + 39 | 96 – 69 |
Подсказка
Ответ
Решение
|
|
Пояснение
Сложение и вычитание выполняем в столбик
При выполнении вычитания, если единицы уменьшаемого меньше единиц вычитаемого, над десятками уменьшаемого ставим точку, чтобы не забыть о том, что один десяток забрали.
Если есть необходимость, то число, которое запоминают при выполнении сложения в столбик, можно писать сверху над разрядом, к которому это число будут прибавлять.
|
|
Вопрос
6. Начерти отрезок, длина которого 8 см 5 мм.
Подсказка
Ответ
Решение

Пояснение

Вопрос
7.
| 67 – (27 + 3) | 80 – 25 – 15 | 70 : 10 |
| 67 – 27 + 3 | 80 – (25 – 15) | 70 : 7 |
Подсказка
Ответ
Решение
| 67 – (27 + 3) = 37 | 80 – (25 – 15) = 70 |
| 67 – 27 + 3 = 43 | 70 : 10 = 7 |
| 80 – 25 – 15 = 40 | 70 : 7 = 10 |
Пояснение
Если в выражении есть скобки, то сначала выполняют действия в скобках, а затем за скобками.
Если выражении нет скобок и оно содержит только действия сложения и вычитания, то действия выполняют по порядку слева направо.
|
67 – (27 + 3) = 67 – 30 = 37 |
80 – (25 – 15) = 80 – 10 = 70 |
|
67 – 27 + 3 = 40 + 3 = 43 |
70 : 10 = 7, так как 70 – это 7 раз по 10 |
|
80 – 25 – 15 = 55 – 15 = 40 |
70 : 7 = 10, так как 70 – это 10 раз по 7. |
Если есть необходимость, то при решении примеров в два действия, можно записывать промежуточные ответы при выполнении первого действия сверху карандашом над этим действием (у нас промежуточные ответы выделены красным цветом).
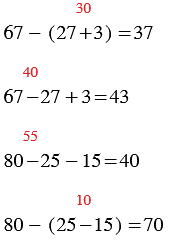
Вопрос
Фермер продал 9 покупателям по 2 л молока. сколько всего литров молока он продал?
Подсказка
Сумму одинаковых слагаемых можно заменить умножением.
Ответ
Решение
2 • 9 = 18 (л)
Ответ: 18 л молока продал фермер.
Пояснение
Пр решении задачи можно использовать следующий схематичный чертеж:

Вопрос
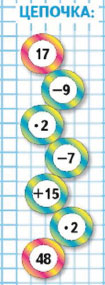
Подсказка
Ответ
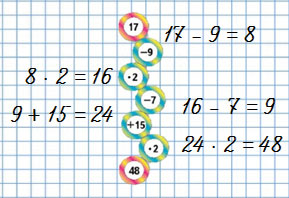
Вернуться к содержанию учебника
Номер 9.
В бассейне занимались три группы пловцов. В первой группе было 12 человек, во второй – на 3 человека меньше, а в третьей – столько, сколько в первой и второй вместе.
Придумай вопрос и реши задачу.
Ответ:

Сколько пловцов в третьей группе?
1) 12 − 3 = 9 (ч.) – во второй группе.
2) 12 + 9 = 21 (ч.) – в третьей группе.
Ответ: 21 человек.
Номер 10.
Ответ:
80 мм = 8 см 28 см = 2 дм 8 см
30 см = 3 дм 65 мм = 6 см 5 мм
Номер 11.
Найди значения:
1) произведения k ∙ 10, если k = 1, k = 3, k = 5, k = 8, k = 10;
2) частного k : 10, если k = 20, k = 60, k = 70, k = 90, k = 100.
Ответ:
1) k ∙ 10
k = 1 1 ∙ 10 = 10
k = 3 3 ∙ 10 = 30
k = 5 5 ∙ 10 = 50
k = 8 8 ∙ 10 = 80
k = 10 10 ∙ 10 = 100
2) k : 10
k = 20 20 : 10 = 2
k = 60 60 : 10 = 6
k = 70 70 : 10 = 7
k = 90 90 : 10 = 9
k = 100 100 : 10 = 10
Номер 12.
Вычисли и сделай проверку.
Ответ:

Номер 13.
Запиши выражения и вычисли их значения.
1) К сумме чисел 31 и 9 прибавить 14.
2) Из суммы чисел 52 и 8 вычесть 40.
Ответ:
1) (31 + 9) + 14 = 40 + 14 = 54
2) (52 + 8) − 40 = 60 − 40 = 20
Номер 14.
На зиму семья заготовила 8 двухлитровых банок компота. Сколько литров компота заготовили?
Составь и реши две задачи, обратные данной.
Ответ:
Заготовили – 8 б. по 2 л
Всего – ? л
1) 8 ∙ 2 = 16 (л) – компота заготовили.
Ответ: 16 литров.
Обратная задача 1:
На зиму семья заготовила 16 л компота по 2 л в каждую банку.
Сколько банок компота получилось?
Заготовили – ? б. по 2 л
Всего – 16 л
1) 16 : 2 = 8 (б.) – компота получилось.
Ответ: 8 банок.
Обратная задача 2:
На зиму семья заготовила 16 л компота в 8 банках.
Сколько литров компота в каждой банке?
Заготовили – 8 б. по ? л
Всего – 16 л
1) 16 : 8 = 2 (л) – компота в одной банке.
Ответ: 2 литра.
Номер 15.
Ответ:
(47 − 7) : 2 = 40 : 2 = 20
(84 − 4) : 10 = 80 : 10 = 8
24 − 8 − 8 − 8 = 24 − 24 = 0
12 − 3 − 3 − 3 − 3 = 12 − 12 = 0
Номер 16.
1) Каких фигур на чертеже больше: треугольников или четырехугольников? На сколько?
2) Найди периметр прямоугольника и каждого треугольника, на которые он разделен.
Ответ:
1) На чертеже 5 треугольников и 5 четырёхугольников. Фигур поровну. 5 = 5.
2) Стороны прямоугольника: 20 мм и 26 мм.
20 + 20 + 26 + 26 = 92 мм
Измеряем стороны каждого треугольника в мм и складываем.
Номер 17.
В двух вазах по 18 яблок в каждой. Из первой вазы переложили во вторую 4 яблока. На сколько больше яблок стало во второй вазе, чем в первой?
Ответ:

1) 18 − 4 = 14 (яб.) – осталось в первой вазе.
2) 18 + 4 = 22 (яб.) – стало во второй вазе.
3) 22 − 14 = 8 (яб.) – разница.
Ответ: на 8 яблок стало больше.
Задание внизу страницы
Проверочные работы с.60
Проверочные работы с.61
|
Что значит “обратная задача” в математике (1, 2, 3, 4 класс)? Как записать и решить обратную задачу, пример?
В математике обратная задача составляется на основании какой-либо имеющейся задачи. В обратных задачах искомые данные уже известны. Требуется найти одну из величин, которые были даны в условии исходной задачи. Пример 1 Исходная задача. В магазине яблоки стоят 120 рублей за 1 килограмм, а груши стоят 150 рублей за 1 килограмм. Требуется узнать, на сколько груши дороже яблок. Для решения этой задачи нужно найти разницу между 2 числами – стоимостью груш и стоимостью яблок. 150 – 120 = 30 (руб.) Таким образом, груши дороже яблок на 30 рублей. _ Обратная задача. Здесь нам будет известна разница в стоимости фруктов, то есть 30 рублей. Будем находить либо стоимость яблок, либо стоимость груш – то есть можно составить 2 разных обратных задачи. 1) Яблоки стоят 120 рублей, а груши на 30 рублей дороже. Сколько стоят груши? Решение: 120 + 30 = 150 (руб.) 2) Груши стоят 150 рублей, а яблоки на 30 рублей дешевле. Сколько стоят яблоки? Решение: 150 – 30 = 120 (руб.) Пример 2 Исходная задача. Покупатель хочет купить 500 грамм говядины, которая стоит 200 рублей за 1 килограмм. Сколько он должен заплатить? Для решения данной задачи нужно вспомнить соотношение между граммами и килограммами. 1 килограмм = 1000 грамм. 500 грамм – это ровно половина от 1000 грамм (или 1 килограмма): 500 / 1000 = 1/2. Таким образом, покупатель заплатит не 200 рублей, а только половину: 200 / 2 = 100 (руб.) _ Обратная задача. Здесь нам будет известна цена покупки, то есть 100 рублей. Можно найти, например, стоимость за 1 килограмм. Вот формулировка подобной задачи: Покупатель купил 500 грамм говядины за 100 рублей. Сколько стоит 1 килограмм говядины? Решение: 1) 1 килограмм – это 1000 грамм. 1000 / 500 = 2, то есть 1 килограмм будет в 2 раза больше, чем 500 грамм. 2) Стоимость 1 килограмма составляет 100 * 2 = 200 (руб.) модератор выбрал этот ответ лучшим
Математический термин “обратная задача” включает два слова. С существительным задача все понятно. Возникает вопрос: что значит обратная. Данное прилагательное по отношению к задаче можно определить как противоположная или ведущая назад, к исходному состоянию. Для того, чтобы составить обратную задачу, нужно иметь задачу исходную. И исходную задачу необходимо решить. Это нужно для того, чтобы использовать полученный результат в качестве исходных данных для обратной задачи. Если сказать еще проще, то то, что дано ( известно ) в исходной задача, в обратной ей нужно будет искать. А решение исходной задачи станет тем, что известно по условию обратной задачи. Это мое определение термину “обратная задача”, простого определения для начальной школы я не нашла. Проще пояснить на примерах. Исходная задача: Мама купила 5 пирожных и 7 кексов к чаю. Сколько всего кексов и пирожных купила мама? Решение 5+7=12 (шт.) выпечки купила мама. Обратная ей задача: Обратных задач можно в этом случае составить две: 1) Мама всего купила 12 пирожных и кексов к чаю, из них 5 пирожных. Сколько кексов купила мама? Решение 12-5=7 (к.) купила мама. 2) Мама всего купила 12 пирожных и кексов к чаю, из них 7 кексов. Сколько пирожных купила мама? Решение 12-7=5 (п.) купила мама.
Марина Вологда 3 года назад Обратная задача – это такая задача, в которой все искомые величины уже известны. Из этих известных величин и составляем обратную задачу. Например, нам дана задача: В автопарк заехало три красных машины и пять белых. Сколько всего машин заехало в автопарк? Решение: 3+5 = 8 машин. Составляем обратную задачу: 1) Сколько машин заехало в автопарк красного цвета, если известно, что всего машин было 8. А белых машин было 5. Решение: 8-5 = 3 машины красного цвета. 2) Известно, что в автопарк заехало 8 машин. Из них три были красного цвета. Остальные машины были белые. Сколько машин белого цвета? Решение: 8-3 = 5 машин белого цвета.
Алиса в Стране 3 года назад Многие из нас, наверное, уже забыли, что такое обратная задача, но на самом деле ничего сложного в ней нет. Приведу пример. Допустим, у нас есть расстояние (путь) и время, за которое человек его прошел, все мы знаем, как просто определить скорость, нужно расстояние (путь) разделить на время.
Так вот к этой элементарной задачке можно составить две обратные задачи: на определение пути (расстояния), если известна скорость и время (чтобы решить эту задачу, нужно скорость умножить на время):
Второй обратной задачей будет задача на определение времени, если известно расстояние (путь) и скорость (нужно путь поделить на скорость):
Не знаю, кто их назвал “обратными” потому что задача это всегда, как минимум, поиск третьего неизвестного по двум известным, и какая разница какое из них будет неизвестным. Составить их проще простого, просто поменять неизвестное с известным, ну и вероятно математическое действие будет другое – вместо сложения – вычитание, вместо деления – умножение (как и наоборот) Вот пример. У Васи было две конфеты, Валя дала Васе еще три конфеты, сколько у Васи конфет теперь? Ответ – пять. Якобы обратная задача. У Васи было пять конфет, две из которых были его, сколько конфет ему дала Валя что бы у него получилось пять? Ответ – три.
Zummy out off 3 года назад Обратная задача в математике – это такая задача, которая составляется по исходной задаче, но ответ исходной задачи включается в условие обратной задачи, а требуется найти то, что было одним из условий исходной задачи. Составление обратных задач тренирует «мозги» для решения задач в математике. Пример составления обратной задачи. Исходная задача. У Маши было 20 рублей, она купила тетрадь за 12 рублей. Сколько денег осталось у Маши? Решение: 20-12=8. Ответ: 8 рублей осталось у Маши. Обратная задача. В условие задачи надо включить сумму сдачи 8 руб. Составляем задачу: Маша купила тетрадь за 12 руб и у неё осталась сдача 8 руб. Сколько денег было у Маши до покупки тетради? Решение: 12+8=20. Ответ: 20 рублей было у Маши.
Бархатные лапки 3 года назад Обратная задача составляется на основе уже имеющейся решенной задачи. В обратной задаче требуется узнать то, что было известно в нашей задаче. Объясним, что такое обратная задача, на примере простейшей задачки для начальных классов. У Иры 10 яблок, у Маши 5 яблок. Нужно найти, сколько яблок у обоих девочек вместе. Это наша задача, решается она так: общее количество яблок равно: яблоки Иры плюс яблоки Маши = 5 + 10 + 15 Обратная задача к этой задаче: у двух девочек, Иры и Маши 15 яблок, сколько яблок у Иры, если у Маши 5 яблок. Решение: 15 – 5 = 10 яблок у Иры. Также обратную задачу можно составить и так: у Иры и Маши 15 яблок, сколько яблок у Маши, если у Иры 10 яблок. Решение: 15 – 10 = 5, у Маши 5 яблок.
KritikSPb 4 года назад Обратная задача в математике требует найти то, что было известно в первоначальной задаче. То есть обязательным условием составления обратной задачи является наличие прямо задачи, от которой и отталкиваются для составления обратной. Например, первоначально известно, что человеку нужно дойти из дома до магазина. Расстояние 10 км. Идёт он со скоростью 5 км в час. Через сколько времени он будет на месте? Решение: 10 / 5 = 2 часа. А теперь обратная задача: За два часа человек дошёл от дома до магазина. Определите расстояние, если известно, что скорость человека 5 км в час. Решение: 2 * 5 = 10 км. Для составления обратной задачи необходимо решить исходную.
Бекки Шарп 3 года назад Обратные задачи бывают в разных науках и в математике тоже. Обратная составляется на основании уже полученных данных. Когда то что требовалось найти уже известно. Например. У Миши было 7 яблок, а у Васи 8 яблок. Сколько всего было яблок у мальчиков. Решение: 7+8=15 (яблок) Обратная задача к нашей будет такая. Всего у Миши и Васи 15 яблок. У Миши – 7 яблок. Сколько у Васи яблок? Решение: 15-7=8 (яблок) Еще одна обратная задача к нашей. У Миши и Васи 15 яблок, у Васи – 8. Сколько яблок у Миши? Решение: 15-8=7 (яблок) Val111111 4 года назад Обратная задача- это когда то, что требовалось найти, теперь известно, а то, что было в дано нужно найти. Пример, есть три яблока. Два забрали. Сколько осталось? Обратная задачка: Забрали два яблока, осталось одно, сколько было? TheSun 3 года назад В обратной задаче неизвестным является дано, именно его и нужно найти. Но, при этом известен результат. Рассмотрим на примере. У Маши было 4 синих мяча и 3 зелёных мяча. Сколько всего у Маши мячей? 4+3=7 (шт.) мячей у Маши. Теперь обратная задача. У Маши всего 7 мячей. Из них синих мячей 4, а остальные мячи зелёного цвета. Сколько у Маши зелёных мячей? 7-4=3 (шт.) зелёных мяча у Маши. Знаете ответ? |





