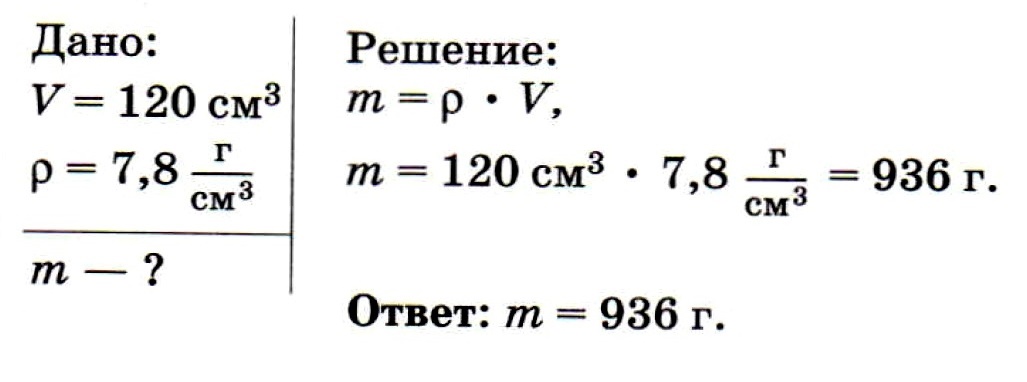МБОУ Уршельская средняя общеобразовательная школа
Разработка урока по теме:
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ФОРМУЛ СОКРАЩЁННОГО УМНОЖЕНИЯ
( педагогическая разработка учителя естественно –
математического цикла
« Современный урок: метапредметный подход»)
Выполнила: Круглова Ольга Николаевна
учитель
математики и информатики
МБОУ Уршельская сош
2014г.
Общие
сведения.
|
Фамилия, |
Круглова |
|
Стаж |
16 |
|
Квалификационная |
высшая |
|
Предмет |
алгебра |
|
УМК |
«Алгебра 7» , М:Просвещение – 2011г. |
|
Ф. |
Ю.Н. Макарычев, Н.Г. |
|
Тема |
Решение задач с помощью |
|
Класс |
7 |
|
Краткая |
В классе 21 учащийся: 9 мальчиков, 13 девочек. |
Пояснительная
записка к уроку.
Организация учебной деятельности в современной школе
предполагает переход от преимущественно информационных форм к активным методам
и формам обучения с включением элементов проблемности, научного поиска,
широкого использования резервов самостоятельной работы обучающихся.
Данный урок входит в заключительную серию уроков по
теме «Формулы сокращённого умножения». Рассчитан на 45 минут. Урок состоит из
трёх основных блоков, на каждом из которых максимально создана ситуация
активного включения ребенка в учебный процесс.
1 блок –Мотивационно – ориентировочный.
Задает
общее настроение последующих 45 минут, определяя ключевые действия учащихся на
уроке: исследовать, рассуждать, искать, открывать. Здесь анализируются
имеющиеся знания и умения по теме урока., происходит обращение к
индивидуальному опыту учащихся, связанному с метапредметной темой урока. Данный
анализ должен натолкнуть ребят на проблему, решение которой предлагается
рассмотреть на уроке. Вместе с учащимися ставится цель урока.
2 блок –организационно – деятельностный.
Учащиеся
решают задачи на применение уже известных формул, но в новых ситуациях. Для
решения этих задач составляют математические модели с использованием формул
сокращённого умножения. Активно дискутируют, обсуждают решения. Демонстрируют
свои решения, которые получили при выполнении задания. Сравнивают свои решения
с решениями сверстников и учителя. В результате, знания, полученные учениками
на уроке становятся более обобщёнными и цельными и учащиеся самостоятельно
смогут ответить на вопрос: «Где и как применяются формулы сокращенного
умножения?». Одновременно учащиеся стараются дать адекватную оценку своей
деятельности и своим результатам, работая с картой самооценивания.
3 блок –рефлексивно
– оценочный. Здесь ученики осознают свою деятельность,
полученные результаты, возникшие трудности и проблемы. И отвечают на вопросы:
Что
нового каждый из нас узнал на уроке? Что каждый из нас делал сегодня на
занятии? Что было главным? Какая цель была нашего
урока? Каковы основные результаты? Достигли
ли мы цели? Подводят итоги своей работы – выставляют две оценки за урок: за
полученный результат и за процесс получения результата. Конечно же, наша
сегодняшняя система оценивания предполагает выставление оценки в журнал за
результат( нам до сих пор твердят: «не важно как, главное результат» и требует
от учителей дать этот результат), но ведь деятельность, которую осуществляет
ученик на пути достижения к результату тоже очень важна. Поэтому можно
выставить в журнал оценку за процесс получения результата, например, хотя – бы
одну оценку за имеющуюся положительную динамику при изучении какой – то темы
(не за каждый урок!). Конечно она «погоды» не сделает, зато поощрение за
небольшие успехи стимулирует ребёнка к дальнейшему продвижению. И, что тоже
важно – ученики учатся оценивать собственные
умения, сравнивая себя не с одноклассниками, а только с собой вчерашним.
Конспект – сценарий урока.
·
Тема: Решение
задач с помощью формул сокращённого умножения.
·
Класс: 7 класс.
·
Цель: Формирование
оценочной деятельности на уроке математики при решении задач с помощью формул
сокращённого умножения.
·
Учебные задачи, направленные на развитие учащихся:
– в личностном
направлении:
Ø
продолжать
развивать умение ясно, точно и грамотно излагать свои мысли в устной и
письменной речи;
Ø
развивать
умение контролировать процесс и результат учебной математической
деятельности;
Ø
прививать
умение ответственного отношения к результатам своего труда;
Ø
расширить
кругозор;
Ø развить навыки сотрудничества
со сверстниками, воспитать чувство товарищества, чувство ответственности за
общее дело;
Ø развить умение
оценивать свою деятельность, усваиваемое содержание;
Ø продолжать развивать
умение адекватно понимать причины успеха (неуспеха) в учебной деятельности;
Ø развить логическое и
алгоритмическое мышление.
– в метапредметном
направлении:
Ø научить применять полученные
знания в повседневной жизни;
Ø
формировать
понимание сущности алгоритмических предписаний и развивать
умение действовать в соответствии с предложенным алгоритмом;
Ø
развивать
умение выражать свои мысли, вступать в диалог и сотрудничать с другими людьми в
поиске необходимой информации;
Ø
продолжать
развивать умение вести поиск и выделять необходимую информацию, анализировать
ход и способ действий, выбирать наиболее эффективный способ решения задач;
Ø
развивать
способность строить логическую цепь рассуждений и способность структурировать
найденную информацию в нужной форме;
Ø
развить
умение интерпретировать результат, аргументировать своё мнение и позицию;
Ø
формировать
умение составлять модель и преобразовывать её в случае необходимости, используя
знаково – символические средства;
Ø
продолжить
развивать умение осуществлять операции: анализ, синтез, сравнение, обобщение,
аналогия..
– в предметном направлении:
Ø развить умения читать
и записывать информацию в виде различных математических моделей;
Ø развить умения составлять
математическую модель задачи, переводить условия задачи с обычного языка на
математический;
Ø развить умение планировать
действия в соответствии с поставленной задачей;
Ø формировать умение применять
формулы сокращённого умножения в различных ситуациях;
Ø развивать вычислительные навыки .
- Формы
работы: парная, индивидуальная, фронтальная. - Оборудование
урока: мультимедийное оборудование, интерактивная доска. - Методы: проблемно
–поисковый.
- Технологическая карта
урока:
|
№п/п |
Этап |
Планируемый |
Действия |
Действия |
Формируемые |
Время |
ЭОР (№ слайда) |
|
|
|||||||
|
1.1 |
Этапа актуализации |
Обращение понимание |
1.Побуждает 2.Задаёт Предлагает 3.Организует Задаёт 4.Предлагает разгадать кроссворд: 1. Свойство 2. Способ 3. Значение 4. Равенство, 5. Выражение, 6. Слагаемые, 7. Числовой 5.Задаёт вопрос: Ребята, а 6.Организует фронтальную работу: -прочитать правильно выражения: а2, с2, 0,62, 2ах, 3аb, 4ху, ас, 6ак; (а+с)2, (с-2)2, а2-с2, – возвести в степень числа и выражения, представить виде квадрата и куба числа (выражения): Возвести 72, Представить в виде квадрата: куба: -заменить звёздочку одночленом так, чтобы 7.Задаёт вопросы: Что такое тождество? Какие формулы вы применили? Почему их назвали формулами сокращённого умножения? 8.Предлагает 1. Формулы 2. Формула 3. Формулы суммы 4. Ещё (а-b)2 9.Задаёт С какой целью применяют формулы сокращённого 10.Задаёт |
1.Слушают 2. 3.Отвечают 4.Отвечают 1.распределительное 2. 3.корень 4.тождество 5.многочлен 6.подобные 7.коэффициент 5.Отвечают 6.читают Выполняют Предлагают 7.Отвечают -Тождество –Формулы -Можно 8.Называют 9.Отвечают 10. |
Извлечение использование знаково-символических средств (П); осознанное и выполнение волевая саморегуляция выражение аргументация своего мнения и позиции в коммуникации использование |
8 |
1-10 |
|
1.2 |
Этап проблематизации |
Формулируют |
1.Ставит -составьте 2. 1) 2) 3) x2-4xy+4y2 (Л) (2x-7y)2 3.Знакомит (a + b)² = а² использовал
|
1.Стараются составить фамилию. 2.Обсуждают способ решения 3.Анализируют, высказывают свои |
анализ, синтез, сравнение, обобщение, подведение структурирование осознанное и волевая выражение своих мыслей с достаточной полнотой и аргументация своего мнения и позиции в коммуникации контроль и самооценка |
6 |
11-15 |
|
1.3 |
Этап |
Осмысление планирование |
1.Задаёт Предлагает 2.Задаёт А как вы 3.У 4.Подводит Планирует(вместе с учащимися) деятельность (исходя из цели, –Вспомним формулы сокращённого умножения; -Потренируемся в решении задач на применение этих формул; -сконструируем собственные модели для решения задач; -Будем учиться оценивать свою деятельность. 5.Предлагает |
1.Отвечают -При – у кого -высказывают 2. -Будем – вывод: 3. 4.Вместе 5.Оценивают |
самоопределение смыслообразование анализ, синтез, сравнение, обобщение, аналогия (П); поиск и планирование прогнозирование осознанное и волевая выражение своих мыслей с достаточной полнотой и аргументация своего мнения и позиции в коммуникации учет разных мнений (К); использование критериев для обоснования своего контроль и оценка процесса и результатов самооценка на основе критерия успешности(Л). |
3 |
16,17 |
|
|
|||||||
|
2.1 |
Этап |
Решать |
1.Организует Я задумала два одночлена, нашла их сумму, нашла их 2.Какие одночлены я задумала? Как ты узнал? Какую формулу вы использовали? Сформулируй ее. 3.Учитель 4.Предлагает |
1.Предлагают 2.Отвечают 2x и 3y Так как здесь Разность 4х2 3. Задают возникшие вопросы. 4.Работают с |
анализ, моделирование использование установление выполнение действий по алгоритму осознанное и произвольное построение выражение своих мыслей с адекватное формулирование использование критериев для обоснования своего следование в управление осознание контроль и самооценка |
5 |
18 |
|
2.2 |
Физкультминутка |
Сменить |
1.Предлагает |
1.Выполняют несложные физические |
выполнение действий по образцу |
3 |
19-29 |
|
2.3 |
Этап конструирования |
Сконструировать |
1.Предлагает Задумайте Отгадывает 2.Предлагает 3.Предлагает 4..Предлагает Задача Пифагора: 5.Предлагает 6.Знакомит В школе Действительно, 7.Предлагает |
1.Загадывают число и выполняют 2.Учащиеся Составляют Приводят 5·5 3. 4.Дети учатся находить информацию в (n+1)2 – n2 2 способ. (n+1)2 – n2 5. Демонстрируют 6.Слушают 7.Оценивают |
анализ, извлечение из математических текстов осознанное и произвольное доказательство (П); контроль, коррекция, оценка (Р); волевая саморегуляция в ситуации затруднения (Р); осознанное выражение своих мыслей с использование критериев для обоснования контроль и самооценка |
9 |
30,31 |
|
2.4 |
Этап |
Организовать коллективно – где они смогли бы выявить границы |
1.Предлагает 2.Предлагает 3.Предлагает |
1.Предлагают Приводят 452=4(4+1) 2.Решают 3.Оценивают |
нравственно-этическое анализ, понимание использование установление выведение самостоятельное выполнение построение доказательство осознанное и контроль, выражение формулирование и аргументация своего мнения в постановка адекватное контроль и самооценка |
6 |
32 |
|
|
|||||||
|
3.1 |
Рефлексия |
отследить |
1.Предлагает Что Что Что было Каковы 2.Ответить 3.Предлагает Сравните 4.Предлагает Красный Зелёный Жёлтый |
1.Кратко 2.Работают 3.Подводят Отвечают Сравнивают сдают 4.Выбирают |
рефлексия способов и условий контроль и оценка процесса и результатов деятельности (П); самооценка на основе критерия адекватное выражение своих мыслей с формулирование и аргументация использование следование в |
3 |
33 |
|
3.2 |
Домашнее |
Организовать |
Предлагает 1.Составьте На «5» – три На «4» – две На «3» – одну (предполагается, 2. Подумайте, Поставьте |
Записывают |
самоопределение(Л); смыслообразование(Л); выражение своих мыслей с достаточной |
2 |
34 |
Цель:
- Обобщить и систематизировать знания учащихся
по данной теме, их умения и навыки применять
формулы при решении задач; - Развивать логическое мышление, познакомиться с
новой формулой.
Оборудование: таблицы, дидактические
карточки.
Ход урока
I. Организационная часть
II. Актуализация прежних знаний
Учитель: Ребята мы с вами изучили
формулы сокращенного умножения. Теперь
посмотрим, как их можно применить при решении
задач.А теперь мы еще раз вспомним эти формулы.
II-1. Пока мы работаем устно один из вас, сделает
домашнюю работу.
1. Доказать, что при любом натуральном значении
а значение выражения:
(3а – 4)2 – а2 кратно 8.
2. Сторона одного квадрата на 2 см меньше стороны
другого квадрата а разность площадей этих
квадратов равна 24 см2 . Найти сторону
большего квадрата.
II-2 Устная работа.
Выбрать правильный ответ:
| 1) (а + в)2
2) (а – в)2 3) а2 – в2 4) а3 – в3 5) а3 + в3 |
1) (а + в)(а – в)
2) (а + в)(а2 3) (а – в)(а2 + ав + в2) 4) а2 + 2ав + в2 5) а2 – 2ав + в2 |
II-3 Нужно заполнить пустые клетки.
1) (* – 10а2)(* + *) = 0,49х6-*
2) (* – *)2 = * – 2а4х2 + *
3) * + 6х3у2 + * = (* + *)2
4) (5х – *)(* + 10 ху + 4у2) = *3-*3
5) *3 + *3 = (* + m)(9а2 – 3аm
+ *)
III. Применение формул сокращенного умножения
при решении задач
1) Представить в виде многочлена:
а) (3р – 4с)2
в) (2а + 7в)2
2) Разложить на множители :
а) 16m2 – 25n4
в) х3-1000
с) 8у3 + 27
3) Доказать, что при любом натуральном значении n
значение выражения (n+9)2-(n-7)2
кратно 32.
4) Известно, что разность квадратов двух
последовательных натуральных чисел равна 81.
Восстановите эти числа.
5) Докажите, что разность квадратов двух
последовательных нечетных чисел кратна 8.
6) Отрезок длиной в 20см разделен на две части, и
на каждой из них построен квадрат. Найдите
стороны квадратов, если разность их площадей
равна 40см2.
С задачами мы справились. В каждом из этих задач
мы с вами применяли формулы сокращенного
умножения.
Мы с вами знаем возведение в квадрат только
двух слагаемых.
Еще Евклид в древности знал эти формулы. А
почему только двух слагаемых, а может быть,
возьмем три слагаемых, четыре слагаемых или
больше. Каким будет результат, давайте попробуем.
(а + в + с)2 = (а + в + с)(а
+ в + с) = а2 + в2 + с2
+ 2ав + 2вс + 2ас.(а + в + с + d)2 = (а + в + с
+ d)((а + в + с + d) = а2 + в2
+ с2 + d2 + 2ав + 2вс + 2сd + 2ас
+ 2аd + 2вd
А теперь сделаем вывод и попробуем дать
определение этой формуле.
Квадрат суммы нескольких выражений равен сумме
квадратов этих выражений, сложенной с удвоенными
произведениями выражений, взятых по два.
А теперь попробуем на примере:
1) (2х + у + 3z)2
2) (а + 2в + 4с)2
IV. Работа по тестам, где применяются формулы
сокращенного умножения.
V. Итоги урока.
VI. Домашнее задание
№520, возвести в квадрат 5 и 6 слагаемых.
Задачи на плотность, массу и объем с решением
Формулы, используемые по теме «Задачи на плотность, массу и объем с решением»
Название величины |
Обозначение |
Единицы измерения |
Формула |
Масса |
m |
кг |
m = ρ * V |
Объем |
V |
м3 |
V = m / ρ |
Плотность |
ρ |
г/см3,
|
ρ = m / V |
Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Найдите плотность молока, если 206 г молока занимают объем 200 см3?
Задача № 2.
Определите объем кирпича, если его масса 5 кг?
Задача № 3.
Определите массу стальной детали объёмом 120 см3
Задача № 4.
Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?
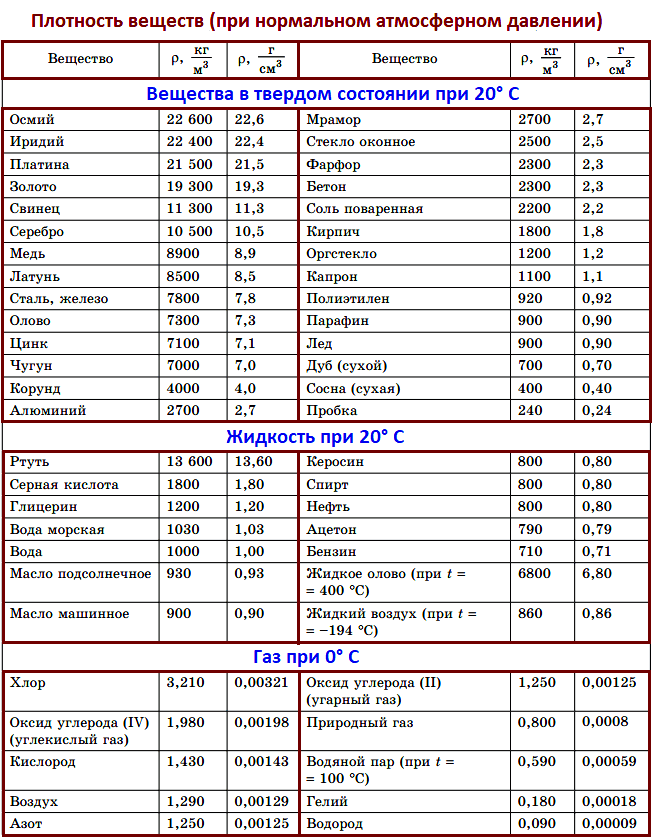
Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ2 = 7000 кг/м3) меньше плотности стали (ρ1 = 7800 кг/м3). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.
Задача № 5.
Определите плотность мела, если масса его куска объемом 20 см3 равна 48 г. Выразите эту плотность в кг/м3 и в г/см3.
Ответ: Плотность мела 2,4 г/см3, или 2400 кг/м3.
Задача № 6.
Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м2 ?
ОТВЕТ: 160 кг.
Указания к решению. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.
Вычисляем: m = 800 кг/м3 • 0,04 м2 • 5 м = 160 кг.
Задача № 7.
Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.
ОТВЕТ: Брусок сделан из алюминия.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 8 (повышенной сложности).
Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?
ОТВЕТ: 5 мм.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 9 (олимпиадный уровень).
Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.
ОТВЕТ: 8000 кг/м3
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задачи на плотность,
массу и объем с решением
Справочный материал для
«Задачи на плотность, массу и объем«
Таблица плотности веществ.
Как, зная только массу, рассчитать плотность?
- Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
- Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
- Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
- Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
- Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
- Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
- Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.
Задачи на плотность,
массу и объем с решением
ВОПРОСЫ ОТ ПОЛЬЗОВАТЕЛЕЙ САЙТА
Публикуем популярные вопросы от наших пользователей, оставленные в поле Комментариев. Прежде чем написать свой вопрос, проверьте: нет ли похожей задачи в начале статьи в разделе «Примеры решения задач» или среди вопросов в данном разделе!
Вопрос № 1. Длина стального листа 120 см, ширина 60 см, толщина 10 мм. Определить массу одного листа.
ОТВЕТ:≈ 56 кг.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 2. Какова масса платинового стержня, объём которого равен 21 дм3 ?
ОТВЕТ: 451,5 кг.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 3. Определить плотность бензина, если бак с бензином ёмкостью 20 литров имеет массу 14,2 кг?
Ответ: 710 кг/м3
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 4. Масса бетонного блока, имеющего форму параллелепипеда, равна 12 кг. Какой станет масса блока, если одну его сторону увеличить в 2 раза, вторую – в 2,5 раза, а третью оставить без изменения?
ОТВЕТ: 60 кг.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 5. Сколько рейсов должен сделать самосвал грузоподъемностью 5 т, чтобы перевезти 100 м3 гранита? Плотность гранита 2600 кг/м3.
ОТВЕТ: 52 рейса.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 6. Плотность некоторого раствора 1300 кг/м3. После того как в этот раствор добавили 10 л воды (деминерализованной) плотность этого раствора стала 1290 кг/м3. Сколько литров раствора было с исходной плотностью?
ОТВЕТ: 290 литров.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Конспект урока по физике в 7 классе «Задачи на плотность, массу и объем с решением». Выберите дальнейшие действия:
- Перейти к теме: «ЗАДАЧИ на силу тяжести и вес тела».
- Вернуться к Списку конспектов по физике для 7-11 классов
- Найти конспект через Кодификатор ОГЭ по физике
- Найти конспект через Кодификатор ЕГЭ по физике
В 7 классе курс алгебры усложняется. В программе появляется много интересных тем. В 7 классе решают задачи на разные темы, например: «на скорость (на движение)», «движение по реке», «на дроби», «на сравнение величин». Мастерство с легкостью решать задачи указывает на высокий уровень математического и логического мышления. Безусловно,с удовольствием решаются только те, которые легко поддаются и получаются.

Инструкция
Разберем, как решать более распространенные задачи.
При решении задач на скорость надо знать несколько формул и уметь правильно составить уравнение.
Формулы для решения :
S=V*t – формула пути;
V=S/t – формула скорости;
t =S/V – формула времени, где S – расстояние, V – скорость, t – время.
На примере разберем, как решать задания такого типа.
Условие: Грузовой автомобиль на путь из города «А» в город «Б» потратил 1,5часа. Второй грузовой автомобиль потратил 1,2 часа. Скорость второго автомобиля больше на 15 км/ч., чем скорость первого. Найти расстояние между двумя городами.
Решение: Для удобства применяйте следующую таблицу. В ней укажите то, что известно по условию:
1 авто 2 авто
S X X
V X/1,5 X/1,2
t 1,5 1,2
За Х примите то, что надо найти, т.е. расстояние. При составлении уравнения будьте внимательнее, обратите внимание, чтобы все величины были в одинаковом измерении (время – в часах, скорость в км/ч). По условию скорость 2-го авто больше скорости 1-го на 15 км/ч, т.е. V1 – V2=15. Зная это, составим, и решим уравнение:
X/1,2 – X/1,5=15
1,5Х – 1,2Х – 27=0
0,3Х=27
Х=90(км) – расстояние между городами.
Ответ: Расстояние между городами 90 км.
При решении задач на “движение по воде” необходимо знать, что существуют несколько видов скоростей: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость против течения (Vпр. теч.), скорость течения (Vтеч.).
Запомните следующие формулы:
Vпо теч=Vс+Vтеч.
Vпр. теч.=Vс-Vтеч.
Vпр. теч=Vпо теч. – 2Vтеч.
Vпо теч.=Vпр. теч+2Vтеч.
Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.
Vтеч.=(Vпо теч. – Vпр. теч)/2
На примере, разберем, как их решать.
Условие: Скорость катера по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость катера и скорость течения реки.
Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. – Vпр. теч)/2, найдем:
Vтеч = (21,8 – 17,2)/2=4,62=2,3 (км/ч)
Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)
Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
Задачи на сравнение величин
Условие: Масса 9 кирпичей на 20 кг больше, чем масса одного кирпича. Найти массу одного кирпича.
Решение: Обозначим за Х (кг), тогда масса 9 кирпичей 9Х (кг). Из условия следует, что:
9Х – Х=20
8х=20
Х=2,5
Ответ: Масса одного кирпича 2,5 кг.
Задачи на дроби. Главное правило при решении таких такого типа задач: Чтобы найти дробь от числа, надо это число умножить на данную дробь.
Условие: Турист был в пути 3 дня. В первый день он прошел? всего пути, во второй 5/9 оставшегося пути, а в третий день – последние 16 км. Найти весь путь туриста.
Решение: Пусть весь путь туриста равен Х (км). Тогда в первый день он прошел? х (км), во второй день – 5/9(х -?) = 5/9*3/4х = 5/12х. Так как в третий день он прошел 16 км, то:
1/4х+5/12х+16=х
1/4х+5/12х-х= – 16
– 1/3х=-16
Х=- 16:(-1/3)
Х=48
Ответ: Весь путь туриста равен 48 км.
Полезный совет
Чтобы с легкостью решать задачи, надо научиться переводить их на “язык чисел”, используя некоторые хитрости. Составление таблиц и схем максимально помогает понять условие задачи, отношения величин. Так же облегчает процесс составления уравнений. Безусловно, надо знать необходимы формулы.
Источники:
- Информация и задачи взяты из книги “Большой справочник. Математика. Для школьников и поступающих в вузы” Издательский дом “Дрофа”.
- расстояние скорость время решение задач
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
По теме: методические разработки, презентации и конспекты
Проектная работа Методика подготовки учащихся к решению задач по темам «Задачи на движение» и «Задачи на смеси и сплавы», включенных в ЕГЭ по математике.
Доминирующей идеей федерального компонента государственного образовательного стандарта по математике является интенсивное развитие логического мышления, пространственного воображения, алг…
Применение задач с военным содержанием на уроках математики по теме: «Решение задач на движение с помощью систем уравнений второй степени».
Имеющийся опыт в применении военной составляющей показывает, что учащиеся с большим интересом занимаются вопросами военного дела, особенно, если предлагаемые для решения задачи ставить не в сухой мате…
ГИА Задачи на движение(движение протяженных тел)
Обучающий модуль для дистанционной самоподготовки…
Методическая разработка по математике “Решение тестовых задач Единого Государственного Экзамена по математике: задачи на движение”
Решения тестовых задач ЕГЭ по математике по теме “Задачи на движение” всегда вызывают сложности у учащихся. Методическая разработка сделана для того ,чтоб было более ясно и проще выполнять данные зада…
Проектная работа по тема «Методика подготовки учащихся решению задач по теме «Задачи на движение, включенные в ЕГЭ по математике. Разработка системы индивидуальных заданий»
Проблема Методика подготовки учащихся решению задач по теме «Задачи на движение, включенные в ЕГЭ по математике»Цели:Собрать информацию о разнообразных задачах на движение, включенные в ЕГЭ, о ме…
Скорость, движение, время. Задачи на движение.
В данном пособии собраны задачи на движение. При составлении систем для таких задач обычно не требуется никаких особенных математических знаний. Требуется лишь здравый смысл и понимание того, что расс…
«Применение технологии подводящих задач при подготовке обучающихся к государственной итоговой аттестации в 9 классе по теме: «Текстовые задачи на движение»
Суть технологии подводящих задач – это планомерная корекционная работа с любым учащимся по любой теме для подготовки к ГИА, и не только. В данной статье приводится метод технологии подводящих задач пр…