п.1. Алгоритм решения задач с помощью систем уравнений
1. Обозначить неизвестные величины переменными («от смысла к буквам»).
2. По условию задачи записать уравнения, связывающие обозначенные переменные.
3. Решить полученную систему уравнений.
4. Истолковать результат в соответствии с условием задачи («от букв к смыслу»).
Например:
Найдите два положительных числа, если известно, что сумма квадратов этих чисел равна 185, а разность квадратов равна 57.
Шаг 1
«От смысла к буквам»:
Пусть x > 0 и y > 0 – задуманные числа.
Шаг 2
Уравнения по условию задачи:
( left{ begin{array}{ l } mathrm{x^2+y^2=185} & \ mathrm{x^2-y^2=57} & end{array}right. )
Шаг 3
Решение системы уравнений:
( left{ begin{array}{ l } mathrm{x^2+y^2=185} & \ mathrm{x^2-y^2=57} & end{array}right.Rightarrow )
( Rightarrow left{ begin{array}{ l } mathrm{2x^2=185+57=242} & \ mathrm{2y^2=185-57=128} & end{array}right.Rightarrow )
( Rightarrow left{ begin{array}{ l } mathrm{x^2=121} & \ mathrm{y^2=64} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=pm 11} & \ mathrm{y=pm 8} & end{array}right. )
Шаг 4
«От букв к смыслу»:
Выбираем положительные корни $$ mathrm{x=11, y=8} $$ Задуманы числа 11 и 8.
п.2. Примеры
Пример 1. Диагональ прямоугольника равна 10 см. Если меньшую сторону прямоугольника увеличить на 2 см, а большую уменьшить на 2 см, то диагональ не изменится. Найдите стороны прямоугольника.
Пусть a и b – стороны прямоугольника, a > b. Диагональ через стороны выражается по теореме Пифагора. По условию получаем: $$ left{ begin{array}{ l } mathrm{a^2+b^2=10} & \ mathrm{(a-2)^2+(b+2)^2=10^2} & end{array}right. $$ Найдём линейную зависимость между a и b из уравнения: begin{gather*} mathrm{a^2+b^2=(a-2)^2+(b+2)^2}\ mathrm{a^2+b^2=a^2-4a+4+b^2+4b+4}\ mathrm{4a-4b=8Rightarrow a-b=2Rightarrow a=b+2} end{gather*} Подставим a в верхнее уравнение системы: ( mathrm{(b+2)^2+b^2=100} ) begin{gather*} mathrm{b^2+4b+4+b^2-100=0}\ mathrm{2b^2+4b-96=0Rightarrow b^2+2b-48=0Rightarrow (b+8)(b-6)=0}\ mathrm{b_1=-8, b_2=6} end{gather*} Выбираем положительный корень: b = 6
Тогда a = b + 2 = 8
Ответ: 8 см и 6 см.
Пример 2. (задача Диофанта, III в.) Отношение двух чисел равно 3, а отношение суммы квадратов этих чисел к их сумме равно 5. Найдите эти числа.
Пусть x и y – искомые числа. По условию: $$ left{ begin{array}{ l } mathrm{frac{x}{y}=3} & \ mathrm{frac{x^2+y^2}{x+y}=5} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=3y} & \ mathrm{x^2+y^2=5(x+y)} & end{array}right. $$ Подставляем верхнее уравнение в нижнее и решаем: begin{gather*} mathrm{(3y)^2+y^2=5(3y+y)Rightarrow 9y^2+y^2=20yRightarrow 10y^2-20y=0Rightarrow}\ mathrm{Rightarrow 10y(y-2)=0Rightarrow} left[begin{array}{ l } mathrm{y_1=0} & \ mathrm{y_2=2} & end{array}right. end{gather*} Т.к. y в первом уравнении системы стоит в знаменателе, он не может быть равен 0. Получаем: begin{gather*} left{begin{array}{ l } mathrm{x=3y=6} & \ mathrm{y=2} & end{array}right. end{gather*} Ответ: 6 и 2.
Пример 3. Двое рабочих могут выполнить работу за 12 дней. Если сначала один из них сделает половину всей работы, а потом остальное сделает другой, то им понадобится 25 дней. За сколько дней каждый рабочий может выполнить задание самостоятельно?
Пусть x и y – производительность каждого рабочего, A – работа.
По условию: $$ left{ begin{array}{ l } mathrm{frac{A}{x+y}=12} & \ mathrm{frac{A}{2x}+frac{A}{2y}=25} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{A=12(x+y)} & \ mathrm{frac{A}{2}left(frac{1}{x}+frac{1}{y}right)=25} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{A=12(x+y)} & \ mathrm{A=frac{50}{frac{1}{x}+frac{1}{y}}=frac{50xy}{x+y}} & end{array}right. $$ Получаем уравнение: begin{gather*} mathrm{12(x+y)=frac{50xy}{x+y}Rightarrow 12(x+y)^2=50xyRightarrow 6(x+y)^2=25xy}\ mathrm{6(x^2+2xy+y^2)-25xy=0}\ mathrm{6x^2-13xy+6y^2=0 |:y^2}\ mathrm{6left(frac{x}{y}right)^2-13frac{x}{y}+6=0}\ mathrm{D=13^2-4cdot 6cdot 6=25=5^2, frac{x}{y}=frac{13pm 5}{12}=} left[begin{array}{ l } mathrm{frac23} & \ mathrm{frac32} & end{array}right. end{gather*} Пусть для определенности x > y. Тогда ( mathrm{frac{x}{y}=frac{3}{2}Rightarrow x=1,5y}. )
Работа: ( mathrm{A=12(x+y)=12(1,5y+y)=12cdot 2,5y=30y}. )
Второй рабочий может выполнить работу самостоятельно за: ( mathrm{frac{A}{y}=frac{30y}{y}=30} дней. )
Первый рабочий работает в 1,5 раза быстрей, ему понадобится ( mathrm{frac{30}{1,5}=20} дней. )
Ответ: 30 дней и 20 дней.
Пример 4. Бригада выполнила работу за 20 дней. Если бы в бригаде было на 4 человека больше, а рабочий день – на 1 ч дольше, то работа была бы выполнена за 10 дней. Если бы в бригаде было на 1 человека меньше, а рабочий день – на 1 ч короче, то работа была бы выполнена за 30 дней. Сколько человек было в бригаде, и сколько часов в день они работали?
Пусть A – вся работа, n – количество человек в бригаде, t – продолжительность рабочего дня. По условию: $$ left{ begin{array}{ l } mathrm{20nt=A} & \ mathrm{10(n+4)(t+1)=A} & \ mathrm{30(n-1)(t-1)=A} & end{array}right. $$ Исключаем A и получаем систему из двух уравнений: begin{gather*} left{begin{array}{ l } mathrm{20nt=10(n+4)(t+1)} & \ mathrm{20nt=30(n-1)(t-1)} & end{array}right.Rightarrow left{begin{array}{ l } mathrm{2nt=nt+4t+n+4} & \ mathrm{2nt=3(nt-t-n+1)} & end{array}right.Rightarrow\ Rightarrow left{begin{array}{ l } mathrm{nt=4t+n+4} & \ mathrm{nt=3t+3n-3} & end{array}right. end{gather*} Найдём линейную зависимость между n и t из уравнения: $$ mathrm{4t+n+4=3t+3n-3Rightarrow t-2n=-7Rightarrow t=2n-7}. $$ Подставим t в верхнее уравнение системы: begin{gather*} mathrm{n(2n-7)=4(2n-7)+n+4}\ mathrm{2n^2-7n=8n-28+n+4Rightarrow 2n^2-16n+24=0Rightarrow n^2-8n+12=0}\ mathrm{ (n-2)(n-6)=0Rightarrow} left[begin{array}{ l } mathrm{n_1=2} & \ mathrm{n_2=6} & end{array}right. end{gather*} Находим время ( mathrm{t=2n-7: } left[begin{array}{ l } left{begin{array}{ l } mathrm{n_1=2} & \ mathrm{t_1=-3} & end{array}right. &\ left{begin{array}{ l } mathrm{n_2=6} & \ mathrm{t_2=5} & end{array}right. end{array}right. )
Выбираем решение с ( tgt 0: left{begin{array}{ l } mathrm{n=6} & \ mathrm{t=5} & end{array}right. )
Ответ: 6 человек, 5 часов.
На прошлом уроке нами была установлена взаимозависимость между математическим языком и математической моделью. Теоретический базис заложен, так что теперь самое время переходить к практике. Далее мы подробнее рассмотрим составление математической модели и простые задачи, решаемые с помощью математической модели.
На первых порах тема может даваться с трудом. Но есть хорошая новость. Составление математической модели — это во многом навык.
Чем больше типовых задач вы нарешаете, тем проще вам будет ориентироваться в моделировании.
Этапы составления математической модели
Ранее мы описывали, что этапы составления математической модели включают в себя:
| 1. Наблюдение | 2. Моделирование | 3. Предсказание |
|---|---|---|
| Анализ задачи; на основе анализа подготовка частей будущей математической модели. | Логическое объединение частей и составление математической модели. | Использование составленной математической модели для заключений по вопросу задачи. |
С практической точки зрения наибольшую сложность представляют два первых этапа — наблюдение и моделирование. Чтобы их успешно завершать, необходимо умение правильно переводить текстовые утверждения на язык математики.
Что нужно хорошо понимать. На этапе наблюдения обычно переводятся части будущего алгебраического выражения. В процессе этапа моделирования эти части объединяются.
«Типовая задача»?
Еще раз подчеркнем, что задачи для седьмого класса, решаемые с помощью математической модели, являются типовыми. Что это означает? Они отличаются одинаковостью алгоритма решения.
Логика вычислений в них зациклена. А составление математической модели от задачи к задаче также следует одной схеме.
Например, пусть дана части задачи:
«Стоимость яблочного сока $x$ рублей, а томатного — $y$ рублей. Известно, что $5$ стаканов яблочного сока стоят столько же, сколько $6$ стаканов томатного…»
То, как составлена задача, подводит нас к двум концепциям — приравниванию и умножению. Опорным для решения будет следующее алгебраическое выражение:
$$5x=6y$$
Раз задача типовая, то выражения наподобие «$ax=by$» непременно встретятся еще раз, просто уже, так скажем, не в контексте сока. Вот почему мы выше говорили про то, что составление математической модели — это навык. Оно же умение отбросить текст и увидеть алгебру за ним.
Задачи на наблюдение и моделирование
Рассмотрим далее некоторые задачи, решаемые с помощью математической модели, в которых опущен этап наблюдения — где нет вывода ответа. Это поможет освоиться в основных типах учебных задач и научит выражать важные части текста алгебраически.
Операции сложения и вычитания
Задача. Первый рабочий выполняет порученное задание за $x$ часов, второй то же задание — за $y$ часов, при этом первый работает на три часа больше, чем второй.
Решение
Между производительностью двух рабочих можно установить отношение равенства, но с учетом условия «на три часа больше». Для начала составим каркасное тождество, которое дополним далее:
$$x=y$$
«Полноправно» приравнять данные переменные мы можем, только дополнив, что первый рабочий ($x$) работает на три часа больше. Интуитивно так и хочется переписать тождество следующим образом:
$$x+3=y$$
Однако это неверное составление математической модели для данной задачи. Мало того, что по условию очевидно неравенство $x>y$, так еще и тождество с частью «$x+3$» увеличивает разрыв между значениями $x$ и $y$ на лишние три раза.
Чтобы производительность рабочих все-таки приравнять, у первого, наоборот, нужно «отобрать» три часа и «отдать» их тому, кто работает быстрее:
$$x=y+3$$
Операции умножения и деления
Задача. На двух стройках трудится одинаковое количество рабочих. На первой стройке работает 5 бригад по $x$ человек в каждой, на второй стройке — 3 бригады по $y$ человек в каждой.
РЕШЕНИЕ
Первая стройка. В одной бригаде трудится $x$ человек. По условию таких бригад пять. Откуда получаем количество человек всего, трудящихся на первой стройке: $5x$.
Вторая стройка. Здесь же в одной бригаде трудится $y$ человек. По условию имеем три бригады. Следовательно количество работников, трудящихся на второй стройке: $3y$.
Также нам известно, что на двух стройках работает одно и то же количество рабочих. Остается данные части приравнять, чтобы получить тождество:
$$5x=3y$$
Вот, буквально мгновение — и мы вновь увидели составление математической модели коэффициентного типа «$ax=bx$».
Задачи, решаемые с помощью математической модели, со смешанной арифметикой
Задача. У Кати $x$ марок, а у Димы $y$ марок. Если Катя отдаст Диме 5 марок, то у Димы станет марок вдвое больше, чем останется у Кати.
РЕШЕНИЕ
Внимание на следующие части текста задачи:
| «Отдаст пять марок…» | «Вдвое больше» |
| Сложение/вычитание | Умножение/деление |
В зависимости от того, какая часть тождества отражает данные положения, операция может быть как прямой («Катя отдаст, $x-5$»), так и обратной («Дима возьмет, $y+5$).
Разделим составление математической модели задачи на два шага.
1. Катя отдает Диме 5 марок и у нее остается $x-5$ марок. Теперь у Димы $y+5$ марок.
2. В результате у Димы марок в два раза больше.
Однако нам нужно количество марок ребят приравнять. Раз у Димы их по условию задачи больше, то для равенства с количеством марок Кати у него их должно быть меньше. Значит, мы можем либо умножить количество марок Кати на 2, либо разделить количество марок Димы на 2:
| $$2(x-5)=y+5$$ | $$x-5=frac{y+5}{2}$$ |
Составление математической модели — полные задачи
Самое время усложнить содержание задач и ввести все этапы составления математической модели, включая этап планирования. Далее мы решим ряд показательных задач, где требуется дать ответ.
Задача. В двух залах кинотеатра 460 мест. Сколько мест в большом зале, если в нем в 3 раза больше мест, чем в малом?
РЕШЕНИЕ
Заметим, что в данном случае составление математической модели задачи будет вестись в двух направлениях. С одной стороны, устанавливается алгебраическое равенство между количеством мест в залах. С другой стороны, нам известна их сумма. Составим эти выражения.
Приравнивание. Пусть количество мест в большом зале равняется $x$. Вместо того, чтобы вводить лишнюю переменную $y$ для количества мест в малом зале, выразим места малого зала через уже введенную переменную $x$ — как $frac{x}{3}$. Это краткая модель записи:
$$y=frac{x}{3}$$
Сложение. Всего в залах 460 мест. Количество мест в большом зале $x$, в малом — $frac{x}{3}$, одна треть от мест в большом. Вместе:
$$x+frac{x}{3}=460$$
Задаче требуется ответ; этапы составления математической модели должны завершаться в полном объеме. С этой целью мы и взяли за «главную» переменную количество мест в большом зале. Остается решить уравнение выше.
$$frac{4}{3}x=460\x=345$$
Ответ: 345.
Составление математической модели — задачи на движение
Задача. От пристани отошел теплоход со скоростью 22 км/ч, а от другой пристани навстречу ему через три часа отошел теплоход со скоростью 26 км/ч. Расстояние между пристанями составляет 306 км. Сколько времени в пути был каждый из теплоходов до встречи?
Для решения нам понадобится формула пути:
$$S=vt$$
Этап наблюдения
Время в пути — искомый параметр, введем его в качестве переменной $t$.
Пусть $t_1$ — это количество времени, затраченное первым теплоходом на преодоление всего своего пути. Сколько при этом затратил времени второй теплоход? На три часа меньше, ведь по условию от пристани он отошел в сравнении с первым с задержкой:
$$t_1-3$$
Этап моделирования
Каркасная модель выглядит так:
$$v_{1}t_1+ v_{2}t_2=S,$$
где $S$ — расстояние между пристанями, $v_1$ — скорость первого теплохода, $v_2$ — скорость второго, $t_1$ и $t_2$ — соответствующее время в пути.
Откуда взялась модель? Зарисуем перемещение теплоходов, что бывает иногда очень полезно при решении задач на движение. Теплоходы двигаются навстречу друг другу. Значит, в сумме они проходят расстояние между пристанями.
Доработаем модель и добавим в нее имеющиеся у нас данные:
$$22t_1+26(t_{1}-3)=306$$
Этап предсказания
Остается решить уравнение, найти значение $t_1$ и вычесть из него 3, чтобы получить $t_2$.
$$22t_1+26t_1=306+78\t_1=8$$
Первый теплоход затратил 8 часов. Второй, соответственно, 5 часов.
Ответ: 8 и 5.
Решите сами!
Показать решение
Спрятать решение
🔵 РЕШЕНИЕ
Не очевидно, но за переменную $x$ удобно взять количество учащихся в старших классах. Почему — увидите далее.
Выразим количество учащихся в начальных и средних классах также через $x$. Для этого проанализируем утверждения, заданные условием задачи.
Утверждение первое: «В начальных классах учащихся в три раза больше, чем в старших». Раз их в три раза больше, то количество учеников в начальных классах через $x$ — это $3x$.
Утверждение второе: «В начальных классах учащихся в два раза меньше, чем в средних». Количество учащихся в начальных классах мы выразили ранее как $3x$. Сколько тогда учеников в средних классах? В два раза больше, то есть $2cdot{3x}=6x$.
Остается составить модель:
$$x+3x+6x=900$$
Решаем и находим количество учеников в старших классах ($x$):
$$10x=900\x=90$$
Откуда получаем, что в начальных классах учится 270 учеников ($3x$), а в средних классах — 540 учеников ($6x$).
Ответ: 270, 540, 90.
11.08.2021
Составление математической модели при решении текстовых задач
![]()
Решение задач является наиболее трудной частью изучения математики для большинства детей. В этой статье приведу несколько примеров составления математических моделей. Данный способ для многих учащихся позволяет проще решать ряд текстовых задач.
Оценить![]()
![]()
![]()
![]()
![]()
631
Содержимое разработки
Составление математической модели при решении текстовых задач
Решение задач является наиболее трудной частью изучения математики для большинства детей.
В этой статье приведу несколько примеров составления математических моделей. Данный способ для многих учащихся позволяет проще решать ряд текстовых задач. Примеры задач, представленные в данной работе, больше подойдут для учащихся 5, 6, 7 классов. Но данную методику можно освоить и для более сложных задач. Модель получается составлением из двух, трёх равенств одного. В некоторых случаях предварительно равенства составляются из неравенств. Это является увлекательным и мотивирует учащихся к работе. Составление подобных моделей можно использовать на элективных курсах по математике.
Во-первых, дадим понятие задачи и её структуры. Задача — вопрос, который требует решения посредством использования определенных умений, знаний и размышлений Задача — единство условия и цели. Условие задачи — сведения об объектах и некоторых величинах, характеризующих данные объекты, об известных и неизвестных значениях этих величин, об отношении между ними. Условие может быть достаточным, недостаточным, избыточным. Требование задачи — указание того, что нужно найти (в повелительной или вопросительной форме). Решить математическую задачу — найти такую последовательность математических действий, применяя которые к условию задачи, получим то, что требуется найти.
Основная особенность текстовых задач состоит в том, что в них не указывается прямо, какие именно действия должны быть выполнены для получения ответа на требование задачи.
Существуют различные методы решения текстовых задач: арифметический, алгебраический, практический и др. Чаще всего используется алгебраический метод решения, опираясь на следующую схему:
– выделить величины о которых идет речь в задаче и установить зависимость между ними
– ввести переменные
– с помощью введенных переменных и данных задачи составить уравнение или систему уравнений
– решить полученные уравнения или систему
– проверить найденные значения по условию задачи и записать ответ.
В данном случае можно обратиться к составлению математической модели задачи.
Математическая модель задачи – компактная запись условия задачи на языке математики с помощью математических символов: цифр, скобок, знаков действий. Различные задачи могут иметь одну и ту же математическую модель. Например, нам нужно посчитать расходы (Р) на покупки в магазине. Надо купить две булки (Б) и три пачки масла (М). Мы знаем цену булки (ЦБ) и цену масла (ЦМ). Легко можно записать:
Р = 2·ЦБ + 3·ЦМ
Вот эта запись и будет математической моделью расходов на наши покупки.
Для тренировки составления математической модели можно выполнить ряд следующих заданий:
-
Переведите фразы на математический язык:
-
Лена за сыр и колбасу заплатила 200 руб
-
Часы стоят столько же, сколько ваза и подсвечник вместе
-
Площадь треугольника и квадрата составляла 56 см кв
-
Сумма двух чисел равна наименьшему трехзначному числу
-
Если Виталий купит за 5 рублей шоколадку, то у него денег останется столько же, сколько сейчас у Павла
-
Если переложить 8 ручек из одного пенала во второй, а затем 2 убрать из первого и положить ещё во второй 6 то число ручек в пеналах сравняется
-
Перчатки дешевле сумки в 2 раза, поэтому за них заплатили на 500 рублей меньше, чем за сумку
-
Если из второй канистры с бензином вылить половину первой, тогда в канистрах будет одинаковое количество бензина.
-
Запишите неравенства и превратите их в равенства:
-
Число А меньше числа В на 3
-
Число В больше числа Г в 6 раз
-
Пальто дороже шляпы в 4 раза
-
Один кусок ленты дороже другого на 50 см
-
Разница между периметром прямоугольника и периметром квадрата 28 см
-
Из двух равенств получить одно:
Р+Л=15
А+С=В
Р=К+Л
Т+Е=52
П=Ж+К
К=Т+А
С=К+Т
Р+В=32
Е=А+Б
20=П+Т
-
Запишите формулу с учетом условий
-
Периметр треугольника F см. Одна его сторона — 4 см, другая сторона 7 см, третья сторона — Z см
-
Периметр равностороннего треугольника равен 34 см
-
Площадь прямоугольника равна 60 см2. Ширина на 13 см больше длины, которая равна Б см.
-
Составьте задачу по математической модели
а) (Б-8)+Б=16d) М+5=(15-М)-5
в) (К+12) +2К=99е) (21-Б)+5=Б
с) (В+8)-10+В=50f) 5В-25=В+15
Задач в мире – бесконечное количество. Поэтому предложить чёткую пошаговую инструкцию по составлению математической моделилюбой задачи – невозможно.
Опираясь на схему решения алгебраических задач приведу примеры составления математических моделей задач разного типа:
-
ПРОСТЕЙШИЕ ЗАДАЧИ. (Отношения«НА»и«В»)
За рубашку и галстук заплатили 1000 руб. Галстук дешевле рубашки на 300 руб. Сколько заплатили за галстук?
-
Выделим величины, о которых идет речь в задаче
Рубашка-Р
Галстук-Г
2. Установим зависимость между ними из условия задачи
1. Р+Г=1000
2. Г<Р=300
-
Для составления модели из неравенства запишем равенства
Р=Г+300
-
Из двух равенств запишем одно
|
Р+Г=1000 |
|
Р=Г+300 |
|
Г+300+Г=1000 |
-
Решим составленную модель
Г+300+Г=1000
2Г+300=1000
2Г=1000-300
2Г=700
Г=700:2
Г=350
Ответ: 350 р
-
ЗАДАЧИ «ЕСЛИ БЫ КОГДА…»(Равенства)
В одной коробке вдвое больше карандашей, чем в другой. Когда в первую коробку добавили еще 12 карандашей, то в двух коробках стало 99 карандашей. Сколько карандашей было в каждой коробке?
В данном случае условие задачи представим в виде таблицы
|
Было |
Стало |
||
|
1 кор-Х к |
Х =2У |
Добавили 12 к |
Х=2У+12 |
|
2 кор-У к |
У |
У |
|
|
Всего |
Х+У=99 к |
Составим из двух равенств одно:
Решим составленную модель:
2У+12+У=99
3У=99-12
3У=87
У=29
29 к. было во 2 коробке
Х=2*29=58к было в 1 коробке
Ответ: 58 к. и 29 к.
-
ТРИ СЛАГАЕМЫХ
Собрали 2100 кг картофеля и разместили его в трех хранилищах. В первое хранилище поместилось в 3 раза больше картофеля, чем во второе. В третье хранилище поместили 500 кг картофеля.Сколько картофеля разместили в первое хранилище?
|
Было |
|
|
1 хранилище-Х кг |
Х=3У кг |
|
2 хранилище-Укг |
Укг |
|
3 хранилище- Z кг |
500кг |
|
Всего |
Х+У+500=2100кг |
Составим из двух получившихся равенств одно:
|
Х+У+500=2100 |
|
Х=3У |
|
3У+У+500=2100 |
Решим составленную модель
3У+У+500=2100
4У=2100-500
4У=1600
У=400
400кг поместили во второе хранилище
Х=3*400=1200 кг поместили в первое хранилище
Ответ: 1200 кг
-
ПЛОЩАДЬ, ПЕРИМЕТР
Ширина прямоугольника в 2 раза меньше его длины. Если увеличить ширину на 5 см, а длину прямоугольника уменьшить на 10 см, получится квадрат. Найдите площадь получившегося квадрата.
|
Прямоугольник |
Было |
Стало- квадрат |
|
|
Ширина –Шсм |
Ш |
Увеличили на 5 см |
Сторона А=Ш+5 |
|
Длина-Дсм |
Д=2Ш |
Уменьшили на 10см |
Сторона А=Д-10 |
|
Площадь-S |
S=А*А |
Составим из трёх равенств одно:
|
А=Ш+5 |
Ш+5=Д-10 |
Ш+5=2Ш-10 |
|
А=Д-10 |
||
|
Д=2Ш |
Д=2Ш |
Решим составленную модель
Ш+5=2Ш-10
5+10=2Ш-Ш
Ш=15
15 см –ширина прямоугольника
Найдём сторону квадрата: А=15+5=20 см
Найдём площадь квадрата: S=20*20=400см^2
Ответ: 400см^2
-
БОЛЕЕ СЛОЖНЫЕ УРАВНЕНИЯ
На трех лодках и четырех яхтах плывут 25 человек. На каждой лодке разместилось на 1 человека меньше, чем на яхте. Сколько человек было в лодке?
|
Количество человек на 1 лодке и яхте (ч) |
Общее количество человек |
|
|
Лодка-Л |
Л |
3Л |
|
Яхта-Я |
Я=Л+1 |
4Я |
|
Всего |
3Л+4Я=25 ч |
Составим из двух равенств одно
|
3Л+4Я=25 |
|
Я=Л+1 |
|
3Л+4(Л+1)=25 |
Решим составленную модель:
3Л+4(Л+1)=25
3Л+4Л+4=25
7Л=25-4
7Л=21
Л=3
По 3ч было в каждой лодке
Ответ:3ч
-
«ГОЛОВЫ И НОГИ»
Сергей Викторович разводил индюшек и поросят. В его хозяйстве всего было 12 голов и 32 ноги. Сколько индюшек и поросят было в хозяйстве у Сергея Викторовича?
|
Количество голов |
Количество ног |
|
|
Индюшки-И |
И |
2И |
|
Поросята -П |
П |
4П |
|
Всего |
И+П=2г |
2И+4П=32 н |
Составим из двух равенств одно
|
И+П=12 |
И=12-П |
|
2И+4П=32 |
2И+4П=32 |
|
2(12-П)+4П=32 |
Решим составленную модель:
2(12-П)+4П=32
24-2П+4П=32
4П-2П=32-24
2П=8
П=4
В хозяйстве поросят –4
Индюшек: И=12-4=8
Ответ: поросят-4, индюшек-8
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/458822-sostavlenie-matematicheskoj-modeli-pri-reshen

«Свидетельство участника экспертной комиссии»
Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!
Текстовые задачи — это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами.
Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.
Пример:
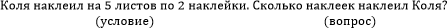
Решение любой текстовой задачи можно разделить на несколько основных этапов:
- Работа с условием
- Составление математической модели
- Проверка ответа
Работа с условием
Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица.
Пример: Петя выше Коли, Сережа ниже Коли. Кто выше?
Иллюстрация:
Из рисунка сразу понятен ответ: Петя выше всех.
Пример.
Два поезда идут навстречу друг другу. Скорость одного из них 45 км/ч, скорость другого — 55 км/ч. Сейчас между ними 200 км. Через сколько часов они встретятся?
Иллюстрация:
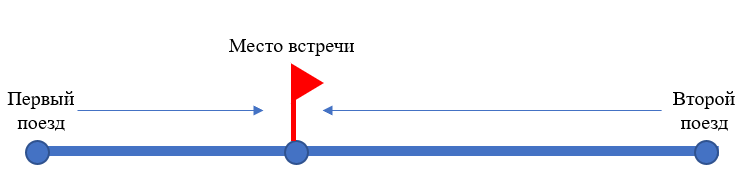
Пусть х часов — время движения обоих поездов, тогда по рисунку видно, что первый проедет 45х км, а второй — 55х км.
Составим математическую модель:
45х + 55х = 200
100х = 200
х = 2 ч
Ответ: 2 ч.
Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.
Математическая модель
Математика, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке. В таблице приведены различные ситуации и их математические модели.
x — число девочек
y — число мальчиков
| Реальная ситуация | Математическая модель |
|---|---|
| В классе поровну мальчиков и девочек | $ { x=y} $ |
| Девочек на 5 больше, чем мальчиков | $ { x=y+5, ; или; x-y=5,; или; x-5=y} $ |
| Мальчиков в 2 раза больше, чем девочек | $ { y=2x, ; или; frac{y}{2}=x,; или; frac{y}{x}=2} $ |
| Если в класс перейдут 3 мальчика, то девочек станет в два раза больше | $ { y=2(y+3)} $ |
Алгебраическая зависимость
Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.
При составлении уравнения особое значение играют используемые предлоги: «в» и «на».
Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?
Решение: Пусть П — рост Пети, К — рост Коли, С — рост Сережи.
Кстати, обратите внимание на этот приём — выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением.
Выразим рост мальчиков.
Петя выше Коли на 20 см: П – 20 = К
Сережа ниже Коли на 10 см: К = С + 10
Подставим в первое уравнение рост Коли: П – 20 = С + 10
Нам нужно найти, на сколько см Петя выше Сережи: П – С
П – 20 = С + 10
П – С = 20 + 10
П – С = 30
Получаем, что Петя выше Сережи на 30 см.
Пример: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?
Решение:
Пусть М — количество снежинок, которое сделала Маша, К — снежинки Коли, Р — снежинки Ромы.
Маша сделала в два раза больше снежинок, чем Коля: К = М/2
Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4
Вместе ребята сделали 12 снежинок: М + К + Р = 12
Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12
М = 4.
Маша сделала 4 снежинки.
Процентная зависимость
С процентами нам постоянно приходиться сталкиваться в повседневной жизни. “Скидка 30%”, “Кредит без процентов за 5 минут”, “Арендная плата выросла на 12%” — со всех сторон на нас сыпятся рекламные слоганы и призывы. Но что же значит это таинственное слово “проценты”? И как ими оперировать?
Сегодня мы с вами дадим определение процентов, поймём, как находится процент от некоторого числа, как можно найти одно количество процентов, уже зная другое. И, конечно, рассмотрим каждый из этих случаев на конкретном примере.
Как кирка у каменщика, камертон у настройщика или световой меч у Джедая, в математике тоже существуют свои инструменты, нужные для выполнения тех или иных операций. И проценты как раз и являются таким удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываясь на них.
Так что же такое один процент?
Процент — это всегда доля какого-то числа.
100% — все число
50% — половина
25% — четверть
Чтобы найти 1%, необходимо поделить всё число на 100.
Пример:
Есть 100 яблок.
$ 1% ;от ;всех ;яблок; –frac{100}{100} = 1 ;яблоко. $
Есть 200 груш
$ 1% ;от ;всех ;груш; –frac{200}{100} = 2 ;груши. $
Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом — соответствующие проценты.
Пример:
200 груш — 100 %
2 груши — 1 %
Пропорция отражает зависимость величин. По-другому это можно записать в виде двух дробей.
$ frac{200}{2}=frac{100}{1} $
Исходя из правил работы с дробями, получаем правила работы с пропорцией.
1. Внутри одной дроби можно сокращать значения.
2. Произведение накрест лежащих значений равно: 200 · 1 = 2 · 100
Эту тему мы еще подробно пройдем на курсе.
Рассмотрим несколько примеров работы с процентами в текстовых задачах.
Ситуация при работе с процентами усложняется, когда изначально нам известен не 1%, а несколько — например, 20. А требуют найти какое-нибудь неудобное число процентов
Пример: 38% населения деревни — это 76 человек. Сколько человек составляет 15% от общего населения?
Так как мы не можем сразу найти 15%, то нам вначале понадобится сделать промежуточный шаг — найти 1%. Если 38% — это 76 человек, то, разделив на 38, мы получим так нужный нам 1%. 38% = 76 человек ⇒1% = 2 человека. Тогда 15% = 30 человек
Но неугомонные математики не остановились и на этом. Что будет, если мы возьмём процент от какого-то числа, вычтем или прибавим к начальному числу, а затем снова возьмём то же количество процентов?
Пример: В 2010 дом стоял 2 тысячи рублей. В 2011 его цена увеличилась на 20%, а в 2012 — ещё на 20%. Сколько дом стоил к концу 2012 года?
На примере этой задаче мы посмотрим не только на то, как нужно брать проценты от разных величин, но и как переводить проценты в дроби. Решим её двумя способами:
Способ 1 Для начала давайте выясним, сколько стоил дом в 2011. Его стоимость увеличилась на 20%, т.е. на 400 рублей (1% = 2000:100 = 20, 20% = 400) и стала, соответственно, равна 2400. Теперь нам нужно узнать, сколько он стал стоить в 2012. Важно! Сейчас мы будем брать 20% от новой цены, т.е. той, которая была на дом в 2011 году. Если 1% = 2400:100 = 24, то 20% = 480, то есть новая цена в 2012 году — 2400 + 480 = 2880
Способ 2 Если 1% — это 0,01 от чего-то, то 20% — это 0,2. Тогда 20% от первоначальной цены это 2000⋅0,2 = 400, и цена на дом в 2011 году стала 2400. Теперь находим 20% от новой стоимости 2400⋅0,2 = 480 и итоговую стоимость в 2012 году: 2400 + 480 = 2880
Отлично! Итак, мы не только узнали, что такое проценты, как можно с ними обращаться, но и выяснили, как можно брать проценты от разных величин и как сопоставлять проценты с дробями. Больше интересных фактов и приёмов работы с процентами вы узнаете в процессе курса.
Также текстовые задачи могут быть посвящены прогрессиям, производительности, темпу — обо всем этом мы поговорим на нашем курсе. А сейчас приступайте к задачам для тренировки.
МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ТЕКСТОВЫХ ЗАДАЧАХ.
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Суслова Д.А. 1
1МОУ “Темповская средняя общеобразовательная школа Ртищевского района Саратовской области”
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение.
Текстовые задачи – одни из самых сложных задач в школьном курсе математики. Алгебраический метод решения не всегда бывает удобным для решения задач подобного типа – нередко бывает сложным выбрать нужную неизвестную величину так, чтобы решение было максимально простым и понятным.
С каждым годом текстовые задачи в школьном курсе математики усложняются, причем времени на совершенствование решений этих задач практически не выделяется. И если раньше их решение не вызывало особых затруднений, то теперь с этим могут возникнуть некоторые трудности. Поэтому решить задачу стандартным способом вряд ли получится. Решая одну из текстовых задач, я решила обратиться к математическому моделированию.
Для того чтобы устранить эти трудности, я решила рассмотреть другие возможные методы решения этих задач, а в частности задач на движение по окружности. Предметом моего исследования является математическое моделирование, как процесс, без которого, на мой взгляд, решение подобных задач будет наиболее трудоемким или даже невозможным.
Цель моей работы – рассмотреть основные виды математических моделей, применяемых к решению математических задач, и выбрать наиболее оптимальные к конкретной из них. К постановке этой цели меня привела следующая проблема: в современном мире, насыщенном информацией, необходимо умение представлять информацию в доступном (упрощенном) виде с целью достижения результата (решения задачи).
Исходя из цели, были поставлены следующие задачи:
-
Проанализировать научно-учебную литературу по теме работы.
-
Рассмотреть процесс математического моделирования и этапы создания модели для конкретной задачи.
-
Рассмотреть этапы создания математической модели.
-
Научиться составлять математические модели различного типа.
-
Выявить оптимальный метод математического моделирования для решения конкретной задачи (подобрать оптимальные модели для решения определённого типа задач).
Гипотеза: Существует универсальная математическая модель, с помощью которой можно решить любую текстовую задачу.
Объект исследования: текстовые задачи различного типа.
Методы исследования: анализ, аналогия, обобщение, прогнозирование, эксперимент.
Основная часть.
Глава I. Что такое математическая модель?
1.1 Краткая теоретическая справка.
Заинтересовавшись математическим моделированием, я проанализировала литературу, подробно описывающую данный метод. Существуют различные трактовки и классификации этого понятия. Я остановилась на учебном пособии [1] И.А. Печерских и А.Г. Семенова, которые дают следующее определение математической модели:
Математическая модель представляет собой формализованное описание системы на некотором абстрактном языке, например, в виде совокупности математических соотношений, т. е. такое математическое описание, которое обеспечивает имитацию работы систем или устройств на уровне, достаточно близком к их реальному поведению. Любая математическая модель описывает реальный объект, явление или процесс с некоторой степенью приближения к действительности. Целью математического моделирования является анализ реальных процессов математическими методами.
1.2 Этапы математического моделирования.
-
Постановка задачи.
На этом этапе требуется четкое понимание поставленной задачи.
-
Изучение теоретических основ и сбор информации об объекте оригинала.
На этом этапе подбирается или разрабатывается подходящая теория
-
Формализация.
Заключается в выборе системы условных обозначений.
-
Выбор метода решения.
На этом этапе устанавливаются окончательные параметры моделей с учетом условия функционирования объекта.
-
Реализация модели.
Выполнятся построение математической модели (строится график, таблица, рисунок или эскиз, граф) и решается задача исходя из новых условий.
-
Анализ полученной информации.
Сопоставляется полученное и предполагаемое решение.
7. Проверка адекватности реальному объекту.
Результаты, полученные по модели, сопоставляются с условиями исходной задачи.
Глава II. Применение моделирования к решению задачи.
Для достижения поставленной цели я составила несколько математических моделей, и постаралась к решению одной задачи (на движение по окружности) применить этот метод.
Задача.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 18 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 25 км/ч больше скорости другого?
Данную задачу решим с помощью математических моделей:
1. Таблица.
2. «Математический маятник».
3. Графическая модель.
2.1 Таблица – математическая модель, которая помогает упорядочить все данные в задаче для более удобного восприятия.
(Приложение 1. Таблица. Стр. 14.)
Решение.
Пусть x кмч – скорость первого мотоциклиста, тогда скорость 2-го мотоциклиста (x + 25) км/ч. Пусть первый раз мотоциклисты поравняются через t часов. Для того, чтобы мотоциклисты поравнялись, более быстрый (то есть второй ) должен преодолеть изначально разделяющее их расстояние, равное половине длины всей трассы ( т.к. мотоциклисты расположены в диаметрально противоположных точках )
( x + 25 )t – xt = 9
tx + 25t – tx = 9
25t = 9
t = 21,6 (минут)
Ответ: 21,6 минут.
2.2 «Математический маятник».
Математическим маятником [2] называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. Математический маятник имеет следующие характеристики: период, частота колебаний, количество колебаний и длина нити, но для решения этой задачи я остановилась на двух из них: период частота. Если связать эти величины со скоростью, временем и расстоянием, то задачу на движение по окружности можно будет решать с помощью формул, которые свойственны математическому маятнику.
T – период – это время, затраченное на один круг.
ʋ – частота колебаний – это величина обратная периоду.
Составим математическую модель.
(Приложение 2. «Математический маятник». Стр.14).
Пусть х км/ч – скорость первого мотоциклиста, тогда скорость второго мотоциклиста (х+25) км/ч. Длина всей трассы 18 км.
Т1 = время, затраченное 1-ым мотоциклистом на прохождение полного круга (период).
Т2 = время, затраченное 2-ым мотоциклистом на прохождение полного круга (период).
Для того чтобы мотоциклисты поравнялись в первый раз их частоты должны совпасть, значит:
– частота первого мотоциклиста.
– частота второго мотоциклиста.
Тогда разность – частота с которой будут происходить встречи при старте из одной точки.
Так как мотоциклисты расположены в диаметрально противоположных точках, то частота увеличится в 2 раза:
Тогда (ч) = 21,6 (мин.)
Ответ: 21,6 мин.
2.3 Графическая модель.
Графики законов, которые описывают зависимость S от t, строятся в системе координат SOt. Поскольку t > 0 и S > О, то построения выполняются в первой координатной четверти.
График движения тела по окружности можно заменить графиком движения по прямой. Обход телом окружности и возвращение в исходную точку равносильны достижению телом на прямой точки, удаленной от начальной на расстояние S0, равное длине окружности.
Изобразим схематически в системе SOt движение мотоциклистов.
Так как все величины положительны, то достаточно рассмотреть графики в первой четверти.
Пусть x ч – время, за которое первый мотоциклист догнал второго, y км – путь, пройденный вторым мотоциклистом до момента встречи с первым. Решение сводится к решению геометрической задачи.
(Приложение 3. Графическая модель. Стр. 15)
Ответ: 21, 6 минуты.
На примере решения данной задачи были выявлены следующие преимущества решения задач с помощью геометрической модели: наглядность, оперативность, простота решения.
Глава 3. Выявление оптимальных моделей для решения конкретных
задач.
3.1 Задачи на совместную работу.
Задачи подобного типа удобнее всего решать с помощью таблицы, потому что производительность, объем работы и время на выполнение всей работы можно легко связать со скоростью, временем и расстоянием. Роль скорости выполняет производительность труда, роль расстояния – вся работа, время выполняет свою роль.
Задача.
Двое рабочих, работая вместе, могут выполнить производственное задание за 40 дней. За сколько дней может выполнить задание каждый из них, работая самостоятельно, если одному из них для этого надо на 18 дней больше, чем другому?
Решение:
Примем весь объем работы за единицу. Пусть 2-ой рабочий, работая самостоятельно, может выполнить все задание за x дней, тогда 1-ый — за (x+18) дней.
(Приложение 4. Таблица. Стр. 15)
Вместе за 1 день рабочие выполняют задания. За 40 дней рабочие выполнят всю работу. Составим уравнение:
40× ( ) = 1
→
→
Второй корень не подходит по смыслу задачи (так как время не может быть отрицательным числом). Значит, 2-ой рабочий, работая самостоятельно, может выполнить всю работу за 10 дней, а 1-ый — за 10+9=19 дней.
Ответ: 10 дней, 19 дней.
3.2 Задачи на движение.
Задачи на движение по прямой удобнее всего решать с помощью графической модели.
Задача: Два пешехода вышли одновременно из своих сел W и C навстречу друг другу. После встречи первый шел 25 минут до села C, а второй шел 16 минут до села W. Сколько минут они шли до встречи?
(Приложение 5. Графическая модель. Стр. 16)
Решение:
Пусть ОЕ расстояние между сёлами W и C. OD – график движения первого пешехода ( который шёл медленнее), а EF – график движения второго. М – место встречи.
1) ∆ MND~∆MPO,
2) ∆MNE~∆MPF,
3)
4) => что t = 20 (мин.)
Ответ: 20 мин.
3.3 Задачи на движение по окружности.
Два велосипедиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение:
Используя модель «математического маятника», описанного выше, задача решается практически устно.- частота с которой будут происходить встречи при старте из одной точки.
Так как мотоциклисты расположены в диаметрально противоположных точках, то частота увеличится в 2 раза:
Тогда (ч) = (ч) = 20 (мин.)
Ответ: через 20 минут.
С помощью этой модели можно также быстро решать задачи, в которых отставание составляет не половину трассы, а конкретное расстояние. Решим эту же задачу, изменив в ней условие.
Два велосипедиста стартуют одновременно в одном направлении из двух точек круговой трассы, расстояние между которыми равно 3 км. Длина трассы равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение: Задача будет иметь 2 решения в зависимости от направления
движения по круговой трассе.
Составим математическую модель (для данной задачи их будет две).
(Приложение 6. «Математический маятник». Стр. 16)
В первом случае решение будет таким:
– частота, с которой будут происходить встречи при старте из одной точки. – часть периода (отставание), тогда
∙ = 7; тогда Т = (ч).
Во втором случае
– частота, с которой будут происходить встречи при старте из одной точки. – часть периода (отставание), тогда
=∙ = ; тогда Т = (ч).
Ответ: через часа; или через часа.
Таким образом, модель «Математический маятник» подходит для решения задач на движение по окружности. Применение такого способа решения значительно сокращает время на решение задачи, что позволит при выполнении контрольных работ и на экзамене увеличить время на решение более трудных задач.
Заключение.
В результате исследования были получены следующие результаты:
-
Был изучен процесс математического моделирования и этапы создания модели для конкретной задачи.
-
В ходе исследования была опровергнута гипотеза, о существовании универсальной математической модели для решения всех типов задач.
-
Я научилась составлять математические модели различного типа.
-
Были выявлены оптимальные математические модели для решения конкретной задачи.
Я думаю, что за моделированием – будущее. Умение составлять математические модели сможет помочь в решении задач из различных отраслей науки, а также жизненных задач. Хочется отметить, что решение задач с применением моделирования активизирует мыслительную деятельность, помогает лучше понять задачу, самостоятельно найти рациональный путь ее решения, установить подходящий способ проверки, определить условия, при которых задача имеет (или не имеет) решения. Работа с моделью позволяет яснее увидеть зависимости между данными и искомыми величинами, оценить задачу в целом, продемонстрировать разные варианты решения.
Библиографический список.
1. Рецензенты Черкасов В.С., кандидат физ.-мат. наук, доцент;
Чуешев А.В., кандидат физ.-мат. наук, доцент; Печерских, И.А. П 31 Математические модели в экономике: учебное пособие / И.А. Печерских, А.Г. Семенов; Кемеровский технологический институт пищевой промышленности. – Кемерово, 2011. – 191 с.
2. Перышкин, А. В.
П27 Физика. 9 кл. : учебник для общеобразоват. учреждений / А. В.
Перышкин, Е. М. Гутник. – 14-е изд., стереотип. – М. : Дрофа, 2009, – 300,
с, : ил, ; 1 л, цв. Вкл.
3. http://www.pedsovet.info/info/pages/referats/inf_00002.htm
Приложения
Приложение 1. Таблица
|
V (км/ч) |
t (ч) |
S (км) |
|
|
1-ый мотоциклист |
X |
t |
xt |
|
2-ой мотоциклист |
(х+25) |
t |
( x + 25 )t |
Приложение 2. «Математический маятник».
Приложение 3. Графическая модель.
18
A
O
y
D
9
C
t
x
Приложение 4. Таблица.
|
Производительность труда |
Время работы |
Работа |
|
|
1-ый рабочий |
ч/день |
(x+18) дней |
1часть |
|
2-ой рабочий |
ч/день |
1часть |
Приложение 5. Графическая модель.
25 минут
Приложение 6. «Математический маятник».
1) 2)
х
х
х+21
х+21
25
Просмотров работы: 9076
