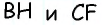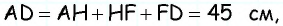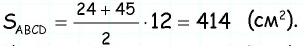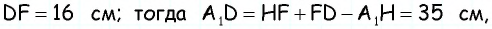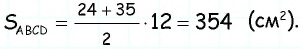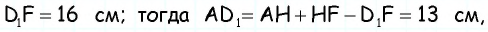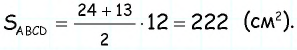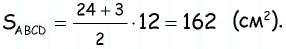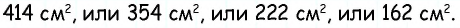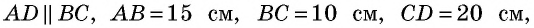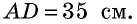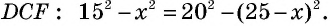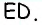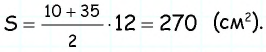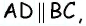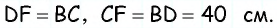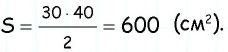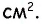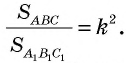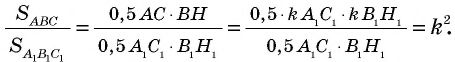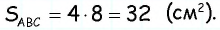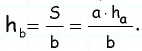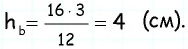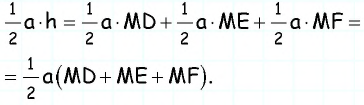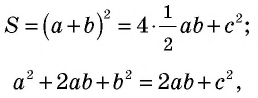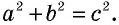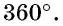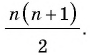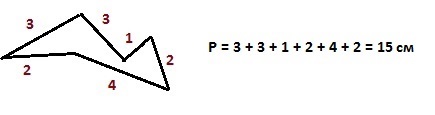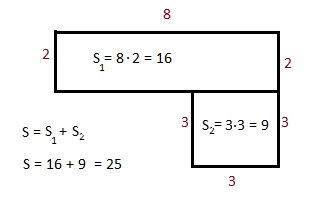Задача 1
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Решение:
- 1) 8 ∙ 7 = 56
- Ответ: Площадь прямоугольника 56 м².
Задача 2
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Решение:
- 1) 1) 64 : 8 = 8 (сторна витрины)
- 2) 2) 8 ∙ 4 = 32 (периметр витрины)
- Ответ: 32 м.
Задача 3
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Решение:
- 1) 1) 90 ∙ 7 = 630
- Ответ: 630 см².
Задача 4
Два прямоугольных участка имеют одинаковую площадь. Длина первого – 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Решение:
- 1) 48 ∙ 30 = 1440 (площадь первого участка)
- 2) 30 + 6 = 36 (ширина второго участка)
- 3) 1440 : 36 = 40
- Ответ: длина второго участка 40 м.
Задача 5
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Решение:
- 1) 36 ∙ 20 = 720 (площадь первого участка)
- 2) 36 – 6 = 30 (длина другого участка)
- 3) 720 : 30 = 24
- Ответ: ширина другого участка 24 м.
Задача 6
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Решение:
- 1) 4 ∙ 4 = 16 (площадь квадрата)
- 2) 2 ∙ 6 = 12 (площадь прямоугольника)
- 3) 16 – 12 = 4
- Ответ: площадь квадратата больше на 4 см.
Задача 7
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Решение:
- 1) 6 ∙ 6 = 36
- 2) 6 ∙ 4 = 24
- Ответ: площадь квадрата 36 см², периметр квадрата 24 см.
Задача 8
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Решение:
- 1) 7 ∙ 5 = 35
- 2) 7 ∙ 2 = 14
- 3) 5 ∙ 2 = 10
- 4) 10 + 14 = 24
- Ответ: площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 9
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
- 1) 8 ∙ 8 = 64 (площадь клумбы)
- 2) 64 : 16 = 4(1/16 клумбы)
- 3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
- 4) 64 – 28 = 36
- Ответ: незабудками засажено 36 м².
Задача 10
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Решение:
- 1) 6 ∙ 2 = 12
- 2) 18 – 12 = 6
- 3) 6 : 2 = 3 (ширина прямоугольника)
- 4) 3 ∙ 6 = 18
- Ответ: площадь прямоугольника 18 м².
Задача 11
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
- 1) 4800 : 60 = 80 (длина стола)
- 2) 60 ∙ 2 = 120 см
- 3) 80 ∙ 2 = 160 см
- 4) 120 + 160 = 280 см
- Ответ: периметр стола 280 см.
Задача 12
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
- 1) 5 ∙ 2 = 10
- 2) 40 – 10 = 30
- 3) 30 : 2 = 15 (другая сторона прямоугольника)
- 4) 5 ∙ 15 = 75
- Ответ: площадь прямоугольника 75 см².
Задача 13
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
- 1) 49 : 7 = 7 (сторона квадрата)
- 2) 7 ∙ 4 = 28 (периметр квадрата)
- Ответ: периметр квадрата равен 28 дм.
Задача 14
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
- 1) 4 ∙ 2 = 8 (длина окна)
- 2) 4 ∙ 8 = 32
- Ответ: площадь окна равна 32 м².
Задача 15
Длина участка земли 54 м. ширина – 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
- 1) 54 ∙ 48 = 2592 (площадь участка земли)
- 2) 2592 : 9 = 288 (1/9 площади)
- 3) 288 ∙ 5 = 1440 (5/9 площади)
- 4) 2592 – 1440 = 1152
- Ответ: капустой засадили 1152 м².
Простые задачи
- Простые задачи на движение
Составные задачи
- Задачи на встречное движение
- Задачи на движение в одном направлении
- Задачи на противоположное движение
- Задачи на нахождение неизвестного по двум разностям
- Задачи на нахождение числа по доле и доли по числу
- Задачи на нахождение площади
- Задачи на сложение и вычитание многозначных чисел
- Задачи на умножение и деление многозначных чисел
- Задачи на приведение к единице и пропорциональное деление
- Задачи на определение цены, количества, стоимости
Примеры решения задач разной сложности на нахождение периметра и площади
Условные обозначения и формулы
- a — длина
- b — ширина
- P — периметр
- S — площадь
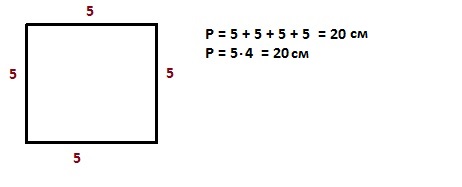
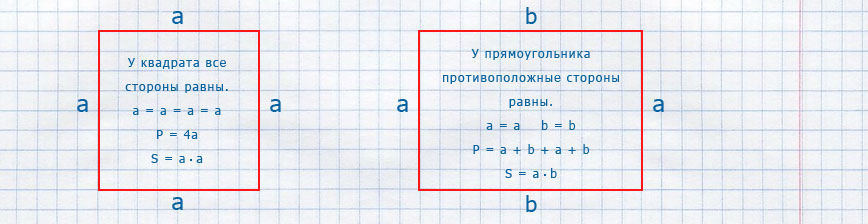
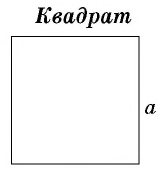
Квадрат → определение
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
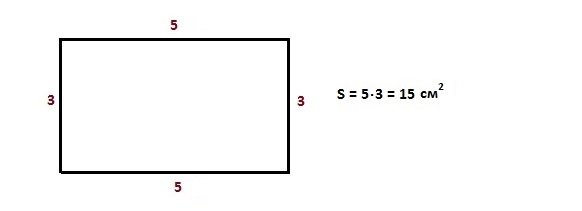
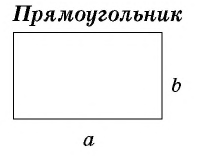
Прямоугольник → определение
P = a + b + a + b; P = 2a + 2b; P = (a + b) · 2 – периметр прямоугольника
S = a · b — площадь прямоугольника
Задачи
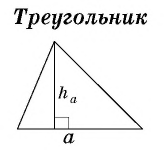
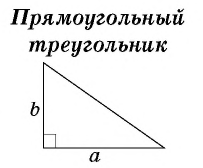
Треугольник → определение
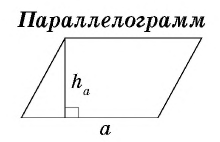
S = ½ · a · h – площадь треугольника
P = a + b + c – периметр треугольника
Задачи
Круг → определение
P = πD; P = 2πR — длина окружности
S = πR2; S = πD2 : 4 – площадь круга
Задачи
30 задач – от простого к сложному
Задача №1
Найди периметр квадрата со стороной 8 см.
Решение:
8 · 4 = 32 (см)Ответ: периметр квадрата 32 см.
Задача №2
Найди периметр квадрата со стороной 16 см.
Решение:
16 · 4 = 64 (см)Ответ: периметр квадрата 64 см.
Задача №3
Периметр квадрата 16 см. Найди его сторону.
Решение:
16 : 4 = 4 (см)Ответ: сторона квадрата 4 см.
Задача №4
Найди периметр прямоугольника со сторонами 9 и 6 см.
Решение:
(9 + 6) · 2 = 30 (см)Ответ: периметр прямоугольника 30 см.
Задача №5
Найди периметр прямоугольника со сторонами 7 и 8 см.
Решение:
(7 + 8) · 2 = 30 (см)Ответ: периметр прямоугольника 30 см.
Задача №6
Найди длину прямоугольника, если его ширина 7 см, а периметр равен 40 см.
Решение:
Вариант Ⅰ
У прямоугольника противоположные стороны равны, то есть две равных ширины и две равных длины.
Если одна ширина (сторона) 7 см, то и другая (противоположная) тоже 7 см.
7 + 7 = 14 (см)
Периметр состоит из суммы длин четырёх сторон прямоугольника, сумму двух противоположных сторон мы уже узнали, тогда сумма двух других противоположных сторон (длин) будет равна:
40 – 14 = 26 (см)
Теперь узнаем длину одной стороны:
26 : 2 = 13 (см)Ответ: длина прямоугольника 13 см.
или
Вариант Ⅱ
P = (a + b) · 2 — периметр прямоугольникаили
(a + b) · 2 = P, где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.
Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 – 14
2а = 26
а = 26 : 2
а = 13Ответ: длина прямоугольника 13 см.
Задача №7
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Решение:
Вариант Ⅰ
У прямоугольника противоположные стороны равны, то есть две равных ширины и две равных длины.
Если одна длина (сторона) 10 см, то и другая (противоположная) тоже 10 см.
10 + 10 = 20 (см)
Периметр состоит из суммы длин четырёх сторон прямоугольника, сумму двух противоположных сторон мы уже узнали, тогда сумма двух других противоположных сторон будет равна:
30 – 20 = 10 (см)
Теперь узнаем ширину одной стороны:
10 : 2 = 5 (см)Ответ: ширина прямоугольника 5 см.
или
Вариант Ⅱ
P = (a + b) · 2 — периметр прямоугольникаили
(a + b) · 2 = P, где a — длина = 10 см, b — ширина = ?, P — периметр = 30 см.
Составим уравнение:
(10 + b) · 2 = 30
20 + 2b = 30
2b = 30 – 20
2b = 10
b = 10 : 2
b = 5Ответ: ширина прямоугольника 5 см.
Задача №8
Ширина прямоугольника 14 см. Длина на 5 см больше. Найди его периметр и площадь.
Решение:
14 + 5 = 19 (см)
(19 + 14) · 2 = 66 (см)
19 · 14 = 266 (см²)Ответ: периметр прямоугольника 66 см; площадь прямоугольника 266 см².
Задача №9
Длина прямоугольника 7 см. Ширина на 3 см меньше. Найди его периметр и площадь.
Решение:
7 – 3 = 4 (см)
(7 + 4) · 2 = 22 (см)
7 · 4 = 28 (см²)Ответ: периметр прямоугольника 22 см; площадь прямоугольника 28 см².
Задача №10
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)Ответ: площадь квадрата 36 см².
Задача №11
Периметр квадрата 36 см. Найди его площадь.
Решение:
36 : 4 = 9 (см)
9 · 9 = 81 (см²)Ответ: площадь квадрата 81 см².
Задача №12
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см.
На сколько см² он ошибся?Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 – 45 = 3 (см²)Ответ: он ошибся на 3 см².
Задача №13
Ученику нужно было начертить прямоугольник со сторонами 10 см и 8 см, а он начертил его со сторонами 8 см и 6.
На сколько см² он ошибся?Решение:
10 · 8 = 80 (см²)
8 · 6 = 48 (см²)
80 – 48 = 32 (см²)Ответ: он ошибся на 32 см².
Задача №14
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Решение:
4 + 4 = 8 (см)
36 – 8 = 28 (см)
28 : 2 = 14 (см)
14 · 4 = 56 (см²)Ответ: площадь прямоугольника 56 см².
Задача №15
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см)
3 + 3 = 6 (см)
24 – 6 = 18 (см)
18 : 2 = 9 (см)Ответ: длина прямоугольника 9 см.
Задача №16
Сторона квадрата 18 см. Найди длину прямоугольника с таким же периметром и шириной 14 см.
Решение:
18 · 4 = 72 (см)
14 + 14 = 28 (см)
72 – 28 = 44 (см)
44 : 2 = 22 (см)Ответ: длина прямоугольника 22 см.
Задача №17
Площадь прямоугольника 40 см². Ширина его 4 см.
Чему равен периметр прямоугольника?Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)Ответ: периметр прямоугольника 28 см.
Задача №18
Площадь прямоугольника 40 см². Длина его 8 см.
Чему равен периметр прямоугольника?Решение:
40 : 8 = 5 (см)
(8 + 5) · 2 = 26 (см)Ответ: периметр прямоугольника 26 см.
Задача №19
Ширина прямоугольника 15 см, длина 20 см.
Найди длину другого прямоугольника с той же площадью, если его ширина в 3 раза меньше ширины первого прямоугольника.Решение:
в первом действии узнаём площадь по формуле a · b = S
15 · 20 = 300 (см²) — S одного и другого прямоугольника
теперь ширину второго
15 : 3 = 5 (см) — ширина другого прямоугольника
и отвечаем на вопрос задачи применив формулу S : a = b
300 : 5 = 60 (см)Ответ: длина другого прямоугольника 60 см.
Задача №20
Длина прямоугольника b = 32 см. Ширина a = 4 см.
Найди длину другого прямоугольника с такой же площадью, если его ширина в 2 раза больше ширины первого прямоугольника.Решение:
узнаем площадь прямоугольников по формуле a · b = S
32 · 4 = 128 (см²) — S первого прямоугольника
теперь ширину второго прямоугольника
4 · 2 = 8 (см) — ширина другого прямоугольника
применив формулу S : a = b узнаем длину другого
128 : 8 = 16 (см)Ответ: длина другого прямоугольника 16 см.
Задача №21
Какой участок земли потребует большую ограду: прямоугольный размерами 32 м и 2 м или квадратный, имеющий ту же площадь?
Решение:
Ⅰ. Прямоугольный участок
32 · 2 = 64 (м²) — S прямоугольного участка = 64 (м²)
(32 + 2) · 2 = 68 (см) — P прямоугольного участка = 68 (см)Ⅱ. Квадратный участок (имеющий площадь прямоугольного = 64 м²)
Если S квадрата = a · a, тогда, из формулы, узнаем сторону квадратного участка S : a = a
(у квадрата все стороны равны, тогда a · a = S — таблицу умножения мы знаем, подберём значения a и заменим их — 8 · 8 = S или 8 · 8 = 64 или 64 = 8 · 8 или 64 : 8 = 8)
64 : 8 = 8 (м) — любая сторона квадратного участка = 8 (м)
8 · 4 = 32 (м) — периметр квадратного участка = 32 (м)Ⅲ. P прям. – P квадр. = разница периметров
68 – 32 = 36 (м) — разница периметровОтвет: потребует большую ограду прямоугольный на 36 м.
Задача №22
Какая комната потребует больше плинтуса: прямоугольная размерами 4 м и 9 м или квадратная, имеющая ту же площадь?
Решение:
(4 + 9) · 2 = 26 (м) — P периметр прямоугольной комнаты
4 · 9 = 36 (м²) — S площадь прямоугольной комнаты
(из условия задачи квадратная комната имеет ту же площадь 36 м², а из определения площади квадрата знаем, что все стороны равны a = a = a = a, смотрим таблицу умножения и видим 6 · 6 = 36, то есть любая из сторон a = 6
запишем (приведём) формулу площади квадрата S = a · a в форму нахождения её стороны S : a = a
36 : 6 = 6 (м) — любая из сторон квадратной комнаты
6 · 4 = 24 (м) — P периметр квадратной комнаты
26 – 24 = 2 (м)Ответ: потребует больше плинтуса прямоугольная на 2 м.
Задача №23
Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)Ответ: площадь всех граней куба равна 24 см².
Задача №24
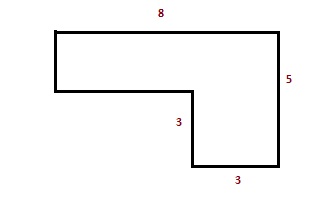
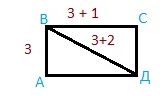
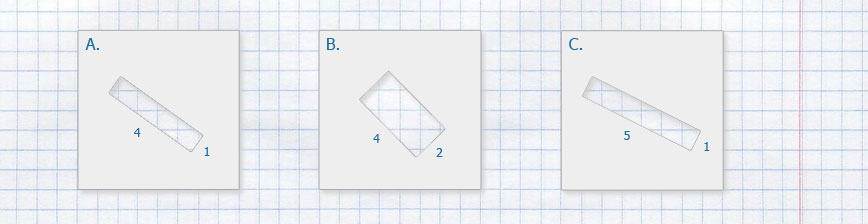
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Решение:
Для решения потребуются формулы:
S = a · a; S = a² — площадь квадрата (у квадрата все стороны равны)
S = a · b — площадь прямоугольника (у прямоугольника противоположные стороны равны)
Далее всё очень просто:Квадрат A.
S = a · a или a · a = S — формула площади квадрата, тогда
8 · 8 = 64 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
4 · 1 = 4 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь вырезанного прямоугольника
64 – 4 = 60Ответ: площадь получившейся фигуры равна 60.
Квадрат B.
S = a · a или a · a = S — формула площади квадрата, тогда
7 · 7 = 49 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
4 · 2 = 8 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь прямоугольника
49 – 8 = 41Ответ: площадь получившейся фигуры равна 41.
Квадрат C.
S = a · a или a · a = S — формула площади квадрата, тогда
7 · 7 = 49 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
5 · 1 = 5 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь прямоугольника
49 – 5 = 44Ответ: площадь получившейся фигуры равна 44.
Задача №25
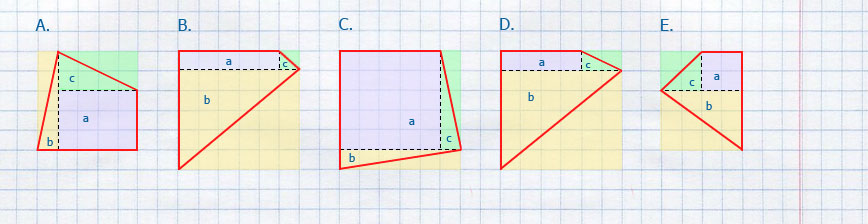
- Найдите площадь фигуры, изображённой на рисунке A.
- Найдите площадь фигуры, изображённой на рисунке B.
- Найдите площадь фигуры, изображённой на рисунке C.
- Найдите площадь фигуры, изображённой на рисунке D.
- Найдите площадь фигуры, изображённой на рисунке E.
(!) Фигуры расположены на листе в клетку, где каждая клетка – квадрат со стороной равной 1см.
Определение:
Неправильный четырехугольник – фигура, у которой стороны не равны и не параллельны.
Решение:
разобьём неправильные четырехугольники A, B, D на два прямоугольных треугольника и прямоугольник, а неправильные четырехугольники C, E на два прямоугольных треугольника и квадрат.
Применив формулы площади треугольника , квадрата и прямоугольника легко решим поставленную задачу
Фигура A.
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²Ответ: площадь фигуры A 18,5 см²
Фигура B.
S = a · b — формула площади прямоугольника, тогда
5 · 1 = 5 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 6 · 5 = 15 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 1 = 0,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры B
5 + 15 + 0,5 = 18,5 см²Ответ: площадь фигуры B 20,5 см²
Фигура C.
S = a · a; S = a² — формула площади квадрата, тогда
5 · 5 = 25 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 6 = 3 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры C
25 + 3 + 2,5 = 30,5 см²Ответ: площадь фигуры C 30,5 см²
Фигура D.
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры D
12 + 2,5 + 4 = 18,5 см²Ответ: площадь фигуры A 18,5 см²
Фигура E.
S = a · a; S = a² — формула площади квадрата, тогда
2 · 2 = 4 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 3 · 4 = 6 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 2 = 2 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры E
4 + 6 + 2 = 12 см²Ответ: площадь фигуры E 12 см².
Задача №26
Найдите площади и периметры фигурок. Сделайте вывод.
Определение:
Периметр – сумма длин всех сторон фигуры выраженый в милиметрах, сантиметрах, дециметрах, метрах и т.д.Площадь фигуры – геометрическое понятие, размер плоской фигуры выраженый в мм², см², дм², м² и т.д.
Пусть каждая из сторон клетки равна 1 см, тогда
применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура A имеет четыре стороны, тогда
1 + 4 + 1 + 4 = 10 см — периметр фигуры.Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура B имеет четыре стороны, тогда
2 + 2 + 2 + 2 = 8 см — периметр фигуры.Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура C имеет шесть сторон, тогда
3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура D имеет восемь сторон, тогда
1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура E имеет восемь сторон, тогда
1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.Вывод:
Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат.
У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача №27
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см
Найдём гипотенузу прямоугольного треугольника по формуле: a² + b² = c²Решение:
6² + 8² = c²
6 · 6 + 8 · 8 = c²
36 + 64 = с²
с² = 36+64
с² = 100
с = 10
Найдём периметр прямоугольного треугольника по формуле: p = a + b + c
p = 6 + 8 + 10 = 24Ответ: периметр прямоугольника равен 24 см.
см. Площадь треугольника
Задача №28
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (гипотенуза) с = 10 см
Найдём гипотенузу прямоугольного треугольника по формуле: a² + b² = c²Решение:
6² + b² = 10²
6 · 6 + b² = 10 · 10
36 + b² = 100
b² = 100 – 36
с² = 64
с = 8
Найдём периметр прямоугольного треугольника по формуле: p = a + b + c
p = 6 + 8 + 10 = 24Ответ: периметр прямоугольника равен 24 см.
см. Площадь треугольника
Задача №29
В треугольной пластине abc у которой один из углов 90°, сторона a равна 20 сантиметрам, а сторона b равна 10 сантиметрам просверлили отверстие диаметром 3 сантиметра. Какую оставшуюся площадь пластины нужно покрасить?
Решение:
Мы знаем что площадь – S треугольника равна половине – ½ произведения его основания – a умноженная на высоту – h,
то есть S = ½ · a · h, а Формула площади круга S = πd² : 4, число π ≈ 3,14.
1) По условию задачи пластина имеет форму прямоугольника со сторонами abc, в данном случае сторона b является высотой треугольника.
Тогда формула будет выглядеть так – S = ½ · a · b
подставим значения в эту формулу
½ · 10 · 20 = 100 (см²) — площадь треугольника
2) Подставим значения в формулу и узнаем площадь круга S = πd² : 4
3,14 · 3² : 4 = 3,14 · 9 : 4 = 7,065 (см²)
3) Теперь мы можем ответить на вопрос поставленный в задаче
100 – 7,065 = 92,935 см² — оставшуюся площадь пластиныОтвет: нужно покрасить 92,935 см².
Задача №30
На садовом участке Петя построил для цыплят круглый вольер радиусом 5 метров. Участок имеет прямоугольную форму с длинной 120 метров и шириной равной 8 диаметрам вольера. Сколько потребуется метров металлической сетки чтобы огородить участок и вольер?
Решение:
Для решения задачи нам потребуются вычислить периметры участка и вольера.
1) В первом действии узнаем диаметр вольера, нам известен радиус 5 метров, тогда по формуле диаметр равен двум радиусам D = 2R
5 · 2 = 10 (м) — диаметр вольера
2) Если ширина участка равна 8 диаметрам вольера, тогда
10 · 8 = 80 м — ширина участка
3) Далее по формуле P = (a + b) · 2 — периметр прямоугольника
120 + 80 · 2 = 400 (м)
4) Теперь по формуле P = 2πR — длина окружности (периметр) вольера
2 · 3,14 · 5 = 2 · 3,14 · 5 = 31,4 (м)
5) В последнем действии сложим периметры участка и вольера ответим на вопрос задачи
400 + 31,4 = 431,4 (м)Ответ: потребуется 431,4 метров металлической сетки.
Коротко:
Известные и великие математики
ученые древности, средневековья и современности, и их вклад в мировую науку
Рене Декарт
математик, философ
Дата рождения: 31 марта 1596 г.
Место рождения: Декарт, Турень, Абсолютная монархия во Франции
Дата смерти: 11 февраля 1650 г. (53 года), Стокгольм, Швеция
Биография
Родился 31 марта 1596 года в городе Ла-Э-ан-Турен (ныне Декарт), департамент Эндр и Луара, Франция. Декарт происходил из старинного, но обедневшего дворянского рода, был младшим (третьим) сыном в семье. Начальное образование Декарт получил в иезуитском колле́же Ла Флеш, где его учителем был Жан Франсуа.
В коллеже Декарт познакомился с Мареном Мерсенном (тогда — учеником, позже — священником), будущим координатором научной жизни Франции, и Жаком Валле де Барро. Религиозное образование только укрепило в молодом Декарте скептическое отношение к тогдашним философским авторитетам. Позже он сформулировал свой метод познания: дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.
В 1612 году Декарт закончил коллеж, некоторое время изучал право в Пуатье, затем уехал в Париж, где несколько лет чередовал рассеянную жизнь с математическими исследованиями. Затем он поступил на военную службу (1617) — сначала в революционной Голландии (в те годы — союзнице Франции), затем в Германии, где участвовал в недолгой битве за Прагу (Тридцатилетняя война).
В Голландии в 1618 году Декарт познакомился с выдающимся физиком и натурфилософом Исааком Бекманом, оказавшим значительное влияние на его формирование как учёного. Несколько лет Декарт провёл в Париже, предаваясь научной работе, где, помимо прочего, открыл принцип виртуальных скоростей, который в то время никто ещё не был готов оценить по достоинству.
Затем — ещё несколько лет участия в войне (осада Ла-Рошели). По возвращении во Францию оказалось, что свободомыслие Декарта стало известно иезуитам, и те обвинили его в ереси. Поэтому Декарт переезжает в Голландию (1628), где проводит 20 лет в уединённых научных занятиях.
В 1634 году он заканчивает свою первую, программную книгу под названием «Мир» (Le Monde), состоящую из двух частей: «Трактат о свете» и «Трактат о человеке». Вскоре, однако, одна за другой, появляются другие книги Декарта.
Кардинал Ришельё благожелательно отнёсся к трудам Декарта и разрешил их издание во Франции. Протестантские же богословы Голландии наложили на них проклятие (1642)
В 1649 году Декарт, измученный многолетней травлей за вольнодумство, поддался уговорам шведской королевы Кристины (с которой много лет активно переписывался) и переехал в Стокгольм. Почти сразу после переезда он серьёзно простудился и вскоре умер.
Его труды:
- Сформулировал (хотя и не доказал) основную теорему алгебры
- Методы решения алгебраических уравнений
- Классификация алгебраических кривых
- Сформулировал точное «правило знаков» для определения числа положительных корней уравнения
- Исследовал алгебраические функции (многочлены)
- Исследования Декарта в области к механики, оптики и общему строению Вселенной
- Математически вывел закон преломления света
- Понятие о рефлексе
- Классическое построение философии рационализма
- Теория близкодействия
- Метод радикального сомнения
- Картезианский дуализм
В память о Декарте:
- Великий физиолог И. П. Павлов поставил памятник-бюст Декарту возле своей лаборатории
- В честь учёного названы его родной город
- Назван кратер на Луне
- Назван астероид (3587) Descartes
- Декартова система координат
- Декартов лист
- Декартов овал
- Декартово дерево
- Декартово произведение
***
Цитата: У одного человека зачастую больше шансов сделать открытие, нежели у нескольких, занимающихся одной проблемой.
Решение задач на вычисление площадей многоугольников чаще всего сводится к поиску величин отдельных элементов рассматриваемых фигур и дальнейшему применению соответствующих формул площадей.
Во многих задачах наряду с сугубо геометрическими приемами решения (дополнительные построения, применение равенства фигур и т. п.) используются и методы алгебры (составление уравнений или систем уравнений на основе метрических соотношений между элементами фигуры).
В ходе решения особое внимание следует уделить тому, однозначно ли данные задачи определяют взаимное расположение элементов фигуры.
Пример:
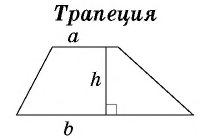
Найдите площадь трапеции, в которой одно из оснований равно 24 см, высота 12 см, а боковые стороны — 13 см и 20 см.
Решение:
Пусть
1) Для трапеции 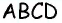
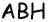
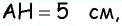
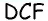
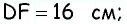
2) Для трапеции 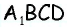
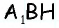
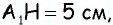
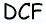
3) Для трапеции 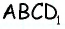
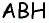
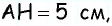
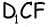
4) Для трапеции 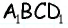
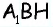
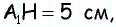
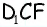
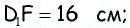
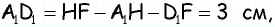
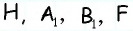
Ответ:
Рассмотренная задача наглядно демонстрирует одну из причин, по которым в процессе решения геометрической задачи может возникать многовариантность. Но даже если такая ситуация не возникает, взаимное расположение элементов фигур нуждается в обосновании.
Пример:
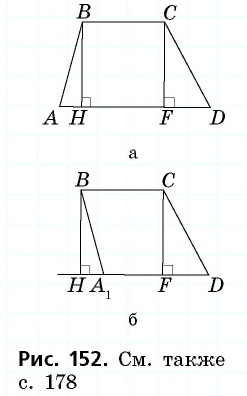
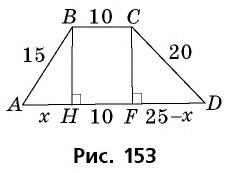
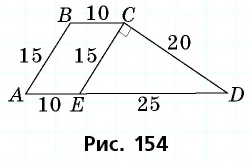
Основания трапеции равны 10 см и 35 см, а боковые стороны — 15 см и 20 см. Найдите площадь трапеции.
Прежде всего заметим, что решение данной задачи фактически сводится к нахождению высоты трапеции. Итак, пусть дана трапеция
Естественно было бы провести, как в предыдущей задаче, высоты 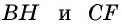
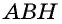
Такое решение позволит получить правильный ответ, но не будет полным, ведь принадлежность точек 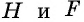
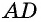
Решение:
Проведем через вершину 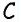
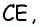

Поскольку по построению 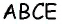
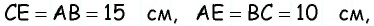
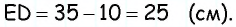
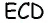
По формуле 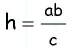
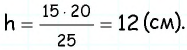
Ответ: 270
Как видим, этот способ намного более рационален, в частности, с точки зрения вычислений. Рассмотрим еще одну задачу, для решения которой используется дополнительное построение.
Пример:
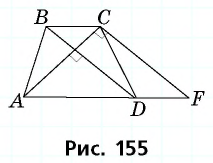
Диагонали трапеции равны 30 см и 40 см и пересекаются под прямым углом. Найдите площадь трапеции.
Попробуем решить эту задачу чисто геометрическими методами. Основная сложность заключается в том, что данные отрезки не являются сторонами одного треугольника. Попробуем «исправить» эту ситуацию.
Решение:
Пусть дана трапеция 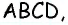
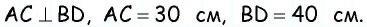
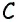
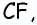
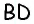
Очевидно, что по построению угол 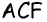
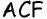
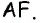
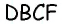
Обратим внимание на то, что треугольники 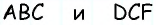
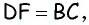
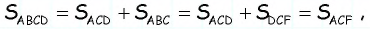

Ответ: 600
Применение площадей
Теорема (об отношении площадей подобных треугольников)
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
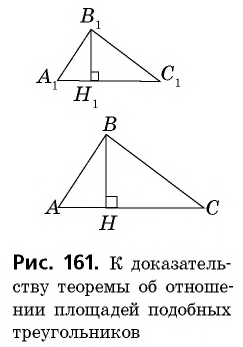
Доказательство:
Пусть 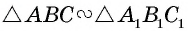
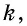
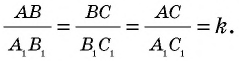
Проведем в данных треугольниках высоты 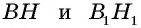
Прямоугольные треугольники 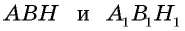
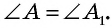
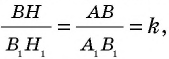
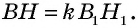
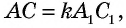
Пример:
Средняя линия отсекает от данного треугольника треугольник с площадью 8 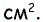
Решение:
Пусть 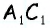
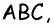

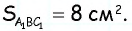
Треугольники 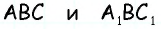
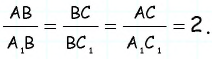
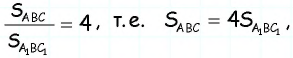
Ответ:
Метод площадей
Понятия площади и формулы ее вычисления могут применяться даже в тех задачах, в условиях которых площадь не упоминается. Рассмотрим такой пример.
Пример:
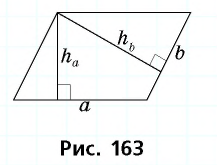
Стороны параллелограмма равны 16 см и 12 см. Высота параллелограмма, проведенная к большей стороне, равна 3 см. Найдите высоту, проведенную к меньшей стороне.
Решение:
Пусть дан параллелограмм со сторонами 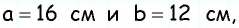

По формуле площади параллелограмма 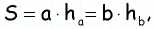
Таким образом,
Ответ: 4 см.
При решении этой задачи площадь параллелограмма вычислялась двумя разными способами. Поскольку площадь многоугольника независимо от способа ее вычисления определяется однозначно, то полученные выражения приравнивались, благодаря чему удалось связать известные величины с искомой. Такой метод, основанный на использовании площади как вспомогательной величины, называется методом вспомогательной площади или просто методом площадей.
Заметим, что из формул площади параллелограмма 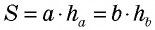
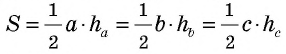
Метод площадей используется как в задачах на вычисление, так и для доказательства утверждений.
Пример:
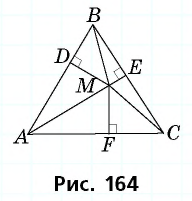
Сумма расстояний от точки, взятой внутри равностороннего треугольника, до его сторон не зависит от выбора точки и равна высоте треугольника. Докажите.
Решение:
Пусть точка 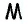
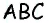
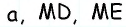
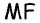
Соединим точку 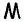
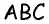
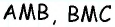
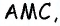
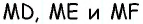
Отсюда 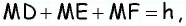
Другие доказательства теоремы Пифагора
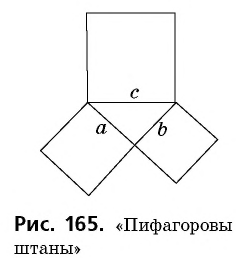
Исторически появление и доказательство теоремы Пифагора связаны с вычислением площадей. Поэтому в классической формулировке этой теоремы речь идет не о квадратах сторон прямоугольного треугольника, а о площадях соответствующих фигур:
- площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Рисунок 165, который наглядно воплощает эту формулировку, стал своеобразным символом геометрии и среди гимназистов позапрошлого столетия получил название «пифагоровы штаны».
Шутливый стишок про «пифагоровы штаны» школьники запоминали на всю жизнь.
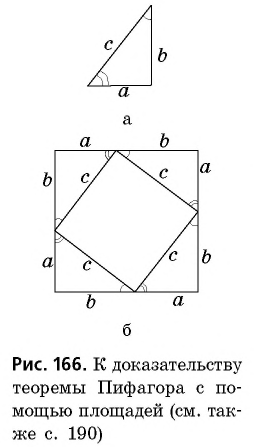
Докажем теорему Пифагора с помощью площадей.
Доказательство:
Пусть дан прямоугольный треугольник с катетами 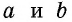
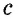
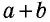
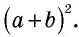
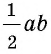
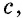
т.е.
Теорема доказана.
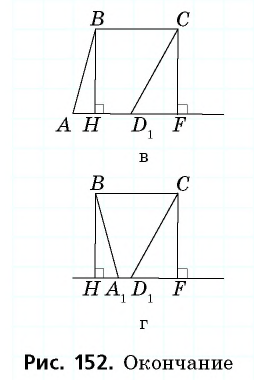
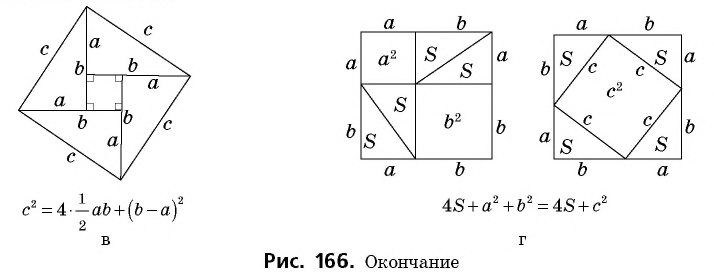
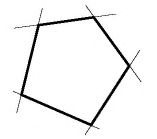
На рисунках 166, в, г показаны другие способы доказательства теоремы Пифагора с помощью площадей. В трактатах индийского математика XII ст. Бхаскари один из них сопровождался только одним словом: «Смотри!». В целом сегодня известно более 150 разных способов доказательства этой знаменитой теоремы. Но каждый из вас может изобрести и свой собственный способ.
Итоги главы 3.
Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону
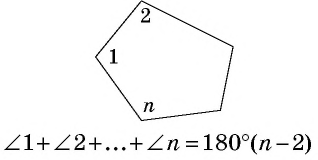
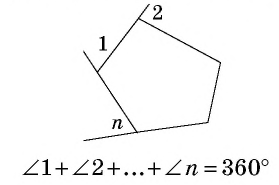
Сумма углов многоугольника
Сумма углов выпуклого 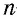
Сумма внешних углов выпуклого 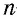
Описанный многоугольник
Многоугольник называется вписанным в окружность, если все его вершины лежат в этой окружности.
Описанный многоугольник.
Многоугольником называют описанным около окружностей, если все его стороны касаются этой окружности.
Аксиомы площадей
- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Площадь квадрата со стороной, равной единице длины, равна единице площади
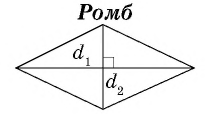
Две фигуры называются равновеликими, если они имеют равные площади
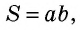
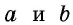
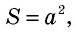
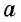
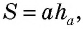
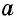
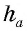
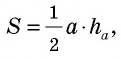
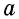
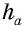
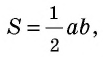
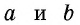
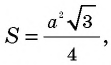
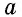
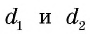
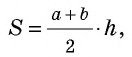
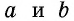
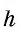
Теорема об отношении площадей подобных треугольников Отношение площадей подобных треугольников равно квадрату коэффициента подобия
Историческая справка:
Вычисление площадей многоугольников — первая среди тех практических задач, благодаря которым появилась геометрия как наука. Но не всегда представление об измерении площадей было таким, как сегодня.
Например, древние египтяне при вычислении площади любого треугольника брали половину произведения двух его сторон. Так же пять столетий назад измеряли площадь треугольника и в Древней Руси. Чтобы найти площадь четырехугольника, который не является квадратом, в Вавилоне использовали формулу произведения полусумм его противолежащих сторон.
В Средние века для вычисления площади треугольника со стороной и проведенной к ней высотой, которые выражаются целым числом 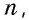
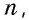
Кстати, в то время знали и правильную формулу площади этого треугольника 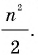
Древние вавилоняне еще четыре тысячи лет назад умели правильно вычислять площадь квадрата, прямоугольника, трапеции. Немало формул площадей и объемов, с которыми вы познакомитесь в старших классах, открыл знаменитый греческий ученый Архимед (ок. 287-212 гг. до н. э.). И это все при том, что в те древние времена не было даже алгебраической символики!
Сегодня, благодаря значительно более широкому применению алгебры в геометрии, мы имеем возможность дать куда более простые и понятные решения многих задач, чем это было возможно в те далекие времена.
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Площади фигур в геометрии
- Площади поверхностей геометрических тел
- Эллипс
- Гипербола
- Парабола
- Многогранник
ПЕРИМЕТР
Периметр – сумма длин всех сторон плоской геометрической фигуры. Чаще всего периметр измеряется в сантиметрах, метрах и километрах.
Чаще всего периметр обозначается буквой P.
Периметр прямоугольника – удвоенная сумма длины и высоты – 2∙(a+b)
Периметр квадрата – произведение любой его стороны на 4, так как стороны равны.
ПЛОЩАДЬ
Площадь – характеристика замкнутой геометрической фигуры, которая показывает ее размер. Чаще всего площадь измеряется в квадратных сантиметрах, квадратных метрах и квадратных километрах.
В отличие от периметра, не существует универсальной формулы площади. Для каждого типа фигур площадь вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольники, квадраты и составные фигуры из прямоугольников и квадратов.
Чаще всего площадь обозначается буквой S.
Площадь прямоугольника – произведение длины на высоту.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
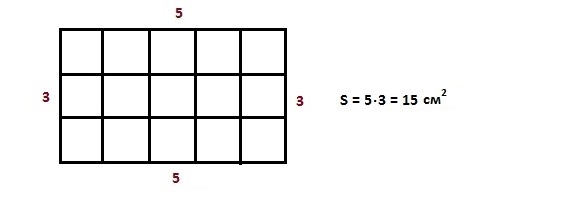
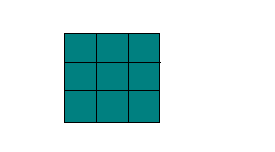
Разделим этот прямоугольник на квадраты
Мы получили 15 квадратов внутри этого прямоугольника – это и есть те самые 15 квадратных сантиметров, которые составляют площадь прямоугольника.
Площадь квадрата – произведение длины стороны на саму себя.
СОСТАВНЫЕ ФИГУРЫ
Разделим эту фигуру на прямоугольник и квадрат
Высота прямоугольника составит 5 – 3 = 2
СООТНОШЕНИЕ ПЛОЩАДИ И ПЕРИМЕТРА
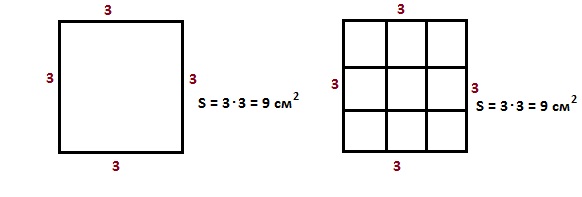
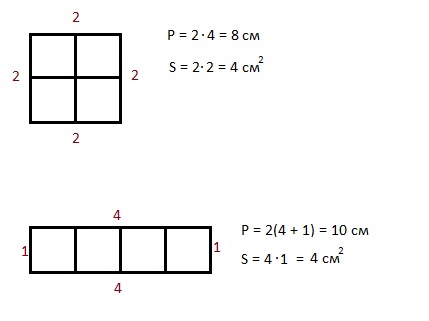
Фигуры с одной и той же площадью могут иметь разный периметр
Почему у нас изменился периметр, хотя площадь, т.е. число квадратиков внутри фигуры, осталась прежней?
Потому что изменилось число граней квадратиков, которые участвуют в формировании сторон фигуры, т.е. перметра. В первой фигуре – большом квадрате, в формировании сторон участвовали по две внешних грани каждого маленького квадратика – общее число таких граней 8, и периметр равен 8.
Во второй фигуре у нас в формировании сторон участвуют по три грани у двух крайних квадратиков и по две грани внутренних квадратов. Общее число таких граней 10, и периметр равен 10.
ОБЪЁМ
Объём – количественная характеристика пространства, занимаемого телом или веществом. Чаще всего объём измеряется в кубических сантиметрах, кубических дециметрах, кубических метрах и литрах.
1 л = 1 дм3
Не существует универсальной формулы объема. Для каждого типа фигур объём вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольные параллелепипеды.
Чаще всего объём обозначается буквой V.
Прямоугольный параллелепипед – замкнутая фигура, у которой 6 прямоугольных граней (передняя, задняя, нижняя, верхняя и две боковые), и каждая из граней расположены под прямым углом к соседним.
Объём прямоугольного параллелепипеда – произведение его длины, ширины и высоты
Зная объём и две стороны, мы можем найти третью сторону:
c = (V:a):b = V:S
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
ЗАДАЧИ
Задача 1. Найдите периметр и площадь прямоугольника, у которого ширина 10 см, и она меньше длины на 6 см.
x = 10 см – ширина
1. Найдём длину
y = 10 + 6 = 16 см
2. Найдём периметр
P = 2∙(10+16) = 52 см
3. Найдём площадь
S = 10∙16 = 160 см2
Ответ: P = 52 см, S = 160 см2
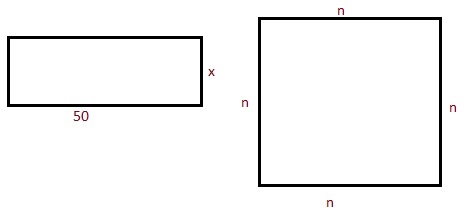
Задача 2. Какую ширину имеет прямоугольник, длина которого 50 см, а площадь совпадает с площадью квадрата периметром 80 см?
1. Вычислим сторону квадрата
4∙n = 80 – периметр
n = 20 см
2. Вычислим площадь квадрата
20∙20 = 400 см2
3. Вычислим ширину прямоугольника
50∙x = 400 см2
x = 8 см
Ответ: 8 см
Задача 3. Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм2 ?
1 дм = 10 см, 1 м = 100 см, 1 м = 10 дм
1. Переведём длину прямоугольника в дм
x = 15∙10 = 150 дм
2. Найдём ширину прямоугольника
150∙y = 7500
y = 7500:150 = 50 дм
Ответ: 50 дм
Задача 4. Длина прямоугольника равна 60 см, и она в 3 раза больше ширины стороны.
1. Найдите площадь этого прямоугольника.
2. Найдите площадь квадрата, который имеет такой же периметр, как и прямоугольник.
3. Найдите периметр квадрата, площадь которого в 12 раз меньше площади прямоугольника.
1. Найдём ширину прямоугольника
x = 60:3 = 20 см
2. Найдём площадь прямоугольника
S = 60∙20 = 1200 см
2. Найдём периметр прямоугольника
P = 2∙(60+20) = 160 см
3. Найдём сторону квадрата
y = 160:4 = 40 см
4. Найдём площадь квадрата
Sкв = 40∙40 = 1600 см2
5. Найдём площадь квадрата, которая в 12 раз меньше площади прямоугольника:
Sкв2 = 1200:12 = 100 см2
6. Найдём сторону такого квадрата
Площадь квадрата = 100 см2
Из таблицы умножения мы знаем, что 10∙10 = 100, значит сторона квадрата = 10 см
7. Найдём периметр такого квадрата
P = 10∙4 = 40 см
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Задача 5. В прямоугольнике АВСД сторона АВ 3 см, сторона ВС на 1 см длиннее, а диагональ ВД на 2 см длиннее АВ. Найдите периметр и площадь прямоугольника АВСД и треугольника АВД.
1. Найдём сторону ВС
ВС = 3+1 = 4
2. Найдём диагональ ВД
ВД = 3+2 = 5
3. Найдём периметр АВСД
P = 2∙(3+4) = 14 см
4. Найдём площадь АВСД
Sавсд = 3∙4 = 12 см2
5. Найдём периметр треугольника АВД
Pавд = 3 + 5 + 4 = 13 см
6. Найдём площадь треугольника АВД
Треугольник АВД занимает половину площади прямоугольника АВСД
Sавд = Sавсд:2
Sавд = 12:2 = 6 см2
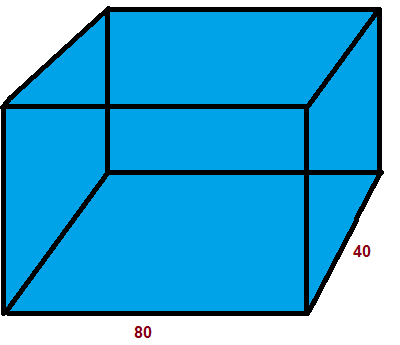
Задача 6. В аквариум в форме прямоугольного параллелепипеда, основание которого имеет стороны 80 и 40 см, налили до краёв 160 л. воды. Какова высота аквариума?
Решение
1. Переведём литры в кубические дециметры
1 л = 1 дм3, 160 л = 160 дм3
2. Переведём стороны аквариума в дециметры
1 дм = 10 см, 80 см = 8 дм, 40 см = 4 дм
3. Найдём высоту аквариума
V = a∙b∙c, a = 8, b = 4
c = (V:a):b
c = (160:8):4 = 5 дм
c = 5∙10 = 50 см
Ответ: 50 см
Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:
a — длина
b — ширина
P — периметр
S — площадь
Формулы площади и периметра для квадрата
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
Формулы площади и периметра для прямоугольника
P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника
Примеры решения задач разной сложности на нахождение периметра и площади
Задача 1
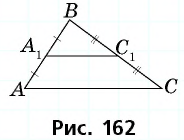
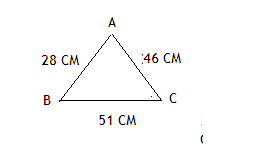
Каков периметр треугольника ABC?
Ответ: периметр треугольника равен 125 см.
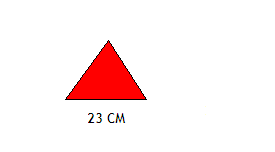
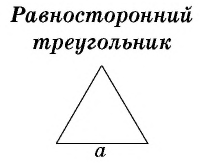
Задача 2
Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?
Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.
Задача 3
Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?
Ответ: Равнобедренный треугольник имеет две равные стороны. Сумма равных сторон будет 37 – 9 = 28 см. Значит, каждая из них будет равна 28 : 2 = 14 см.
Задача 4
У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?
Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.
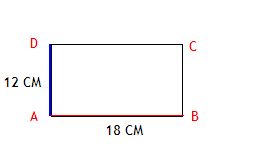
Задача 5
В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?
Ответ: Периметр прямоугольника равен 60 см.
Задача 6
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Ответ: Площадь прямоугольника 56 м².
Задача 7
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Ответ: Периметр витрины равен 32 м.
Задача 8
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Ответ: Площадь прямоугольника равна 630 см².
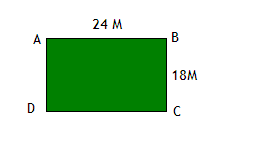
Задача 9
Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?
Ответ: 42 дерева.
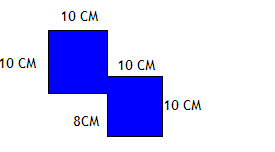
Задача 10
Каков периметр синей фигуры?
Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.
Задача 11
Два прямоугольных участка имеют одинаковую площадь. Длина первого – 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Ответ: Длина второго участка 40 м.
Задача 12
Найди периметр квадрата со стороной 8 см.
Ответ: Периметр квадрата 32 см.
Задача 13
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см) -находим периметр квадрата
3 + 3 = 6 (см) -сумма ширины прямоугольника
24 — 6 = 18 (см)- сумма двух длин прямоугольника
18 : 2 = 9 (см)
Ответ: Длина прямоугольника 9 см.
Задача 14
Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.
Решение:
120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)
Ответ: Периметр бассейна 46 метров
Задача 15
Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.
Решение:
8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)
Ответ: Периметр прямоугольника 16 см.
Задача 16
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?
Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)
Ответ: Ученик ошибся на 3 см²
Задача 17
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
Решение:
4·2=8 (дм) -длина окна
8·4=32 (дм²)
Ответ: Площадь окна 32 дм²
Задача 18
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Ответ: Ширина другого участка 24 м.
Задача 19
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Ответ: Площадь квадрата больше на 4 см.
Задача 20
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.
Задача 21
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 22
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36
Ответ: Незабудками засажено 36 м².
Задача 23
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Решение:
1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18
Ответ: Площадь прямоугольника 18 м².
Задача 24
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см
Ответ: Периметр стола 280 см.
Задача 25
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75
Ответ: Площадь прямоугольника 75 см².
Задача 26
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)
Ответ: Периметр квадрата равен 28 дм.
Задача 27
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32
Ответ: Площадь окна равна 32 м².
Задача 28
Длина участка земли 54 м. ширина – 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152
Ответ: Капустой засадили 1152 м².
Задача 29
Найди периметр квадрата со стороной 16 см.
Ответ: Периметр квадрата 64 см.
Задача 30
Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.
Решение:
P = (a + b) · 2 — периметр прямоугольника
или
(a + b) · 2 = P,
где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.
Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 – 14
2а = 26
а = 26 : 2
а = 13
Ответ: Длина прямоугольника 13 см.
Задача 31
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Ответ: Ширина прямоугольника 5 см.
Задача 32
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)
Ответ: Площадь квадрата 36 см².
Задача 33
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Ответ: Площадь прямоугольника 56 см².
Задача 34
Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?
Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)
Ответ: Периметр прямоугольника 28 см.
Задача 35
Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)
Ответ: Площадь всех граней куба равна 24 см².
Задача 36
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Ответ: Площадь получившейся фигуры равна 44.
Задача 37
Площадь одной клетки равна 1см.
- Найдите площадь фигуры, изображённой на рисунке A.
- Найдите площадь фигуры, изображённой на рисунке B.
- Найдите площадь фигуры, изображённой на рисунке C.
- Найдите площадь фигуры, изображённой на рисунке D.
- Найдите площадь фигуры, изображённой на рисунке E.
Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².
Задача 38
Найдите площади и периметры фигурок. Сделайте вывод.
Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²
Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.
Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.
Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.
Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача 39
Квадрат в данной фигуре имеет периметр 24 см. Синий треугольник – периметр 15 см. Каков периметр красной фигуры?
Ответ: Периметр красной фигуры равен 27 см.
Задача 40
Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?
Ответ: Периметр равен 36 см.
Задача 41
Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?
Ответ: Длина прямоугольника равна 12 см. а ширина – 6 см.
Задача 42
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.
Ответ: Периметр прямоугольника равен 24 см.
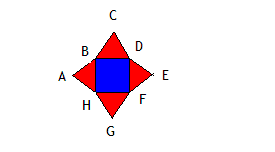
Задача 43
Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?
Ответ: Расстояние пройденное улиткой будет равно 28 см.
Задача 44
В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?
Ответ: 2400 плиток.
Задача 45
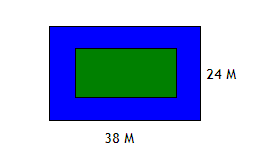
Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?
Ответ: Периметр зеленой зоны равен 100 метров.






 Применив формулы площади треугольника , квадрата и прямоугольника легко решим поставленную задачу
Применив формулы площади треугольника , квадрата и прямоугольника легко решим поставленную задачу