7 класс. Графики. Решение текстовых задач с помощью графика.
Рассмотрим следующий пример.
1. Ученики 7-«О» класса отправились пешком из города к озеру в 9 часов утра. Имеется траектория движения учащихся. Можно ли по графику движения определить:
а) сколько времени ученики были в пути?
б) с какой скоростью они двигались в 13 часов дня?
в) когда скорость ребят была большей
в 10 часов или в 12 часов?


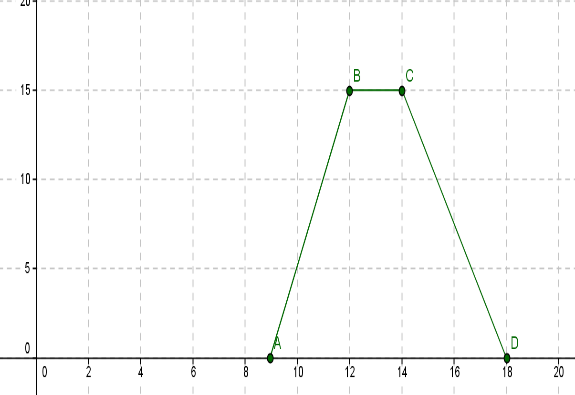
Рис. 1.
С помощью графика можно ответить на все эти вопросы. По оси ОХ отмечаем время, а по оси ОУ – расстояние.
а) ученики были в пути с 9-12 ч и с 14-18 ч; итого: (12-9)+(18-14)=3+4=7.
б) ученики в 13 ч шли со скоростью 0, т.е. они находились у озера и их маршрут не менялся. На графике этот маршрут ВС, этот отрезок параллелен оси ОУ.
в) определим в какой момент времени скорость ребят была наибольшей., где v– скорость в км/ч, S- расстояние в км, а t- время в часах. = 5 км/ч т.к. t =10-9=1ч, S=5 км; в 12 ч: = 5 км/ч т.к. t=12-9=3ч, S=15 км и ; или в 11ч S=10 км, а в 12 ч S=15 км, найдем их разности и вычислим скорость, с которой шли ребята. Следовательно скорость, с которой шли ученики и в 10ч и в 12ч, была одинаковой.
Используя траектории, можно решать много задач на движение.
Задача 2. Из пунктов А и В навстречу друг другу с постоянными скоростями вышли 2 путника. Первый вышел из А в 7 часов и пришёл в В в 13 часов. Второй путник вышел из В в 7часов и пришёл в А в 19 часов. В какое время путники встретились?
Решение. 1) Построим траектории движения путников. Расстояние от А до В неизвестно, поэтому на оси расстояний отложим любой отрезок, например, 6 см (рис.2). По оси времени возьмём масштаб: 1 см – 1час. 2) Соединив отрезком прямой точки начала и конца пути каждого путника, получим траектории их движения. Точка пересечения этих траекторий соответствует моменту встречи. 3) Время встречи – 11 часов.
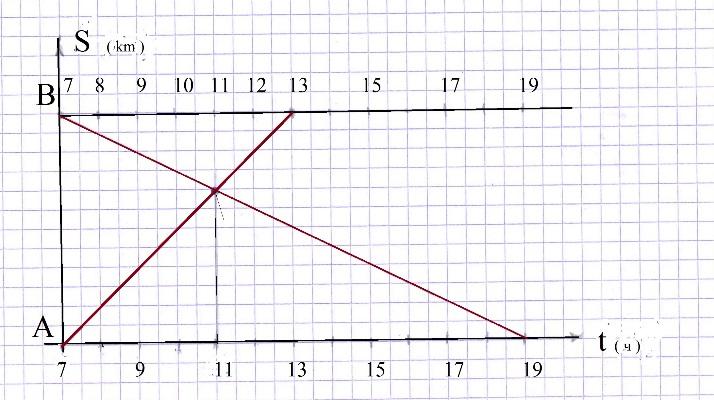
Рис.2
Задача 3. Алдар Косе приехал в 8 часов утра на поезде в Астану и пошел с вокзала в аул к своему другу, живущему недалеко от города, планируя прийти туда в 17 часов. В 9 часов из этого аула вышел Айдар в город Астану. Успеет ли Айдар на поезд, отходящий из Астаны в 20 часов, если встреча Алдара Косе и Айдара произошла в 13 часов?

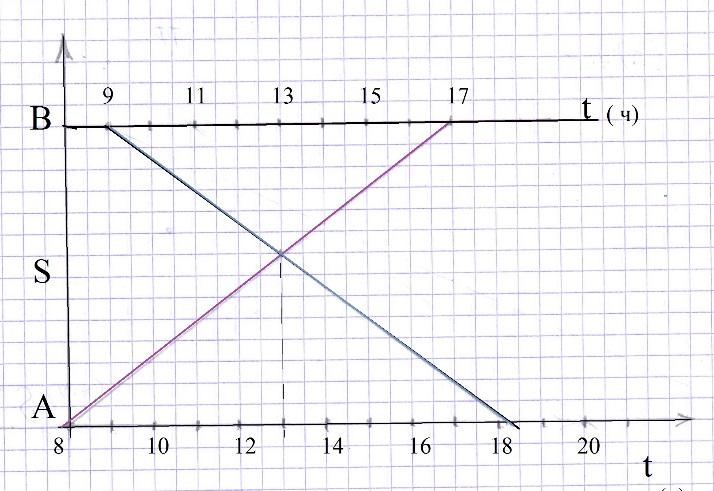
Встреча произошла в 13 ч, Айдар прибывает в город после 18 часов, следовательно он успевает на поезд.
Рис. 3
Задачи для самостоятельного решения. Решите задачи с помощью построения графиков.
№ 1. Из аула в сторону озера вышел Алдар Косе. Первые 2 часа он шёл со скоростью 4 км/ч, затем один час со скоростью 2 км/ч и оставшиеся 3 часа – со скоростью 6 км/ч. Найти расстояние между аулом и озером. На каком расстоянии от аула был Айдар Косе через 6 часов?

№ 2. Малыш выехал из города Астаны на автомашине, а навстречу ему летит Карлсон из Караганды. Расстояние между городами 300 км. На каком расстоянии от Астаны и через какое время произойдет их встреча, если скорость автомашины 60 км/ч, а Карлсона 15 км/ч.
№ 3. Из аула в направлении гор вышла Жалмауз Кемпир со скоростью 5 км/ч. Спустя 3 часа вслед за ней выехал джигит на коне со скоростью 10 км/ч. Через какое время джигит догонит старуху?


№ 4. Из пункта А в пункт В выехал велосипедист со скоростью 10 км/ч. Одновременно с ним из пункта В в пункт А вышел пешеход со скоростью 5 км/ч. Через какое время произойдет их встреча, если расстояние от А до В составляет 75 км/ч?
№ 5. Бригада каменщиков может справиться с определенной работой за 8 недель. Через 3 недели после начала работы ей стала помогать другая бригада, которая может справиться с этой работой за 12 недель. За какое время бригады закончат работу?
№ 6. Из пунктов А и В навстречу друг другу вышли 2 путника. Первый вышел из пункта А в 8 часов и пришел в пункт В в 17 часов. Второй вышел из пункта В в 9 часов и пришел в А в 20 часов. Успели ли путники встретится до 13 часов?
№ 7. Из Астаны в Кокчетав навстречу друг другу выехали 2 поезда. Первый поезд выехал из Астаны в 7 часов и прибыл в Кокчетав в 15 часов. Второй выехал из Кокчетава в 9 часов и прибыл в Астану в 16 часов. Успеют ли машинисты поездов при встрече поприветствовать друг друга гудками до полудня?
№ 8. Два туриста из 7-го класса «О», Адай и Гани вышли из А в В навстречу друг другу. Адай вышел из В в 8 часов и пришел в А в 19 часов.Гани вышел из А в 10 часов. Успеет ли Гани до полуночи прийти в пункт В, если они встретились в 15 часов?
№ 9. Путешественник, находившийся в 100 м от домика лесника, продолжил движение со скоростью 4м/с вдоль дороги. На каком расстоянии он окажется через 15 с от домика?
№ 10. Из пункта А в пункт В выехал мотоциклист со скоростью 30 км/ч. Через 2 часа из пункта В навстречу мотоциклисту выехал автобус со скоростью 60 км/ч. На каком расстоянии от пункта А и через какое время после выезда автобуса произойдет встреча, если расстояние между А и В равно 150 км?
№ 11. Кот Леопольд выехал на велосипеде из пункта А в 8 часов и двигался со скоростью 10 км/ч в направлении пункта В. Нарисовать траекторию его движения до 18 часов. 

№ 12. Расстояние между пунктами А и В равно 100 км. В 8 ч. утра выехал велосипедист, двигаясь с постоянной скоростью, в 12 часов он находился на расстоянии 40 км от А. Постройте график движения велосипедиста.
№ 13. Из пунктов А и В навстречу друг другу с постоянными скоростями вышли 2 путника. Первый вышел из А в 7 часов и пришел в В 13 часов. Второй путник вышел из В в 7 ч и пришел в А 19 ч. В какое время путники встретились?
Выполнила работу учитель математики:
Сергазиева Кулара Пернебаевна
НИШ ХБН г. Шымкент
Математушка
- Наши выпускники
- Оставить заявку
- ЕГЭ
- Статьи
- Контакты
- Цены
- Заочное обучение
- Войти
Задачи ЕГЭ по математике
Задача № 1

Показать ответ
Показать решение
Задача № 2

Показать ответ
Показать решение
Задача № 3

Показать ответ
Показать решение
Задача № 4

Показать ответ
Показать решение
Задача № 5

Показать ответ
Показать решение
Задача № 6

Показать ответ
Показать решение
Задача № 7
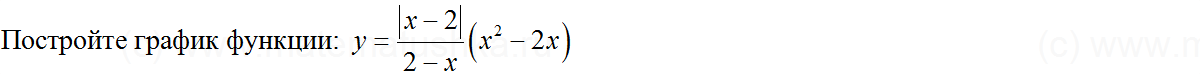
Показать ответ
Показать решение
Задача № 8

Показать ответ
Показать решение
Задача № 9

Показать ответ
Показать решение
Задача № 10

Показать ответ
Показать решение
Задача № 11

Показать ответ
Показать решение
Задача № 12

Показать ответ
Показать решение
Задача № 13
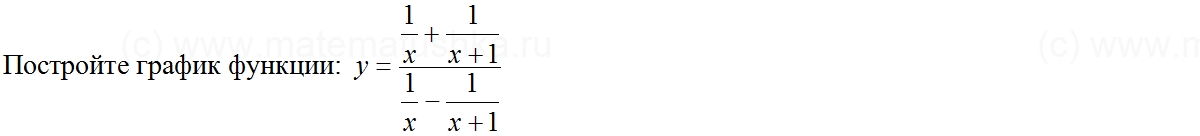
Показать ответ
Показать решение
Задача № 14
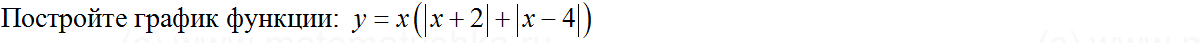
Показать ответ
Показать решение
Задача № 15

Показать ответ
Показать решение
Задача № 16
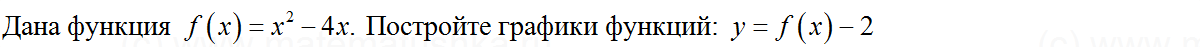
Показать ответ
Показать решение
Задача № 17
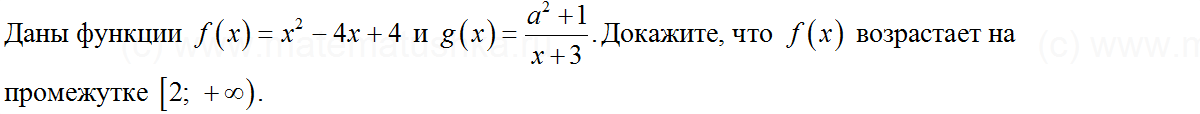
Показать ответ
Показать решение
Задача № 18
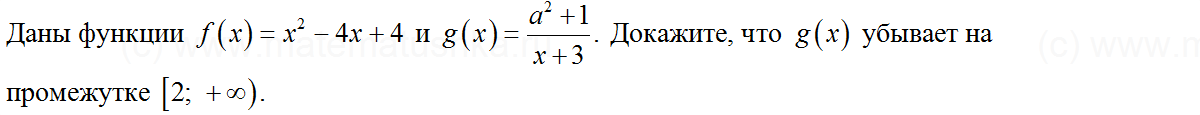
Показать ответ
Показать решение
Задача № 20
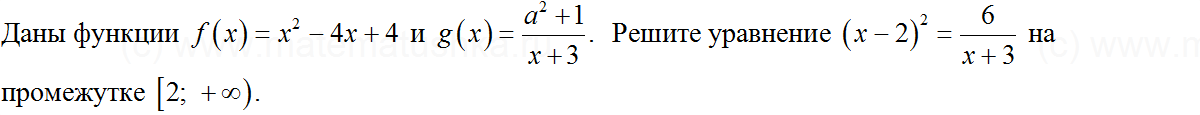
Показать ответ
Показать решение
Задача № 21

Показать ответ
Показать решение
Сначала идёт подробная теория по функциям, а потом примеры решения задач по функциям.

Функция
К оглавлению…
Функция 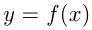 считается заданной, если каждому
считается заданной, если каждому 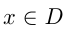 соответствует единственное по определенному правилу вычисленное
соответствует единственное по определенному правилу вычисленное 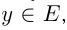 , где
, где 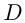 и
и 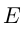 — числовые множества. Говорят, что
— числовые множества. Говорят, что 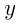 зависит от
зависит от 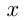 , и функция — это зависимость переменной
, и функция — это зависимость переменной 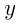 от переменной
от переменной 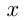 . Множество
. Множество 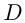 называется областью определения функции, множество
называется областью определения функции, множество 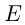 — областью значений функции. Переменную
— областью значений функции. Переменную 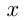 называют независимой переменной, а переменную
называют независимой переменной, а переменную 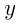 — зависимой. Переменная
— зависимой. Переменная 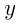 является функцией от
является функцией от 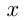 , что записывается
, что записывается 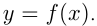 Для записи функций используются и другие буквы:
Для записи функций используются и другие буквы: 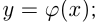
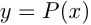 и т. п.
и т. п.
Переменная 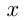 называется аргументом функции,
называется аргументом функции, 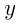 — ее значением.
— ее значением.
Функция может быть задана формулой, таблицей и другими способами. Если функция задана формулой, и область определения функции не указана, то считается, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.
Например, если 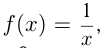 то область определения функции все
то область определения функции все 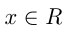 , кроме
, кроме 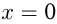 , т. е.
, т. е. 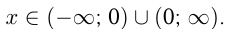
Если 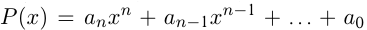 — многочлен, то
— многочлен, то 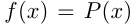 называется целой рациональной функцией; если
называется целой рациональной функцией; если 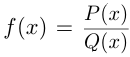 — это дробно-рациональная функция. Например,
— это дробно-рациональная функция. Например, 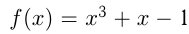 — целая рациональная функция 3-й степени;
— целая рациональная функция 3-й степени; 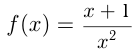 —— дробно-рациональная функция.
—— дробно-рациональная функция.
Введем понятие координатной плоскости. Проведем на плоскости через точку 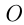 две взаимно перпендикулярных прямые
две взаимно перпендикулярных прямые 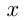 и
и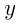 — оси координат. Ось
— оси координат. Ось 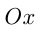 называется осью абсцисс, ось
называется осью абсцисс, ось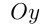 — осью ординат, точка
— осью ординат, точка 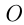 — началом координат. Этой точкой каждая из осей разбивается на две полуоси, одна из которых — положительная, другая — отрицательная.
— началом координат. Этой точкой каждая из осей разбивается на две полуоси, одна из которых — положительная, другая — отрицательная.
Каждой точке плоскости ставится в соответствие пара чисел 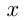 ;
; 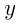 — координаты точки. Это записывается
— координаты точки. Это записывается 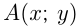 ,
, 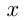 — абсцисса точки,
— абсцисса точки, 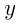 — ордината. Значение
— ордината. Значение 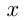 определяется как расстояние от начала координат до основания перпендикуляра, опущенного из точки
определяется как расстояние от начала координат до основания перпендикуляра, опущенного из точки 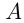 на ось
на ось 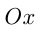 ; значение
; значение 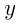 — расстояние от начала координат до основания перпендикуляра, опущенного из точки
— расстояние от начала координат до основания перпендикуляра, опущенного из точки 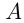 на
на 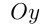 .Для определения значений
.Для определения значений 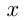 и
и 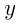 на осях выбираются единичные отрезки.
на осях выбираются единичные отрезки.
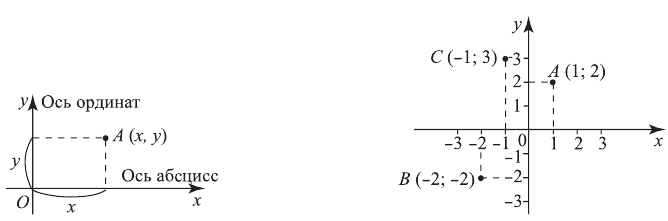
Оси координат разбивают плоскость на 4 четверти: I, II, III и IV. В I четверти обе координаты положительны, во II — координата 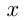 отрицательна,
отрицательна, 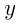 положительна, в III — обе координаты отрицательны, в IV —
положительна, в III — обе координаты отрицательны, в IV — 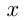 положительна,
положительна, 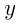 отрицательна. Приведенное описание — это прямоугольная декартова система координат. Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. График представляет собой линию на плоскости, непрерывную или разрывную.
отрицательна. Приведенное описание — это прямоугольная декартова система координат. Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. График представляет собой линию на плоскости, непрерывную или разрывную.
Линейная функция
К оглавлению…
Функция вида 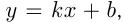 где
где 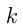 и
и 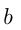 — числа, называется линейной функцией, ее область определения
— числа, называется линейной функцией, ее область определения 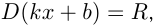 т.е.
т.е. 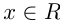 . Область значений линейной функции
. Область значений линейной функции 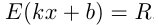 , т. е.
, т. е.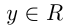 , если
, если 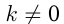 ; если
; если 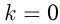 , то
, то 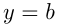 .
.
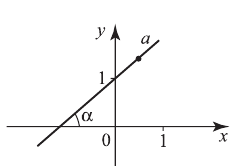
График линейной функции — прямая линия, угол наклона которой к оси 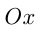 определяется числом
определяется числом 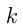 (угловой коэффициент). Если
(угловой коэффициент). Если 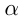 — угол наклона, то
— угол наклона, то 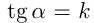 если
если 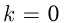 , то прямая параллельна
, то прямая параллельна 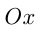 .
.
Например, график функции 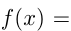
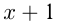 — прямая
— прямая 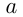 .
.
![]()
График линейной функции строится по двум точкам, т. к. две точки определяют прямую единственным образом.
Квадратичная функция
К оглавлению…
Функция 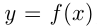 , где
, где 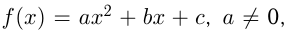 называется квадратичной. Область определения квадратичной функции
называется квадратичной. Область определения квадратичной функции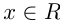 , или
, или 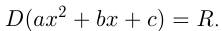 График квадратичной функции называется параболой, ее ветви направлены вверх, если
График квадратичной функции называется параболой, ее ветви направлены вверх, если 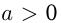 , и вниз, если
, и вниз, если 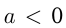 . И в том, и в другом случае парабола имеет вершину, координаты которой вычисляются по следующим формулам:
. И в том, и в другом случае парабола имеет вершину, координаты которой вычисляются по следующим формулам: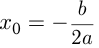 ;
;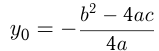 . Обычно при необходимости по формуле вычисляют
. Обычно при необходимости по формуле вычисляют 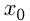 , a
, a 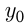 получают подстановкой
получают подстановкой 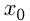 в формулу
в формулу 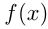 , т. е.
, т. е. 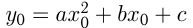 . Парабола имеет вертикальную ось симметрии, проходящую через вершину. Построение параболы часто сводится к нахождению точек пересечения графика с
. Парабола имеет вертикальную ось симметрии, проходящую через вершину. Построение параболы часто сводится к нахождению точек пересечения графика с 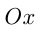 т.е. корней уравнения
т.е. корней уравнения 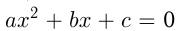 , если они существуют, и координат вершины. Если корней нет, то находят еще несколько точек.
, если они существуют, и координат вершины. Если корней нет, то находят еще несколько точек.
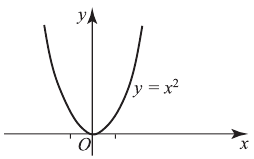
Например, график функции 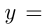
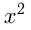 имеет вершину в т.
имеет вершину в т. 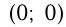 , т.к.
, т.к. 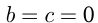 и проходит через точки
и проходит через точки 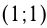 и
и 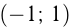 . Построим графики функций
. Построим графики функций 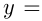
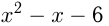 и
и 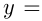
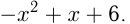
1) 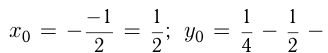
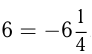
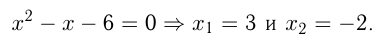
2)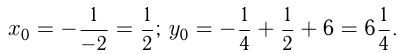 Корни уравнения те же
Корни уравнения те же
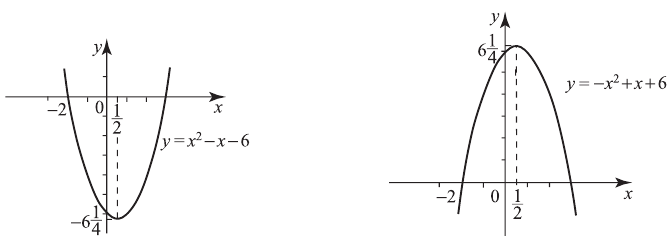
Из графиков видно, что множество значений квадратичной функции 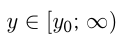 , если
, если 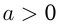 , и
, и 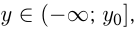 если
если 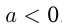
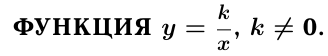
Эта функция называется обратной пропорциональностью. Область ее определения 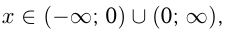 т. к.
т. к. 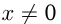 .
.
Множество значений 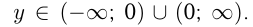 График этой функции называется гиперболой;
График этой функции называется гиперболой;
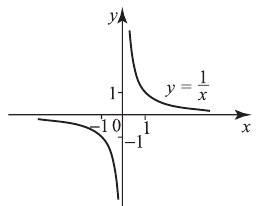
он не имеет точек пересечения с осями 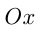 и
и 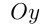 и имеет эти оси в качестве асимптот, т. е. прямых, к которым кривая бесконечно приближается.
и имеет эти оси в качестве асимптот, т. е. прямых, к которым кривая бесконечно приближается.
График расположен в I и III четвертях, если 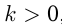 и во II и IV четвертях, если
и во II и IV четвертях, если 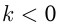 .
.
Например, построим график 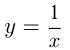 . Он проходит через точки
. Он проходит через точки 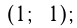
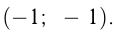 График симметричен относительно начала координат.
График симметричен относительно начала координат.
Степенная функция с целым показателем
К оглавлению…
Степенной функцией с целым показателем называется функция вида 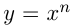 , где
, где 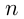 — целое число. Отметим, что частными случаями такой степенной функции являются линейная функция
— целое число. Отметим, что частными случаями такой степенной функции являются линейная функция 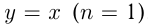 , квадратичная функция
, квадратичная функция 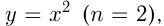 обратная пропорциональность
обратная пропорциональность 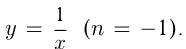 Графики этих функций представлены ниже.
Графики этих функций представлены ниже.
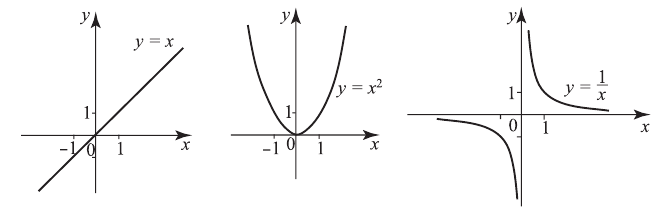
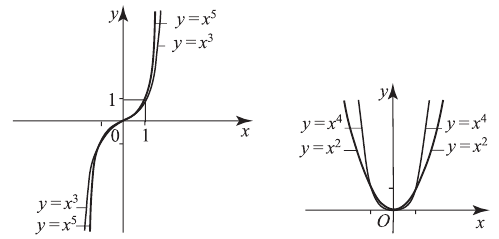
1) Показатель степени 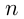 — нечетное положительное число
— нечетное положительное число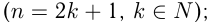
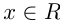 ,
, 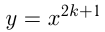 например,
например, 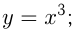
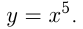
График 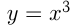 называется кубической параболой.
называется кубической параболой.
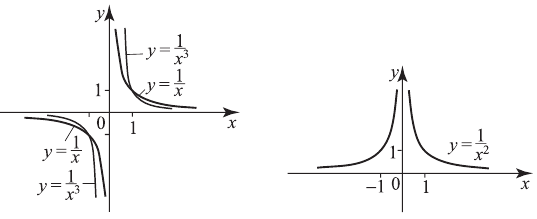
2) 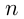 — четное положительное число
— четное положительное число 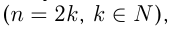
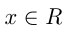 .
.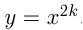 , например,
, например, 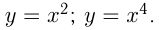
3) 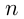 — нечетное отрицательное число
— нечетное отрицательное число 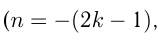
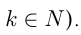
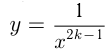 например,
например, 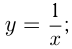
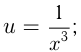
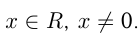
4) 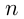 — четное отрицательное число
— четное отрицательное число 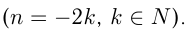
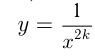 например ,
например , 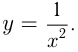
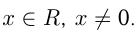
Показательная функция
К оглавлению…
Функция 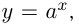 где
где 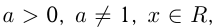 называется показательной. При этом
называется показательной. При этом 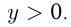 Функция имеет различные графики при
Функция имеет различные графики при 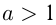 и
и 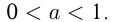
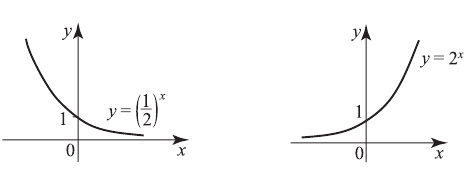
1) 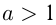 ; если
; если 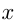 возрастает, то
возрастает, то 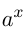 также возрастает, например,
также возрастает, например, 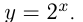
2) 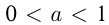 ; если
; если 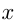 возрастает, то
возрастает, то 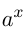 убывает, например,
убывает, например, 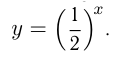
Логарифмическая функция
К оглавлению…
Функция 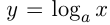 , где
, где 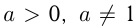 и
и 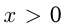 , называется логарифмической. Так же, как и в случае показательной функции, существуют 2 графика логарифмической функции: при
, называется логарифмической. Так же, как и в случае показательной функции, существуют 2 графика логарифмической функции: при 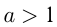 и при
и при 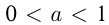 . Например,
. Например, 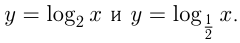
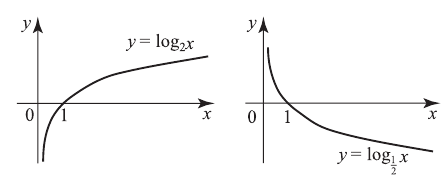
Тригонометрические функции
К оглавлению…
Тригонометрическими функциями называются функции 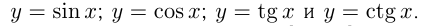
1) 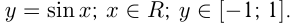 График — синусоида, период
График — синусоида, период 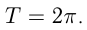
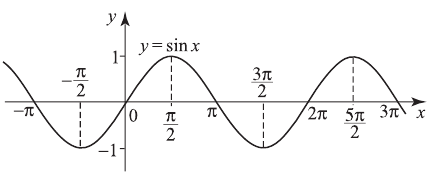
2) 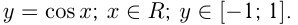 График — синусоида, период
График — синусоида, период 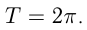
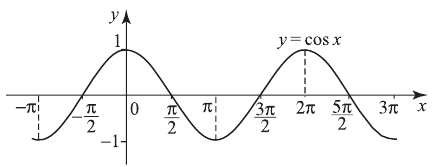
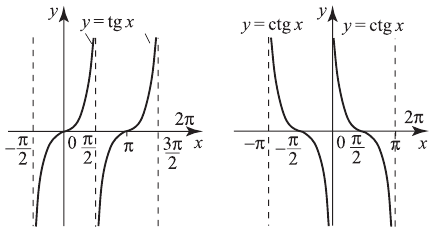
3) 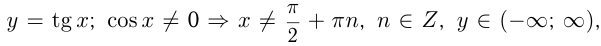 период
период 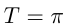
4) 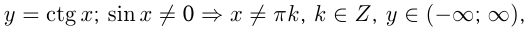 период
период 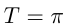 .
.
Функции: 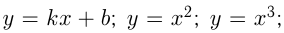
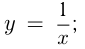
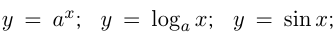
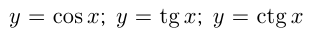 относятся к элементарным. К ним присоединяют еще
относятся к элементарным. К ним присоединяют еще 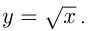
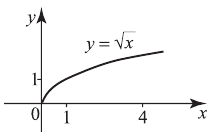
График функции 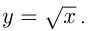
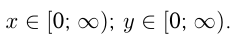
Преобразование графиков функции
К оглавлению…
Одним из способов построения графиков является способ получения из графика функции 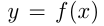 графиков функций следующего вида:
графиков функций следующего вида:
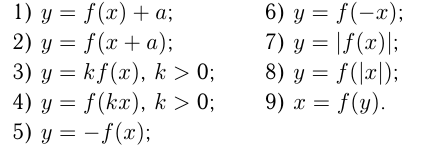
Построение нового графика происходит на основе графика элементарной функции путем его преобразования.
В 1-м случае график 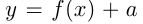 получается из графика
получается из графика 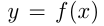 путем сдвига этого графика как единого целого вдоль оси ординат на
путем сдвига этого графика как единого целого вдоль оси ординат на 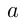 единиц. Например, построим график функции
единиц. Например, построим график функции 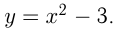 Сначала построим график
Сначала построим график 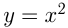 и затем сдвинем его на 3 единицы вниз.
и затем сдвинем его на 3 единицы вниз.
Во 2-м случае график 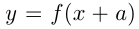 получается из графика
получается из графика 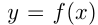 путем сдвига вдоль оси абсцисс на
путем сдвига вдоль оси абсцисс на 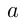 единиц влево, если
единиц влево, если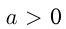 , и вправо, если
, и вправо, если 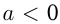 . Например, построим график
. Например, построим график 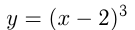
В 3-м случае для построения графика 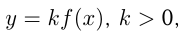 надо растянуть график
надо растянуть график 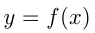 в
в 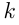 раз вдоль оси ординат при неиз —
раз вдоль оси ординат при неиз —
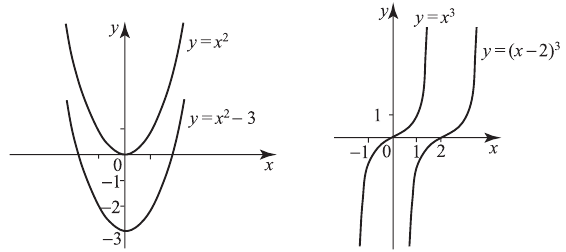
менной оси абсцисс. Если 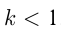 , то растяжение часто называют сжатием. Например, построим графики:
, то растяжение часто называют сжатием. Например, построим графики: 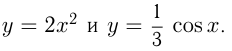
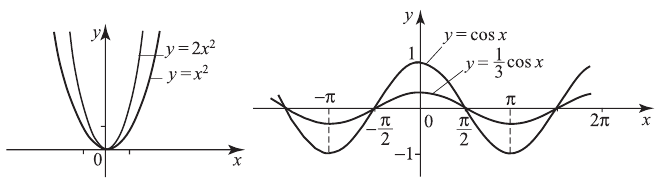
В 4-м случае для построения графика 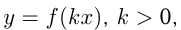 надо растянуть или сжать вдоль оси абсцисс при неизменной оси ординат график
надо растянуть или сжать вдоль оси абсцисс при неизменной оси ординат график 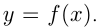 Если
Если 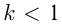 , происходит растяжение, если
, происходит растяжение, если 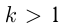 — сжатие. Например, построим графики
— сжатие. Например, построим графики 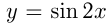 и
и 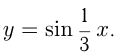
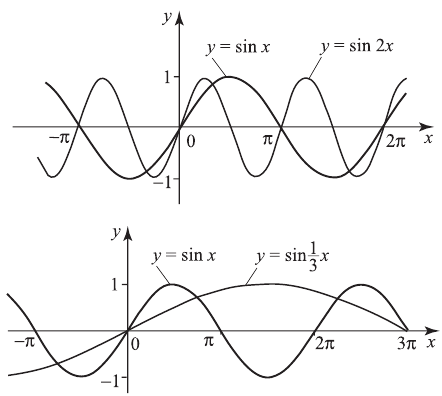
В 5-м случае для получения графика 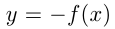 из графика
из графика 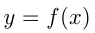 нужно отразить его симметрично относительно оси абсцисс. Например, построим график функции
нужно отразить его симметрично относительно оси абсцисс. Например, построим график функции 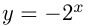 .
.
В 6-м случае для получения графика 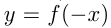 из графика
из графика 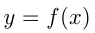 нужно отразить его симметрично относительно оси ординат. Например, построим график функции
нужно отразить его симметрично относительно оси ординат. Например, построим график функции 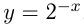 .
.
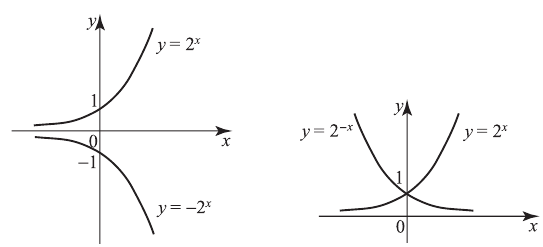
В 7-м случае для получения графика 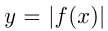 из графика
из графика 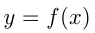 нужно отразить симметрично относительно оси абсцисс часть графика, лежащую ниже этой оси. Например, построим график
нужно отразить симметрично относительно оси абсцисс часть графика, лежащую ниже этой оси. Например, построим график 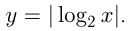
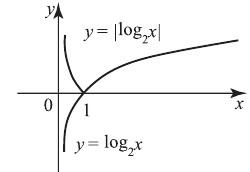
В 8-м случае для получения графика 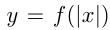 из графика
из графика 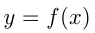 нужно заменить часть графика, лежащую слева от оси ординат, графиком, симметричным части графика, лежащей справа от оси ординат. Например, построим график
нужно заменить часть графика, лежащую слева от оси ординат, графиком, симметричным части графика, лежащей справа от оси ординат. Например, построим график 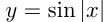
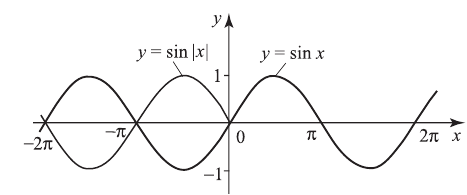
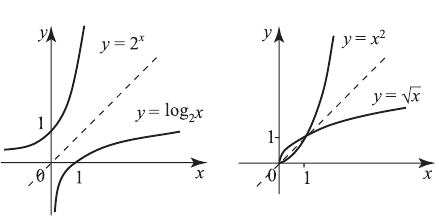
9-й случай — это получение обратной функции. Такими взаимно обратными функциями являются 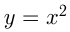 и
и 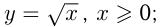
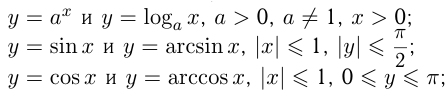
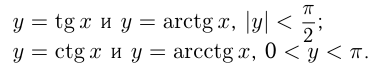
Для построения обратной функции нужно функцию 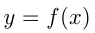 симметрично отразить относительно биссектрисы прямого угла I четверти координатной плоскости. Например, графики
симметрично отразить относительно биссектрисы прямого угла I четверти координатной плоскости. Например, графики 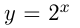 и
и 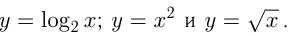
Свойства функций
К оглавлению…
1) Четность. Функция 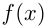 называется четной, если на всей области определения
называется четной, если на всей области определения 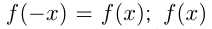 называется нечетной, если на всей области определения
называется нечетной, если на всей области определения 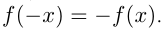 Например,
Например,
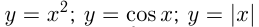 — четные функции.
— четные функции.
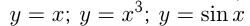 — нечетные функции.
— нечетные функции.
График четной функции симметричен относительно оси ординат; график нечетной функции симметричен относительно начала координат.
2) Периодичность. Функция 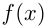 называется периодической, если на всей области определения
называется периодической, если на всей области определения 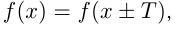 где
где 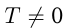 — период.
— период.
Например, функции 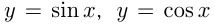 — периодические с периодом
— периодические с периодом 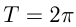 ; функции
; функции 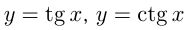 — периодичес-кие с периодом
— периодичес-кие с периодом 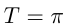 . Период функции
. Период функции 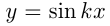 равен
равен 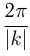 , аналогично для
, аналогично для 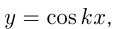
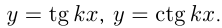
3) Возрастание. Функция 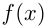 возрастает на некотором интервале из области определения, если для любых
возрастает на некотором интервале из области определения, если для любых 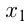 и
и 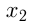 из этого интервала таких, что
из этого интервала таких, что 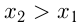 , выполняется
, выполняется 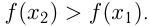
4) Убывание. Функция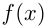 убывает на некотором интервале из области определения, если для любых
убывает на некотором интервале из области определения, если для любых 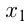 и
и 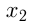 из этого интервала таких, что
из этого интервала таких, что 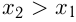 выполняется
выполняется 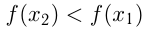 .
.
5) Экстремумы. Точка 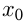 называется точкой минимума функции
называется точкой минимума функции 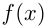 , если для всех
, если для всех 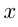 из некоторой окрестности
из некоторой окрестности 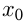 выполняется
выполняется 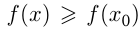 . Само значение
. Само значение 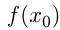 — минимум функции (min). Точка
— минимум функции (min). Точка 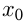 называется точкой максимума функции
называется точкой максимума функции 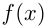 , если для всех
, если для всех 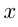 из некоторой окрестности
из некоторой окрестности 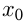 выполняется
выполняется 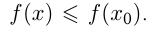 Само значение
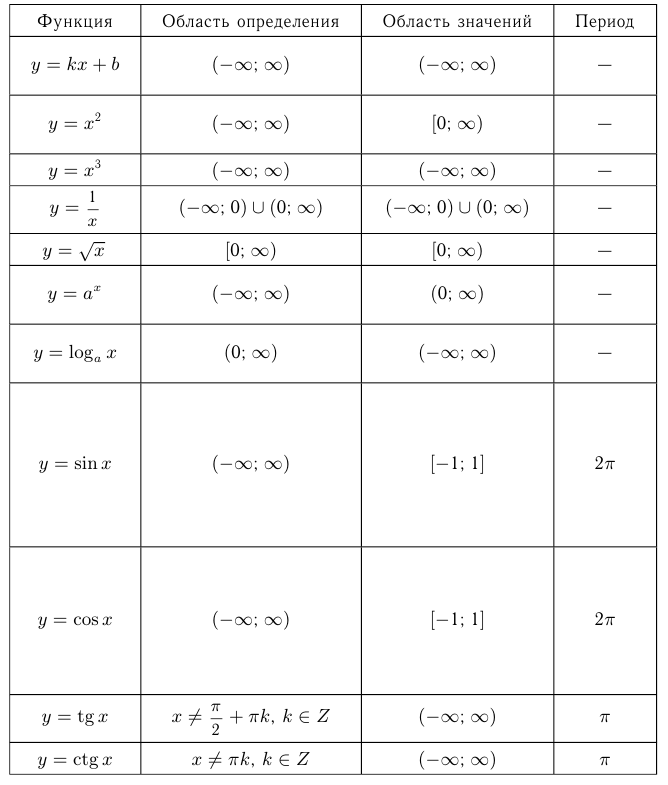
Само значение 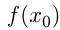 в этом случае называется максимумом функции (max). Выше приведена таблица свойств элементарных функций.
в этом случае называется максимумом функции (max). Выше приведена таблица свойств элементарных функций.

Производная функции
К оглавлению…
Допустим, областью определения функции 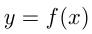 является интервал
является интервал 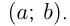 Возьмем точку
Возьмем точку 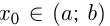 и точку
и точку 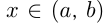 в окрестности точки
в окрестности точки 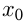 ; тогда разность
; тогда разность 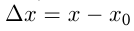 называется приращением аргумента в точке
называется приращением аргумента в точке 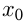 .
.
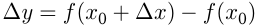 — приращение функции в точке
— приращение функции в точке 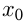 .
.
Число 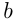 называется пределом функции
называется пределом функции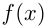 в точке
в точке 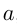 , если для любого
, если для любого 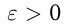 при всех
при всех 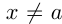 , достаточно близких к
, достаточно близких к 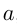 , выполняется неравенство
, выполняется неравенство  . Обозначается
. Обозначается 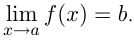
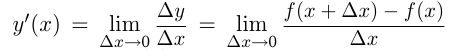
производная функции 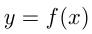 равна пределу отношения приращения функции к приращению аргумента, если такой предел существует и конечен. Производная функции
равна пределу отношения приращения функции к приращению аргумента, если такой предел существует и конечен. Производная функции 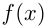 также обозначается
также обозначается 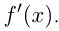
Производные элементарных функций
К оглавлению…
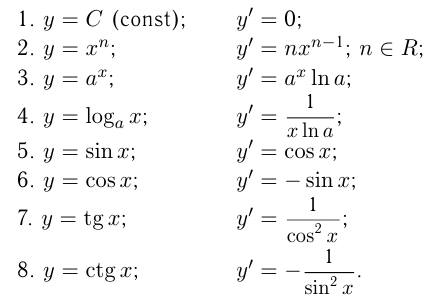
Правила вычисления производных
К оглавлению…
Если для функций 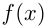 и
и 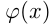 существуют производные
существуют производные 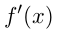 и
и 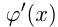 , то:
, то:
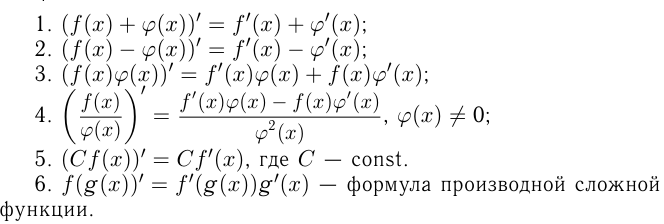
Если функция имеет производную на некотором интервале, то она называется дифференцируемой на этом интервале.
Если в каждой точке интервала 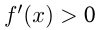 , то
, то 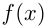 возрастает на этом интервале.
возрастает на этом интервале.
Если в каждой точке интервала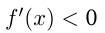 , то на этом интервале
, то на этом интервале 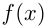 убывает.
убывает.
Если на интервале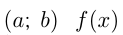 имеет производную
имеет производную 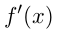 и
и 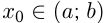 и если
и если 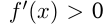 при
при 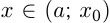 и
и 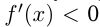 при
при 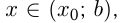 то точка
то точка 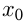 является точкой максимума функции
является точкой максимума функции 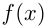 ; при этом
; при этом 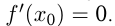
И наоборот, если при тех же условиях 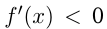 при
при 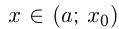 и
и 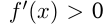 при
при 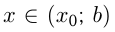 , то точка
, то точка 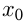 — точка минимума функции
— точка минимума функции 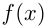 , при этом
, при этом 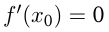 .
.
Уравнение касательной к графику функции
К оглавлению…
Касательная к графику 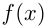 в точке
в точке 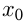 , если
, если 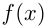 дифференци-руема в точке
дифференци-руема в точке 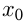 , — это прямая, проходящая через точку
, — это прямая, проходящая через точку 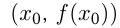 и имеющая угловой коэффициент
и имеющая угловой коэффициент 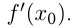 Уравнение касательной:
Уравнение касательной: 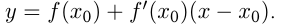
Например, напишем уравнение касательной к функции 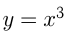 в точке
в точке 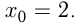
![]()
Уравнение касательной: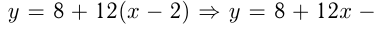
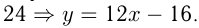
Исследование функций и построение графиков
К оглавлению…
Исследование функции, т.е. наиболее полное описание ее свойств, производится, как правило, для построения ее графика и состоит из нескольких пунктов:
- область определения функции;
- область значений функции;
- четность, нечетность функции;
- периодичность функции;
- определение нулей функции, т.е. значений
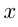 , в которых функция обращается нуль, и значения
, в которых функция обращается нуль, и значения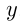 , которое принимает функция при
, которое принимает функция при 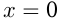 ;
; - интервалы возрастания и убывания функции;
- экстремумы функции;
- нахождение, если это необходимо, дополнительных точек для построения графика.
Иногда к перечисленным пунктам добавляют еще нахождение интервалов знакопостоянства функции.
Однако для построения графика не всегда бывает необходимо проводить исследование по полной схеме, достаточно тех пунктов, которые дают возможность построить график. Так, бывает трудно найти область значений функции и нули функции.
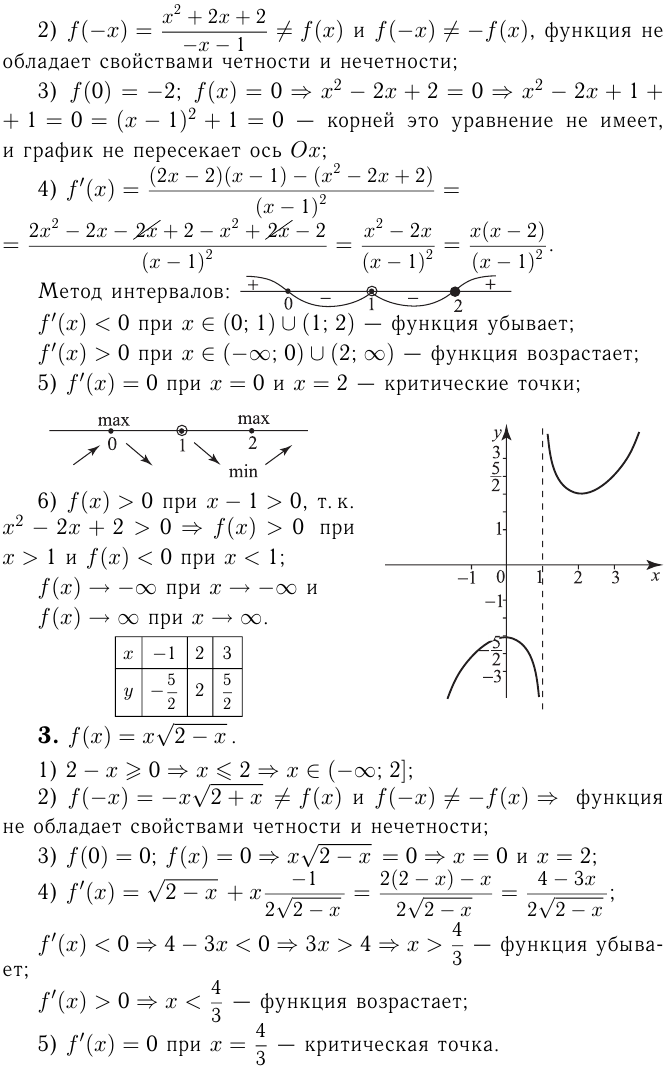
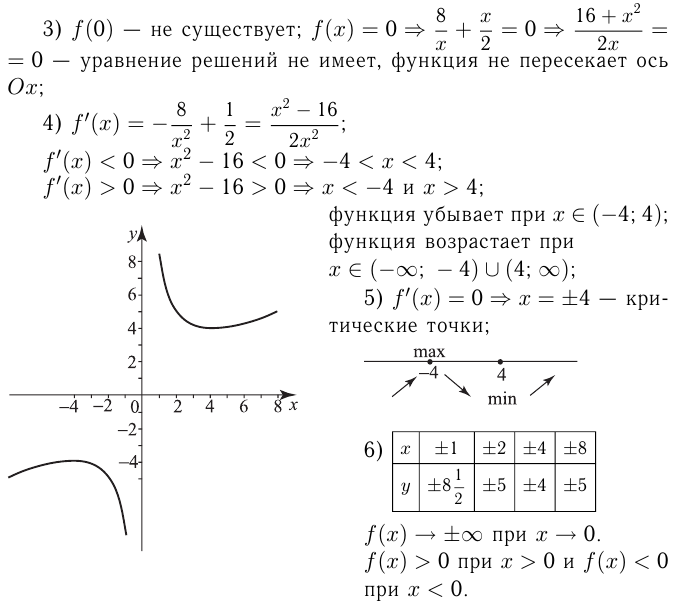
Пример. Исследовать функцию и построить ее график.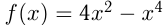 .
.
1.Область определения 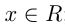 .
.
3.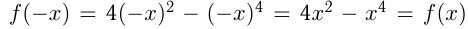 функция четная.
функция четная.
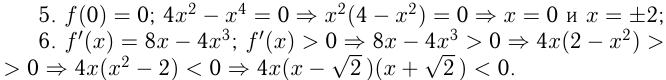
Метод интервалов:
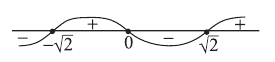
Функция возрастает на интервалах: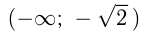 и
и 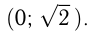
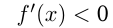 при
при 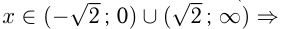 на этих интервалах функция убывает.
на этих интервалах функция убывает.
7.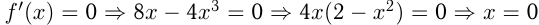 и
и 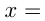
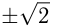 — эти значения
— эти значения 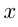 называют критическими точками.
называют критическими точками.
Только там, где 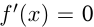 , возможны экстремумы функции. Экстремумы легко определить по схеме.
, возможны экстремумы функции. Экстремумы легко определить по схеме.
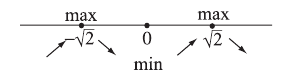
Стрелка, направленная вверх, означает возрастание функции, вниз — убывание.
Если в критической точке возрастание функции сменяется убыванием, то в этой точке — максимум, если наоборот — минимум.
8.Составим небольшую таблицу:

Строим график. Область значений функции, которую сразу определять было сложно, 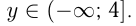
Наибольшее и наименьшее значения функции
К оглавлению…
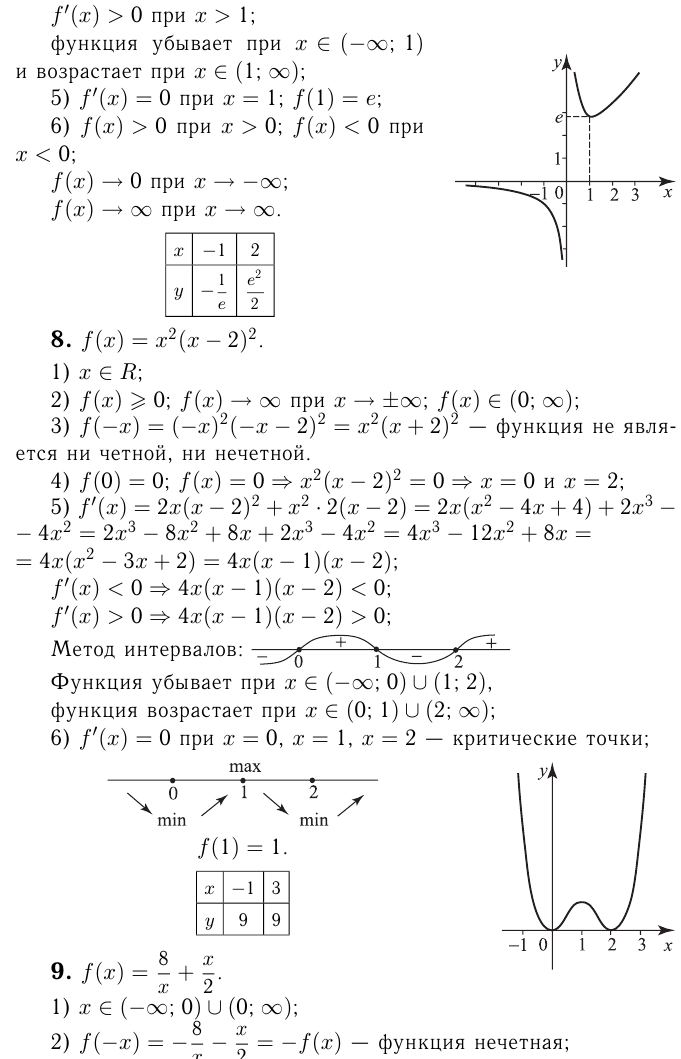
Решение многих практических задач часто сводится к нахождению наибольшего и наименьшего значений непрерывной на отрезке функции. Правило нахождения этих значений таково: чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
Например, найдем наименьшее и наибольшее значения функции 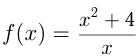 на отрезке
на отрезке 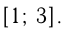
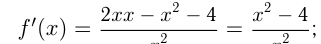
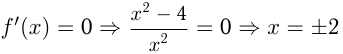 критические точки.
критические точки.
Составим таблицу: 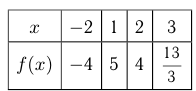
Итак, наименьшее значение 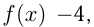 а наибольшее 5, часто это записывают так:
а наибольшее 5, часто это записывают так: 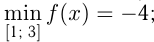
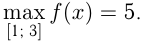
Первообразная и интеграл
К оглавлению…
Функция 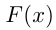 называется первообразной для функции
называется первообразной для функции 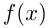 на некотором промежутке, если для всех
на некотором промежутке, если для всех 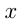 из этого промежутка
из этого промежутка
Например, функция 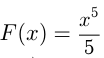 -первообразная для функции
-первообразная для функции 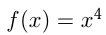 при
при 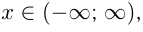 так как
так как
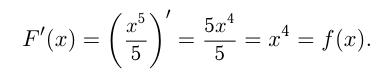
Любая первообразная для 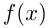 при
при 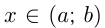 может быть записана как
может быть записана как 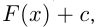 где
где 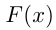 — одна из первообразных для
— одна из первообразных для 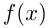 при
при 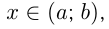 а
а 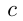 — произвольное число.
— произвольное число.
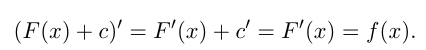
Нахождение первообразной для функции — действие, обратное нахождению производной. Исходя из этого, можно составить таблицу первообразных некоторых функций.
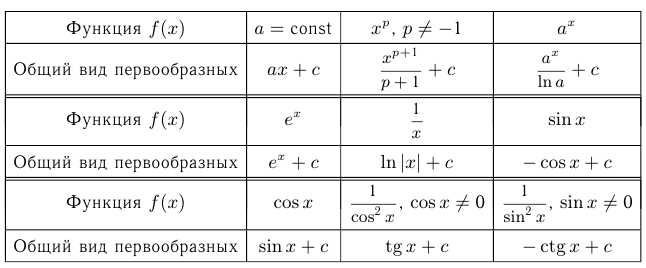
Три правила нахождения первообразных
К оглавлению…
- Если
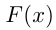 — первообразная для
— первообразная для 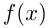 , a
, a 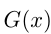 — первообразная для
— первообразная для 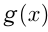 , то
, то 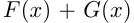 — первообразная для
— первообразная для 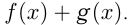
- Если
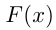 — первообразная для
— первообразная для 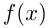 и
и 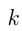 — число, то
— число, то 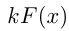 — первообразная для
— первообразная для 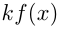 .
. - Если
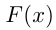 — первообразная для
— первообразная для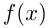 ,
, 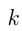 и
и 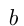 — числа и
— числа и 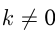 , то
, то 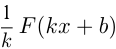 — первообразная для
— первообразная для 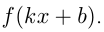
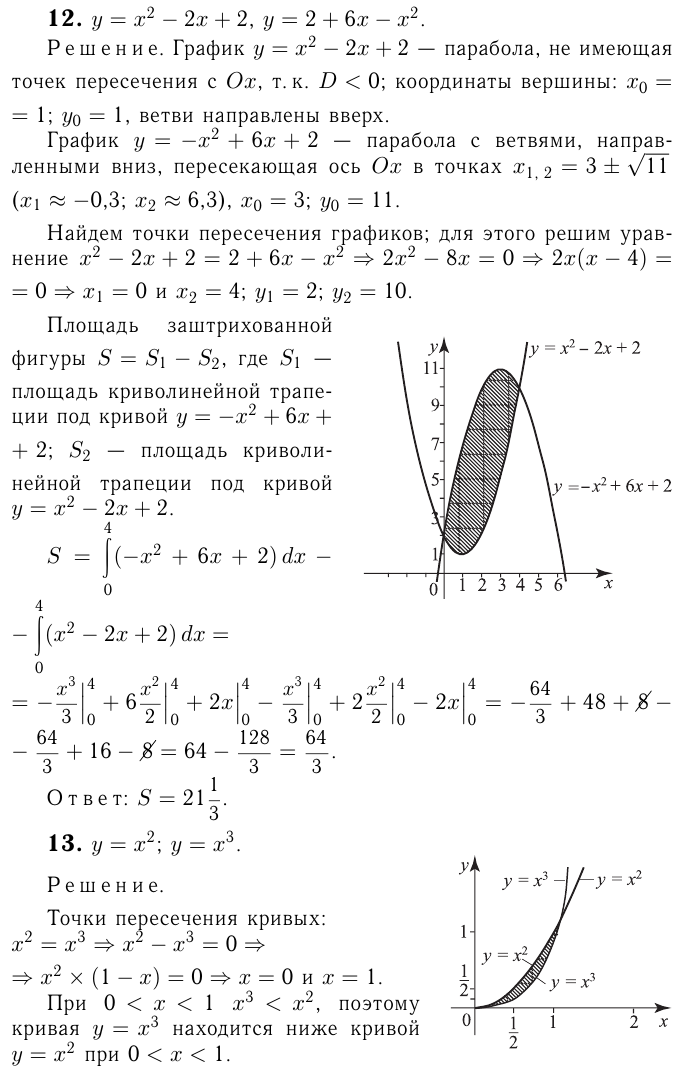
Например, найдем первообразные.
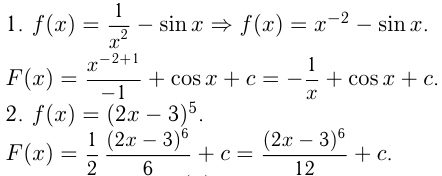
Пусть функция 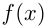 непрерывна на отрезке
непрерывна на отрезке 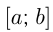 и не меняет знака на этом отрезке. Тогда фигуру, ограниченную графиком этой функции, отрезком
и не меняет знака на этом отрезке. Тогда фигуру, ограниченную графиком этой функции, отрезком 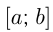 и прямыми
и прямыми 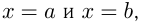 называют криволинейной трапецией.
называют криволинейной трапецией.
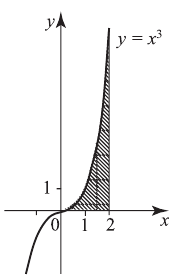
Например, 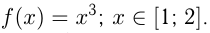
Заштрихованная фигура — криволинейная трапеция.
Для вычисления площади криволинейной трапеции применяется формула:
![]()
В нашем примере 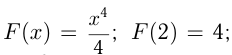
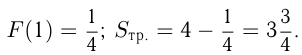
Площадь криволинейной трапеции может быть получена так же, как 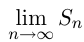 где
где 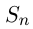 — сумма площадей
— сумма площадей 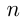 прямоугольников, на которые разбивается криволинейная трапеция. Основания прямоугольников
прямоугольников, на которые разбивается криволинейная трапеция. Основания прямоугольников 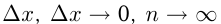 и
и 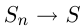 (площадь трапеции). Суммирование площадей называется интегрированием, а площадь трапеции выражается как интеграл, т.е.
(площадь трапеции). Суммирование площадей называется интегрированием, а площадь трапеции выражается как интеграл, т.е.
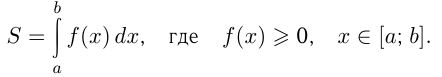
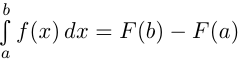 — формула Ньютона-Лейбница.
— формула Ньютона-Лейбница.
Для удобства используют запись:
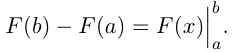
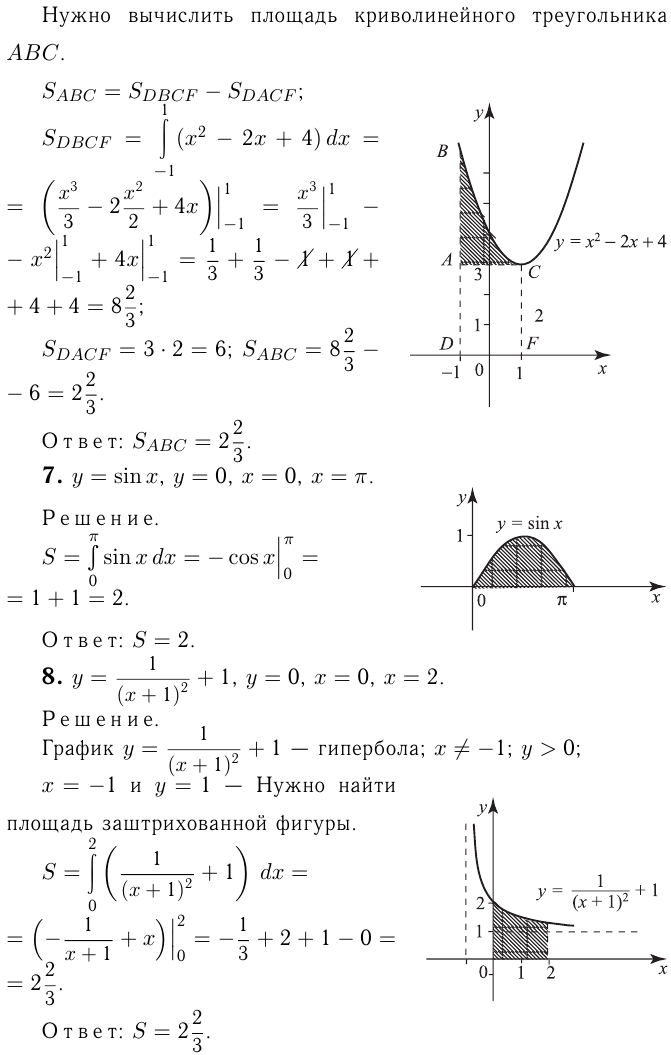
Например, 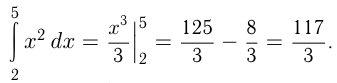
Вычислим площадь фигуры, ограниченной линиями: 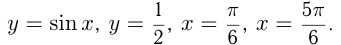
Сделаем чертеж.
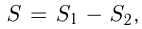 где
где 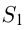 — площадь криволинейной трапеции,
— площадь криволинейной трапеции,
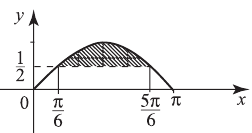
ограниченной синусоидой, осью 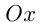 и прямыми
и прямыми 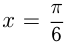 и
и 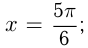
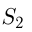 — площадь 6 6 прямоугольника, ограниченного прямыми
— площадь 6 6 прямоугольника, ограниченного прямыми 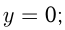
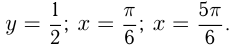
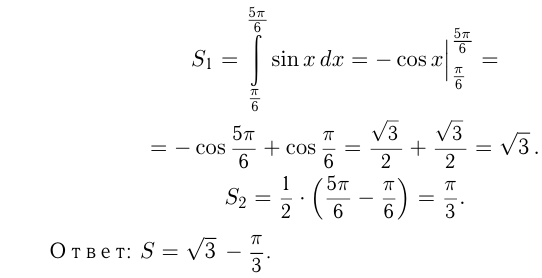
Решение задач на функции
К оглавлению…
Найти область определения функций
К оглавлению…



Найти область значений функции
К оглавлению…
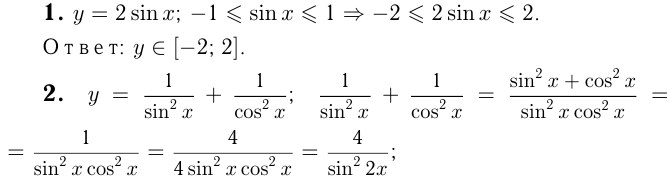
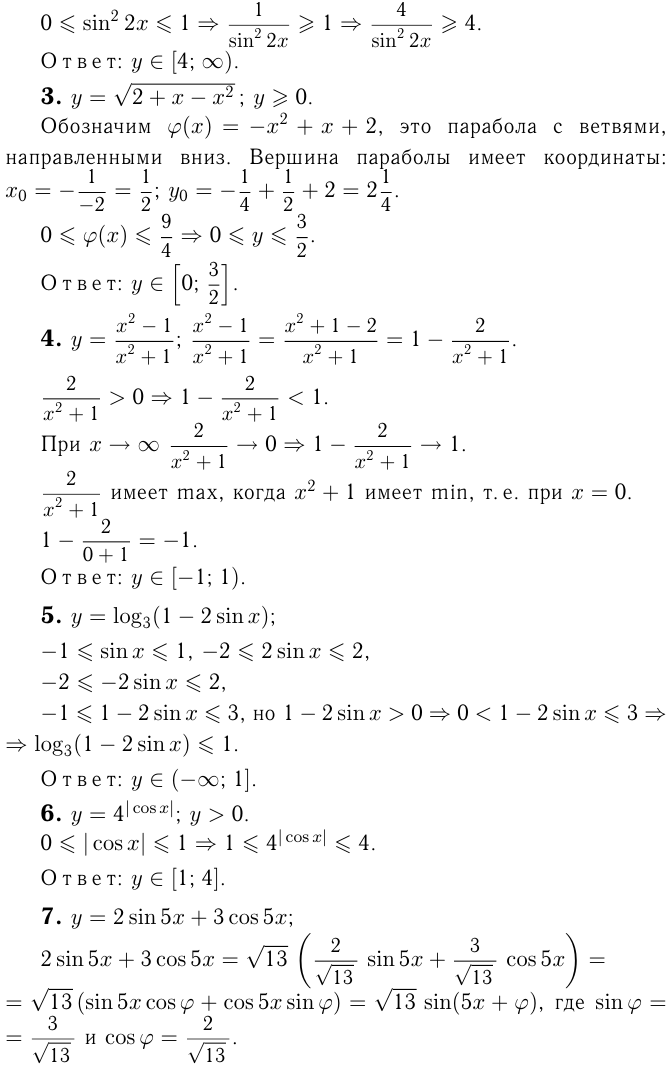

Построить график функций методом преобразования
К оглавлению…
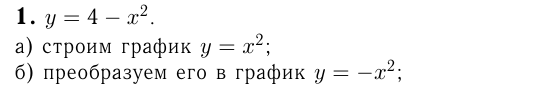
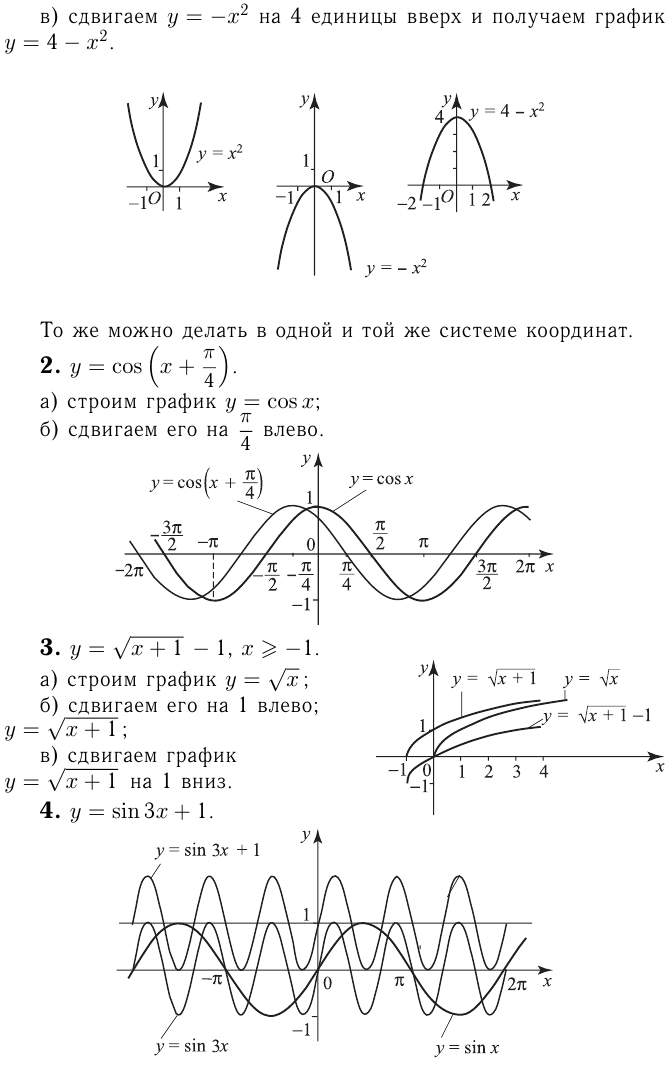
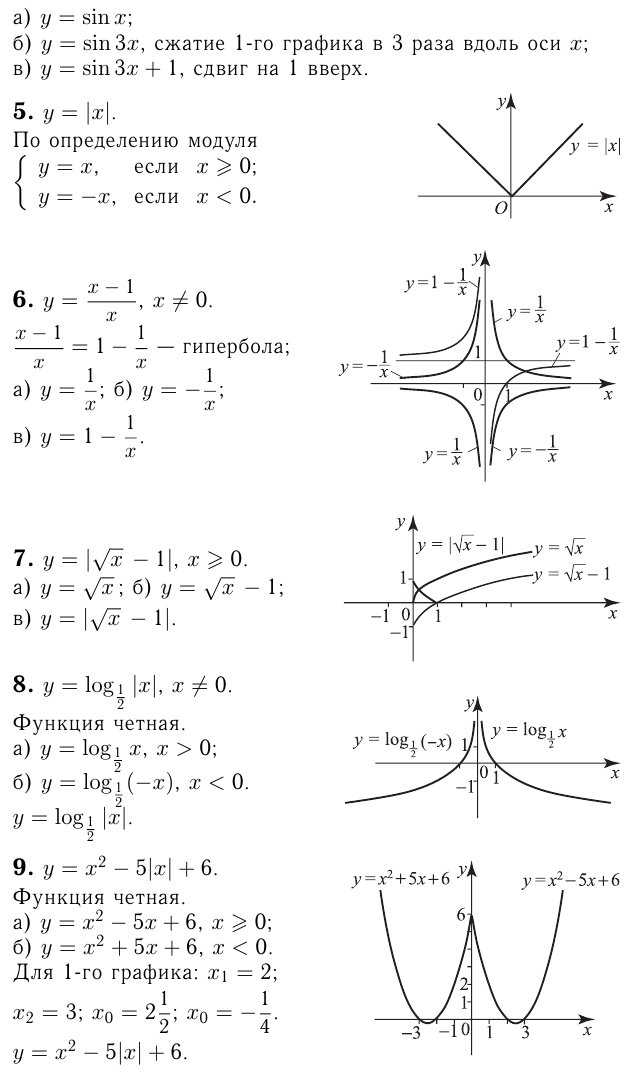
Какие из следующих функций являются чётными? нечётными? не являются ни чётными, ни нечётными?
К оглавлению…

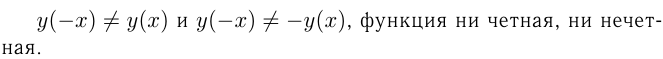
Определить период функций
К оглавлению…

Найти производные функций
К оглавлению…
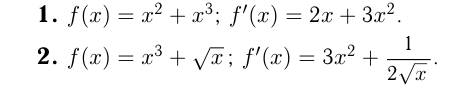

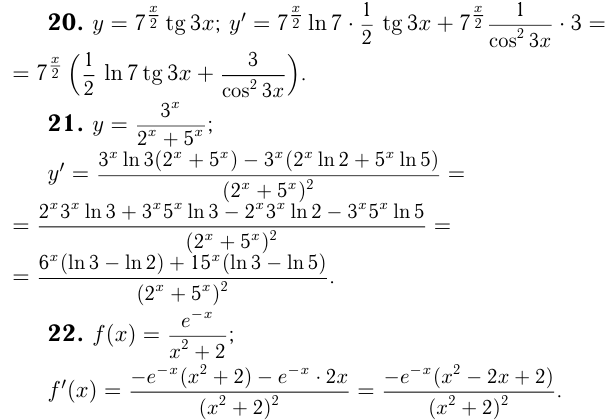
Касательная к графику функции
К оглавлению…
Задача №160
Написать уравнение касательной к графику функции в точке 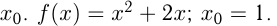
Решение, 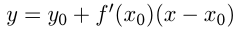 — уравнение касательной, где
— уравнение касательной, где 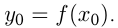
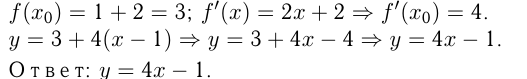
Задача №161
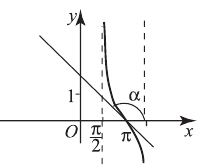
Найти тангенс ума наклона касательной, проходящей через точку 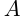 графика функции
графика функции 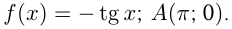
Решение:
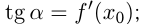
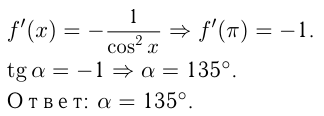
Задача №162
Написать уравнение касательной к графику функции 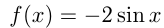 в точке
в точке 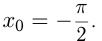
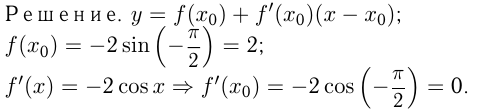
![]()
Задача №163
Найти точки графика функции 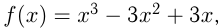 в которых касательная параллельна оси абсцисс.
в которых касательная параллельна оси абсцисс.
Решение:
Если прямая 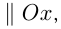 , то угол между ними равен
, то угол между ними равен 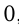 , т. е.
, т. е.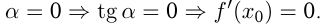
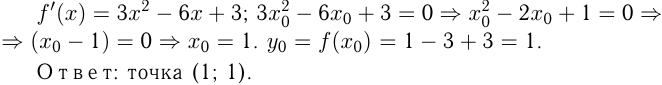
Задача №164
Под каким углом пересекается с осью 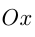 график функции
график функции 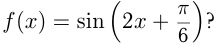
Решение:
Угол пересечения определяется углом между касательной к графику в точке пересечения и осью 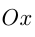 .
.
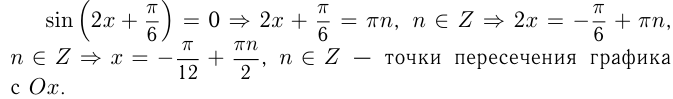
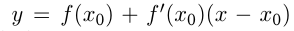 — уравнение касательной, где
— уравнение касательной, где 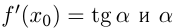 — угол наклона касательной к
— угол наклона касательной к 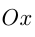 в точке
в точке 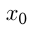 .
.
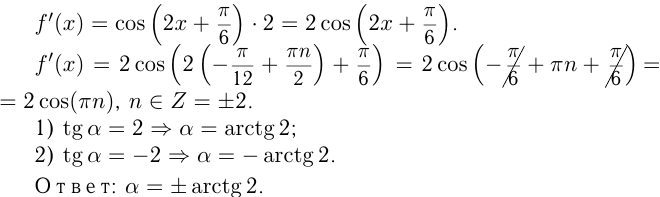
Задача №165
Под каким углом пересекается с осью 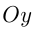 график функции
график функции 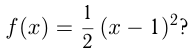
Решение. График пересекается с 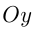 в точке
в точке 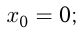
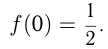
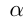 — угол наклона касательной в точке
— угол наклона касательной в точке 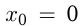 к
к 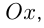
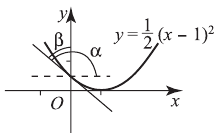
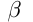 — угол наклона касательной в этой же точке к
— угол наклона касательной в этой же точке к 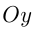 ;
;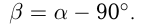
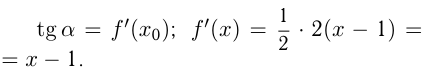
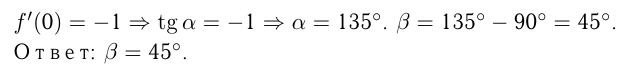
Задача №166
Найти все значения 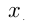 , при которых касательные к графикам функций
, при которых касательные к графикам функций 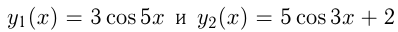 в точках с абсциссой
в точках с абсциссой 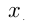 параллельны.
параллельны.
Решение:
Параллельность касательных означает равенство их угловых коэффициентов. Поэтому 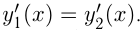
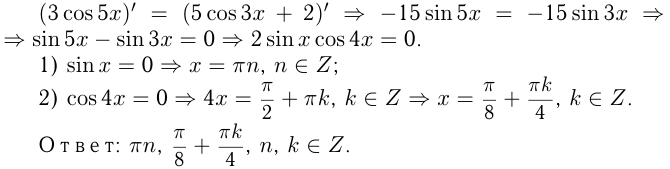
Задача №167
К параболе 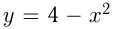 в точке с абсциссой
в точке с абсциссой 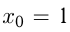 проведена касательная. Найти точку пересечения этой касательной с
проведена касательная. Найти точку пересечения этой касательной с 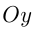 .
.
Решение:
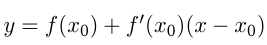 — уравнение касательной.
— уравнение касательной.
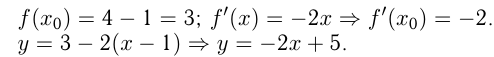
При пересечении с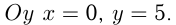
Ответ: точка 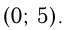
Задача №168
Найти координаты точки пересечения двух касательных, проведенных к графику функции 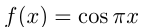 в точке с абсциссой
в точке с абсциссой 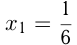 и в точке с абсциссой
и в точке с абсциссой 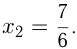
Решение:
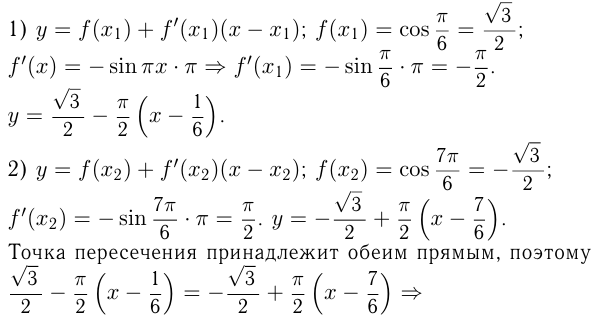
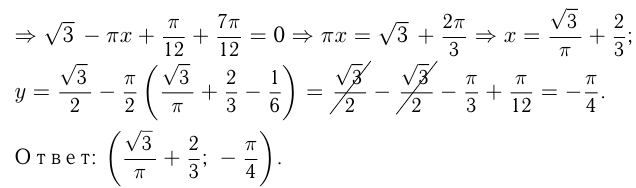
Задача №169
Найти уравнения общих касательных к параболам 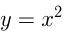 и
и 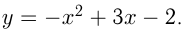
Решение:
1) Касательная к 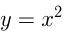 проходит через точку с абсциссой
проходит через точку с абсциссой 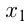 этой параболы. Уравнение касательной:
этой параболы. Уравнение касательной: 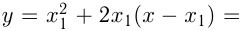
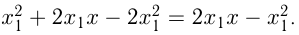
2) Касательная к 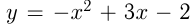 проходит через точку с абсциссой
проходит через точку с абсциссой 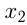 этой параболы. Уравнение касательной:
этой параболы. Уравнение касательной:
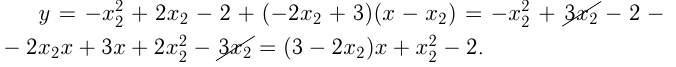
Эти касательные — одна и та же прямая, следовательно их угловые коэффициенты и свободные члены совпадают.
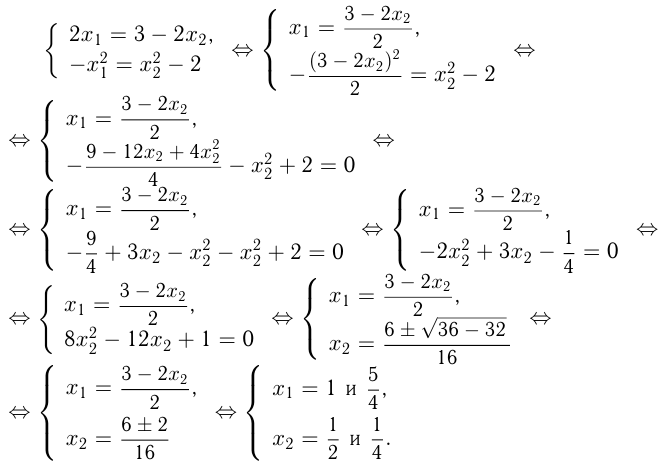
Уравнения касательной к функции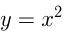 в точке с абсциссой
в точке с абсциссой
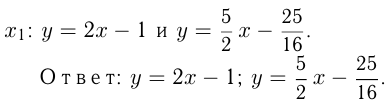
Задача №170
Вычислите площадь треугольника, ограниченного осями координат и касательной к графику функции 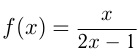 в точке с абсциссой
в точке с абсциссой 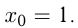
Решение:
Сделаем схематический чертеж. Функция 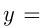
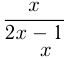 гипербола, т. к.
гипербола, т. к.
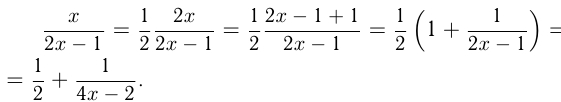
Эта гипербола имеет асимптоты 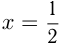 и
и 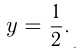 Т. к.
Т. к. 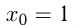 , начертим только одну ветвь гиперболы.
, начертим только одну ветвь гиперболы.
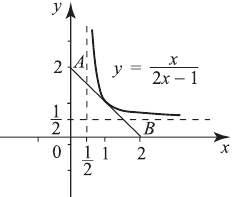
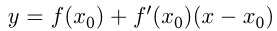 — Уравнение касательной.
— Уравнение касательной.
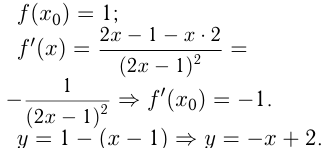
Эта прямая пересекается с 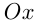 при
при 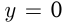 в точке
в точке 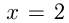 и пересекается с
и пересекается с 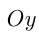 при
при 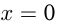 в точке
в точке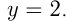
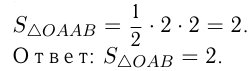
Задача №171
Найти угол между касательными, проведенными из точки 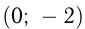 к параболе
к параболе 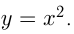
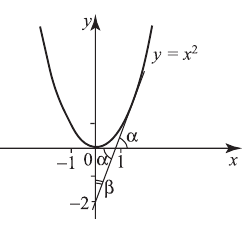
Решение:
Сделаем чертеж. 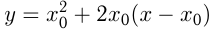 касательной к графику
касательной к графику 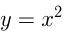 в точке с абсциссой
в точке с абсциссой 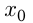 .
.
![]()
Эта прямая проходит через точку 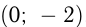 , поэтому
, поэтому 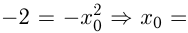
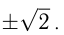 Возьмем касательную к правой ветви параболы;
Возьмем касательную к правой ветви параболы; 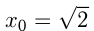 и
и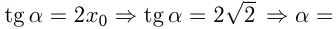
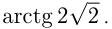
![]()
Угол между касательными 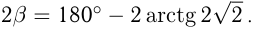
Ответ: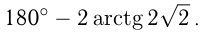
Задача №172
В точке 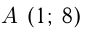 к графику функции
к графику функции 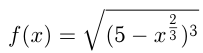 проведена касательная. Найти длину ее отрезка, заключенного между осями координат.
проведена касательная. Найти длину ее отрезка, заключенного между осями координат.
Решение:
Уравнение касательной к графику функции при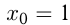 .
.
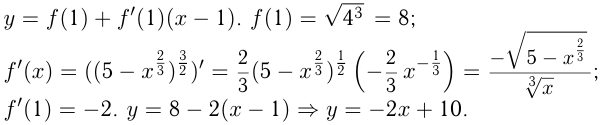
Прямая 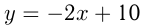 пересекает ось
пересекает ось 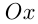 в точке
в точке 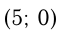 и ось
и ось 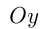 в точке
в точке 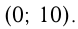 Расстояние между этими точками:
Расстояние между этими точками: 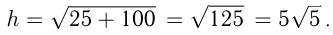
Ответ: 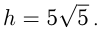
Задача №173
Найти уравнения тех касательных к графику функции 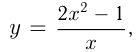 которые вместе с осями координат ограничивают треугольник площади
которые вместе с осями координат ограничивают треугольник площади 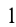 .
.
Решение:
Прямая 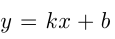 отсекает на осях
отсекает на осях 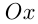 и
и 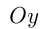 следующие отрезки:
следующие отрезки:
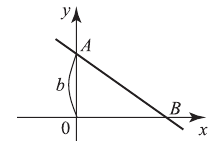
при 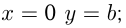
при 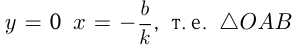 имеет катеты
имеет катеты 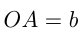 и
и 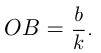
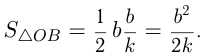
Уравнение касательной
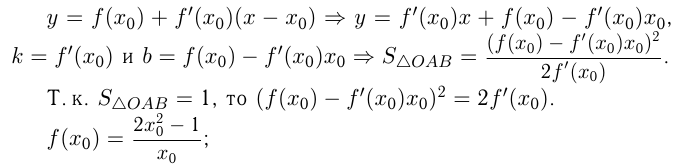
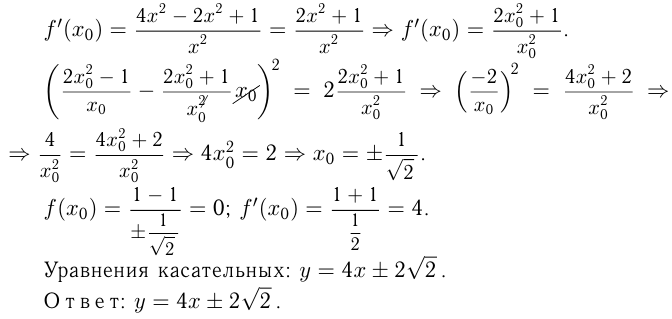
Исследование функций и построение графиков
К оглавлению…




Наибольшее и наименьшее значение функции
К оглавлению…

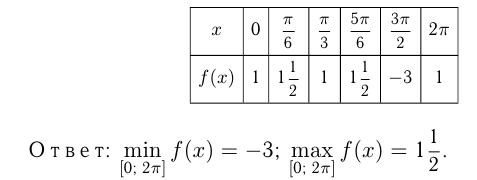



Первообразная и интеграл
К оглавлению…



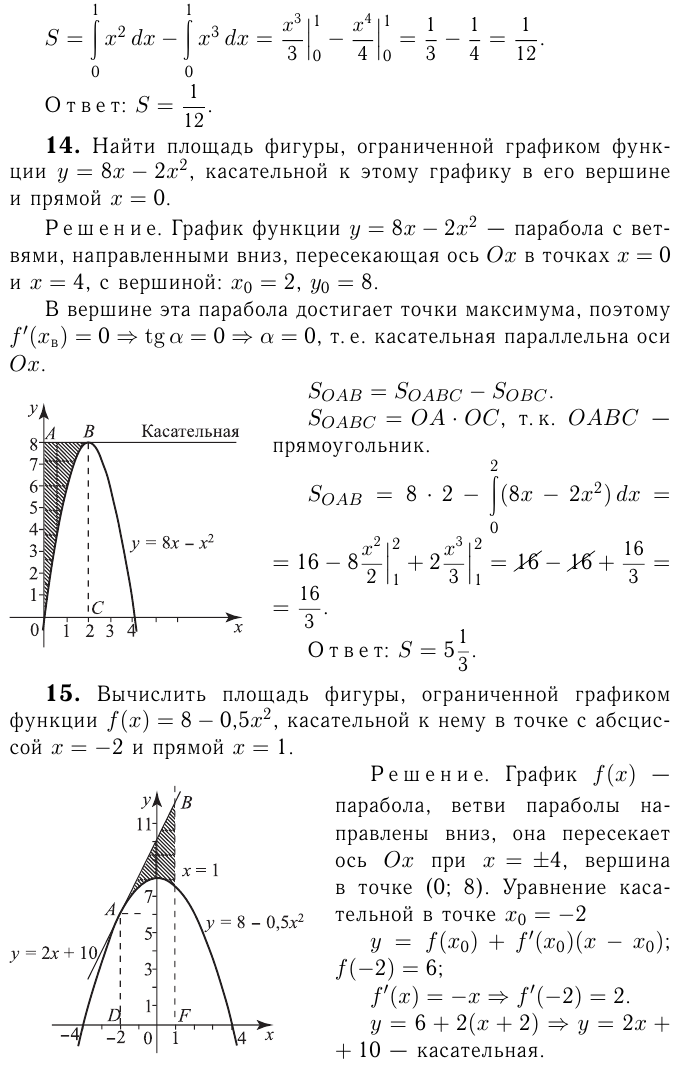
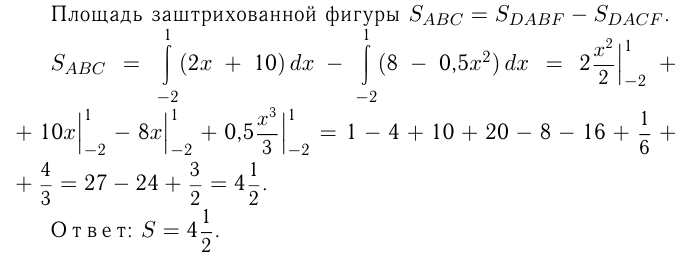
Эта лекция взята со страницы решения задач по математике:
Решение задач по математике
Возможно вам будут полезны эти страницы:

Я уже рассматривала несколько сложных графиков из сборника Ященко и работы СтатГрад от 2 октября. Так что открывай в новой вкладке ссылки и смотри решение других типов этого задания!
А пока задание на сегодня такое:
ПОСТРОЕНИЕ
1) График состоит из 2-ух стандартных графиков (парабола и гипербола), каждый из которых располагается в своей “зоне” на координатной плоскости. Парабола в “зоне”, где Х больше или равен (-3), а гипербола, где Х меньше (-3):
на координатной плоскости (с единичным отрезком=2 клетки) условно показала эти “зоны” желтым и зеленым цветом.
2) Строим параболу в “желтой” части координатной плоскости:
- Находим координаты вершины. Заметим, что в функции легко выделяется полный квадрат по формуле сокращенного умножения
тогда понимаем, что вершина смещена по оси Х на “-2”, а по оси У не смещается. Значит координаты вершины:
- Определяем направление веток параболы. В этом случае а>0 и ветки смотрят вверх.
- Находим дополнительные точки. Одна из точек должна обязательно быть “граничной”, т.е. при х=-3 в нашем случае.
- Отмечаем найденные точки (в том числе вершину) и проводим часть параболы. В “зеленую” часть координатной плоскости не заходим!
3) Строим гиперболу в “зеленой” зоне
- Определяем ось симметрии и расположение веток в четвертях
т.е. если наглядно “схематично” изобразить этот график, то он выглядит так:
НО в нашем задании будет видна только часть гиперболы, та часть, которая левее х=-3 (схематично отсекаю её красной линией)
- Понятно, что будет виден “хвост” ветки гиперболы расположенной во II координатной четверти. Он будет идти в левую сторону от “граничной” точки постепенно приближаясь к оси Х, но никогда не касается ее!
Поэтому точка, необходимая для построения, граничная точка. Найдем значение У при Х=-3:
Построим весь график:
Ответ на вопрос:
Прямая y=m параллельна оси ОХ, пересекает ось ОУ в точке со значением m.
При таком расположении
прямая не пересекает и не касается графика ни в одной точке.
Если перемещать эту прямую визуально вверх, то при совпадении с осью ОХ (У=0) прямая касается графика в вершине параболы, т.е. будет иметь с графиком одну общую точку:
Значит у=0 подходит условию задания, и m=0.
Если прямая поднимется еще немного выше, то уже будет пересекать график в трех точках (2 раза параболу и один раз “хвост” гиперболы).
Поднимаем еще выше прямую и видим, что в таком положении она пересекает график в двух точках:
Это подходит. Значит m=1
Смотрим, что происходит выше:
Видно, что выше единицы прямая пересекает график по ветке параболы ровно один раз всегда.
Значит m>1 (любое число больше 1)
Собираем все в один ответ: m=0 , m>1
Если вы знаете того, кто готовится к ОГЭ, не забудьте поделиться с ним этой информацией. Всегда пригодится.
Продолжение следует…
Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность
(✿◠‿◠)
Решение текстовых задач с помощью графиков линейной функции
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Данилкин П.С. 1
1МАОУ Новоселезневская СОШ
Черноскутова Н.П. 1
1МАОУ Новоселезневская СОШ
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
ВВЕДЕНИЕ
Математика является одним из основных предметов школьного образования, ее мы изучаем с 1-го класса. Уже в начальных классах мы нередко решаем текстовые задачи. Вообще решению текстовых задач в школе уделяется достаточно много внимания, так как современный человек, независимо от рода деятельности и уровня образования, должен уметь решать задачи. В этом я убедился, работая над проектом «Нужна ли математика?» в 5 классе. До 5 класса мы решали задачи по действиям, начиная с 5 класса, некоторые задачи мы решаем с помощью уравнения.
В этом учебном году на уроках алгебры мы изучили тему «Линейная функция, ее свойства и график», а на уроках физики при изучении темы «Механическое движение» чертили графики зависимости пути от времени движения, это были графики линейной функции. У меня сложилось мнение, что графики служат обычно для иллюстрации и лучшего запоминания свойств изучаемых функций, а построение чертежей дает возможность «увидеть» задачу. Мне стало интересно узнать, применяются ли свойства и графики линейной функции при решении задач на движение, а также других текстовых задач.
В связи с этим возникла тема моего исследования «Применение графиков линейной функции при решении текстовых задач». Работа посвящена текстовым задачам, при решении которых применяются графики линейной функции.
Актуальность моей работы заключается в том, что знание нескольких методов решения задачи увеличивает возможность её правильного решения и позволяет выбрать наиболее рациональный в данной ситуации.
Цель работы: изучить применения графиков линейной функции при решении текстовых задач.
Цель исследования обусловила следующие задачи:
1. Изучить литературу по данной теме.
2. Рассмотреть способы решения текстовых задач с помощью графиков линейной функции.
3. Провести сравнительный анализ различных методов решения текстовых задач.
4. Привести примеры решения задач из типовых экзаменационных вариантов.
Гипотеза: графический метод упрощает решение текстовых задач.
Объект исследования – текстовые задачи.
Предмет исследования – способ решения задач с помощью графиков линейной функции.
СПОСОБЫ РЕШЕНИЯ ТЕКСТОВЫХ ЗАДАЧ
Для умения решать текстовые задачи важна всесторонняя работа над одной задачей, в частности решение её различными способами. Следует отметить, что решение задач различными способами позволяет убедиться в правильности решения задачи, даёт возможность глубже раскрыть зависимости между величинами, рассмотренными в задаче.
В качестве основных способов в математике различают арифметический и алгебраический.
Решить задачу арифметическим способом значит выполнить арифметические действия над числовыми данными из условия задачи, составив числовое выражение, а конечный результат вычислений – ответ на вопрос задачи.
Решить задачу алгебраическим способом – это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений (или неравенств).
Если использовать чертёж при решении, то можно легко дать ответ на вопрос задачи. Такой способ решения называется графическим. Графический способ даёт возможность более тесно установить связь между алгебраическим и геометрическим материалом. Следует отметить, что благодаря применению графического способа можно сократить время решения задач. В то же время умение графически решать задачу – это важное политехническое умение. Графический способ иногда даёт возможность ответить на вопрос такой задачи, которую сложно решить алгебраическим способом.
Графический способ решения любых задач и проблем очень удобен своей наглядностью, так как вырисовывается вся картина целиком, и не нужно удерживать в памяти разрозненные куски.
РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ С ПОМОЩЬЮ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ
Графический метод решения задач появился во времена Евклида (III век до нашей эры) и использовался не только в геометрии, но и в алгебре. Особенность его применения в алгебре состояла тогда в том, что он предполагал решение задач только с помощью построений и законов геометрии.
Решить задачу графическим способом – значит решить задачу с помощью графиков в прямоугольной системе координат. Решение задач графическим методом требует творческого подхода и глубокого понимания процессов, описанных в задаче. Изображая графики процессов, можно находить зависимости между величинами, применяя геометрические знания, а можно решать задачу привычным способом. Построенная модель зависимости между величинами помогает увидеть отношения между этими величинами. На этих двух подходах основано использовании графиков при решении текстовых задач.
В школьных задачах, как правило, описываются процессы с постоянной скоростью его протекания. Поэтому, независимо от вида процесса, его характеристики связаны одной и той же линейной зависимостью: результат процесса равен произведению скорости и времени его протекания.
Действие движения характеризуется тремя компонентами: пройденный путь s, скорость v и время t Известно соотношение между ними s= vt. Работу характеризуют также три компонента действия: время работы t, объем работы V и производительность N (количество произведенной работы в единицу времени). Существует следующее соотношение между этими компонентами: V = N t. В задачах на смеси и сплавы обычно присутствуют тоже три величины: концентрация (доля чистого вещества в смеси (или сплаве)), количество чистого вещества в смеси (или сплаве), масса смеси (сплава). Соотношение между этими величинами: масса смеси концентрация = количество чистого вещества.
Решение текстовой задачи графическим способом осуществляется в три этапа:
Построение графической модели задачи.
Решение получившейся графической задачи.
Перевод полученного ответа с графического языка на естественный.
Рассмотрим подробно реализацию этих этапов в процессе решения текстовых задач.
РЕШЕНИЕ ЗАДАЧ НА ДВИЖЕНИЕ
Большое значение в математике имеют задачи на движение. Задачи на движение подразделяются на следующие типы: по количеству движущихся объектов, по направлению движущихся объектов, по времени начала движения.
Методы решения текстовых задач на движение, использующие графики, обладают большой простотой и изяществом. При решении задач на движение вводится система координат, причем на оси абсцисс откладывается время, а на оси ординат – пройденное расстояние, отсчитываемое от некоторой фиксированной точки. Движущийся объект в любой момент времени занимает определённое положение, т.е. находится на определённом расстоянии от этой фиксированной точки, а значит, изображается некоторой точкой в данной системе координат. В процессе движения объект изменяет своё положение, и изображающая его точка вычерчивает некоторую линию – график движения. Приведу примеры нескольких задача, в них будем считать движение равномерным и графики движения прямолинейными.
Задача 1. Из пункта A вышла грузовая машина со скоростью 60 км/ч. Через 2 ч вслед за ней из А вышла легковая машина со скоростью 90 км/ч. На каком расстоянии от пункта А легковая машина догонит грузовую?
Р ешение 1. За начальный отсчет времени берется момент выхода грузовой машины (рис. 1), тогда момент выхода легковой машины будет через два часа. Зная скорости движения объектов, построим графики движения. По чертежу видно, что точка пересечения графиков показывает встречу машин, она состоялась на расстоянии 360 км.
(рис. 1) Ответ: 360 км.
Решение 2. Пусть х ч. – время движения легковой машины, тогда (х+2) ч. – время движения грузовой машины. Составляем уравнение 60(х+2)=90х. Решив уравнение, получим, что легковая машина двигалась 4 часа, отсюда расстояние равно 360 км.
Задача 2. С противоположных концов катка длиной 120 м бегут навстречу друг другу два мальчика. Через сколько секунд они встретятся, если второй начнет бег через 5 секунд после первого и если первый пробегает 6 м/с, а второй – 9 м/с? Решение 1. Отрезок ОМ – график движения . (рис.2) первого мальчика. Так как мальчики движутся навстречу друг другу, то возникает необходимость ввести вторую систему координат, где оси Оt сонаправлены, и масштабы на них одинаковые. Вертикальные оси противоположно направлены. График движения второго мальчика – отрезок O1K. Абсцисса точки С пересечения графиков показывает время, через которое мальчики встретятся. Ответ: 11с.
Решение 2. Пусть х с.– время (рис. 2) движения второго мальчика, тогда время первого – (х+5) с. Составим уравнение, учитывая, что сумма расстояний равна 120м: решив которое, получим, что х = 6 с. Тогда время, через которое они встретятся – 11 с.
Задача 3. Из городов, расстояние между которыми равно 40 км, вышли одновременно навстречу друг другу два лыжника. Скорость одного из них была на 2 км/ч больше скорости другого. Через 2 часа лыжники оказались на расстоянии 8 км друг от друга. С какой скоростью шёл каждый лыжник?
Р ешение 1. Пусть лыжники двигались с одинаковыми скоростями. Учитывая, что они двигались навстречу друг другу и, что между ними расстояние – 8 км, построим графики движения. По графику видно, что их скорость равна 8 км/ч. Но т.к. разница в скоростях составляет 2 км/ч, получаем, что скорость первого лыжника 7 км/ч, а второго 9 км/ч. Но может быть ещё случай, когда 8 км было оооооо (рис. 3) между лыжниками после встречи. Тогда одинаковая скорость – 12км/ч, значит скорость первого лыжника 11км/ч, а второго–13км/ч.
Решение 2. Пусть х км/ч скорость первого лыжника, тогда скорость второго – (х+2) км/ч. Составим уравнение по условию задачи: 40 – (2х +2(х+2)) = 8. Решив уравнение, получим, что скорость первого лыжника 7 км/ч, а второго 9 км/ч. Во втором случае уравнение составим так: (2х +2(х+2)- 40 =8. Получим, что скорость первого лыжника 11 км/ч, а второго – 13 км/ч.
Если сравнивать способы решения, то графический метод позволяет быстрее и нагляднее решить задачу, особенно для тех учащихся, кто ошибается при составлении уравнения по условию задачи или при его решении.
РЕШЕНИЕ ЗАДАЧ НА СМЕСИ И СПЛАВЫ
Графический метод можно применить при решении задач, не связанных с движением каких-либо объектов. Сложными считаются задачи на смеси и сплавы. Рассмотрим решение таких задач двумя способами.
Задача 1. Один сплав содержит металлы в отношении 1: 5, другой сплав содержит эти же металлы в отношении 5: 7. В какой пропорции нужно взять первый и второй сплавы, чтобы получить сплав, содержащий те же металлы в отношении 1: 3?
Р ешение 1. По вертикальной оси отложим вес сплава в условных единицах (рис.1). По горизонтальной оси – вес первого металла в тех же условных единицах. Первый металл в первом сплаве составляет 1/6 часть. Взяв по горизонтали 1 у.е., а по вертикали 6 у.е., получим точку С. Прямая ОС будет характеризовать первый сплав. Взяв произвольную точку на этой прямой и спроецировав ее на оси, мы определим, сколько условных единиц весит весь сплав и сколько условных единиц составляет в . (рис.1) нем вес первого металла. Взяв по горизонтали точку 5 и по вертикали точку 12, получим точку D. Соединив ее прямой линией с началом координат, получим график, характеризующий второй сплав. Аналогично получим характеристику третьего сплава. Из любой точки вертикальной оси, например, на уровне точки D, проведем горизонтальную
прямую, пересекающую характеристики в точках М, N и D. Отношение длины отрезка ND к длине отрезка MN даст пропорцию, в которой нужно взять сплавы I и II соответственно, так как в данном случае отрезок ND в 2 раза больше отрезка MN, то необходимо взять 2 части первого сплава и 1 часть второго сплава. Можно просто измерить отрезки линейкой. Ответ: сплавы необходимо брать в пропорции 2: 1.
Решение 2. Пусть х кг – первого сплава, у кг – второго сплава. Тогда, вес первого металла в новом сплаве
, вес второго металла в новом сплаве . Новый сплав содержит металлы 1:3, тогда . Преобразовав данное выражение, получим 8у = 4х, отсюда . Ответ: 2: 1.
Задача 2. Сплавили два слитка. Первый весил 100 г и содержал 40% меди, второй весил 400 г и содержал 60 % меди. Какой процент меди содержится в получившемся сплаве? [1]
Решение 1. По вертикальной оси отложим количество чистого вещества, на горизонтальной – массу сплава (рис.2).
Построим графики, характеризующие первый и второй сплавы. Учитывая, что в 500 г получившегося сплава содержится 280 г чистого вещества, построим прямую, х арактеризующую новый сплав. По графику видно, что в 100 г нового сплава содержится 56 г чистого вещества. Следовательно, в оооо (рис. 2) получившемся сплаве содержится 56% меди.
Решение 2. Пусть х % – меди в новом сплаве, вес нового сплава 500 г. Используя условие задачи, получаем уравнение: + = . Решив уравнение, получим ответ: х = 56%.
В данном случае графики также позволяют наглядно увидеть ответ задачи, причем временные затраты меньше, чем решение задачи с помощью уравнения.
РЕШЕНИЕ ЗАДАЧ НА СОВМЕСТНУЮ РАБОТУ
При решении задач на совместную работу, на вертикальной оси откладывается отрезок, соответствующий количеству работы, а на горизонтальной время работы объектов, данных в задаче. Рассмотрим примеры решений задач двумя способами.
З адача 1. Чтобы выкачать воду из котлована, поставили два насоса. Оба насоса могли бы выкачать всю воду за 10 часов. Однако после 3 часов совместной работы один насос сломался, и другому насосу пришлось работать ещё 14 часов, чтобы выкачать оставшуюся воду. За сколько часов, действуя отдельно, каждый насос мог бы выкачать всю воду из котлована? Решение 1. По вертикали отложим отрезок, условно соответствующий количеству воды в котловане. По горизонтали – время работы насосов (пусть они начнут работу в 6 ч. утра). (рис.1). По графику видно, что если второй насос один начал (рис 1.) бы выкачивать воду в 3 часа, то окончил бы работу в 23 часа. Значит, второму насосу потребуется для выкачивания всей воды 20 часов. Т.к. оба насоса вместе выкачивают воду за 10 часов, то первому насосу потребуется также 20 часов для работы.
Решение 2. Пусть за х ч. выкачает весь котлован первый насос, за у ч.- второй насос.
Производительность в час обоих насосов , тогда за 3 часа совместной работы насосы выкачали котлована, значит осталось выкачать котлована.
Так как 14 часов работал один второй насос, то составляем уравнение: 14 . Решив это уравнение, получим х = 20. Значит, второй насос всю работы выполнит за 20 часов. Чтобы найти время работы первого насоса, решим уравнение: . Отсюда у = 20. Ответ: каждому нужно по 20 часов.
Задача 2. Игорь и Паша могут покрасить забор за 30 часов, Паша и Володя могут покрасить этот же забор за 36 часов, а Володя и Игорь – за 45 часов. За сколько часов мальчики покрасят забор, работая втроём?
Р ешение 1. На вертикальной оси отметим отрезок условно соответствующий всей работе (рис 2). На горизонтальной оси – время. Удобный масштаб: 3 часа– 1 клетка. Прямая ОD – производительность Володи и Игоря, прямая ОК – производительность Паши и Володи, прямая ОМ – Игоря и Паши. Проведя (рис.2) через любую точку горизонтальной оси, например, отметку 3 часа, вертикальную линию и отметив на ней точки пересечения ее с прямыми ОМ, ОК и OD, построим на ней сумму отрезков, соответствующих производительности каждой пары ребят. Получим точку F. Спроецировав точку F на вертикальную ось, мы можем узнать, какую часть забора покрасят 2 первых, 2 вторых и 2 третьих мальчика при совместной работе в течение одного часа. Проведя прямую ОF до пересечения с верхней горизонтальной осью, мы попадем в точку А, соответствующую времени 12 часов. Это половина необходимого времени, так как каждый мальчик участвует дважды в работе. Значит, для того, чтобы покрасить забор трем мальчикам потребуется 24 часа. Ответ: 24 часа
Решение 2. Пусть х – производительность Паши, у – производительность Володи, z – Игоря. Тогда: х+у = , у+z = , х+z = . Проссумируем : (х+у)+ (у+z) + (х+z)= + + .Из этого следует : х + у+ z = = . Значит, на всю работу потребуется 24 часа.
Трудность в данной задаче была в том, что масштаб был выбран не сразу. Мы видим, что такие задачи удобнее решать графическим методом, если задано небольшое количество часов, тогда на горизонтальной оси 1 час будет крупнее, и тогда удобнее отмечать точку F.Ответ будет читаться нагляднее.
ЗАКЛЮЧЕНИЕ
Целью данной работы было изучение применения графиков линейной функции в решении текстовых задач. В процессе работы над данной темой, выяснилось, что при решении текстовых задач наряду с традиционными методами, можно использовать и графический метод, который предполагает построение графиков линейных функций.
Были изучены материалы учебно-методической литературы, материалы из интернета. Решено множество задач из экзаменационных материалов разными способами, проведен сравнительный анализ.Гипотеза подтвердилась частично. Конечно, алгебраический способ – универсальный, но знание различных способов часто упрощает решение задачи. И, если есть сомнения, что получен правильный ответ, то можно решить задачу другим способом.
По результатам исследования можно сделать следующие выводы:
Одно из преимуществ графического метода перед алгебраическим состоит в наглядности решения, что позволяет лучше понять задачу.
Использование этого метода упрощает решение задач: нет громоздких вычислений.
Графическим методом решаются задачи не только на движение, но и на совместную работу, на смеси и сплавы.
Графический способ даёт возможность более тесно установить связь между алгебраическим и геометрическим материалами, развить функциональное мышление.
График дает возможность определить, есть ли у данной задачи решение и единственно ли оно.
Есть и «минусы»: иногда получаются приближённые значения в случаях неудачного масштаба.
Настоящее исследование значительно расширило представление о линейной функции, способствовало глубокому пониманию взаимосвязи этой функции с реальными ситуациями, возникающими в нашей жизни. Есть планы продолжить исследование в этом направлении: при решении некоторых задач применяется графико-геометрический метод, который основан на подобии треугольников.
Следует отметить, что решение задач различными способами позволяет убедиться в правильности решения задачи, даёт возможность глубже раскрыть зависимости между величинами, рассмотренными в задаче. Результаты работы можно использовать на уроках и дополнительных занятиях по математике при подготовке обучающихся к экзаменам. Этот материал позволит повысить образовательный уровень обучающихся.
СПИСОК ЛИТЕРАТУРЫ
Кочагин В.В. ОГЭ 2018. Математика: тематические тренировочные задания: 9 класс. – Москва: Эксмо, 2017. – 192 с.
Лунина Л.С. Обучение решению алгебраических задач геометрическим методом //Математика в школе: М.: Изд. «Школа-Пресс»,1996.-№4.- с.34-39.
Рудин В.Н., Рудина Е.И. Графическое решение текстовых задач. Учебное пособие по математике для учителей и учащихся. Издание Томского института повышения квалификации работников образования, 1995 г.
Ященко И.В., Волчкевич М.А. и др. ЕГЭ 2018. Математика. Профильный уровень. 50 вариантов. Типовые тестовые задания от разработчиков ЕГЭ. – М.: Издательство «Экзамен», 2018. – 263 с.
https://infourok.ru/
Просмотров работы: 1490
