Решение
задач с помощью чертежей – диаграмм
Диаграмма
– это чертеж или рисунок, на котором условно изображены в виде отдельных фигур
различные значения одной и той же величины или несколько сравнимых величин.
Графико-вычислительные
приемы помогают решать разнообразные арифметические и геометрические задачи.
Построение этих чертежей дает возможность «увидеть» задачу, установить и
исследовать связи, существующие между величинами, входящими в задачу, выбрать
кратчайший путь решения.
Применяя
диаграммы к решению задач, будем изображать отрезками численные значения
величин, входящих в условие задачи. Действия над числами заменяют соответствующими
построениями на диаграмме.
Самостоятельное
решение задач таким путем требует определенного навыка, изобретательности. В
некоторых случаях этот путь может заменить чисто вычислительные приемы, в
других – облегчить наилучший выбор неизвестного для составления уравнения, или
подсказать ход рассуждений для отыскания арифметического решения.
Очень важное
достоинство такого пути – в наглядности: на рисунке сразу видна связь между
величинами, входящими в условие задачи; чертеж помогает расширить задачу –
поставить и решить более общие вопросы, глубже проникнуть в существо задачи,
оценить реальность результата и промежуточных действий. Особенно целесообразно
применять этот путь в тех случаях, когда требуется ответить не на один, а на
несколько вопросов.
Задача.
В одном бидоне вдвое больше молока, чем в другом. Когда из обоих бидонов отлили
по 20 литров молока, то в первом бидоне оказалось втрое больше молока, чем во
втором. Сколько литров молока было первоначально в каждом бидоне?
Решение.
Начертим
два вертикальных отрезка «бидоны», один по высоте в два раза больше, чем
другой, т.к. одном бидоне вдвое больше молока, чем в другом.
Допустим:
8 и 4 клетки.
Сколько
взять клеток, чтобы показать, что отлили по 20 литров молока, учтем условие: в
первом бидоне оказалось втрое больше молока, чем во втором. На рисунке должна
остаться одна часть во втором «бидоне» и три части в первом.

Тогда
20 л молока – это две клетки. Останется во втором «бидоне» две клетки, в первом
– шесть клеток.
Выходит, что 20
литров – это часть, таких частей в первом бидоне 4, тогда 4∙20=80 л, во втором
бидоне – две части 2∙20= 40 л.
Эту задачу легко
решить, используя алгебраический метод.
|
I бидон |
II бидон |
|
|
Было |
2x |
x |
|
стало |
2x-20 |
x-20 |
Составить
уравнение помогает фраза «в первом бидоне оказалось втрое больше молока, чем во
втором».
2х
– 20= 3(х-20), х=40, 40∙20=80
Ответ:
в первом бидоне 80 л, во втором -40 л молока.
Ученик 7класса
справится с такой задачей, используя введение переменной, и решит уравнение.
Но интересен другой факт: ученик 5, 6 классов тоже способен решить такую
задачу, используя рисунок и логически рассуждая.
Задача.
Коля уплатил в кассу кафе за три блюда, Саша – за два блюда (все пять блюд
одинаковой стоимости). Когда они сели за стол, к ним присоединился Юра, и они
втроем съели все пять блюд поровну. При расчете приятелей между собой
выяснилось, что Юра должен уплатить за съеденный им обед 500 рублей. Сколько из
этих денег следует отдать Коле и сколько Саше?
Решение.

Пусть отрезок в 15
клеток – это вся стоимость обеда (Юра должен отдать 500 рублей), ведь они
втроем съели поровну блюда, то поровну и заплатили за обед. Из рисунка
очевидно, что 1 клетка – 100 рублей. И Коля за три блюда заплатил 900 рублей,
Саша – 600 рублей. Полный обед из пяти блюд стоил 1500 рублей. Следовательно,
Коле нужно отдать 900-500=400 рублей, Саше 600-500=100 рублей.
Ответ:
Коле нужно отдать 400 рублей, Саше 100 рублей.
Задача.
На трех деревьях уселось 36 галок. Когда с первого дерева перелетели на второе
6 галок, а со второго перелетели на третье 4 галки, то на всех трех деревьях
галок стало поровну. Сколько галок сидело первоначально на деревьях?
Решение.
Рисунок
подсказывает, что на втором дереве после перелетов добавились две птицы, и их
стало 12, следовательно, первоначально их было 12-2=10. Конечно, если на
рисунок вынести общее число галок, то решение будет еще более очевидным.

Ответ:
1 дерево -18 галок, 2-10 галок, 3 – 8 галок.
Задача.
Рабочие отремонтировали дорогу длиной 820 метров за три дня. Во вторник они
отремонтировали ![]() этой дороги, в среду
этой дороги, в среду ![]() остальной части дороги.
остальной части дороги.
Сколько метров дороги отремонтировали рабочие в четверг?
Решение.
Возьмем отрезок длиной в 15 клеток – это длина всей отремонтированной дороги
(НОК (5;3)=15). Ведь нам нужно показать сначала две части из пяти, а потом две
части из трех.

Из рисунка
становится очевидным, что вся дорога разделена на пять частей, и, чтобы узнать,
какая часть осталась на четверг (это одна часть), нужно 820:5=164 метра.
Обычный путь
решения:
1)
820 ∙ ![]() =328 м была
=328 м была
отремонтирована во вторник,
2)
820-328=492 м осталось отремонтировать в среду и четверг,
3)
492∙![]() =328 м отремонтировали в
=328 м отремонтировали в
среду,
4)
(820-328) -328=164 м отремонтировали в четверг.
Рисунок
позволяет решить задачу без громоздких вычислений.
Ответ.
164 метра дороги отремонтировали в четверг.
Графики
можно использовать для геометрической иллюстрации движения (перемещения).
Например, расписание движения поездов раньше разрабатывались при помощи
графиков, которые назывались «графики движения поездов». Наиболее просто
графиком изображается равномерное движение.
На
графике обычно, но не всегда, по направлению оси ОХ отсчитывают время, а по
направлению оси OY – расстояние. В
таком случае абсцисса всякой точки графика движения любого тела указывает
момент времени, а ордината – положение этого тела. Следовательно, график дает
возможность ответить на вопрос: «Где в данный момент находится тело? Когда оно
находилось или будет находиться в данном месте?»
Если
на одном чертеже построить два графика движения пешеходов, и если эти два
графика пересекаются в некоторой точке, то координаты этой точки показывают
место и время встречи пешеходов. Вот две задачи на движение, которые можно
решить с помощью графика равномерного движения. Геометрия придет на помощь
алгебре.
Задача.
Два туриста выезжают одновременно навстречу друг другу из двух пунктов А и В.
При встрече оказалось, что первый проехал на 30 км больше второго и что через
четыре дня он будет в В. Второй попадет в А через 9 дней после встречи. Найти
расстояние АВ.
Решение.
Берем произвольный отрезок АВ, изображающий расстояние между пунктами Аи В.
Отрезки АВꞌ и ВАꞌ – это графики движения первого и второго туриста (№1, №2).
Место и момент встречи определяются точкой О пересечения графиков.

Через точку О
проведем KL ‖ AB.
По условию KAꞌ =9 дней и LBꞌ =4 дня. Обозначим число дней от момента выхода туристов до их встречи
через х, тогда x=AK=BL.
Имеем
две пары подобных треугольников:
▲AOK
∞ ▲Bꞌ OL,
откуда x:4=OK:
OL
▲Aꞌ
OK ∞ ▲BOL, откуда 9:х= OK:
OL.
Отсюда
получаем x:4=9:х,
решая,
получим х=6 дней.
Обозначим
расстояние BC через y.
Тогда
LO=BC=y,
AC=KO=y+30.
Из
подобия треугольников AOK , BꞌOL
следует OK:OL=AK:
Bꞌ L или (y+30):y=6:4.
Упрощая
эту пропорцию, получим 30:y=2:4,
y=60
км.
Таким
образом, AB=2y+30=150
км.
Ответ:
расстояние между пунктами 150 км
Кроме
того, мы можем определить скорость каждого туриста.
Скорость
первого: v1=OL:LBꞌ
=60:4=15 км в день.
Скорость
второго v2
=OL:LB=60:6=10
км в день.
Задача.
Два пешехода идут навстречу друг другу, один из пункта А, другой из пункта В.
Первый выходит из А на 6 часов позже, чем второй из В. При встрече оказывается,
что он прошел на 12 км меньше второго. Продолжая после встречи дальней путь с
той же скоростью, первый приходит в В через 8 часов, второй в А – через 9
часов. Найти скорость каждого пешехода.
Решение.
Изобразим расстояние между пунктами А и В произвольным отрезком АВ. Ось времени
теперь направим вертикально. На перпендикуляре АЕ отмечаем точку С, принимая,
что АС=6 часам. Пусть прямая СD является
графиком движения первого пешехода, а прямая ВЕ – графиком движения второго. F
– точка пересечения графиков – это место встречи пешеходов, G
– проекция на АВ точки F.

Через
точку F проведем HJ ‖ AB.
По
условию, HE=9 часов, JD=
8 часов, JB – AG=12
км.
Пусть
CH=y,
тогда BJ=AH=(y+6)
часов.
▲BGF∞▲FHE
и ▲FJD∞▲
FHC
(▲FGB=▲FBJ)
Отсюда
получаем (y+6) : 9=FJ : FH=8 : y,
Следовательно,
(y+6)
∙y=8
∙ 9
или
y2+6y
– 72=0 , y=6 часов.
Далее,
![]() ,
, ![]() ,
, ![]() , FH=36
, FH=36
км,
FJ=48
км.
FH
– это путь, который прошел первый пешеход за время, равное y=6
часов; FJ – путь, который прошел
второй пешеход за y+6=12 часов.
Следовательно,
первый пешеход шел со скоростью 36:6=6 км/час,
а
второй – со скоростью 48:12=4 км/час.
Ответ:
6 км/час – скорость первого пешехода, 4 км/час – скорость второго пешехода.
Вот второй вариант
решения данной задачи – алгебраический, привычный для ученика и учителя. Пусть
х – путь, пройденный первым пешеходом до встречи.
|
S, км |
V, км/ч |
t, час |
||
|
До |
1-й |
x |
|
|
|
2-й |
x+12 |
|
|
|
|
После |
1-й |
x+12 |
|
8 |
|
2-й |
x |
|
9 |
Составить
уравнение поможет фраза «первый выходит из А на 6 часов позже, чем второй из
В», следовательно, разница во времени между ними 6 часов:![]()
После
преобразований получим: 5х2 – 12∙12х – 12∙12∙9=0, решив квадратное
уравнение, получаем х=36.
Следовательно,
второй пешеход прошел после встречи 36 км, а до встречи 36+12=48 км. Эти же 48
км прошел первый пешеход после встречи.
Первый пешеход шел
со скоростью 48:8=6 км/ч, второй – 36:9=4 км/ч.
Невозможно пройти
мимо интереснейшей задачи из рассказа Чехова «Репетитор». Чтобы освежить в
памяти, о чем идет речь, вот небольшой отрывок из этого рассказа.
«Теперь
по арифметике… Берите доску. Какая следующая задача?
Петя
плюет на доску и стирает рукавом. Учитель берет задачник и диктует:
—
«Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько
аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3
руб.?» Повторите задачу.
Петя
повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.
—
Для чего же это вы делите? Постойте! Впрочем, так… продолжайте. Остаток
получается? Здесь не может быть остатка. Дайте-ка я разделю!
Зиберов
делит, получает 3 с остатком и быстро стирает.
«Странно…
— думает он, ероша волосы и краснея. — Как же она решается? Гм!.. Это задача на
неопределенные уравнения, а вовсе не арифметическая»…
Учитель
глядит в ответы и видит 75 и 63.
«Гм!..
странно… Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то».
—
Решайте же! — говорит он Пете.
—
Ну, чего думаешь? Задача-то ведь пустяковая! — говорит Удодов Пете. — Экий ты
дурак, братец! Решите уж вы ему, Егор Алексеич.
Егор
Алексеич берет в руки грифель и начинает решать. Он заикается, краснеет,
бледнеет.
—
Эта задача, собственно говоря, алгебраическая, — говорит он. — Ее с иксом и
игреком решить можно. Впрочем, можно и так решить. Я, вот, разделил…
понимаете? Теперь, вот, надо вычесть… понимаете? Или, вот что… Решите мне
эту задачу сами к завтраму… Подумайте…
Петя
ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство
учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из
угла в угол.
—
И без алгебры решить можно, — говорит Удодов, протягивая руку к счетам и
вздыхая. — Вот, извольте видеть…
Он
щелкает на счетах, и у него получается 75 и 63, что и нужно было.
—
Вот-с… по-нашему, по-неученому.
Учителю становится
нестерпимо жутко. С замиранием сердца поглядывает он на часы и видит, что до
конца урока остается еще час с четвертью — целая вечность!»
Задачу из рассказа
А. П. Чехова можно решать по-разному.
Для учеников,
осваивающих тему «Решение задач с помощью системы уравнений», можно предложить
такой способ.
Пусть
х – количество аршин синего сукна,
y
– количество аршин черного сукна,
тогда
5х – стоимость синего сукна,
3y
– стоимость черного сукна.
Учитывая
условие задачи, составим систему уравнений
![]()
Выразим
х через y,
получим x=138-y,
5∙(138-y)+3y=540,
y=75,
138-75=63.
Ответ:
купец
купил 75 аршин черного сукна и 63 аршина синего сукна.
Еще вариант
размышлений: если бы купец приобрел только 138 аршин синего сукна, то ему
пришлось бы заплатить 138 ∙ 5 = 690 рублей. А он заплатил 540 рублей, на 150
рублей меньше. Заменяя один аршин синего сукна на аршин черного, можно
уменьшить стоимость сукна на 2 рубля. А чтобы уменьшить стоимость 138 аршин
сукна на 150 рублей, надо заменить 150 : 2 = 75 аршин синего сукна на такое же
количество черного. Выходит, что купец купил 75 аршин черного сукна и 138-75 =
63 аршина синего.
Есть ли
какой-то смысл в действиях чеховских героев? Петя разделил 540 на 138. У него
получилось 3 и 126 в остатке. Если купить 138 аршин черного сукна, то 138∙3=414
– стоимость черного сукна, и при делении его стоимости на 138, получается 3 без
остатка. Замена 1 аршина черного сукна на аршин синего увеличивает общую
стоимость сукна 2 рубля, и остаток от деления общей стоимости на 138
увеличивается на 2. Для того, чтобы остаток стал равен 126, надо 126 : 2 = 63
аршина черного сукна заменить таким же количеством синего. Следовательно, было
куплено 63 аршина синего сукна и 138 – 63 = 75 аршин черного.
Учитель-гимназист
хотел сложить пять и три, а потом 540:3. Посмотрим, что из этого получается.
540: (5 + 3) = 67 и 1/2 аршина черного и синего сукна, Как купить на те же
деньги 138 аршин? Для того, чтобы купить еще 3 аршина черного сукна, нужно 3 ∙
3 = 9 рублей. Эти 9 рублей можно выиграть от замены 9: 2 = 4 и 1/2 аршина
синего сукна на такое же количество черного. При этом синего сукна останется 63
аршина, а черного 75 аршин.
Вот еще одно
решение с применением ломаных графиков.

Один
аршин синего сукна стоит 5 рублей, следовательно, 100 аршин стоят 500 рублей.
Отмечаем точку М и строим луч ОМ – это график стоимости синего сукна.
Один
аршин черного сукна стоит 3 рубля, следовательно, 100 аршин стоят 300 рублей.
Отмечаем точку N и строим
луч ON – это график стоимости
черного сукна.
Т.к.
точка С (138 аршин, 540 рублей) оказывается между лучами OM и ON, то,
следовательно, купили и черное, и синее сукно.
Проведем
CA‖
NO до пересечения с OM,
получим точку А. Ломаная OAС – график
нарастающей стоимости сукон – синего (OA)
и черного (AC).
Проекции
точки А на оси OX и OY
указывают, что синего сукна купили 63 аршина на 315 рублей. Задача решена.
Найти количество и стоимость черного сукна уже легко.
Можно поступить и
немного иначе: провести CB ‖ MO;
тогда ломаная OBC -график нарастающей
стоимости сукон – черного (OB)
и синего (BC). Проекции точки В на
оси OX,
OY показывают, что черного сукна купили 75 аршин на 225 рублей. Проверка:
63+75=138 аршин и 315+225=540 рублей.
Приведенные
выше пути решения задач на первый взгляд могут показаться неожиданными и
непривычными. И возникает закономерный вопрос: «Зачем нужно использовать
нестандартные приемы задач, если для усвоения стандартного пути решения очень
мало времени и не все учащиеся отрабатывают каждый прием до конца?»
Показывать
нестандартные приемы решений задач можно на факультативных занятиях, кружковых,
а самые простые рисунки и схемы для понимания смысла задачи обязательно
включать в урочную деятельность.
Если
включить в уроки, кружки, факультативы подобные пути решения заданий, то
появляется вероятность привлечь учащихся в реальную для них творческую
деятельность. И это будет важным условием формирования разных творческих
качеств мышления школьников. Это один из путей развития креативности.
Работа с таблицами и диаграммами
Задача 1.
На диаграмме представлены площади нескольких озёр. Пользуясь диаграммой, ответьте на вопрос.
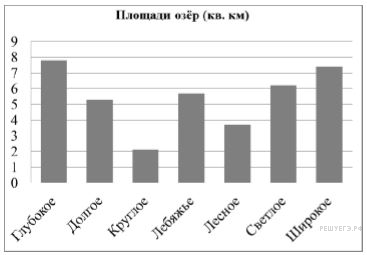
Какое озеро занимает третье место по величине площади среди представленных на диаграмме?
Задача 2.
Чемпионат по хоккею проходил в четыре круга. Алексей следил за количеством заброшенных шайб своих любимых команд и записывал результаты в таблицу. Используя данные этой таблицы, ответь на вопрос.
|
Номер игрового |
«Металлург» |
«Салават |
«Ак Барс» |
|
Первый круг |
32 |
35 |
29 |
|
Второй круг |
40 |
45 |
34 |
|
Третий круг |
37 |
38 |
30 |
|
Четвёртый круг |
44 |
31 |
46 |
Сколько шайб было заброшено командой «Металлург» в четвёртом круге?
Задача 3.
Ниже приведены данные за три года о количестве дождливых дней в июне-октябре в Старом Осколе. Используя эти данные, ответь на вопрос.
|
Месяц |
2013 год |
2014 год |
2015 год |
|
Июнь |
11 |
6 |
8 |
|
Июль |
8 |
3 |
8 |
|
Август |
9 |
5 |
0 |
|
Сентябрь |
13 |
4 |
1 |
|
Октябрь |
7 |
3 |
5 |
Сколько дождливых дней было в Старом Осколе в сентябре 2014 года?
Задача 4.
На игре КВН судьи поставили оценки командам за конкурсы:
|
Команда |
Баллы |
Баллы |
Баллы за |
|
«Диоды» |
23 |
20 |
24 |
|
«Шарм» |
28 |
21 |
22 |
|
«Блеск» |
21 |
18 |
27 |
|
«Лирики» |
27 |
22 |
20 |
Какая команда набрала наибольшее число баллов в конкурсе «Приветствие»?
В ответе укажите одно слово — название команды в именительном падеже.
Задача 5.
В таблице приведены цены на пирожные в трёх кондитерских (в рублях). Используя эти данные, ответьте на вопрос.
|
Название |
Цена в рублях в кондитерской |
||
|
«Сладкая жизнь» |
«Наслаждение» |
«Домашняя» |
|
|
«Эклер» |
15 |
13 |
11 |
|
«Картошка» |
20 |
21 |
25 |
|
«Корзинка» |
32 |
35 |
29 |
|
«Ромовая баба» |
14 |
10 |
13 |
В какой кондитерской пирожное «Корзинка» самое дорогое?
В ответе укажите одно слово — название кондитерской в именительном падеже.
Задача 6.
В таблице приведены данные о количестве девочек и мальчиков в пяти четвёртых классах школы. Используя эти данные, ответьте на вопрос.
|
Количество школьников |
|||||
|
4 «А» |
4 «Б» |
4 «В» |
4 «Г» |
4 «Д» |
|
|
Мальчики |
13 |
10 |
15 |
16 |
17 |
|
Девочки |
15 |
14 |
14 |
12 |
9 |
В каком классе наибольшая разница между числом мальчиков и девочек?
Задача 7.
В таблице приведены данные о численности населения трёх областей России в разные годы (в тыс. человек). Используя эти данные, ответьте на вопрос.
|
Область |
Численность населения |
||||
|
1970 г. |
1979 г. |
1990 г. |
2000 г. |
2010 г. |
|
|
Астраханская |
1400 |
1467 |
1575 |
1390 |
1230 |
|
Мурманская |
800 |
965 |
1191 |
941 |
795 |
|
Калининградская |
730 |
807 |
881 |
959 |
940 |
В каком году численность населения в Астраханской области была наибольшей?
В ответе укажите число — год.
Задача 8.
Баскетбольная команда детской спортивной школы встречалась с командами нескольких школ. Количество очков, набранных игроками, тренер записывал в таблицу. Используя таблицу, ответьте на вопрос.
|
Номер игры |
Артём |
Тимур |
Владимир |
|
Первая игра |
2 |
9 |
9 |
|
Вторая игра |
6 |
5 |
8 |
|
Третья игра |
8 |
2 |
7 |
|
Четвёртая игра |
4 |
10 |
9 |
Сколько очков набрал Владимир в третьей игре?
Задача 9.
Ниже приведены данные о количестве различных отметок по математике за четвёртую четверть в разных классах одной школы. Используя эти данные, ответь на вопросы.
|
Класс |
Отметка «3» |
Отметка «4» |
Отметка «5» |
|
4 «А» |
6 |
11 |
6 |
|
4 «Б» |
2 |
13 |
8 |
|
4 «В» |
5 |
12 |
5 |
|
4 «Г» |
7 |
9 |
10 |
Сколько пятёрок по математике в 4 «Г» классе?
Задача 10.
В течение трёх лет учитель фиксировал количество «пятёрок» за контрольные работы по математике для одной и той же группы детей. Эти данные представлены в таблице.
|
Месяц |
Год |
||
|
2013 год |
2014 год |
2015 год |
|
|
Сентябрь |
16 |
14 |
17 |
|
Октябрь |
6 |
4 |
10 |
|
Ноябрь |
8 |
16 |
5 |
|
Декабрь |
16 |
5 |
18 |
В каком месяце 2014 года было наибольшее количество «пятёрок»?
В ответе укажите одно слово — название месяца в именительном падеже.
Задача 11.
Пётр Иванович выращивает морковь, лук и свёклу. Каждый овощ он выращивал на отдельном участке в течении четырёх лет. Пётр Иванович заносит в таблицу количество килограммов урожая, которое он получает с каждого участка за год. Используя таблицу, ответьте на вопрос.
|
Годы по порядку |
Морковь |
Лук |
Свёкла |
|
Первый год |
750 кг |
560 кг |
690 кг |
|
Второй год |
720 кг |
380 кг |
740 кг |
|
Третий год |
630 кг |
730 кг |
680 кг |
|
Четвёртый год |
690 кг |
710 кг |
620 кг |
Урожайность какого овоща была наибольшей за второй год?
В ответе укажите одно слово — название овоща в именительном падеже.
Задача 12.
Используя диаграмму, ответьте на вопрос.
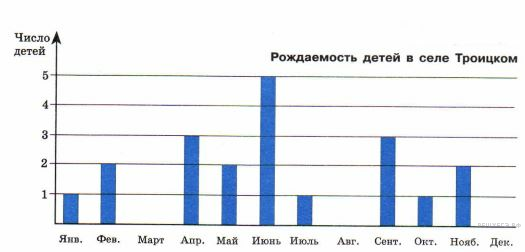
Сколько детей родилось в марте?
Задача 13.
Используя диаграмму, ответьте на вопрос.

В каком месяце родилось 600 детей?
В ответе укажите одно слово — название месяца в именительном падеже.
Задача 14.
Используя диаграмму, ответьте на вопрос.
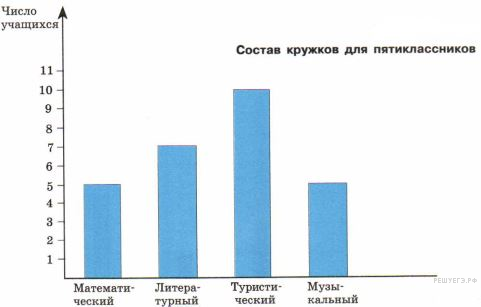
В каком кружке больше всего учащихся?
В ответе укажите одно слово — название кружка в именительном падеже.
Задача 15.
На диаграмме показано распределение дневной нормы питания, которую рекомендуют врачи. Используя диаграмму, ответьте на вопрос.
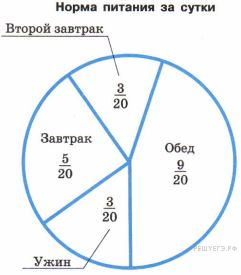
Сколько раз в день рекомендуют питаться врачи?
В ответе укажите цифру — количество раз.
Задача 16.
На диаграмме показано количество осадков, выпавших за год в Новинске. Используя диаграмму, ответьте на вопрос.
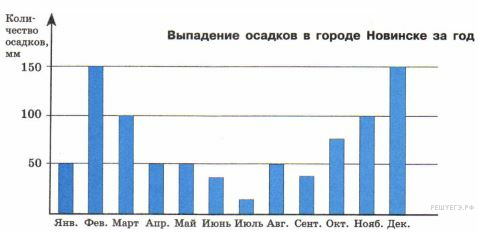
В каком месяце было меньше всего осадков?
В ответе укажите одно слово — название месяца в именительном падеже.
Задача 17.
Изображённая ниже диаграмма посадок в саду наглядно показывает, какая часть сада отведена под яблони, груши и кусты смородины. Используя диаграмму, ответьте на вопрос.
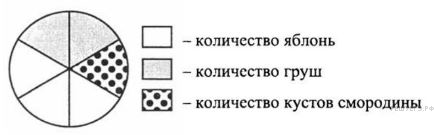
Какие деревья занимают большую часть сада?
Задача 18.
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8-го класса по математике в 2007 году (по 1000-балльной шкале). Используя диаграмму ответьте на вопрос.
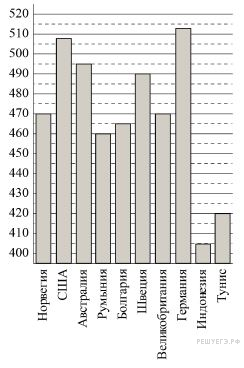
Какой средний балл у участников из Австралии?
Задача 19.
На диаграмме показана средняя температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — средняя температура в градусах Цельсия. Используя диаграмму, ответьте на вопрос.
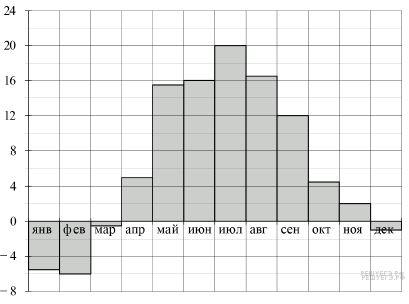
Какая самая высокая температура была летом?
Задача 20.
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по математике в 2007 году (по 1000-балльной шкале). Используя диаграмму, ответьте на вопрос.
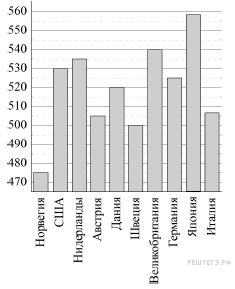
Сколько баллов набрали участники из Дании?
Задача 21.
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по естествознанию в 2007 году (по 1000-балльной шкале). Используя диаграмму, ответьте на вопрос.
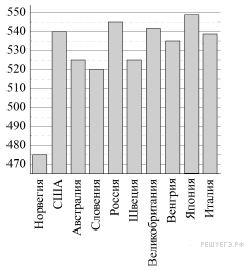
Участники каких стран набрали одинаковое количество баллов?
В ответе перечисляйте пары стран без пробелов и других знаков, в порядке, в котором они встречаются в диаграмме.
Задача 22.
На диаграмме показано распределение выплавки цинка (в тысячах тонн) в 11 странах мира за 2009 год. Среди представленных стран первое место по выплавке цинка занимало Марокко, одиннадцатое место — Болгария. Используя диаграмму, ответьте на вопрос.
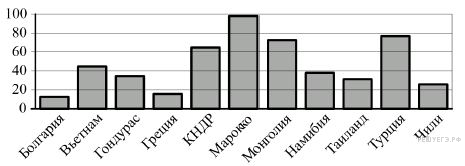
Какое место по выплавке цинка занимала КНДР?
Задача 23.
На диаграмме приведены данные о протяжённости восьми крупнейших рек России. Первое место по протяжённости занимает Лена. Используя диаграмму, ответьте на вопрос. Ответ напишите с точностью до десятых.

Какая примерно протяжённость у реки Волги? Ответ дайте в тыс. км.
Задача 24.
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Используя диаграмму, ответьте на вопрос.
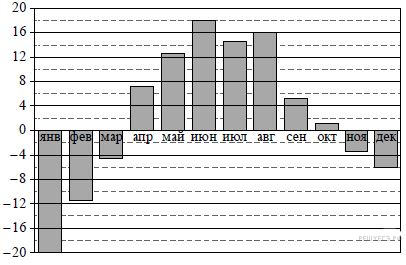
Какая примерно температура была в декабре?
Задача 25.
На диаграмме показано количество посетителей сайта РИА «Новости» в течение каждого часа 8 декабря 2009 года. По горизонтали указывается час, по вертикали — количество посетителей сайта на протяжении этого часа. Используя диаграмму, ответьте на вопрос.
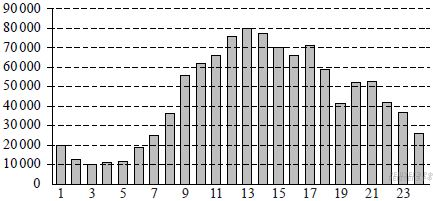
В течение какого часа было наименьшее число посетителей?
Задача 26.
На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Используя диаграмму, ответьте на вопрос.
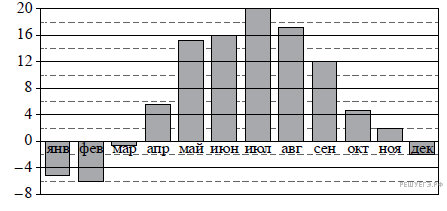
Какой месяц лета был самым холодным?
Задача 27.
На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Используя диаграмму, ответьте на вопрос.
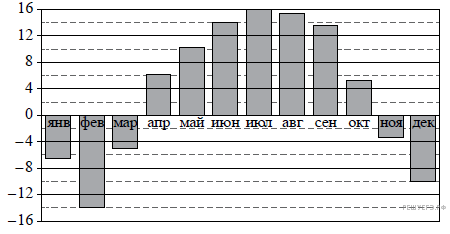
На протяжении какого месяца температура была примерно −10 °С?
Задача 28.
На игре КВН судьи поставили следующие оценки командам за конкурсы.
|
Команда |
Баллы за конкурс «Приветствие» |
Баллы за конкурс «СТЭМ» |
Баллы за музыкальный конкурс |
|
«АТОМ» |
28 |
22 |
25 |
|
«Шумы» |
29 |
20 |
23 |
|
«Топчан» |
26 |
21 |
27 |
|
«Лёлек и Болек» |
24 |
24 |
29 |
Какая команда набрала больше всего баллов за конкурс «Приветствие»?
Задача 29.
На диаграмме показано распределение выплавки меди в 10 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке меди занимали США, десятое место — Казахстан. Используя диаграмму, ответьте на вопрос.
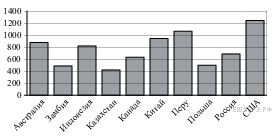
Какое место по выплавке меди занимала Польша?
Задача 30.
В таблице показано распределение медалей на Летних Олимпийских играх 1980 года в Москве среди команд, занявших первые пять мест по количеству золотых медалей.
|
Места |
Команды |
Медали |
||
|
Золотые |
Серебряные |
Бронзовые |
||
|
1 |
СССР |
80 |
69 |
46 |
|
2 |
ГДР |
47 |
37 |
42 |
|
3 |
Болгария |
8 |
16 |
17 |
|
4 |
Куба |
8 |
7 |
5 |
|
5 |
Италия |
8 |
3 |
4 |
Какая из этих стран получила наибольшее число серебряных медалей?
Задача 31.
В Северной Долине есть пять авиакомпаний: «Стрела», «Омикрон», «Компас», «Сванегольм» и «Небесный Скороход». В таблице дано число самолётов, принадлежащих каждой компании. По этим данным построена круговая диаграмма, но на ней подписаны названия только двух авиакомпаний.
|
Авиакомпания |
Количество самолётов |
|
Стрела |
162 |
|
Омикрон |
145 |
|
Компас |
75 |
|
Сванегольм |
144 |
|
Небесный Скороход |
194 |
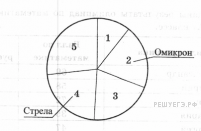
Какой авиакомпании соответствует сектор 3?
Задача 32.
В Зелёном Лесу есть пять авиакомпаний: «Лесные авиалинии», «Ласточка», «Вихрь», «Ариэль» и «Пчела». В таблице дано число самолётов, принадлежащих каждой компании. По этим данным построена круговая диаграмма, но ней подписаны названия только двух авиакомпаний.
|
Авиакомпания |
Количество самолётов |
|
Лесные авиалинии |
251 |
|
Ласточка |
134 |
|
Вихрь |
170 |
|
Ариэль |
180 |
|
Пчела |
115 |
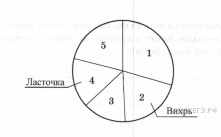
Какой авиакомпании соответствует сектор 5?
Задача 33.
На диаграмме показано, сколько побед одержали команды четырёх европейских стран в чемпионатах мира (ЧМ) и чемпионатах Европы (ЧЕ) по футболу. Пользуясь этими данными, выполните задания.
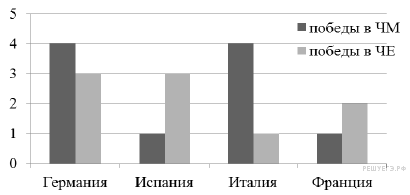
Перечислите страны, команды которых побеждали в чемпионатах мира больше, чем в чемпионатах Европы.
В ответе перечисляйте названия стран, без пробелов и других знаков, так как они подписаны на диаграмме.
Задача 34.
На диаграмме показано, сколько плюшек съедал Карлсон в каждый день недели. Пользуясь этими данными, ответьте на вопросы
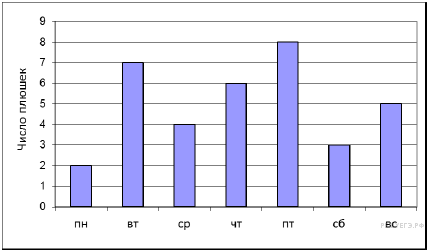
Сколько плюшек съел Карлсон в среду?
Задача 35.
Юра повесил кормушку для птиц. На диаграмме показано, сколько воробьёв и синиц прилетало к кормушке каждый день в течение недели. Сколько птиц прилетало в воскресенье?
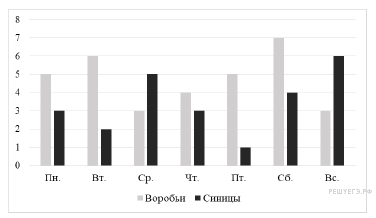
Задача 36.
Максим повесил кормушку для птиц. На диаграмме показано, сколько воробьёв и синиц прилетало к кормушке каждый день в течение недели. Сколько птиц прилетало в субботу?
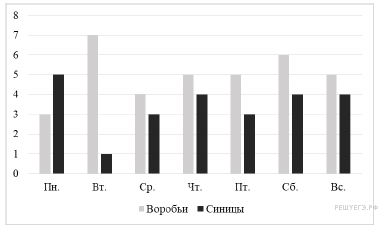
Задача 37.
Директор зоопарка рассказал, сколько рублей в день в среднем тратится на питание (содержание) различных животных в зоопарке.
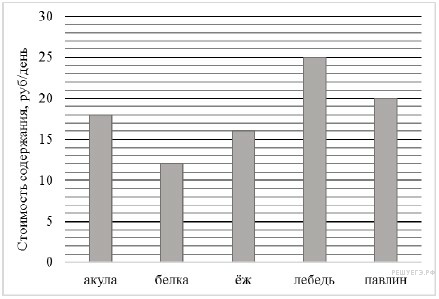
Сколько рублей в среднем тратится в день на питание одного ежа?
Задача 38.
Директор зоопарка рассказал, сколько рублей в день в среднем тратится на питание (содержание) различных животных в зоопарке.
Сколько рублей в среднем тратится в день на питание одной акулы?
Задача 39.
На диаграмме показано, сколько золотых и серебряных медалей завоевали российские спортсмены на Олимпийских играх в разные годы.
Сколько золотых медалей завоевали российские спортсмены в 2008 году?
Задача 40.
На диаграмме показано, сколько золотых и серебряных медалей завоевали российские спортсмены на Олимпийских играх в разные годы.
Сколько серебряных медалей завоевали российские спортсмены в 1996 году?
Задача 41.
На диаграмме показано, сколько золотых и серебряных медалей завоевали российские спортсмены на Олимпийских играх в разные годы.
Сколько золотых медалей завоевали российские спортсмены в 2000 году?
Задача 42.
На диаграмме показано, сколько раз в Большом театре шли балеты «Щелкунчик» и «Лебединое озеро» в течение пяти лет.
В каком году в Большом театре балет «Щелкунчик» шёл больше раз, чем в другие годы?
Задача 43.
На диаграмме показано, сколько раз в Большом театре шли балеты «Щелкунчик» и «Лебединое озеро» в течение пяти лет.
В каком году в Большом театре балет «Щелкунчик» шёл меньше раз, чем в другие годы?
Задача 44.
На диаграмме показано, сколько раз в Большом театре шли балеты «Щелкунчик» и «Лебединое озеро» в течение пяти лет.
В каком году в Большом театре балет «Лебединое озеро» шёл больше раз, чем в другие годы?
Задача 45.
На диаграмме показано, сколько раз в Большом театре шли балеты «Щелкунчик» и «Лебединое озеро» в течение пяти лет.
В каком году в Большом театре балет «Лебединое озеро» шёл меньше раз, чем в другие годы?
В прошлом уроке мы научились работать с транспортиром. Мы выяснили, что градусная мера развернутого угла равняется $180°$, это также градусная мера полуокружности. А следовательно, градусная мера самой окружности в два раза больше: $180°cdot2=360°$
Градусная мера любой окружности равняется $360°$.
В этом уроке мы познакомимся с круговыми диаграммами.
Круговая диаграмма — это схема с секторами, которая помогает наглядно показать какое-либо соотношение.
Задача №1
Рассмотрим ситуацию: у Образавра есть два яблока, три апельсина и одна груша. Давайте поможем ему наглядно показать соотношение фруктов в виде круговой диаграммы.
Для начала найдем общее количество фруктов: $$2 space яблока + 3 space апельсина + 1 space груша = 6 space фруктов$$
Теперь начертим окружность и расчертим в ней $6$ равных секторов. Как нам это сделать? Вспомним, что в окружности $360°$. Тогда разделим $360°$на $6$: $$360°:6=60°$$
Выходит, каждый сектор должен занимать по $60°$. С помощью транспортира построим все секторы, получаем рисунок 3.
Теперь вспомним, что яблоки занимают два сектора, апельсины – три сектора, а груша – один. Изобразим все фрукты в секторах, получим рисунок 4.
Остается стереть линии между одинаковыми фруктами и получить окончательную круговую диаграмму, рисунок 5. Каждый сектор обязательно подписываем!
Таким образом, круговая диаграмма дает нам возможность сравнить количество фруктов, не сравнивая их численные значения. По полученной диаграмме видно, что у Образавра больше всего апельсинов, а меньше всего — груш.
Бывают ситуации, когда градусные меры секторов не получаются такими же удобными, как в случае с фруктами. И тогда первый способ построения становится сложным.
Рассмотрим второй вариант построения круговых диаграмм.
Задача №2
В классах 5 «А» и 5 «Б» по $20$ детей. Оба класса написали контрольную работу по математике. Результаты 5 «А»: $12$ пятерок, $4$ четверки, $3$ тройки и $1$ двойка. Результаты 5 «Б»: $10$ пятерок, $5$ четверок и $5$ троек.
Для сравнения результатов этих классов построим две круговые диаграммы.
В данном случае неудобно вычерчивать по $20$ одинаковых секторов, как мы это делали раньше. В работе с большим количеством вариантов проще сразу работать с разными секторами.
Начнем с класса 5 «А». Всего в классе $20$ детей, а в окружности $360°$, значит говорим, что $20$ — это $360°$. Тогда найдем, сколько градусов занимает один ребенок: $$20 — 360°$$ $$1 — X°$$
$$X=frac{1cdot360°}{20}=18°$$
Теперь найдем, сколько градусов занимают ученики с разными оценками, для этого умножаем их количества на $18°$:
$12cdot18°=216°$ — такое количество градусов в диаграмме занимают дети из класса 5 «А», написавшие контрольную на пятерки.
$4cdot18°=72°$ — написали на четверки;
$3cdot18°=54°$ — написали на тройки;
$1cdot18°=18°$ — написали на двойки.
Аналогично для класса 5 «Б», сразу запишем ответ:
$10spaceдетей$ – $180°$ — такое количество градусов в диаграмме занимают дети из класса 5 «Б», написавшие контрольную на пятерки.
$5spaceдетей$ – $90°$ — столько детей написали на четверки;
$5spaceдетей$ – $90°$ — столько написали на тройки;
Теперь мы можем воспользоваться транспортиром и изобразить две диаграммы с результатами контрольной работы для двух классов:
Далее закрасим сектора для наглядности и подпишем каждый из них. Получаем конечные диаграммы:
С помощью круговых диаграмм мы можем сравнить результаты двух классов. Пусть «5» и «4» — хорошие оценки, а «3» и «2» — плохие. Тогда по диаграммам мы можем сказать, что результаты контрольной работы в классе 5 «А» лучше, чем в классе 5 «Б», потому что в классе «А» площадь зелёных зон больше.
Построение круговой диаграммы по процентам
Среди учеников начальной школы был проведен опрос на тему: «Какое ваше любимое время года?» $55%$ учеников выбрали лето, $20%$ выбрали зиму, $15%$ выбрали весну, и $10%$ — осень. Воспользуйтесь транспортиром, чтобы изобразить результаты опроса в виде круговой диаграммы.
Всего у нас есть $100%$, значит $100%$ занимают всю площадь окружности, то есть все $360°$. $$100% — 360°$$ $$1% — X°$$ $$X°=frac{360°}{100}=3.6°$$
Умножьте $3.6°$ на $55%, 20%, 15%spaceиspace10%$, чтобы узнать, сколько градусов в диаграмме займёт каждый сектор. По полученным результатам начертите круговую диаграмму.
Сравните свою диаграмму с рисунком 8. Вы могли расположить сектора с временами года в другой последовательности. Чтобы понять, правильно ли вы начертили диаграмму, посмотрите, сколько градусов занимают ваши секторы, правильный ответ:
$55% -198°$
$20% -72°$
$15% -54°$
$10% -36°$
В этой статье я рассмотрю решение третей задачи в 14 задании. Здесь нужно построить диаграмму. Прежде, чем ее строить надо найти значения, по которым ее строить и обязательно при построении диаграммы включить в нее легенду и подписи данных.
Смотрим на примере:
3. Постройте круговую диаграмму, отображающую соотношение числа участников из округов с кодами «В», «Зел» и «З». Левый верхний угол диаграммы разместите вблизи ячейки G6.
Делаем сначала выборку, сколько участников были из округов с кодами «В», «Зел» и «З». Для этого опять же воспользуемся фильтрацией: выделяем ячейку Округ, нажимаем на верхней панели Данные – фильтрация – Быстрый фильтр. Нажимаем на треугольник в столбце Округ и выбираем код “В”.
Напротив первого ученика в пустом столбце ставим 1 и копируем ее вниз до последнего ученика, выделяем столбец с 1 и справа внизу смотрим чему равна сумма этих 1. Получилось 132.
Далее, в фильтре выбираем код окгруга “ЗЕЛ”. И точно так же находим, сколько учащихся было из этого округа. Вышло 29.
Осталось тем же способом выяснить, сколько учащихся было из округа “З”. Таких 108.
Убираем фильтр: выделяем ячейку Округ – Нажимаем Данные – Фильтрация – кнопка Быстрый фильтр. Удаляем лишние 1.
Теперь составляем таблицу:
Строим диаграмму: выделяем таблицу – нажимаем Вставка – Диаграмма. Выйдет окно Мастера диаграмм. Выбираем круговую – разделенную диаграмму и нажимаем Готово.
Устанавливаем окно с диаграммой правым углом в нужную ячейку (указана в задании). Проверяем наличие легенды и делаем подписи данных на диаграмме. Для этого нажимаем по самой диаграмме правой кнопкой мыши и выбираем Подписи данных.
В итоге ответ на все это задание будет таким:
Если остались вопросы, пишите в комментариях. Обязательно отвечу. Если нужно разобрать конкретный пример, также – в комментарии.
Читайте: Задание 1, Задание 2, Задание 3, Задача 4, Задание 5, Задание 6, Задание 7, Задание 8, Задание 9, Задание 10, Задание 11, Задание 12, Задание 13.1, Задание 13.2, Задание 14-1, Задание 14-2, Задание 15.1, Задание 15.2.
Математика
6 класс
Урок № 13
Круговые диаграммы
Перечень рассматриваемых вопросов:
- Круговые диаграммы.
- Построение круговой диаграммы.
- Решение математических задач с использованием круговых диаграмм.
Тезаурус
Одну сотую часть числа (величины) называют процентом этого числа (величины).
Диаграмма – графическое представление данных, чтобы наглядно показать соотношение целого и его частей.
Центральный угол – это угол, вершина которого совпадает с центром окружности.
Прямой угол равен 90 градусов.
Развёрнутый угол равен 180 градусов.
Острый угол больше 0 градусов, но меньше 90 градусов.
Тупой угол больше 90 градусов, но меньше 180 градусов.
Основная литература
- Никольский С. М. Математика. 6 класс: Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н.Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е.Ф. Шершнёв, О.Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И.Ф. Задачи на смекалку: 5-6 кл. // И.Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Диаграмма в переводе с греческого языка – это изображение, рисунок или чертёж.
Круговые диаграммы – позволяют наглядно показывать соотношение целого и его частей.

Рассмотрим круговую диаграмму на примере:
В 8А классе 32 ученика, из них 16 – девочек и 16 – мальчиков.

В 8Б классе 30 учеников, из них 12 – девочек и 18 – мальчиков.

Разберём подробнее диаграмму 8Б.
Все ученики 8Б – это весь круг.


Круг разбит на равные части по числу ребят, так что каждой девочке и каждому мальчику соответствует один угол с вершиной в центре круга (такие углы называются центральными углами).

Для построения круговой диаграммы:
Выясняем, сколько градусов приходится на одну часть.


Имеем две группы учащихся:
12 учащихся класса – девочки.
18 учащихся класса – мальчики.



Покажем на круговой диаграмме результаты выполнения контрольной работы по алгебре в 9В классе.
Оценка «5» – 5 человек;
Оценка «4» – 10 человек:
Оценка «3» – 7 человек;
Оценка «2» – 2 человека.
Всего писали контрольную работу:


На диаграмме отражено количество жителей города, имеющих домашних питомцев:
70 % жителей – не содержат домашних питомцев;
30 % жителей – содержат домашних питомцев.

Чтобы построить такую диаграмму, надо определить величину центрального угла, соответствующего 30 и 70 % жителей.

Круговые диаграммы хорошо использовать при небольшом количестве частей, необходимых к изображению на диаграмме. Желательно не использовать круговые диаграммы для изображения более чем 15 различных совокупностей, так как при таком их количестве наглядность преподносимой информации может сильно снижаться.
Разбор заданий тренировочного модуля
№ 1. Единичный выбор.
Выберите верный ответ.
В голосовании должно было принять участите 120 работников предприятия. Используя круговую диаграмму, определите, сколько человек не участвовало в голосовании.

Варианты ответов: 12, 120, 24, 60.
Решение.
Пусть х человек не участвовали в голосовании. На диаграмме оранжевым цветом отмечен соответствующий им центральный угол, и сделана соответствующая их количеству в процентах подпись.

№ 2. Подчеркивания элементов.
Подчеркните верное утверждение.
Градусная мера углов.

