Как составить задание на соотношение

Текстовые задачи на отношения

Отношения встречаются в различных задачах и важно понимать, как с ними работать. Отношение – это какая-то уже сокращенная дробь. То есть данные в заданиях отношения – не реальная величина, а уже сокращенная, и мы должны узнать, на сколько.

Отношение = дробь, можно сокращать и расширять.

Если это тяжело принять, то можно поступить проще: представить, что в отношениях даны не величины, а какие-то деления. Отношение обычно записывается через двоеточие, например 3:5.

Например, рассматриваем отношение конфет на двух столах – представляем, что единицы отношения – это вазочки с одинаковым количеством конфет, мы должны узнать, сколько вазочек находится на одном столе, а сколько – на другом; если рассматриваем отношение цветов, то единицы отношения – это клумбы с одинаковым количеством цветов.

Пример 1

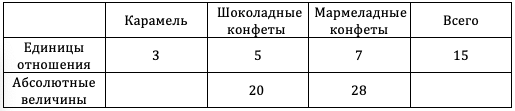
В магазине в наличии есть карамель, шоколадные конфеты и мармеладные конфеты в соотношении (3:5:7) соответственно.

1. Каково отношение между карамелью и шоколадными конфетами?​

Необходимо поделить количество коробок с карамелью на количество коробок с шоколадными конфетами, то есть (3:5).

2. Каково отношение между карамелью и мармеладными конфетами?​

Необходимо поделить количество коробок с карамелью на количество коробок с мармеладными, то есть (3:7.)

3. Какую часть составляют мармеладные конфеты от всех конфет?

Нужно сложить количество всех коробок. Всего у нас (3 + 5 + 7 = 15) единиц отношения. Далее поделим единицы отношения мармеладных конфет на единицы отношения всех конфет. Таким образом, мармеладные конфеты по отношению ко всем конфетам составляют (7:15. )

4. Если в магазине есть 20 шоколадных конфет, то каково количество мармеладных? ​

В этом вопросе мы встречаемся с переходом от единиц отношения к абсолютной величине. Вспоминаем, что наши конфеты разложены по коробкам. То есть у нас есть 5 коробок, в которых 20 шоколадных конфет. Коробки — это единицы отношения, а шоколадные конфеты – это абсолютная величина.

Количество шоколадных конфет разделим на количество клеток (20:5 = 4), т.е. в каждой коробке 4 шоколадные конфеты.

Помним, что размер единицы отношения равен для всех элементов этого отношения. Значит, что во всех коробках в магазине находится по 4 конфеты.​

Тогда всего в магазине 28 мармеладных конфет.

Пример 2

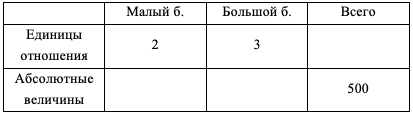
Отношение объема воды в большом и малом бассейне равно 3:2. Для того, чтобы поменять воду в этих двух бассейнах, потребуется 500 воды. Сколько воды в малом бассейне?

Решение:

Представим, что вся вода из большого бассейна хранится в 3 бочках, из малого в 2 точно таких же, это будут единицы отношения. Абсолютная величина – это весь объем бассейна.

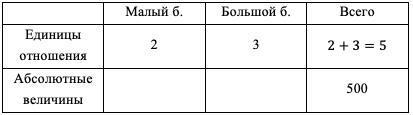
Если у нас 2 бочки от малого бассейна и 3 от большого, то всего их 5.

Мы знаем, что в 5 бочках находится 500 воды. Узнаем сколько в одной:

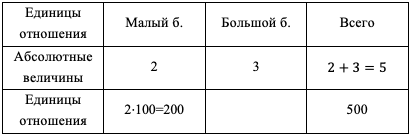
(500) : 5 = 100

Итак, узнаем, во сколько бочек вместится вся вода из малого бассейна, знаем их размерность, найдем объем малого бассейна.

Ответ: 200

Единицы отношения в геометрии

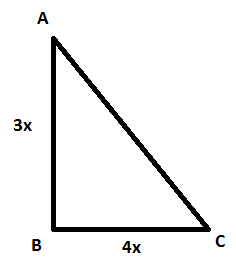
Единицы отношений могут встретиться и в задачах по геометрии. Смысл останется тем же: отношение — это какая-то сокращенная дробь. Например, может быть дано соотношение сторон или углов в задаче: стороны прямоугольного треугольника ABC AB и BC относятся как 3:4.

Так как отношение — это некая сокращенная дробь, то отношение сторон должно быть представлено следующим образом:

(frac{text{AB}}{text{BC}} = frac{3x}{4x})

То есть мы вводим переменную, чтобы показать, что отношение не является реальным значением сторон.

Стороны могут составлять 3 и 4, 6 и 8, 333 и 444 соответственно, а также принимать любые другие значения при условия сохранения данного соотношения.

Аналогичным образом можно представить углы или другие измеряемые величины.

Кратко пробежимся по теории.

Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным.

Пропорция – это равенство двух отношений.

Отношение – это частное двух чисел. Отношение показывает, во сколько раз одно число больше другого или какую часть одно число составляет от другого.

Основное свойство пропорции: в верной пропорции произведение крайних членов равно произведению средних.

Задачи на пропорции из учебников

Основная сложность в задачах такого типа – составить пропорцию и определить, прямо или обратно пропорциональны величины.

В шестом классе условие задач на пропорции записывают таблицей, а пропорциональность обозначают стрелкам в одном либо противоположных направлениях.

Решите с помощью пропорции задачи:

1) Для изготовления 8 одинаковых приборов необходимо 18 кг металла. Сколько таких приборов можно изготовить из 27 кг металла?

Пусть из 27 кг металла возможно изготовить x приборов.
К-во приборов   Масса металла
   ↓  8                       18 кг ↓
      х                        27 кг
$frac8x=frac{18}{27}$
18x = 8 * 27
$x=frac{8ast27}{18}$
$x=frac{4ast3}1$
x = 12
Значит, 12 приборов можно изготовить из 27 кг металла
Ответ: 12 приборов.

2) За 5 ч турист прошел 24 км. Какое расстояние он пройдет за 8 ч с той же скоростью?

Пусть x км пройдет турист за 8 ч.
Время    Путь
↓ 5 ч       24 км ↓
   8 ч       х км
$frac58=frac{24}x$
5x = 8 * 24
$x=frac{8ast24}5$
$x=frac{192}5$
$x=38frac25=38,4$
Значит, 38,4 км пройдет турист за 8 ч с той же скоростью
Ответ: 38,4 км.

3) Из 140 кг свежих вишен получают 21 кг сушеных. Сколько килограммов сушеных вишен получится из 160 кг свежих? Сколько килограммов свежих вишен необходимо взять, чтобы получить 31,5 кг сушеных?

Пусть из 160 кг свежих вишен возможно получить x кг сухих вишен.
Масса свеж.   Масса сух
↓ 140 кг              21 кг ↓
   160 кг               х кг
$frac{21}x=frac{140}{160}$
140x = 160 * 21
$x=frac{160ast21}{140}$
$x=frac{8ast3}1$
x = 24 
Значит, 24 кг  сушеных вишен получится из 160 кг свежих

Пусть из x кг свежих вишен необходимо взять, чтобы получить 31,5 кг сухих вишен.

$frac{21}{31,5}=frac{140}x$
21x = 31,5 * 140
$x=frac{31,5ast140}{21}$
$x=frac{1,5ast140}1$
x = 210
Значит, 210 кг свежих вишен необходимо взять, чтобы получить 31,5 кг сухих вишен
Ответ: 24 кг; 210 кг.

4) Объем бруска, изготовленного из древесины вишни, равен 800 см³, а его масса − 528 г. Какова масса бруска, изготовленного из этого же материала, если его объем равен 1500 см³?

Пусть x г масса бруска, если его объем равен 1500 см³.

$frac{800}{1500}=frac{528}x$
800x = 1500 * 528
$x=frac{1500ast528}{800}$
$x=frac{15ast66}1$
x = 990
Значит, 990 г масса бруска, если его объем равен 1500 см³.
Ответ: 990 г .

5) Из 45 т железной руды выплавляют 25 т железа. Сколько требуется тонн руды, чтобы выплавить 10 т железа?

Пусть x т руды требуется, чтобы выплавить 10 т железа.

$frac{45}x=frac{25}{10}$
25x = 45 * 10
$x=frac{45ast10}{25}$
$x=frac{9ast2}1$
x = 18
Значит, 18 т руды требуется, чтобы выплавить 10 т железа.
Ответ: 18 т руды.

6) Площадь поля 480 га. Пшеницей засеяли 24% площади поля. Сколько гектаров земли засеяли пшеницей?

Пусть x га земли засеяли пшеницей.

$frac{480}x=frac{100}{24}$
100x = 480 * 24
$x=frac{480ast24}{100}$
$x=frac{96ast6}5$
$x=frac{576}5=115frac15=115,2$
Значит, 115,2 га земли засеяли пшеницей.
Ответ: 115,2 га земли.

7) За первый час автомобиль проехал 70 км, что составило 14% всего пути. Сколько километров составляет весь путь?

Пусть x км составляет весь путь.

$frac{70}x=frac{14}{100}$
14x = 70 * 100
$x=frac{70ast100}{14}$
$x=frac{5ast100}1$
x = 500
Значит,  500 км составляет весь путь.
Ответ: 500 км.

8) Сплав содержит 12% цинка. Сколько килограммов цинка содержится в 80 кг сплава?

8) Пусть x кг цинка содержится в 80 кг сплава.

$frac{80}x=frac{100}{12}$
100x = 80 * 12
$x=frac{80ast12}{100}$
$x=frac{4ast12}5$
$x=frac{48}5=frac{96}{10}=9,6$ 
Значит, 9,6 кг цинка содержится в 80 кг сплава
Ответ: 9,6 кг цинка.

9) На пошив 14 одинаковых костюмов израсходовали 49 м ткани. Сколько таких костюмов можно сшить из 84 м ткани?

Пусть x костюмов можно сшить из 84 м ткани.

$frac{14}x=frac{49}{84}$
4x = 14 * 84
$x=frac{14ast84}{49}$
$x=frac{2ast12}1$
x = 24 
Значит, 24 костюма можно сшить из 84 м ткани.
Ответ: 24 костюма.

10) За 7 ч в бассейн налилось 224 л воды. За какое время в него нальется 288 л воды?

Пусть за x часов в бассейн нальется 288 л воды.

$frac7x=frac{224}{288}$
224x = 7 * 288
$x=frac{7ast288}{224}$
$x=frac{1ast72}8$
x = 9
Значит, 9 часов в бассейн будет наливаться 288 л воды.
Ответ: 9 часов.

11) Из 150 кг картофеля получают 27 кг крахмала. Сколько килограммов крахмала получат из 420 кг картофеля? Сколько килограммов картофеля необходимо, чтобы получить 30,6 кг крахмала?

Пусть x кг крахмала получат из 420 кг картофеля.

$frac{27}x=frac{150}{420}$
150x = 27 * 420
$x=frac{27ast420}{150}$
$x=frac{27ast14}5$
$x=frac{378}5$
$x=frac{756}{10}=75,6$ 
Значит, 75,6 кг крахмала получат из 420 кг картофеля.
Ответ: 75,6 кг крахмала.

Пусть x кг картофеля необходимо, чтобы получить 30,6 кг крахмала.

$frac{27}{30,6}=frac{150}x$
27x = 30,6 * 150
$x=frac{30,6ast150}{27}$
$x=frac{3,4ast50}1$
x = 170 
Значит, 170 кг картофеля необходимо, чтобы получить 30,6 кг крахмала.
Ответ: 170 кг картофеля.

12) В саду растет 320 деревьев, из которых 40% составляют яблони. Сколько яблонь растет в саду?

Пусть x яблонь растет в саду.
К-во деревьев   Проценты
  320 д                   100 %
    х    д                   40 %
$frac{320}x=frac{100}{40}$
100x = 320 * 40
$x=frac{320ast40}{100}$
$x=frac{32ast4}1$
x = 128
Значит, 128 яблонь растет в саду
Ответ: 128 яблонь. 

13) Масса соли составляет 24% массы раствора. Сколько килограммов раствора необходимо взять, чтобы он содержал 96 кг соли?

Пусть x килограммов раствора необходимо взять, чтобы он содержал 96 кг соли.

$frac{100}{24}=frac x{96}$
24x = 100 * 96
$x=frac{100ast96}{24}$
$x=frac{100ast4}1$
x = 400
Значит, 400 килограммов раствора необходимо взять, чтобы он содержал 96 кг соли.
Ответ: 400 кг.

14) На изготовление 3,5 кг ржаного хлеба требуется 2,5 кг муки. Сколько хлеба можно испечь из 17,5 т ржаной муки?

Пусть х кг хлеба можно испечь из 17,5 т муки.
17,5 т = 17500 кг
Масса хлеба   Масса муки
↓ 3,5 кг                 2,5 кг    ↓
   х кг                  17500 кг
3,5 кг − 2,5 кг
x кг − 17500 кг
$frac{3,5}{2,5}=frac х{17500}$
$х=frac{3,5ast17500}{2,5}$   умножим по 1 числу в числ. и знам. на 10
$х=frac{35ast17500}{25}$
x = 24500
Значит, 24500 кг = 24,5 т хлеба можно испечь из 17,5 т ржаной муки.
Ответ: 24,5 т

В задачах выше зависимость между величинами была прямо пропорциональная, но бывают задачи и с обратно пропорциональной зависимостью.

1) Самолет со скоростью 200 км/ч преодолевает расстояние от Москвы до Тюмени за 2 часа, за сколько он преодолеет это же расстояние со скоростью 150 км/ч?

Пусть за х часов самолет преодолеет то же расстояние со скоростью 150 км/ч
Скорость     Время
↑ 200 км/ч      2 ч ↓
  150 км/ч      х ч
Зависимость обратно пропорциональная, исходя из этого составляем пропорцию:
$frac{200}{150}=frac х2$
150 х = 200 * 2
$х=frac{200ast2}{150}$
$х=2frac23$
Значит,  за $2frac23$ часа он преодолеет это же расстояние со скоростью 150 км/ч.
Ответ: за $2frac23$ часа.

2) Три трактора вспахали поле за 7 часов. Сколько нужно тракторов, чтобы вспахать такое же поле за 5 часов?

Пусть нужно х тракторов, чтобы вспахать поле за 5 часов.
К-во тракторов   Время
 ↓3                          7 ч ↑
   х                          5 ч
$frac3х=frac57$
5 х = 3 * 7
х = 4,2
Так как количество тракторов не может быть дробным числом, округлим до большей величины.
х ≈ 5
Значит, 5 тракторов нужно, чтобы вспахать такое же поле за 5 часов.
Ответ: 5 тракторов.

3)  Для покрытия пола требуется 45 м линолеума шириной 2,2 м. Сколько потребуется линолеума шириной 1,5 м для покрытия пола той же площади?

Пусть х м линолеума шириной 1,5 м потребуется для покрытия пола той же площади.
Длина лин.   Ширина лин.
↓ 45 м                2,2 м ↑
  x м                  1,5 м
$frac{45}х=frac{1,5}{2,2}$
$frac{45}х=frac{15}{22}$
15 х = 22 * 45
$х=frac{22ast45}{15}$
x = 66
Значит, 66 м линолеума шириной 1,5 м потребуется для покрытия пола той же площади..
Ответ: 66 метров.

Нестандартные задачи на пропорции

Задача 1. Поп нанял работника Балду на год, обещал ему 120 рублей и красный кафтан. Однако, проработав 7 месяцев, Балда стал просить у попа расчет и получил за работу 50 рублей и красный кафтан. Сколько стоит кафтан у Балды?

Эту задачу можно решить, не прибегая к уравнению и пропорции, однако можно и пропорцией.

Решение

Пусть x – цена кафтана. Тогда за 12 месяцев Балда мог получить 120 руб. и кафтан, т.е. 120 + x. Но за 7 месяцев он получил 50 + x. Запишем в привычном для шестиклассника виде:

 | 12       120 + х |
↓ 7          50 + х  ↓

Записываем пропорцию

$frac{12}7=frac{120+х}{50+х}$

Применяя основное свойство пропорции, получаем уравнение:

7 * (120 + х) = 12 * (50 + х)
840 + 7 х = 600 + 12 х
12 х – 7 х = 840 – 600
5 х = 240
х = 48

Ответ: 48 рублей стоил кафтан у Балды.

Гораздо сложнее ученикам даются задачи на пропорциональную зависимость трёх и более величин. Причем настолько, что когда в 7 классе в учебнике геометрии (например, в учебнике Погорелова) встречается задача, где в условии говорится, что углы треугольника пропорциональны числам 2, 3, 4 (т.е. относятся как 2:3:4), некоторые ученики приходят в замешательство и утверждают, что не понимают условие. 

В последнее время задачи на пропорциональное деление стали встречаться в некоторых сборниках по занимательной, нестандартной и олимпиадной математике. Рассмотрим задачу такого плана.

Задача 2 на деление в данном отношении. Три предпринимателя – Давыдов, Петров и Максимов вложили в совместную организацию предприятия по производству мебели деньги. Первый вложил 60 тыс. руб., второй – 90 тыс. руб., а третий – 150 тыс. руб. Они получили прибыль в размере 117 тыс. руб. Сколько денег из прибыли получит каждый из предпринимателей при условии распределения ее пропорционально их вкладам?

Решение.

Найдём, каким числам пропорциональны вклады предпринимателей. Все числа запишем в тыс. руб.
60 : 90 : 150, т.е. 2 : 3 : 5.
Исходя из этого, можно записать, что 2x + 3x + 5x = 117, где 2x – часть прибыли, которую должен получить Давыдов, 3x – часть прибыли, которую должен получить Петров, 5x – часть прибыли, которую должен получить Максимов, исходя из пропорциональности вкладов. Отсюда x = 11,7 тыс. руб., т.е. Давыдов получит 23,4 тыс. руб., Петров – 35,1 тыс. руб., а Максимов – 58,5 тыс. руб.
Задачу можно решить и немного иначе:
1) 60 + 90 + 150 = 300 тыс. руб.
2) 117 : 300 x 60 = 23,4 тыс. руб.
3) 117 : 300 x 90 = 35,1 тыс. руб.
4) 117 : 300 x 150 = 58,5 тыс. руб.
Ответ: 23, 4 тыс. руб., 35,1 тыс., руб., 58,5 тыс. руб.

Классика нестандартных задач на пропорциональность трёх и более величин:

Задача 3. Три курицы за 3 дня снесли три яйца. Сколько яиц снесут 12 кур за 12 дней?

И сразу аналогичная, коих может быть бесконечное множество, а решаются они одинаково:

Задача 4. Пять землекопов за 5 часов выкапывают 5 метров канавы. Сколько потребуется землекопов, чтобы за 100 часов выкопать 100 м канавы?

Напрашивается ответ 12 в задаче про куриц и 100 в задаче с канавой, но это не верно. В задаче про куриц правильный ответ 48, а в задаче про землекопов правильный ответ – 5.

Задача 5. 2 робота за 3 часа собирают 1 компьютер. Сколько компьютеров соберут 10 роботов за 12 часов?

Иногда условия таких задач выписывают примерно также как обычную пропорцию и делают стрелочки. Например:

Роботы   Часы   Компьютеры
| 2             | 3             | 1
↓10          ↓12            ↓ х

Решение.

Если 2 робота за 3 часа собирают 1 компьютер, то сколько компьютеров соберут те же два робота за 12 часов?
12 : 3 = в 4 (раза) – больше будет времени у 2х роботов на сборку компьютеров
Если у двух роботов будет времени в 4 раза больше, то и соберут они в 4 раза больше компьютеров, т.е.
1 * 4 = 4 (компьютера)  – собирают 2 робота за 12 часов.

Если роботов будет 10, то сколько компьютеров они соберут за 12 часов?
10 : 2 = в 5 (раз) – больше роботов
Так как роботов будет в 5 раз больше, то и соберут они за 12 часов в 5 раз больше компьютеров.
4 * 5 = 20 (компьютера)  – соберут 10 роботов за 12 часов.

Ответ: 20 компьютеров.

Задача 6. 3 маляра за 5 дней могут покрасить 60 окон. Сколько окон покрасят 5 маляров за 4 дня?

Решение.

60 : 3 =  20 (окон) – может покрасить 1 маляр за 5 дней,
20 : 5  = 4 (окна) – маляр покрасит за 1 день
4 * 4 = 16 (окон) –  он покрасит за 4 дня.
А если таких маляров будет 5, то окон будет покрашено
5 : 16 = 80 (окон) – покрасят 5 маляров за 4 дня
Ответ: 80 окон.

Лишь только тогда, когда ученик приобретает опыт в решении таких задач поэтапно, можно показать ему решение подобной задачи пропорцией.

3 маляра за 5 дней выполнят работу, которую можно измерить как 3 х 5 человеко-дней. Можно пояснить, что человеко-дни – единица, с помощью которой учитывается рабочее время на производстве. И по условию эта работа выражается в 60-ти окнах. В задаче требуется узнать, чему равна работа, которая измеряется как 4 х 5 человеко-дней.
Значит, можно составить пропорцию:

К-во окон   К-во человеко-дней
60 окон        3*5 человеко-дней
х окон          4*5 человеко-дней

$frac{60}х=frac{3ast5}{4ast5}$

$х=frac{4ast5ast60}{3ast5}=80$ (окон) –  покрасят 5 маляров за 4 дня

Ответ: 80 окон.

Однако надо быть внимательным. В некоторых задачах имеет место быть и обратно пропорциональная зависимость. Если, например, количество рабочих увеличивается, то количество дней, за которые им надо выполнить заданную работу, уменьшается.

Задача 7. 3 маляра за 5 дней могут покрасить 60 окон. За сколько дней 5 маляров смогут покрасить 80 окон?

Решение.

За 1 день один маляр покрасит 4 окна, а 5 маляров за 1 день – 20 окон. А 80 окон 5 маляров смогут покрасить за 4 дня (80 : 20 = 4).

Через пропорцию:

Кол-во маляров Скорость покраски
3 м.                        60/5 окон/день
5 м.                        80/х  окон/день

$5astfrac{60}5=3astfrac{80}х$
…
х = 4

В заключение обзора сложных задач на пропорцию и методов их решения рассмотрим задачу, с четырьмя величинами. Такие задачи сегодня могут встречаться на олимпиадах. Но было время, когда они входили в курс школьной математики (учебник Киселева). 

Задача 8. На 5 одинаковых керосинок, горевших 24 дня по 6 часов ежедневно, израсходовано 120 л керосина. На сколько дней хватит 216 л керосина, если 9 таких же керосинок будут гореть по 8 часов в день?

Решение.

С тем, чтобы не запутаться в условии, выпишем все данные в виде таблички. В учебнике Киселева таблицы отсутствуют, а условие записано двумя строчками. Последуем его примеру:

5 керосинок 24 дня по 6 часов – 120 л
9 керосинок x дней по 8 часов – 216 л

Далее, если следовать логике решений задач, приведённых на этой странице, а также логике Киселева, решим задачу поэтапно. Сначала решим такую задачу: На сколько дней хватит 216 л керосина, если те же 5 керосинок будут гореть по 6 часов в день? То есть:

120 л – на 24 дня
216 л – на y дней

$у=frac{216ast24}{120}=43,2$ (дня)

То есть 216 л керосина хватит на 43,2 дня, если будет работать 5 керосинок.

Теперь найдём, на сколько дней хватит 216 л керосина, если керосинок будет не 5, а 9. То есть, если 5 керосинок могут работать 43,2 дня, то 9 керосинок меньше в 1,8 раза (9 : 5 = 1,8). То есть 9 керосинок, работая по 6 часов в день при запасе в 216 литров, проработают 24 дня.

Осталось найти, на сколько дней хватит 216 л керосина, если 9 таких же керосинок будут гореть по 8 часов в день. То есть:

24 дня – по 6 часов в день
х дней – по 8 часов в день

Таким образом,

$х=frac{24ast6}8=18$ (дней)

Все выполненные действия можно записать одной дробью и сократить ее:

$х=frac{24ast216ast5ast6}{120ast9ast8}=18$ (дней)

Ответ: 18 дней.

Надеемся, что способы решения задач на пропорцию, изложенные в этой статье, помогут пятиклассникам и шестиклассникам, стремящимся изучить школьный материал, в том числе и тот, который выходит за рамки программы обычной школы, но который может быть полезен при подготовке к олимпиадам.

Ранее мы рассматривали отношения. Сегодня рассмотрим различные задачи на отношения.

Многие задачи посвящены тому, чтобы разделить заданное число на два или три в том или ином отношении. Например, необходимо разделить 30 конфет в отношении 2:3. То есть мы делим конфеты равным образом между друзьями, при этом зная, что сегодня в гости придет 2 друга, а завтра еще 3. То есть на сегодня надо оставить 2 части конфет, а на завтра – 3 части, итого 5 частей конфет. Делим 30 на 5 и получаем то количество конфет, которыми мы угостим одного друга. Но сегодня надо оставить 2 части, так как в гости придут 2 друга, а на следующий день останется 3 части, для 3 друзей.

В некоторых учебниках предлагается ввести переменную, обозначив ее как коэффициент пропорциональности k. Далее составляется уравнение относительно k, а затем через этот коэффициент пропорциональности находятся части отношения.

В более сложных задачах используются отношения трех чисел. Два разных отношения можно объединить в одно, если значение соответствующей части совпадает. Например, x:y=3:4, а y:z=2:1. Для объединения в одно отношение нужно, чтобы число, соответствующее y было одним и тем же в обоих отношениях. Других совпадающих переменных в этих отношениях нет. Воспользуемся свойством отношения и умножим правую и левую часть второго отношения на два, получим y:z=4:2. Можем приравнять: x:y:z=3:4:2

И еще одна задача из сборника Сканави, кажется сложной, но все достаточно просто решается.

Надеемся, теперь Вы с легкостью сможете решать задачи на отношения. Задавайте вопросы в комментариях, пишите, какие темы Вы хотели бы разобрать в следующий раз.

Представьте себе вот такую задачу – “Размер прямоугольного тента 6×2 метра весит 2 кг. Сколько весит тент размерами 15×2 метра?”.

В общем виде методика решения понятна – раз тент один и тот же, но разной площади, то нужно вычислить площадь первого тента, вычислить площадь второго, поучить соотношение этих площадей – то есть то, во сколько раз второй тент больше первого, и умножить это соотношение его на массу первого тента. Однако, в данной задаче площадь первого тента – 6∙2 = 12 м², площадь второго – 15∙2 = 30 м², а 30 на 12 без остатка не делится, а дети в 4-м классе с дробями работать ещё не умеют. Поэтому для решения данной задачи нужен несколько более хитрый подход. Решению таких задач и посвящён этот урок.

Первые задачи, которые мы будем разбирать в этом уроке, могут показаться очень простыми. Однако, они нужны нам для того, чтобы провести путь от простых задач к сложным задачам на соотношение площадей и масс и прочих параметров.

Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

Задача 1

Круглый лист железа площадью 2 дм² весит 117 г. Сколько весит прямоугольный лист такого же железа такой же толщины размером 2 дм в ширину и 4 дм в длину?

Решение:

Площадь второго листа – произведение длины на высоту – 2∙4 = 8 дм².

Его площадь в 4 раза больше (8:2 = 4), чем площадь круглого листа железа. Так как железо одно и то же, то для того, чтобы узнать, сколько весит прямоугольный лист железа, надо массу круглого листа умножить на то, во сколько раз прямоугольный лист больше круглого, то есть на 4.

Масса второго листа:

117 * 4= 468 г

Обратим внимание, что в этой задаче не имеет значение, что первый лист круглый, а второй – прямоугольный. Важно только соотношение их площадей.

Ответ: 468 г

Задача 2

Лист железа площадью 1 м² весит 3999 г. Сколько весит лист такого же железа такой же толщины площадью 70000 квадратных сантиметров.

Решение:

Для решения этой задачи надо привести величины к одинаковым единицам измерения. Проще всего квадратные сантиметры перевести в метры. 1 м – это 100 см, 1 м² – это 10000 см².

Таким образом, 70000 см²:10000 это 7 м².

Если первый лист железа имеет площадь 1 м², а второй – 7 м², то, при условии, что железо одно и то же, масса второго листа в 7 раз больше.

Масса второго листа:

3999 *7 = 27993 г.

Ответ: 27993 г.

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

Задача 3

Прямоугольный лист картона размером 15 на 10 см весит 70 г. Сколько весит лист такого же картона такой же толщины со сторонами 75 на 10 см?

Решение:

Площадь первого листа: 15∙10 = 150 см²

Площадь второго листа: 75∙10 = 750 см²

Так как картон один и тот же, то второй лист будет весить больше первого листа во столько раз, во сколько больше его площадь, то есть в 5 раз, так как 750:150 = 5.

Масса второго листа: 70∙5 = 350 г.

Эту же задачу можно решить не вычисляя напрямую площади. Так как оба листа прямоугольные, у обеих одна сторона одинаковая – 10 см. Значит для того, чтобы найти, во сколько раз один лист больше второго, надо длину второй стороны одного листа разделить на длину второй стороны другого листа, то есть 75:15 = 5. То есть мы получили то же самое соотношение площадей, что и при делении 750:150. Соответственно, и масса второго листа при таком варианте решения будет той же, что и при первом варианте.

Ответ: 350 г

Прямоугольный лист меди размером 15 на 10 см весит 70 г. Сколько весит прямоугольный лист такой же меди размером 75 на 50?

Аналогично предыдущей задачи, эту можно решить двумя способами.

Способ первый – нахождение площадей

Площадь первого листа: 15∙10 = 150 см².

Площадь второго листа: 75∙50 = 3750 см².

Вычислим, во сколько раз второй лист больше первого:

3750:150 = 25.

Следовательно, масса второго листа в 25 раз больше массы первого: 70*25 = 1750 г.

Способ первый – нахождение соотношения сторон листов

Для того, чтобы не иметь дела с площадью и большими числами, можно найти, как соотносятся каждые из двух сторон этих двух листов, а потом перемножить эти соотношения.

Длина первого листа – 15, длина второго листа – 75.

Соотношение длин: 75:15 = 5

Ширина первого листа – 10, ширина второго листа – 50.

Соотношение ширин: 50:10 = 5

Произведение соотношений: 5∙5 = 25.

Таким образом, вторым способом мы тоже получили, что второй лист в 25 раз больше первого.

Следовательно, масса второго листа в 25 раз тоже в 25 раз больше массы первого.

Ответ: 1750 г

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

Задача 5

Размер прямоугольного тента 6×2 метра весит 2 кг. Сколько весит тент размерами 15×2 метра?

Это как раз та самая задача, про которую мы говорили в начале этого урока.

Как уже писалось выше, площади двух тентов (15∙2 = 30 и 6∙2 = 12) не делятся без остатка друг на друга. Если мы будем искать соотношение сторон по отдельности, то увидим, что 15 на 6 тоже не делится без остатка.

15 не делится нацело на 6, но делится на 3. Воспользуемся этим, и найдём массу тента со сторонами 3×2. Этот тент будет в два раза меньше первого тента 6×2. Одна сторона одинаковая – 2 метра, а вторая сторона в два раза меньше (6:3 = 2). Соответственно, масса тента со сторонами 3×2 = 2:2 = 1 кг.

Теперь рассмотрим тенты 3×2 и 15×2.

Одна сторона у этих тентов одинаковая – 2 м, а вторая сторона второго тента в 5 раз больше аналогичной стороны первого тента (15:3 = 5).

Таким образом, масса тента 15×2 в 5 раз больше массы тента 3×2. то есть 5∙1 = 5 кг.

Итак, для решения этой задачи нам нужно было придумать ещё один тент, стороны которого были бы кратны сторонам и первого тента и сторонам второго тента. Благодаря этому приёму мы сначала вычислили массу такого тента, зная массу первого тента, а потом легко вычислили массу нужного нам второго тента, пользуясь тем, что обе стороны этого тента кратны (делятся без остатка) сторонам нашего придуманного тента.

Ответ: 5 кг