Как составить задания разного типа

Актауский городской координационный центр образования

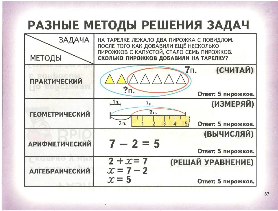
Решение разных типов задач

г. Актау-2016

«Утверждаю»

на заседании Совета

ГУ «АГКЦО»

«___»______________2016г

Составитель:

Юркина Надежда Михайловна

учитель начальных классов

школы-лицея №7 г. Актау

Рекомендовано

экспертной комиссией

ГУ «АГКЦО»

протокол №___________________

«____»___________________2016г

Введение

На протяжении многих лет, наблюдая за детьми, я заметила, что детям трудно дается решение видов задач. Решила, что этому надо уделить больше внимания на уроках.

   Решение задач – это важнейшее средство формирования математических знаний, умений,

навыков учащихся, но в то же время- это одна из основных форм изучения математики, а также средство математического развития ребенка. С  методической точки зрения для полноценной работы над задачей ученик должен:

– уметь хорошо читать и понимать смысл прочитанного;

– уметь анализировать текст задачи, выявлять его структуру и взаимоотношения между данными и искомыми;

– уметь правильно выбирать и выполнять арифметические действия;

– уметь записывать решение задач с помощью соответствующей математической символики.

    Можно научить решать задачи конкретных видов, но если  не выработать общий метод подхода к задаче, общий способ её анализа, то дети самостоятельно решать задачи не научаться.

     При обучении решению задач ставлю такие цели:

– учиться анализировать и самостоятельно решать задачи;

– умение составлять задачи;

– развивать умение решать задачи;

– развивать логическое мышление;

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ОБУЧЕНИЮ РЕШЕНИЮ СОСТАВНЫХ ЗАДАЧ В НАЧАЛЬНОЙ ШКОЛЕ.

        В начальном курсе математике понятие «задача»  обычно используется тогда, когда речь идет об арифметических задачах. Они формируются в виде текста, в котором находят отражение количественные отношения между реальными объектами. Поэтому их называют «текстовыми», « сюжетными», «вычислительными» или «практическими».

        Начальный курс математики ставит основной целью научить младших школьников решать задачи арифметическим методом, который сводится к выбору арифметического действия или действий, моделирующих связи между данными и искомыми величинами. Оно оформляется в виде последовательности числовых равенств или выражением, к которым даются пояснения.

Определение составной задачи.

        Задача, для решения которой надо выполнить несколько действий, связанных между собой, называется составной задачей. Она включает в себя ряд простых задач. Связанных между собой, так что искомые одних простых задач служат данными других. Решение составной задачи сводится к расчленению ее на ряд простых задач и к последовательному их решению.

Работа над условием составной задачи.

        В подготовительный период перед знакомством с составной задачей одной из форм работы является решение простых задач. Простые задачи являются составными частями одного из способов  введения составных задач.

        Решение составной задачи всегда начинается знакомством с условием и вопросом к ней. Пока дети не научатся читать бегло, условие  и вопрос  к нему рассказывает или прочитывает учитель. Но когда дети овладели навыком беглого чтения, тогда целесообразно предлагать читать задачи одному из учеников; а в некоторых случаях всем ученикам про себя. В процесс чтения входит не только произношение вслух или про себя слов текста, но и осмысление содержания прочитанного так, чтобы после чтения передать содержание, не пропуская, ни одного существенного элемента.

        Если в тексте задачи встречаются незнакомые детям слова или выражения, то рекомендуется разъяснить их значение до начала чтения.

        Повторять чтение текста задачи следует как можно реже, когда, например, при первом чтении текст ошибочно искажен. Детей полезно приучать запоминать содержание задачи после одного чтения, чтобы не расходовать время на повторное чтение. Если условие задачи учащиеся поняли недостаточно хорошо, то задачу можно повторить по вопросам учителя, а затем в виде связного пересказа содержания ее повторяет один из учеников.

Формы краткой записи условий задачи.

        После ознакомления с содержанием задачи можно приступить к поиску ее решения.

        При введении задач нового типа поиском решения руководит учитель, а затем учащиеся выполняют это самостоятельно. В том и другом случае используются  специальные приемы, которые помогают детям вычленить величины, данные и искомые числа, установить связи между ними. К таким приемам относятся и иллюстрация задачи.

 Наряду с предметной иллюстрации, начиная с 1 класса, используется и схематическая – это краткая запись условия задачи. В краткой записи фиксируются в удобной форме величины, числа данные и искомые, а также некоторые слова, показывающие, о чем говорится в задаче: «было», «улетело», «осталось», и т.п., и слова обозначающие отношения: «больше», «меньше» и т.п., и слова, указывающие на величины, данные в условии задачи: «скорость», «время», «расстояние» и другие.

        Для того чтобы краткая запись в максимальной степени способствовала решению задачи, нужно:

        1).    Краткую запись составлять на основе анализа текста задачи;

        2).    В краткой записи должно быть минимальное количество условных обозначений;

        3). Количество вопросительных знаков в краткой записи должно соответствовать количеству действий в задачи;

        4).    Форму краткой записи выбирать такую, чтобы она более наглядно представляла условие задачи.

        Краткую запись задачи можно выполнять в виде опорной схемы, таблицы, чертежа, с помощью геометрических фигур.

Способы анализа задачи.

        В формировании умения решать текстовые задачи велика роль правильно организованного разбора задачи. В методике обычно говорят о двух способах проведения такой работы: о разборе от данных к искомым значениям и, наоборот. От искомых (вопроса задачи) к данным (известным) значениям. Первый называется синтетическим, второй – аналитическим. Возможна их комбинация – аналитико-синтетический способ рассуждений.

Составление задач по краткой записи.

        Составление задач по краткой записи – важный этап  в работе над составной задачей и отработке навыков решения ее. Эту работу надо начинать еще при работе над простой задачей  и параллельно с записью краткого условия задачи. Сначала рекомендуется научить составлять краткое условие составной задачи, решать ее, затем предложить аналогичную краткую запись, но с другими числами и попросить сформулировать задачу, аналогичную данной. Затем постепенно, работая над составлением задач, менять формы краткой записи условия задачи и исключать предварительную работу с заданной задачей и ее краткой записью.

Пояснения к решению задач.

        Эта форма работы над составной задачей предусматривает проверку умения учащихся по данным действиям решения задачи пояснить, на какой вопрос и с какой целью отвечает действие. Она может быть использована при первоначальном закреплении решения задач, при индивидуальной работе, как со слабыми, так и сильными учениками, при разборе нового способа решения задачи, который не предложил ни один ученик. Такая форма работы помогает учащимся увидеть другие отношения, вести необходимую цепочку логических  рассуждений, анализировать и делать выводы.

        Овладение основами математики немыслимо без решения и разбора задач, что является одним из важнейших звеньев в цепи познания математики. Этот вид занятий не только активизирует изучение математики, но и прокладывает пути к глубокому пониманию ее. Работа по осознанию хода решения той или иной математической задачи дает импульс к развитию мышления ученика. Кроме того, нельзя забывать, что решение задач воспитывает у детей многие положительные качества характера и развивает их эстетически.

При изучении задач в курсе математики, как простых, так и сложных, как обычных арифметических, так и типовых оказывается высокоэффективным систематическое применение так называемого метода обратных задач.

Успех обучения решению задач посредством преобразования прямой задачи в обратные задачи объясняется как первопричиной тем, что такой путь заставляет поднимать из сферы подсознания наибольшее разнообразие связей, заключенных в содержании задачи. Это и обеспечивает – на языке дидактики – глубокое и прочное усвоение материала.

На составление и решение обратной задачи уходит несравненно меньше времени, чем на решение новой задачи, так как числовые данные и сюжет остаются прежними; производится здесь лишь логическая операция по переосмыслению ролей чисел; неизвестное в прямой задаче становится известным и наоборот.

На мой взгляд, самое трудное в начальной школе – научить ребенка грамотно писать, а самое трудное в математике – научить решать задачи.

В процессе работы мне хотелось повысить процент способных детей и уменьшить процент слабых.

Кроме того, в своей работе я стремлюсь к тому, чтобы как можно больший процент детей имел качественный показатель знаний по математике. Далее я опишу, как я этого добиваюсь и каковы результаты работы.

Я ознакомилась с мнением различных ученых-методистов (смотреть список литературы) по вопросу классификации задач и решению взаимно обратных задач, как по традиционной, так и по развивающей методике.

                                                 Виды задач

• Простые

• Текстовые

• Составные

• Обратные.

  Обучению решению задач начинаю с 1 класса. В 1 классе  использую предметную модель, она способствует выяснению способа решения задач.

Например: У Марины и Кати вместе 5 яблок. У Марины 3 яблока. Сколько яблок у Кати?

На I этапе обучаю решению:                                                            

 -2 яблока отдала

– Каким действием узнаем, сколько яблок у Кати? (-)

На I I  этапе учу детей переходить от предметной модели к образной модели. 

В конце года при проведении проверочной работы в 1 классе выяснила, что дети хорошо владеют образной моделью и без труда справляются с решением простых задач.

Во 2 классе я продолжила работу с задачами. Это стало III  этапом в моей работе.

На этом этапе использую краткую запись и графический чертеж, где ответ задачи не виден и решение скрыто.

    Для более эффективной работы с задачами разных  видов использую приемы преобразования и составления задач.

    При составлении задач  на уроках использую разные таблицы:

– нахождение суммы двух чисел;

– уменьшение числа на несколько единиц;

– разностное сравнение;

Во 2 классе наряду с решением взаимосвязных простых задач провожу подготовительную работу к  введению составных задач и предлагаю задания:

– с постановкой вопроса к задаче;

Например: На садовом участке посадили 8 кустов смородины, а крыжовника – на 5 кустов меньше.

-задачи с недостающими данными;

Например: В одной вазе       груш, а в другой на         груш …. Сколько груш в другой вазе?

– задачи двумя вопросами;

Например: В одной вазе 5 груш, а в другой на 3 груши больше. Сколько груш в другой вазе? Сколько груш в двух вазах? При анализе итоговой контрольной работы за 2 класс выяснила, что ребята справляются с решением задач определенного вида.

   В 3 классе продолжила работу над решением задач и уделила внимание составлению и решению текстовых задач. При решении текстовых задач применяю разные приемы на развитие мышления:

1. изменение вопроса задачи.

Цель: научить отличать простые задачи от составных; осознавать выбор действий; подбор вопросов познавательного характера.

2.Поиск различных способов решения.

Цель:  более глубокое раскрытие взаимосвязи между величинами.

3.Прием сравнения и их решения.

Цель:  развивать творческую активность, мышление.

4.Выявить неверное решение

Цель: развивать умения выбора арифметического действия, логическое мышление.

5.Прием, основанный на предложенных объектах, сюжете, вспомогательной модели.

Цель: сформулировать правильный подход к решению задачи.

 6.Выбери слова, характеризующие сюжет задачи.

Цель: научить выделять ключевые слова для краткой записи.

 7.Соотнесите предложенные объекты со схемой, указав количественные характеристики.

Цель: уметь составлять схемы и таблицы по данным задачи.

8.Прием составления задачи по предложенной программе действий. 

Цель: научиться самостоятельному разбору задачи.

    При составлении текстовых задач предлагаю детям пользоваться алгоритмом решения

               1.Придумай сюжет.

               2. Назови объекты, о которых будет говориться в задаче.

               3. Дай количественную характеристику объектам.

4. Сформулируй требование задачи.

               5. Сформулируй текст задачи

При проведении итоговой контрольной работы за 3 класс выявила, что дети поняли принцип решения задачи, но ещё есть трудности.

    В 4 классе я закрепляла и развивала умение решать задачи.

     При решении задач использовала разные виды работ с задачами:

  – фронтальное (коллективное) под руководством учителя;

– фронтальное под руководством учащихся;

– самостоятельное решение (решение задач с недостающими данными; решение задач определенного вида.)

-выполнение части решения.

     Для развития интереса к задаче использовала виды работ с решенной задачей:

1)      изменение условий так, чтобы решалась другим действием;

2)      постановка нового вопроса;

3)      решение задачи другим способом;

4)      изменение числовых данных.

    На уроках применяла виды работ, которые не включают в себя полное решение задачи:

1)      установление соответствия между содержанием задачи и схемой, чертежом, таблицей и краткой записи.

2)      выбор среди  задач – задач данного вида ( как решали на уроке или прошлом уроке)

3)      выбор задач, ответ на вопрос которых может быть найден заданной последовательностью действий:  1) +     2):    3) +

4)      обнаружение ошибок в решении задач;

5)      решение вспомогательной задачи или цепочки таких задач перед решением трудной задачи;

6)      выбор тех задач, которые можно решить устно;

7)      с заменой чисел на буквы.

      Реализовать разнообразные функции задач поможет и выполнение такого вида работы с задачами- как составление задач самими учащимися.

      Часто при решении задач у учащихся вызывает затруднение нахождения разных способов решения задач. Для помощи использую следующие приемы:

1)      прием разъяснения плана решения задачи;

2)      прием пояснения готовых способов решения;

3)      прием соотнесения пояснения с решением;

4)      прием продолжения начатого способа решения;

5)      нахождение «ложного» способа решения.

В своей работе я постаралась описать то многообразие видов и форм работы с задачей на уроке, использование которых сделает встречу учеников с задачами интересной и увлекательной.

       Предложенные различные методические приемы при составлении текстовых задач соответствуют совершенствованию логического мышления и творческих способностей детей.

Следует отметить существенно важные дидактические достоинства метода обратных задач.

Во время преобразования задачи учащийся выявляет и использует взаимно обратные связи между величинами задачи:

Прямая задача	Ц.	К.	С.
30 тг.	6 шт.	?тг.
Обратная задача	Ц.	К.	С.
30 тг.	? шт.	180 тг.

Во время преобразования учащийся практически познает связи между действиями. Полезно, например, обратить внимание учащихся на то, что количество действий при решении прямой и обратной задач совпадает (это правило нарушается крайне редко). Кроме того, полезно знать учащимся следующее явление: каждому действию прямой задачи соответствует действие той же ступени в обратной задаче.

Количество комбинаций при составлении обратной задачи ограниченно: оно равно количеству данных в задаче.

Решая обратную задачу, учащийся перестраивает суждения и умозаключения, использованные при решении прямой задачи, преодолевая при этом в мышлении инерцию действий, выполненных при решении прямой задачи.

Решение обратной задачи представляет проверку решения прямой задачи, то есть при этом возникают благоприятные условия для потоков информации по целям обратных связей в мыслительных процессах (систематическое сочетание прямых и обратных задач вырабатывает важное качество личности – чувство самоконтроля).

Учащиеся, составляя обратные задачи, знакомятся со значительно большим разнообразием задач, чем в традиционных задачниках.

При составлении и решении обратных задач выдвигается на первый план анализ и видоизменение математических зависимостей.

Итак, для развития мышления ценны не столько прямые и обратные задачи, взятые вне времени сами по себе, сколько сам познавательный элемент, который заключается в процессе преобразования одной задачи в другую, в сравнении условий, решений, ответов задач, то есть тех “невидимых”, трудно уловимых и трудноизобразимых при логическом анализе элементов мысли, связывающих решения обеих задач (прямой и обратной).

Однако нельзя забывать, что переходы эти осуществляются во времени: чем меньше интервал времени между противоположными процессами решения взаимно обратных задач, тем быстрее и чаще будут совершаться эти переходы и тем прочнее будут сохраняться в памяти следы этих переходов, то есть тем более глубокими и основательными окажутся осваиваемые знания.

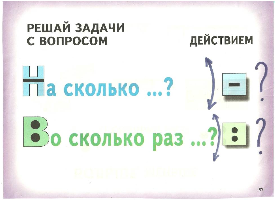
Решение простых задач на сложение и вычитание.

Разновидности задач на сложение и вычитание в учебниках математики по традиционной системе как бы перетасованы, что затрудняет возникновение циклических связей мысли.

Задачи на сложение и вычитание целесообразно рассматривать следующими циклами:

• задачи на нахождение суммы и неизвестного слагаемого;

• задачи на нахождение разности, уменьшаемого, вычитаемого;

• задачи на увеличение и уменьшение числа на несколько единиц;

• задачи на разностное сравнение величин.

Задачи на нахождение суммы и неизвестного слагаемого.

Прямая задача

Катя купила 9 открыток, а Надя 8 открыток. Сколько всего открыток купили девочки?

Краткая запись:

К.	Н.	Всего
9 от.	8 от.	? от.

Решение: 9 + 8 = 17 (от.)

Ответ: девочки купили 17 открыток.

Дается название вида задачи, вводится таблица видов простых задач.

Обратная задача.

Какие числа были даны в задаче?

Какие числа мы нашли, решая задачу?

Составим новую задачу, для чего неизвестным числом сделаем одно из двух других чисел, например, 9 открыток. Сформулируйте эту задачу.

Катя купила несколько открыток, а Надя 8 открыток. Всего девочки купили 17 открыток. Сколько открыток купила Катя?

Краткая запись:

К.	Н.	Всего
? от.	8 от.	17 от.

Решение: 17 – 8 = 9 (от.)

Ответ: Катя купила 9 открыток.

Сравните решения задач:

1. Обе задачи решаются одним действием.

2. Прямая задача – действием сложения, обратная – действием вычитания.

Вводится термин – обратная задача. Определяется вид задачи – нахождение неизвестного слагаемого.

Аналогично вводится вторая обратная задача.

Введение обратных задач не изолированно от прямой, а через нее имеет следующие положительные стороны.

1. Достигается ознакомление не только с новой задачей, но и повторение старой.

2. Учащиеся усваивают связи между задачами, умозаключения здесь возникают в цикле, во взаимопревращениях друг в друге.

3. На следующем этапе мы учимся делать обратные преобразования: дается одна обратная задача, решается, а к ней составляется прямая и другая обратная. Причем, здесь уместно ввести решение задачи уравнением.

Саша купил несколько тетрадей в линейку и 7 тетрадей в клетку. Всего он купил 13 тетрадей. Сколько тетрадей в линейку купил Саша?

1. Читаем условие: “Саша купил несколько тетрадей в линейку”. Сколько было – неизвестно, обозначаем “окошечком”.

2. Читаем дальше: “и 7 тетрадей в клетку”. Пишем: 7 .

3. Всего у него было 13 тетрадей. Пишем: 13 (? 7 13)

4. При каком действии получается 13? (? + 7 = 13)

Вместо “окошечка” обозначаем неизвестное число буквой Х. Получается уравнение: Х + 7 = 13

Как решить задачу? (Найти неизвестное слагаемое)

Решение:

Х = 13 – 7

Х = 6

6 + 7 = 13

13 = 13

Эта задача преобразуется в прямую и взаимообратную.

Совершенно аналогично проводим обучение решению задач на нахождение третьего (четвертого) слагаемого.

В одном ящике 23 кг яблок, во втором – 20 кг, а в третьем 18 кг яблок. Сколько кг яблок в трех ящиках?

Решение: 23 + 20 + 18 = 61 (кг)

Составим обратную задачу:

1 ящ.	2 ящ.	3 ящ.	Всего
? кг	20 кг	18 кг.	61 кг

Как найти неизвестное слагаемое? (Из суммы вычесть известное слагаемое)

Как это можно сделать?

1 способ: 61 – (20 + 18) = 23 (кг)

2 способ: (61 – 18) – 20 = 23 (кг)

3 способ: (61 – 20) – 18 = 23 (кг)

Таким образом. При решении задач на нахождение неизвестного слагаемого появляется возможность ознакомления с несколькими способами решения одной и той же задачи.

Сколько еще обратных задач можно составить? (Еще 2 задачи, каждую решить разными способами)

Часто учителя начальных классов выбирают из нескольких способов простейший и им ограничиваются. Но нужно помнить старое дидактическое правило: иногда полезнее одну задачу решить разными способами, чем несколько задач одним и тем, же способом.

Естественно, не всегда задачи на уроке мы решаем с преобразованием в обратные. Можно обратную задачу сформулировать и р6ешить устно, сформулировать условие без ее решения, выяснив, какие числа даны, что надо найти и т.д.

Задачи на нахождение разности, уменьшаемого и вычитаемого.

Прямая задача.

У Веры было 87 тенге. Она купила книгу за 37 тенге. Сколько денег у нее осталось?

Краткая запись:

Было	Израсходовано	Осталось
87 тг.	37 тг.	? тг.

Решение: 87 – 37 = 50 (тг.)

Какие числа были даны в задаче?

Что мы узнали после решения? (50тг. – сколько осталось, разницу между числами)

Определяем вид задачи: нахождение остатка (разности).

Составим обратную задачу, сделав известным число 50 тг., а неизвестным то, что было.

У Веры было несколько тенге. Она купила книгу за 37 тенге, после этого у нее осталось 50 тенге. Сколько денег было у Веры до покупки?

Эту задачу уместно решить уравнением.

1. Сколько денег было у Веры? (Неизвестно – Х)

2. Сколько денег она израсходовала?

3. Сколько у нее осталось?

4. Вопрос задачи?

Запись на доске: Х 37 50

1. Чтобы получилось уравнение, нужно эти числа связать знаками. Если человек уплатил (истратил, израсходовал) деньги. То у него их стало больше или меньше?

2. Какое действие надо выполнить? (Х – 37 = 50)

3. У веры осталось 50 тг., да она израсходовала 37 тг. Сколько денег у нее было вначале: больше, чем 50, или меньше?

4. Почему больше?

5. На сколько больше?

6. Как узнать, сколько денег было вначале?

Х – 37 = 50

Х = 37 + 50

Х = 87

87 – 37 = 50

50 = 50

Ответ: у Веры было 87 тг.

Какой компонент находили?

Каким действием?

Вид задачи: нахождение уменьшаемого.

Сравнение прямой и обратной задач:

Решены одним действием, прямая задача – вычитанием, обратная – сложением.

На последующих уроках решаются задачи в иной последовательности: сначала на нахождение уменьшаемого, затем она преобразуется в задачу на нахождение разности.

Затем мы решаем задачи на нахождение разности, когда вычитаемых несколько.

Прямая задача.

В магазине было 90 коробок конфет. В первый день продали 30 коробок, во второй день – 32 коробки. Сколько коробок конфет продали в третий день?

К этому времени мы изучили следующие свойства:

• прибавление суммы к числу,

• прибавление числа к сумме,

• вычитание суммы из числа,

• вычитание числа из суммы.

Поэтому решение подобных задач разными способами не вызывает особых затруднений у детей.

Краткая запись:

Было	Израсходовано	Осталось
90 к.	30 к. и 32 к.	? к.

Решение: 1 способ – 90 – (30 + 32) = 28 (к.)

2 способ – (90 – 30) – 32 = 28 (к.)

3 способ – (90 – 32) – 30 = 28 (к.)

Что мы находим в этой задаче?

Составьте обратную задачу на нахождение уменьшаемого.

В магазине было несколько коробок конфет. В первый день продали 30 коробок, во второй – 32 коробки, в третий – оставшиеся 28 коробок. Сколько коробок конфет было в магазине первоначально?

Краткая запись: ? к. 30 к. и 32 к. 28 к.

Решение:

1 способ – (30 + 32) + 28 = 90 (к.)

2 способ – (30 + 28) + 32 = 90 (к.)

3 способ – (32 + 28) + 30 = 90 (к.)

Вслед за задачей на нахождение уменьшаемого вводится задача на нахождение вычитаемого.

Прямая задача.

К обеду в столовой сделали 70 бутербродов. За обедом съели 62 бутерброда. Сколько бутербродов осталось в столовой?

Краткая запись:

Было	Израсходовано	Осталось
70 б.	62 б.	? б.

Решение: 70 – 62 = 8 (б.)

Изменим краткую запись: 70 б.? б. 8б.

Составьте по ней обратную задачу. К обеду в столовой сделали 70 бутербродов. После обеда осталось 8 бутербродов. Сколько бутербродов съели за обедом?

Эту задачу удобнее решить уравнением.

Сколько было сделано бутербродов?

Сколько съели?

Сколько осталось? 70 Х 8

Как связать эти три числа?

70 – Х = 8

Х = 70 – 8

Х = 62

70 – 62 = 8

8 = 8

Какой компонент находили?

Определите вид задачи. (Нахождение вычитаемого)

Далее решаются задачи на преобразование задач на нахождение вычитаемого в задачи на нахождение разности.

В конце изучения данной темы необходимо решать изолированные задачи без составления к ним обратных, а иногда решать все три задачи по одной и той же ситуации.

Задачи на уменьшение и увеличение числа на несколько единиц и задачи на разностное сравнение величин.

К введению понятия разностного сравнения мы находим через прямую задачу на увеличение и уменьшение числа на несколько единиц.

Прямая задача.

Набор цветных карандашей стоит 160 тенге, а набор фломастеров на 120 тенге дороже. Сколько стоит набор фломастеров?

Краткая запись:

К.	Ф.
16о тг.	на 120 тг. дороже	? тг.

Решение: 160 + 120 = 280 (тг.)

Обратная задача: ? тг. на 120 тг. дороже 280 тг.

Набор карандашей стоит несколько тенге. Набор фломастеров на 120 рублей дороже. Он стоит 280 рублей. Сколько стоит набор карандашей?

Производим рассуждения и преобразования: Набор фломастеров на 120 тенге. дороже, значит, набор карандашей на 120 тенге. дешевле. Поэтому получаем следующую задачу:

Набор фломастеров стоит 280 тенге., набор карандашей на 120 тенге. дешевле. Сколько стоит набор карандашей?

Краткая запись:

К.	Ф.
? тг. на 120 тг. дешевле	280 тг.

Решение: 280 – 120 = 160 (тг.)

Преобразовываю схему:

К.	Ф.
160 тг.	280 тг.

на? тг. дешевле

Составьте обратную задачу:

Набор карандашей стоит 160 тенге, а набор фломастеров 280 тенге. На сколько тенге фломастеры дороже карандашей? (На сколько тенге карандаши дешевле фломастеров?)

Решение: 280 – 160 = 120 (тг.)

Обязательно сравниваем решение прямой и обратных задач.

На следующих уроках сначала решается задача на разностное сравнение, которая преобразуется в две другие задачи. После этого решаем задачи на сложение и вычитание, выраженные в косвенной форме.

Таким образом, взаимосвязь между задачами на сложение и вычитание укладывается в таблицу (прилагается). В ней обозначены три вида задач на сложение и шесть видов задач на вычитание.

Чтобы обобщить эти задачи и подготовить почву для свернутого решения этих задач, полезно упражнять учащихся по мере изучения материала в составлении нескольких видов задач к одному выражению, например,15+3.

Составьте три задачи, чтобы в них использовались слова:

“больше на…”

“сколько вместе”

“сколько было вначале”

Например:

1. В одном ящике было 15 кг яблок, в другом на 3 кг больше. Сколько килограмм яблок во втором ящике?

2. В одной коробке 15 кг конфет, в другой – 3 кг. Сколько конфет в двух коробках.

3. За обедом съели 3 яблока, после чего в вазе осталось 15 яблок. Сколько яблок было в вазе вначале?

4. Эти упражнения содействуют развитию множественных связей (ассоциаций). В данном случае множественная связь имеет следующее строение:

Сложение –

“увеличить на”

“сколько вместе”

“сколько всего”

“сколько было вначале”.

– Составьте четыре задачи на вычитание: 700 – 300.

1. У мамы было 700 тенге. Она купила апельсинов на 300 тенге . Сколько денег у неё осталось?

2. У мамы было 700 тенге. Она истратила несколько тенге на покупку апельсинов, после чего у нее осталось 300 тенге. Сколько денег мама истратила на апельсины?

3. У Коли 700 марок, у Пети на 300 марок меньше. Сколько марок у Пети?

4. Зеленая лента 700 см, белая – 300см. на сколько см зеленая лента длиннее белой?

Здесь формируется следующий пучок ассоциаций:

Вычитание –

“сколько осталось”

“сколько истратили”

“меньше на”

“на сколько меньше (больше)”.

Формы работы младших школьников на уроках математики

Формы организации обучения (организационные формы) – это внешнее выражение согласованной деятельности учителя и учащихся, осуществляемой в определенном порядке и режиме. Они имеют социальную обусловленность, возникают и совершенствуются в связи с развитием дидактических систем [29]. Учебный процесс предполагает органическое единство средств, методов и приемов работы с организационными формами обучения. Каждому методу, приему обучения соответствует своя организационная форма, определяющаяся отношениями между учителем и учащимися и учащихся между собой. Учитель управляет всей учебной деятельностью на уроке, используя при этом различные ее формы. В дидактике принята следующая классификация форм учебной деятельности, в основе которой лежит количественная характеристика коллектива учащихся, взаимодействующих с учителем в данный момент урока:

• общие или фронтальные (работа со всем классом);

• индивидуальные (с конкретным учащимся);

• групповые (звено, бригада, пара и т. д.).

Первая предполагает совместные действия всех учащихся класса под руководством учителя, вторая — самостоятельную работу каждого ученика в отдельности; групповая — учащиеся работают в группах из трех-шести человек или в парах. Задания для групп могут быть одинаковыми или разными. Названные формы организации учебной деятельности учителя и учеников выступают на уроке в различных сочетаниях и последовательностях. В современных условиях обучения достаточно четко ставится вопрос о применении и сочетании таких организационных форм работы на уроке, которые обеспечивали бы эффективное приобретение школьниками не только знаний, умений и навыков, но и ценного опыта нравственных и коллективистских отношений. Огромная роль в достижении дидактических целей урока принадлежит коллективным формам работы (по сравнению с другими формами), поскольку они:

– позволяют уплотнять время урока,

– создают ситуации взаимообучения учащихся,

– существенно влияют на развитие личности.

Фронтальной формой организации учебной деятельности учащихся называется такой вид совместной деятельности учителя и учащихся на уроке, когда все ученики одновременно выполняют одинаковую, общую для всех работу, всем классом обсуждают, сравнивают и обобщают ее результаты. Учитель ведет работу со всем классом одновременно, общается с учащимися непосредственно в ходе своего рассказа, объяснения, показа, вовлечения школьников в обсуждение рассматриваемых вопросов и т.д. Это способствует

• установлению особенно доверительных отношений и общения между учителем и учащимися, а также учащихся между собой;

• воспитывает в детях чувство коллективизма;

• позволяет учить школьников рассуждать и находить ошибки в рассуждениях своих товарищей по классу;

• формировать устойчивые познавательные интересы школьников;

активизировать их деятельность.

Индивидуальную работу допустимо проводить на всех этапах урока, при решении различных дидактических задач ― для усвоения новых знаний и их первичного закрепления, для формирования и закрепления умений и навыков, для обобщения и повторения изученного, для контроля, для овладения исследовательским методом и т.д.

Недостатком индивидуальной формы организации работы учащихся на уроке является то, что при выполнении заданий школьники практически не общаются друг с другом, приобретаемый опыт самостоятельной деятельности не становится достоянием коллектива, не обсуждается вместе с товарищами по классу и учителем. Эти недостатки можно компенсировать в практической работе учителя сочетанием индивидуальной формы организации учебной деятельности школьников с групповой либо фронтальной (звеньевой, бригадной, кооперативно-групповой, парной). Кроме того, подготовка и реализация индивидуальной формы работы на уроке требует от учителя существенной затраты времени уже на этапе замысла и разработки, а также высокого мастерства при управлении самим процессом и при анализе полученных результатов.

Для организации групповой (звеньевой) формы учебной работы учащихся учителю необходимо тщательно продумать все вопросы, которые связаны с образованием групп, распределением обязанностей внутри групп и объемом работы каждой группы.

Величина групп может быть различной. Она колеблется в пределах от двух до шести человек. Состав групп меняется в зависимости от содержания и характера предстоящей работы. При этом не менее половины группы должны составлять ученики, способные успешно заниматься самостоятельной работой.

Учащиеся подбираются по принципу объединения школьников разного уровня обученности, внеурочной информированности по данному предмету, совместимости учащихся, что позволяет им взаимно дополнять и компенсировать достоинства и недостатки друг друга. В группе не должно быть негативно настроенных друг к другу учащихся.

Групповая работа может быть однородной и неоднородной. Однородная групповая работа предполагает выполнение небольшими группами учащихся одинакового для всех задания, а дифференцированная – выполнение различных заданий разными группами. В ходе работы членам одной группы разрешается совместное обсуждение хода и результатов работы, обращение за советом друг к другу.

При групповой форме работы учащихся на уроке в значительной степени возрастает и индивидуальная помощь каждому нуждающемуся в ней ученику, как со стороны учителя, так и со стороны учащихся-консультантов.

Групповая форма работы учащихся на уроке наиболее применима и целесообразна при проведении практических, лабораторных работ и работ-практикумов по естественнонаучным предметам, при отработке навыков разговорной речи на уроках иностранного языка (работа в парах), на уроках трудового обучения при решении конструктивно-технических задач, при изучении текстов, копий исторических документов и т.п.

На уроках математики в начальной школе групповая работа может быть применена на этапе отработки вычислительных навыков, при закреплении знаний некоторых теоретических фактов (связи между компонентами арифметических действий, решение уравнений, действия с величинами).

Фронтальная, групповая и индивидуальная формы работы учащихся по-разному способствуют реализации образовательных, воспитательных и развивающих задач. Поэтому необходимо рациональное их сочетание, продуманный выбор той или иной формы с учетом особенностей учебного предмета, содержания изучаемого материала, методов обучения, возрастных особенностей учащихся.

Литература:

1. «Преподавание математики в начальной школе» –

Плоткина С.М., Шишера Е.Б. / Издат-во «Ранок –Веста» – 2004г.

1. «Библиотека учителя начальной школы» – Волкова Н.Т., Издат- во «Астрель АСТ» – 2003 г.

2. «Учимся решать задачи» – Истомина Н.Б. /Тетради по математике 1 – 4 классы./Издат-во «Линка – Пресс» 2004г.

Содержание:

1.Введение…………………………………………………………….3

2. Методические рекомендации по обучению решению составных задач в начальной школе …………………………………………….4

3.Виды задач………………………………………………………….8

4.Решение разных видов задач……………………………………..13

5.Формы работы младших школьников на уроках математики..22

6.Литература……………………………………………………….26

8

Тип задания

Цель задания

Слова-помощники

Примеры

Узнавание

Формирование умений узнавать, распознавать и различать понятия (объекты изучения)

Найди, соотнеси, выбери, определи

Найди примеры, в которых используется сочетательный закон.

Определи, на каком рисунке изображено….

Выбери правильное определение…

Воспроизведение

Формирование умений воспроизводить учебный материал (объекты изучения)на уровне памяти

Назови, перескажи, перечисли, опиши, воспроизведи, заполни пропуски, приведи примеры

Воспроизведи последовательность…

Опиши по плану…

Назови группы объектов

Понимание

Формирование умений воспроизводить учебный материал (объектов изучения) на уровне понимания; описывать и анализировать действия с объектами изучения

Реши, объясни, докажи, классифицируй, выдели, сравни, сопоставь, дополни предложение, закончи фразу

Подели на группы.

Объясните, почему…?

Найдите закономерность…

Дополни предложение «Все народы России называют братскими, потому что….»

Применение в знакомых условиях

Формирование умений применять знания в знакомой ситуации по образцу; объяснять сущность объектов изучения; выполнять действия с четко обозначенными правилами; применять знания на основе обобщенного алгоритма для решения новой учебной задачи

Примени, используй, сконструируй, выполни задание по образцу

Составь 3 вопроса к тексту

Приготовь презентацию, сообщение…

Напиши рассказ о..

Найди ошибки…

Проложи безопасный маршрут от дома до школы.

Применение в новых условиях

Формирование умений применять знания в незнакомых, нестандартных ситуациях для решения качественно новых задач; самостоятельно действовать по описанию, объяснению и преобразованию объектов изучения

Сочини, составь, спроектируй, разработай алгоритм

Относятся творческие задания:

Придумай герб класса…

Придумай задачу, обратную этой.

Напиши сказку от имени героя.

Создай задание для одноклассника (квест-комната).

Создай календарь- наблюдений.

Работа
с задачами разных видов, как средство формирования логических умений учащихся
начальной школы.

Учитель
 Приймак Н.А.

Государственное
бюджетное общеобразовательное учреждение г. Москвы

«Школа
с углубленным изучением английского языка»

Работа
с задачами разных видов на уроках математики.

Текстовые задачи на уроке математики
в начальных классах могут быть использованы для самых разных целей: для
подготовки к введению новых понятий (в частности математических действий) для
ознакомления с новыми понятиями, свойствами понятий; для показа области
применимости изучаемых понятий; для углубления и расширения формируемых
математических знаний и умений; для формирования вычислительных навыков; для обучения
методам и приемам решения задач на разных этапах этого обучения. Очевидно, что
и методика работы с задачей на уровне должна определятся прежде всего тем, с
какой целью эта задача включена в урок.

Цель – разработать алгоритм действия
по организации работы с текстовыми задачами.

Наиболее распространенный вид работы
с задачами на уроке – это решение задач.

Решение задач на уроке может
отличаться формой организации деятельности детей, характером и степенью
руководства процессом решения, содержанием решаемых задач, способом оформления
решения и т.п. Исходя их сказанного даже решение задач на разных уроках,  в
разных классах в зависимости от целей урока может осуществляться по-разному.
Приведу несколько вариантов организации и содержания решения задач на уроке.

1.Фронтальное
(коллективное) решение задачи под руководством учителя.

Этот вид работы с задачей на уроке
наиболее известен. Коллективное решение может использоваться для знакомств
детей с решением (со способом решения) задач определенного вида. В этом случае
оно должно быть ориентированно на запоминание учащимися отличительных
особенностей задач этого вида,  и на понимание и запоминание основных шагов
такого решения.

Например: коллективное решение задачи
для ознакомления учащихся с решением задач на нахождение числа по двум
разностям:

Купили два куска ленты. За второй
кусок уплатили на 1 р. Меньше чем за первый. Сколько рублей стоит каждый кусок?

Коллективную работу с этой задачей
полезно начать так:

– Прочитайте задачу. Скажите, решили
ли вы раньше такие задачи? ( Нет не решали)

– Что нового в содержании задачи,
из-за чего вы сделали вывод, что такие задачи не решали? (Новое здесь то, что в
ней не дана ни цена ленты, ни стоимость  какого-либо количества метров ленты. А
сказано только, на сколько меньше стоит один кусок, чем другой.)

– Сегодня на уроке вы будете учиться
это делать. Для этого решим задачу. Внимательно следите за тем. Какие вопросы я
буду задавать.

После решения задачи полезно вновь
задать вопрос об особенностях задач этого вида и особенностях их решения,
обобщить ход решения.

Коллективное решение под руководством
учителя полезно также использовать для того, чтобы дети запомнили этапы
решения, ознакомились каким – либо приемом, помогающим решению.

2.Фронтальное (коллективное)
решение задач под руководством учащихся.

Этот вид работы чаще всего может быть
использован для овладения учащимися умением последовательно выполнять этапы
решения задачи, для закрепления умения пользоваться определенными приемами и
методами решения. Учитель в этом случае только побуждает детей к руководству
решением. Работа также должна завершаться обобщенными выводами в соответствии с
ее целями.

3.Самостоятельно решение
задачи учащимися.

1) Самостоятельный выбор средств,
методов, способов и форм решения;

2) Применение указанных учителем или
учебником средств, методов и способов решения.

Самостоятельное решение – один из
наиболее распространенных видов работы с задачами на уроке. Однако и здесь
возможна ориентация на разные цели: на формирование умения решать задачи
определенного вида , решать задачи с помощью определенных средств, приемов и
методов; проводить проверку и самопроверку, оценку и самооценку.

В зависимости от содержания решаемых
задач можно выделить следующие виды решения задач:

1.Решение задач с лишними данными.

2.Решение задач с недостающими
данными.

3.Решение нестандартных задач разных
видов (логических, комбинаторных, на смекалку и т.п.)

Другой вид работы  –  выполнение
части решения.

Основные цели выполнения части
решения – формирование у учащихся умение выполнять определенный этап решения,
обучение общим приемам решения, формирование представлений учащихся об
математических действиях.

Приведу примеры заданий, которые
определяют этот вид работы на уроке.

Сделайте рисунок (чертеж) к этой
задаче. (Само построение рисунка (чертежа) может проводиться под руководством
учителя, под руководством учащихся или самостоятельно;  при частичном
руководстве учителя или учащихся.)

Прочитайте задачу. Представьте то, о
чем говорится в задаче, так, чтобы ее было легче решить. Расскажите, что вы
представили.

Пользуясь схемой разбора задачи от
вопроса к данным, составьте план решения задачи. Известно, что данная задача
решается так … (дается запись математического решения и по действиям). Запишите 
это же решение в виде выражения, найдите его значение и ответьте на вопрос
задачи.

Проверьте, правильно ли решена эта
задача, определив смысл каждого действия (решив задачу другим способом, решив
задачу графически,  с помощью кружочков и т.п.)

Цели дополнительной работы над
решенной задачей могут быть самые различные: формирование у учащихся смысла
математических действий; обучение умениям находить другие способы решения,
решать задачи  разными методами, проводить анализ содержания задачи, ставить
вопросы к условиями задачи. Целью дополнительной работы может быть также
выявление особенностей способа решения задач определенного вида, обучение
элементам исследования задачи, обучение умению обосновывать правильность
решения задачи и т.п.

Виды дополнительной работы с решенной
задачей:

1.Изменение условия задачи так, чтобы
задача решалась другим действием.

2.Постановка нового вопроса к уже
решенной задаче, постановка всех вопросов, ответы на которые еще можно найти по
данному условию.

3.Сравнение содержаний данной задачи
и ее решения с содержанием и решением другой задачи.

4.Решение задачи другим способом или
с помощью других средств – другим методом: графическим, алгебраическим и др.

5.Изменение числовых данных задачи
так, чтобы появился способ решения или, наоборот, чтобы один из способов
решения стал невозможен.

6.Исследование решения. (Сколько способов
решения имеет задача? При каких условиях она не имела бы решения? Какие приёмы
наиболее целесообразны для поиска решения этой задачи? Возможны ли другие

методы решения?)

7.Обоснование правильности решения ( проверка
решения задачи любым из известных приёмов ).

Виды работы с задачами не включает в себя
явное и полное решение задачи. Основным содержанием
большинства этих видов работы являются сравнение, сопоставление, анализ, а
потому выполнение их способствует развитию мышленияучащихся, повышает интерес к
математике, в частности к решению задач,позволяет учителю целенаправленнее формировать
компоненты общего умения решать задачи.

К сожалению, именно эти виды работы реже используются
в практике. Причина заключается в том, что в методике математики до сих пор ещё
наблюдается отождествление выражений ” методика обучения решению
задач”,” методика использования текстовых задач в обучении
математике”, “методика решения текстовых задач”,отчего негласно
считается, что если есть задача ( в учебнике, в пособии для учителя ),то она прежде
всего должна быть решена,а на потом уже, если останется время, можно ещё
какое-нибудь задание выполнить. Такая постановка исключает проблему соответствия
характера работы с задачей на уроке и цели включения этой задачи в урок.

Виды работы:

1.Установление соответствия между
содержанием задачи и схематическим рисунком (чертежом, таблицей, какой-либо
иной формой краткой записи ) и наоборот, между рисунком ( чертежом и т. д.) и
содержанием задачи.

Примеры заданий.

Соответствует ли данный рисунок (чертёж,
таблица и т.п.) данной задаче?

Как нужно изменить данный рисунок (что
нужно изменить в этом рисунке), чтобы он соответствовал данной задаче?

Как нужно изменить задачу, чтобы данный
рисунок соответствовал этой задаче?

2. Выбор среди данных задач (среди задач
на данной странице учебника, задач, записанных на доске, карточке и т. п.) той,
которая соответствует данному рисунку (чертежу, таблице, краткой записи).

3.Выбор среди нескольких данных рисунков (чертежей,
таблиц, кратких записей ) того , который соответствует данной задаче).

4.Нахождение ошибок в данномрисунке,
чертеже, таблице и т.п.( построенных к данной задаче). Цель видов работы
1,2,3.4 – формирование умения пользоваться различными моделями задачи для
поиска её решения, так как обоснование соответствия содержания задачи рисунку, чертежу,
таблице и т.д. является обязательной операцией при решении задачи с

помощью этих моделей.

5.Выбор среди данных задач (задач на
данной странице или страницах учебника) задач данного вида (таких же, какие
решали сегодня на уроке, или

задач, которые решаются так же, как только
что решённая.) Этот вид работы необходим для формирования умения решать задачи
определённого вида: например,умения решать задачи с отношением ” больше
(меньше) на …”,

” больше ( меньше ) в … раз;задачи
на нахождение четвёртого пропорционального;простые задачи с величинами ”
цена ” количество ” и ” стоимость ” и т.п.

6.Классификация простых задач по
действиям, с помощью которых они могут быть решены.

Возможны формы этой работы. Прочитайте все
задачи на странице

учебника. Укажите, какие из задач могут
быть решены с помощью сложениям, а какие – с помощью вычитания ( действие может
быть указано устно, отмечено карандашом в учебнике или показано на карточке и
т.п.).

Этот вид работы полезен для закрепления
понимания детьми смысла математических действий.Однако полезность его зависит
от подбора задач: задачи должны содержать разные словесные задания основного

отношения, определяющего действие. Полезно
включать и задачи, ответ на вопрос которых не требует выполнения никаких
действий, задачи с

нетрадиционными текстами, нетрадиционными вопросами,
задачи разных видов, разной структуры текстов.

7.Выбор задач, ответ на вопрос которых
может быть найден заданной последовательностью действий.

Пример.

Найдите среди данных задач такие, ответ на
 вопрос которых можно было бы найти с помощью математических действий в такой
последовательности:

1)” +”; 2 ) ” : ” ;
3)” +

Этот вид работы полезен для закрепления
умения обосновывать выбор действий,для закрепления умения решать задачи
определённого вида.

В число предлагаемых задач целесообразно
включать задачи, допускающие несколько способов решения, доступных детям. Тогда
на уроке может возникнуть дискуссия о том, правильно ли отнесена задача к заданной

последовательности. В результате дети
устно обоснуют несколько способов решения.

8.Выбор задач, при решении которых
необходимо ( или можно ) применить данные вычислительные приёмы.

Пример.

Вы сейчас учились делить двузначное число
на двузначное. Просмотрите задачи на этих двух страницах учебника и найдите те
, для решения которых нужно будет выполнить деление двузначного числа на двузначное.
Обоснуйте свой ответ. Этот вид работ полезен для закрепления соответствующих
вычислительных навыков,для закрепления смысла действий,умения обосновывать выбор
действия умения решать задачи.

9.Выбор задач, с помощью которых можно
научиться тому или иному приёму, помогающему решению; тому или иному приёму
решения ( графическому, табличному  практическому,  математическому).

Пример.

Найдите на странице задачи, которые могут
быть решены с помощью чертежа; задачи, при решении которых полезно представить
себя участником

ситуации,сделать схематический рисунок,составить
план решения задачи,рассуждая от вопроса к данным,и т.п. Ответы обоснуйте путём
выполнения соответствующих действий.

Этот вид работы нужен для овладения определенными
приёмами.Он интересен учащимся.

10.Определение числа математических способов,которыми
может быть решена данная задача.

Пример.

Рядом с номером каждой задачи на этой
странице ( на карточке) поставьте карандашом число возможных различных способов
её решения.

Учитель просит нескольких человек
обосновать свои ответы.Возможна и организация взаимопроверки,когда соседи по
парте рассказывают друг другу способы решения,чтобы подтвердить обоснованность
названного ими числа способов. Эта работа очень помогает закрепить общее умение

решать задачи,находить различные способы
решения.

11 Обнаружение ошибок в решении задачи.

12.Определение смысла выражений, составленных
из чисел, имеющихся в тексте ( причём целесообразно составлять всевозможные
выражениям том числе и не имеющие смысла в рамках данной задачи ).

Цель такой работы – обучению анализу
решения, анализу содержания задачи, умению проверять решение задачи; формирование
понимания смысла действий и т.п.

13.Решение вспомогательной задачи или
цепочки таких задач перед решением трудной для детей задачи. Этот вид работы способствует
формированию умения решать задачи при ознакомлении с новым видом задач, при
тренировке в решение задач. Он заменяет скучное и утомительное коллективное решение
с подробным разбором, даёт возможность учащихся самостоятельно найти способ
решения незнакомой задачи.

14.Исключение из текста задачи лишних данных,лишних
условий.

Пример.

Не решая задачи, скажите, какие данные
здесь лишние.Объясните почему. Подтвердите это же,выполнив решение. Этот вид
работы помогает формировать умения анализировать содержание задачи. С
аналогичной целью полезно выполнять на уроке и следующие виды работы.

15.Дополнение содержания задачи
недостающими  данными для

решения данными или отношениями.

16.Выбор на странице тех задач , которые
ученик может решить устно ( знает,как решить ).

Примеры.

Прочитайте на странице учебника все задачи.Выпишите
номера и ответы на вопросы тех задач,которые можно решить устно. Выпишите
номера тех задач,которые знаете,как решить.Запишите рядом с номером знаки
действий в том порядке,в каком нужно выполнить действия для ответа

на вопрос задачи. Основная цель этого вида
работы – закрепление умения решать задачи,осознание смысла действий. Реализовать
разнообразные функции задач поможет и выполнение такого известного вида работы
с задачами, как составление задач самими учащимися. Само составление задач тоже
может осуществляться в разных видах работы,с разной степенью полноты.Это: 1)дополнение
задачи недостающими данными;

2)постановка вопроса к данному условию; 3)
составление задачи по краткой записи,рисунку,чертежу,числовым данным и т.п.; 4)
составление задачи,аналогичной данной по способу решений (те же действиям том
же

порядке ),по сюжету; стакими же числовыми
данными,но с другим решением; аналогичной данной по количеству действий,по
величинам,о которых идёт речь в задаче; 5)дополнение условия задачи сведениями,меняющими
способ решения; 6) составление задачи по данной записи решения5по уравнению; 7)
составление и решение задачи,обратной данной; 8) устное сочинение “О чём
может рассказать данное математическое выражение? “

Важно только помнить, что нет и не может
быть раз и навсегда принятого  с помощью задач полностью зависит от цели, для достижения
которой задача включена в урок.

Литература

1.    
Бантова М.А. «Методика  преподавая
математики в начальной школе.» _М.: Просвещение, 2000г.

2.    
Белошистая А.В. «Методика обучения
математики в начальной школе.» _М.: Владос, 2007г.

3.    
Истомина Н.Б. « Методика обучения
математики в начальных классах.»_М.: Линка – Пресс 2010г.

4.    
Лавриненко Т.А. «Как научить детей решать
задачи: Методические рекомендации для учителей нач. классов» Саратов, 2000г.

5.    
Царева С.Е. «Виды работы с задачами на
уроке математики» М.: школа  2012г.

Методические рекомендации по составлению тестовых заданий

1. При создании тестов для проверки остаточных знаний по соответствующей дисциплине или для проверки итоговых знаний обучающегося/студента на основании программы дисциплины определяется область содержания теста и цели тестирования.

План теста (Приложение 1) для промежуточного контроля знаний должен охватывать знания, умения и навыки по одной или нескольким дидактическим единицам, для итоговой аттестации – по всем дидактическим единицам дисциплины в соответствии с программой дисциплины, для проверки остаточных знаний по всем дидактическим единицам дисциплины в соответствии с ГОСом по профессии/специальности.

2.  Содержание теста должно соответствовать содержанию учебной дисциплины. Задания теста должны в правильной пропорции охватывать все важные аспекты области содержания.

3.   Необходимо включение в тесты только наиболее важных, базовых знаний, выражающих сущность, содержание, законы и закономерности рассматриваемых явлений. Все спорные точки зрения, допустимые в научном споре, следует исключить из тестовых заданий.

4.       Каждый учебный элемент должен иметь некоторую усредненную меру трудности, которую необходимо учитывать в процессе контроля знаний.

1. При разработке плана тестовых заданий по дисциплине делается примерная раскладка процентного содержания разделов и определяется необходимое число заданий (но не менее 3-х) по каждому разделу дисциплины (по каждой дидактической единице) исходя из его важности и числа часов, отведенных на его изучение в программе.

2. Общие рекомендации к тестовым заданиям

Содержание тестового задания должно быть ориентировано на получение от тестируемого однозначного заключения.

Основные термины тестового задания должны быть явно и ясно определены.

Тестовые задания должны быть прагматически корректными и рассчитаны на оценку уровня учебных достижений студентов по конкретной области знаний.

Тестовые задания должны формулироваться в виде свернутых кратких суждений.

В содержании тестового задания определяющий признак должен быть необходимым и достаточным.

Следует избегать тестовых заданий, которые требуют от тестируемого развернутых заключений на требования тестовых заданий.

При конструировании тестовых ситуаций можно применять различные формы их представления, а также графические и мультимедийные компоненты с целью рационального предъявления содержания учебного материала.

Количество слов в тестовом задании не должно превышать 10-12, если при этом не искажается понятийная структура тестовой ситуации. Главным считается ясное и явное отражение содержания фрагмента предметной области.

Среднее время  на тестовое задание не должно превышать 1,5 минуты.

1. Рекомендуется соблюдать следующие параметры тестов:

Соответствие содержания тестовых заданий государственному образовательному стандарту по учебной дисциплине (базовая часть тестовых заданий –70%- 85%), а также включение дополнительных тестовых заданий (вариативная часть  тестовых заданий – 15%-30%).

Необходимо проводить подбор заданий, комплексно отображающих основные темы учебной дисциплины.

Тестовые задания по конкретной учебной дисциплине должны наиболее полно отображать ее содержание и ключевые понятия, чтобы иметь качественную объективную оценку знаний студентов. Включение в тест второстепенных элементов содержания может привести к неоправданным выводам о знании или незнании учебной дисциплины.

Необходимо соблюдать пропорции в количестве тестовых заданий по темам учебной дисциплины.

Необходимо проверять соответствие  содержания тестовых заданий знаниям, навыкам и умениям, оцениваемым у студентов.

В каждом тестовом задании необходима определенность, логичность, отсутствие некорректных формулировок, выделение одного предмета измерения  (ключевого  понятия,  термина,  правила,  определения  и  т.д.).

1. Спецификация теста включает:

Цель создания теста, обоснование выбора подхода к его созданию,  описание возможных сфер его применения.

Перечень нормативных документов (базисных программ, требований к уровню подготовки выпускников и др.), используемых при планировании содержания теста.

Количество заданий различной формы с указанием числа ответов к закрытым заданиям, общее число заданий в тесте.

Вес каждого задания, рекомендуемый автором теста.

Рекомендуемое время выполнения теста, среднее время выполнения одного задания с учетом специфики формы.

Охват требований государственных образовательных стандартов по дисциплине.

1. Рекомендации к формулировкам тестовых заданий

Основными элементами тестового задания являются инструкция,  задание (содержательная часть), ответы к заданию.

Инструкция к тестовым заданиям определяет перечень действий  при прохождении тестирования. Она должна быть адекватна форме и содержанию задания («укажите правильный ответ (ответы)», «установите соответствие», «определите правильную последовательность», «введите правильный ответ»).

Используемая терминология не должна выходить за рамки основных учебников и нормативных документов.

Содержательная часть задания не должна включать элементы инструкции.

Содержательная часть задания формулируется в логической форме высказывания, а не в форме вопроса; в ней не должны быть двусмысленные и неясные формулировки, вводные фразы, двойное отрицание, оценочное суждение, выясняющее субъективное мнение испытуемого.

Все повторяющиеся слова должны быть исключены из ответов и вынесены в содержательную часть задания.

В содержательной части и в ответах необходимо исключить слова «большой, небольшой, много, мало, меньше, больше, часто, всегда, редко, никогда …».

Все варианты ответов должны быть грамотно согласованы с содержательной частью задания, однообразны по содержанию и структуре, равнопривлекательны. Между ответами необходимы четкие различия. Правильный ответ однозначен и не должен опираться на подсказки.

Среди ответов должны отсутствовать ответы, вытекающие один из другого.

В варианты ответов нельзя включать формулировки «все перечисленное выше», «все утверждения верны», «перечисленные ответы не верны»,  так как такие ответы нарушают логическую конструкцию тестового задания или несут подсказку.

Число тестовых заданий с отрицанием должно быть минимальным. При этом частица «не» выделяется жирным шрифтом.

1.     Виды и типы тестовых заданий. Их особенности, преимущества и недостатки

Существуют два типа заданий, которые объединяют шесть видов

Схема 1. Типы и виды тестовых заданий

К заданиям открытого типа относятся два вида – задания дополнения и задания свободного изложения. Их отличительной особенностью является то, что для их выполнения ученику необходимо записать одно или несколько слов (цифр, букв, словосочетаний, предложений).

Задания закрытого типа (альтернативных ответов, множественного выбора, восстановления соответствия и восстановления последовательности) предусматривают различные варианты ответа на поставленный вопрос: из ряда предлагаемых выбираются один или несколько правильных ответов, выбираются правильные (или неправильные) элементы списка и др. Эти задания предполагают наличие ряда предварительно разработанных вариантов ответа на заданный вопрос.

Задания закрытого типа

1. Задания альтернативных ответов.

К каждой задаче альтернативных ответов дается только два варианта ответов. Испытуемый должен выбрать один из них – “да – нет”, “правильно – неправильно” и др. 

Форма задания

Текст задания (вопрос)	Ответ
Утверждение 1	да	нет
Утверждение 2	да	нет
Утверждение 3	да	нет

…        …        

Инструкция для задания альтернативных ответов: Вам необходимо выбрать один вариант ответа, который Вы считаете правильным.

Задания альтернативных ответов в большей степени подходят для выявления уровня овладения сложными определениями, знания достаточно сложных графиков, диаграмм, схем и др.Особенностью заданий альтернативных ответов является то, что вопрос должен быть сформулирован в форме утверждения, поскольку он предполагает согласие или несогласие, которое можно отнести к утверждению.

2. Задания множественного выбора.

Это основной вид заданий, применяемый в тестах достижений. Задачи с множественным выбором предполагают наличие вариативности в выборе. Испытуемый должен выбрать один из предложенных вариантов, среди которых чаще всего только один правильный.

Рекомендации к заданиям с выбором ответа

1. В тексте задания должна быть устранена всякая двусмысленность или неясность формулировок;

2. Основная часть задания формулируется очень кратко, не более одного предложения из семи-восьми слов;

3. Задание должно иметь предельно простую синтаксическую конструкцию;

4. В основную часть задания включается как можно больше слов, оставляя для ответа 2-3 ключевых слова для данной проблемы;

5. Все ответы к одному заданию должны быть примерно одной длины, либо в некоторых заданиях правильный ответ может быть короче других;

6. Из текста должны быть исключены все ассоциации, способствующие выбору правильного ответа с помощью догадки;

7. Частота выбора одного и того же номера места для правильного ответа в различных заданиях должна быть примерно одинакова;

8. Из ответов исключаются все повторяющиеся слова за счет ввода их в основной текст заданий;

9. В ответах не рекомендуется использовать слова «все», «ни одного», «никогда», «всегда», «ни один из перечисленных», «все перечисленные», т.к. в отдельных случаях они способствуют угадыванию правильного ответа;

10. Из числа неправильных должны исключаться ответы, вытекающие один из другого;

11. Из числа тестовых должны исключаться задания, содержащие оценочные суждения или мнения испытуемого по какому-либо вопросу;

12. Все варианты ответов должны быть равновероятно привлекательны для испытуемых;

13. Ни один из вариантов ответов не должен являться частично правильным, превращающимся при определенных дополнительных условиях в правильный;

14. Основная часть задания формулируется в форме утверждения, которое обращается в истинное или ложное высказывание после подстановки ответов;

15. Ответ на одно задание не должен служить ключом к правильным ответам на другие задания теста, т.е. не следует использовать дистракторы из одного задания в качестве ответов к другим заданиям теста;

16. Если задание содержит среди прочих альтернативные ответы, не следует сразу после правильного приводить альтернативный ответ, так как внимание отвечающего обычно сосредотачивается только на этих двух ответах;

17. Все ответы должны быть параллельны по конструкции и грамматически согласованы с основной частью задания теста.

Форма предоставления заданий множественного выбора:

Вопрос (утверждение):

A. Вариант ответа 1

B. Вариант ответа 2

C. Вариант ответа 3

Инструкция для заданий множественного выбора: Выберите букву (ы), соответствующую (ие) варианту (ам) правильного (ых) ответа (ов). 

3. Задания на восстановление соответствия.

К заданиям данного типа относятся задания на восстановление соответствия между элементами двух списков, порядка ряда. Состоит из двух групп элементов и четкой формулировки критерия выбора соответствия между ними. Соответствие устанавливается по принципу 1:1 (одному элементу первой группы соответствует только один элемент второй группы) или 1:M (одному элементу первой группы соответствует М элементов второй группы). Внутри каждой группы элементы должны быть однородными. Количество элементов во второй группе должно превышать количество элементов первой группы, но не более чем в 1,5 раза. Максимально допустимое количество элементов во второй группе не должно превышать 10. Количество элементов в первой группе должно быть не менее двух.

Форма представления заданий на восстановление соответствия:

Инструкция: Соотнесите написанное в столбцах 1 и 2.

Вопрос:

Варианты ответа:

Столбец 1	Столбец 2
А.	1.
Б.	2.
В.	3.
Г.	4.
Д.	5.

Ответ: А. 3.  Б. 2.  В. 5.  Г. 1.  Д. 4.

Главными преимуществами заданий этого вида являются: возможностью быстрой оценки знаний, умений и навыков в конкретной области знаний, и экономичность размещения задач в тесте. 

4. Задания на восстановление последовательности

Задания на восстановление последовательности можно рассматривать как вариант задания на восстановления соответствия, когда одним из рядов является время, расстояние, или иной континуальный конструкт, который подразумевается в виде ряда.

Задания на восстановление последовательности – это очень качественная форма тестовых заданий, обладающая значительными преимуществами: краткостью, простотой проверки.

Задание.

Инструкция: Расположите в правильной последовательности.

Вопрос.

Варианты ответа.

1. А.

2. B.

3. С.       …….                             Ответ: 1. А. 2. D. 3. В. 4. Е. 5. С. 6. F.

Преимущества заданий закрытого типа

Задания могут быть надежны, поскольку отсутствуют факторы, связанные с субъективными оценками, которые снижают надежность.

Оценивание заданий полностью объективно: между оценками различных проверяющих не может быть различий.

Не учитывается умение испытуемых хорошо формулировать ответы.

Задания этого типа легко обрабатываются, тестирование быстро проводится.

Простой алгоритм заполнения снижает количество случайных ошибок и описок.

Эти задания позволяют охватить большие области знания, что для тестов достижений особенно важно.

Возможна машинная обработка ответов.

Низкая вероятность угадывания правильных ответов.

Возможно получение точной оценки содержательности теста, что особенно важно для определения соответствия теста целям исследования

Задания открытого типа

Требует сформулированного самим тестируемым заключения на требования задания. Имеет вид неполного утверждения, в котором отсутствует один или несколько ключевых элементов. В качестве ключевых элементов могут быть: число, слово или словосочетание. При формулировке задания на месте ключевого элемента, необходимо поставить прочерк или многоточие. Отсутствующий элемент (правильный вывод) в задании открытой формы вводит тестируемый  на месте прочерка и/или в специальном поле, хорошо видимом испытуемым.

К ним относятся задания двух видов:

1) дополнения (задачи с ограничением на ответы). В этих заданиях испытуемые также самостоятельно давать ответы на вопросы, однако их возможности ограничены.

Ограничения обеспечивают объективность оценивания результата выполнения задания, а формулировка ответа должна дать возможность однозначного оценивания.

Инструкция для заданий дополнения: вместо многоточия впишите только одно слово (символ, знак и т.д.).

Пример задания дополнения.

Инструкция: Вместо многоточия впишите только одно слово.

Вопрос: Фирма, предоставляющая сетевые услуги – это …

Ответ: провайдер.

2) Свободного изложения или свободного конструирования. Они предполагают свободные ответы испытуемых по сути задания. На ответы не накладываются ограничения. Однако формулировки заданий должны обеспечивать наличие только одного правильного ответа.

Инструкция для заданий свободного изложения: закончите предложение (фразу), впишите вместо многоточия правильный ответ (словосочетание, фразу, предложение или несколько предложений).

Пример задания свободного изложения.

Инструкция: Закончите предложение.

Вопрос: Специальная программа, реализующая правила передачи информации между компьютерами – это … …

Ответ: сетевой протокол.

Трудность в применении этого вида задач заключается в сложности с формализацией ответов, необходимость подготовки оценочных схем затрудняет стандартизацию, громоздкость процедуры и большие затраты времени на проведение.

Основная трудность при составлении заданий открытого типа – соблюдения основного требования к тестовым заданиям (наличия однозначного правильного ответа).

Положительными сторонами хорошо составленных заданий дополнения и свободного изложения являются:

1) невозможность угадать ответ;

2) краткость и однозначность ответов;

3) необходимость воспроизведения ответа по памяти;

4) отсутствие необходимости искать несколько вариантов ответа;

5) простота формулировки вопроса;

6) простота проверки.

1.    Критерии выставления оценки

Оценка «удовлетворительно» ставится, если обучающийся/студент ответил на от 55 до 70% вопросов. Оценка «хорошо» ставится, если обучающийся/студент получил от 71 до 85%. Оценка «отлично» ставится, если обучающийся/студент получил 86% и более.

Приложение 1 Пример плана теста

Номер задания	Тема	Шифр темы	Вид задания*
А1	Основные законы химии. Количество вещества. Молярная масса.(Задача)	1	2
А2	Молярный объем газа. (Задача)	1	2
А3	Число Авогадро (Задача)	1	1
А4	Основные типы химических реакций	3.2, 3.3	2
А5	Периодическая система Д.И.Менеделеева и свойства химических элементов	3.1	1
А6	Химическая связь и строение вещества	3.4	2
А7	Химическая  кинетика и катализ. Скорость реакций. Катализ. (Задача)	2. 2.3 1.3	2
А8	Химическое равновесие. Константа равновесия. Смещение равновесия.	2.1, 2.2	3
А9	Дисперсные системы. Общие свойства растворов. Энергетика растворения.	1.1 1.2	2
А10	Состав растворов. Массовая доля. Молярная концентрация.	1.1,	3
А11	Растворы электролитов. Диссоциация кислот, оснований, солей.	1.1 3.2	2
А12	Кислотно-основные реакции. Гидролиз солей.	3.2	2
А13	Реакции ионного обмена. Выпадение осадка, образование  газа.	3, 3.2	2
А14	Химические свойства простых веществ, оксидов, кислот, оснований	3	1

Шифр темы	Количество заданий	% от всего теста
1
1.1
..
Всего

*Примечание. Виды тестовых заданий:

1 – задания с выбором одного или нескольких правильных ответов;

2 – задания открытой формы, т. е. без указания ответов (дополнения и свободного изложения)

3 – задания на установление соответствия

4 – задания на установление правильной последовательности

5 – задания альтернативных ответов

Иллюстрация: Rawpixel / Nakaridore / Pikisuperstar / Kstudio / Master1305 / Freepic / Ambur / Cleanpng / Meery Mary для Skillbox Media

Редактор направления «Образование» Skillbox Media.

Из этой статьи вы узнаете:

• почему для подготовки домашнего задания важно хорошо знать целевую аудиторию курса и при чём тут популярные сериалы;
• правда ли, что тесты — это плохо, а текст домашнего задания должен быть коротким (спойлер: нет!);
• как оценить креативность и почему студенты могут быть недовольны заслуженной пятёркой;
• для чего нужны дополнительные материалы к заданию и какими они могут быть;
• какой шаблон используют в Skillbox, чтобы спикерам было проще составить задания для учащихся, методистам — их проверить, а студентам — выполнить;
• как поддержать учащихся и мотивировать их сделать домашку.

---

Каждый опытный методист знает, что составить для учащихся хорошее самостоятельное задание — отдельный вид искусства. Для тех, кто только начинает проектировать образовательные программы или подумывает создать свой курс, полезно будет познакомиться с ключевыми этапами разработки таких заданий.

Казалось бы, домашки — та часть программы онлайн-курса, которую можно продумать быстро. Это, конечно, совсем не так. Задания для самостоятельного выполнения проектируются вместе с основной программой и требуют от методиста столь же серьёзной подготовки, как разработка содержания лекций.

Для создания хороших домашних заданий важно ориентироваться на:

• Образовательные результаты.

В практических курсах задания должны помочь студенту сформировать определённые навыки, а не только усвоить ключевые определения. Особенно это касается курсов дополнительного профессионального образования. Чтобы понять, какие образовательные результаты должны быть у студентов после курса, нужно исследовать рынок труда: какие запросы у работодателей к знаниям и навыкам представителей той специальности, которой посвящён курс, что потребуется студентам в будущей работе. «Например, если по итогам исследования мы поняли, что студент должен уметь писать текст рекламного объявления, то эта тема ляжет в основу одного или нескольких уроков, а в качестве практического задания учащемуся нужно будет написать текст рекламного объявления», — комментирует методист Skillbox Юлия Прокофьева.

• Финансовые и технические возможности.

Безусловно, чем больше форматов самостоятельных заданий можно предложить студенту, тем лучше, однако если бюджет ограничен, то и красивую симуляцию реальной рабочей задачи построить тоже вряд ли получится.

• Опыт самих студентов.

Важно учитывать их уровень знаний, возможности для обучения, возраст, увлечения. Практическое задание должно быть для них посильным и с точки зрения необходимого на выполнение времени, и с точки зрения умений, которые для этого потребуются.

«Поскольку в асинхронном онлайн-обучении все учатся порознь, то у нас нет возможности увидеть, как студент воспринял задание, всё ли ему понятно, загорелись ли у него глаза и появилось ли желание его выполнить. Невозможно быстро поправить все недочёты, на ходу адаптировать задание под целевую аудиторию. Поэтому в онлайне особенно важно заранее изучить, кто и для чего придёт на ваш курс, что им интересно, и разработать задание с учётом специфики разных сегментов аудитории», — отмечает Юлия Прокофьева.

Для подготовки практических заданий есть также несколько основных правил, которые полезно учитывать:

• Задания должны быть основаны на информации из того урока или модуля, к которому они относятся. «Забежать вперёд» — значит вынудить студента самостоятельно изучать новую тему, повысить уровень сложности, а то и вовсе сделать задачу непонятной для учащегося.
• Материал задания не должен превышать сложности урока, к которому это задание относится, а выполнение не должно требовать слишком много времени. Даже если студент приступит к чересчур сложному заданию, его выполнение может сильно затянуться — и чем дальше, тем больше будет падать уровень мотивации.
• Все задания должны быть сформулированы подробно и понятно.
• В подготовке заданий по возможности стоит опираться на знакомый студентам опыт. Им будет куда интереснее проанализировать кейс из любимого сериала или сделать что-то по мотивам популярной у всех возрастов компьютерной игры, чем тренироваться на более скучном примере. Однако даже задача с «заимствованными» героями или обстоятельствами должна быть максимально приближена к реальной.

Идеального и «единого» формата самостоятельных заданий, конечно же, не существует — всё зависит от подходов к проектированию программы, аудитории и целей. Но есть несколько видов заданий, которые будут актуальны практически для любого онлайн-курса:

• Тесты.

Этот формат поможет проверить, как студент запомнил и понял материал. Подходит как для практико-ориентированных курсов, так и для тех, которые направлены на освоение чисто теоретических дисциплин (например, курсов по философии, истории или литературе).

«Как ни странно, студенты любят проходить тесты, несмотря на некоторое предвзятое отношение к такой форме проверки: они помогают им систематизировать знания, запомнить ключевые тезисы уроков, термины и формулы», — говорит Юлия Прокофьева.

• Практические задания.

Составляют основу курсов дополнительного профессионального образования или, например, курсов по творческим хобби, ведь именно они дают студенту возможность освоить желаемый навык. Такие домашние работы могут быть как индивидуальными, так и групповыми. А ещё они должны быть аутентичными — то есть максимально приближенными к реальным задачам, с которыми студенту придётся работать в будущем (особенно в курсах ДПО).

• Тренажёры.

У них есть множество форм — от разветвлённых квестов до больших VR-симуляций, однако во многом использование тренажёров зависит от технических возможностей. Но выход есть, даже если ресурсы ограничены: например, тот же квест можно сделать благодаря нехитрым программам (например, Twine, Branch Track и TextAdventure).

• Задания на целеполагание и рефлексию.

Статистика показывает, что мотивация взрослых студентов как минимум нестабильна — даже до первой лекции доходят далеко не все записавшиеся на курс. Поэтому в онлайн-обучении задачи на целеполагание особенно полезны. Правда, по словам Юлии Прокофьевой, не все студенты воспринимают их позитивно, поскольку могут просто не видеть в них смысла. Это может быть связано с тем, что в России в принципе не очень развиты культура и навык рефлексии.

Форматы самостоятельных заданий можно смело миксовать, а не концентрироваться только на одном из них.

«Лучше, чтобы форматы заданий были разнообразными. Тогда они будут тренировать разные навыки и помогут задействовать разные способы мышления, а студентам будет интереснее их выполнять. Но при этом всегда нужно отталкиваться от карты компетенций, которая закладывается на курс, и делать акцент именно на тех навыках и способах мышления, которые мы хотим отработать на этом курсе», — объясняет методист Skillbox Елена Мозговая.

При этом важно не перегружать курс самостоятельными заданиями, здесь нужно соблюдать баланс. Например, в Skillbox задание даётся в конце каждого модуля длительностью 60–90 минут и закрепляет один навык, объясняет Юлия Прокофьева. Когда теория чередуется с практикой, даже в асинхронном обучении не возникнет «перекоса».

«Мы любим делать так, чтобы студент практиковал новый для него материал, при этом не накапливая его слишком много. В противном случае домашки превращаются в слишком объёмные и сложные, а риск, что студент их не сдаст и остановится в своём обучении, увеличивается», — комментирует Елена Мозговая.

Чем больше информации и подробностей даст эксперт, участвующий в курсе, тем лучше получится прописать задание. Казалось бы, всё необходимое будет включено в теоретическую часть, но иногда именно обсуждение самостоятельной работы для студентов приводит к интересным примерам, лайфхакам и возможности под другим углом посмотреть на обучение в целом.

Просто попросить эксперта курса подготовить несколько заданий, скорее всего, не получится. Опыт методистов показывает, что эксперты часто присылают в качестве задания буквально одну-две реплики, максимум — абзац с расплывчатыми формулировками. Даже если дать эксперту шаблон для заполнения и инструкцию, каким должно быть задание, это не всегда помогает.

«У экспертов очень замылен взгляд на тему. Самая частая их реплика: „Здесь же и так всё понятно“. Экспертам бывает сложно посмотреть на учебный материал с точки зрения студента, но вещи, которые для погружённого в тему специалиста могут быть очевидными, не будут такими для учащихся. Студентам всегда нужно что-то „подсветить“, где-то дать рекомендации, лишний раз напомнить определение, потому что у них в головах новая информация ещё не сложилась в единую картинку», — объясняет Юлия Прокофьева.

Именно поэтому общению с экспертами стоит уделить особое внимание, чтобы в итоге задание оказалось качественным. Методисты Skillbox отмечают, что наибольшим успехом у студентов пользуются домашние задания, которые сделаны с особой любовью — дополнены интересными деталями, необычными фишками и так далее.

Обычно критерии оценки определяются исходя из того, чему должен научиться студент на том или ином этапе обучения. «Например, если мы рассказываем про рекламные тексты, то на этапе разработки курса определяем, что на этом уровне студенту достаточно уметь писать текст по трём продающим формулам. А можем решить, что ему нужно использовать в основе креативное решение», — объясняет Юлия Прокофьева.

Критерии должны быть прозрачны, измеримы и достижимы, причём это касается и творческих заданий. Казалось бы, как можно оценить креативность? «Оценка креативности — очень субъективная задача. Поэтому мы стараемся прописывать в критериях оценки не „креативность“, а, например, „новизну“. Новизна может характеризовать либо результат задания (студент сделал что-то новое, нестандартное по сравнению с общепринятым результатом), либо подход к его выполнению (студент сделал что-то по-новому, не так, как принято)», — рассказывает Елена Мозговая.

Не меньшее внимание стоит уделить выбору формата оценивания. Например, в Skillbox используется система «зачёт/незачёт», однако в других онлайн-школах можно найти примеры и с пятибалльной шкалой оценки. В любом случае, отмечают методисты, студенту будет важна не столько оценка, сколько качественная обратная связь. Юлия Прокофьева приводит пример из собственного опыта: когда учащиеся получали пятёрки за работу без комментариев, они всё равно оставляли жалобы — в их глазах даже хорошая отметка была просто отпиской.

«Студенту важно понимать, на каком уровне он сейчас находится, что у него хорошо получается, а над чем нужно больше работать. Без этого сложно оценивать себя и двигаться дальше. Иногда студенты просто не верят, что сделали с первого раза работу на пять, и поэтому считают отсутствие комментариев с замечаниями и рекомендациями подозрительным», — отметила она.

Студенты хотят совершенствоваться, и удовлетворить это желание без обратной связи невозможно, соглашается с коллегой Елена Мозговая. Поэтому, даже если работа выполнена идеально и проверяющему преподавателю совершенно не к чему «придраться», нужно всё равно что-то написать — объяснить, что именно так замечательно сделано в этой безупречной работе.

Не менее важно качество обратной связи, если задание студент сделал неправильно или неудачно. В таком случае стоит начать с позитивных моментов: отметить прогресс, сделанный во время обучения, упорство, старание, а уже дальше указать на моменты, с которыми ещё предстоит поработать. Отдельно нужно пояснить, как именно подступиться к сложностям (напомнить алгоритм, добавить примеры и так далее), отмечает Елена.

В самостоятельное задание можно (и зачастую нужно) включить дополнительную информацию, которая поможет в работе над ним. «В текст домашнего задания надо включать любые материалы, которые помогут студенту его выполнить. Речь идёт, конечно, не об ответах, а о рекомендациях, шаблонах и правилах», — комментирует Юлия Прокофьева.

Учащимся могут помочь:

• Рекомендуемые материалы.

Это, например, полезные статьи или видео по теме урока, выдержки из книг. Но подобных материалов не должно быть слишком много и они не должны быть слишком объёмными.

Елена Мозговая приводит такой пример: «В нашем курсе по дизайну интерьеров возникает много вопросов по эргономике. До сих пор основной опорный материал по этой теме — книга Эрнста Нойферта, очень объёмная. Поэтому мы даём из неё только выжимку с основными величинами, а вот тем, кто хочет узнать больше, предлагаем прочитать всю книгу».

Если примеров действительно много и хочется дать студентам побольше материала, то можно сделать отдельный список рекомендуемой литературы, но в основной включать только самое необходимое и полезное.

• Чек-листы, памятки и инструкции.

Сюда можно отнести и инструкции к каким-то сервисам, которыми студенту предстоит воспользоваться, и определённые правила работы, и рекомендации по оформлению задания. А иногда — памятки с понятиями или определениями, которые уже упоминались в уроке, но сложны для понимания. Особенно если есть вероятность, что студент их не запомнил или не до конца уловил суть.

• Референсы и образцы.

Это материалы, которые либо задают определённый стандарт выполнения задания, либо указывают студенту общее направление для работы. В любом случае не стоит перегружать эту дополнительную информацию подробными подсказками на десять страниц — учащийся вряд ли дойдёт до конца первой из них.

Мы уже упоминали, что задание для студента должно быть сформулировано максимально подробно и понятно. Но что такое «подробно» и «понятно»? В Skillbox, например, для составления задания методисты используют шаблон из пяти шагов:

• Объясните цель выполнения задания — что получит студент в результате его выполнения, какие навыки сможет освоить.
• Расскажите, что именно нужно сделать. Чем подробнее это будет сделано, тем больше шансов, что студент это задание выполнит. Формулировки должны быть чёткими — нужно постараться избежать двусмысленности. Включить в этот пункт можно:

  список задач, необходимых для выполнения;

  описания задач, то есть что нужно делать, как, в каком формате и, если обучение синхронное, в какие сроки. Также необходимо прописать итоговый результат: что получится, когда студент выполнит задание;

  необходимую информацию. Например, ссылки на сервис, с которым придётся работать.

  В некоторых случаях также могут потребоваться шаблоны. Например, если студентам какого-то управленческого курса в качестве практического задания надо составить бизнес-план в формате Excel, то лучше дать им готовый шаблон таблицы — ведь они учатся делать бизнес-план, а не верстать таблицы.

• Предложите советы и рекомендации. Это могут быть лайфхаки, помогающие настроиться на выполнение задания, дополнительные нюансы, которые стоит учесть в работе над домашкой и, главное, напоминание о важных деталях, про которые студенты часто забывают.
• Сформулируйте критерии для оценки работы. Это важно и для студентов, и для проверяющих преподавателей, поэтому напомним, что критерии должны быть ясными, измеримыми и достижимыми.
• Пропишите, как студенту действовать после выполнения задания, — когда, куда и в какой форме его отправить, в течение какого времени ждать обратную связь.

В то же время очень важно не перегрузить задание инструкциями и подробностями — тут нужно уловить баланс. Например, если для творческого задания предложить слишком подробный алгоритм выполнения, то в итоге это будет не творчество, а работа по образцу в жёстких рамках. И если список дополнительных материалов, необходимых для выполнения задания, превышает одну страницу, велика вероятность, что студент не прочтёт их до конца.

Стоит также заранее продумать, будут ли у вас какие-то ограничения по выполнению самостоятельных работ. Это зависит от формата обучения и методологии курса. Например, формат потоковых курсов предполагает дедлайны для сдачи заданий, а некоторые сервисы ограничивают количество попыток пройти тест — чтобы избежать механической зубрёжки. В Skillbox, например, домашние работы чаще всего принимают в строгой последовательности (нельзя сначала выполнить задание 2, а потом — 1), поскольку новое задание может напрямую зависеть от предыдущего — «перескочить» будет сложно. Если какие-либо ограничения у вас будут, предупреждайте о них в формулировке каждого задания.

Итак, само задание вроде бы собрано, но станут ли выполнять его студенты? Всё зависит от содержания, уверены методисты.

Мотивировать студента выполнить работу помогут:

• Элементы сторителлинга.

Интересные кейсы, которые позволяют студенту примерить на себя новую роль, необычные персонажи, а иногда — целые текстовые сериалы (на курсах, где и формат соответствует) — чем лучше студент «прочувствует» задание, тем интереснее будет его выполнять.

• Моральная поддержка и ориентация на опыт студента.

«Путь студента подразумевает, что человек начинает обучение с определённого уровня и настроения. В процессе и то и другое будет меняться, поскольку меняется учебный материал, появляются трудности. Это означает и боль от процесса их преодоления, и радость от победы. В идеале настроение текста домашнего задания должно соответствовать настроению студента в той точке, на которой он находится на этом пути. Если мы понимаем, что задание будет сложным, то говорим ему: „Не волнуйся, мы только начинаем, нелегко будет только поначалу. А пока мы вместе посмотрим, попробуем и дальше всё хорошо пойдёт“», — комментирует Елена Мозговая.

• Мотивирующая обратная связь.

Студентам нравится получать подробные ответы преподавателей, а ещё — возможность оперативно что-то уточнить, поделиться проблемой. Чем дольше они ждут ответа, тем выше риск, что домашка останется заброшенной.

Хотя это и не напрямую относится к работе методиста, всё же это имеет значение для общего результата курса:

• Обратная связь требует оперативности, и при разработке самостоятельных заданий стоит предусмотреть, сколько времени потребуется на то, чтобы их проверить и дать ответ студенту. Вряд ли кому-то понравится неделю ждать результатов, а практика показывает, что даже несколько часов могут показаться учащимся долгим сроком.
• Не менее важно, чтобы у студента была возможность быстро что-то уточнить (например, в общем чате или у помощника по обучению), чем дольше он ждёт — тем меньше желание выполнить работу.
• Лучше также заложить возможность для студента провести работу над ошибками или что-то доделать при необходимости.

В каких ситуациях студент не захочет выполнять задание? «Точно демотивирует проходить курс ситуация, когда материал урока не даёт базы для выполнения задания, инструкции сформулированы абстрактно, задания никак не применимы к реальным условиям, куратор не отвечает в чате на уточняющий вопрос, проверяющий преподаватель долго не отвечает, а обратная связь — очень обрывочная или грубая», — объясняет Юлия Прокофьева.

Больше интересного про образование — в нашем телеграм-канале. Подписывайтесь!

Научитесь: Онлайн-репетитор
Узнать больше