Как составлять уравнение движения тела по графику
Задачи по физике – это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики по кинематике.
Задача на составление описания движения и составление уравнения движения по заданному графику движения
Дано: график движения тела
Найти:
1. составить описание движения
2. составить уравнение движения тела.
Проекцию вектора скорости определяем по графику, выбрав любой удобный для рассмотрения отрезок времени.
Здесь удобно взять t=4c
Составляем уравнение движения тела:
Записываем формулу уравнения прямолинейного равномерного движения.
Подставляем в нее найденный коэффициент Vx (не забываем о минусе!).
Начальная координата тела (Xо) соответствует началу графика, тогда Xо=3
Составляем описание движения тела:
Желательно сделать чертеж, это поможет не ошибиться!
Не забываем, что все физические величины имеют единицы измерения, их необходимо указывать!
Тело движется прямолинейно и равномерно из начальной точки Xо=3м со скоростью 0,75 м/с противоположно направлению оси X.
Задача на определение места и времени встречи двух движущихся тел (при прямолинейном равномерном движении)
Движение тел задано уравнениями движения для каждого тела.
Дано:
1. уравнение движения первого тела
2. уравнение движения второго тела
Найти:
1. координату места встречи
2. момент время (после начала движения), когда произойдет встреча тел
По заданным уравнениям движения строим графики движения для каждого тела в одной системе координат.
Точка пересечения двух графиков движения определяет:
1. на оси t – время встречи ( через сколько времени после начала движения произойдет встреча)
2. на оси X – координату места встречи (относительно начала координат)
В результате:
Два тела встретятся в точке с координатой -1,75 м через 1,25 секунд после начала движения.
Для проверки полученных графическим способом ответов можно решить систему уравнений из двух заданных
уравнений движения:
Для тех, кто почему-то забыл, как построить график прямолинейного равномерного движения:
График движения – это линейная зависимость ( прямая), строится по двум точкам.
Выбираем два любых удобных для простоты расчета значения t1 и t2.
Для этих значений t подсчитываем соответствующие значения координат X1 и X2.
Откладываем 2 точки с координатами (t1, X1) и (t2, X2) и соединяем их прямой – график готов!
Задачи на составление описания движения тела и построение графиков движения по заданному уравнению прямолинейного равномерного движения
Задача 1
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Заданное уравнение сравниваем с формулой и определяем коэффициенты.
Не забываем делать чертеж, чтобы еще раз обратить внимание на направление вектора скорости.
Задача 2
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Задача 3
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Задача 4
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Тело находится в состоянии покоя в точке с координатой X=4м (состояние покоя – это частный случай движения, когда скорость тела равна нулю).
Задача 5
Дано:
начальная координата движущейся точки xo=-3 м
проекция вектора скорости Vx=-2 м/с
Найти:
1. записать уравнение движения
2. построить график движения
3. показать на чертеже векторы скорости и перемещения
4. найти координату точки через 10 секунд после начала движения
Как составлять уравнение движения тела по графику
1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Типовая задача «Уравнение координаты (нахождение неизвестной величины)»
Задача № 1. В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.

Типовая задача «Уравнение координаты. Движение двух тел»
Задача № 2. Движение двух тел задано уравнениями x1 = 20 – 8t и х2 = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.

Типовая задача «График координаты»
Задача № 3. Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите: а) начальную координату тела; б) проекцию скорости тела; в) направление движения тела (по оси х или против оси х); г) запишите уравнение координаты.


Типовая задача «График координаты. Движение нескольких тел»
Задача № 4. На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите: а) начальную координату; б) скорость; в) направление движения; г) запишите уравнение координаты.


ЗАДАЧИ ПОСЛОЖНЕЕ
Задача № 5. На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.

РЕШЕНИЕ: 
Задача № 6. По графикам на рисунке напишите уравнения движения x = x(t) . Из уравнений и графиков найдите координаты тел через 5 с , скорости движения тел, время и место встречи второго и третьего тел.

РЕШЕНИЕ: 
Задача № 7. ОГЭ Расстояние ( S ) между городами М и К = 250 км . Одновременно из обоих городов навстречу друг другу выезжают автомашины. Машина из города М движется со скоростью = 60 км/ч , из города К — со скоростью ν2 = 40 км/ч . Построить график зависимости пути от времени для каждой из машин и по ним определить место встречи и время их движения до встречи.

Задача № 8. ЕГЭ Скорость течения реки vp = 1 м/с , скорость лодки относительно воды v0 = 2 м/с . Под каким углом к берегу следует держать курс, чтобы лодка двигалась перпендикулярно берегу? За какое время t она переправится через реку, ширина которой d = 200 м ?

Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.
Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.
Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.
При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.
В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.
Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия:
Уравнение движения, графики равномерного прямолинейного движения
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.

Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin x=x_0+s=x_0+vt\ x=20+10t end

Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin x=x_0-st=x_0-vt\ x=20-10t end Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
 |
Построим графики зависимости координаты от времени для нашего примера: |
x=20+10t – машина движется вправо (в направлении оси OX)
x=20-10t – машина движется влево (в направлении, противоположном оси OX)
x=20 – машина стоит
п.5. Как найти уравнение движения по графику движения?

п.6. График скорости vx=vx(t)
Для рассмотренного примера:
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости: 
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

По графику находим: begin x_1=x(5)=8cdot 5=40 text<(м)>\ x_2=x(10)=8cdot 10=80 text <(м)>end
б) Скорость (v_x=8) м/с – постоянная величина, её график:

$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text <(м)>$$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).

Найдем скорость корабля (v_x): $$ v_x=frac=frac<56-38><2-1>=18 (text<тыс.км/ч>) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text<тыс.км/ч>) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text<тыс.км>) $$
г) Переведем скорость в км/с: $$ 18000frac<text<км>><text<ч>>=frac<18000 text<км>><1 text<ч>>=frac<18000 text<км>><3600 text>=5 text <км/c>$$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
[spoiler title=”источники:”]
http://reshator.com/sprav/fizika/7-klass/uravnenie-dvizheniya-grafiki-ravnomernogo-pryamolinejnogo-dvizheniya/
[/spoiler]
Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.
Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.
Будем отдельно рассматривать:
- движение без ускорения (равномерное), и
- движение с ускорением (неравномерное).
1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec{a} =0).
2). Неравномерное движение — скорость меняется и появляется ускорение.
Пусть ускорение есть и, оно не изменяется: (vec{a} =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:
- Равноускоренное движение — скорость тела увеличивается.
- Равнозамедленное движение — скорость уменьшается.
Примечание: Когда изменяется скорость, всегда появляется ускорение!
Движение будем изображать графически, используя две перпендикулярные оси.
На графиках будем откладывать:
- по горизонтали — время в секундах.
- по вертикали — координаты тела, или проекции скорости и ускорения.
Для каждого вида движения получим три графика. Графики будем называть так:
- x(t) – зависимость координаты от времени;
- v(t) – зависимость проекции скорости от времени;
- a(t) – зависимость проекции ускорения от времени.
Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.
Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_{0}) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_{0}]

Рис.1. Тело покоится, график координаты x(t) — горизонтальная прямая рис. б).
Скорость «v» и ускорение «a» — это прямые, лежащие на оси Ox. График скорости – рис. в). График ускорения – рис. г)
Скорость и ускорение неподвижного тела равны нулю:
[vec{v}=0]
[vec{a}=0]
Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.
Скорость не меняется — движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка (x_{0}), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.

Рис.2. Тело движется равномерно в направлении оси Ox – рис а). Зависимость координаты от времени – это возрастающая прямая x(t) – рис. б). График скорости в) – это горизонтальная прямая, а график ускорения г) лежит на оси времени, так как ускорение равно нулю
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
[ x = x_{0} + v cdot t ]
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
[ v = v_{0} = const ]
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
[ a = 0 ]
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).

Рис.3. Тело движется равномерно противоположно направлению оси Ox – рис. а). Такому движению соответствуют: убывающая зависимость координаты от времени – рис б), отрицательная проекция скорости на ось – рис. в) и, нулевое ускорение – рис. г)
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Равноускоренное движение в направлении оси, скорость увеличивается
Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.

Рис.4. Тело движется равноускорено – рис. а) по направлению оси Ox. Изменение координаты от времени x(t) описывается правой ветвью параболы – рис. б), график v(t) скорости изображен наклонной возрастающей прямой – рис. в), а график неизменного ускорения a(t) – рис. г) изображается горизонтальной прямой, лежащей выше оси времени
Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.
Уравнение, которое описывает квадратичное изменение координаты, выглядит так:
[ x = frac{a}{2}cdot t^{2} + v_{0} cdot t + x_{0} ]
Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:
[ v = v_{0} + a cdot t ]
Ускорение есть (рис. 4г) и оно не меняется:
[ a = const ]
Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.
Примечания:
1). Координата «x» будет изменяться:
- по линейному закону, когда скорость не меняется — остается одной и той же.
- по квадратичному закону, когда скорость будет изменяться (расти, или убывать).
2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.
3). Квадратичный закон – это уравнение второй степени, на графике — парабола.
4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.
Равноускоренное движение против оси
Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).
Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).

Рис.5. Тело движется равноускорено противоположно оси Ox – рис. а). Координата меняется параболически – рис. б), ветвь правая, так как скорость растет. Скорость — рис. в), и ускорение — рис. г), направлены против оси Ox, их графики лежат ниже оси времени
Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).
Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec{v}) и (vec{a}) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.
Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.
Скорость уменьшается — движение равнозамедленное
Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).

Рис.6. Тело движется равнозамедленно по оси Ox – рис. а), его координата растет по левой ветви параболы – рис. б), график скорости — убывающая наклонная прямая – рис. в), ускорение направлено против оси Ox, горизонтальный график ускорения — рис. г) лежит ниже оси времени
Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).
Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).
А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).
Равнозамедленное движение против оси
Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).
Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).

Рис.7. Тело движется равнозамедлено против оси Ox – рис. а), его координата убывает по левой ветви параболы – рис. б), скорость отрицательная и уменьшается к нулю, график скорости — наклонная прямая – рис. в), ускорение направлено по оси Ox, горизонтальный график ускорения — рис. г) лежит выше оси времени
Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).
Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.
Выводы
1). Все, что лежит:
- выше оси t – положительное;
- ниже оси t – отрицательное;
- на горизонтальной оси t – равно нулю.
2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).
3). Если скорость не меняется, ускорения нет.
- График x(t) координаты – это прямая линия.
- График v(t) скорости – горизонтальная прямая.
- График a(t) ускорения лежит на оси t.
4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.
- График x(t) координаты – это правая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.
- График x(t) координаты – это левая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
- Прямолинейное равномерное движение на координатной прямой
- Уравнение прямолинейного равномерного движения
- Удобная система отсчета для решения задачи о прямолинейном движении
- График движения x=x(t)
- Как найти уравнение движения по графику движения?
- График скорости vx=vx(t)
- Как найти путь и перемещение по графику скорости?
- Задачи
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.

Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin{gather*} x=x_0+s=x_0+vt\ x=20+10t end{gather*}

Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin{gather*} x=x_0-st=x_0-vt\ x=20-10t end{gather*} Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Основная задача механики – уметь определять положение тела в пространстве в любой момент времени.
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
Назовем проекцией вектора скорости (overrightarrow{x}) на параллельную ему ось координат OX величину (v_x=pm|overrightarrow{v}|=pm v).
Знак проекции определяется следующим правилом:
- если направление вектора (overrightarrow{v}) совпадает с направлением оси OX, то (v_x=vgt 0)
- если направление вектора (overrightarrow{v}) противоположно направлению оси OX, то (v_x=-vlt 0)
В любой момент времени t координата тела x(t) при прямолинейном равномерном движении описывается уравнением: $$ x(t)=x_0+v_x t $$ где (x_0) – координата в начальный момент времени, (v_x) – проекция вектора скорости движения.
Проекция перемещения (overrightarrow{r}) на параллельную ему ось координат OX в любой момент времени t определяется формулой: $$ triangle x=x(t)-x_0 $$ Знак (triangle x) указывает на направление совершенного перемещения:
- если (triangle xgt 0), перемещение (overrightarrow{r}) произошло в направлении оси OX;
- если (triangle xlt 0), перемещение (overrightarrow{r}) произошло противоположно направлению оси OX.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Прямолинейное движение описывается с помощью координатной прямой, параллельной направлению движения тела.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
В осях (t) и (x) график (x(t)=x_0+v_x t) является прямой.
Эта прямая:
- возрастает, если (v_xgt 0)
- убывает, если (v_xlt 0)
- постоянна (параллельна оси (t)), если (v_x= 0)
 |
Построим графики зависимости координаты от времени для нашего примера:
x=20+10t – машина движется вправо (в направлении оси OX) |
п.5. Как найти уравнение движения по графику движения?

Шаг 1. Выбрать на прямой любые две точки (A(t_1,x_1)) и (B(t_2,x_2)).
Шаг 2. Найти проекцию скорости как отношение: $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{triangle x}{triangle t} $$ Шаг 3. Найти начальную координату по одной из формул: $$ x_0=x_1-v_x t_1 text{или} x_0=x_2-v_x t_2 $$ Шаг 4. Записать найденное уравнение движения: $$ x(t)=x_0+v_x t $$
п.6. График скорости vx=vx(t)
В осях (t) и (x) график (v_x(t)=v_x=const) является прямой, параллельной оси (t).
Эта прямая:
- расположена над осью (t), если (v_xgt 0)
- расположена под осью (t), если (v_xlt 0)
- совпадает с осью (t), если (v_x=0)
Для рассмотренного примера:
Внимание!
В отличие от алгебры, в физике масштабы на осях, как правило, разные.
Поэтому обязательно нужно:
1) указывать обозначения и единицы измерения физических величин, которым соответствуют оси графика;
2) подбирать масштабы так, чтобы с графиком было удобно работать.
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости: 
На графике скорости путь, пройденный за промежуток времени (triangle t=t_2-t_1) равен площади прямоугольника, длина которого равна (triangle t), а ширина (triangle |v_x|): $$ s=|v_x|triangle t $$
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
На графике скорости проекция перемещения на ось OX за промежуток времени (triangle t=t_2-t_1) равна площади (v_xtriangle t), с учетом знака: $$ triangle x=v_xtriangle t $$
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

По графику находим: begin{gather*} x_1=x(5)=8cdot 5=40 text{(м)}\ x_2=x(10)=8cdot 10=80 text{(м)} end{gather*}
б) Скорость (v_x=8) м/с – постоянная величина, её график:
$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text{(м)} $$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).
Найдем скорость корабля (v_x): $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{56-38}{2-1}=18 (text{тыс.км/ч}) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text{тыс.км/ч}) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text{тыс.км}) $$
г) Переведем скорость в км/с: $$ 18000frac{text{км}}{text{ч}}=frac{18000 text{км}}{1 text{ч}}=frac{18000 text{км}}{3600 text{c}}=5 text{км/c} $$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
I. Механика
Тестирование онлайн
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают 
Графики равномерного движения
Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Скорость со временем не изменяется, график v(t) – прямая линия, параллельная оси времени.

Правило определения пути по графику v(t): Численное значение перемещения (пути) – это площадь прямоугольника под графиком скорости.
Зависимость пути от времени. График s(t) – наклонная линия.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Графики равноускоренного движения
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном движении путь изменяется, согласно линейной зависимости  . В координатах
. В координатах  . Графиком является наклонная линия.
. Графиком является наклонная линия.


Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.


Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости  . В координатах зависимость имеет вид
. В координатах зависимость имеет вид  . Графиком является ветка параболы.
. Графиком является ветка параболы.
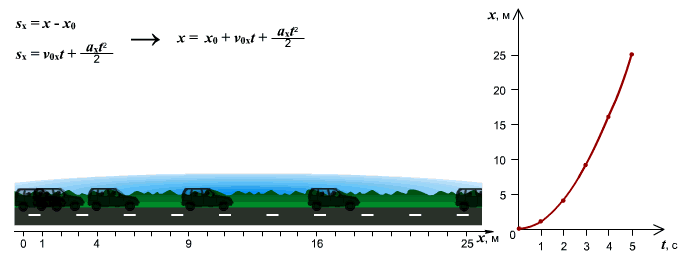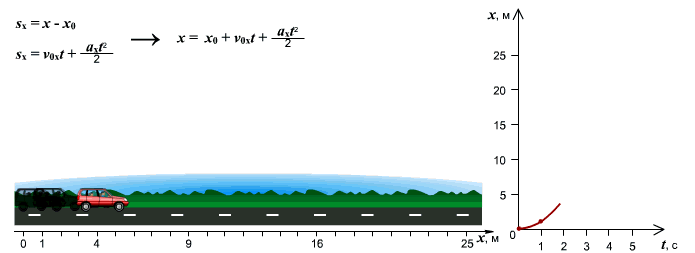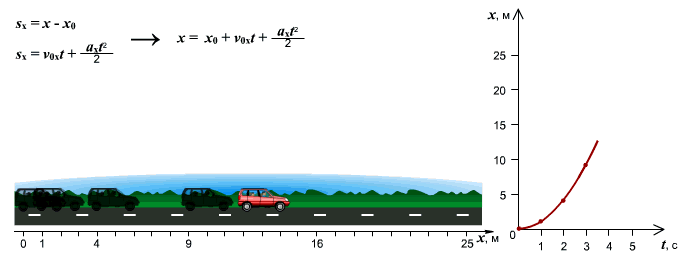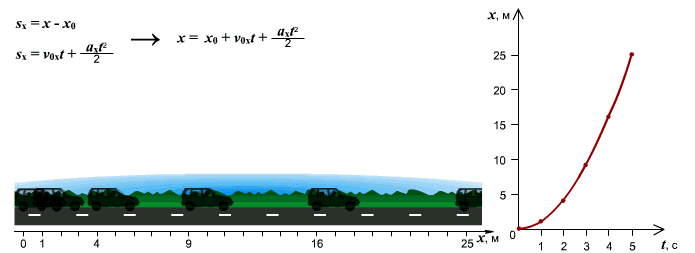


График движения при  . График движения при
. График движения при 


График движения при  . График движения при
. График движения при 
Сравнительная таблица графиков

Графическое представление
равномерного прямолинейного движения
Механическое движение представляют графическим
способом. Зависимость физических величин выражают при помощи функций.
Обозначают:
V(t) – изменение
скорости со временем
S(t) –
изменение перемещения (пути) со временем
a(t) –
изменение ускорения со временем

Зависимость ускорения от времени.
Так как при равномерном движении ускорение равно нулю, то зависимость a(t) –
прямая линия, которая лежит на оси времени.

Зависимость скорости от времени.
Так как тело движется прямолинейно и равномерно (v = const), т.е. скорость со временем не изменяется,
то график с зависимостью скорости от времени v(t) – прямая линия, параллельная
оси времени.

Проекция перемещения тела
численно равна площади прямоугольника АОВС под графиком, так как величина
вектора перемещения равна произведению вектора скорости на время, за которое
было совершено перемещение.

Правило определения пути по графику v(t):
при прямолинейном равномерном движении модуль вектора перемещения равен площади
прямоугольника под графиком скорости.

Зависимость перемещения от
времени. График s(t) – наклонная линия:
Из графика видно, что
проекция скорости равна:

Рассмотрев эту формулу, мы
можем сказать, чем больше угол, тем быстрей движется тело и оно проходит
больший путь за меньшее время.
Правило
определения скорости по графику s(t): Тангенс угла наклона графика к оси
времени равен скорости движения.
Неравномерное
прямолинейное движение.
Равномерное
движение это движение с постоянной скоростью. Если скорость тела меняется,
говорят, что оно движется неравномерно.
Движение, при
котором тело за равные промежутки времени совершает неодинаковые перемещения,
называют неравномерным или переменным движением.
Для
характеристики неравномерного движения вводится понятие средней скорости.

Средняя
скорость движения равна отношению всего пути, пройденного материальной
точкой к промежутку времени, за который этот путь пройден.
В физике наибольший интерес представляет не
средняя, а мгновенная скорость, которая определяется как
предел, к которому стремится средняя скорость за бесконечно малый промежуток
времени Δt:

Мгновенной скоростью переменного
движения называют скорость тела в данный момент времени или в данной точке
траектории.
Мгновенная скорость тела в любой точке
криволинейной траектории направлена по касательной к траектории в этой точке.
Различие между средней и мгновенной скоростями
показано на рисунке.

Движение тела, при котором его скорость за
любые равные промежутки времени изменяется одинаково, называют равноускоренным
или равнопеременным движением.
Ускорение — это
векторная физическая величина, характеризующая быстроту изменения скорости,
численно равная отношению изменения скорости к промежутку времени, в течение
которого это изменение произошло.
Если скорость изменяется
одинаково в течение всего времени движения, то ускорение можно рассчитать по
формуле:

Обозначения:
Vx — Скорость
тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
ax — Ускорение тела
t — Время движения тела
Ускорение показывает, как
быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость
тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит
скорость уменьшается, движение замедленное.
Единица измерения ускорения в
СИ [м/с2].
Ускорение измеряют акселерометром
Уравнение скорости для
равноускоренного движения: vx = vxo + axt
Уравнение равноускоренного прямолинейного
движения (перемещение при равноускоренном движении):

Обозначения:
Sx—
Перемещение тела при равноускоренном движении по прямой
Vx o —
Начальная скорость тела
Vx — Скорость тела при равноускоренном
движении по прямой
ax — Ускорение тела
t— Время
движения тела
Еще формулы, для нахождения перемещения при
равноускоренном прямолинейном движении, которые можно использовать при решении
задач:

–
если известны начальная, конечная скорости движения и ускорение.

–
если известны начальная, конечная скорости движения и время всего движения
Графическое представление неравномерного
прямолинейного движения
Механическое
движение представляют графическим способом. Зависимость физических величин
выражают при помощи функций. Обозначают:
V(t) – изменение
скорости со временем
S(t) –
изменение перемещения (пути) со временем
a(t) –
изменение ускорения со временем
Зависимость ускорения от времени.
Ускорение со временем не изменяется, имеет постоянное значение, график a(t) –
прямая линия, параллельная оси времени.

Зависимость скорости от времени. При
равномерном движении скорость изменяется, согласно линейной зависимости vx = vxo + axt .
Графиком является наклонная линия.

Правило определения пути по графику v(t):
Путь тела – это площадь треугольника (или трапеции) под графиком скорости.

Правило определения ускорения по графику v(t):
Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело
замедляет движение, ускорение отрицательное, угол графика тупой, поэтому
находим тангенс смежного угла.

Зависимость пути от времени. При
равноускоренном движении путь изменяется, согласно квадратной зависимости:

.
В координатах зависимость имеет
вид:

Графиком является ветка параболы.


