Каждый обращал внимание на все многообразие видов движения, с которыми он сталкивается в своей жизни. Однако любое механическое движение тела сводится к одному из двух типов: линейное или вращательное. Рассмотрим в статье основные законы движения тел.
О каких типах движения пойдет речь?
Как было отмечено во введении, все виды движения тела, которые рассматриваются в классической физике, связаны либо с прямолинейной траекторией, либо с круговой. Любые другие траектории можно получить благодаря комбинации этих двух. Далее в статье будут рассмотрены следующие законы движения тела:
Равномерное движение, или состояние покоя
 Вам будет интересно:Преподаватели СПБГУ: педагогический состав, факультеты, направления
Вам будет интересно:Преподаватели СПБГУ: педагогический состав, факультеты, направления
Этим движением с научной точки зрения начал интересоваться впервые Галилей в конце XVI – начале XVII века. Изучая инерционные свойства тела, а также введя понятие о системе отсчета, он догадался, что состояние покоя и равномерного движения – это одно и то же (все зависит от выбора объекта, относительно которого рассчитывают скорость).
 Вам будет интересно:Характеристика движения под углом к горизонту: формулы, решение задачи с лучником
Вам будет интересно:Характеристика движения под углом к горизонту: формулы, решение задачи с лучником
Впоследствии Исаак Ньютон сформулировал свой первый закон движения тела, согласно которому скорость последнего является постоянной величиной всегда, когда нет внешних сил, изменяющих характеристики движения.

Равномерное прямолинейное перемещение тела в пространстве описывается следующей формулой:
s = v * t
Где s – расстояние, которое преодолеет тело за время t, двигаясь со скоростью v. Это простое выражение также записывается в следующих формах (все зависит от величин, которые известны):
v = s / t; t = s / v
Перемещение по прямой с ускорением
Согласно второму закону Ньютона, наличие внешней силы, действующей на тело, неминуемо приводит к появлению ускорения у последнего. Из определения ускорения (быстрота изменения скорости) следует выражение:
 Вам будет интересно:Тюркизмы в русском языке: понятие, история появления, звучание и примеры
Вам будет интересно:Тюркизмы в русском языке: понятие, история появления, звучание и примеры
a = v / t или v = a * t
Если действующая на тело внешняя сила будет оставаться постоянной (не будет изменять модуля и направления), то ускорение также не изменится. Такой тип движения называется равноускоренным, где ускорение выступает коэффициентом пропорциональности между скоростью и временем (скорость растет линейно).
Для этого движения пройденный путь рассчитывается с помощью интегрирования скорости по времени. Закон движения тела для пути при равноускоренном перемещении приобретает форму:
s = a * t2 / 2
Самым распространенным примером этого движения является падение любого предмета с высоты, при котором сила тяжести сообщает ему ускорение g = 9,81 м/с2.
Прямолинейное ускоренное (замедленное) движение с наличием начальной скорости
По сути, речь идет о комбинации двух видов перемещения, рассмотренных в предыдущих пунктах. Представим простую ситуацию: автомобиль ехал с некоторой скоростью v0, затем водитель нажал на тормоза, и транспортное средство через некоторое время остановилось. Как описать движение в этом случае? Для функции скорости от времени справедливо выражение:
v = v0 – a * t
Здесь v0 – начальная скорость (до торможения авто). Знак минус говорит о том, что внешняя сила (трения скольжения) направлена против скорости v0.

Как и в предыдущем пункте, если взять интеграл по времени от v(t), то получаем формулу для пути:
s = v0 * t – a * t2 / 2
Отметим, что по этой формуле вычисляется только путь торможения. Чтобы узнать расстояние, пройденное автомобилем за все время его движения, следует найти сумму двух путей: для равномерного и для равнозамедленного движения.
В примере описанном выше, если бы водитель нажал не на педаль тормоза, а на педаль газа, тогда в представленных формулах поменялся бы знак “-” на “+”.
Движение по окружности
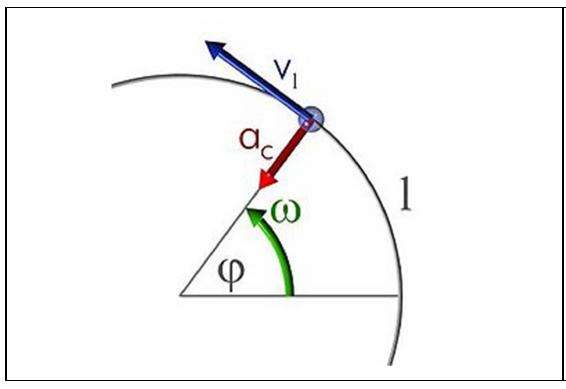
Любое движение по окружности не может происходить без ускорения, поскольку даже при сохранении модуля скорости изменяется ее направление. Ускорение, которое связано с этим изменением, называется центростремительным (именно оно искривляет траекторию тела, превращая ее в окружность). Модуль этого ускорения вычисляют так:
ac = v2 / r, r – радиус
В этом выражении скорость может зависеть от времени, как это происходит в случае равноускоренного движения по окружности. В последнем случае ac будет быстро расти (квадратичная зависимость).
Центростремительное ускорение определяет силу, которую нужно прикладывать, чтобы удерживать тело на круговой орбите. Примером являются соревнования по метанию молота, когда спортсмены прикладывают значительные усилия, чтобы раскрутить снаряд до его метания.

Вращение вокруг оси с постоянной скоростью
Этот вид движения идентичен предыдущему, только описывать его принято не с использованием линейных физических величин, а с применением угловых характеристик. Закон вращательного движения тела, когда угловая скорость не изменяется, в скалярной форме записывается так:
L =I * ω
Здесь L и I – моменты импульса и инерции, соответственно, ω – угловая скорость, которая с линейной связана равенством:
v = ω * r
Величина ω показывает, на сколько радиан повернется тело за секунду. Величины L и I имеют такой же смысл, как импульс и масса для прямолинейного движения. Соответственно, угол θ, на который повернется тело за время t, вычисляется так:
θ = ω * t
Примером этого типа движения является вращение маховика, находящегося на коленчатом вале в двигателе автомобиля. Маховик – это массивный диск, которому очень тяжело придать какое-либо ускорение. Благодаря этому он обеспечивает плавность изменения крутящего момента, который передается от двигателя к колесам.

Вращение вокруг оси с ускорением
Если к системе, которая способна вращаться, прикладывать внешнюю силу, то она начнет увеличивать свою угловую скорость. Такая ситуация описывается следующим законом движения тела вокруг оси вращения:
F * d = I * dω / dt
Здесь F – внешняя сила, которая приложена к системе на расстоянии d от оси вращения. Произведение в левой части равенства носит название момента силы.
Для равноускоренного движения по окружности получаем, что ω зависит от времени следующим образом:
ω = α * t, где α = F * d / I – угловое ускорение
В этом случае угол поворота за время t можно определить, проинтегрировав ω по времени, то есть:
θ = α * t2 / 2
Если же тело уже вращалось с некоторой скоростью ω0, а затем начал действовать внешний момент силы F*d, то по аналогии с линейным случаем можно записать такие выражения:
ω = ω0 + α * t;
θ = ω0 * t + α * t2 / 2
Таким образом, появление внешнего момента сил является причиной наличия ускорения в системе с осью вращения.
Для полноты информации отметим, что изменить скорость вращения ω можно не только с помощью внешнего момента сил, но и благодаря изменению внутренних характеристик системы, в частности ее момента инерции. Эту ситуацию видел каждый человек, который наблюдал за вращением фигуристов на льду. Группируясь, спортсмены увеличивают ω за счет уменьшения I, согласно простому закону движения тела:
I * ω = const
Движение по эллиптической траектории на примере планет Солнечной системы
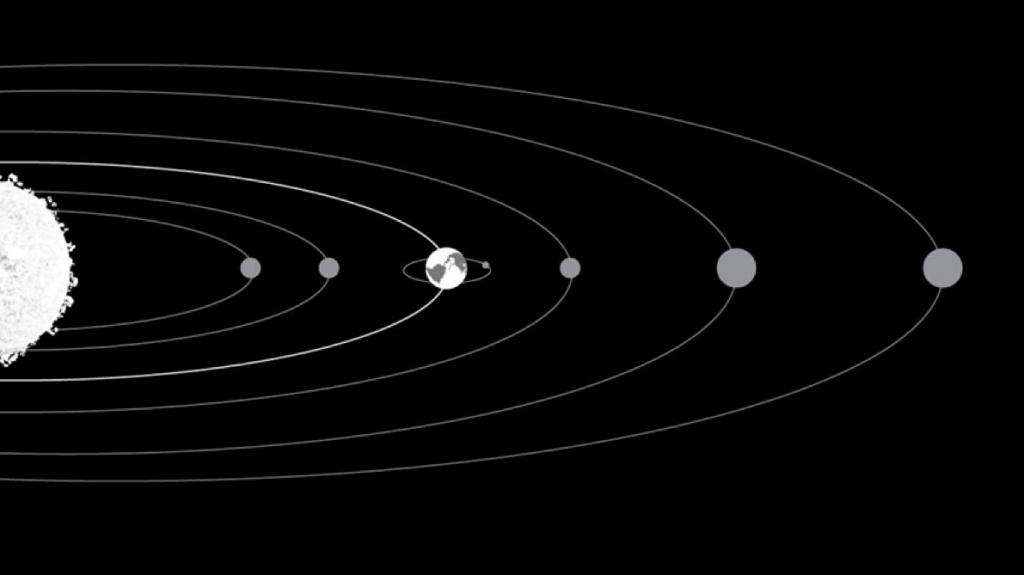
Как известно, наша Земля и другие планеты Солнечной системы вращаются вокруг своей звезды не по окружности, а по эллиптической траектории. Впервые математические законы для описания этого вращения сформулировал знаменитый немецкий ученый Иоганн Кеплер в начале XVII века. Используя результаты наблюдений своего учителя Тихо Браге за движением планет, Кеплер пришел к формулировке своих трех законов. Они формулируются следующим образом:
T2 / a3 = С = const
Впоследствии Исаак Ньютон, используя эти законы движения тел (планет), сформулировал свой знаменитый закон всемирной гравитации, или тяготения. Применяя его, можно показать, что константа C в 3-м законе Кеплера равна:
C = 4 * pi2 / (G * M)
Где G – гравитационная универсальная константа, а M – масса Солнца.
Отметим, что движение по эллиптической орбите в случае действия центральной силы (тяготения) приводит к тому, что линейная скорость v постоянно меняется. Она максимальна, когда планета находится ближе всего к звезде, и минимальна вдали от нее.
Закон движения — математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют все данные о движении точки.
В классической механике материальной точки закон движения представляет собой три зависимости трёх пространственных координат от времени, либо зависимость одной векторной величины (радиус-вектора) от времени, вида
.
Закон движения может быть найден, в зависимости от задачи, либо из дифференциальных законов механики (см. Законы Ньютона), либо из интегральных (см. Закон сохранения энергии, Закон сохранения импульса), либо из так называемых вариационных принципов.
Частные случаи[править | править код]
Равномерное прямолинейное движение[править | править код]
Простейшим случаем движения материальной точки является равномерное и прямолинейное движение, то есть движение с постоянной по модулю и направлению скоростью. В этом случае её закон движения выглядит следующим образом:
,
где 


Если ось x выбрать направленной вдоль направления вектора скорости, а в качестве нуля выбрать положение материальной точки в момент времени 
,
где 
Равноускоренное прямолинейное движение[править | править код]
Другим важным частным случаем является прямолинейное движение с постоянным ускорением. В этом случае закон движения имеет вид:
,
где 


Если ось x выбрать направленной вдоль направления вектора ускорения, а в качестве нуля выбрать положение материальной точки в момент времени 
,
где 


Равномерное движение по окружности[править | править код]
При движении по окружности с постоянной по модулю скоростью (или, что то же самое с постоянной угловой скоростью) вектор ускорения направлен строго перпендикулярно вектору скорости в сторону центра окружности. В этом случае закон движения может быть записан в следующем виде:
,
где 






Удобнее при рассмотрении движения по окружности перейти к угловым переменным: углу 


Равноускоренное движение по окружности[править | править код]
При равноускоренном движении по окружности вектор ускорения меняет как своё направление, так и величину модуля. Постоянным остаётся только так называемая тангенциальная составляющая ускорения, равная проекции вектора ускорения на прямую, вдоль которой направлен вектор скорости (эта же прямая является касательной к окружности, по которой движется материальная точка). Закон движения может быть при этом записан в следующем виде:
,
где 






В угловых переменных закон равноускоренного движения по окружности имеет более простой вид:
,
где 
Литература[править | править код]
- Сивухин Д. В. Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — 520 с.
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Здесь – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость

Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
Каждый обращал внимание на все многообразие видов движения, с которыми он сталкивается в своей жизни. Однако любое механическое движение тела сводится к одному из двух типов: линейное или вращательное. Рассмотрим в статье основные законы движения тел.
О каких типах движения пойдет речь?
Как было отмечено во введении, все виды движения тела, которые рассматриваются в классической физике, связаны либо с прямолинейной траекторией, либо с круговой. Любые другие траектории можно получить благодаря комбинации этих двух. Далее в статье будут рассмотрены следующие законы движения тела:
- Равномерное по прямой линии.
- Равноускоренное (равнозамедленное) по прямой линии.
- Равномерное по окружности.
- Равноускоренное по окружности.
- Движение по эллиптической траектории.
Равномерное движение, или состояние покоя
Этим движением с научной точки зрения начал интересоваться впервые Галилей в конце XVI – начале XVII века. Изучая инерционные свойства тела, а также введя понятие о системе отсчета, он догадался, что состояние покоя и равномерного движения – это одно и то же (все зависит от выбора объекта, относительно которого рассчитывают скорость).
Впоследствии Исаак Ньютон сформулировал свой первый закон движения тела, согласно которому скорость последнего является постоянной величиной всегда, когда нет внешних сил, изменяющих характеристики движения.

Равномерное прямолинейное перемещение тела в пространстве описывается следующей формулой:
s = v * t
Где s – расстояние, которое преодолеет тело за время t, двигаясь со скоростью v. Это простое выражение также записывается в следующих формах (все зависит от величин, которые известны):
v = s / t; t = s / v
Перемещение по прямой с ускорением
Согласно второму закону Ньютона, наличие внешней силы, действующей на тело, неминуемо приводит к появлению ускорения у последнего. Из определения ускорения (быстрота изменения скорости) следует выражение:
a = v / t или v = a * t
Если действующая на тело внешняя сила будет оставаться постоянной (не будет изменять модуля и направления), то ускорение также не изменится. Такой тип движения называется равноускоренным, где ускорение выступает коэффициентом пропорциональности между скоростью и временем (скорость растет линейно).
Для этого движения пройденный путь рассчитывается с помощью интегрирования скорости по времени. Закон движения тела для пути при равноускоренном перемещении приобретает форму:
s = a * t2 / 2
Самым распространенным примером этого движения является падение любого предмета с высоты, при котором сила тяжести сообщает ему ускорение g = 9,81 м/с2.
Прямолинейное ускоренное (замедленное) движение с наличием начальной скорости
По сути, речь идет о комбинации двух видов перемещения, рассмотренных в предыдущих пунктах. Представим простую ситуацию: автомобиль ехал с некоторой скоростью v0, затем водитель нажал на тормоза, и транспортное средство через некоторое время остановилось. Как описать движение в этом случае? Для функции скорости от времени справедливо выражение:
v = v0 – a * t
Здесь v0 – начальная скорость (до торможения авто). Знак минус говорит о том, что внешняя сила (трения скольжения) направлена против скорости v0.

Как и в предыдущем пункте, если взять интеграл по времени от v(t), то получаем формулу для пути:
s = v0 * t – a * t2 / 2
Отметим, что по этой формуле вычисляется только путь торможения. Чтобы узнать расстояние, пройденное автомобилем за все время его движения, следует найти сумму двух путей: для равномерного и для равнозамедленного движения.
В примере описанном выше, если бы водитель нажал не на педаль тормоза, а на педаль газа, тогда в представленных формулах поменялся бы знак “-” на “+”.
Движение по окружности
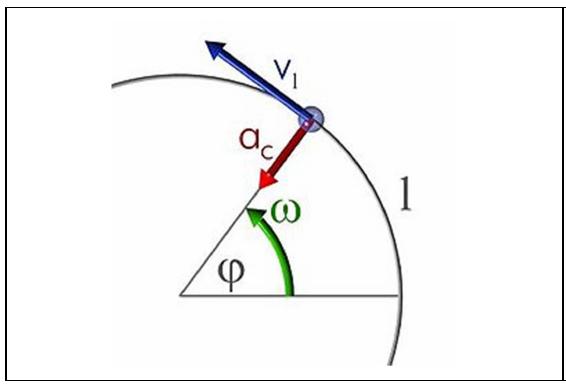
Любое движение по окружности не может происходить без ускорения, поскольку даже при сохранении модуля скорости изменяется ее направление. Ускорение, которое связано с этим изменением, называется центростремительным (именно оно искривляет траекторию тела, превращая ее в окружность). Модуль этого ускорения вычисляют так:
ac = v2 / r, r – радиус
В этом выражении скорость может зависеть от времени, как это происходит в случае равноускоренного движения по окружности. В последнем случае ac будет быстро расти (квадратичная зависимость).
Центростремительное ускорение определяет силу, которую нужно прикладывать, чтобы удерживать тело на круговой орбите. Примером являются соревнования по метанию молота, когда спортсмены прикладывают значительные усилия, чтобы раскрутить снаряд до его метания.

Вращение вокруг оси с постоянной скоростью
Этот вид движения идентичен предыдущему, только описывать его принято не с использованием линейных физических величин, а с применением угловых характеристик. Закон вращательного движения тела, когда угловая скорость не изменяется, в скалярной форме записывается так:
L =I * ω
Здесь L и I – моменты импульса и инерции, соответственно, ω – угловая скорость, которая с линейной связана равенством:
v = ω * r
Величина ω показывает, на сколько радиан повернется тело за секунду. Величины L и I имеют такой же смысл, как импульс и масса для прямолинейного движения. Соответственно, угол θ, на который повернется тело за время t, вычисляется так:
θ = ω * t
Примером этого типа движения является вращение маховика, находящегося на коленчатом вале в двигателе автомобиля. Маховик – это массивный диск, которому очень тяжело придать какое-либо ускорение. Благодаря этому он обеспечивает плавность изменения крутящего момента, который передается от двигателя к колесам.

Вращение вокруг оси с ускорением
Если к системе, которая способна вращаться, прикладывать внешнюю силу, то она начнет увеличивать свою угловую скорость. Такая ситуация описывается следующим законом движения тела вокруг оси вращения:
F * d = I * dω / dt
Здесь F – внешняя сила, которая приложена к системе на расстоянии d от оси вращения. Произведение в левой части равенства носит название момента силы.
Для равноускоренного движения по окружности получаем, что ω зависит от времени следующим образом:
ω = α * t, где α = F * d / I – угловое ускорение
В этом случае угол поворота за время t можно определить, проинтегрировав ω по времени, то есть:
θ = α * t2 / 2
Если же тело уже вращалось с некоторой скоростью ω0, а затем начал действовать внешний момент силы F*d, то по аналогии с линейным случаем можно записать такие выражения:
ω = ω0 + α * t;
θ = ω0 * t + α * t2 / 2
Таким образом, появление внешнего момента сил является причиной наличия ускорения в системе с осью вращения.
Для полноты информации отметим, что изменить скорость вращения ω можно не только с помощью внешнего момента сил, но и благодаря изменению внутренних характеристик системы, в частности ее момента инерции. Эту ситуацию видел каждый человек, который наблюдал за вращением фигуристов на льду. Группируясь, спортсмены увеличивают ω за счет уменьшения I, согласно простому закону движения тела:
I * ω = const
Движение по эллиптической траектории на примере планет Солнечной системы
Как известно, наша Земля и другие планеты Солнечной системы вращаются вокруг своей звезды не по окружности, а по эллиптической траектории. Впервые математические законы для описания этого вращения сформулировал знаменитый немецкий ученый Иоганн Кеплер в начале XVII века. Используя результаты наблюдений своего учителя Тихо Браге за движением планет, Кеплер пришел к формулировке своих трех законов. Они формулируются следующим образом:
- Планеты Солнечной системы движутся по эллиптическим орбитам, причем Солнце расположено в одном из фокусов эллипса.
- Радиус-вектор, который соединяет Солнце и планету, за равные промежутки времени описывает одинаковые площади. Этот факт следует из сохранения момента импульса.
- Если поделить квадрат периода обращения на куб большой полуоси эллиптической орбиты планеты, то получается некоторая константа, которая одинакова для всех планет нашей системы. Математически это записывается так:
T2 / a3 = С = const
Впоследствии Исаак Ньютон, используя эти законы движения тел (планет), сформулировал свой знаменитый закон всемирной гравитации, или тяготения. Применяя его, можно показать, что константа C в 3-м законе Кеплера равна:
C = 4 * pi2 / (G * M)
Где G – гравитационная универсальная константа, а M – масса Солнца.
Отметим, что движение по эллиптической орбите в случае действия центральной силы (тяготения) приводит к тому, что линейная скорость v постоянно меняется. Она максимальна, когда планета находится ближе всего к звезде, и минимальна вдали от нее.
Билет
1
1.
|
Рис. 1 |
1. Естественный
способ. Этим
способом пользуются, если известна
траектория движения точки. Траекторией
называется совокупность точек
пространства, через которые проходит
движущаяся материальная частица.
Это линия, которую она вычерчивает в
пространстве. При естественном
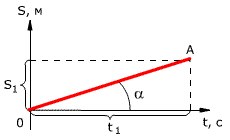
способе необходимо задать (рис. 1):
а)
траекторию движения (относительно
какой-либо системы координат);
б)
произвольную точку на ней нуль, от
которого отсчитывают расстояние S до
движущейся частицы вдоль траектории;
в)
положительное направление отсчета
S (при смещении точки М в противоположном
направлении S отрицательно);
г)
начало отсчета времени t;
д)
функцию S(t), которая называется законом
движения*точки.
2. Координатный
способ. Это
наиболее универсальный и исчерпывающий
способ описания движения. Он предполагает
задание:
а)
системы координат (не обязательно
декартовой) q1, q2, q3;
б)
начало отсчета времени t;
в)
закона движения точки, т.е. функций
q1(t), q2(t), q3(t).
Говоря
о координатах точки, мы всегда будем
иметь в виду (если не оговорено противное)
ее декартовы координаты.
3. Векторный
способ. Положение
точки в пространстве может быть определено
также и радиус-вектором, проведенным
из некоторого начала в данную точку
(рис. 2). В этом случае для описания
движения необходимо задать:
а)
начало отсчета радиус-вектора r;
б)
начало отсчета времени t;
в)
закон движения точки r(t).
Поскольку
задание одной векторной величины r эквивалентно
заданию трех ее проекций x, y, z на оси
координат, от векторного способа
легко перейти к координатному. Если
ввести единичные векторы i, j, k ( i = j = k =
1), направленные соответственно вдоль
осей x, y и z (рис. 2), то, очевидно, закон
движения может быть представлен в виде*)
r(t)
=
x(t)i +y(t)j+z(t)k. (1)
Преимущество
векторной формы записи перед координатной в
компактности (вместо трех величин
оперируют с одной) и часто в большей
наглядности.
2.В
динамике решают две задачи. Эти задачи
называются первой или прямой, второй
или обратной. Обратная задача является
основной. Прямой задачей, по заданным
законам
движения,
определяют силы и моменты сил. Во второй
задаче, по приложенным силам и моментам,
вычисляют законы движения
Билет
2
Закон движения:
зависимость r=r(t)
Закон движения
материальной точки:
Положение
материальной точки в любой момент
времени относительно данной системы
отсчета:
x=x0+V0t
x=x0+V0t+(at2)/2
m(dV/dt)
– уравнение движения
y=y(x)
– уравнение траектории
2. Инерциальные системы отсчета. Первый закон Ньютона, две его формулировки.
Инерциальная
система отсчёта (ИСО) — система
отсчёта,
в которой справедлив первый закон
Ньютона (закон инерции): все свободные
тела (то есть такие, на которые не
действуют внешние силы или действие
этих сил компенсируется) движутся
прямолинейно и равномерно или покоятся.
Первый
закон Ньютона
постулирует наличие такого явления,
как инерция тел.
Поэтому он также известен как Закон
инерции.
Инерция — это явление сохранения
телом скорости движения (и по величине,
и по направлению), когда на тело не
действуют никакие силы. Чтобы изменить
скорость движения тела, на него необходимо
подействовать с некоторой силой.
Естественно, результат действия
одинаковых по величине сил на различные
тела будет различным. Таким образом,
говорят, что тела обладают инертностью.
Инертность — это свойство тел
сопротивляться изменению их текущего
состояния. Величина инертности
характеризуется массой тела.
Современная
формулировка:
Существуют
такие системы
отсчёта,
называемые инерциальными,
относительно которых материальная
точка при
отсутствии внешних воздействий сохраняет
величину и направление
своей скорости неограниченно
долго.
Закон
верен также в ситуации, когда внешние
воздействия присутствуют, но взаимно
компенсируются (это следует из 2-го
закона Ньютона, так как скомпенсированные
силы сообщают телу нулевое суммарное
ускорение)
Историческая
формулировка:
Всякое
тело продолжает удерживаться в состоянии
покоя или равномерного и прямолинейного
движения, пока и поскольку оно не
понуждается приложенными силами изменить
это состояние.
С
современной точки зрения, такая
формулировка неудовлетворительна.
Во-первых, термин «тело» следует заменить
термином «материальная точка», так как
тело конечных размеров в отсутствие
внешних сил может совершать и вращательное
движение. Во-вторых, и это главное, Ньютон
в своём труде опирался на существование
абсолютной неподвижной системы
отсчёта,
то есть абсолютного пространства и
времени, а это представление современная
физика отвергает. С другой стороны, в
произвольной (скажем, вращающейся)
системе отсчёта закон инерции неверен.
Поэтому ньютоновская формулировка
нуждается в уточнениях.
Билет
3
1.
Путь(S) – это скалярная величина, равная
длине траектории. Путь всегда положительная
величина.
Перемещение
– вектор, соединяющий начальной положение
материальной точки с ее конечным
положением на траектории. Перемещение
векторная величина.
Траектория
– линия, вдоль которой движется тело.
2.
Второй закон ньютона
Современная
формулировка
В
инерциальной системе отсчёта ускорение,
которое получает материальная точка,
прямо пропорционально равнодействующей
всех приложенных к ней сил и обратно
пропорционально её массе.
a=F/m
Си́ла
— векторная физическая величина,
являющаяся мерой интенсивности
воздействия на данное тело других тел,
а также полей.
Масса
– мера инертности тела, физическая
величина. Она определяет отношение
модуля ускорения талона массы к модулю
ускорения тела при их взаимодействии.
Билет
4
1.
Средняя скорость – это физическая
величина, равная отношению вектора
перемещения
![]()
точки
к промежутку времени Δt, за который
произошло это перемещение. Направление
вектора средней скорости совпадает с
направлением вектора перемещения
.
Средняя скорость определяется по
формуле:
М![]()
гновенная
скорость – это физическая величина,
равная пределу, к которому стремится
средняя скорость при бесконечном
уменьшении промежутка времени Δt:
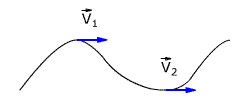
Иными
словами, мгновенная скорость в данный
момент времени – это отношение очень
малого перемещения к очень малому
промежутку времени, за который это
перемещение произошло.
Вектор
мгновенной скорости направлен по
касательной к траектории движения тела
(рис. 1.6).
2.


Билет
5
1![]()
.Отношение
приращения вектора скорости промежутку
времени, в течение которого произошло
это приращение, называется средним
ускорением 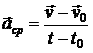
М![]()
гновенное
ускорение (или просто, ускорение) a – это
вектор ускорения материальной точки в
любой момент времени a=dv/dt.
или мгновенное ускорение есть вторая
производная по времени от радиус-вектора:
2.

Билет
6
1.

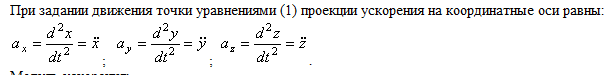
2.
Билет
7
1.
Равноме́рное движе́ние — механическое
движение, при котором тело за любые
равные отрезки времени проходит равные
перемещения. Равномерное движение
материальной точки — это движение, при
котором скорость точки остаётся
неизменной.
2.
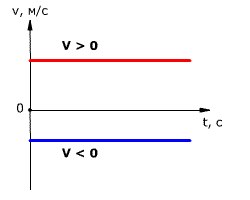
третий закон ньютона Современная
формулировка
Материальные
точки взаимодействуют друг с другом
силами, имеющими одинаковую природу,
направленными вдоль прямой, соединяющей
эти точки, равными по модулю и
противоположными по направлению:
F12=-F21
Закон
отражает принцип парного взаимодействия.
То есть все силы в природе рождаются
парами.
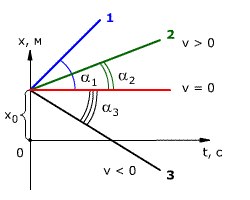
Билет
8
1.Самый
простой вид неравномерного движения —
это равноускоренное движение.
Равноускоренным называется движение
с ускорением, постоянным по модулю и
направлению:
![]()
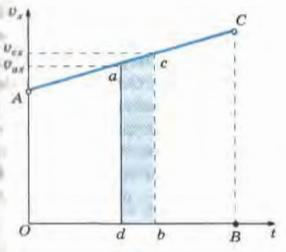
S=((V0x+Vx)/2)*t.
Sx=V0x*t+(ax*t^2)/2
равноускоренным
движением называют
такое движение, при
котором
вектор ускорения остается
неизменным по модулю и направлению.
Примером такого движения является
движение камня, брошенного под некоторым
углом к горизонту (без учета сопротивления
воздуха). В любой точке траектории
ускорение камня равно ускорению
свободного падения g.
Для кинематического описания движения
камня систему координат удобно выбрать
так, чтобы одна из осей, например ось OY,
была направлена параллельно вектору
ускорения. Тогда криволинейное движение
камня можно представить как сумму двух
движений – прямолинейного
равноускоренного движения вдоль
оси OY и равномерного
прямолинейного движения в
перпендикулярном направлении, т. е.
вдоль оси OX (рис. 1.4.1).
Таким
образом, изучение равноускоренного
движения сводится к изучению прямолинейного
равноускоренного движения. В случае
прямолинейного движения векторы
скорости V и
ускорения a направлены
вдоль прямой движения. Поэтому скорость υ и
ускорение a в
проекциях на направление движения можно
рассматривать как алгебраические
величины.
V=V0+at
Прoекции
векторов скорости и ускорения на
координатные оси. ax = 0, ay = –g
При
равноускоренном прямолинейном движении
скорость тела определяется формулой
В
этой формуле υ0 –
скорость тела при t = 0 (начальная
скорость),a = const –
ускорение.
2.
Силой трения называют силу, которая
возникает при движении одного тела по
поверхности другого. Она всегда направлена
противоположно направлению движения.
Сила трения прямо пропорциональна силе
нормального давления на трущиеся
поверхности и зависит от свойств этих
поверхностей. Законы трения связаны с
электромагнитным взаимодействием,
которое существует между телами. Сухое
трение возникает между поверхностями
твердых тел в отсутствие смазки. Жидким
(вязким) называется трение между твердым
телом и жидкой или газообразной средой
или ее слоями.
Билет
9
1.
1) Движение — это перемещение тела
относительно других тел. Таким образом,
описывая движение тела, мы всегда
привязываемся к какой-то координатной
системе, относительно которой тело
движется, или к системе отсчета. Движение
тела определяется движением всех его
точек поэтому мы начнем с описания
движения материальной точки. Матеpиальной
точкой называется тело, pазмеpами котоpого
можно пpенебpечь, считая, что вся масса
тела сосpедоточена в одной точке.
Рассмотрим теперь вопрос, как найти
путь 5, проходимый материальной точкой
при ее движении. Путь, пройденный точкой
при неравномерном движении по прямой
с переменной скоростью
![]()
за промежуток времени от
![]()
до
![]()
вычисляется по формуле
![]()
2.
Трение покоя — сила, возникающая между
двумя контактирующими телами и
препятствующая возникновению
относительного движения. Эту силу
необходимо преодолеть для того, чтобы
привести два контактирующих тела в
движение друг относительно друга.
Возникает при микроперемещениях
(например, при деформации) контактирующих
тел. Она действует в направлении,
противоположном направлению возможного
относительного движения. Максимальная
сила трения покоя в простейшем приближении:
F=k0*N , где k0 — коэффициент трения покоя,
N — сила нормальной реакции опоры.
Билет
10
1.ВРАЩАТЕЛЬНОЕ
ДВИЖЕНИЕ твердого тела, 1) вокруг оси –
движение, при котором все точки тела,
лежащие на оси вращения, неподвижны, а
остальные точки тела описывают окружности
с центрами на оси; 2) вокруг точки –
движение тела, при котором одна его
точка О неподвижна, а все другие движутся
по поверхностям сфер с центром в точке
О.
Углова́я
ско́рость — векторная физическая
величина, характеризующая скорость
вращения тела.
2.Закон
всемирного тяготения гласит, что сила
гравитационного притяжения между двумя
материальными точками массы m1 и m2 ,
разделёнными расстоянием R, пропорциональна
обеим массам и обратно пропорциональна
квадрату расстояния между ними — то
есть: F=G*m1*m2/R^2
Билет
11
1.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ твердого тела,
1) вокруг оси – движение, при котором все
точки тела, лежащие на оси вращения,
неподвижны, а остальные точки тела
описывают окружности с центрами на оси;
2) вокруг точки – движение тела, при
котором одна его точка О неподвижна, а
все другие движутся по поверхностям
сфер с центром в точке О.
Угловое
ускорение – векторная физическая
величина, характеризующая быстроту
изменения угловой скорости твёрдого
тела. Угловое ускорение равно первой
производной от угловой скорости по
времени.
2.
Сила тяжести – сила, с которой тело
притягивается к Земле под действием
поля тяготения Земли.
По
закону всемирного тяготения на тело
массой m действует сила тяжести
Fт=GMm/(R+h)2
– формула силы тяжести в общем виде.
где
М – масса Земли; R – радиус Земли; h – высота
от поверхности Земли;
Если
h=0, то Fт=GMm/R2 *m= mg, где g= GMm/R2 – ускорение
свободного падения.
Вес
– сила, с которой тело действует на
опору или подвес.
Вес
P тела, покоящегося в инерциальной
системе отсчёта P, совпадает с силой
тяжести, действующей на тело, и
пропорционален массе m и ускорению
свободного падения g в данной точке:
P=mg
При
движении системы тело — опора относительно
инерциальной системы отсчёта c ускорением
a вес перестаёт совпадать с силой тяжести:
P=m(g+a)
, где + , если а ↑
–
, если а ↓
Билет
12
1.
Установим связь между векторами угловой
ω и линейной υ скоростей. Учитывая, что
радианной мерой угла является отношение
соответствующей дуги ds к радиусу dϕ=dsr,
а линейная скорость точки при движении
по окружности численно равна υ=dsdt,
получаем связь между величинами линейной
и угловой скоростей: υ=ω*r, то есть модуль
скорости υ
численно
равен площади прямоугольника, сторонами
которого являются векторы ω и r.
Кратчайший
поворот от ω к r будет происходить против
часовой стрелки, если смотреть с вершины
вектора υ. Таким образом, вектор линейной
скорости υ равен векторному произведению
угловой скорости и радиуса-вектора
точки, в которой определяется υ.
υ=[ω*r].
Для
определения направления векторов
угловых величин удобно пользоваться
правилом правого винта (буравчика): если
поворачивать головку винта в направлении
вращательного движения точки, то его
поступательное движение покажет
направление вектора угловой скорости.
В
отличие от свободных векторов, которые
могут иметь произвольные точки приложения
и направления в пространстве (например,
r, υ , a, …), векторы угловых величин dϕ ,
ω, ε , … являются аксиальными, т.е. они
всегда направлены вдоль оси вращения
(перпендикулярно плоскости вращения).
2.
Искусственные Спутники Земли (ИСЗ),
космические летательные аппараты,
выведенные на орбиты вокруг Земли и
предназначенные для решения научных и
прикладных задач. С помощью этого ИСЗ
впервые была измерена плотность верхней
атмосферы (по изменениям его орбиты),
исследованы особенности распространения
радиосигналов в ионосфере, проверены
теоретические расчёты и основные
технические решения, связанные с
выведением ИСЗ на орбиту.
Первая
космическая скорость — это минимальная
скорость, при которой тело, движущееся
горизонтально над поверхностью планеты,
не упадёт на неё, а будет двигаться по
круговой орбите.
![]()
Билет
13
1.Установим
связь между векторами угловой ω и
линейной υ скоростей. Учитывая, что
радианной мерой угла является отношение
соответствующей дуги ds к радиусу dϕ=dsr,
а линейная скорость точки при движении
по окружности численно равна υ=dsdt,
получаем связь между величинами линейной
и угловой скоростей: υ=ω*r, то есть модуль
скорости υ
численно
равен площади прямоугольника, сторонами
которого являются векторы ω и r.
Кратчайший
поворот от ω к r будет происходить против
часовой стрелки, если смотреть с вершины
вектора υ. Таким образом, вектор линейной
скорости υ равен векторному произведению
угловой скорости и радиуса-вектора
точки, в которой определяется υ.
υ=[ω*r].
Для
определения направления векторов
угловых величин удобно пользоваться
правилом правого винта (буравчика): если
поворачивать головку винта в направлении
вращательного движения точки, то его
поступательное движение покажет
направление вектора угловой скорости.
В
отличие от свободных векторов, которые
могут иметь произвольные точки приложения
и направления в пространстве (например,
r, υ , a, …), векторы угловых величин dϕ ,
ω, ε , … являются аксиальными, т.е. они
всегда направлены вдоль оси вращения
(перпендикулярно плоскости вращения).
2.В
динамике решают две задачи. Эти задачи
называются первой или прямой, второй
или обратной. Обратная задача является
основной. Прямой задачей, по заданным
законам
движения,
определяют силы и моменты сил. Во второй
задаче, по приложенным силам и моментам,
вычисляют законы движения
Билет
14
1.Равномерное
движение по окружности. Центростремительное
(нормальное) ускорение. Равномерное
движение тела по окружности. Это самый
простой вид криволинейного движения.
Вместе с тем любое сложное криволинейное
движение тела на достаточно малом
участке его траектории можно приближенно
рассматривать как равномерное движение
по окружности.
Центростремительное
или Нормальное ускорение
![]()
— возникает (не равно нулю) всегда при
движении точки по окружности (конечного
радиуса) . Является составляющей вектора
ускорения a, перпендикулярной вектору
мгновенной скорости. Вектор нормального
ускорения всегда направлен к центру
окружности, а модуль равен: aЦС=v2 / R
2.
Инерциальные
системы отсчета. Первый закон Ньютона
и две его формулировки.
Первый
закон Ньютона постулирует наличие
такого явления, как инерция тел.
Поэтому он также известен как Закон
инерции.
Инерция — это явление сохранения
телом скорости движения (и по величине,
и по направлению), когда на тело не
действуют никакие силы. Чтобы изменить
скорость движения тела, на него необходимо
подействовать с некоторой силой.
Естественно, результат действия
одинаковых по величине сил на различные
тела будет различным. Таким образом,
говорят, что тела обладают инертностью.
Инертность — это свойство тел
сопротивляться изменению их текущего
состояния. Величина инертности
характеризуется массой тела.
В
современной физике первый закон Ньютона
принято формулировать в следующем виде:
Существуют такие системы
отсчёта, называемые инерциальными,
относительно которых материальная
точка при отсутствии внешних воздействий
сохраняет величину и направление своей
скорости неограниченно долго.
Ньютон
в своей книге «Математические начала
натуральной философии» сформулировал
первый закон механики в следующем виде:
Всякое тело продолжает
удерживаться в состоянии покоя или
равномерного и прямолинейного движения,
пока и поскольку оно не понуждается
приложенными силами изменить это
состояние.
Билет
15
1.
Криволинейные движения – движения,
траектории которых представляют собой
не прямые, а кривые линии. Криволинейное
движение – это всегда движение с
ускорением, даже если по модулю скорость
постоянна.
Полное
ускорение, с которым движется материальная
точка, равно:
a=sqrt(a2t+a2n)
Тангенциа́льное
ускоре́ние — компонента ускорения,
направленная по касательной к траектории
движения. Характеризует изменение
модуля скорости. Величину тангенциального
ускорения – в смысле проекции вектора
ускорения на единичный касательный
вектор траектории – можно выразить так:
at=dV/dt
где
V=dL/dt – путевая скорость вдоль траектории,
совпадающая с абсолютной величиной
мгновенной скорости в данный момент.
2.
Второй закон ньютона
Современная
формулировка
В
инерциальной системе отсчёта ускорение,
которое получает материальная точка,
прямо пропорционально равнодействующей
всех приложенных к ней сил и обратно
пропорционально её массе.
a=F/m
Си́ла
— векторная физическая величина,
являющаяся мерой интенсивности
воздействия на данное тело других тел,
а также полей.
Масса
– мера инертности тела, физическая
величина. Она определяет отношение
модуля ускорения талона массы к модулю
ускорения тела при их взаимодействии.
Билет
16
1.Из
известного выражения для силы тяжести
вблизи поверхности планеты и второго
закона Ньютона непосредственно следует,
что вне
зависимости от начальных условий
движение любого тела характеризуется
постоянным ускорением, равным g:
.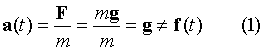
В
общем случае равноускоренного движения
тела его скорость и положение во времени
описываются следующими векторными
равенствами:![]()
,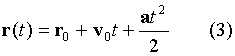
.Приведенные
соотношения (2) и (3), разумеется, справедливы
и для частных случаев падения тела без
начальной скорости и движения тела,
брошенного вертикально вверх, разобранным
в соответствующих разделах.
Применение
формул (2) и (3) для описания движения
тела, брошенного под углом к горизонту
из начала координат с начальной
скоростью v0,
лежащей в плоскости {xOy},
приводит к следующим общеизвестным
соотношениям:
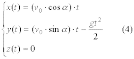
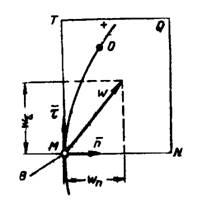
,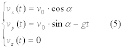
Все
основные соотношения, упоминавшиеся в
разделах, посвященных движению тел
вдоль вертикальной прямой, можно получить
из формул (4) и (5), положив в них угол
равным 900.
В
случае тела, брошенного под произвольным
углом к горизонту, из равенств (4) и (5)
хорошо известные соотношения для времен
полета, подъема и спуска
,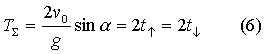
максимальной
высоты подъема:
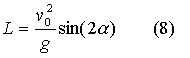
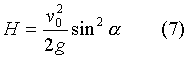
дальности
полета:
Исключая
из двух первых равенств системы (4) время,
легко получить уравнение траектории:
![]()
.
2.
Векторная
форма (2-й закон Ньютона):
![]()
Координатная
форма (2-й закон Ньютона в проекциях на
оси декартовых координат):
![]()
Естественная
(эйлерова) форма (2-й закон Ньютона в
проекциях на оси естественных координат):
![]()
![]()
где
х, у, z – координаты точки массой m; X, Y, Z –
проекции действующей на точку силы (или
равнодействующей действующих на точку
сил) ![]()
на
оси декартовых координат; ![]()
–
проекции силы
на
оси естественных координат: касательную
Т, главную нормаль N и бинормаль В (см.
рис. 1).
Рисунок
1.
Если
точка является несвободной (на движение
точки наложены связи), в число действующих
на точку сил включаются реакции связей.
Силы,
входящие в правую часть дифференциальных
уравнений движения, в общем случае могут
являться функциями от времени t, скорости
v и координат х, у, z точки.
Билет
17


