Кинематика изучает простейшую форму движения – механическое движение. Кинематически определить движение тела – это значит указать его положение относительно выбранной системы отсчета в каждый момент времени.
Движение материальной точки (в дальнейшем будем говорить просто точки) задано, если известен закон движения.
Закон движения. Закон движения – это уравнение, позволяющее определить положение точки относительно выбранной системы отсчета в любой момент времени.
Основная задача кинематики точки. По известному закону движения определить траекторию движения точки, ее положение на траектории, скорость и ускорение точки в ее положении на траектории.
Способы задания движения точки
В зависимости от выбора системы отсчета существуют три способа задания движения точки – векторный, координатный и естественный. Рассмотрим эти способы задания движения в отдельности.
Векторный способ задания движения точки
Пусть точка движется вдоль некоторой линии. В качестве начала отсчета выберем произвольный центр
. Положение точки на линии определяется радиус-вектором
(рис.К.9).

Таким образом, вектор определяет положение движущейся точки в любой момент времени. Следовательно, уравнение
является законом движения при векторном способе задания движения.
Величина называется вектором скорости точки. Вектор скорости точки всегда направлен по касательной к годографу (траектории движения точки) в сторону перемещения точки.
Величина называется вектором ускорения точки.
Определим направление вектора . Направление вектора
определяется направлением вектора
. Пусть точка
движется по некоторой траектории (рис.К.10) от точки
к точке
. Пусть скорость в точке
равна
, а скорость в точке
равна
. Перенесем вектор
параллельно самому себе из точки
в точку
.
Тогда вектор .

Как показано на рис.К.10, вектор направлен в сторону вогнутости траектории движения точки, следовательно и вектор ускорения
всегда направлен в ту же сторону, то есть в сторону вогнутости траектории движения точки.
Координатный способ задания движения точки
Пусть точка движется вдоль некоторой линии. В качестве системы отсчета выберем декартовую систему координат с началом в произвольном центре
. Тогда положение точки
на линии определяются текущими координатами в любой момент времени

Следовательно, система уравнений определяют закон движения точки при координатном способе задания движения. Исключая из закона движения время
, получим уравнение вида
, являющееся уравнением траектории движения точки.
Пример. Закон движения записывается уравнениями . Найти уравнение траектории движения точки.
Решение. Из первого уравнения следует, что или
. Тогда из второго уравнения
. Или
. Таким образом получено, что траекторией движения точки является прямая линия
.
Компоненты скорости и ускорения движущейся точки в любой момент времени определяются по формулам
(К.9)
.
Модули скорости и ускорения
(К.10)
Векторы скорости и ускорения
.
Закон движения — математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют все данные о движении точки.
В классической механике материальной точки закон движения представляет собой три зависимости трёх пространственных координат от времени, либо зависимость одной векторной величины (радиус-вектора) от времени, вида
.
Закон движения может быть найден, в зависимости от задачи, либо из дифференциальных законов механики (см. Законы Ньютона), либо из интегральных (см. Закон сохранения энергии, Закон сохранения импульса), либо из так называемых вариационных принципов.
Частные случаи[править | править код]
Равномерное прямолинейное движение[править | править код]
Простейшим случаем движения материальной точки является равномерное и прямолинейное движение, то есть движение с постоянной по модулю и направлению скоростью. В этом случае её закон движения выглядит следующим образом:
,
где 


Если ось x выбрать направленной вдоль направления вектора скорости, а в качестве нуля выбрать положение материальной точки в момент времени 
,
где 
Равноускоренное прямолинейное движение[править | править код]
Другим важным частным случаем является прямолинейное движение с постоянным ускорением. В этом случае закон движения имеет вид:
,
где 


Если ось x выбрать направленной вдоль направления вектора ускорения, а в качестве нуля выбрать положение материальной точки в момент времени 
,
где 


Равномерное движение по окружности[править | править код]
При движении по окружности с постоянной по модулю скоростью (или, что то же самое с постоянной угловой скоростью) вектор ускорения направлен строго перпендикулярно вектору скорости в сторону центра окружности. В этом случае закон движения может быть записан в следующем виде:
,
где 






Удобнее при рассмотрении движения по окружности перейти к угловым переменным: углу 


Равноускоренное движение по окружности[править | править код]
При равноускоренном движении по окружности вектор ускорения меняет как своё направление, так и величину модуля. Постоянным остаётся только так называемая тангенциальная составляющая ускорения, равная проекции вектора ускорения на прямую, вдоль которой направлен вектор скорости (эта же прямая является касательной к окружности, по которой движется материальная точка). Закон движения может быть при этом записан в следующем виде:
,
где 






В угловых переменных закон равноускоренного движения по окружности имеет более простой вид:
,
где 
Литература[править | править код]
- Сивухин Д. В. Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — 520 с.
В
задачах данного раздела определяются
координаты, скорость, ускорение точки
в любой назначенный момент времени при
различных способах задания движения.
Из всех способов задания движения точки
наибольшее распространение получили
координатный и естественный способы.
Рассмотрим
вначале координатный способ задания
движения точки. Положение в пространстве
движущейся точки определяется тремя
координатами в декартовой системе
координат. Эти координаты задаются как
функции времени:
![]() (1.1)
(1.1)
Зависимости
(1.1) называются уравнениями движения
точки в декартовых координатах.
Если
движение точки происходит в плоскости
ху, то задаются только два уравнения
движения:
x
= x(t);
y = y (t).
При
прямолинейном движении точки достаточно
задать одно уравнение движения:
x
= x(t),
если
принять, что ось х совпадает с прямой,
по которой движется точка.
Скорость
точки представляет собой вектор,
характеризующий быстроту и направление
движения точки в данный момент времени.
При
задании движения точки уравнениями
(1.1) проекции скорости на оси декартовых
координат равны:
![]()
Модуль
скорости
![]() .
.
(1.2)
Направление
скорости определяется направляющими
косинусами:
 .
.
Если
движение точки задается в плоскости
ху, то
![]()
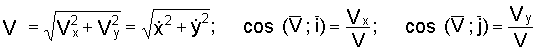 .
.
При
прямолинейном движении по оси х:
![]() .
.
Характеристикой
быстроты изменения скорости является
ускорение
а.
Ускорение точки равно производной от
вектора скорости по времени:
 .
.
При
задании движения точки уравнениями
(1.1) проекции ускорения на координатные
оси равны:

Модуль
ускорения:
![]() .
.
(1.3)
Направление
ускорения определяется направляющими
косинусами
 ;
;
 ;
; .
.
Если
движение точки задается в плоскости
ху, то
![]() ;
;
![]() ;
;
 ;
; .
.
При
прямолинейном движении по оси х
![]() ;
;
![]() .
.
Далее
рассмотрим естественный способ задания
движения точки.
Считается,
что движение точки задано естественным
способом, если указаны ее траектория и
закон изменения криволинейной координаты
s = s(t). Уравнение s = s(t) называется
законом движения точки по траектории.
При этом на траектории указывается
начало отсчета, а также положительное
направление отсчета координаты s в виде
стрелки
![]() .
.
Модуль
скорости точки определяется по формуле
 .
.
(1.4)
Вектор
скорости
V направлен по касательной к траектории
в сторону стрелки
![]() ,
,
если![]() ,
,
и в противоположную сторону, если![]() .
.
Ускорение
точки определяется как векторная сумма
касательного и нормального ускорений
точки:
а
=
а
+
аn
.
Модуль
касательного ускорения определяется
по формуле
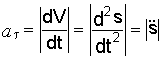 .
.
(1.5)
Вектор
касательного ускорения
а
направлен
по касательной к траектории в сторону
стрелки
![]() ,
,
если![]() ,
,
и в противоположную, если![]() .
.
Модуль
нормального ускорения определяется по
формуле
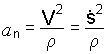 ,
,
(1.6)
где
– радиус кривизны траектории в данной
точке.
Вектор
нормального ускорения
аn
всегда направлен по главной нормали в
сторону центра кривизны траектории.
Модуль
полного ускорения
![]() .
.
(1.7)
Если
движение точки задано координатным
способом, то можно определить параметры
движения, характерные для естественного
способа задания движения.
Так
можно, например, по уравнениям движения
точки (1.1) найти уравнение ее траектории
в форме зависимости между координатами.
Для этого надо из уравнений движения
исключить время t. Затем можно найти
закон движения точки по траектории s =
s(t), используя формулу (1.4). Из этой формулы
следует, что ds = V dt; с учетом формулы
(1.2) имеем
![]() и
и
 .
.
(1.8)
В
законе движения (1.8) за начало отсчета
координаты s принимается начальное
положение точки, когда t = 0. Знак “плюс”
или “минус” перед интегралом ставится
в зависимости от выбора положительного
направления отсчета координаты s: если
движение точки начинается в сторону
стрелки
![]() ,
,
то следует брать знак “плюс”, в противном
случае – знак “минус”.
Рассмотрим
вначале методику решения задач, в которых
движение точки задано координатным
способом. Уравнения (1.1) определяются
либо из геометрических условий, либо в
результате интегрирования дифференциальных
уравнений движения точки. Интегрирование
дифференциальных уравнений движения
точки рассматривается в разделе “Динамика
точки”, который не входит в данное
пособие. Получение уравнений (1.1) с
использованием геометрии движения
рассмотрим на примере исследования
движения точки обода колеса.
Задача
1.1 (3)
Задача
1.2 (1)
Задача
1.3 (2)
Задача
1.4 (4)
Задача
1.5 (4)
Задача
1.6 (5)
Задача
1.7 (6)
Задача
1.8 (7)
Задача
1.1 (3)
Найти
уравнения движения точки М обода колеса
радиуса R вагона, который движется по
прямолинейному участку пути со скоростью
V. Колесо катится без скольжения. Точка
М в начальный момент движения соприкасалась
с рельсом, т.е. занимала положение М0
(рис. 1.1).

Рис.
1.1
Решение
Изобразим
на расчетной схеме (рис. 1.1) оси координат
х и у, начало координат поместим в
начальное положение точки М0.
Рассмотрим
два положения колеса: в начальный момент
t = 0 и в текущий момент времени t.
Отметим
положение точки М на ободе колеса и
положение центра С колеса в момент t,
координаты точки: xм
= М0В,
ум
= МВ.
Расстояние
от центра колеса до рельса остается
постоянным и равным R; это значит, что
центр C колеса движется по прямой,
параллельной оси х. За время t центр
колеса переместится на расстояние C0C
= Vt (закон равномерного движения точки
C), одновременно колесо повернется на
угол
.
Чтобы
получить уравнения движения точки М,
надо координаты этой точки представить
как функции времени.
Из
расчетной схемы (рис. 1.1) видно, что
хм
= C0C
– ЕС, ум
= ВЕ – МЕ;
или
хм
= Vt – ЕС, ум
= R – МЕ.
Из
треугольника МЕС имеем;
МЕ
= Rsin (90
–
) = Rcos
,
ЕC
= Rcos (90
–
) = Rsin
,
Тогда
хм
= Vt – Rsin
, (a)
ум
= R – Rcos
.
Найдем
зависимость угла
от времени t: так как колесо катится без
скольжения, то длина дуги АМ окружности
обода колеса (рис.1.1) равна длине отрезка
М0А.
При
этом
М0А
= С0С
= Vt ,
но
длина дуги АМ равна также произведению
радиуса R на центральный угол
; поэтому Vt = R
, отсюда
![]() .
.
Теперь
уравнения (а) будут иметь вид
 ;
;
 .
.
Полученные
уравнения представляют собой уравнения
движения точки М. В аналитической
геометрии показано, что это параметрические
уравнения циклоиды (параметром в данном
случае является время t). Таким образом,
траектория точки обода колеса, движущегося
по прямолинейному участку пути без
проскальзывания, является циклоидой.
Длина одной ветви циклоиды L (рис. 1.1)
равна 2
R, высота – H = 2R.
Задача
1.2 (1)
Даны
уравнения движения точки:
 ;
;
 (х,
(х,
у – м; t – с).
(б)
-
Определить
уравнение траектории и построить ее. -
Определить
начальное положение точки на траектории. -
Указать
моменты времени, когда точка пересекает
оси координат. -
Найти
закон движения точки по траектории s =
s(t), принимая за начало отсчета расстояний
начальное положение точки. -
Построить
график движения точки.
Решение
1.
Для получения уравнения траектории
вида F(x, y) = 0 исключим из уравнений
движения (б) время t: из первого уравнения
системы (б) найдем
![]() ,
,
подставляя
это выражение во второе уравнение той
же системы, получим уравнение траектории
y
= x + 5.
|
Рис. |
Это
где а– отрезок, отсекаемый прямой на оси |
2.
Для определения положения точки в
начальный момент времени необходимо
подставить значение t = 0 в уравнения
движения (б)
![]() м;
м;
![]() м.
м.
Точка
при t = 0 занимает положение М0
(-1;4).
3.
В момент пересечения точкой оси у
координата х равна нулю, а первое
уравнение системы (б) примет вид:
 .
.
Отсюда

где
n = 0, 1, 2 …
В
момент пересечения точкой оси х координата
у равна нулю, а второе уравнение системы
(б) примет вид:
![]() или
или
![]() .
.
Но
косинус не может быть больше 1.
Следовательно, точка не пересекает ось
х (см. об этом также п. 4 решения задачи).
4.
Для определения закона движения точки
по траектории воспользуемся формулой
(1.8). За начало отсчета координаты s примем
начальное положение точки М0.
Подставляя в уравнения (б) значения t >
0, видим, что с выходом из начального
положения М0
координаты точки х и у увеличиваются.
Это направление движения точки примем
за положительное направление отсчета
координаты s (см. стрелку
![]() на
на
рис. 1.2), а в формуле (1.8) оставим знак
“плюс”:
 .
.
Учитывая,
что


получим

или
 .
.
(в)
Из
закона (в) следует, что координата s не
может быть отрицательной, т.е. точка
движется по полупрямой М0М
(рис.1.2) и ось х не пересекает (см. по этому
поводу п. 3 решения задачи).
5.
График движения точки – это графическое
представление зависимости расстояния
s от времени t. Для построения такого
графика по оси абсцисс откладывают
последовательные значения времени t, а
по оси ординат – соответствующие им
значения расстояния s. Построенные точки
соединяют плавной линией. График
зависимости (в) можно построить быстрее,
если воспользоваться известным графиком
косинуса. Для этого вначале построим
график функции
 (штриховая
(штриховая
линия на рис. 1.3), затем этот график
сместим вдоль оси s на величину![]() м.
м.

Рис.
1.3.
Задача
1.3 (2)
Даны
уравнения движения точки:
![]() ;
;
 (х,
(х,
у – см; t – с ).
(г)
-
Определить
уравнение траектории и построить ее. -
Определить
начальное положение точки на ее
траектории. -
Найти
закон движения точки по траектории s =
s(t), принимая за начало отсчета расстояний
начальное положение точки. -
Определить
время T прохождения точкой полной
окружности.
Решение
|
Рис. |
1. Чтобы найти уравнение траектории
|
сложим
эти уравнения и после преобразования
получим
![]() .
.
Это
уравнение окружности радиуса R = 5 см,
центр окружности расположен в точке
С (-2,5; 5) (рис. 1.4).
2.
Для определения начального положения
точки подставим значение времени t = 0 в
уравнения (г)
х0
= 5 соs0 – 2,5 = 2,5 см; у0
= 5 sin0 – 5 = 5 см;
Точка
при t = 0 занимает положение М0
(2,5; 5).
3.
Для определения закона движения точки
по траектории воспользуемся формулой
(1.8). За начало отсчета координаты s примем
точку M0.
Из системы уравнений (г) видно, что с
увеличением времени t от нуля x уменьшается,
а y увеличивается.
Такое
возможно, если после выхода из начального
положения точка будет двигаться по
окружности против часовой стрелки. Это
направление движения точки примем за
положительное направление отсчета
координаты s (см. стрелку
![]() на
на
рис. 1.4), а в формуле (1.8) перед интегралом
оставим знак “плюс”:
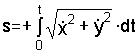 ,
,
где
 ;
; .
.
Отсюда
 ;
;
![]() .
.
(д)
4.
Определим время Т прохождения точкой
полной окружности.
Т – время, по
истечении которого s в формуле (д) станет
равным длине окружности 2
R:
 .
.
Отсюда
![]() с.
с.
Задача
1.4 (4)
Даны
уравнения движения точки:
 ;
;
y = t (x, y – м; t – с ).
(е)
-
Определить
уравнение траектории точки. -
Определить
скорость и ускорение точки при t = 0 и t
= 1 с. -
Построить
траекторию и указать полученные векторы
скорости и ускорения на чертеже.
Решение
1.
Уравнение траектории получается
подстановкой в первое уравнение системы
(е) величины t = y, полученной из второго
уравнения этой системы:
![]() .
.
(ж)
2.
Модуль скорости точки определяется по
формуле
![]() ,
,
где![]()
![]() –
–
проекции вектора скорости на координатные
оси. Для заданного движения (е) имеем
![]() ,
,
![]() м/c.
м/c.
При
t = 0
 ,
,![]() м/c.
м/c.
Модуль
скорости V0
= 1 м/c.
При
t = 1 с,
 м/c,
м/c,![]() м/c.
м/c.
Модуль
скорости V1
= 4,82 м/с.
Модуль
ускорения точки определяется по формуле
![]() ,
,
где![]() ,
,![]() –
–
проекции вектора ускорения на координатные
оси. Для заданного движения (е) имеем
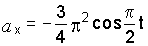 ,
,
![]() .
.
При
t = 0
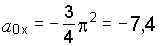 м/с2
м/с2
,
![]() .
.
Модуль
ускорения a0
= 7,4 м/с2.
При
t = 1 с
 ,
,![]() .
.
Модуль
ускорения a1
= 0.
3.
Траектория точки (ж) представляет собой
косинусоиду.
|
Рис.1.5 |
Для |
При
t = 1 с x1
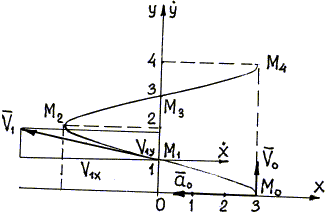
= 0, y1 =
1 м, точка занимает положение М1(0;
1). Для этих положений точки построим
векторы скорости и ускорения. От точки
M0
отложим проекции скорости V0x = 0
и V0y = 1
м/с (см. п.2); направление вектора
V0
показано на рис. 1.5. Вектор скорости
V1
построим следующим образом: через точку
M1
проведем оси
![]() и
и![]() ,
,
ось![]() параллельна
параллельна
оси x, а ось![]() совпадает
совпадает
с осью y. Вдоль этих осей от точки M1
отложим отрезки, равные проекциям V1x
и V1y
(с
учетом их знаков); затем построим
прямоугольник, диагональ которого есть
вектор
V1.
Модуль вектора ускорения
a0
равен модулю проекции a0x
(см. п. 2),
a0
направлен от точки M0
в сторону, противоположную положительному
направлению оси x (cкорости
V0,
V1
должны совпадать с касательными к
траектории соответственно в точках M0
и M1.
Вектор
a0
должен быть направлен от точки M0
внутрь кривой).
Задача
1.5 (4)
Даны
уравнения движения точки:
![]() ;
;
![]() (х,
(х,
у – м; t – с ).
(з)
-
Определить
уравнение траектории точки. -
Определить
скорость и ускорение точки при t = 1 с. -
Построить
траекторию и указать полученные векторы
скорости и ускорения на чертеже.
Решение
1.
Для того чтобы получить уравнение
траектории, необходимо из уравнений
движения (з) исключить время. Запишем
эти уравнения в виде
 ,
,
 .
.
Возведем
оба уравнения в квадрат, вычтем второе
из первого и получим уравнение траектории:
x2
– y2
= 42.
(и)
Это
уравнение равнобочной гиперболы, полуось
которой b = 4 м.
2.
Определим проекции скорости
![]()
![]()
В
заданный момент времени t = 1с, V1x
= 4,68 м/с, V1у
=
6,16 м/с
модуль скорости
![]() м/с.
м/с.
Определим
проекции ускорения
![]() м/с2,
м/с2,
![]() м/с2
м/с2
.
В
момент времени t = 1с, а1x
= 6,16 м/с2,
а1у
=
4,68 м/с2
модуль
ускорения
![]() м/с2.
м/с2.
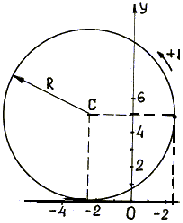
3.
Построим траекторию точки по уравнению
(и). Действительной осью гиперболы
является ось х (рис. 1.6). На траектории
найдем точку М1,
соответствующую моменту времени t = 1 с.
Координаты этой точки: x1 = 2(e +
e-1)
= 6,16 м; y1 = 2(e –
e-1)
= 4,68 м; M1
(6,16; 4,68).

Рис.
1.6
Вектор
скорости построим следующим образом:
через точку М1
проведем оси
![]() и
и![]() ,
,
параллельные соответствующим осям x и
y; вдоль этих осей от точки М1
отложим отрезки, равные проекциям V1x
и V1y
(с учетом их знаков). Диагональ
прямоугольника, построенного на этих
отрезках, есть вектор
V1.
Вектор ускорения
a1
строим подобным образом: от точки М1
вдоль оси
![]() отложим
отложим
отрезок, равный проекцииa1x,
а вдоль оси
![]() отложим
отложим
отрезокa1y.
Затем на этих отрезках строим прямоугольник,
диагональ которого есть вектор
a1.
Вектор скорости
V1
должен быть направлен по касательной
к траектории в точке M1,
а вектор ускорения
a1
должен быть направлен от точки M1
внутрь кривой.
Задача 1.6 (5)
|
Рис. |
Даны уравнения
|
Решение
1.
Чтобы определить уравнение траектории,
следует исключить время из уравнений
движения (к). Учитывая, что
![]() ,
,
получим
 .
.
Траектория
представляет собой эллипс с полуосями
20 см и 40 см.
2.
Определим время Т, когда точка пересечет
прямую у = 20 см, первое уравнение системы
(к) в этот момент примет вид:
20 = 40 sin2
t, отсюда следует
![]() с.
с.
Найдем
величины скорости и ускорения по
значениям их проекций в момент времени
 с:
с:
![]() см/с;
см/с;
![]() см/с.
см/с.
Модуль
скорости
![]() см/с.
см/с.
Проекции
ускорения
 см/с2;
см/с2;
 см/с2.
см/с2.
Модуль
ускорения
![]() см/с2.
см/с2.
Задача
1.7 (6)
Дан
закон движения точки по окружности
радиуса R = 5 м:
![]() (s
(s
– см; t –с ).
(л)
-
Определить
скорость и ускорение точки при t = 0 и t1
= 10 с. -
Определить
моменты остановки точки. -
Определить
путь, пройденный точкой за 10 с.
Решение
|
Рис. 1.8 |
1. На траектории |
Определим
проекцию скорости на касательную
![]() ,
,
учитывая (л),
![]() .
.
(м)
При
t = 0,
V
o
= 162 см/с
и t1
= 10 c
V
1
= 12 см/с.
Теперь
отложим найденные проекции скорости
из точек M0
и M1
по соответствующим касательным: V
o
– по касательной
o,
V
1
– по касательной
1.
Векторы
Vo
и
V1
совпадают со своими проекциями V
o
и V1.
Определим
проекции ускорения на естественные оси
координат, учитывая (л),
![]() см/с2;
см/с2;
 см/с2.
см/с2.
Ускорение
точки
![]() .
.
При
t = 0
![]() см/с2;
см/с2;
 см/с2;
см/с2;
![]() см/с2.
см/с2.
При
t1
= 10 с
![]() см/с2;
см/с2;
![]() см/с2;
см/с2;
![]() см/с2.
см/с2.
Отложим
из точек M0
и M1
по естественным осям проекции аo,
аno,
а
1,
аn1.
Векторы
a0,
a1
изображаются диагоналями прямоугольников,
построенных на проекциях ускорений.
2.
Чтобы найти моменты остановки, необходимо
найти время t*, когда скорость точки
равна нулю. Из уравнения (м) получим
3(t*)2
– 45t* + 162 = 0.
Решив
это уравнение, будем иметь t1*
= 6 с, t2*
= 9 с.
3.
Поскольку за 10 с точка сделала две
остановки (см. п. 2), пройденный ею путь
за 10 с можно найти как сумму пути,
пройденного точкой от начального
положения до первой остановки, пути,
пройденного точкой от первой до второй
остановки, и пути, пройденного точкой
от второй остановки до момента времени
t1
= 10 с, т.е.
![]() ,
,
где
s0
= -15 см;
![]() см;
см;
![]() см;
см;
![]() см.
см.
Путь,
пройденный точкой за 10 с, равен
![]() см.
см.
Задача
1.8 (7)
По
заданным уравнениям движения точки:
![]() ;
;
![]() (х,
(х,
у – м; t – с)
(н)
найти
ее касательное и нормальное ускорение,
а также радиус кривизны траектории для
заданного момента времени t1
= 0,5
с.
Решение
Заданные
уравнения движения точки (н) позволяют
найти проекции скорости точки, м/с,
![]() ;
;
![]() .
.
Модуль
скорости, м/с,
![]() .
.
(о)
В
момент времени t1
= 0,5
с V1
= 2 м/с.
Проекции
ускорения точки, м/с2:
![]()
![]() .
.
Модуль
полного ускорения, м/с2
![]() .
.
(п)
В
момент времени t1
= 0,5
са
= 2 м/с2.
Зная
выражение скорости, как функции времени
t (о), определим модуль касательного
ускорения точки, м/с2,
по формуле (1.5)
 .
.
(р)
В
момент
![]() с
с![]() м/с2.
м/с2.
По
полному ускорению (п) и касательному
ускорению (р) найдем модуль нормального
ускорения точки для
![]() с,
с,
учитывая формулу (1.7)
![]() м/с2.
м/с2.
Нормальное
ускорение аn1
и радиус кривизны траектории
1
связаны зависимостью (1.6), из которой
следует, что при
![]() с
с
 м.
м.


 ,
,
 и
и ;
; ,
,