Монету подбрасывают три раза. Составить закон распределения случайной величины X — числа появлений герба. Найти его математическое ожидание, дисперсию, среднее квадратическое отклонение.
здесь по формуле бернулли с начало теорема Если вероятность p наступления события Α в каждом испытании постоянна, то вероятность того, что событие A наступит k раз в n независимых испытаниях, равна
P(k.n)=Cn k *p^k*q^(n-k) то есть понятно что веротяность выпадение герба такое же что и выпадение другого , то есть аверс и реверс равны 1/2 или 50 на 50!
всего как с уловия 5 раз и нам нужно их распределить ! по формуле бернулли получаем
С 5 0 = 5!/0!(5-0)!= 1*2*3*4*5/1*1*2*3*4*5=1 то ест 1!
С 5 1 =5!/1!(5-1)!=1*2*3*4*5/1*1*2*3*4=5 то есть 5 !
P( 5 и 0)=1*1/2^0*1/2^5=1*1/32=1/32
P( 5 и 1)=5*1/2*1/2^4=5/2*1/16=5/32
P(5 и 6)=10*1/2^2*1/2^3=10/4*1/8=10/32
P(5 и 4)=10*1/2^3*1/2^2=10/8*1/4=10/32
P(5 и 5) =5*1/2^4*1/2=5/32
P( 5 и 5)=1*1/2^5*1/2^0=1/32
то есть вот и будет распрделение обычно ее в таблицу но можно и так
здесь C n k число сочетаний
число сочетаний по формуле чтобы понятней было
Cлучайная величина Х принимает значения:
0; 1; 2; 3
Вероятность появления герба в одном испытании:
p=1/2
Вероятность противоположного события · непоявление герба»
q=1–(1/2)=1/2
Вероятность того, что при трех бросаниях монеты герб не появится ни разу
po=C 0 3·p 0 ·q 3 =1·(1/2) 3 =1/8
p1=C 1 3·p 1 ·q 2 =3·(1/2) 3 =3/8
p2=C 2 3·p 2 ·q 3 =3·(1/2) 3 =3/8
p3=C 3 3·p 0 ·q 3 =1·(1/2) 3 =1/8
Закон распределения ( см. таблицу в приложении)
И по формуле
M(X)=np = 3·(1/2)=3/2
M(X 2 )=0 2 ·(1/8)+1 2 ·(3/8)+2 2 ·(3/8) + 3 2 ·(1/8)=24/8=3
D(X)=M(X 2 )–(M(X)) 2 =3–(3/2) 2 =3–(9/4)=3/4
по формуле
D(X)=npq=3·(1/2)·(1/2)=3/4
Источник
Закон распределения дискретной случайной величины
Дискретная случайная величина
Рассмотрим дискретную случайную величину на примере.
Число появлений герба при трех бросаниях монеты является дискретной случайной величиной Х. Возможные значения числа появлений герба: 0, 1, 2, 3. Следует найти вероятность появления герба в одном испытании.
Вероятность появления герба в одном испытании равна p=1/2. Противоположное ему событие: герб не выпал, вероятность этого события по формуле (4.5) равна q=1-p=1/2.
1) Событие 1. «Три раза бросили монету и ни разу герб не выпал». Это сложное событие состоит из появления трёх совместных и независимых элементарных событий: «герб не выпал в одном испытании». Для события «три раза бросили и ни разу герб не выпал», которое обозначим Р(0), вероятность вычисляется по формуле умножения (4.6а) для независимых событий:
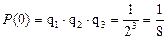 .
.
2) Событие 2. «Три раза бросили монету и один раз герб выпал». Это сложное событие состоит из появления одного из трёх несовместных и независимых событий: «герб выпал в одном из трёх совместных испытаний». Для события «три раза бросили монету и один раз герб выпал» вероятность будет состоять из суммы несовместных событий по формуле (4.2а), где каждое слагаемое вычисляется по формуле умножения (4.6а) для независимых событий:
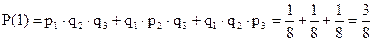 .
.
3) Событие 3. «Три раза бросили и два раза выпал герб». Для этого события вероятность события будет состоять из суммы событий:
 .
.
4) Событие 4. «Три раза бросили и все три раза выпал герб». Вероятность этого события совпадает с первым и вычисляется по формуле умножения (4.6а).
 .
.
Здесь: p1, p2, p3 – вероятность выпадения герба в 1, 2, 3 испытаниях.
q1, q2, q3 – вероятность не выпадения герба в 1, 2, 3 испытаниях.
Результаты вычислений вынесены в таблицу 5.1.
Законом распределениядискретной случайной величины называют соответствие между полученными значениями дискретной случайной величины и их вероятностями. Его можно задать:
1) таблично (рядом распределения);
3) аналитически (в виде формулы).
В примере 1 закон распределения задан в виде ряда распределения (таблицей 5.1), где представлены все возможные значения хi и соответствующие им вероятности рi = Р (Х = хi). При этом вероятности рi удовлетворяют условию:
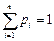 ,
,
 ,
,
где число возможных значений n может быть конечным или бесконечным.
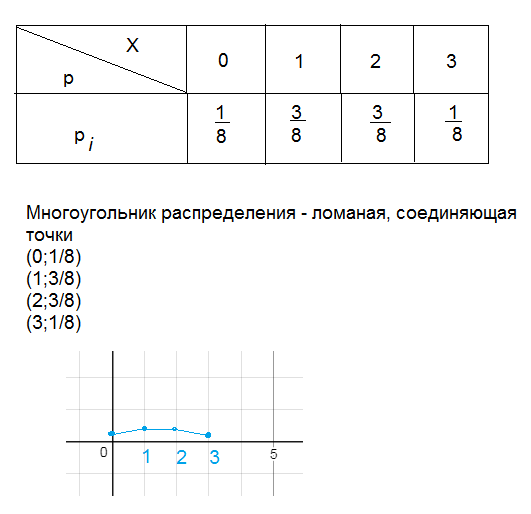
Графическое изображение ряда распределения называется многоугольником распределения. Для его построения возможные значения случайной величины (хi) откладываются по оси абсцисс, а вероятности (рi) – по оси ординат. Точки c координатами (хi, рi) соединяются ломаными линиями.
Функция F(х) для дискретной случайной величины вычисляется по формуле:
 , , |
(5.3) |
где суммирование ведется по всем значениям i, для которых хi 3, то F(х) = Р (Х 3
Условие
![]()
Найти закон распределения дискретной случайной величины Х -числа появлений «герба» при трех бросаниях монеты. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение ДСВ Х, построить многоугольник распределения
предмет не задан
20844
Решение
![]()
★
Cлучайная величина Х принимает значения:
0; 1; 2; 3
Вероятность появления герба в одном испытании:
p=1/2
Вероятность противоположного события * непоявление герба”
q=1-(1/2)=1/2
Вероятность того, что при трех бросаниях монеты герб не появится ни разу
p_(o)=C^(0)_(3)*p^(0)*q^(3)=1*(1/2)^3=1/8
p_(1)=C^(1)_(3)*p^(1)*q^(2)=3*(1/2)^3=3/8
p_(2)=C^(2)_(3)*p^(2)*q^(3)=3*(1/2)^3=3/8
p_(3)=C^(3)_(3)*p^(0)*q^(3)=1*(1/2)^3=1/8
Закон распределения ( см. таблицу в приложении)
M(X)=0*(1/8)+1*(3/8)+2*(3/8) + 3*(1/8)=12/8=3/2
И по формуле
M(X)=np = 3*(1/2)=3/2
M(X^2)=0^2*(1/8)+1^2*(3/8)+2^2*(3/8) + 3^2*(1/8)=24/8=3
D(X)=M(X^2)-(M(X))^2=3-(3/2)^2=3-(9/4)=3/4
по формуле
D(X)=npq=3*(1/2)*(1/2)=3/4
Написать комментарий
kisaiticr13
здесь по формуле бернулли с начало теорема Если вероятность p наступления события Α в каждом испытании постоянна, то вероятность того, что событие A наступит k раз в n независимых испытаниях, равна
P(k.n)=Cn k *p^k*q^(n-k) то есть понятно что веротяность выпадение герба такое же что и выпадение другого , то есть аверс и реверс равны 1/2 или 50 на 50!
всего как с уловия 5 раз и нам нужно их распределить ! по формуле бернулли получаем
С 5 0 = 5!/0!(5-0)!= 1*2*3*4*5/1*1*2*3*4*5=1 то ест 1!
С 5 1 =5!/1!(5-1)!=1*2*3*4*5/1*1*2*3*4=5 то есть 5 !
и так далее!
P( 5 и 0)=1*1/2^0*1/2^5=1*1/32=1/32
P( 5 и 1)=5*1/2*1/2^4=5/2*1/16=5/32
P(5 и 6)=10*1/2^2*1/2^3=10/4*1/8=10/32
P(5 и 4)=10*1/2^3*1/2^2=10/8*1/4=10/32
P(5 и 5) =5*1/2^4*1/2=5/32
P( 5 и 5)=1*1/2^5*1/2^0=1/32
то есть вот и будет распрделение обычно ее в таблицу но можно и так
здесь C n k число сочетаний
число сочетаний по формуле чтобы понятней было
Составить
закон распределения для случайной
величины
X
– числа
гербов, выпавших при бросании трех
монет.
Случайная
величина X
– дискретная. Ее возможные значения
:
{ 0, 1, 2, 3 }.
Запишем
ряд
распределения
для этой случайной величины, т.е. ,
каждому из возможных значений
сопоставим вероятность того, что
случайная величина примет это значение:
p
i
= P( X=x i).
Вероятности
будем подсчитывать по классическому
определению. Для этого запишем все
возможные исходы опыта, заключающего
в бросании трех монет.
(
герб;
герб;
герб
)
; (
цифра ;
герб;
герб
)
;
(
герб;
герб;
цифра )
; (
цифра ;
герб;
цифра )
;
(
герб;
цифра;
герб )
; (
цифра ;
цифра;
герб )
;
(
герб;
цифра;
цифра )
;(
цифра ;
цифра;
цифра )
.
Общее число
исходов опыта равно 8 . Число
благоприятствующих исходов для каждого
из возможных значений подсчитываем
по приведенному списку.
Ряд распределения
оформляем виде таблицы :
|
x |
0 |
1 |
2 |
3 |
||
|
p |
1 |
3 |
3 |
1 |
Должно
выполняться основное свойство ряда
: сумма всех вероятностей действительно
равна 1 .
Ряд
распределения.
(для дискретных с.в.)
Ряд
распределения
– это перечень возможных значений с.в.
и вероятностей этих значений.
Форма
представления ряда:
А) таблица
|
ХI |
Х1 |
Х2 |
ХN |
|
|
PI |
P1 |
P2 |
PN |
 Р2=Р(х=х2)
Р2=Р(х=х2)
Б)
граик
PI
P1
X1
XI
В)
аналитическая функция: Х: Х1
Х2
Х n
pi=f(i)
Вероятность
каждых из этих значений задается одной
общей формулой.
Например: с.В. Х – число
|
ХI |
1 |
2 |
3 |
4 |
5 |
6 |
|
PI |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
Х:
1, 2, 3, 4, 5, 6
Pi
= 1/6
PI

1/6





1
2 3 4 5 6
Основное
свойство ряда распределения.
С обытия
обытия
Х=Х1
Образуют полную группу попарно
несовместных
Х=Х2
событий.
…….
Следовательно:
Х=ХN
Р1
+ Р2
+ … + РN
= 1 (1)
∑РI=1
Например
составить закон распределения для суммы
очков на двух кубиках:
С.в.
Х – сумма очков на двух кубиках (дискретная
с.в.)
|
ХI |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
PI |
1/36 |
2/36 |
3/36 |
4/36 |
5/36 |
6/36 |
5/36 |
4/36 |
3/36 |
2/36 |
1/36 |
∑РI=1
п=36
1
1
2
2
3
3
4
4
5
5
6
6
Если закон распределения
задан – можно прогнозировать поведение
с.в., предсказывать вероятность того,
что она попадет в тот или иной интервал.
Например:
|
ХI |
2 |
5 |
7 |
9 |
11 |
|
|
PI |
0,1 |
0,3 |
0,3 |
0,2 |
0,1 |

-
Р3
– ? Р(х=7) = 1-(0,1+0,3+0,2+0,1)=0,3 -
Р(х=3)
= 0 = Р(V) -
Р(х=11)=0,1
-
Р(х<6)
= Р((х=2)+(х=5))=Р(х=2)+Р(х=5)=0,4

0
2 5 6 7 8 9 11
х
-
Р(х>8)=Р((х=9)+(х=11))=Р(х=9)+Р(х=11)=0,3
-
Р(П<х<3П)=Р(х=5)+Р(х=7)+Р(х=9)=0,8
Случайная величина Х – число появлений герба,
может принимать значения 0,1,2,3,4
Закон распределения биномиальный, т. к. испытания удовлетворяют
схеме Бернулли, m=0,1,2,3,4
Считаешь вероятности по формуле:
Р (Х=m)=C(n,m)*p^m*(q)^(n-m), где
p=0.5,q=1-0.5=0.5,n=4, m=0, 1, 2, 3, 4
C(n,m)=n!/(m!*(n-m)!) – сочетания
Р (4,0)=Р (Х=0)=(q^4)
Р (4,1)=Р (Х=1)=4*p*(q^3)
Р (4,2)=Р (Х=2)=….
Р (4,3)=Р (Х=3)=…
Р (4,4)=Р (Х=0)=(p^4)=…
Дальше проверяешь, суммируешь, дожна получиться 1
нарисуешь таблицу распределения,
где первая строка — Xi = 0, 1, 2, 3, 4
вторая — соответствующие значения вероятности Pi
Матожидание при биномиальном распределении
МО= nр =
Дисперсия при биномиальном распределении
D(X)=npq=
Отсюда среднеквадратическое отклонение находишь.
σ=√D=
График распределения строй сама и функцию распределения
ищи сама. Как строятся, можешь в любом учебнике
по ТВ посмотреть, например у Гмурмана
