Функция распределения дискретной случайной величины
Этот онлайн калькулятор строит график функции распределения по набору значений дискретной случайной величины либо по таблице распределения.
Статьи, описывающие этот калькулятор
- Функция распределения дискретной случайной величины
![]()
Функция распределения дискретной случайной величины
Дискретная случайная величина задана
Таблица распределения
| Значение | Вероятность | ||
|---|---|---|---|
Точность вычисления
Знаков после запятой: 4
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
График распределения
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Функция распределения
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Вероятность возникновения некоторого числа событий при проведении нескольких испытаний. Испытания Бернулли.
- • Таблица независимых испытаний по формуле Бернулли
- • Биномиальное распределение. Функция плотности вероятности, кумулятивная функция распределения, математическое ожидание и дисперсия
- • Наивероятнейшее число появления события в независимых испытаниях
- • Логнормальное распределение
- • Раздел: Математика ( 269 калькуляторов )
PLANETCALC, Функция распределения дискретной случайной величины
Закон распределения дискретной случайной величины (ДСВ) представляет собой соответствие между значениями х1, х2,…,хn этой величины и их вероятностями p1, p2,…,pn
Может быть задан аналитически, графически или таблично.
Самый простой способ представления закона распределения дискретной случайной величины — в виде таблицы ряда распределения, то есть
| X | x1 | x2 | …… | xn |
| P | p1 | p2 | …… | pn |
х1, х2,…,хn — значения дискретной случайной величины;
p1, p2,…,pn — вероятности значений X дискретной случайной величина.
Также должно выполняться условия, что сумма вероятностей равна 1, то есть
∑p=p1+p2+ … +pn=1
Графически закон распределения ДСВ задается в виде многоугольника распределения см. здесь., а аналитически, например, с применением формулы Бернулли.Рассмотрим примеры
Пример 1
Монета подбрасывается 10 раз, герб выпал 6 раз, а орел — 4 раза. Составить закон распределения дискретной случайной величины.
Решение
Вероятности равны:
p1(6)=6/10=0,6;
p2(4)=4/10=0,4
Пример 2
Из корзины извлечено 4 белых шара, 6 черных, 8 синих и 2 красных шара. Найти закон распределения случайной величины X возможного выигрыша на один билет.
Решение
Объем выборки равен
n=4+6+8+2=20
X принимает следующие значения:
x1=4; x2=6; x3=8; x1=2
Найдем их вероятности:
p1(4)=4/20=0,2;
p2(6)=6/20=0,3;
p3(8)=8/20=0,4;
p4(2)=2/20=0,1
Получаем таблицу закона распределения дискретной случайной величины
| X | 4 | 6 | 8 | 2 |
| P | 0.2 | 0.3 | 0.4 | 0.1 |
Пример 3
По контрольной работе по математике школьники получили оценки:
удовлетворительно — 5 человек;
хорошо — 13 человек;
отлично — 7 человек.
Составьте таблицу закона распределения ДСВ
Решение
n=5+13+7=26
Вычислим вероятности:
p1(5)=5/25=0,2;
p2(13)=13/25=0,52;
p3(7)=7/25=0,28
Таблица имеет вид:
| X | 5 | 13 | 8 | 2 |
| P | 0.2 | 0.52 | 0.28 | 0.1 |
Пример 4
Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных.
Решение
Для составления закона распределения воспользуемся формулой комбинаторики сочетание без повторений, то есть всего 8 изделия, а отобрать необходимо 3 изделия получаем:
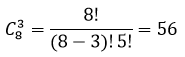
при P(X=0) — вероятность того, что среди трех отобранных изделий не окажется ни одного стандартного;
при P(X=1) — вероятность того, что среди трех отобранных изделий окажется одно стандартное и два нестандартных изделия;
при P(X=2) — вероятность того, что среди трех отобранных изделий окажется два стандартных и одно нестандартное изделие;
при P(X=3) — вероятность того, что среди трех отобранных изделий все три изделия стандартные.
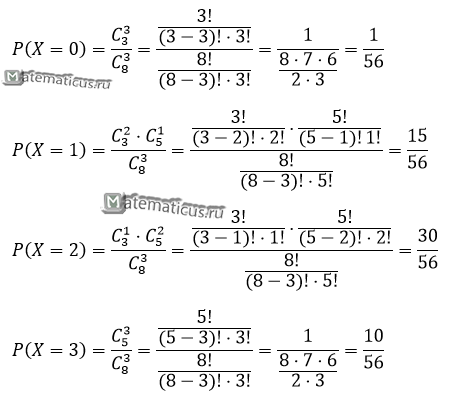
Составим таблицу распределения
| X | 0 | 1 | 2 | 3 |
| P | 0.018 | 0.268 | 0.536 | 0.178 |
Пример 5
В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X — числа стандартных деталей среди отобранных.
Решение
Возможные варианты значений СВ X: 1, 2, 3
$n=C_6^3$ — числу способов, которыми можно выбрать три детали из шести;
$C_4^x$ — число способов, которыми из четырех деталей выбирают х деталей.
$C_2^{3 — x}$ — общее число способов отбора нестандартных деталей
Тогда вероятности события A вычисляются по формуле
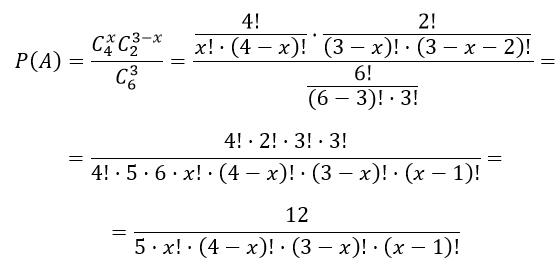
Закон распределения дискретной случайной величины X для составления ряда распределения:
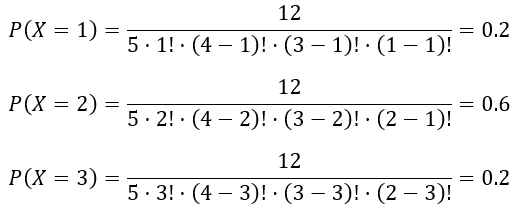
Получаем таблицу ряда распределения ДСВ
| X | 0 | 1 | 2 | 3 |
| P | 0 | 0.2 | 0.6 | 0.2 |
![]() 17267
17267
Uniform distribution is an important & most used probability & statistics function to analyze the behaviour of maximum likelihood of data between two points a and b. It’s also known as Rectangular or Flat distribution since it has (b – a) base with constant height 1/(b – a). It’s one of a continous probability functions popularly used in statistics & probability to characterize the data distribution. The term P(x) represents the probability of maximum likelihood, mean (μ) represents the expected likelihood of data & σ2 represents the variation among the group of data. Whereas the inverse function estimates the negative probability of Uniform distribution between two points.
Formula
The below formula is mathematical representation of Uniform probability density function may help users to know what are all the input parameters are being used in such calculations to characterize the data distribution. Users may use these below uniform distribution formulas for manual calculations and use this calculator to verify the results of manual calculations or generate complete work with steps.

Формулы: законы распределения случайных величин
В данном разделе вы найдете формулы по теории вероятностей, описывающие законы распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, экспоненциальный, равномерный, нормальный.
Каталог формул по теории вероятности онлайн
Законы распределения на этой странице
|
|
Лучшее спасибо – порекомендовать эту страницу
Дискретные случайные величины
Биномиальное распределение ДСВ
Пусть дискретная случайная величина $X$ – количество “успехов” в последовательности из $n$ независимых случайных экспериментов, таких что вероятность “успеха” в каждом из них равна $p$ (“неуспеха” – $q=1-p$).
Закон распределения $X$ имеет вид:
| $x_k$ | 0 | 1 | … | k | … | n |
| $p_k$ | $q^n$ | $ncdot p cdot q^{n-1}$ | $C_n^k cdot p^k cdot q^{n-k}$ | $p^n$ |
Здесь вероятности находятся по формуле Бернулли:
$$
P(X=k) = C_n^k cdot p^k cdot (1-p)^{n-k} = C_n^k cdot p^k cdot q^{n-k}, k=0,1,2,…,n.
$$
Числовые характеристики биномиального распределения:
$$M(X)=np, quad D(X)=npq, sigma(X)=sqrt{npq}.$$
Примеры многоугольников распределения для $n=5$ и различных вероятностей:
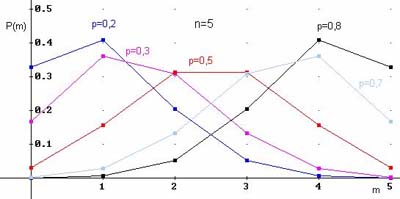
Примеры решенных задач на биномиальный закон ДСВ
Пуассоновское распределение ДСВ
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
При условии $pto 0$, $n to infty$, $np to lambda = const$ закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность $p$ события $A$ в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Ряд распределения по закону Пуассона имеет вид:
| $x_k$ | 0 | 1 | … | k | … |
| $p_k$ | $e^{-lambda}$ | $lambda e^{-lambda}$ | … | $frac{lambda^k}{k!}cdot e^{-lambda}$ | … |
Вероятности вычисляются по формуле Пуассона:
$$
P(X=k)=frac{lambda^k}{k!}cdot e^{-lambda}, k=0,1,2,…
$$
Числовые характеристики для распределения Пуассона:
$$M(X)=lambda, quad D(X)=lambda, sigma(X)=sqrt{lambda}.$$
Разные многоугольники распределения при $lambda = 1; 4; 10$.
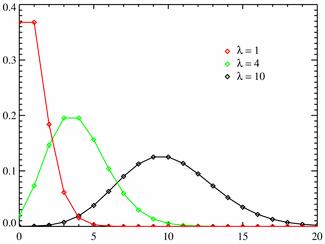
Примеры решенных задач на закон Пуассона
Геометрическое распределение ДСВ
Пусть происходит серия независимых испытаний, в каждом из которых событие может появится с одной и той же вероятностью $p$. Тогда случайная величина $X$ – количество испытаний до первого появления события, имеет геометрическое распределение вероятностей.
Формула для вероятностей:
$$
P(X=k) = q^k cdot p, k=0,1,2,…,n,…
$$
Ряд распределения геометрического закона:
| $x_k$ | 0 | 1 | 2 | … | k | … |
| $p_k$ | $p$ | $qcdot p$ | $q^2 cdot p$ | … | $q^k cdot p$ | … |
Числовые характеристики:
$$M(X)=frac{q}{p}, quad D(X)=frac{q}{p^2}.$$
Примеры решенных задач на геометрическое распределение
Гипергеометрическое распределение ДСВ
Из урны, в которой находятся $N$ шаров ($K$ белых и $N-K$ чёрных шаров), наудачу и без возвращения вынимают $n$ шаров ($n le N$). Найти закон распределения случайной величины $X$ – равной числу белых шаров среди выбранных.
Случайная величина $X$ может принимать целые значения от $0$ до $K$ (если $n lt K$, то до $n$). Вероятности вычисляются по формуле:
$$
P(X=k)=frac{C_K^k cdot C_{N-K}^{n-k}}{C_N^n}, quad 0le k le K.
$$
Числовые характеристики:
$$M(X)=frac{K}{N}cdot n, quad D(X)=frac{K}{N}cdot n cdot frac{N-n}{N} cdot frac{N-K}{N-1}.$$
Примеры задач на гипергеометрическое распределение
Решаем теорию вероятностей на отлично. Закажите сейчас!
Непрерывные случайные величины
Показательное распределение НСВ
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Плотность распределения величины $X$(везде $ lambda gt 0)$:
$$
f(x)=
left{
begin{array}{l}
0, x lt 0\
lambda e^{-lambda x}, xge 0 \
end{array}
right.
$$
Функция распределения величины $X$:
$$
F(x)=
left{
begin{array}{l}
0, x lt 0\
1- e^{-lambda x}, xge 0 \
end{array}
right.
$$
Числовые характеристики можно найти по формулам:
$$M(X)=frac{1}{lambda}, quad D(X)=frac{1}{lambda^2}, quad sigma= frac{1}{lambda}.$$
Плотность распределения при различных значениях $lambda gt 0$:
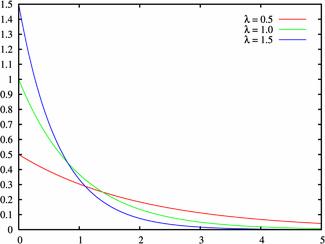
Примеры решенных задач на показательное распределение
Равномерное распределение НСВ
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.
Плотность распределения на отрезке $(a;b)$:
$$
f(x)=
left{
begin{array}{l}
0, x le a\
frac {1}{b-a}, a lt x le b, \
0, x gt b, \
end{array}
right.
$$
Функция распределения:
$$
F(x)=
left{
begin{array}{l}
0, x le a\
frac {x-a}{b-a}, a lt x le b, \
1, x gt b, \
end{array}
right.
$$
Числовые характеристики равномерно распределенной случайной величины:
$$M(X)=frac{a+b}{2}, quad D(X)=frac{(b-a)^2}{12}, quad sigma=frac{b-a}{2sqrt{3}}.$$
График плотности вероятностей:
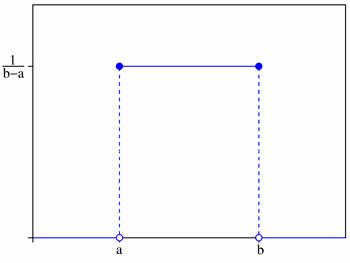
Примеры решенных задач на равномерное распределение
Нормальное распределение или распределение Гаусса НСВ
Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.
Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Плотность распределения нормальной случайной величины $X$ имеет вид:
$$f(x)= frac{1}{sigmasqrt{2pi}} expleft({-frac{(x-a)^2}{2sigma^2}}right). $$
При $a=0$ и $sigma=1$ эта функция принимает вид:
$$varphi(x)= frac{1}{sqrt{2pi}} e^{-x^2/2}.$$
Скачать таблицу для функции $varphi(x)$
Числовые характеристики для нормального распределения:
$$M(X)=a, quad D(X)=sigma^2.$$
Пример графика плотности распределения для различных значений среднего и СКО:
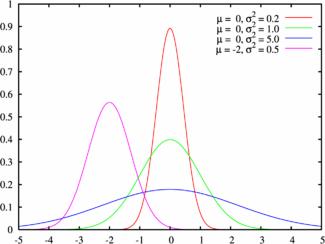
Нормальный закон распределения случайной величины с параметрами $a=0$ и $sigma=1$ называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.
Функция Лапласа определяется как:
$$Phi(x)= frac{1}{sqrt{2pi}}int_0^x e^{-t^2/2} dt$$
Скачать таблицу для функции Лапласа
Вероятность попадания нормально распределенной случайной величины $X$ в заданный интервал $(alpha, beta)$:
$$
P(alpha lt X lt beta) = Phileft( frac{beta-a}{sigma} right) – Phileft( frac{alpha-a}{sigma} right).
$$
Вероятность отклонения нормально распределенной случайной величины $X$ на величину $delta$ от математического ожидания (по модулю).
$$
P(|X -a|lt delta) = 2 Phileft( frac{delta}{sigma} right).
$$
Примеры решенных задач на нормальное распределение
Полезная страница? Сохрани или расскажи друзьям
Решенные задачи по теории вероятностей
Ищете готовые задачи по теории вероятностей? Посмотрите в решебнике:
Подробно решим теорию вероятностей. Закажите сейчас!
Полезные ссылки
|
|
Математическое ожидание
Данный калькулятор предназначен для вычисления математического ожидания дискретной случайной величины онлайн.
Оценка математического ожидания и дисперсии случайной величины имеет большое значение в теории вероятности.
Математическое ожидание – среднее значение случайной величины. Чтобы найти математическое ожидание случайной величины, следует вычислить сумму парных произведений всех возможных значений случайной величины на соответствующие им вероятности.
Свойства математического ожидания заключаются в следующем. Во-первых, математическое ожидание суммы независимых случайных величин равно сумме их математических ожиданий. Во-вторых, математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.
Как найти среднее значение , формула (на примере следующих величин):
xi= 1 ; 2 ; 5 ; 6 (случайные величины)
pi = 0.1 ; 0.3 ; 0.1 ; 0.5 (вероятность)
M[X] = x1p1 + x2p2 + x3p3 + x4p4 = 1×0.1 + 2×0.3 + 5×0.1 + 6×0.5 = 0.1 + 0.6 + 0.5 + 3 = 4.2
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

