Как составить закономерность по математике

Нас повсюду окружают различные типы математических закономерностей. К примеру, неделя состоит из 7 дней, и через 7 календарных дней наступит тот же день недели, что и сегодня. Это пример закономерности, которая имеет свойство повторяться. Зная, какая закономерность задает порядок между элементами, можно прогнозировать события. Поэтому тема математических закономерностей и задач с ними хотя и кажется простой, но является важной для изучения и понимания более сложных вещей.

«Бери и Делай» подсказывает, с помощью каких способов и приемов можно научиться решать задачи с закономерностями.

Какие бывают закономерности в математике

Математическая закономерность — это правило, которое задает порядок элементов в ряду, отражает какое-то изменение этих элементов или их свойств. Математические закономерности бывают:

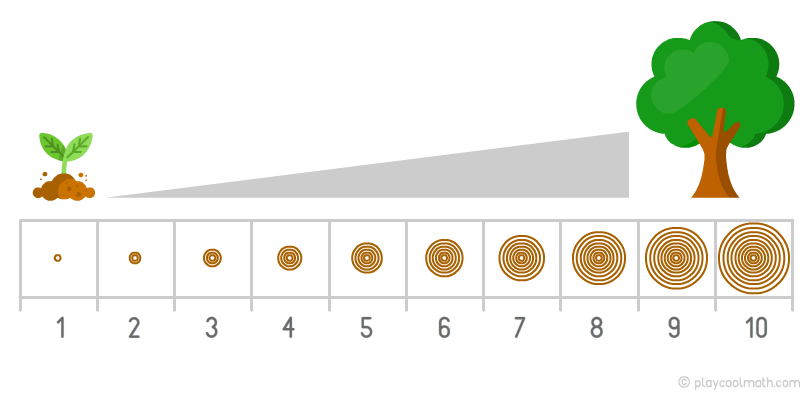
• Возрастающими, если числовое свойство такой закономерности увеличивается согласно какому-то закону или формуле. К примеру, дерево растет, прибавляя каждый год по 1 новому кольцу на стволе. Зная эту закономерность, мы можем определить точный возраст дерева, посчитав число колец на срезе ствола.
• Убывающими, если числовое свойство такой закономерности уменьшается согласно какому-то закону или формуле. Например, зная, сколько бензина тратит машина, преодолевая каждый километр, мы можем определить, в какой момент нужно будет остановиться и дозаправиться.
• Циклическими, если закономерность имеет свойство повторяться. В таком случае полный круг в циклической закономерности называется циклом закономерности. Смена дня и ночи, времен года, дней недели — это примеры циклических закономерностей.
• Сложными, если они состоят из закономерностей нескольких видов или имеют несколько свойств.

Зачем решать задачи на закономерности

Поиск закономерностей в заданиях помогает детям понять, что из себя представляют числа, и развить способности к наблюдению. Когда ребенок видит закономерность, он изучает ее и может прогнозировать то, что произойдет следом по порядку. Это является важным навыком для понимания чисел и в будущем поможет при изучении более сложных тем математики.

Как решать задачи на закономерности

Посмотрите на картинку выше. Это простая задачка, где ребенку предлагают закрасить остальные квадратики, соблюдая заданную закономерность.

Сначала нужно определить цепочку (последовательность цветов), которая повторяется. На картинке выше видно, что цветные квадратики стоят друг за другом в определенном порядке, который не нарушается. Из этого можно сделать вывод, что в данном случае закономерность задана повторением цветов: зеленый, желтый, красный, синий, снова зеленый и так далее. Другими словами, мы имели дело с циклической закономерностью.

Выше представлена более сложная задачка. Чтобы определить, какая фигура должна быть на месте вопросительного знака, нужно разглядеть несколько закономерностей:

1. Закономерность по форме фигуры заметна, если приглядеться к тому, как чередуются звенья цепочки через каждые 4 элемента. Таким образом, можно сделать вывод, что на месте вопросительного знака должен быть круг.

2. Закономерность по размеру фигуры бросается в глаза, если разделить ряд фигур на части, в каждой из которых всего 3 элемента. Получается, что на месте вопросительного знака должен быть маленький круг.

3. Закономерность по цвету становится заметной, если выделить цепочку из 5 элементов. Так мы приходим к выводу, что на месте вопросительного знака находится маленький круг синего цвета. Мы решили задачку, где присутствовала сложная закономерность.

Чтобы решать задачи с закономерностями, удобно сразу выработать алгоритм поиска закономерностей:

• Шаг № 1: Определяем количество свойств цепочки.
• Шаг № 2: Выявляем закономерности для каждого свойства.
• Шаг № 3: Сопоставляем закономерности для определения всех свойств следующего звена в цепочке.

Примеры задач с закономерностями и решения

Задача № 1

Попробуйте отгадать, какая фигура должна быть в последней клетке.

Решение: По горизонтали в ряд после квадрата идет треугольник, после треугольника — круг, а после круга — снова квадрат. По вертикали в ряд после квадрата следует круг, после круга — треугольник, а после него — снова квадрат. Фигуры повторяются по диагонали слева направо. По диагонали справа налево смайлики тоже повторяются в определенном порядке. Получается, что в пустой клетке должен быть квадрат с горизонтальной черточкой вместо улыбки.

Ответ: Квадрат.

Задача № 2

На картинке выше квадраты различаются цветами и числами, записанными внутри них, но располагаются в определенном порядке. Попробуйте определить закономерность.

Решение: В данном случае нужно искать правило, которое задает порядок между числами. Чтобы увидеть закономерность, произведем вычисления:

23 − 14 = 9

14 − 8 = 6

8 − 5 = 3

Получается, что каждое следующее число в цепочке 5, 8, 14, 23 увеличивается на предыдущее значение + 3. Таким образом:

? − 23 = 9 + 3

? = 35

Ответ: Вместо вопросительного знака должно стоять число 35.

Задача № 3

Выше на картинке изображены 3 круга, каждый из которых разделен на 3 сектора. Нужно узнать, какое число кроется за вопросительным знаком.

Решение: В первых 2 кругах число, которое располагается в нижнем секторе, составляет 1/3 от суммы чисел, располагающихся в верхних секторах. Соответственно, чтобы узнать, какое число прячется за вопросительным знаком, нужно сложить числа в 2 верхних секторах 3-го круга и разделить полученное число на 3.

16 + 5 = 21

21 : 3 = 7

Ответ: 7.

Задача № 4

Выше изображена последовательность чисел. Ее надо изучить и найти лишнее число, которое не обладает свойством, характерным для остальных чисел в ряду.

Решение: Все числа в этом ряду делятся на 9, кроме числа 426.

Ответ: 426.

Задача № 5

Посмотрите на картинку выше и определите, какое число скрывается под автомобилем.

Решение: Это загадка с подвохом. Достаточно перевернуть картинку вверх ногами, чтобы увидеть последовательность, где каждое последующее число больше предыдущего на 1. Получается, что у нас есть ряд чисел (86, ?, 88, 89, 90, 91), и машина стоит на числе 87.

Ответ: 87.

Понравилась статья? Заходите к нам на сайт “Бери и Делай” и читайте еще. А также подписывайтесь на наш канал, чтобы не пропускать полезные посты.

Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом. 

В чем смысл игры?

Игры такого рода развивают умение выделять закономерности в последовательном ряде элементов. Для этого сначала нужно внимательно рассмотреть задание: сравнить соседние объекты и попробовать определить правило закономерности.

Решить задачу можно с помощью простого счета, обобщения по какому-либо признаку или простого анализа рисунка, текста или схемы.

Как научить ребенка находить закономерности?

Маленьким детям, для решения задач на поиски закономерностей, понадобится только смекалка и воображение. Достаточно лишь объяснить, как можно установить закономерность между звеньями ряда. Если задачу решить не получается, то вместо прямых подсказок следует задать дополнительные вопросы, не раскрывая решение задачи полностью.

В любом случае, пользы будет больше, если ребенок решит, хотя бы одну задачу самостоятельно, нежели взрослый просто расскажет, как её решать. 

Рассмотрим способы, которые помогут ребенку понять закономерности и последовательности в заданиях.

Инструкция по решению числовых последовательностей:

• Найти разницу между двумя рядом стоящими числами
• Определить алгоритм построения последовательности
• Применить алгоритм к следующей паре чисел
• Использовать алгоритм для определения следующего числа в ряду

Инструкция по нахождению закономерностей в заданиях с геометрическими фигурами:

• Рассмотреть фигуры и разделить их, на повторяющиеся группы
• Определить какой элемент изменился в группе
• Решить, какая именно фигура отсутствует или является лишней.

---

Задания для 1 класса

Задание 1

Раскрась дорожки для зайчика и белочки, сохраняя закономерность.

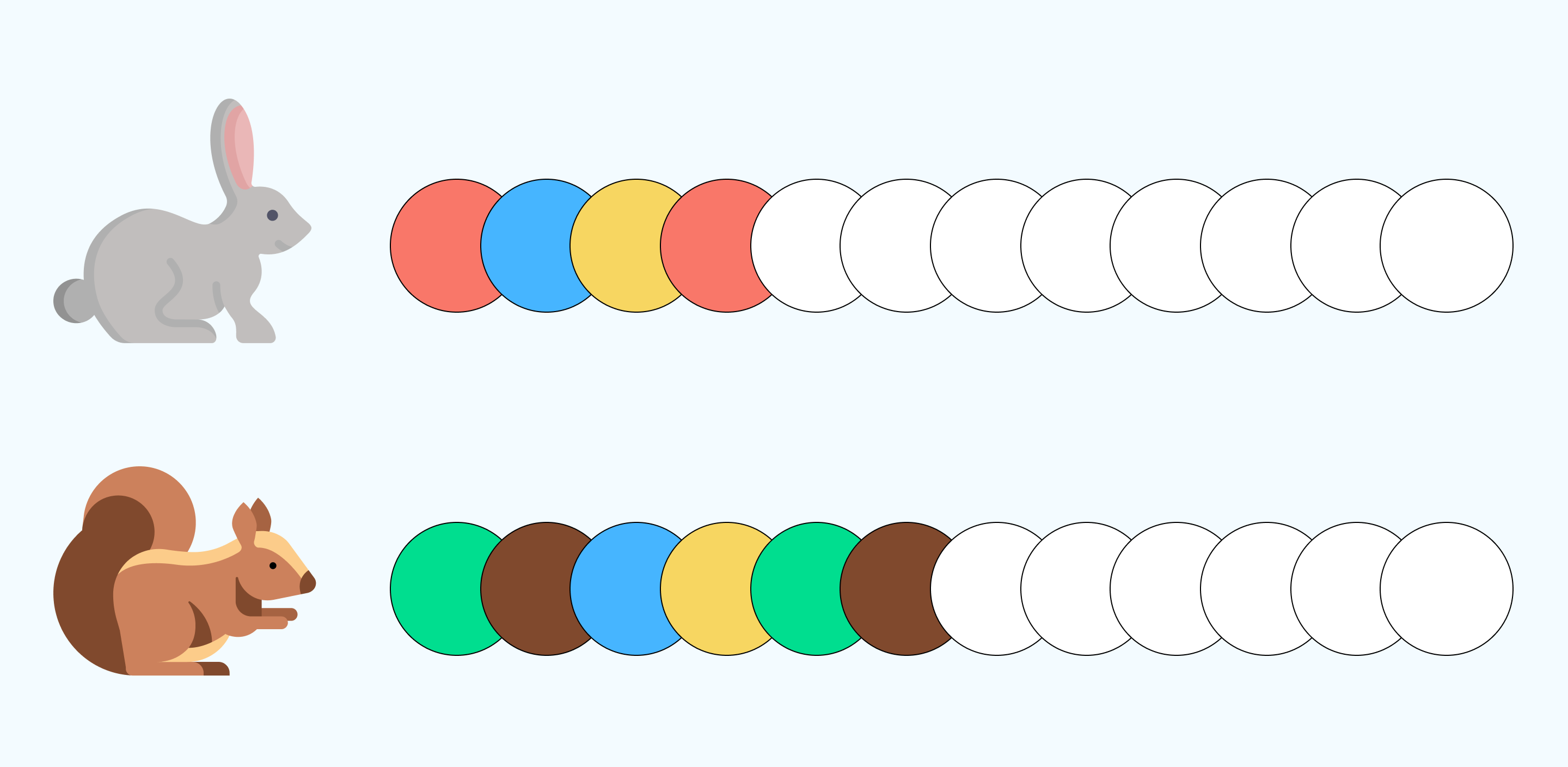
Решение: Белочка и зайчик бегут по разным дорожкам. У каждой дорожки есть своя закономерность. У зайчика повторяется 3 цвета на дорожке: красный, голубой, жёлтый, а у белочки 4: зеленый, коричневый, фиолетовый, жёлтый.

В этом задании можно обратить внимание на то, что обе дорожки состоят из 12 кругов. Но количество повторяющихся цветов разное.

Задание 2

Найди закономерность в ряду геометрических фигур. 

Решение: В этом ряду нужно обратить внимание на размеры фигур, а не на цвет и форму. Сначала идет одна большая фигура, а за ней две маленькие, далее они повторяются.

Задание 3

Нарисуйте в четвертом квадрате правильный ответ. 

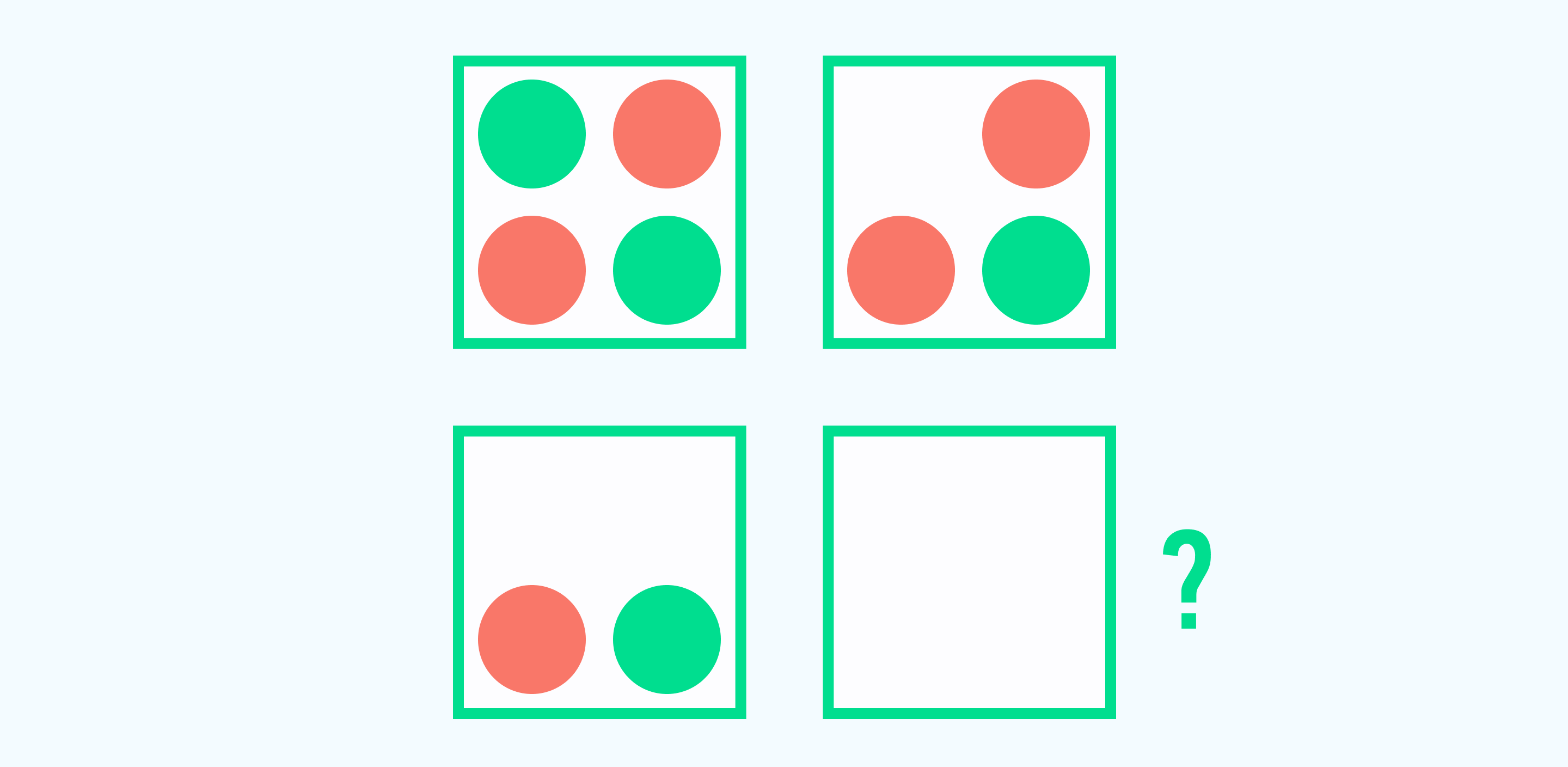
Решение: Рассмотрев внимательно рисунок, мы увидим, что круги в квадратах исчезают по одному, против часовой стрелки. В этой задаче имеет значение только расположение кругов квадрате. Таким образом, в последний квадрат мы должны нарисовать один синий круг в нижнем левом углу.

Задание 4

Соблюдая закономерность, продолжи ряд чисел до 10. Сформулируй правило, которое действует в этой закономерности. Используя это правило, придумай свою закономерность.

• 2, 4, 6,…

Решение: В этом ряду каждая цифра увеличивается на 2 относительно предыдущей – мы вычислили правило для данной закономерности. Значит, чтобы продолжить ряд, мы прибавим к каждой следующей цифре по 2. Ответ будет выглядеть так: 2,4,6,8,10.

Чтобы придумать подобную закономерность, нужно использовать сформулированное выше правило: например, 1,3,5,7,9.

---

Задания для 2 класса

Задание 1

Найди закономерность и в пустом квадрате нарисуй нужное количество кругов.

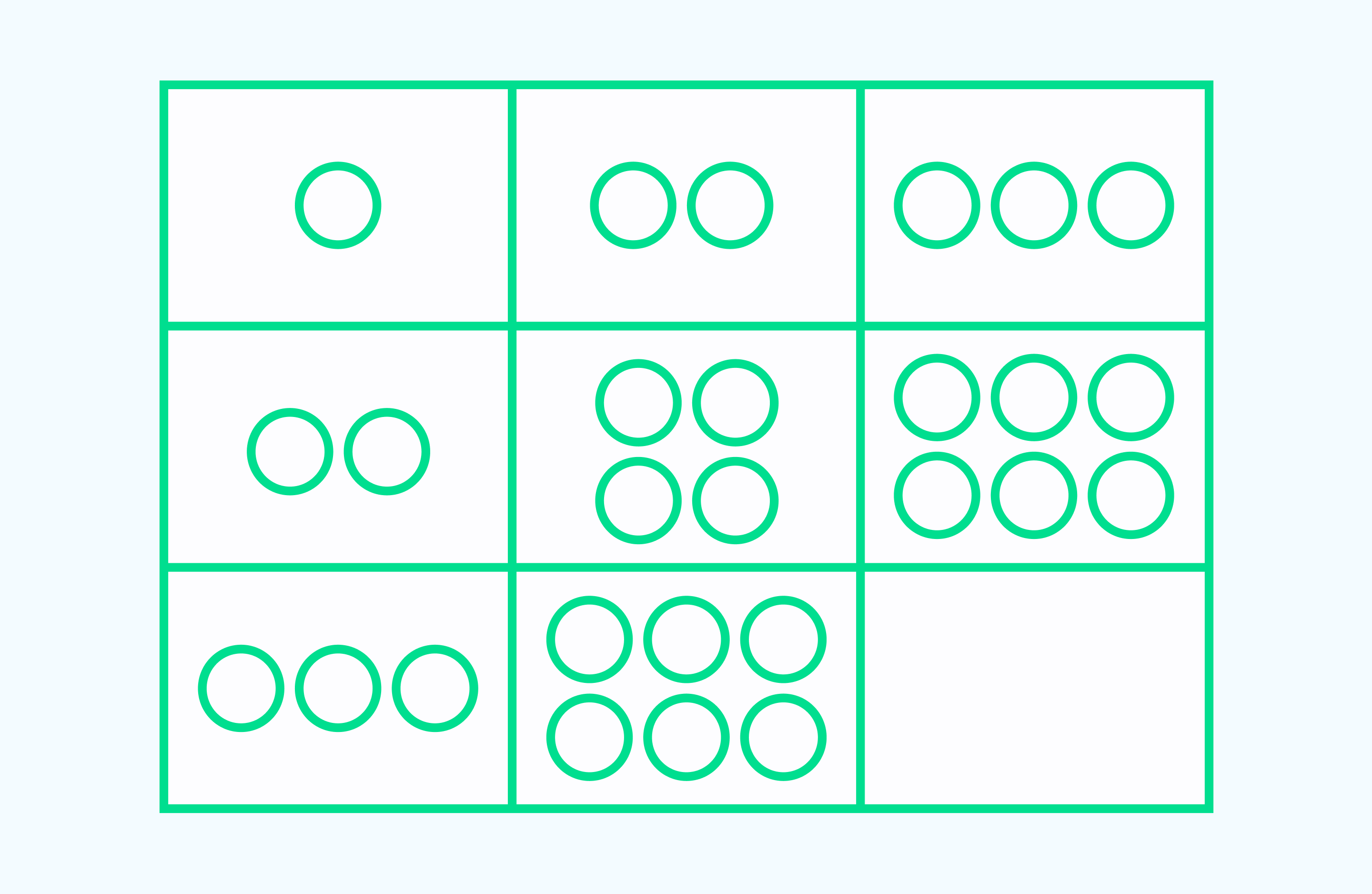
Решение: В таблице в первом горизонтальном ряду количество кругов увеличивается на 1. Во втором ряду увеличивается на 2. Таким образом, можно предположить, что в третьем ряду количество кругов будет увеличиваться на 3 и ответ будет 9. Можно заметить, что и в вертикальных рядах эта закономерность повторяется.

Задание 2

В цепочке чисел найди закономерность и вставь пропущенные числа

• 95, 90, 85, 80, 75,_, 65,_, _,50

Решение: В цепочке чисел можно выделить пары: 95 -90, 85 – 80 и далее. Каждый раз, в паре, число уменьшается на 5. Значит, после 75 запишем 70, после 65 — 60, а затем 55 .

Задание 3

Найди закономерность и продолжи последовательность.

• 2, 3, 5, 8, …, …, …, …

Решение: В этой цепочке чисел к каждому последующему числу прибавляется предыдущее. 2+3=5+3=8+5=13+8=21+13=34 и далее.

Задание 4

В поезде едут геометрические фигуры. Нарисуйте фигуры, в четвёртом вагоне, соблюдая закономерность их расположения.

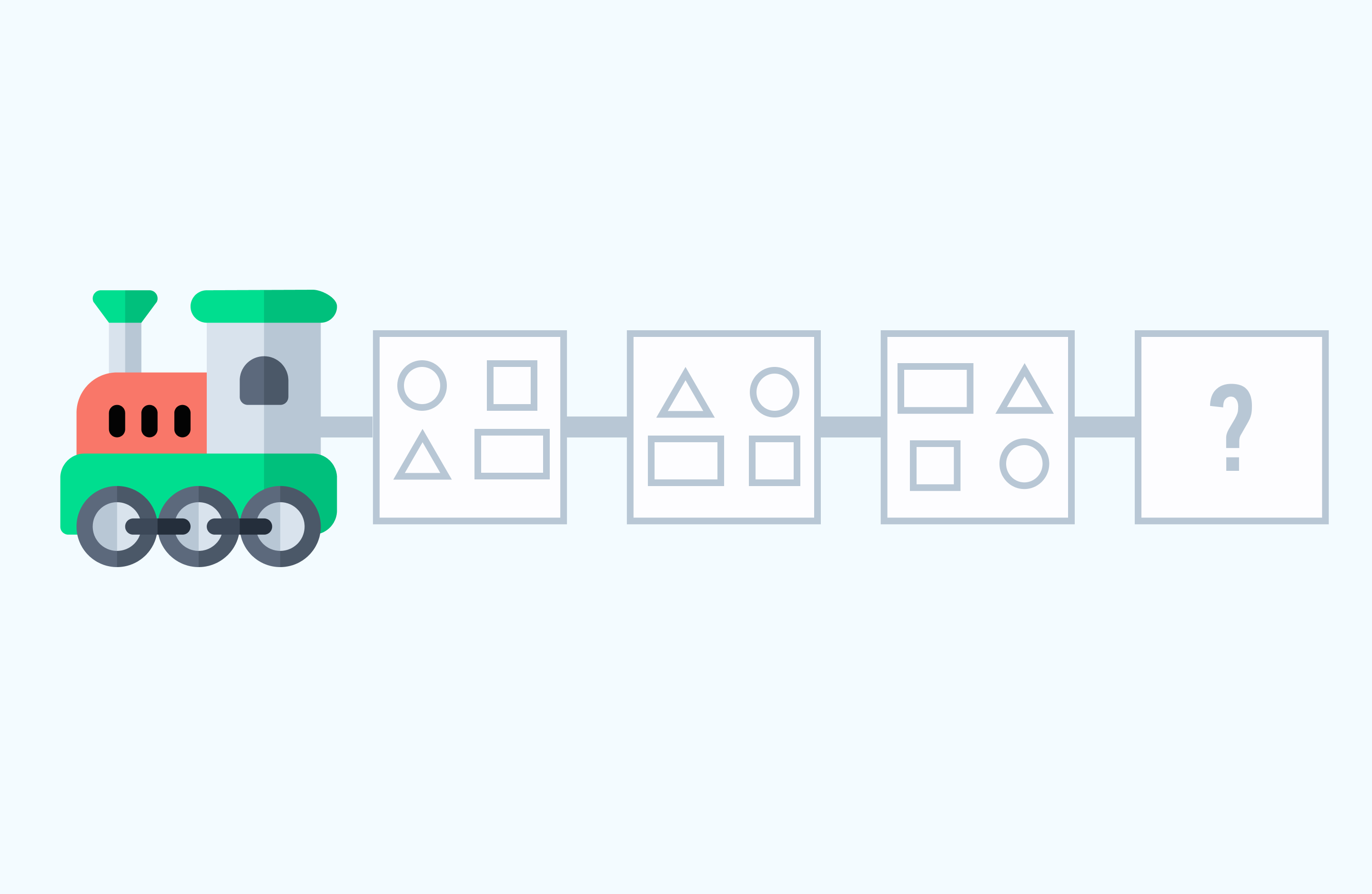
Решение: В поезде едут геометрические фигуры: квадрат, треугольник, прямоугольник и круг. В трёх вагонах все места заняты фигурами, в определённом порядке. Расставим их и в четвертом вагоне: Круг в нём будет располагаться в нижнем левом углу, квадрат в верхнем левом, треугольник поедет в правом нижнем, а прямоугольник – в левом верхнем углу.

---

Задания для 3 класса

Задание 1

Рассмотрите картинку и найдите закономерность в задаче.

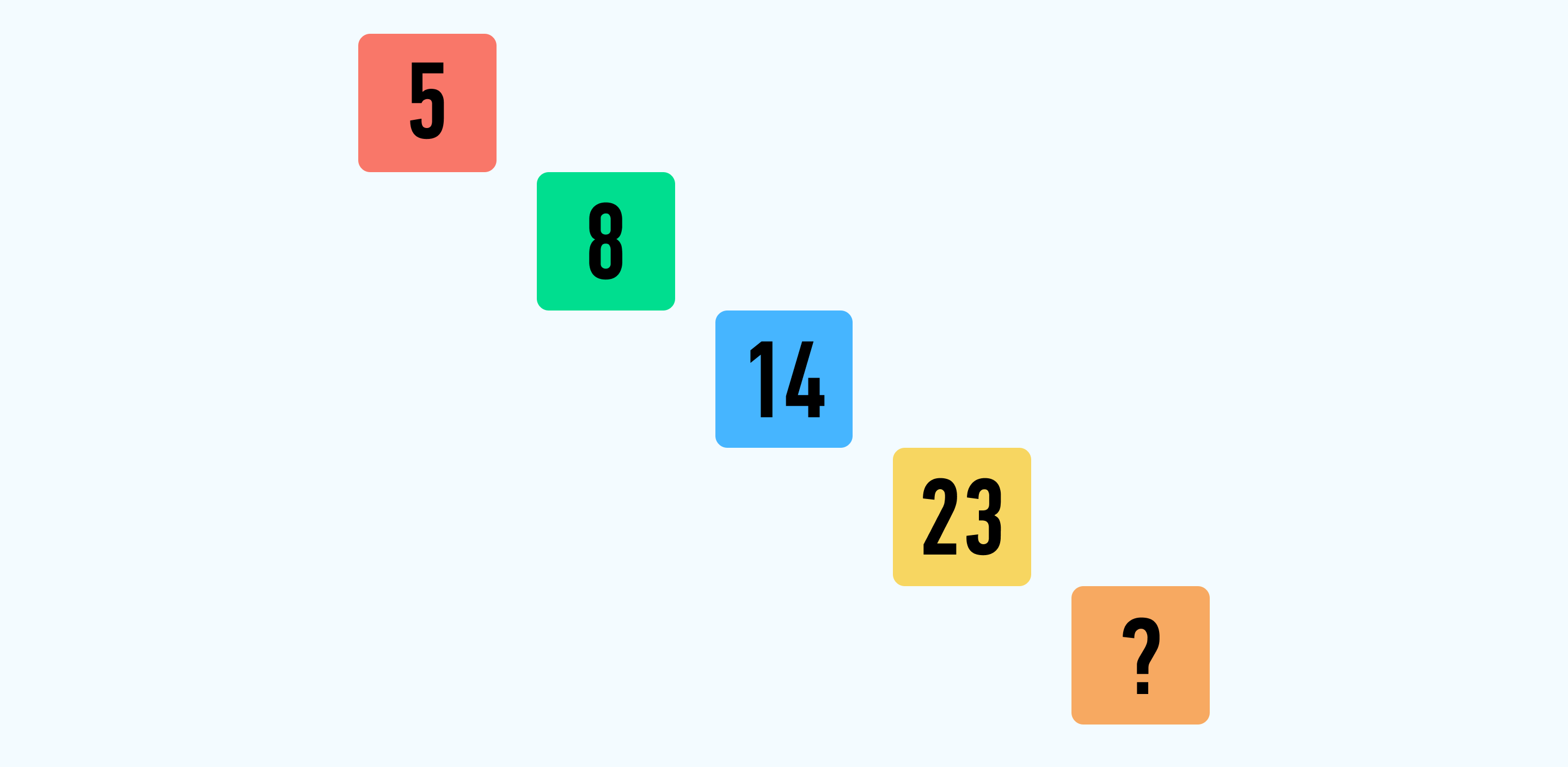
Решение: В таблице мы увидим такую закономерность: 

8-5=3, то есть число увеличилось на 3; далее 14-8=6, соответственно, число увеличилось на 6. В последней связке 23-14=9 число увеличилось на 9. Мы делаем вывод, что каждое следующее число увеличивается на предыдущее значение+3. Таким образом, следующее число увеличивается на 9+3=12. 23 + 12 = 35. Ответ: 35.

Задание 2

 В пустые клетки вставьте геометрические фигуры, сохраняя закономерность.

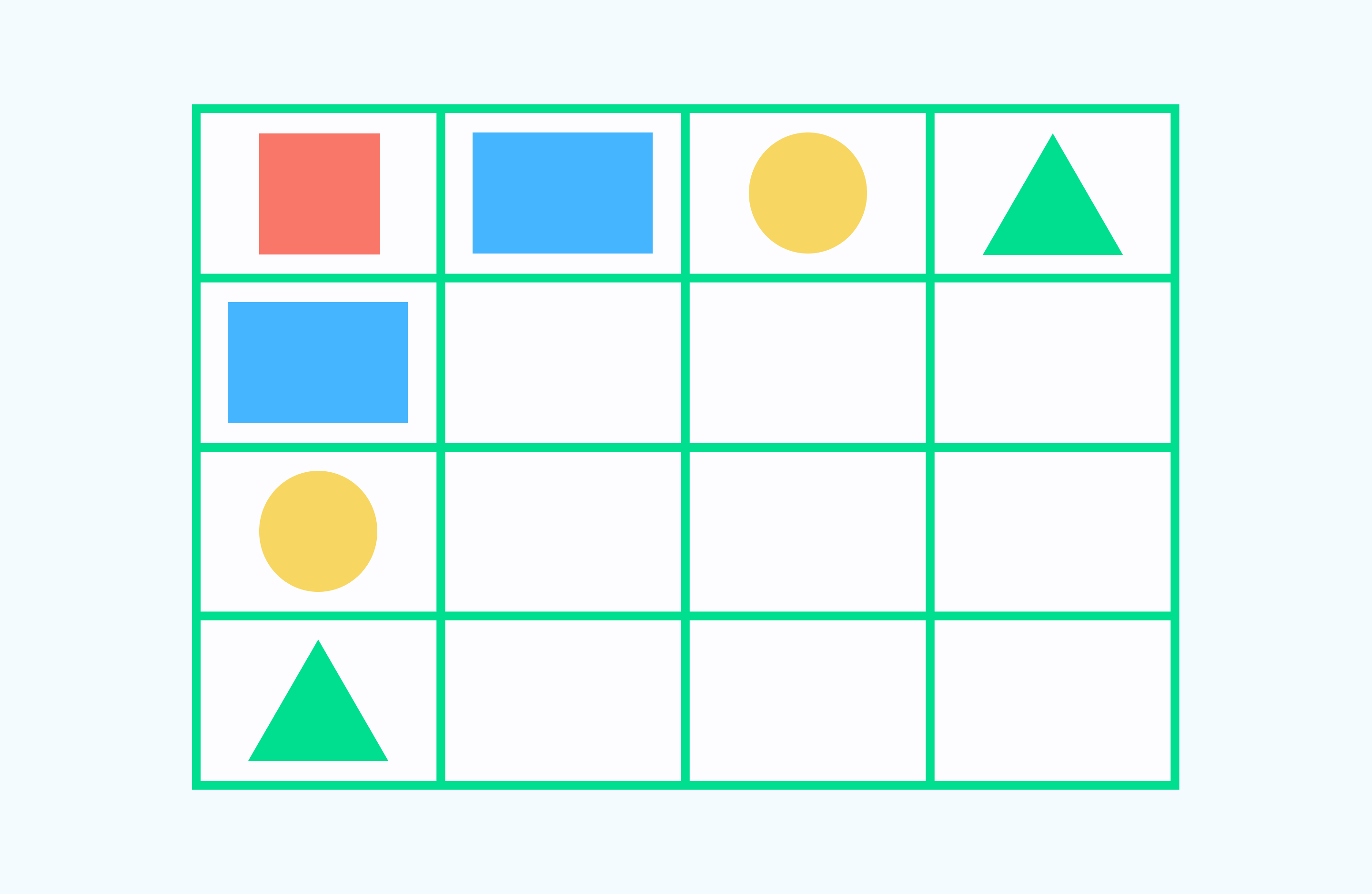
Решение: Чтобы выполнить задание, нужно фигуры расставить по порядку, друг за другом, соблюдая последовательность. Значит, после прямоугольника стоит круг, треугольник и квадрат  и т. д. 

Задание 3

Найди закономерность и продолжи ряды:

• 12, 23, 34, 45, 56…
• 13, 24, 35, 46…

Решение: В этой задаче каждая последующая цифра увеличивается так: десятки на один десяток и единицы на одну единицу. 12=10+2, 23=20+3, 34=30+5 и т. д.  

Задание 4

 Продолжи ряд, сохраняя закономерность.

• 12, 36, 13, 39, 14, 42, 15,…

Решение: В числовой цепочке выделяем пары чисел. Первая пара:12 и 36. 12×3=36, далее по порядку: 13×3=39. Умножая каждый раз на 3, цифры, следующие по порядку (12,13,14,15…), мы продолжаем последовательный ряд. Ответ: 45.

---

Задания для 4 класса

Задание 1

Найди ошибку в бусах.

Решение: В первых бусах повторяются квадрат и круг, значит лишний шестой круг. Во вторых бусах, повторяется закономерность: круг, два треугольника, два круга, лишний – восьмой, по счету, круг.

Задание 2

Определите закономерность. Найдите лишнее число.

• 8, 16, 20, 24, 32, 40, 48, 56, 64, 72.

Решение: В этом числовом ряду таблица умножения на 8. Ответ: число 20 – лишнее.

Задание 3

Каких геометрических фигур не хватает? Дорисуй их, соблюдая закономерность в таблице: 

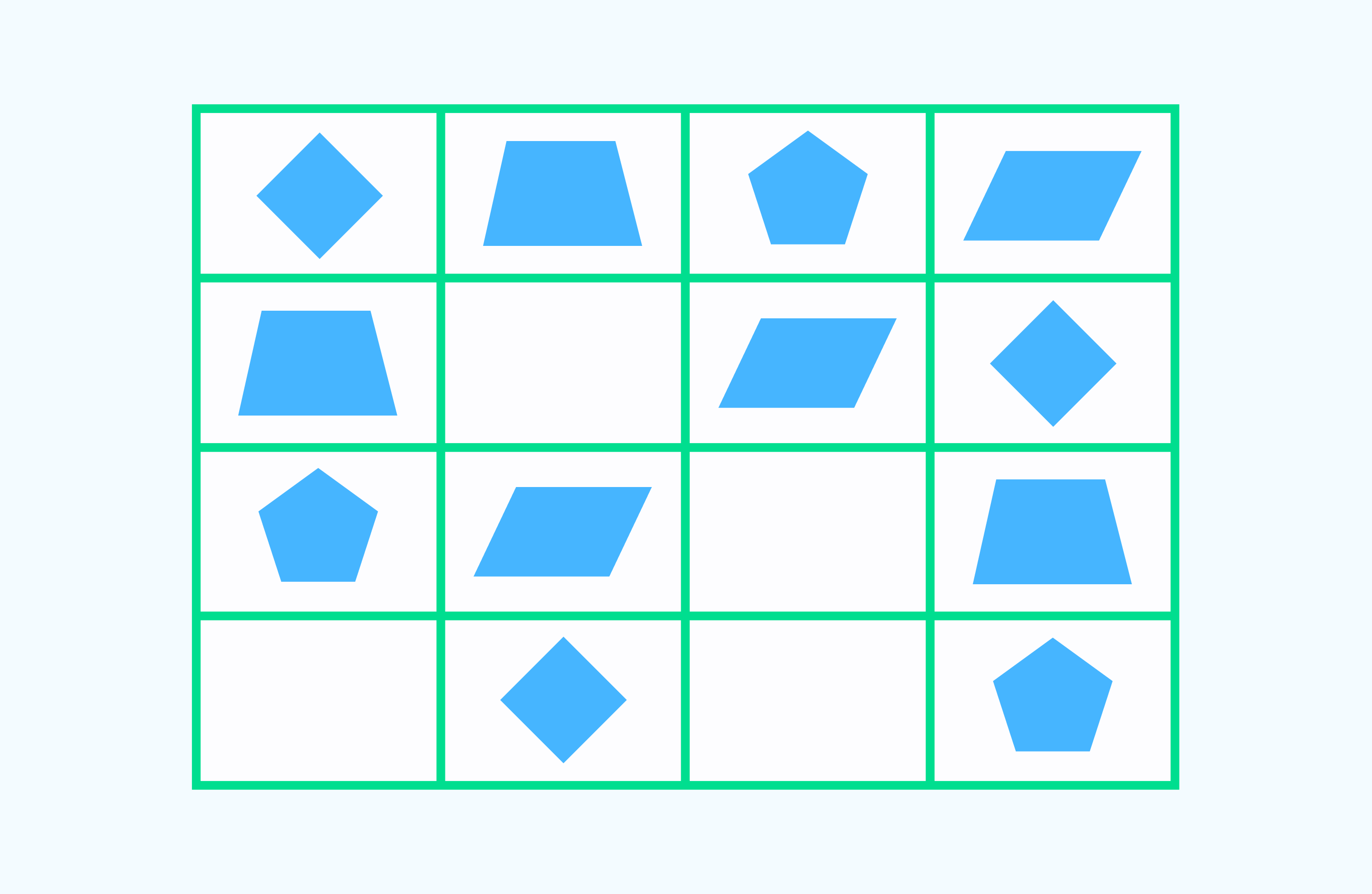
Решение: Определить, какой элемент изменился во втором и последующих рядах, можно, выделив последовательность: ромб, трапеция, шестиугольник и параллелограмм. Во втором ряду недостает шестиугольника, в третьем — ромба, в четвертом – параллелограмма и трапеции. 

Решайте закономерности 4 класс у нас! На странице размещены задания “найти закономерность 4 класс”. Так же задачи на закономерности “продолжи ряд” и различные виды. Удачи!

Начнем сейчас! Мы будем решать:

• Задачи на поиск закономерностей
• Составлять закономерности
• Продолжать ряд
• Продолжать циклические закономерности

Найди закономерность:

1, 5, 10, 16, 23, 31, 40, 50, 61.

2, 3, 5, 8, 13, 21, 34, 55.

100, 90, 80, 70, 60, 50, 40, 30.

60, 62, 64, 66, 68, 70.

2, 4, 12, 48.

Составляем закономерности чисел

Составь закономерность из 7 чисел но с циклом -1, уменьшающимся на 2 каждый раз.

Составь закономерность из 5 чисел чтобы с циклом *2, увеличивающимся на 1 каждый раз.

Придумай закономерность с циклом x, чтобы последнее число было 5x.

Попробуй сделать закономерность с циклом Фиббоначчи – число = сумма 2 предыдущих.

Пример: 2, 3, 5, 8, 13. 2+3=5, 3+5=8, 8+5=13.

Составь эту закономерность из 8 чисел.

Придумай закономерность, чтобы были 2 в 1. Смешанную, чтобы через клетку. Цикл первой – +4, второй – /2.

Продолжи закономерность 4 класс

3, 7, 12, 18, 25, 33, 42, 52, 63, …?

10, 20, 30, 40, 50, 60, 70, …, …?

100, 4, 95, 8, 90, 16, …, …, …?

4, 7, 11, 18, 29, 47, …?

1923453525, 39, 12, …?

1, 3, 7, 13, 21, 31, …, …?

Циклические числовые закономерности

Доделай, чтобы максимальное число не было больше 50.

1, 12, 22, 31, ?

Доделай до 1 (потому что закономерность убывающая).

256, 128, 64, ?

Придумай до 3 в степени 6, но вычисли.

3 в степени 2, 3 в степени 3, 3 в степени 4, ?

Задачи на закономерность

В миске лежит много конфет. Мама в первый день взяла 2, потом – 7, в третий – 12 конфет. Леля – 4, 3 и 2. Сколько конфет они возьмут вместе за пятый день?

В строительстве офиса участвовали 4 рабочих. Первый работник построил 7 этажей. Второй – 14. Работник №3 сделал 28 этажей. Сколько этажей в офисе?

На верхней полке было 200 мандаринов. Семья ела их 4 дня.

Папа – 4, 8, 16

Мама – 3, 6, 9

Ярослав – 5, 9, 13

Сколько мандаринов осталось на полке?

Как решать закономерности и их разновидности? Ответ ниже:

https://matsharik.ru/istoria-zadach/vidy-zakonomernostej

В одном из предыдущих уроков ты узнал о свойствах предметов и как они связаны с математикой. На этом уроке ты познакомишься с понятием – математическая закономерность.

Закономерность – постоянно повторяющаяся взаимосвязь явлений, действий или свойств предметов.

Закономерности, как и свойства предметов связаны с математикой и с логикой. Зная закономерность, ты точно можешь знать, что будет дальше. После четверга точно будет пятница, после 10 часов утра будет 11 часов утра. Последовательность действий, явлений, свойств или событий в закономерности всегда определена, то есть мы точно знаем что будет дальше.

Типы закономерностей

Существует несколько типов закономерностей: убывающие, возрастающие, циклические и сложные закономерности. Давайте познакомимся с каждой подробнее.

Возрастающая закономерность

Закономерность, у которой числовое свойство увеличивается согласно некоторому закону или формуле, называется возрастающей.

Например, дерево растет и на его стволе каждый год добавляется одно новое кольцо. Этот процесс называется простой возрастающей закономерностью. В этой закономерности легко вычислить, сколько колец будет через 2 года или через 10 лет. Количество колец в стволе соответствует возрасту дерева.

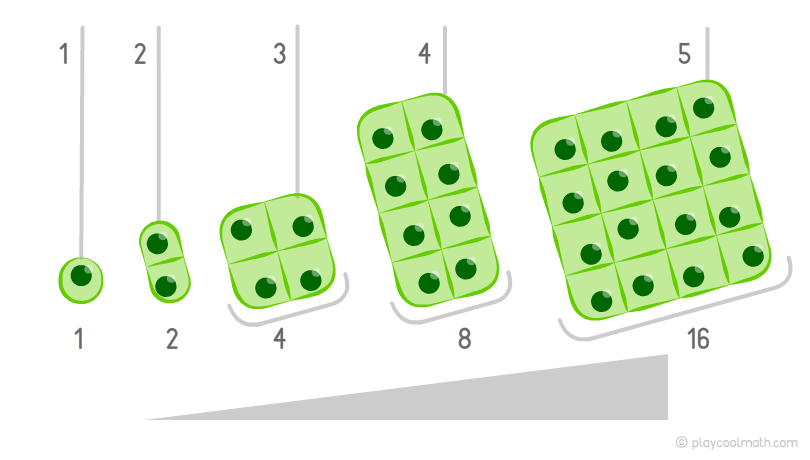
Приведем пример возрастающей закономерности, которая сложнее чем в примере с деревом. Представьте одноклеточный организм, который каждую минуту делится на две клетки. На картинке хорошо видно, что в первую минуту мы видим 1 клетку, во вторую – уже 2 клетки, а затем 4 клетки, 8, 16. Каждую минуту количество увеличивается в 2 раза. Зная предыдущее количество, можно узнать, сколько будет клеток в следующую минуту. Этот процесс называется тоже возрастающей закономерностью. Для настоящих математиков будет несложно установить формулу увеличения закономерности для этого примера. Эта задача для тебя еще сложная, так как ты только начали изучать математику. Главное сейчас чтобы ты понять, что такое закономерность.

Убывающая закономерность

Закономерность, у которой числовое свойство уменьшается согласно некоторому закону или формуле, называется убывающей.

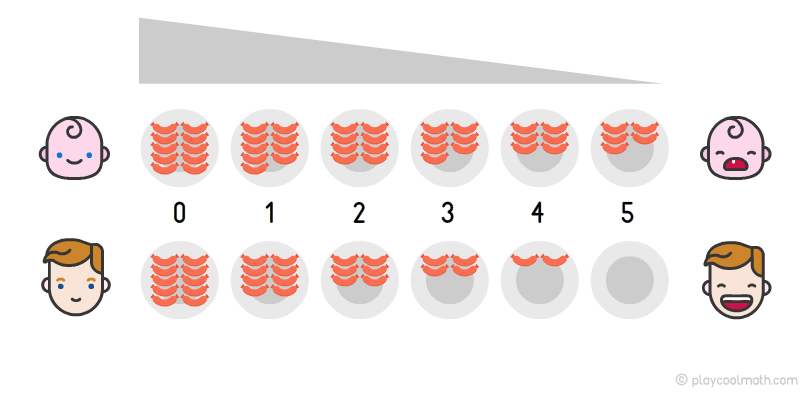
Представьте соревнования по поеданию сосисок на скорость, в которых участвуют два участника. У каждого по 10 сосисок на тарелке (это столько, сколько у тебя пальцев на руках). Первый съедает одну сосиску за минуту, а второй съедает 2 сосиски за минуту. Ясно, что второй участник соревнований победит, так как он съедает больше сосисок за минуту, чем первый участник. Но нам важно увидеть закономерность. На рисунке мы можем увидеть, как в каждой тарелке уменьшается количество сосисок. Этот процесс называется убывающей закономерностью. Второй участник съел всю тарелку сосисок за пять минут и победил!

Циклическая закономерность

Закономерность, которая повторяется каждый раз, называется циклической. Полный круг в циклической закономерности называется циклом закономерности.

Ты точно знаешь закономерность такого типа – это смена времен года. Весна-Лето-Осень-Зима и потом происходит повторение.

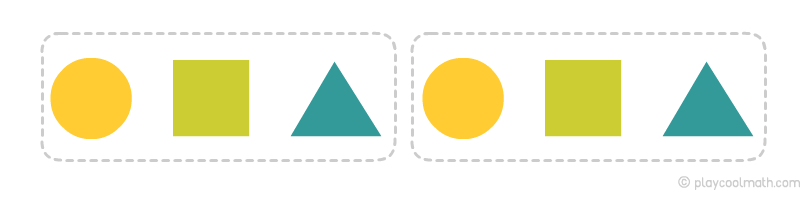
Рассмотрим пример с предметами разной формы. На рисунке ты видишь цепочку из разного количества предметов. Попробуй найти закономерность на рисунке ниже. Продолжи цепочку.

Предметы повторяются через каждые три ячейки. Зная закономерность, мы можем предположить, какие предметы будут дальше. За последним звеном будет треугольник, затем круг, далее квадрат.

Сложные закономерности

Закономерности, которые состоят из нескольких видов закономерностей или имеют несколько свойств, называются сложными.

Рассмотрим пример закономерностей на одной и той же цепочке, но будем искать закономерности в зависимости от свойства звеньев. Попробуй найти следующее звено в примере ниже.

Закономерность по форме

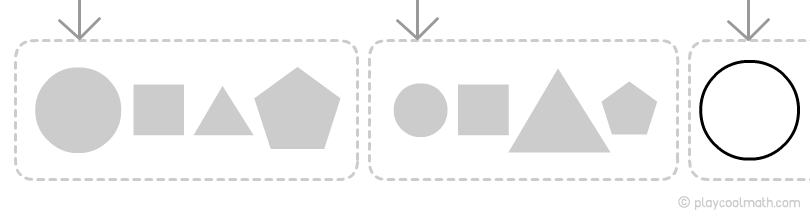
Видим, как чередуются звенья цепочки. Точно знаем, что по форме следующим будет круг, обозначим его как большой круг

Закономерность по размеру

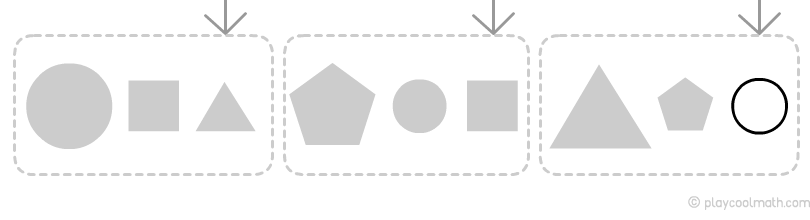
Видим, как чередуются звенья цепочки: большая и затем две маленькие фигуры, то есть следующей будет маленькая фигура.

Закономерность по цвету

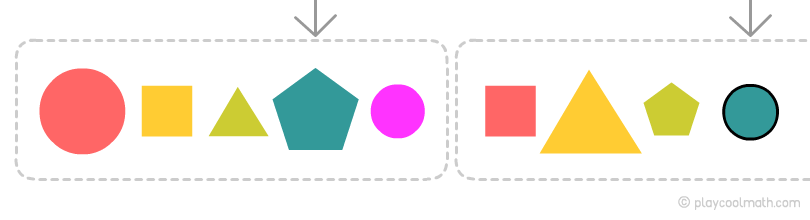
Получилась самая длинная закономерность в цепочке, выделим ее и определим, какой будет следующий цвет.

Как видишь, закономерность зависит от свойств элементов цепочки. Для одной и той же цепочки мы нашли различные закономерности в зависимости от свойства. Объединим полученные результаты и узнаем, какое звено будут следующим.

Алгоритм поиска закономерностей

Давайте еще раз повторим все шаги для выявления закономерностей.

1. Определяем количество свойств цепочки;
2. Определяем закономерность для каждого свойства;
3. Сопоставляем закономерности для определения всех свойств следующего звена в цепочке.

Поиск закономерностей – это очень хороший навык для юного математика. В будущем, когда ты будешь изучать цифры, тебе обязательно этот навык пригодится. Мы создали набор тестов, где ты сможешь потренироваться в поиске закономерностей. Попробуй пройти все тесты с хорошим результатом и двигайся дальше в изучении математики.