Составление плана решения задачи,
пожалуй, является главным шагом на пути
ее решения. Правильно составленный план
решения задачи почти гарантирует
правильное ее решение. Но составление
плана может оказаться сложным и длительным
процессом. Поэтому крайне необходимо
предлагать ученику ненавязчивые вопросы,
советы, помогающие ему лучше и быстрее
составить план решения задачи, “открыть”
идею ее решения:
а) Известна ли решающему какая-либо
родственная задача? Аналогичная задача?
Если такая или родственная задача
известна, то составление плана решения
задачи не будет затруднительным. Но
далеко не всегда известна задача,
родственная решаемой. В этом случае
может помочь в составлении плана решения
совет.
б) Подумайте, известна ли вам задача, к
которой можно свести решаемую. Если
такая задача известна решающему, то
путь составления плана решения данной
задачи очевиден: свести решаемую задачу
к решенной ранее. Может оказаться, что
родственная задача неизвестна решающему
и он не может свести данную задачу к
какой-либо известной. План же сразу
составить не удается.
Стоит воспользоваться советом:
“Попытайтесь сформулировать задачу
иначе”. Иными словами, попытайтесь
перефразировать задачу, не меняя ее
математического содержания.
При переформулировании задачи пользуются
либо определениями данных в ней
математических понятий (заменяют термины
их определениями), либо их признаками
(точнее сказать, достаточными условиями).
Надо отметить, что способность учащегося
переформулировать текст задачи является
показателем понимания математического
содержания задачи.
Некоторые авторы относят к переформулировке
задачи и перевод ее на язык математики,
т. е. язык алгебры, геометрии или анализа.
Это, скорее, формализация задачи,
“математизация” ее. К такому приему
и приходится часто прибегать при решении
многих текстовых задач.
в) Составляя план решения задачи, всегда
следует задавать себе (или решающему
задачу ученику) вопрос: “Все ли данные
задачи использованы?” Выявление
неучтенных данных задачи облегчает
составление плана ее решения.
г) При составлении плана задачи иногда
бывает полезно следовать совету:
“Попытайтесь преобразовать искомые
или данные”. Часто преобразование
искомых или данных способствует более
быстрому составлению плана решения.
При этом искомые преобразуют так, чтобы
они приблизились к данным, а данные –
так, чтобы они приблизились к искомым.
Так, при каждом случае тождественных
преобразований данные преобразуются,
постепенно приближаясь к результату
(искомому). Аналогично уравнение, систему
уравнений, неравенство или систему
неравенств преобразуют в равносильные,
чтобы найти их корни или множество
решений.
д) Нередко случается так, что, следуя
указанным выше советам, решающий задачу
все же не может составить план ее решения.
Тогда может помочь еще один совет:
“Попробуйте решить лишь часть задачи”,
т. е. попробуйте сначала удовлетворить
лишь части условий, с тем чтобы далее
искать способ удовлетворить оставшимся
условиям задачи.
е) Нередко в составлении плана решения
задачи помогает ответ на вопрос: “Для
какого частного случая возможно
достаточно быстро решить эту задачу?”
Обнаружив такой частный случай, решающий
ставит перед собой новую цель –
воспользоваться решением задачи в
найденном частном случае для более
общего (но, может быть, не самого общего)
случая. Так можно поступить, постепенно
обобщая задачу до исходной, решаемой
задачи. Предполагаемый вариант рассуждений
– явное применение полной индукции.
Итак, совет: “Рассмотрите частные
случаи задачной ситуации, решите задачу
для какого-нибудь частного случая,
примените индуктивные рассуждения”.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Образцы оформления задачи
В разделе “Задачи” мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
1. Задачи на нахождение суммы
В вопросе задач такого типа всегда есть “Сколько всего?”
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
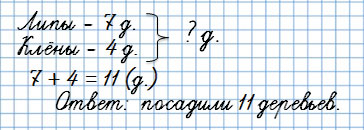
2. Задачи на нахождение остатка
В вопросе “Сколько … осталось?”
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
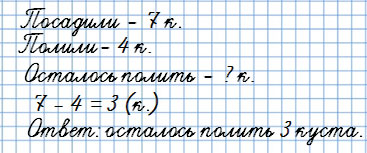
3. Задачи на увеличение или уменьшение числа на несколько единиц
В условии “на … больше”
Папа с Володей собирали грибы. Папа нашёл 8 грибов, а Володя на 3 гриба больше.
Сколько грибов нашёл Володя?
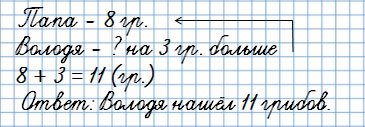
В условии “на … меньше”
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
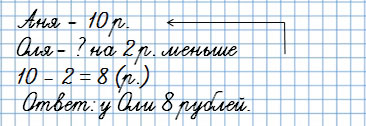
4. Задачи на разностное сравнение
В вопросе “На сколько больше…?”
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
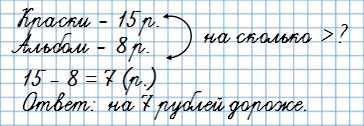
“На сколько меньше…?”
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
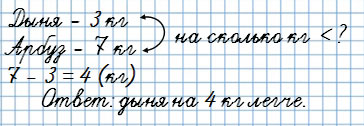
5. Задачи на нахождение неизвестного слагаемого
В условии “Было…Стало…”
В вопросе “Сколько добавили?”
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?

6. Задачи на нахождение неизвестного вычитаемого
В условии “Было… Осталось…”
В вопросе “Сколько уехало?”
“Сколько человек вышло?”
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?

7. Задачи на нахождение неизвестного уменьшаемого
В условии “Убрали… Осталось…”
В вопросе “Сколько было сначала?”
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?

Задачи в 2 и 3 действия
Первый вид
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
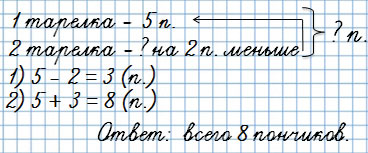
Второй вид
В классе два маленьких аквариума. В первом аквариуме 4 рыбки, а во втором – на 2 рыбки больше.
Сколько рыбок в двух аквариумах?
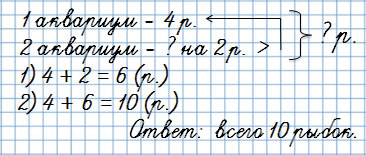
Третий вид
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?

Четвёртый вид
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
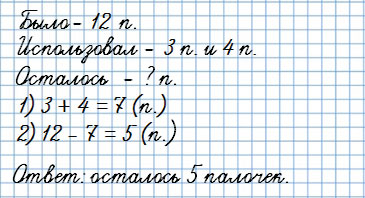
или
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
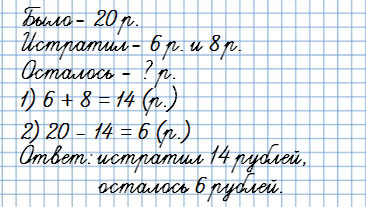
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?

II тип:
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?

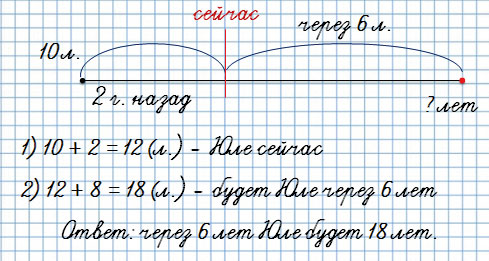
Задачи с составлением рисунка по условию:
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Советуем посмотреть:
Обратные задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 15,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 23,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 24,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 25,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 27,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 28,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 30,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 31,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 5,
Моро, Волкова, Рабочая тетрадь, часть 2
2 класс
Страница 54. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 60,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 110,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 45,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 50,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 46,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 69,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 75,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 33. ПР 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 56,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 64,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 12,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 20,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 79,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 38. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 47,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 57,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 61,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 90,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Номер 82,
Мерзляк, Полонский, Якир, Учебник
Номер 106,
Мерзляк, Полонский, Якир, Учебник
Номер 165,
Мерзляк, Полонский, Якир, Учебник
Номер 245,
Мерзляк, Полонский, Якир, Учебник
Номер 246,
Мерзляк, Полонский, Якир, Учебник
Номер 318,
Мерзляк, Полонский, Якир, Учебник
Номер 480,
Мерзляк, Полонский, Якир, Учебник
Номер 508,
Мерзляк, Полонский, Якир, Учебник
Номер 5,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 361,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 370,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 384,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 412,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 419,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 432,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 437,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 451,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 453,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Этапы работы над задачей
Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала.
Математические задачи отражают различные стороны жизни, несут много полезной информации, их решение является одним из звеньев в системе обучения и воспитания.
- Решение любой задачи – процесс сложной умственной деятельности. Чтобы овладеть им, надо знать основные этапы решения задачи.этап – ознакомление с содержанием задачи;
- этап – поиск решения задачи;
- этап – выполнение решения задачи;
- этап – проверка решения задачи.
- Ознакомление с содержанием задачи.
Ознакомиться с содержанием задачи – значит прочитать ее, представить жизненную ситуацию, отраженную в задаче. Читают задачу, как правило, дети. Учитель читает задачу лишь в тех случаях, когда у детей нет текста задачи или когда они еще не умеют читать. Очень важно научить детей правильно читать задачу: делать ударение на числовых данных и на словах, которые определяют выбор действий, таких как «было», «убрали», «осталось», «стало поровну» и т.п., выделять интонацией вопрос задачи. Если в тексте задачи встретятся непонятные слова, их надо пояснить или показать рисунки предметов, о которых говорится в задаче. Задачу дети читают один – два, а иногда и большее число раз, но постепенно их надо приучать к запоминанию задачи с одного чтения, так как в этом случае они будут читать задачу более сосредоточенно.
- Поиск решения задачи.
После ознакомления с содержанием задачи нужно приступить к поиску ее решения: ученики должны выделить величины, входящие в задачу, данные и искомые числа, установить связи между данными и искомыми и на этой основе выбрать соответствующие арифметические действия.
При введении задач нового вида поиском решения руководит учитель, а затем учащиеся выполняют это самостоятельно.
В том и другом случае используются специальные приемы, которые помогают детям вычленить величины, данные и искомые числа, установить связи между ними. К таким приемам относятся иллюстрация задачи, повторение задачи, разбор и составление плана решения задачи.
Рассмотрим каждый из этих приемов.
Иллюстрация задачи – это использование средств наглядности для вычисления величин, входящих в задачу, данных и искомых чисел, а также для установления связей между ними. Иллюстрация может быть предметной или схематичной. Предметная иллюстрация помогает создать яркое представление той жизненной ситуации, которая описывается в задаче. Ею пользуются только при ознакомлении с решением задач нового вида и преимущественно в 1 классе. Для иллюстрации задачи используются либо предметы, либо рисунки предметов, о которых идет речь в задаче: с их помощью иллюстрируется конкретное содержание задачи.
Наряду с предметной иллюстрацией, начиная с 1 класса, используется и схематическая – это краткая запись задачи.
- При изучении свойств арифметических действий наиболее удобным является словесная краткая запись
Было – 6 книг и 7 книг
Взяли – 4 книги
Осталось – ?
- При решении многих составных задач, особенно в 1 классе, используется следующий вид краткой записи
Коля – 4 рыбки
Вася – ? на 2 больше )?
- При решении задач на зависимость между тройками величин используют табличную краткую запись
|
Скорость |
Время |
Расстояние |
|
одинаковая |
3 ч |
24 км |
|
5 ч |
- Чертёж составляется при решении задачи на движение
- Схематическая краткая запись
Используя иллюстрацию, краткую запись, чертёж ученики могут повторить задачу. При повторении лучше, чтобы дети объясняли, что показывает каждое число и что требуется узнать в задаче.
- Назовите величины в условии задачи.
- Что обозначает число…?
- Что сказано про …?
- Какой вопрос задачи?
При ознакомлении с задачей нового вида, как правило, используется какая- либо одна иллюстрация, но в отдельных случаях полезно выполнить предметную и схематичную иллюстрацию.
В процессе выполнения иллюстрации некоторые дети находят решение задачи, то есть они уже знают, какие действия надо выполнить, чтобы решить задачу. Однако часть детей может установить связи между данными и искомыми выбрать соответствующее арифметическое действие только с помощью учителя. В этом случае учитель проводит специальную беседу, которая называется разбором задачи.
Рассуждение можно строить двумя способами: идти от вопроса задачи к числовым данным (анализ) или же от числовых данных идти к вопросу (синтез).
Чаще следует использовать первый способ рассуждения, так как при этом ученик должен иметь в виду не одно выделенное действие, а все решение в целом. При использовании второго способа разбора учитель прямо подводит их к выбору каждого действия. Кроме того, такое рассуждение может привести к выбору «лишних действий».
Разбор составной задачи заканчивается составлением плана решения – это объяснение того, что узнаем, выполнив то или иное действие, и указание по порядку арифметических действий.
3. Решение задачи.
Решение задачи – это выполнение арифметических действий, выбранных при составлении плана решения. При этом обязательны пояснения, что находим, выполняя каждое действие. Надо учить детей правильно и кратко давать пояснения к выполняемым действиям.
Около школы посадили 8 лип, а берёз на 2 меньше, чем лип. Сколько всего деревьев посадили около школы?
В начальных классах могут быть использованы такие основные формы записи решения:
- Составление по задаче выражения и нахождение его значения;
(8+2) +8=18(д.)
Ответ: 18 деревьев посадили около школы.
- Запись решения в виде отдельных действий с пояснением или без них;
1)8+2=10(д.) – берёзы.
2)10+8=18(д.) – посадили всего.
Ответ: 18 деревьев.
1)8+2=10(д.)
2)10+8=18(д.)
Ответ: 18 деревьев посадил около школы.
- Запись решения по действиям с вопросами;
- Сколько посадили берёз?
8+2=10(д.)
- Сколько всего деревьев посадили около школы?
10+8=18(д.)
Ответ: 18 деревьев
4.Проверка решения задач.
Проверить решение задачи – значит установить, что оно правильно или ошибочно.
В начальных классах используются следующие четыре способа проверки:
- Составление и решение обратной задачи. В этом случае детям предлагается составить задачу, обратную по отношению к данной: то есть преобразовать данную задачу так, чтобы искомое данной задачи стало данным числом, а одно из данных чисел стало искомым.
Володя поймал 4 окуня и 3 леща. Сколько всего рыб поймал Володя?
4+3=7(р.)
Ответ: 7 рыб поймал Володя.
Володя поймал 7 рыб, из них 4 окуня. Сколько лещей поймал Володя?
7-4=3(л.)
Ответ: 3 леща поймал Володя.
Если при решении обратной задачи в результате получится число, которое было известно в данной задаче, то можно считать, что данная задача решена правильно.
- Установление соответствия между числами, полученными в результате решения задачи, и данными числами. При проверке решения задачи этим способом выполняют арифметические действия над числами, которые получаются в ответе на вопрос задачи, если при этом получатся числа, данные в условии задачи, то можно считать, что задача решена правильно.
Школьники собрали три мешка картофеля всего 115 кг. Они взвесили первый и второй мешки, получили102 кг, взвесили второй и третий мешки, получили 99 кг. Сколько кг картофеля было в каждом мешке?
153-102=51 (кг) – масса третьего мешка.
99-51=48(кг) – масса второго мешка.
102-48=54(кг) – масса первого мешка.
Проверка:
54+48+51=153(кг) – масса трёх мешков.
54+48=102(кг) – масса первого и второго мешков.
51+48=99(кг) – масса второго и третьего мешков.
- Решение задачи другим способом. Если задачу можно решать различными способами, то получение одинаковых результатов подтверждает, что задача решена правильно.
В буфете было 12 чашек. Из этих чашек на стол поставили сначала 4 чашки, а потом ещё 3 чашки. Сколько чашек осталось в буфете?
1 способ:
12-4-3=5(ч.)
2 способ:
12-(4+3)=5(ч.)
- Установление границ искомого числа или прикидка ответа – то есть до решения задачи устанавливается больше или меньше какого-то из данных чисел должно быть искомое число.
В мешке было 30 кг картофеля. После того как несколько кг продали, в мешке осталось 10 кг. Сколько кг картофеля продали?
Ответ задачи должен быть меньше 30.
Для выработки навыков самостоятельного решения задачи необходимо иметь памятку работы над задачей.
«Как решить задачу»
1. Прочитай задачу и представь себе то, о чем в ней говорится.
2. Выдели условие и вопрос.
3. Запиши условие кратко или выполни чертёж.
4.Подумай можно ли сразу ответить на вопрос задачи. Если нет, то почему. Что надо узнать сначала, что потом?
5. Составь план решения.
6. Выполни решение.
7. Проверь решение и запиши ответ задачи.
Из вышесказанного можно сделать вывод, что задачи выполняют очень важную функцию в начальном курсе математики — они являются полезным средством развития у детей логического мышления.
Приступая к работе над задачей, необходимо учить ребенка внимательно читать задачу, понимать смысл прочитанного, пересказывать содержание, подмечать, какие события произошли в задаче: что было, что изменилось, что стало; объяснять, что обозначает каждое число в задаче, в чем суть тех или других математических выражений.
Понимая роль задачи и её место в обучении и воспитании ученика, учитель должен подходить к подбору задачи и выбору способов решения обоснованно и чётко знать, что должна дать ученику работа при решении данной им задачи.
Ведь задача способствует воспитанию терпения, настойчивости, воли, способствует пробуждению интереса к самому процессу поиска решения, дает возможность испытать глубокое удовлетворение, связанное с удачным решением.
Математика, 2 класс
Урок № 34. Решение задач.
Перечень вопросов, рассматриваемых в теме:
– Как составить план решения задачи?
Глоссарий по теме:
Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.
Выражение – формула, выражающая какие–либо математические отношения.
Схема – своеобразный чертёж, в котором составные части — его элементы и связи между ними изображены условно, без соблюдения масштаба.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –5-е изд. – М.: Просвещение, 2014. – с.10, 11.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.7, 8.
- Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.18.
Математика. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. С. И. Волкова – М.: Просвещение, 2017. – с.41.
Теоретический материал для самостоятельного изучения
Посмотрите на эти изображения. Знакомы ли нам они? Да, это схемы задач.


Мы умеем составлять схемы к задачам и по схемам находить задачу.
Определим, какая схема подходит к задаче.
В этой задаче мы находим целое.
Подходит такая схема.

Выберем схему ко второй задаче.
В этой задаче мы находим часть
от целого. Подходит данная схема.
И к последней схеме мы составим такую задачу: 

Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?
Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?
Рассмотрите такую схему. 
Знакома ли она вам? С такими схемами мы ещё не встречались. Это схемы рассуждения при поиске решения задачи. Составим схему рассуждения при решении уже известной нам задачи. «Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?». Для решения задачи начнём рассуждать от вопроса, составляя при этом схему. Что нужно найти в задаче? «Сколько всего рыб поймал папа?»
Ставим в схеме знак вопроса.
Что для этого достаточно знать?
Верно, нужно знать, сколько и каких рыб поймал папа.

 Это окуни и лещи. Ставим числа 8 и 6,
Это окуни и лещи. Ставим числа 8 и 6,
рисуем стрелки к вопросу.
Можем ли мы ответить на вопрос задачи?
Да.
8 + 6 = 14 (р.) поймал папа
Попробуем составить схему рассуждения к более сложной задаче.
«Папа поймал на рыбалке 8 окуней, а сын на 2 рыбы меньше. Сколько всего рыб поймали папа и сын?».
 Что нужно узнать в задаче? «Сколько всего рыб поймали папа и сын?»
Что нужно узнать в задаче? «Сколько всего рыб поймали папа и сын?»
Ставим в схеме знак вопроса.
Что для этого достаточно знать?
Верно, нужно знать сколько рыб поймал папа
и сколько рыб поймал сын. Рисуем два круга и стрелки к вопросу.
 Что из этого мы знаем, а что нужно найти?Правильно, мы знаем сколько рыб поймал папа. Ставим число восемь в схему.
Что из этого мы знаем, а что нужно найти?Правильно, мы знаем сколько рыб поймал папа. Ставим число восемь в схему.
Но мы не знаем, сколько рыб поймал сын.
Ставим знак вопроса.
 Что нужно знать, чтобы сосчитать рыб, которых поймал сын?
Что нужно знать, чтобы сосчитать рыб, которых поймал сын?
Нужно знать количество рыб у папы и
на сколько меньше поймал рыб сын.
Рисуем два круга и стрелки к вопросу.
Ставим в схему числа восемь и два.
Каким будет первое действие? Узнаем, сколько рыб поймал сын.
1) 8 – 2 = 6 (р.) поймал сын.
Ответили мы на вопрос задачи? Нет. Каким будет второе действие?
Узнаем, сколько всего рыб поймали папа и сын.
2) 8 + 6 = 14 (р.) поймали всего.
Вывод: Для выбора способа решения задачи, мы выстраиваем цепочку рассуждения. Её можно представить в виде схемы. Составляя схему рассуждения «от вопроса к данным», мы отвечаем на такие вопросы: «Что достаточно знать, чтобы ответить на вопрос задачи? Что мы знаем уже? Как найти то, что ещё неизвестно?». Текст задачи можно моделировать разными способами: в виде схематического чертежа, таблицы, диаграммы.
Тренировочные задания.
1.Выберите схему рассуждения, подходящую к задаче «Юра съел 9 конфет, а Коля на 4 конфеты меньше. Сколько конфет съели мальчики?» 

Правильные ответы:

2. Дополните диаграмму данными из текста.
Сел Миша на пенёк, съел пирожок… А ещё две баранки, пять пончиков и девять яблок.

Правильные ответы:
