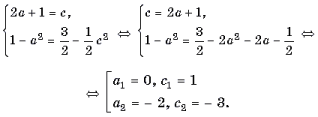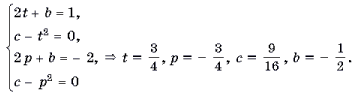Как составьте уравнение касательной к графику функции в точке

Уравнение касательной к графику функции

2 апреля 2011

Пусть дана функция f, которая в некоторой точке x₀ имеет конечную производную f (x₀). Тогда прямая, проходящая через точку (x₀; f (x₀)), имеющая угловой коэффициент f ’(x₀), называется касательной.

А что будет, если производная в точке x₀ не существует? Возможны два варианта:

1. Касательная к графику тоже не существует. Классический пример — функция y = |x| в точке (0; 0).
2. Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π/2).

Уравнение касательной

Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x₀, достаточно знать значение функции и производной в этой точке.

Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x₀ ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:

y = f ’(x₀) · (x − x₀) + f (x₀)

Здесь f ’(x₀) — значение производной в точке x₀, а f (x₀) — значение самой функции.

Задача. Дана функция y = x³. Составить уравнение касательной к графику этой функции в точке x₀ = 2.

Уравнение касательной: y = f ’(x₀) · (x − x₀) + f(x₀). Точка x₀ = 2 нам дана, а вот значения f (x₀) и f ’(x₀) придется вычислять.

Для начала найдем значение функции. Тут все легко: f (x₀) = f (2) = 2³ = 8;
Теперь найдем производную: f ’(x) = (x³)’ = 3x²;
Подставляем в производную x₀ = 2: f ’(x₀) = f ’(2) = 3 · 2² = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.

Задача. Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x₀ = π/2.

В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:

f (x₀) = f (π/2) = 2sin (π/2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f ’(x₀) = f ’(π/2) = 2cos (π/2) = 0;

Уравнение касательной:

y = 0 · (x − π/2) + 7 ⇒ y = 7

В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.

Смотрите также:

1. Правила вычисления производных
2. Вводный урок по вычислению производных степенной функции
3. Что такое логарифм
4. Тест к уроку «Площади многоугольников без координатной сетки» (легкий)
5. Текстовые задачи про рельсы
6. Задача B4: Семья из трех человек едет из Москвы в Нижний Новгород

п.1. Уравнение касательной

Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin{gather*} (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end{gather*}

Уравнение касательной к кривой (y=f(x)) в точке (x_0) имеет вид: $$ y=f'(x_0)(x-x_0)+f(x_0) $$ при условии, что производная (f'(x_0)=aneinfty) – существует и конечна.

Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace{f'(x_0)}_{=k}x+underbrace{f(x_0)-f'(x_0)cdot x_0}_{=b} $$

Уравнение касательной с угловым коэффициентом: begin{gather*} y=kx+b\ k=f'(x_0), b=f(x_0)-f'(x_0)cdot x_0 end{gather*}

п.2. Алгоритм построения касательной

п.3. Вертикальная касательная

В случае, если производная (f'(x_0)=pminfty) – существует, но бесконечна, в точке (x_0) проходит вертикальная касательная (x=x_0).

п.4. Примеры

Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)

Пример 2. Напишите уравнение касательной к графику функции в заданной точке:
a) ( f(x)=frac5x+frac x5, x_0=4 ) begin{gather*} f(x_0)=frac54+frac45=frac{25+16}{20}=frac{41}{20}\ f'(x)=left(frac5xright)’+left(frac x5right)’=-frac{5}{x^2}+frac15=frac{-25+x^2}{5x^2}=frac{x^2-25}{5x^2}\ f'(x_0)=frac{4^2-25}{5cdot 4^2}=-frac{9}{80} end{gather*} Уравнение касательной: $$ y=-frac{9}{80}(x-4)+frac{41}{20}=-frac{9}{80}x+frac{9}{20}+frac{41}{20}=-frac{9}{80}x+2,5 $$
б) ( f(x)=frac{x^2+5}{3-x}, x_0=2 ) begin{gather*} f(x_0)=frac{2^2+5}{3-2}=frac91=9\ f'(x)=frac{(x^2+5)'(3-x)-(x^2+5)(3-x)’}{(3-x)^2}=frac{2x(3-x)+(x^2+5)}{(3-x)^2}=\ =frac{6x-2x^2+x^2+5}{(3-x)^2}=frac{-x^2+6x+5}{(3-x)^2}\ f'(x_0)=frac{-2^2+6cdot 2+5}{(3-2)^2}=13 end{gather*} Уравнение касательной: $$ y=13(x-2)+9=13x-26+9=13x-17 $$

Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin{gather*} 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac{0,4}{2}=-0,2 end{gather*} Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt{0,4^2+(-0,2)^2}=0,2sqrt{2^2+1^2}=frac{sqrt{5}}{5})
Ответ: (frac{sqrt{5}}{5})

Уравнение касательной к графику функции

П. Романов, Т. Романова,
г. Магнитогорск,
Челябинская обл.

Уравнение
касательной к графику функции

Статья опубликована при поддержке Гостиничного комплекса «ИТАКА+». Останавливаясь в городе судостроителей Северодвинске, вы не столкнетесь с проблемой поиска временного жилья. Тут, на сайте гостиничного комплекса «ИТАКА+» http://itakaplus.ru, вы сможете легко и быстро снять квартиру в городе, на любой срок, с посуточной оплатой.

На современном этапе развития
образования в качестве одной из основных его
задач выступает формирование творчески мыслящей
личности. Способность же к творчеству у учащихся
может быть развита лишь при условии
систематического привлечения их к основам
исследовательской деятельности. Фундаментом для
применения учащимися своих творческих сил,
способностей и дарований являются
сформированные полноценные знания и умения. В
связи с этим проблема формирования системы
базовых знаний и умений по каждой теме школьного
курса математики имеет немаловажное значение.
При этом полноценные умения должны являться
дидактической целью не отдельных задач, а
тщательно продуманной их системы. В самом
широком смысле под системой понимается
совокупность взаимосвязанных взаимодействующих
элементов, обладающая целостностью и устойчивой
структурой.

Рассмотрим методику обучения
учащихся составлению уравнения касательной к
графику функции. По существу, все задачи на
отыскание уравнения касательной сводятся к
необходимости отбора из множества (пучка,
семейства) прямых тех из них, которые
удовлетворяют определенному требованию
– являются касательными к графику некоторой
функции. При этом множество прямых, из которого
осуществляется отбор, может быть задано двумя
способами:

а) точкой, лежащей на
плоскости xOy (центральный пучок прямых);
б) угловым коэффициентом (параллельный пучок
прямых).

В связи с этим при изучении
темы «Касательная к графику функции» с целью
вычленения элементов системы нами были выделены
два типа задач:

1) задачи на касательную,
заданную точкой, через которую она проходит;
2) задачи на касательную, заданную ее угловым
коэффициентом.

Обучение решению задач на
касательную осуществлялось при помощи
алгоритма, предложенного А.Г. Мордковичем [2].
Его принципиальное отличие от уже известных
заключается в том, что абсцисса точки касания
обозначается буквой a (вместо x0), в связи с чем
уравнение касательной приобретает вид

y = f(a) + f ‘(a)(x – a)

(сравните с y = f(x₀) + f ‘(x₀)(x
– x₀)). Этот методический прием, на наш
взгляд, позволяет учащимся быстрее и легче
осознать, где в общем уравнении касательной
записаны координаты текущей точки, а где
– точки касания.

Алгоритм
составления уравнения касательной к графику
функции y = f(x)

1. Обозначить буквой a
абсциссу точки касания.
2. Найти f(a).
3. Найти f ‘(x) и f ‘(a).
4. Подставить найденные числа a, f(a), f ‘(a) в
общее уравнение касательной y = f(a) = f ‘(a)(x – a).

Этот алгоритм может быть
составлен на основе самостоятельного выделения
учащимися операций и последовательности их
выполнения.

Практика показала, что
последовательное решение каждой из ключевых
задач при помощи алгоритма позволяет
формировать умения написания уравнения
касательной к графику функции поэтапно, а шаги
алгоритма служат опорными пунктами действий.
Данный подход соответствует теории поэтапного
формирования умственных действий, разработанной
П.Я. Гальпериным и Н.Ф. Талызиной [3].

В первом типе задач были
выделены две ключевые задачи:

• касательная проходит через
  точку, лежащую на кривой (задача 1);
• касательная проходит через
  точку, не лежащую на кривой (задача 2).

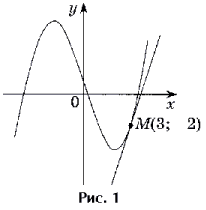Задача 1. Составьте уравнение
касательной к графику функции в точке M(3; – 2).

Решение. Точка M(3; – 2)
является точкой касания, так как

1. a = 3 – абсцисса точки
касания.
2. f(3) = – 2.
3. f ‘(x) = x² – 4, f ‘(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – уравнение
касательной.

Задача 2. Напишите уравнения
всех касательных к графику функции y = – x²
– 4x + 2, проходящих через точку M(– 3; 6).

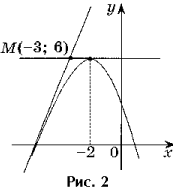Решение. Точка M(– 3; 6) не
является точкой касания, так как f(– 3) ­ 6 (рис. 2).

1. a – абсцисса точки
касания.
2. f(a) = – a² – 4a + 2.
3. f ‘(x) = – 2x – 4, f ‘(a) = – 2a – 4.
4. y = – a² – 4a + 2 – 2(a + 2)(x – a)
– уравнение касательной.

Касательная проходит через
точку M(– 3; 6), следовательно, ее координаты
удовлетворяют уравнению касательной.

6 = – a² – 4a + 2 – 2(a +
2)(– 3 – a),
a² + 6a + 8 = 0 ^ a₁ = – 4, a₂ = – 2.

Если a = – 4, то уравнение
касательной имеет вид y = 4x + 18.

Если a = – 2, то уравнение
касательной имеет вид y = 6.

Во втором типе ключевыми
задачами будут следующие:

• касательная параллельна
  некоторой прямой (задача 3);
• касательная проходит под
  некоторым углом к данной прямой (задача 4).

Задача 3. Напишите уравнения
всех касательных к графику функции y = x³ – 3x²
+ 3, параллельных прямой y = 9x + 1.

Решение.

1. a – абсцисса точки
касания.
2. f(a) = a³ – 3a² + 3.
3. f ‘(x) = 3x² – 6x, f ‘(a) = 3a² – 6a.

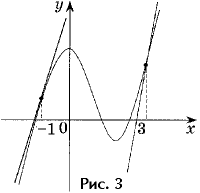Но, с другой стороны, f ‘(a) = 9
(условие параллельности). Значит, надо решить
уравнение 3a² – 6a = 9. Его корни a = – 1, a = 3
(рис. 3).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f ‘(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – уравнение
касательной;

1) a = 3;
2) f(3) = 3;
3) f ‘(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – уравнение
касательной.

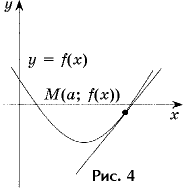Задача 4. Напишите уравнение
касательной к графику функции y = 0,5x² – 3x + 1,
проходящей под углом 45° к прямой y = 0 (рис. 4).

Решение. Из условия f ‘(a) =
tg 45° найдем a:  a – 3 = 1 ^ a = 4.

1. a = 4 – абсцисса точки
касания.
2. f(4) = 8 – 12 + 1 = – 3.
3. f ‘(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – уравнение
касательной.

Несложно показать, что
решение любой другой задачи сводится к решению
одной или нескольких ключевых задач. Рассмотрим
в качестве примера следующие две задачи.

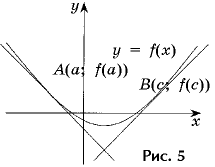1. Напишите уравнения
касательных к параболе y = 2x² – 5x – 2, если
касательные пересекаются под прямым углом и одна
из них касается параболы в точке с абсциссой 3
(рис. 5).

Решение. Поскольку дана
абсцисса точки касания, то первая часть решения
сводится к ключевой задаче 1.

1. a = 3 – абсцисса точки
касания одной из сторон прямого угла.
2. f(3) = 1.
3. f ‘(x) = 4x – 5, f ‘(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – уравнение первой
касательной.

Пусть a – угол наклона первой
касательной. Так как касательные
перпендикулярны, то – угол наклона второй касательной. Из
уравнения y = 7x – 20 первой касательной имеем tg a = 7. Найдем

Это значит, что угловой
коэффициент второй касательной равен .

Дальнейшее решение сводится к
ключевой задаче 3.

Пусть B(c; f(c)) есть точка
касания второй прямой, тогда

1.  – абсцисса второй точки касания.
2. 
3. 
4. 
– уравнение
второй касательной.

Примечание. Угловой
коэффициент касательной может быть найден проще,
если учащимся известно соотношение
коэффициентов перпендикулярных прямых k₁•k₂
= – 1.

2. Напишите уравнения всех
общих касательных к графикам функций

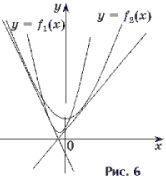Решение. Задача сводится к
отысканию абсцисс точек касания общих
касательных, то есть к решению ключевой задачи 1 в
общем виде, составлению системы уравнений и
последующему ее решению (рис. 6).

1. Пусть a – абсцисса
точки касания, лежащей на графике функции y = x²
+ x + 1.
2. f(a) = a² + a + 1.
3. f ‘(a) = 2a + 1.
4. y = a² + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a².

1. Пусть c – абсцисса
точки касания, лежащей на графике функции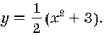  
2.
3. f ‘(c) = c.
4. 

Так как касательные общие, то

Итак, y = x + 1 и y = – 3x – 3
– общие касательные.

Основная цель рассмотренных
задач – подготовить учащихся к
самостоятельному распознаванию типа ключевой
задачи при решении более сложных задач,
требующих определенных исследовательских
умений (умения анализировать, сравнивать,
обобщать, выдвигать гипотезу и т. д.). К числу
таких задач можно отнести любую задачу, в которую
ключевая задача входит как составляющая.
Рассмотрим в качестве примера задачу (обратную
задаче 1) на нахождение функции по семейству ее
касательных.

3. При каких b и c прямые y = x и
y = – 2x являются касательными к графику функции
y = x² + bx + c?

Решение.

Пусть t – абсцисса точки
касания прямой y = x с параболой y = x² + bx + c; p
– абсцисса точки касания прямой y = – 2x с
параболой y = x² + bx + c. Тогда уравнение
касательной y = x примет вид y = (2t + b)x + c – t², а
уравнение касательной y = – 2x примет вид y = (2p +
b)x + c – p².

Составим и решим систему
уравнений

Ответ:

 Задачи для
самостоятельного решения

1. Напишите уравнения
касательных, проведенных к графику функции y = 2x²
– 4x + 3 в точках пересечения графика с прямой y = x +
3.

Ответ: y = – 4x + 3, y = 6x – 9,5.

2. При каких значениях a
касательная, проведенная к графику функции y = x²
– ax в точке графика с абсциссой x₀ = 1,
проходит через точку M(2; 3)?

Ответ: a = 0,5.

3. При каких значениях p
прямая y = px – 5 касается кривой y = 3x² – 4x – 2?

Ответ: p₁ = – 10, p₂
= 2.

4. Найдите все общие точки
графика функции y = 3x – x³ и касательной,
проведенной к этому графику через точку P(0; 16).

Ответ: A(2; – 2), B(– 4; 52).

5. Найдите кратчайшее
расстояние между параболой y = x² + 6x + 10 и
прямой

Ответ:

6. На кривой y = x² – x + 1
найдите точку, в которой касательная к графику
параллельна прямой y – 3x + 1 = 0.

Ответ: M(2; 3).

7. Напишите уравнение
касательной к графику функции y = x² + 2x –
| 4x |, которая касается его в двух точках.
Сделайте чертеж.

Ответ: y = 2x – 4.

8. Докажите, что прямая y = 2x
– 1 не пересекает кривую y = x⁴ + 3x² + 2x.
Найдите расстояние между их ближайшими точками.

Ответ:

9. На параболе y = x²
взяты две точки с абсциссами x₁ = 1, x₂ = 3.
Через эти точки проведена секущая. В какой точке
параболы касательная к ней будет параллельна
проведенной секущей? Напишите уравнения секущей
и касательной.

Ответ: y = 4x – 3 – уравнение
секущей; y = 4x – 4 – уравнение касательной.

10. Найдите угол q между касательными
к графику функции y = x³ – 4x² + 3x + 1,
проведенными в точках с абсциссами 0 и 1.

Ответ: q = 45°.

11. В каких точках
касательная к графику функции образует с осью Ox угол в 135°?

Ответ: A(0; – 1), B(4; 3).

12. В точке A(1; 8) к кривой 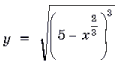проведена
касательная. Найдите длину отрезка касательной,
заключенного между осями координат.

Ответ:

13. Напишите уравнение всех
общих касательных к графикам функций y = x² –
x + 1 и y = 2x² – x + 0,5.

Ответ: y = – 3x и y = x.

14. Найдите расстояние между
касательными к графику функции параллельными оси абсцисс.

Ответ:

15. Определите, под какими
углами парабола y = x² + 2x – 8 пересекает ось
абсцисс.

Ответ: q₁ = arctg 6, q₂ = arctg (– 6).

16. На графике функции найдите все
точки, касательная в каждой из которых к этому
графику пересекает положительные полуоси
координат, отсекая от них равные отрезки.

Ответ: A(– 3; 11).

17. Прямая y = 2x + 7 и парабола y
= x² – 1 пересекаются в точках M и N. Найдите
точку K пересечения прямых, касающихся параболы в
точках M и N.

Ответ: K(1; – 9).

18. При каких значениях b
прямая y = 9x + b является касательной к графику
функции y = x³ – 3x + 15?

Ответ: – 1; 31.

19. При каких значениях k
прямая y = kx – 10 имеет только одну общую точку с
графиком функции y = 2x² + 3x – 2? Для найденных
значений k определите координаты точки.

Ответ: k₁ = – 5, A(– 2;
0); k₂ = 11, B(2; 12).

20. При каких значениях b
касательная, проведенная к графику функции y = bx³
– 2x² – 4 в точке с абсциссой x₀ = 2,
проходит через точку M(1; 8)?

Ответ: b = – 3.

21. Парабола с вершиной на
оси Ox касается прямой, проходящей через точки A(1;
2) и B(2; 4), в точке B. Найдите уравнение параболы.

Ответ:

22. При каком значении
коэффициента k парабола y = x² + kx + 1 касается
оси Ox?

Ответ: k = д 2.

23. Найдите углы между
прямой y = x + 2 и кривой y = 2x² + 4x – 3.

Ответ:

24. Определите, под какими
углами пересекаются графики функций y = 2x² +
3x – 3 и y = x² + 2x + 3.

Ответ:

25. При каком значении k угол
между кривыми y = x² + 2x + k и y = x² + 4x + 4
будет равен 45°?

Ответ: k = – 3.

26. Найдите все значения x0,
при каждом из которых касательные к графикам
функции y = 5cos 3x + 2 и y = 3cos 5x в точках в
абсциссой x₀ параллельны.

Ответ:

27. Под каким углом видна
окружность x² + y² = 16 из точки (8; 0)?

Ответ:

28. Найдите геометрическое
место точек, из которых парабола y = x² видна
под прямым углом?

Ответ: прямая

29. Найдите расстояние между
касательными к графику функции образующими с
положительным направлением оси Ox угол 45°.

Ответ:

30. Найдите геометрическое
место вершин всех парабол вида y = x² + ax + b,
касающихся прямой y = 4x – 1.

Ответ: прямая y = 4x + 3.

Литература

1. Звавич Л.И., Шляпочник Л.Я.,
Чинкина М.В. Алгебра и начала анализа: 3600 задач
для школьников и поступающих в вузы. – М., Дрофа,
1999.
2. Мордкович А. Семинар четвертый для молодых
учителей. Тема «Приложения производной». – М.,
«Математика», № 21/94.
3. Формирование знаний и умений на основе
теории поэтапного усвоения умственных действий.
/ Под ред. П.Я. Гальперина, Н.Ф. Талызиной.
– М., МГУ, 1968.

Геометрический смысл производной

Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!

Рассмотрим график какой-то функции ( y=fleft( x right)):

Выберем на линии графика некую точку ( A). Пусть ее абсцисса ( {{x}_{0}}), тогда ордината равна ( fleft( {{x}_{0}} right)).

Затем выберем близкую к точке ( A) точку ( B) с абсциссой ( {{x}_{0}}+Delta x); ее ордината – это ( fleft( {{x}_{0}}+Delta x right)):

Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).

Обозначим угол наклона прямой к оси ( Ox) как ( alpha ).

Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.

Какие значения может принимать угол ( alpha )?

Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – ( 180{}^circ ), а минимально возможный – ( 0{}^circ ).

Значит, ( alpha in left[ 0{}^circ ;180{}^circ right)). Угол ( 180{}^circ ) не включается, поскольку положение прямой в этом случае в точности совпадает с ( 0{}^circ ), а логичнее выбирать меньший угол.

Возьмем на рисунке такую точку ( C), чтобы прямая ( AC) была параллельна оси абсцисс, а ( BC) – ординат:

По рисунку видно, что ( AC=Delta x), а ( BC=Delta f).

Тогда отношение приращений:

Давай теперь уменьшать ( Delta x).

Тогда точка ( B) будет приближаться к точке ( A). Когда ( Delta x) станет бесконечно малым ( left( Delta xto 0 right)), отношение ( frac{Delta f}{Delta x}) станет равно производной функции в точке ( {{x}_{0}}).

Что же при этом станет с секущей?

Точка ( B) будет бесконечно близка к точке ( A), так что их можно будет считать одной и той же точкой.

Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки ( A), но этого достаточно).

Говорят, что при этом секущая занимает предельное положение.

Угол наклона секущей к оси ( displaystyle Ox) назовем ( varphi ). Тогда получится, что производная

( {f}’left( {{x}_{0}} right)underset{Delta xto 0}{mathop{=}},frac{Delta f}{Delta x}= {tg}varphi ),

то есть

Производная равна тангенсу угла наклона касательной к графику функции в данной точке

Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:

( y=kx+b).

За что отвечает коэффициент ( displaystyle k)? За наклон прямой. Он так и называется: угловой коэффициент.

Что это значит? А то, что равен он тангенсу угла между прямой и осью ( displaystyle Ox)!

То есть вот что получается:

( {f}’left( {{x}_{0}} right)= {tg}varphi =k).

Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?

Посмотрим: Теперь углы ( alpha ) и ( displaystyle varphi ) тупые. А приращение функции ( Delta f) – отрицательное.

Снова рассмотрим ( triangle ABC): ( angle B=180{}^circ -alpha text{ }Rightarrow text{ } {tg}angle B=- {tg}alpha ).

С другой стороны, ( {tg}angle B=frac{AC}{BC}=frac{-Delta f}{Delta x}).

Получаем: ( frac{-Delta f}{Delta x}=- {tg}alpha text{ }Rightarrow text{ }frac{Delta f}{Delta x}= {tg}alpha ), то есть все, как и в прошлый раз.

Снова устремим точку ( displaystyle B) к точке ( displaystyle A), и секущая ( displaystyle AB) примет предельное положение, то есть превратится в касательную к графику функции в точке ( displaystyle A).

Итак, сформулируем окончательно полученное правило:

Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:

( {f}’left( {{x}_{0}} right)= {tg}varphi =k)

Это и есть геометрический смысл производной.

Окей, все это интересно, но зачем оно нам? Вот пример:

На рисунке изображен график функции ( displaystyle y=mathsf{f}left( x right)) и касательная к нему в точке с абсциссой ( {{x}_{0}}).

Найдите значение производной функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}).

Решение.

На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!

Таким образом, производная функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}) равна ( displaystyle 1,2).

Ответ: ( displaystyle 1,2).

Теперь попробуй сам.

Уравнение касательной к графику функций

А сейчас сосредоточимся на произвольных касательных.

Предположим, у нас есть какая-то функция, например, ( fleft( x right)=left( {{x}^{2}}+2 right)). Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке ( {{x}_{0}}). Например, в точке ( {{x}_{0}}=2).

Берем линейку, пристраиваем ее к графику и чертим:

Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости?

Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты ( k) и ( b) в уравнении

( y=kx+b).

Но ведь ( k) мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:

( k={f}’left( {{x}_{0}} right)).

В нашем примере будет так:

( {f}’left( x right)={{left( {{x}^{2}}+2 right)}^{prime }}=2x;)

Графически ( b) – это координата пересечения прямой с осью ординат (ведь ( displaystyle x=0) во всех точках оси ( displaystyle Oy)):

Проведём ( BCparallel Ox) (так, что ( triangle ABC) – прямоугольный).

Тогда ( angle ABC=alpha )(тому самому углу между касательной и осью абсцисс). Чему равны ( displaystyle AC) и ( displaystyle BC)?

По рисунку явно видно, что ( BC={{x}_{0}}), а ( AC=fleft( {{x}_{0}} right)-b). Тогда получаем:

( {f}’left( {{x}_{0}} right)= {tg}alpha =frac{AC}{BC}=frac{fleft( {{x}_{0}} right)-b}{{{x}_{0}}}text{ }Rightarrow text{ }b=fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right)).

Соединяем все полученные формулы в уравнение прямой:

( y=kx+b={f}’left( {{x}_{0}} right)cdot x+fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right);)

Пример:

Найди уравнение касательной к графику функции ( fleft( x right)={{x}^{2}}-2x+3) в точке ( {{x}_{0}}=3).

Решение:

На этом примере выработаем простой…

Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике

ЕГЭ №7. Производная функции — геометрический смысл, дифференцирование

На этом видео мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5. 

Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ. Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.  

Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.

P.S. Не забудьте потом посмотреть родственную тему: «Интегралы на ЕГЭ. Первообразные элементарных функций».