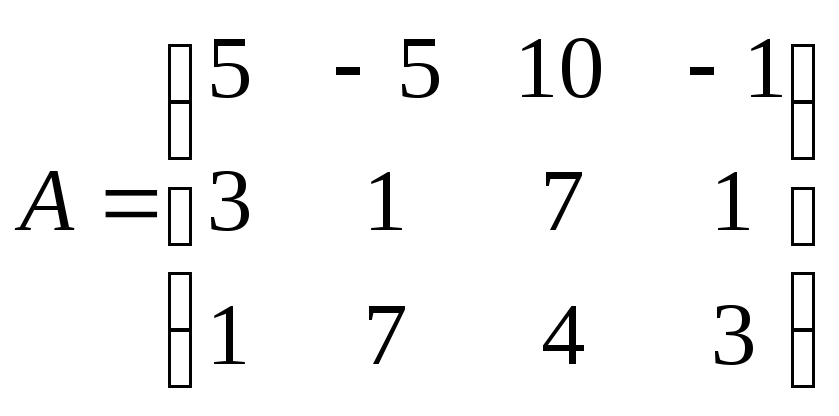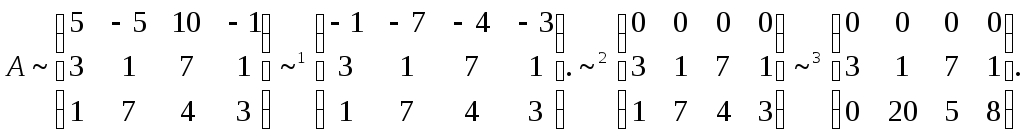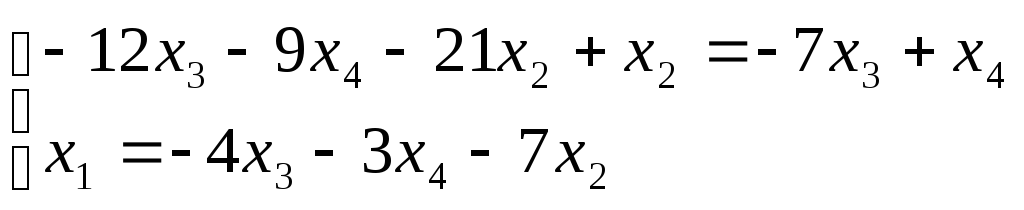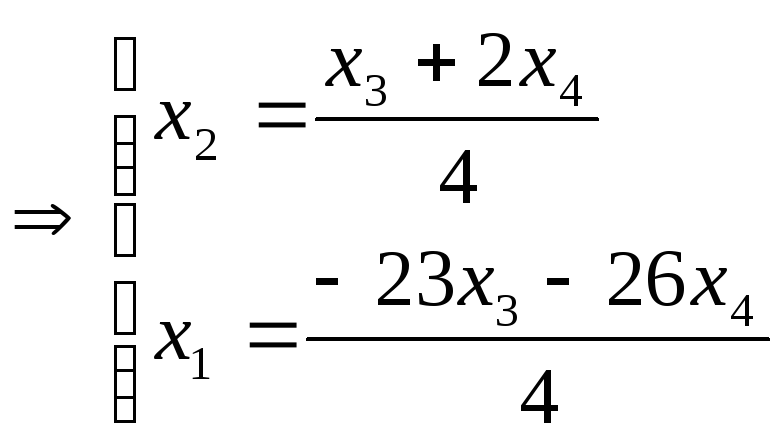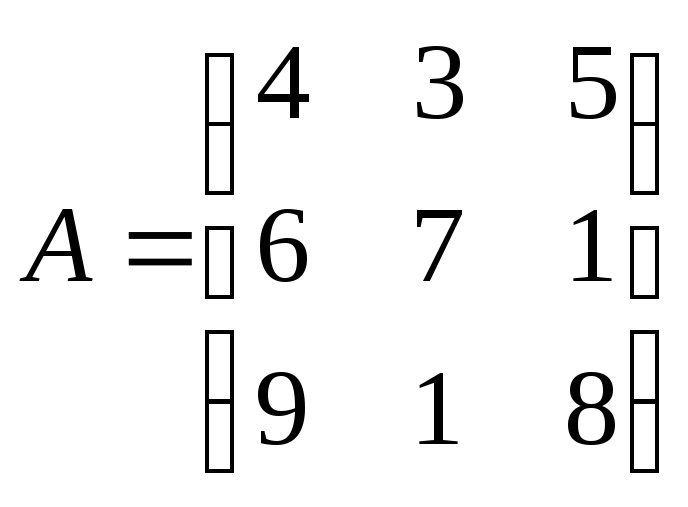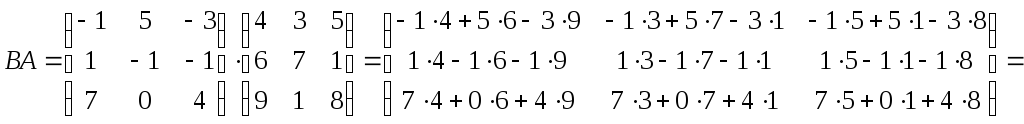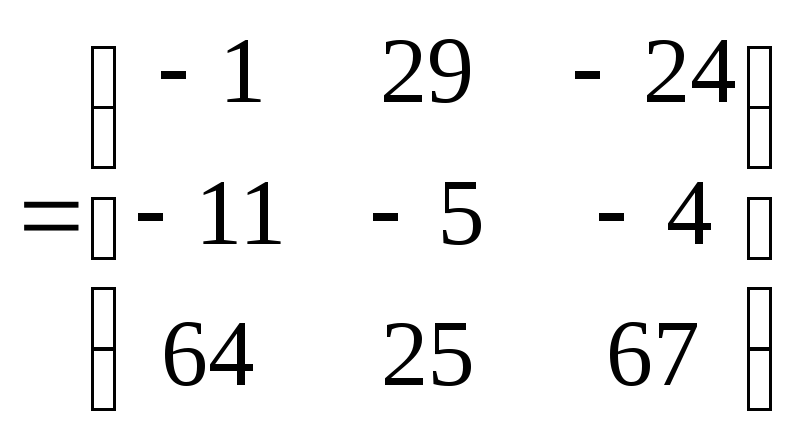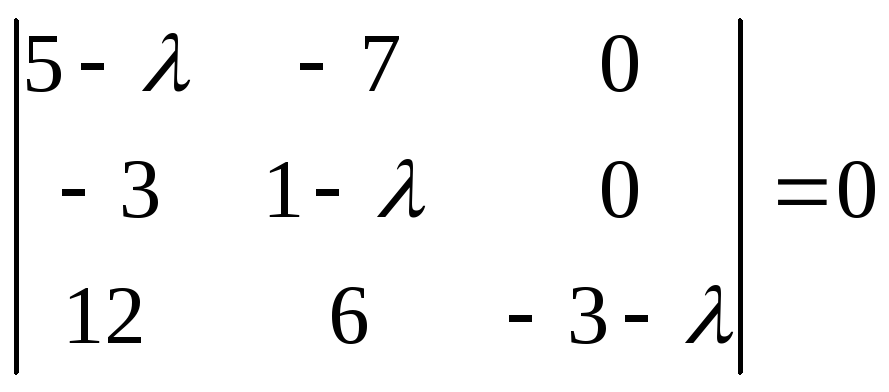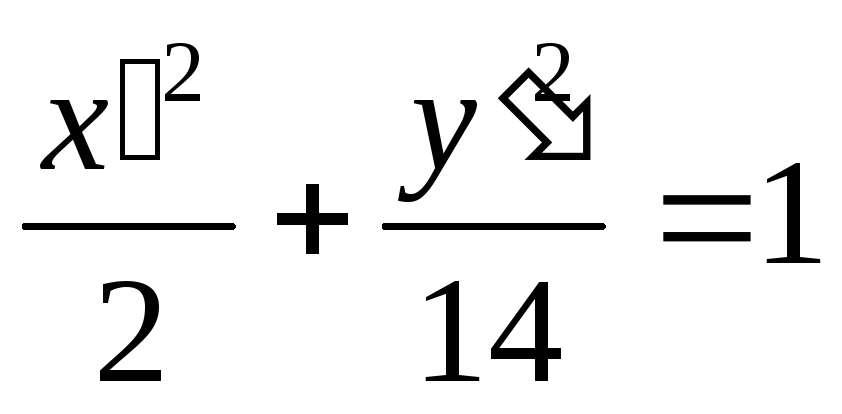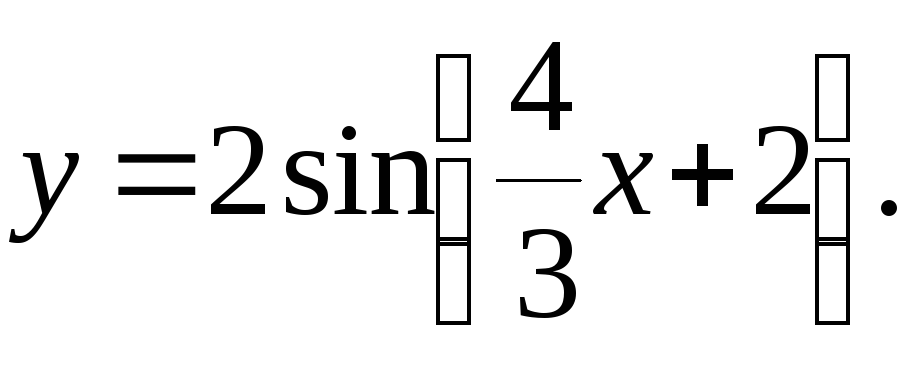Как средствами матричного исчисления найти преобразования

Как средствами матричного исчисления найти преобразования

Решение:

Данная
система имеет размер 2×3. Она однородна,
т.к. свободный член в каждом уравнении
равен нулю. Число уравнений меньше числа
неизвестных. Следовательно, множество
решений системы бесконечно.


Проведем
преобразования:

Для
этого проведём преобразования матрицы
А:

  1. Отнимем
    от элементов первой строки элементы
    второй строки, умноженные на 2;

  2. К
    первой строке добавим третью;

  3. Третью
    строку умножим на 3 и вычтем из неё
    вторую строку;

Ранг
матрицы системы равен двум, так как
только среди ее миноров

второго
порядка есть отличный от нуля, например
минор

Следовательно,
данная система эквивалентна системе

,

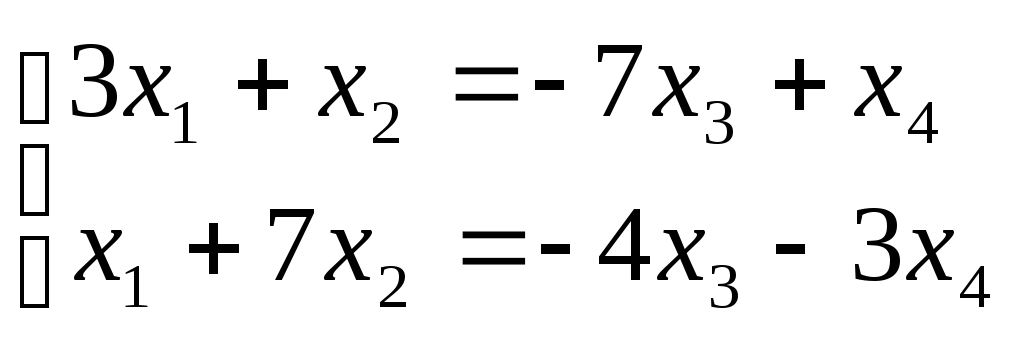
Отсюда

Следовательно,
множество решений системы имеет вид

.

Задача 74.
Даны два линейных преобразования.
Средствами матричного исчисления найти
преобразование, выражающее

через

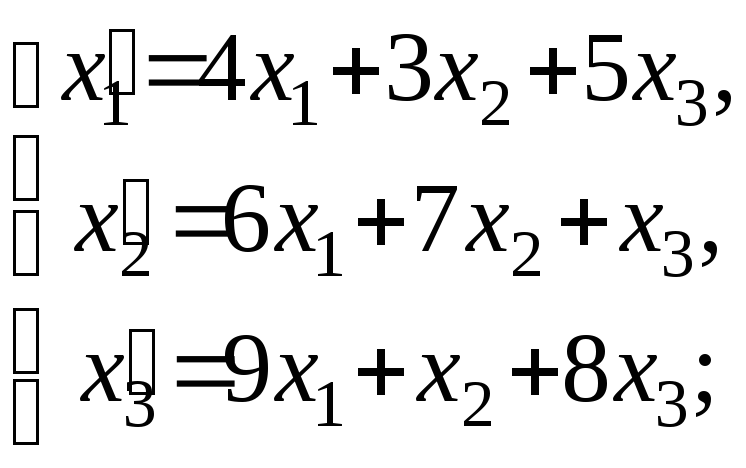
Решение:

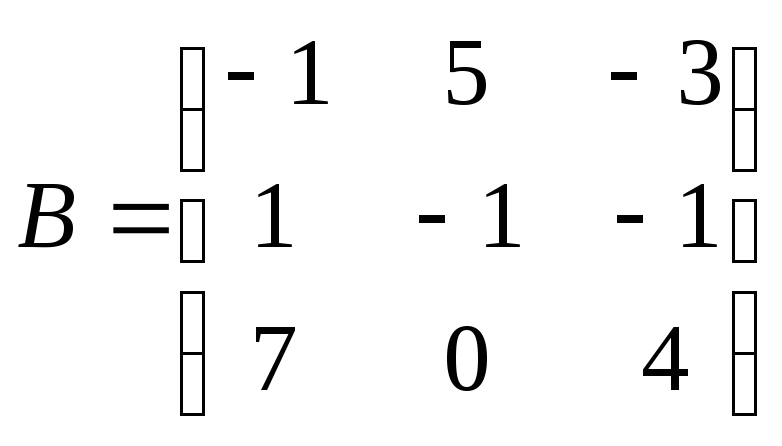
Составим две
матрицы:


и

найдем их
произведение:

Поэтому искомое
линейное преобразование имеет вид:

Задача
54.
Найти собственные значения и собственные
векторы линейного преобразования,
заданного в некотором базисе матрицей.

Решение:

  1. Характеристическое
    уравнение данного преобразования имеет
    вид:

Корни
этого уравнения следующие:
;
;

  1. Все
    корни являются собственными числами.

  1. Чтобы
    найти собственный вектор с собственным
    числом
    ,
    полагаем в системе
    .
    Получим

Решение
этой системы можно записать в виде

;
;

Вектор
,
где

и

— любые числа, удовлетворяющие условию
,
является собственным вектором данного
преобразования с собственным числом
.

  1. Аналогично
    находим собственный вектор с собственным
    числом
    :

;
;

Вектор
,
где

— любое число, удовлетворяющее условию
,
является собственным вектором данного
преобразования с собственным числом
.

  1. Аналогично
    находим собственный вектор с собственным
    числом
    :

;
;

Вектор
,
где

— любое число, удовлетворяющее условию
,
является собственным вектором данного
преобразования с собственным числом
.

Задача
64.
Привести к каноническому виду уравнение
линии второго порядка, используя теорию
квадратичных форм.

Решение:

Введем
обозначение.
Тогда матрица данной квадратичной формы

.

Найдем
собственные значения этой матрицы. Ее
характеристическое уравнение имеет
вид

,

откуда
;
.
Тогда квадратичная форма имеет следующий
канонический вид:
.
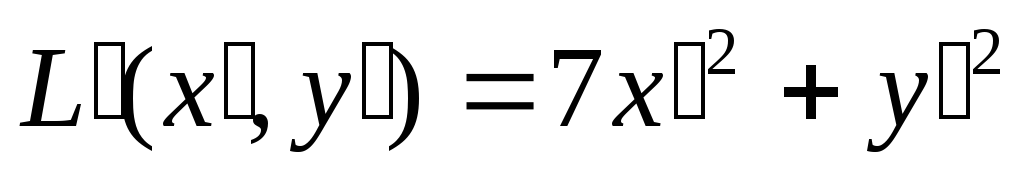
Переходя к исходному уравнению, получаем
.
Т.е. имеем эллипс

Задача
74.
Построить график функции

преобразованием графика функции
.

Решение:

  1. Построим
    график функции
    :

  1. График
    общей синусоиды

    с амплитудой
    ,
    круговой частотой
    и
    фазой
    получим
    синусоиды последствием преобразований:

растяжением
в
раз
в направлении оси
,

растяжением
в
=
раз в направлении оси

и
последующим параллельным переносом по
оси

на
.

Задача
84.
Дана функция

на отрезке
.
Требуется:

1)
построить график функции в полярной
системе координат по точкам, давая 
значения через промежуток /8,
начиная от =0;

2) найти
уравнение полученной линии в прямоугольной
декартовой системе координат, начало
которой совпадает с полюсом, а положительная
полуось абсцисс – с полярной осью, и по
уравнению определить, какая это будет
линия.

Соседние файлы в предмете Высшая математика

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #

    01.04.2014456.19 Кб17ВМ.doc

Источник
  • |
  • Библиотека решений
  • |
  • Даны два линейных преобразования (см.рис.) Средствами матричного исчисления найти преобразование, выражающее x//1, x//2, x//3 через x1, x2, x3.

Ирина Эланс

Автор который поможет с любыми образовательными и учебными заданиями

Заказ: 1027925

Даны два линейных преобразования (см.рис.) Средствами матричного исчисления найти преобразование, выражающее x//1, x//2, x//3 через x1, x2, x3.

Описание

Подробное решение в WORD

Даны два линейных преобразования (см.рис.) Средствами матричного исчисления найти преобразование, выражающее x//1, x//2, x//3 через x1, x2, x3. (Решение → 15106)

Даны два линейных преобразования (см.рис.) Средствами матричного исчисления найти преобразование, выражающее x//1, x//2, x//3 через x1, x2, x3. (Решение → 15106)

  • Даны два линейных преобразованияСредствами матричного исчисления найти преобразование, выражающее x”1, x”2, x’3 через x1, x2, x3
  • Даны два простых четырёхполюсника. Составьте из них сложный, используя соединение заданного вида. Определите первичные параметры простых и составного четырёхполюсников.Тип соединения: последовательное
  • Даны два простых четырёхполюсника. Составьте из них сложный, используя соединение заданного вида. Определите первичные параметры простых и составного четырёхполюсников.Тип соединения: последовательное
  • Даны два текстовых файла X.TXT и Y.TXT. Создать третий файл с произвольным именем, в который поместить сначала все строки файла X.TXT, а затем все строки файла Y.TXT. Подсчитать число строк в полученном файле, максимальную и среднюю длину строки.
  • Даны две вершины A(−3,3), B(5,−1) и точка D(4,3) пересечения высот треугольника. Составить уравнения его сторон.
  • Даны две вершины A(-6;-5) и B(2;4) параллелограмма ABCD и точка M(3;1) пересечения его диагоналей. Найти координаты вершин C и D, уравнения сторон параллелограмма.
  • Даны две координаты вектора х = 4, y = -12. Определить, его третью координату z при условии, что
  • Даны выборки из генеральных совокупностей для двух непрерывных случайных величин x1 и x2 соответственно: 1. Построить вариационный ряд и статистическое распределение выборки 2. Построить гистограмму относительных частот, разбив интервал на 5 – 7 частей 3. Получить несмещенные точечные оценки для математического ожидания и дисперсии случайной величины (выборочная средняя и исправленная выборочная дисперсия). 4. Найти 95%-е доверительные интервалы для математического ожидания и дисперсии случайной величины, предполагая нормальное распределение. 5. Проверить гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона (“хи-квадрат”) для уровня значимости a=0.01. 6. Получить матрицу парных коэффициентов корреляции для x1 и x2 7.По полученным результатам вычислений сделать выводы о взаимозависимости случайных величин: существует или не существует корреляционная зависимость, прямая она или обратная 8. Считая, что существует линейная регрессионная зависимость между x1 и x2, оценить значения коэффициентов линейных функций регрессии. 9. Построить прямые линии регрессии x1 на x2 и x2 на x1
  • Даны два вектора a = 2i – 3i + 5k. b =4i + j – 6k. Найти: 1) скалярное произведение векторов 2) длины векторов 3) косинус угла между векторами 4) проекцию вектора α на вектор b
  • Даны два вектора a = 2i – j + 3k, b = 3i + 4j – 5k. Найти векторы (а + b), (a – b), 3a, -2b, (5a – 4b)
  • Даны два вектора a и b. Вычислить:
  • Даны два вектора α = 2m + n, b = m – 3n, |m| = 2, |n| = 3, (m,n) = 120° Найти 1) скалярное произведение векторов 2) длины векторов 3) косинус угла между векторами 4) проекцию вектора α на вектор b
  • Даны два комплексных числа z1 = 2 – 4i , z2 = -3 + 5i , найти сумму, разность, произведение и частное, результаты изобразить на комплексной плоскости:
  • Даны два круга с общим центром и радиусами R1 и R2 (R1> R2). Найти и вывести на экран площади этих кругов S1 и S2, а также площадь S3 кольца, внешний радиус которого равен R1 , а внутренний радиус равен R2. (Sкруга= π∙R2)

Предварительный просмотр

Даны два линейных преобразования (см.рис.) Средствами матричного исчисления найти преобразование, выражающее x//1, x//2, x//3 через x1, x2, x3.

Источник

Тема: Средствами матричного исчисления найти преобразование …  (Прочитано 32004 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Даны 2 преобразования. Средствами матричного исчисления найти преобразование, выражающее z1, z2, z3 через x1, x2, x3.
Система 1:

  • 1)y1=x1+2x2+2x3
  • 2)y2=-3x2+x3
  • 3)y3=2x1-x2+3x3

Система 2:

  • 1)z1=3y1+y2
  • 2)z2=y1-2y2-y3
  • 3)z3=3y2+2y3

Или хотя бы киньте ссылку где есть такая тема, буду ОЧЕНЬ БЛАГОДАРЕН!!!

« Последнее редактирование: 07 Декабря 2010, 22:31:33 от Asix »

Запишите систему 1 и систему 2 в матричной форме.

« Последнее редактирование: 07 Декабря 2010, 22:31:40 от Asix »

Сделал:)) Но как из элементов одной матрицы выразить элементы другой? Может, есть какой алгоритм? А то весь нет уже обшарил… ???

« Последнее редактирование: 07 Декабря 2010, 22:31:47 от Asix »

« Последнее редактирование: 07 Декабря 2010, 22:32:03 от Asix »

Ну можно сказать, что начало, но не решение полностью.

« Последнее редактирование: 07 Декабря 2010, 22:32:10 от Asix »

« Последнее редактирование: 07 Декабря 2010, 22:32:22 от Asix »

Привет. У меня проблема с данной системой. И мне к сожалению совсем не понятно что дальше делать. :( Сориентируйте пожалуйста

С какой именно системой? После чего дальше?

Источник

Линейные операторы

Преобразование матричной формы оператора при замене базиса

Из самого определения матричной формы линейного оператора следует, что она зависит от выбора базиса. Пусть в векторном пространстве ( mathit{L}) заданы линейный оператор (A) и два базиса, ({e}) и ({f}), так что
[
Ae_k=sum _{r=1}^nalpha _{rk}e_r, quad k=1,2,…,n, quad quad (56)
]
[
Af_m=sum _{s=1}^nbeta _{sm}f_s, quad m=1,2,…,n, quad quad(57)
]
[
f_t=sum _{p=1}^nc _{pt}e_p, quad t=1,2,…,n. quad quad(58)
]
Здесь в правой части (56) определена матричная форма оператора (A), соответствующая базису ({e}), в правой части (57) – определена матричная форма оператора (A), соответствующая базису ({f}), в правой части (58) – матрица перехода от базиса ({e}) к базису ({f}). Наша задача – установить связь между матрицами (alpha ) и (beta ). Для этого мы подставляем (58) в правую и левую части (57). В левой части имеем:
[
Af_m=Aleft ( sum _{p=1}^nc _{pm}e_p right )=sum _{p=1}^nc _{pm}left (A e_p right )=sum _{p=1}^nc _{pm}left (sum _{r=1}^nalpha _{rp}e_r right )=
]
[
sum _{r=1}^n e_r left (sum _{p=1}^n alpha _{rp}c _{pm} right ).
]
В правой части:
[
sum _{s=1}^nbeta _{sm}f_s=sum _{s=1}^nbeta _{sm}left ( sum _{r=1}^nc _{rs}e_rright )=sum _{r=1}^n e_r left (sum _{s=1}^nc _{rs} beta _{sm} right ).
]
Разложение вектора по базису однозначно, так что, сравнивая результаты, получаем:
[
sum _{p=1}^n alpha _{rp}c _{pm}=sum _{s=1}^nc _{rs} beta _{sm}, quad r,m=1,2,…,n.
]
В этих формулах можно опознать результат матричного умножения, так что в матричном виде имеем:
[
alpha C^T=C^T beta,
]
или, в окончательном виде,
[
beta=(C^T)^{-1}alpha C^T.
]
Эта формула связывает матричные формы линейного оператора, соответствующие различным базисам векторного пространства.

1. Даны два линейных преобразования
[
left{ begin{array} {c} y_1=a_{11}x_1+a_{12}x_2+a_{13}x_3, \ y_2=a_{21}x_1+a_{22}x_2+a_{23}x_3, \ y_3=a_{31}x_1+a_{32}x_2+a_{33}x_3, end{array} right. quad left{ begin{array} {c}z_1=b_{11}y_1+b_{12}y_2+b_{13}y_3, \ z_2=b_{21}y_1+b_{22}y_2+b_{23}y_3, \ z_3=b_{31}y_1+b_{32}y_2+b_{33}y_3. end{array} right.
]

Средствами матричного исчисления найти преобразование, выражающее (z_1,z_2,z_3) через (x_1,x_2,x_3).

а)
[
left{ begin{array} {c} y_1=x_1+2x_2+2x_3, \ y_2=-3x_2+x_3, \ y_3=2x_1+3x_3, end{array} right. quad left{ begin{array} {c}z_1=3y_1+y_2, \ z_2=y_1-2y_2-y_3, \ z_3=3y_1+2y_3. end{array} right.
]

б)
[
left{ begin{array} {c} y_1=2x_2, \ y_2=-2x_1+3x_2+2x_3, \ y_3=4x_1-x_2+5x_3, end{array} right. quad left{ begin{array} {c}z_1=-3y_1+y_3, \ z_2=2y_2+y_3, \ z_3=-y_2+3y_3. end{array} right.
]

в)
[
left{ begin{array} {c} y_1=4x_1+3x_2+2x_3, \ y_2=-2x_1+x_2-x_3, \ y_3=3x_1+x_2+x_3,, end{array} right. quad left{ begin{array} {c}z_1=y_1-2y_2-y_3, \ z_2=3y_1+y_2+2y_3, \ z_3=y_1+2y_2+2y_3. end{array} right.
]

Предыдущий раздел

Назад

Далее Следующий раздел

Источник

Добавить комментарий