Тупой угол
Тупой угол — это угол, больший прямого, но меньший развёрнутого.
Градусная мера тупого угла — от 90º до 180º.
∠ABC, ∠DEF, ∠PTK — тупые углы.
Построить тупой угол заданной градусной меры можно с помощью транспортира.
Построить с помощью транспортира угол 140º.
1) Отмечаем точку — вершину угла.
2) От точки проводим луч — сторону угла.
3) Отметку в центре транспортира (у разных моделей отметка может располагаться в разных местах) совмещаем с вершиной угла таким образом, чтобы отметка 0º находилась на стороне угла.
4) Находим 140º на той шкале, где находится 0º, и ставим точку.
5) От вершины угла к отмеченной точке проводим луч — вторую сторону угла.
На рисунках показано построение угла 140º с началом отсчёта по разным шкалам — по нижней и по верхней.
Чтобы найти тупой угол на рисунке при помощи угольника, нужно приложить вершину угольника к вершине угла так, чтобы сторона угольника проходила вдоль одной из сторон угла. Если угол тупой, то его другая сторона выйдет за вторую сторону угольника.
Четырехугольники
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.
 Определение
Определение
Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.
 На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь
На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь 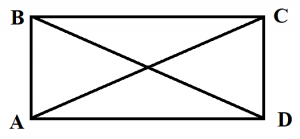
- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
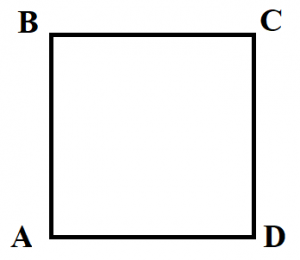 Свойства квадрата
Свойства квадрата
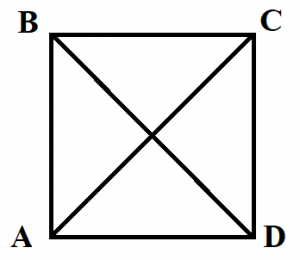
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Ромб – это параллелограмм, у которого все стороны равны.

Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.

Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.

углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Прямой, тупой, острый и развернутый углы
Давайте начнем с определения того, что такое угол. Во-первых, он является геометрической фигурой. Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол – геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре – прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:

Его градусная мера всегда составляет 90 о , иначе говоря, прямой угол – это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:

Градусная мера тупого угла всегда больше 90 о , но меньше 180 о . Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:

Градусная мера острого угла всегда меньше 90 о . Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:

В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол – это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить смежные углы, проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:

Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о , а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие – он не должен равняться 0 о , 90 о , 180 о , 270 о .
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла – от 0 о до 180 о .
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о .
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные

Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о .
2. Смежные

Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о .
3. Вертикальные

Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный

Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный

Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных – острого, тупого, прямого и развернутого – в геометрии существует много других их видов.
[spoiler title=”источники:”]
http://fb.ru/article/73397/pryamoy-tupoy-ostryiy-i-razvernutyiy-ugol
[/spoiler]
Определение
Тупой угол — это угол, больший прямого, но меньший развёрнутого.
Градусная мера тупого угла — от 90º до 180º.
Например,

∠ABC, ∠DEF, ∠PTK — тупые углы.
Построить тупой угол заданной градусной меры можно с помощью транспортира.
Пример.
Построить с помощью транспортира угол 140º.
1) Отмечаем точку — вершину угла.
2) От точки проводим луч — сторону угла.
3) Отметку в центре транспортира (у разных моделей отметка может располагаться в разных местах) совмещаем с вершиной угла таким образом, чтобы отметка 0º находилась на стороне угла.
4) Находим 140º на той шкале, где находится 0º, и ставим точку.
5) От вершины угла к отмеченной точке проводим луч — вторую сторону угла.
На рисунках показано построение угла 140º с началом отсчёта по разным шкалам — по нижней и по верхней.
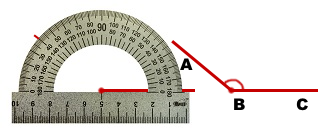
∠ABC=140º

∠MNK=140º
Чтобы найти тупой угол на рисунке при помощи угольника, нужно приложить вершину угольника к вершине угла так, чтобы сторона угольника проходила вдоль одной из сторон угла. Если угол тупой, то его другая сторона выйдет за вторую сторону угольника.
Здравствуйте, дорогие читатели. В прошлом выпуске разбирали как вычислять углы в параллелограмме, используя накрест лежащие углы и односторонние. В этой статье рассмотрим еще несколько разновидностей задач, для нахождения углов в четырехугольнике.
Задача №1
В этой задаче неважно какой угол вы возьмете равным в 51 градус, главное в ответе указать острый угол. А острый угол, это угол меньше 90 градусов.
Вспомним свойство диагоналей прямоугольника:
Диагонали прямоугольника равны, и точкой пересечения делятся пополам.
В прямоугольнике образуются четыре равнобедренных треугольника. Углы при основании в равнобедренном треугольнике равны.
Как видите, не важно между какой стороной и диагональю взять угол, но правильно только на первом рисунке, где “нарисован” острый угол, и по градусам также получился острый угол. На втором рисунке “нарисован” тупой угол, а получился при решении острый.
В таком типе задачи в вопросе может стоять найти тупой угол. Тогда в ответ, записываем угол, который больше 90 градусов. В этом случае тупой угол будет равен 180-78=102.
Задача №2
Из условия задачи понимаем, что трапеция ABCD равнобедренная, т.к. АВ=CD, значит и углы при основаниях равны.
Так же для решения воспользовались теоремой о сумме углов в треугольнике: Сумма углов в треугольнике равна 180 градусам.
Задача №3
Запомни! Ромб – это параллелограмм, у которого все стороны равны. Значит треугольник АВС – равнобедренный. Диагонали ромба делят его углы пополам.
Задача №4
Так как АС в 2 раза больше чем АВ, и диагонали параллелограмма в точке пересечения делятся пополам, то АО=АВ
Задача №5
Решение: Проведем диагональ ВD. Треугольники BCD равен треугольнику BAD по трем сторонам. Значит угол С равен углу А. Сумма углов выпуклого четырехугольника равна 360. Угол А равен:
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Содержание:
- Определение тупого угла
- Примеры решения задач с тупыми углами
Определение тупого угла
Определение
Угол называется тупым, если его
градусная мера лежит в пределах от
$90^{circ}$ до
$180^{circ}$ (рис. 1).
$angle alpha$ – тупой, если
$90^{circ} lt angle alpha < 180^{circ}$.
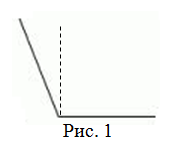
То есть тупой угол больше
прямого и меньше, чем
развернутый.
Примеры решения задач с тупыми углами
Пример
Задание. Найти тупой угол параллелограмма
$ABCD$, если известно, что его
острый угол равен
$30^{circ}$.
Решение. Известно, что сумма углов параллелограмма, прилежащих к одной стороне, равна
$180^{circ}$. Тогда искомый тупой угол равен
$$angle alpha=180^{circ}-30^{circ}=150^{circ}$$
Ответ. $angle alpha=150^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два угла треугольника равны
$30^{circ}$ и
$40^{circ}$. Найти третий угол треугольника, определить
тупым или острым он является.
Решение. Пусть $alpha$ – искомый угол.
Согласно теореме про сумму углов треугольника имеем, что
$$angle alpha+30^{circ}+40^{circ}=180^{circ}$$
Отсюда получаем
$$angle alpha=110^{circ}$$
Так как $90^{circ} < angle alpha=110^{circ} < 180^{circ}$, то он является тупым.
Ответ. $angle alpha=110^{circ}$
Читать дальше: что такое плоский угол.
|
Как выглядит фигура, приведите пример по возможности. В четырехугольнике может быть три тупых угла. Начертите квадрат АВСD. Представьте, что вершины это четыре иголки, воткнутые в пластину, а стороны сделаны из резины. Теперь приподнимите Вершину (иголку) D, и оттяните ей резинку подальше от центра. Если увести ее бесконечно далеко, то угол D будет стремиться к нулю, а углы С и А к 135 градусам. А теперь, чуть-чуть отведите подальше от центра квадрата вершины А и С. Тогда угол В станет чуть больше 90 градусов, т.е. он тупой. Углы А и С будут чуть меньше 135 градусов, т.е тоже тупые, а угол D будет очень малым. Итак три тупых угла. Или так. Возьмите обыкновенную шестигранную гайку, положите ее плашмя на лист бумаги, и обведите контуры трех последовательных граней. У Вас получится три угла по 120 градусов и две параллельные прямые. Если их свободные концы чуть свести, чтобы они перестали быть параллельными, и продолжить до пересечения, то получим четырехугольник, один угол которого 120 градусов, еще два чуть меньше 120 градусов, и один очень острый, чуть больше 0. Конечно можно начертить и множество промежуточных вариантов, необязательно симметричных. Просто приведенные примеры наиболее наглядны. система выбрала этот ответ лучшим
Татьяна Ьеглова 6 лет назад
В четырёхугольнике может быть один, два, три тупых углов. Это утверждение проистекает из следующих рассуждений и примеров. 1) Два тупых угла. Классические примеры – трапеция или ромб. Но могут быть варианты четырёхугольников с неравными и непараллельными сторонами и двумя тупыми углами. 2) Три тупых угла. Как известно, сумма внутренних углов четырёхугольника равна 360 градусов. Исходя из этого, если три его угла больше 90 градусов (хотя бы 91), то четвёртый угол будет меньше 90 градусов, т. е. будет острым, например: 360-91х3=87. 3) Один тупой угол. По аналогии с предыдущим рассуждением, если три угла меньше 90 градусов (хотя бы 89), будем иметь: 360-89х3=93, т. е. три угла острых, один тупой (> 90 градусов).
Помощни к 6 лет назад Чтобы узнать сколько может быть тупых или острых углов в четырехугольнике, давайте вспомним или узнаем чему равна сумма углов у этой геометрической фигуры. Любой четырехугольник можно разделить на два треугольника, а у последнего сумма углов всегда равна 180 градусов, а поскольку в четырехугольнике два треугольника, то сумма углов равняется 360 градусам. Тупой угол – это угол больше, чем 90 градусов. Допустим, если есть 3 угла по 100 градусов, то третий угол равен 60 гр. – он острый. Если 3 угла по 91 градусу, то последний, третий угол уже будет меньше 90 градусов, а значит он будет острым. Выходит, что больше 3 тупых углов в четырехугольнике быть не может.
-Irinka- 4 года назад Четырехугольники может иметь по одному, двум или трём тупым углам. Ниже примеры таких четырехугольников. Пример четырехугольника с 1 тупым углом.
Пример четырехугольника с 2 тупыми углами.
Пример четырехугольника с 3 тупыми углами.
Нептун 8 лет назад Четырёхугольником может быть абсолютно любая фигура, имеющая 4 угла, а не только квадрат, прямоугольник, трапеция, ромб и прочие. Сначала мне показалась, что максимум может быть 2 угла, но немного поразмыслив с карандашом и бумагой понял, что могут быть и 3 угла. Rafail в своём ответе объяснил, как можно начертить, а же ниже приведу рисунок ранее мной начерченной фигуры, которую я приберегал до первого правильного ответа. Рисунок мой соответствует фигуре, которую описал Rafail. Напоминает немного ромб с разными выступами, чем больше вытягивать правую сторону, тем меньше будет угол справа и больше 2 угла, расположенные посередине.
Бархатные лапки 4 года назад Как мы знаем из курса геометрии четырехугольник может быть разным: квадрат, трапеция, ромб, прямоугольник и другие. В четырехугольнике может быть один тупой угол. Может быть и два тупых угла – как пример этому – это такие геометрические фигуры, как ромб или трапеция. Как ни странно, но в четырехугольнике может быть и три тупых угла, правда сама фигура выглядит несколько странно, но тем не менее это возможно. Ниже смотрим пример четырехугольника с тремя тупыми углами, мне эта фигура напоминает трапецию.
Но вот четыре тупых угла в четырехугольнике быть точно не может, максимум – это три тупых угла.
m3sergey 8 лет назад Существует теорема, справедливая для любого многоугольника, как выпуклого, так и невыпуклого, что сумма его углов равна 180*(n-2), где n – количество углов многоугольника. Для четырехугольника, таким образом, сумма углов равна 360 град., что составляет 4 * 90 град. Следовательно, в любом четырехугольнике может быть не более 2 тупых углов, ведь тупой угол – это угол больше 90 град., а значит 2 других угла четырехугольника будут острыми – меньше 90 град. Примеры таких фигур – ромб, трапеция. Четырехугольник с одним тупым углом тоже возможен, например, невыпуклый четырехугольник стреловидной формы.
владсандрович 6 лет назад По урокам геометрии, мы знаем, что таких углов, которые считаются прямыми, два. На уроках геометрии, ученикам в таком случае, в качестве примера, как правило приводят трапецию. Причем в трапеции их два, и это по максимуму, а бывает случаи, когда может быть только один такой угол.
Андрей В Б 8 лет назад По моему в четырёхугольнике может быть только два тупых угла. И простой пример этому – обыкновенная трапеция или ромб. Хотя возможно я и ошибаюсь, но так нам говорили на уроках геометрии в школе, и это вроде даже как-то там доказывается теоремой.
morsusdoctor 8 лет назад Сумма углов выпуклого четырехугольника равна 360 грудусов. Тупых углов в четырехугольнике может быть два из четырех. Примером таких четырехугольников – параллеллограмм, трапеция, ромб. Плюс четырехугольник может быть и не правильной формы.
terli4eno4ka 6 лет назад В четырехугольнике может быть 3 тупых угла. Как мы помним из школьной программы геометрии, сумма углов такой фигуры, как четырехугольник равна 360 градусов, а тупым углом считается угол, который больше 90 градусов. Вот и считайте, что если в четырехугольнике будет три угла, размер которых больше 90 градусов, то как ни крути, четвертый угол будет меньше 90 градусов, то есть острым. Знаете ответ? |











