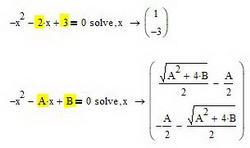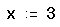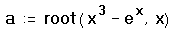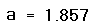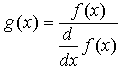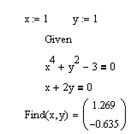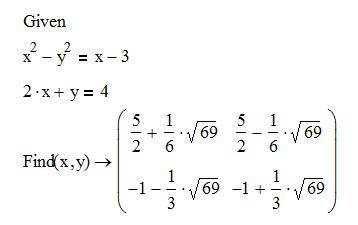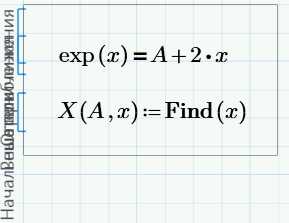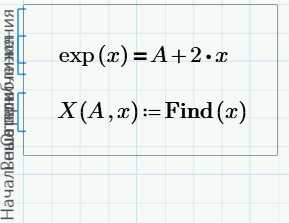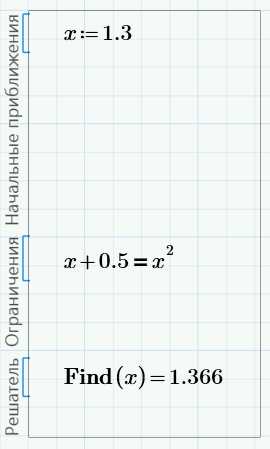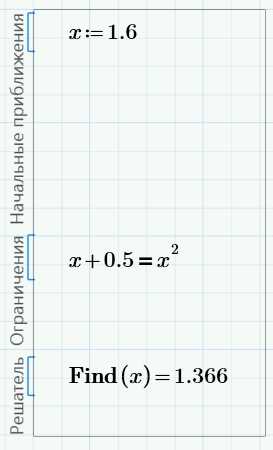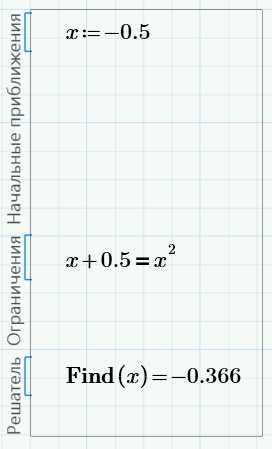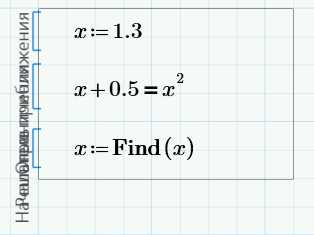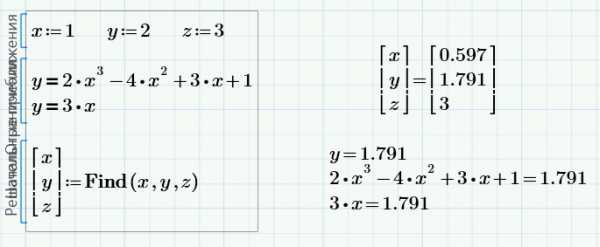Для решения уравнений в Mathcad можно воспользоваться двумя способами:
- Метод Given – Find
- Метод Solve
Использование метода Given – Find:
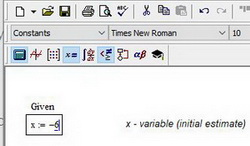
Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения уравнения численными методами.
Затем указывается начальное приближение для искомой переменной. Это нужно для увеличения скорости и точности решения уравнения. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю
Рис. 1. Ввод данных в поле mathcad
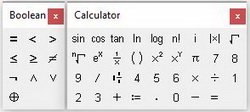
Далее вводится уравнение. Его можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа “ровно”. На панели Boolean он выделен жирным шрифтом (см. рис. 2)
Рис. 2. Панели Boolean и Calculator
После уравнения вводится функция Find(x) (где х – переменная). Это функция, которая возвращает результат. Значение функции Find(x) можно присвоить какой-либо переменной с помощью символа “:=” и использовать ее далее в расчетах
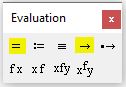
Для получения результата, после Find(x) следует поставить символ “→” либо “=” из панели Evaluation (см. рис. 3). Причем, если вы используете символ “→“, то mathcad определит все корни уравнения и сформирует матрицу результатов. Но если вы используете символ “=“, то mathcad выведет единственный корень, который был наиболее близок к начальному приближению. Так что, если вы не знаете сколько корней имеет уравнение, то лучше использовать стрелочку
Рис. 3. Панель “Evaluation”
В зависимости от сложности уравнения через определенное время MathCad выведет результат. На рис.4 можно рассмотреть синтаксис и различие результатов выводимых mathcad. Обратите внимание, что выводимые результаты одного и того же уравнения различны
Рис. 4. Результат численного решения уравнения
Mathcad позволяет решать уравния в символьном виде. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, то результат выведется в символьном виде (см. рис. 5). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ “→” для вывода результата
Рис. 5. Результат символьного решения уравнения
Использование метода Solve:
Этот метод отличается от выше рассмотренного синтаксисом. На свободном поле вводим уравнение с использованием логического символа “ровно” из панели Boolean. После ввода уравнения, не смещая курсор ввода, на панели Symbolic нажимаем кнопку solve (см. рис. 6)
Рис. 6. Панель Symbolic
Затем ставим запятую и вводим переменную, относительно которой нужно решить уравнение (в нашем случае это x). Нажимаем Enter на клавиатуре и смотрим результат (см. рис. 7)
Рис. 7. Результат решения уравнения методом Solve
Обратите внимание, что метод подходит как для численного так и для символьного представления результатов
Как показывает моя личная инженерная практика, иногда не удается решить уравнения с помощью Given – Find, но получается в Solve. При этом, к сожалению, метод Solve не очень удобен для далнейшего использования результатов решения уравнения
Как найти неизвестную переменную в уравнении маткад
Mathcad дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно пятидесяти. В первой части этого раздела описаны процедуры решения систем уравнений. В заключительной части приведены примеры и проведено обсуждение некоторых часто встречающихся ошибок. Результатом решения системы будет численное значение искомого корня. Для символьного решения уравнений необходимо использовать блоки символьного решения уравнений. При символьном решении уравнений искомый корень выражается через другие переменные и константы.
Для решения системы уравнений выполните следующее:
- Задайте начальные приближения для всех неизвестных, входящих в систему уравнений. Mathcad решает уравнения при помощи итерационных методов. На основе начального приближения строится последовательность, сходящаяся к искомому решению.
- Напечатайте ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений. При печати слова Given можно использовать любой шрифт, прописные и строчные буквы. Убедитесь, что при этом Вы не находитесь в текстовой области или параграфе.
- Введите уравнения и неравенства в любом порядке ниже ключевого слова Given. Удостоверьтесь, что между левыми и правыми частями уравнений стоит символ =. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов , , и .
- Введите любое выражение, которое включает функцию Find. При печати слова Find можно использовать шрифт любого размера, произвольный стиль, прописные и строчные буквы.
| Find(z1, z2, z3, . . . ) | Возвращает решение системы уравнений. Число аргументов должно быть равно числу неизвестных. |
Функция Find возвращает найденное решение следующим образом:
- Если функция Find имеет только один аргумент, то она возвращает решение уравнения, расположенного между ключевым словом Given и функцией Find.
- Если функция Find имеет более одного аргумента, то она возвращает ответ в виде вектора. Например, Find(z1, z2) возвращает вектор, содержащий значения z1 и z2 , являющиеся решением системы уравнений.
Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называются блоком решения уравнений.
На Рисунке 5 показан рабочий документ, который использует блок решения уравнений для решения одного уравнения с одним неизвестным. Так как имеется только одно уравнение, то только одно уравнение появляется между ключевым словом Given и формулой, включающей функцию Find. Так как уравнение имеет одно неизвестное, то функция Find имеет только один аргумент. Для решения одного уравнения с одним неизвестным можно также использовать функцию root, как показано ниже:
Рисунок 5: Блок решения уравнений для одного уравнения с одним неизвестным.
Между ключевым словом Given и функцией Find в блоке решения уравнений могут появляться выражения строго определенного типа. Ниже приведен список всех выражений, которые могут быть использованы в блоке решения уравнений. Использование других выражений не допускается. Эти выражения часто называются ограничениями. В таблице, приведенной ниже, через x и y обозначены вещественнозначные скалярные выражения, а через z и w обозначены любые скалярные выражения.
| Условие | Как ввести | Описание |
| w = z | [Ctrl] = | Булево равенство возвращает 1, если операнды равны; иначе 0 |
| x > y | > | Больше чем. |
| x |
Следующие выражения недопустимы внутри блока решения уравнений:
- Ограничения со знаком .
- Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.
- Неравенства вида a -15 .
Причиной появления этого сообщения об ошибке может быть следующее:
- Поставленная задача может не иметь решения.
- Для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число. Если решение задачи комплексное, то оно не будет найдено, если только в качестве начального приближения не взято также комплексное число. На Рисунке 11 приведен соответствующий пример.
- В процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Метод поиска решения, который используется в Mathcad, не позволяет в этом случае построить следующее приближение, которое бы уменьшало невязку. Для поиска искомого решения пробуйте использовать различные начальные приближения или добавьте ограничения на переменные в виде неравенств, чтобы обойти точку локального минимума.
- В процессе поиска решения получена точка, которая не является точкой локального минимума, но из которой метод минимизации не может определить дальнейшее направление движения. Метод преодоления этой проблемы — такой же, как для точки локального минимума: измените начальное приближение или добавьте ограничения в виде неравенств, чтобы миновать нежелательную точку остановки.
- Возможно, поставленная задача не может быть решена с заданной точностью. Если значение встроенной переменной TOL слишком мало, то Mathcad может достигнуть точки, находящейся достаточно близко к решению задачи, но уравнения и ограничения при этом не будут выполнены с точностью, задаваемой переменной TOL. Попробуйте увеличить значение TOL где-нибудь выше блока решения уравнений.
Что делать, когда имеется слишком мало ограничений
Если количество ограничений меньше, чем количество переменных, Mathcad вообще не может выполнить блок решения уравнений. Mathcad помечает в этом случае функцию Find сообщением об ошибке “слишком мало ограничений”.
Задача, аналогичная той, которая приведена на Рисунке 12, называется недоопределенной. Ограничений в ней меньше, чем переменных. Поэтому ограничения не содержат достаточной информации для поиска решения. Поскольку функция Find имеет пять аргументов, Mathcad определяет, что требуется решить два уравнения с пятью неизвестными. Вообще говоря, такая задача обычно имеет бесконечное число решений.
При использовании блока решения уравнений в Mathcad необходимо задать количество уравнений по крайней мере не меньшее, чем число искомых неизвестных. Если зафиксировать значения некоторых переменных, удастся решить уравнения относительно оставшихся переменных. На Рисунке 13 показано, как, зафиксировав часть переменных, решить недоопределенную задачу из Рисунка 12. Поскольку функция Find содержит только два аргумента, z и w, Mathcad определяет переменные x, y и v как имеющие фиксированные значения 10, 50 и 0 соответственно. Блок решения уравнений становится в этом случае корректно определенным, потому что теперь имеются только две неизвестных, z и w, и два уравнения.
Рисунок 12: Функция Find имеет пять аргументов, поэтому Mathcad определяет, что требуется решить два уравнения с пятью неизвестными.
Рисунок 13: Проблема может быть решена, если уменьшить количество аргументов функции Find.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Как найти неизвестную переменную в уравнении маткад
Mathcad для студентов
Mathcad для начинающих
Скачать программы бесплатно
Уравнения с одним неизвестным в Mathcad
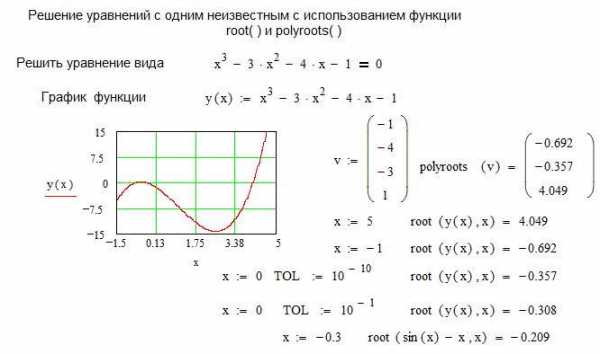
Простейший способ найти корень уравнения с одним неизвестным в Mathcad обеспечит функция root ( ). Аргументами функции root ( ) являются вид функции определяющей решаемое уравнение и имя переменой, относительно которой ищется решение – root (f(x),x) Если уравнение в Mathcad содержит несколько корней, то функция обеспечивает нахождение единственного корня, ближайшего к заданному начальному значению для искомой переменной. Точность вычислений может быть увеличена или уменьшена посредством задания значения переменной TOL, равной по умолчанию 10-3 и определённой в меню Math, Options (Математика, Опции). Установленное значение TOL также оказывает влияние на точность вычислений.
В случае, если решаемое уравнение в Mathcad представлено полиномом, то все его решения могут быть получены с помощью функции polyroots (v). В качестве аргументов этой функции выступает вектор коэффициентов полинома –v, а результат представляется в виде вектора корней полинома. На листинге представлен пример нахождения корней уравнений с использованием функций root ( ) и polyroots ( ).
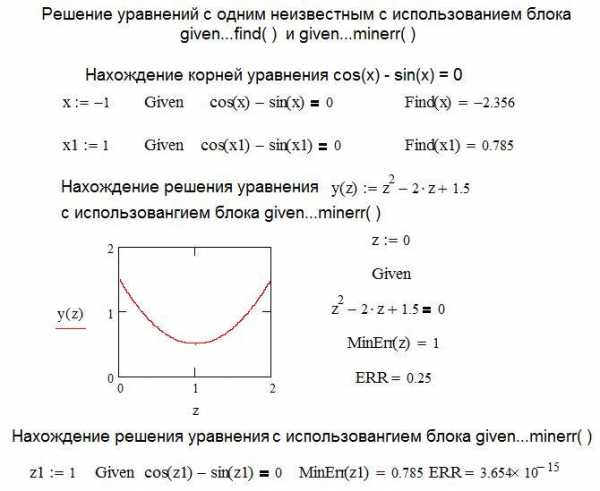
Другим способом решения уравнений в Mathcad является применение специального вычислительного блока, начинающегося с ключевого слова given с использованием функций find( ) и minerr ( ).
Блок имеет следующую структуру:
Начальное значение искомой переменной
Выражение с использованием функции find( ) или minerr ( )
Нахождение корней уравнения в Mathcad с использованием блока given…find ( ) в чем – то аналогично использованию функции root ( ). В Mathcad задается начальное значение для искомой переменной, после находится решение, ближайшее к заданному начальному условию. Использовании блока given…minerr ( ) имеет существенные особенности. Решение будет найдено в любом случае, даже при его отсутствии. Дело в том, что ищется не решение системы, а минимальная невязка уравнений. На листинге рассмотрена функция, заведомо не имеющая действительных корней и при использовании блока given…minerr ( ) найдено решение, значение, которое наиболее приближено к оси х, то есть обеспечивает минималь-ную невязку. Значение невязки (ошибки) показывает системная переменная ERR.
Mathcad find переменная не определена
MathCad | ANSYS CFX | MS Office
Поиск по сайту
Выбор языка
Решение уравнений в MathCad
Часто в курсовом проекте, либо в лабораторной работе встает вопрос о решении какого-либо сложного большого уравнения с одним неизвестным. Не всегда хочется тратить 10 — 20 минут на рутинные преобразования в процессе которых, велика вероятность допущения ошибки. Целесообразно воспользоваться математической программой (в данном случае MathCad), которая быстро и правильно сможет дать ответ. Мы рассмотрим пример использования 2-ух способов решения уравнений, причем как в числах так и в символьном виде.
Способ №1: использование вычислительного блока Given — Find:
Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем первое слово Given. Это служебное слово. Оно “подключает” определенные программные модули mathcad, необходимые для решения уравнения. Эти модули в своем составе содержат основные численные методы решения: метод бисекции, простой итерации и пр. Далее пишется наше уравнение в любом — явном или неявном виде. Само уравнение набирается с клавиатуры с использованием логического символа “равно”. На панельке Boolean (Булева алгебра) он выделен жирным шрифтом (см. рис. 1).
Рис. 1. Панель “Булевая алгебра”
Далее пишется слово Find(x) (где х — переменная). Это функция, которая и получает ответ. Функцию Find(x) можно присвоить какой-либо переменной и использовать далее в расчетах. Для получения результата, после Find(x) следует поставить символ “→” либо “=” (см. рис. 2).
Рис. 2. Панель “Вычисления”
В зависимости от сложности уравнения через некоторое время MathCad выведет результат.
Возможности MathCad позволяют определить корень как в численном виде (т. е. результат решения уравнения представляет собой число) так и в символьном (результат — выражение). Для численного определения корня необходимо задать (определить) ВСЕ переменные входящие в уравнение и даже искомую переменную. MathCad воспринимает задание искомой переменной как начальное приближение корня. Крайне важно задаться начальным приближением, поскольку без него корень уравнения невозможно определить в силу особенностей используемых численных методов. Нужно отметить, что некорректное задание начального приближения часто становится причиной получения неверного результата либо его отсутствия вообще. Но не стоит забывать также и о том, что корня может не быть, потому что само уравнение его не имеет.
В том случае, если необходимо решить уравнение относительно какой-либо переменной в символьном виде, то нет необходимости задаваться значениями всех входящих в уравнение параметров и начальным приближением переменной. В этом случае достаточно ввести уравнение (также через “жирное равно”) и после оператора Find(x) поставить “→”. При этом будут работать уже другие функции MathCad, которые заточены под символьное преобразование и упрощение выражений. Результатом решения будет выражение. Стоит отметить, что MathCad сможет записать решение далеко не всякого уравнения. В этом смысле его возможности ограничены.
Для подтверждения и закрепления выше сказанного, Вам предлагается скачать и познакомиться с примерами решения уравнений как в численном так и в символьном виде.
Пример №1. Решение уравнения в MathCad с помощью блока Given Find численно: Скачать
Пример №2. Решение уравнения в MathCad с помощью блока Given Find символьно: Скачать
Способ №2: Применение метода solve:
Этот метод по существу не отличается от выше рассмотренного, поскольку процедура нахождения корня аналогична. Разница лишь в оформлении. В этом случае наше уравнение записывается без операторов Given и Find. После ввода уравнения на панели Symbolic нажимаем кнопку solve (см. рис. 3), определяем через запятую искомую переменную, жмем “→” и получаем ответ.
Рис. 3. Панель “Символьные”
Иногда, то что не получается найти с помощью Given Find получается в solve.
Пример №3. Решение уравнения в MathCad с помощью solve: Скачать
РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
4 Решение уравнений и систем средствами Mathcad
Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.
Функция root, блоки Given…Find, Given…Minerr
В ходе численного решения обычно выделяют два этапа:
- отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
- уточнение корней – нахождение численного значения корня с указанной точностью.
Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.
Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается
root(f(x), x, [a, b])
и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:
- f(x) – функция левой части уравнения f(x) = 0;
- x – переменная, относительно которой требуется решить уравнение;
- a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде
Этот прием используется в Mathcad так:
- задается матрица коэффициентов при неизвестных системы A;
- задается столбец свободных членов b;
- вводится формула для нахождения решения системы X:=A -1 b;
- выводится вектор решений системы X=.
Кроме того, пакет Mathcad имеет встроенную функцию
lsolve(A, b),
возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).
Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.
Порядок выполнения лабораторной работы
- Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
- Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
- Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:
Лабораторная работа № 4
Решение уравнений и систем в Mathcad.
- В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
- Выполнить задание 1.
Задание 1. Решить уравнение .
Решение.
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:
Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:
Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).
Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).
Для появления графика щелкнем левой клавишей мыши вне графической области.
Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.
Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.
После указанных преобразований график функции f(x) будет выглядеть следующим образом:
Из графика функции f(x) видно, что уравнение имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.
Этап отделения корней завершен.
Уточним теперь корни уравнения с помощью функции root.
Присвоим начальное приближение переменной x и укажем точность поиска корня:
Уточним заданное приближение к значению корня с помощью функции root:
Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:
Задание 2. Решить уравнение .
Решение.
Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:
Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.
Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.
Для получения результата напечатаем polyroots(v) =:
Задание 3. Решить систему линейных уравнений Сделать проверку.
Решение.
1-й способ. Использование блока Given … Find.
Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:
Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).
После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом
После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.
2-й способ. Использование блока Given…Minerr.
Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:
3-й способ. Решение системы линейных уравнений матричным способом.
Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:
Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:
Решим систему матричным способом по формуле
Решим систему с помощью функции lsolve:
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:
программирование mathcad скалярный трехмерный
Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given — Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Если задано уравнение f(x) = 0, то его можно решить следующим образом с помощью блока Given — Find:
— задать начальное приближение
— ввести служебное слово
- — записать уравнение, используя знак боулево равно
- — написать функцию find с неизвестной переменной в качестве параметра
В результате после знака равно выведется найденный корень.
Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.
В Mathcad можно писать программы двух видов
- 1)в виде скриптов(последовательность команд)
- 2)в виде настоящих программ с входными и выходными параметрами.
Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вы0числениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.
Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT).
Mathcad имеет интуитивный и простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов.
Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования. При создании документов-приложений используется принцип WYSIWYG (What You See Is What You Get — «что видишь, то и получаешь»).
Несмотря на то, что эта программа в основном ориентирована на пользователей-непрограммистов, Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования, путем использования распределённых вычислений и традиционных языков программирования. Также Mathcad часто используется в крупных инженерных проектах, где большое значение имеет трассируемость и соответствие стандартам.
Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов. Открытая архитектура приложения в сочетании с поддержкой технологий .NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения. Есть возможность создания электронных книг (e-Book).
Программа содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.
[spoiler title=”источники:”]
http://allmathcad.com/ru/uravneniya-s-odnim-neizvestnym.html
http://web-shpargalka.ru/mathcad-find-peremennaja-ne-opredelena.php
[/spoiler]
Как в маткаде найти неизвестное из уравнения
Mathcad для студентов
Mathcad для начинающих
Скачать программы бесплатно
Уравнения с одним неизвестным в Mathcad
Простейший способ найти корень уравнения с одним неизвестным в Mathcad обеспечит функция root ( ). Аргументами функции root ( ) являются вид функции определяющей решаемое уравнение и имя переменой, относительно которой ищется решение — root (f(x),x) Если уравнение в Mathcad содержит несколько корней, то функция обеспечивает нахождение единственного корня, ближайшего к заданному начальному значению для искомой переменной. Точность вычислений может быть увеличена или уменьшена посредством задания значения переменной TOL, равной по умолчанию 10-3 и определённой в меню Math, Options (Математика, Опции). Установленное значение TOL также оказывает влияние на точность вычислений.
В случае, если решаемое уравнение в Mathcad представлено полиномом, то все его решения могут быть получены с помощью функции polyroots (v). В качестве аргументов этой функции выступает вектор коэффициентов полинома –v, а результат представляется в виде вектора корней полинома. На листинге представлен пример нахождения корней уравнений с использованием функций root ( ) и polyroots ( ).
Другим способом решения уравнений в Mathcad является применение специального вычислительного блока, начинающегося с ключевого слова given с использованием функций find( ) и minerr ( ).
Блок имеет следующую структуру:
Начальное значение искомой переменной
Выражение с использованием функции find( ) или minerr ( )
Нахождение корней уравнения в Mathcad с использованием блока given…find ( ) в чем – то аналогично использованию функции root ( ). В Mathcad задается начальное значение для искомой переменной, после находится решение, ближайшее к заданному начальному условию. Использовании блока given…minerr ( ) имеет существенные особенности. Решение будет найдено в любом случае, даже при его отсутствии. Дело в том, что ищется не решение системы, а минимальная невязка уравнений. На листинге рассмотрена функция, заведомо не имеющая действительных корней и при использовании блока given…minerr ( ) найдено решение, значение, которое наиболее приближено к оси х, то есть обеспечивает минималь-ную невязку. Значение невязки (ошибки) показывает системная переменная ERR.
Как в маткаде найти неизвестное из уравнения
Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.
| root( f(z), z) | Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. |
Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.
Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
Рассмотрим пример, как найти a — решение уравнения e x = x 3 . Для этого выполните следующие шаги:
- Определите начальное значение переменной x. Введите x:3. Выбор начального приближения влияет на корень, возвращаемый Mathcad (если выражение имеет несколько корней).
- Определите выражение, которое должно быть обращено в ноль. Для этого перепишите уравнение e x = x 3 в виде x 3 — e x = 0. Левая часть этого выражения и является вторым аргументом функции root
- Определите переменную a как корень уравнения. Для этого введите a:root(x^3[Space]-e^x[Space],x).
- Напечатайте a=, чтобы увидеть значение корня.
При использовании функции root имейте в виду следующее:
- Удостоверьтесь, что переменной присвоено начальное значение до начала использования функции root.
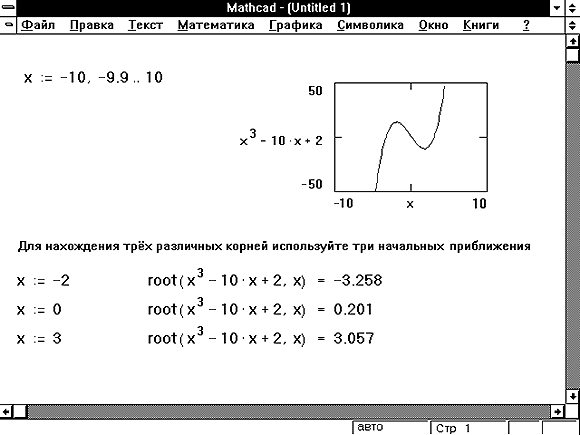
- Для выражения с несколькими корнями, например x 2 — 1 = 0, начальное значение определяет корень, который будет найден Mathcad. На Рисунке 1 приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального приближения.
- Mathcad позволяет находить как комплексные, так и вещественные корни. Для поиска комплексного корня следует взять в качестве начального приближения комплексное число.
- Задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) — g(x) =0. Для этого функция root может быть использована следующим образом:
Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 1: Использование графика и функции root для поиска корней уравнения.
Что делать, когда функция root не сходится
Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.
Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”. Эта ошибка может быть вызвана следующими причинами:
- Уравнение не имеет корней.
- Корни уравнения расположены далеко от начального приближения.
- Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.
- Выражение имеет разрывы между начальным приближением и корнями.
- Выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find
Некоторые советы по использованию функции root
В этом разделе приведены несколько советов по использованию функции root:
- Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL.
- Если уравнение имеет несколько корней, пробуйте использовать различные начальные приближения, чтобы найти их. Использование графика функции полезно для нахождения числа корней выражения, их расположения и определения подходящих начальных приближений. Рисунок 1 показывает пример. Если два корня расположены близко друг от друга, можно уменьшить TOL, чтобы различить их.
- Если f(x) имеет малый наклон около искомого корня, функция может сходиться к значению r, отстоящему от корня достаточно далеко . В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x)=0 на g(x)=0, где
Решение уравнений с параметром
Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции
Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.
Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.
Рисунок 2: Определение функции пользователя с функцией root.
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.
| polyroots(v) | Возвращает корни полинома степени . Коэффициенты полинома находятся в векторе v длины n+1. Возвращает вектор длины n, состоящий из корней полинома. |
Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.
Рисунок 4: Использование функции polyroots для поиска корней полинома.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Электронная библиотека
Задача ставится следующим образом:
Пусть имеется алгебраическое уравнение с одним неизвестным х или система алгебраических уравнений
Требуется решить данное уравнение или систему уравнений, т.е. найти те значения х, в которых уравнения превращаются в верное равенство.
Отыскание корней численными методами связано с несколькими задачами:
Ø Исследование существования корней в принципе, определение их количества и примерного расположения;
Ø Отыскание корней с заданной погрешностью
Всевозможные функции MathCAD нацелены на решение второй задачи, т.е. предполагается, что корни уже приблизительно локализированы. Выбор встроенных функций для решения уравнений и систем уравнений осуществляется в зависимости от специфики уравнения.
Решение одного уравнения с одним неизвестным
Рассмотрим алгебраическое уравнение f(x)=0 с одним неизвестным х, например, sin(x)=0.
Для решения таких уравнений MathCAD имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному.
Мнемоника команды выглядит следующим образом:
root (f(x), x) или root (f(x), x, a, b),
где f(х) – скалярная функция, определяющая уравнение; х – скалярная переменная, относительно которой решается уравнение; а, b – границы интервала, внутри которого происходит поиск корня.
Первый тип функции root требует дополнительного задания начального значе
ния переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.
Приведем пример решения очень простого уравнения sin(x)=0, корни которого известны заранее (рис. 38).
Обратите внимание, что, хотя уравнение имеет бесконечное количество корней MathCAD находит (с заданной точностью) только один из них, х0, лежащий наиболее близко к х = 0,5. Если задать другое начальное значение, например х = 3, то решением будет другой корень уравнения х1 = π и т.д. Таким образом, для поиска корня средствами MathCAD требуется его предварительная локализация. Это связано с особенностями выбранного численного метода, который называется методом секущих.
Если уравнение неразрешимо, то при попытке найти его корень будет выдано сообщение об ошибке. Кроме того, к ошибке или выдаче неправильного корня может привести и попытка применить метод секущих в область локального экстремума. В этом случае секущая может иметь направление, близкое к горизонтальному, выводя точку следующего приближения далеко от предполагаемого корня. Для решения таких уравнений лучше применять функцию Minerr.
Рис. 7.1. Функция Minerr
Примечание: Для решения уравнения с одним неизвестным применимы и градиентные методы, относящиеся в MathCAD к системам уравнений.
Иногда удобнее задавать не начальное приближение к корню, а интервал [а, b], внутри которого корень заведомо находится. В этом случае следует использовать функцию root с четырьмя аргументами, а присваивать начальное значение х не нуж
но. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента). Явный вид функции f(x) может быть определен непосредственно в теле функции root (рис. 39).

Ø внутри интервала [а, b] не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно;
Ø значения f(а) и f(b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.

При задании начального значения 0,5 численный метод отыскивает первый корень (отрицательную мнимую единицу –i), а при начальном значении –0,5 находится и второй корень i.
Для решения этого уравнения второй вид функции root (с четырьмя, а не с двумя аргументами) неприменим, поскольку f(х) является положительно определенной, и указать интервал, на границах которого она имела бы разный знак, невозможно.
Нахождение корней полинома
Если функция f(x) является полиномом, то все его корни можно определить, использую встроенную функцию polyroots(v), где v – вектор, составленный из коэффициентов полинома.
Поскольку полином n-й степени имеет ровно n корней (некоторые из них могут быть кратными), вектор v должен состоять из n+1 элемента. Результатом действия функции polyroots является вектор, составленный из n корней рассматриваемого полинома. При этом нет надобности вводить какое-либо начальное приближение, как для функции root.
Например, найдем корни полинома четвертой степени f(x)=х 4 -6х 3 +12х 2 -10х+3 с
помощью функции polyroots (рис. 41).
Рис. 7.2. Функция Polyroots
Запишем коэффициенты рассматриваемого в примере полинома в виде вектора. Первым в векторе должен идти свободный член полинома, вторым – коэффициент при х 1 и т.д. Соответственно, последним n+1 элементом вектора должен быть коэффициент при старшей степени x N .
Совет: Иногда исходный полином имеется не в развернутом виде, а, например, как произведение нескольких полиномов. В этом случае определить все его коэффициенты можно, выделив его и выбрав в меню Symbolics (Символика) пункт Expand (Разложить). В результате символьный процессор MathCAD сам преобразует полином в нужную форму, пользователю надо будет только корректно ввести ее в аргументы функции polyroots.
Далее показано действие функции polyroots. Обратите внимание, что численный метод вместо двух из трех действительных единичных корней (иными словами, кратного корня 1) выдает два мнимых числа. Однако малая мнимая часть этих корней находится в пределах погрешности, определяемой константой TOL, и не должна вводить пользователей в заблуждение. Просто нужно помнить, что корни полинома могут быть комплексными, и ошибка вычислений может сказываться как на действительной, так и на комплексной части искомого корня.
Для функции polyroots можно выбрать один из двух численных методов – метод полиномов Лаггера (он установлен по умолчанию) или метод парной матрицы.
Решение системы линейных алгебраических уравнений
Рассмотрим систему уравнений вида
В матричной форме СЛАУ записывается в эквивалентном виде:
где А – матрица коэффициентов СЛАУ размерности n×n; x – вектор неизвестных; В – вектор правых частей уравнений.
СЛАУ имеет единственное решение, если матрица А является невырожденной, т. е. ее определитель не равен нулю. С вычислительной точки зрения, решение СЛАУ не представляет трудностей, если матрица А не очень велика.
В MathCAD СЛАУ можно решить как в более наглядной форме (1), так и в более удобной для записи форме (2). Для первого способа следует использовать вычислительный блок Given/Find, а для второго – встроенную функцию решения системы линейных уравнений lsolve. Мнемоника написания команды следующая:
где А – матрица коэффициентов системы; В – вектор правых частей.
Применение функции lsolve показано на рис. 42.
В некоторых случаях, для большей наглядности представления СЛАУ, его можно решить точно так же, как систему нелинейных уравнений. Не забывайте, что при численном решении всем неизвестным требуется присвоить начальные значения (это сделано в первой строке листинга) (рис. 43). Они могут быть произвольными, так как решение СЛАУ с невырожденной матрицей единственно.
Решение системы нелинейных уравнений
Рис. 7.4. Решение системы
Рассмотрим решение системы N нелинейных уравнений с m неизвестными
Здесь fi(x1, … , xm) – некоторые скалярные функции от скалярных переменных x1, x2, …, хm и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему можно формально переписать в виде f(x)=0, где х – вектор, составленный из переменных x1, x2, …, хm; f(x) – соответствующая векторная функция.
Для решения систем имеется специальный вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом:
1) Given – ключевое слово;
2) Система, записанная логическими операторами в виде равенств и, возможно, неравенств;
3) Find (х1, …, хm) – встроенная функция для решения системы относительно переменных х1, …, хm.
Вставлять логические операторы следует, пользуясь панелью инструментов Boolean (Булевы операторы). Если вы предпочитаете ввод с клавиатуры помните, что логический знак равенства вводится сочетанием клавиш + . Блок Given/Find используется для поиска решения итерационные методы, поэтому, как и для функции root, требуется задать начальные значения для всех х1, …, хm. Сделать это необходимо до ключевого слова Given. Значение функции Find есть вектор, составленный из решения по каждой переменной. Таким образом, число элементов вектора
Find равно числу аргументов.
В листинге (рис 44) приведен пример решения системы двух уравнений.
В первой строке листинга переменным х и у, относительно которых она будет решаться, присваиваются начальные значения. После этого следует ключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. Завершает вычислительный блок функция Find, содержащая вектор решения. Первый элемент вектора есть первый аргумент функции Find, второй элемент – ее второй аргумент.
Совет: Часто бывает очень полезно проверить точность решения уравнений, вычислив значения образующих их функций в найденных вычислительным процессором корнях.
Рис. 7.6. Точность
В листинге найдено только одно из двух решений – находящееся в правой нижней части графика (рис. 45). Чтобы отыскать и второе решение, следует повторить вычисления, изменив начальные значения так, чтоб они лежали ближе к другой точке пересечения графиков, например, х=–1, y=–1.
Пока мы рассмотрели пример системы из двух уравнений и таким же числом
неизвестных, что встречается наиболее часто. Но число уравнений и неизвестных может и не совпадать. Более того, в вычислительный блок можно добавить дополнительные условия в виде неравенств. Например, введение ограничения на поиск только отрицательных значений х (рис. 46).
Рис. 7.7. Ограничение на поиск
Обратите внимание, что, несмотря на те же начальные значения, что и в предыдущем листинге мы получили другой корень. Это произошло именно благодаря введению дополнительного неравенства, которое определено в блоке Given в предпоследней строке.
Если предпринять попытку решить несовместную систему, MathCAD выдаст сообщение об ошибке, гласящее, что ни одного решения не найдено, и предложение попробовать поменять начальные значения или значение погрешности.
Примечание: Вычислительный блок использует константу CTOL в качестве погрешности выполнения уравнений, введенных после ключевого слова Given. Другая константа TOL определяет условие прекращения итераций численным алгоритмом. Значение CTOL может быть задано пользователем, так же как и TOL, например, CTOL:=0,01. По умолчанию принято, что CTOL=TOL=0,001, но по желанию можно переопределить их.
Рис. 7.8. Переопределение
Вычислительным блоком с функцией Find можно найти и корень уравнения с одним неизвестным. Действие Find в этом случае совершенно аналогично уже рас
смотренным в данном разделе примерам. Задача поиска корня рассматривается как решение системы, состоящей из одного уравнения. Единственным отличием будет скалярный, а не векторный тип числа возвращаемого функцией Find (рис 47).
Символьное решение уравнений
Некоторые уравнения можно решить точно с помощью символьного процессора MathCAD. Делается это очень похоже на численное решение уравнений с применением вычислительного блока. Присваивать неизвестным начальные значения нет необходимости. Рассмотрим листинги символьного решение уравнения с одним неизвестным и системы двух уравнений с двумя неизвестными.
Как видно, вместо знака равенства после функции Find в листингах (рис. 48) следует знак символьных вычислений, который можно ввести с панели Symbolic, или, нажав клавиши + .
Рис. 7.9. Пример вычисления
Не забывайте, что сами уравнения должны иметь вид логических выражений, т.е. знаки равенства нужно вводить с помощью панели Booleans (Булевы операторы). Обратите внимание, что во втором листинге вычислены как два первых действительных корня, которые мы уже находили численным методом, так и два других мнимых корня. Эти два последних корня чисто мнимые, так как множитель
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
источники:
http://old.exponenta.ru/soft/MathCAD/usersguide/chapter15/15_1.asp
http://libraryno.ru/7-reshenie-uravneniy-v-srede-mathcad-prog_sr_z_2013/

Любой численный метод решения уравнения основан на уточнении какого-либо начального значения корня до заданной точности. Точность вычислений в MathCAD задается встроенной переменной TOL и по умолчанию равна 0,001. Для задания начального значения корня удобно сначала построить график функции, задающей уравнение.
Одно уравнение с одним неизвестным
1. Решение уравнения с помощью специальноговычислительного блока, состоящего из трех частей, идущих последовательно друг за другом:
–Given – ключевое слово, определяющее начало цикла или вычислительного блока;
–Уравнение, записанное с использованием жирного равно;
|
– |
Find(xn) – |
встроенная |
функция |
для |
решения |
уравнения |
|
|
относительно переменной xn. |
|||||||
|
Вставлять логический |
оператор |
следует, |
пользуясь |
панелью |
|||
|
инструментов Boolean |
(Булевы |
операторы). |
Если |
вы |
предпочитаете ввод с |
клавиатуры, помните, что логический знак равенства вводится сочетанием клавиш<Ctrl>+<=>. Блок Given/Find использует для поиска решения итерационные методы, поэтому требуется задать xn – начальные значения для неизвестной. Сделать это необходимо до ключевого словаGiven. Если начальные значения неизвестной задать в виде вектора(уравнение имеет несколько корней), то значение функции Find будет тоже вектор, составленный
из решения по каждому начальному значению неизвестной переменной.
2. Для решения уравнений с одной неизвестнойMathCAD имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента , исоответственно, работает несколько по-разному.
–root(y(х),х,а,b);
–root(y(х),х); где
y(х) – скалярная функция, определяющая уравнение;
31

х – скалярная переменная, относительно которой решается уравнение;
а, b – границы интервала, внутри которого происходит поиск корня.
Второй тип функции root требует дополнительного задания начального значения xn переменной х. Для этого нужно просто предварительно присвоить хn некоторое число. Поиск корня будет производиться вблизи этого числа.
Решение задачи 2 в Mathcad |
задание функции |
||
|
y (x) := 5 × sin(3 × x + 2) – 2.5 × x |
+ exp(x) |
||
|
10 |
|||
|
5 |
|||
|
y(x) |
0 |
1 |
2 |
|
– 1 |
|||
|
– 5 |
|||
|
– 10 |
|||
|
x |
|||
|
Первый способ |
|
æ –0.7 ö |
начальные приближения к корням, взятые из |
|||||
|
ç |
÷ |
|||||
|
xn := ç |
0.4 |
÷ |
графика и заданные в виде вектора |
|||
|
è |
1.5 |
ø |
||||
|
Given |
начало цикла |
|||||
|
y (xn) |
0 |
тело цикла, равенство с жирным равно |
||||
|
k := Find(xn) |
конец цикла, функция Find ищет корни уравнения |
|||||
|
с заданной точностью |
||||||
|
æ –0.635 ö |
||||||
|
ç |
÷ |
решение уравнение в виде вектора |
||||
|
k = ç |
0.452 |
÷ |
||||
|
è |
1.506 |
ø |
32

|
k1 := k0 = –0.635 |
k2 := k1 = 0.452 |
k3 := k2 = 1.506 |
||||
|
три корня, вывод ответа |
||||||
|
проверка |
y (k1) = 0 y (k2) = 0 y (k3) = 0 |
|||||
|
Второй способ: |
||||||
|
Использование встроенной функции root на интервале приближений |
||||||
|
xk1 := root(y (x) ,x ,-1 ,0) |
(–1 ,0) |
– интервал значения корня |
||||
|
xk1 = –0.635 первый корень |
||||||
|
xk2 := root(y (x) ,x ,0 ,1) |
xk2 = 0.452 |
второй корень |
||||
|
xk3 := root(y (x) ,x ,1 ,2) |
xk3 = 1.506 |
третий корень |
||||
|
Третий способ: |
||||||
|
Использование встроенной функции root с точкой начального приближения |
||||||
|
xn := –0.7 |
начальное приближение к корню |
|||||
|
kk1 := root(y (xn) ,xn) |
kk1 = –0.635 первый корень |
|||||
|
xn := 0.4 |
начальное приближение к корню |
|||||
|
kk2 := root(y (xn) ,xn) |
kk2 = 0.452 |
второй корень |
||||
|
xn := 1.5 |
начальное приближение к корню |
|||||
|
kk3 := root(y (xn) ,xn) |
kk3 = 1.506 |
третий корень |
||||
|
10 |
||||||
|
y(x) |
||||||
|
y(k) |
5 |
|||||
|
y(xk1) |
||||||
|
y(xk2) |
||||||
|
y(xk3) |
– 1 |
0 |
1 |
2 |
||
|
y(kk1) |
||||||
|
y(kk2) |
– 5 |
|||||
|
y(kk3) |
||||||
|
– 10 |
||||||
|
x,k ,xk1,xk2,xk3 ,kk1 ,kk2 ,kk3 |
||||||
|
33 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:
Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:
В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:
При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “
This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.
Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:
Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения
solve в сочетании со знаком символьного равенства система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера. Например:
Пример использования блока given…find для решения системы уравнений:
allmathcad.com
Уравнения с одним неизвестным в Mathcad
Простейший способ найти корень уравнения с одним неизвестным в Mathcad обеспечит функция root ( ). Аргументами функции root ( ) являются вид функции определяющей решаемое уравнение и имя переменой, относительно которой ищется решение — root (f(x),x) Если уравнение в Mathcad содержит несколько корней, то функция обеспечивает нахождение единственного корня, ближайшего к заданному начальному значению для искомой переменной. Точность вычислений может быть увеличена или уменьшена посредством задания значения переменной
TOL, равной по умолчанию 10-3 и определённой в меню Math, Options (Математика, Опции). Установленное значение TOL также оказывает влияние на точность вычислений.
В случае, если решаемое уравнение в Mathcad представлено полиномом, то все его решения могут быть получены с помощью функции polyroots (v). В качестве аргументов этой функции выступает вектор коэффициентов полинома –v, а результат представляется в виде вектора корней полинома. На листинге представлен пример нахождения корней уравнений с использованием функций root ( ) и polyroots ( ).
Другим способом решения уравнений в Mathcad является применение специального вычислительного блока, начинающегося с ключевого слова given с использованием функций find( ) и minerr ( ).
Блок имеет следующую структуру:
Начальное значение искомой переменной
given
Решаемое уравнение
Выражение с использованием функции find( ) или minerr ( )
Нахождение корней уравнения в Mathcad с использованием блока given…find ( ) в чем – то аналогично использованию функции root ( ). В Mathcad задается начальное значение для искомой переменной, после находится решение, ближайшее к заданному начальному условию. Использовании блока given…minerr ( ) имеет существенные особенности. Решение будет найдено в любом случае, даже при его отсутствии. Дело в том, что ищется не решение системы, а минимальная невязка уравнений. На листинге рассмотрена функция, заведомо не имеющая действительных корней и при использовании блока
given…minerr ( ) найдено решение, значение, которое наиболее приближено к оси х, то есть обеспечивает минималь-ную невязку. Значение невязки (ошибки) показывает системная переменная ERR.
allmathcad.com
Решение системы уравнений в Mathcad
Первоначально рассмотрим СЛАУ в Mathcad. Для их решения может использоваться блок given …find() или специальная функция lsolve(). Применение блока given …find() предопределяет необходимость задания начальных значений искомых переменных. Далее после ключевого слова given описывается СЛАУ и с помощью find() находится решение. Следует указать, что в том случае, когда
СЛАУ в Mathcad имеет бесконечное множество решений блок given …find() дает конкретный результат, что несомненно следует отнести к недостаткам. В случае отсутствия решения будет выдано сообщение “Matrix is singular. Cannot compute its inversу – Матрица сингулярная. Нельзя вычислить эту инверсию”.
Применение функции lsolve( ) позволяет избежать этого недостатка. Функция lsolve(M,b) имеет два аргумента. M – матрица коэффициентов при неизвестных, b – вектор свободных членов. На листинге приведен пример решения СЛАУ.
Пример решения СЛАУ:

given…find() и given…minerr () для решения систем нелинейных уравнений.
allmathcad.com
Урок 24. Решение уравнений в Mathcad – использование функций
Решение уравнений является важным для решения практических задач. Поэтому уделим уравнениям еще один урок.
Блок решения в функции
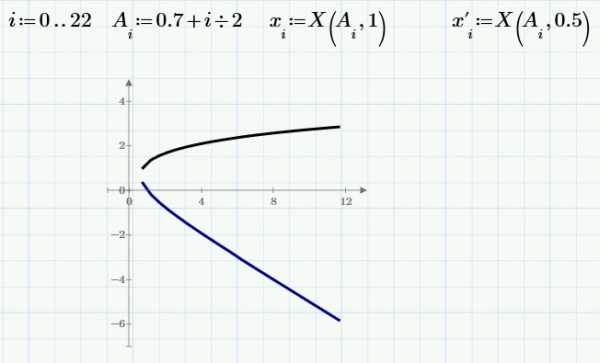
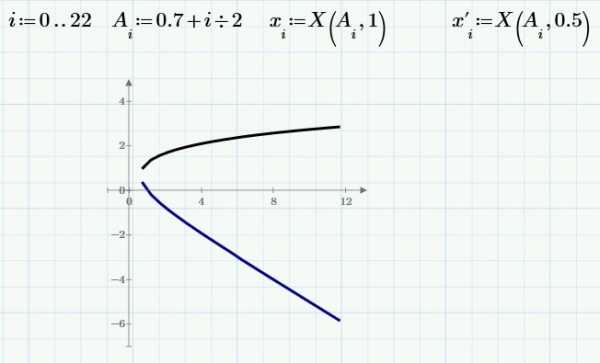
Если Вы хотите исследовать изобразить на графике поведение уравнения в зависимости от значения определенного параметра, Вам, возможно, придется решить систему уравнений много раз. Вы можете сделать это, используя блок решения в функции. Покажем на примере: предположим, мы хотим исследовать поведение решения следующего уравнения в зависимости от различных значения параметра
A:
Блоку решения не нужно ни значение параметра, ни начальное приближение, поскольку решение есть функция этих двух значений. Эти значения мы будем задавать при вызове функции.
Функцию можно использовать сколько угодно раз:
Использовать функцию можно с диапазоном переменных:
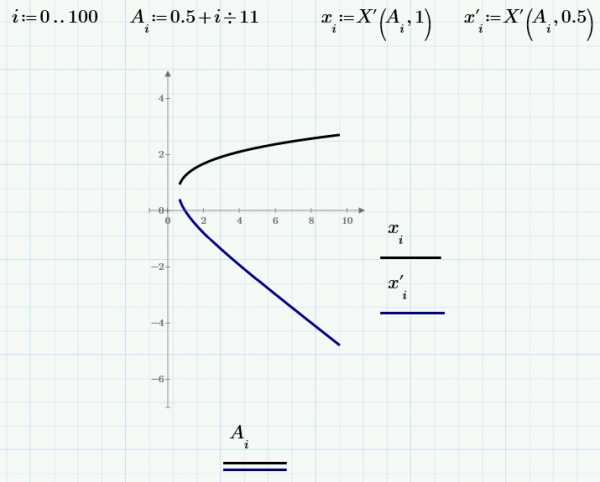
Такая техника решения не самая надежная. Если хотя бы одно решение не может быть найдено, Вы не получите и решений для других параметров (это произойдет, если задать
A<0.7). Поэтому лучше заранее проверить свою функцию.
Сообщения об ошибке можно избежать, написав маленькую программу:
Если блок решения выдает сообщение об ошибке, на выходе получим значение NaN (Not a Number – «Не Число»), которое просто не отображается на графике:
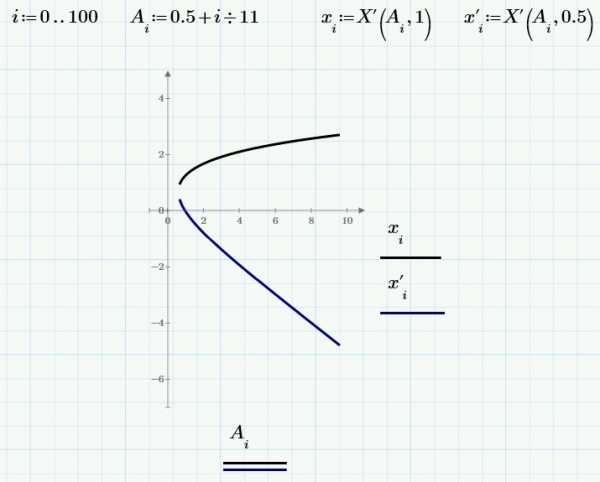
Построим две ветки уравнения с использованием этого приема:
Когда переменных много
Расчеты часто содержат несколько переменных, но Вам, возможно, придется использовать лишь некоторые из них. В качестве примера рассмотрим систему восьми уравнений, где нам нужно получить только значения X и Y. Начальные приближения следует задать для всех переменных:
Решение представляет собой вектор из восьми элементов, но нам нужны лишь элементы с индексами 0 и 1.
Минимизация ошибки
Find() – не единственный решатель в Mathcad. Еще один полезным решателем является Minnerr(), находящий решения, которые минимизируют ошибку в системе уравнений. Рассмотрим пример: есть набор данных, которые мы хотим аппроксимировать уравнением Бейтмена:
Мы хотим подобрать три константы в уравнении Бейтмена таким образом, чтобы ошибка приближения была минимальна. У нас есть семь уравнений (по одной для каждого эксперимента) и три константы, так что в системе избыток данных. Minerr() может обработать эту проблему:
Замечания:
- Три константы являются переменными для этой системы.
- Переменные не могут иметь счетных индексов.
- У параметров (t и c) могут быть счетные индексы.
Возможно, Вам хотелось бы использовать цикл
for для семи уравнений, но в блоке решений этого сделать нельзя.
Для полностью определенных систем (с одинаковым числом независимых уравнений и неизвестных) функция Minerr() дает тот же ответ, что и Find().
Резюме
В этом уроке мы определили способы расширенного использования блоков решения:
- Вы можете определить вывод блока решения как функцию. Таким образом в блок решения можно передавать параметры и начальные приближения.
- Если при вычислении точек для графика хотя бы одно решение не будет найдено, то график не будет построен. Этой ошибки можно избежать, написав небольшую программу с использованием “try/on error”, которая выводит NaN (Not a Number – Не Число), если результат отсутствует.
- Для двух и более неизвестных (и уравнений) вывод блока решения является вектором. Если нужен один или два элемента этого вектора, их можно вывести, используя подстрочные индексы.
- Вместо функции Find() можно использовать Minerr() – она минимизирует ошибку для заданного набора ограничений, в том числе, если данные избыточны. Minerr() часто может дать приближенный результат, когда Find() выдает ошибку.
Другие интересные материалы
sapr-journal.ru
2. Решение уравнений в Mathcad
2.1. Численное решение уравнения
Для простейших уравнений
вида f(x) = 0
решение в Mathcad находится с помощью
функции root
root(
f(х1,
x2,
…),
х1,
a,
b
)
Возвращает значение х1,
принадлежащее отрезку [a,
b],
при котором выражение или функция f(х)
обращается в 0. Оба
аргумента этой функции должны быть
скалярами. Функция возвращает скаляр.
Аргументы:
f(х1,
x2,
…)
— функция,
определенная где-либо в рабочем документе,
или выражение. Выражение должно возвращать
скалярные значения.
х1
— — имя переменной,
которая используется в выражении. Этой
переменной перед использованием функции
root
необходимо присвоить
числовое значение. Mathcad использует его
как начальное приближение при поиске
корня.
a,
b
– необязательны, если
используются, то должны быть вещественными
числами, причем a
< b.
Наиболее распространен
графический способ
определения начальных приближений.
Принимая во внимание, что действительные
корни уравнения f(x)
= 0 — это точки пересечения графика функции
f(x)
с осью абсцисс, достаточно построить
график функции f(x)
и отметить точки пересечения f(x)
с осью Ох,
или отметить на оси Ох
отрезки, содержащие по одному корню.
Построение графиков часто удается
сильно упростить, заменив уравнение
f(x)
= 0 равносильным
ему уравнением:
|
, |
где функции
f1(x)
и f2(x)
— более простые, чем функция
f(x).
Тогда, построив графики функций у
=
f1(x)
и у
= f2(x),
искомые корни получим как абсциссы
точек пересечения этих графиков.
Пример.
Графически отделить
корни уравнения:
Уравнение (1) удобно
переписать в виде равенства:
lg x=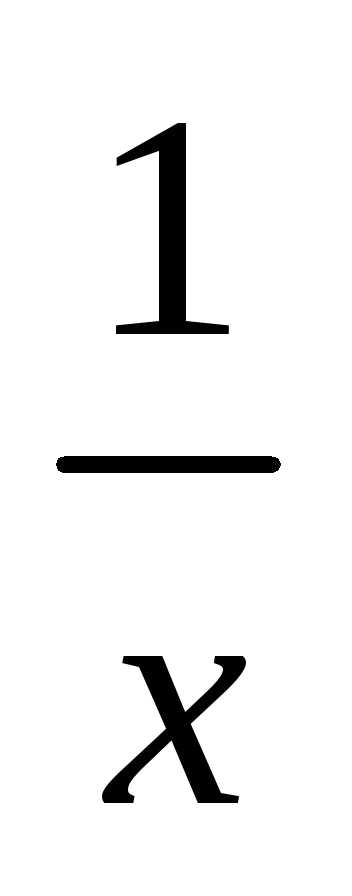
Отсюда ясно, что корни
уравнения (1) могут быть найдены как
абсциссы точек пересечения логарифмической
кривой y
= lg x и
гиперболы y
=
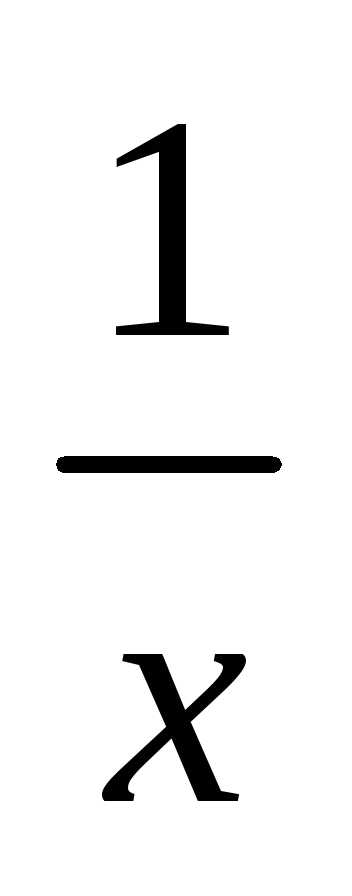
Построив эти кривые, приближенно найдем
единственный корень
уравнения (1) или определим его содержащий
отрезок [2, 3].
Упражнение 1.
Построить график
функции f(x)
(Таблица 1) и приблизительно
определить один из корней уравнения.
Решить уравнение f(x)=
0 с
помощью встроенной функции Mathcad root.
Таблица 1
Варианты упражнения 1
-
x3
+ x2
-2sin(x)
=05x
— 8ln(x) = 8x2
+ x — cos(3x) = 1x2
— sin(4x) = 03x
— 2ln(x) = 52x
-2,2x =0x2
— 2x -sin(3x) =1x
— sin(x)
-0.25
= 03x —
ex
= 03x
— 2ln(x) = 5ex
+ e-3x
= 4x
+4sin(x) = 22.7x
— 1.5ln(x) = 2.8x3
+ x2
-2sin(x)
=0ex
-6x =3
studfiles.net
Решение уравнений в MathCad – использование функций
Одной из самых важных математических задач является решение уравнений. Поэтому нам стоит остановиться на них еще подробнее.
Блок решения в функциях
Если вам нужно просмотреть на графике действие уравнения, относительно определенных параметров, вам, судя по всему, придется решить данное уравнение огромное количество раз. Давайте обратимся к визуальному примеру. Попробуем просмотреть поведение решения уравнений в зависимости от разных значений параметра А.
Блок решения не нуждается в значениях параметров, изначальных приближениях. Решением будет считаться функция двух указанных значений. Их мы будем оформлять во время вызова функций.
Каждая функция может быть использованной неограниченное количество раз.
Так, можно воспользоваться функцией с диапазонами переменных.
Данная методика решения задач не считается самой проверенной и надежной. Если хотя бы одно решение не удастся найти, пользователь не сможет перейти к решению остальных параметров. Вот почему нужно быть максимально уверенным в правильности заданных функций.
Чтобы избежать появления ошибок, достаточно написать небольшую программу.
Когда блок решения начинает выдавать ошибки, мы получим значение NaN (Not a Number – «Не Число». Впрочем, на графике мы его не увидим.
Теперь разработаем две ветки уравнения при использовании данного опционала:
Что делать в случаях, когда переменных много
Бывают расчеты, в которых вмещено несколько переменных. Вполне возможно, что когда-то с ними столкнетесь и вы. Для примера мы возьмем систему, которая состоит из восьми уравнений. Нам понадобится получить только X и Y. Сначала же зададим всем переменным начальное приближение.
Решение становится вектором из восьми пунктов. Нам потребуются исключительно те элементы, которые вмещают индексы 0 и 1.
Устранение ошибки
Теперь давайте на примере просмотрим набор данных, которые будут аппроксимированны в соответствии с уравнениями Бейтмена.
Сейчас мы собираемся разработать три константы при помощи уравнения Бейтмена таким образом, чтобы актуальная ошибка приближения была минимизирована. Что мы имеем? Систему из семи уравнений. Каждая из них соответствует отдельному эксперименту. Также у нас есть три константы, а, следовательно, система пострадала от преизбытка данных. Опция Minerr () станет оптимальным инструментом для обработки данной проблемы.
Константы – это переменные нашей системы. Переменные не имеют математических индексов. Параметры имеют индексы счетного типа.
archicad-autocad.com
Урок 23. Нелинейные уравнения в Mathcad
Mathcad может решать системы линейных и нелинейных уравнений с помощью встроенных алгоритмов. На самом деле, «решать» — не совсем верное определение того, что делает программа. Лучше рассуждать так: Вы задаете приближенное значение, затем программа уточняет эту оценку. Поэтому, используя такую технологию решения, нужно знать, что Вы делаете. Вы должны понимать, как ведет себя функция, которую исследуете. Иначе Вы можете быть разочарованы.
Изучение «решения» начнем с уравнений с одной переменной. В этом случае поведение уравнения можно понять, построив график. Позже мы рассмотрим системы уравнений.
Уравнения с одной переменной
Уравнение, которое мы рассмотрим, достаточно простое:
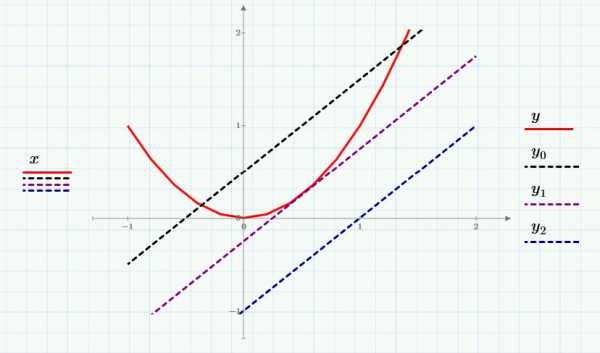
Рассмотрим это уравнение как пересечение прямой линии (левая часть) и парабола (правая часть). Построим графики трех прямых линий и посмотрим, что произошло:
Первая (самая верхняя) линия дважды пересекается с параболой около точек x=-0.3 и x=1.3. У второй линии – одно пересечение (или два близко расположенных) возле точки x=0.5. Пересечений с третьей прямой (самой нижней) нет.
Решения
Сначала рассмотрим самую верхнюю линию. Чтобы получить решение, нам нужен Блок решения (вкладка Математика –> Области –> Блок решения). Заполним блок для решения первого уравнения:
Здесь есть три области для различных записей:
— начальные приближения;
— ограничения;
— решатель.
В области ограничений мы записали уравнение, которое хотим решить. В первой области мы задали приближенное решение этого уравнения. Функция Find(), которую мы записали в последней области – это решатель.
Как видно, решение 1.366 – это правое пересечение прямой и параболы. Начальное приближение не критично – можно ввести 1.6, щелкнуть мышью вне блока и получить тот же результат:
Изменим начальное приближение на значение, близкое к левому пересечению, скажем, -0.5. Решение изменится на -0.366:
Измените начальное приближение обратно на 1.3.
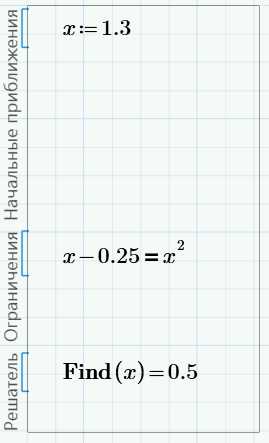
Теперь поменяем константу 0.5 в уравнении на -0.25. Решение изменится на 0.5:
Этот же ответ мы будем получать для любого значения начального приближения – это единственное решение.
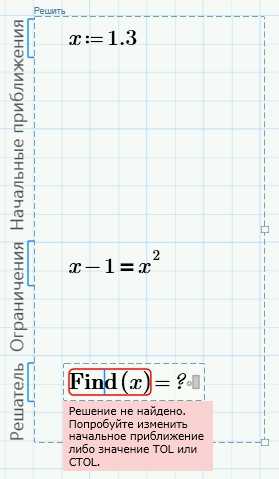
Наконец, изменим константу в уравнении на -1 (последнее уравнение). Щелкнем вне блока и получим сообщение об ошибке:
Решения нет. Изменим константу обратно на 0.5.
Вывод решения
Переменные в блоке решений локальны. Вы не можете использовать их значения вне блока. Вернемся к уравнению, где приближенное значение задано 1.3. Мы решили уравнение, чтобы найти более точное решение x=1.366. Однако если мы попробуем вывести значение x, мы получим вектор, которые определили для нашего графика.
Если Вы хотите использовать результат решения в дальнейших вычислениях, нужно присвоить функцию решателя переменной:
Тогда получим верный результат:
Решение систем уравнений
Для примера решим систему трех уравнений: два линейных и одно кубическое. Здесь три неизвестных – начальное приближение даем для всех трех:
Все три ответа можно вывести в вектор:
Удалите последнее из трех уравнений. Решение все равно будет найдено, с учетом двух оставшихся уравнений:
Однако, такое решение может быть не тем, которое Вам нужно.
Обратите внимание еще на некоторые детали. В блоке решения используются два вида знака «равно»: знак присваивания для начальных приближений и для решателя Find, и знак булева равенства в уравнении. Эта разница очень важна. Еще один момент – щелкните по слову Find в области решателя, откройте вкладку Математика. В строке Обозначения должно быть отмечено «Ключевое». Некоторые другие ключевые слова мы рассмотрим в последующих уроках.
Растворимость вещества
Рассмотрим растворение вещества DOH. Это двухстадийный процесс: сначала растворяется твердая фаза, затем растворенные части диссоциируют на D и OH. Малую растворимость можно повысить, добавив небольшое количество сильной кислоты HA. Она диссоциирует, и ионы водорода вступают в реакцию с гидроксильной группой:
Как зависит общая растворимость D от количества добавленной кислоты? Концентрацию будем считать в моль/л. Концентрация насыщения нерастворенной кислоты:
Начнем с концентрации кислоты:
Константы равновесия реакции:
Блок решения начинается с трех неизвестных и их начальных приближений:
Решение:
Общая концентрация вещества:
Расчет для построения графика (подробнее о таких расчетах поговорим в следующем уроке):
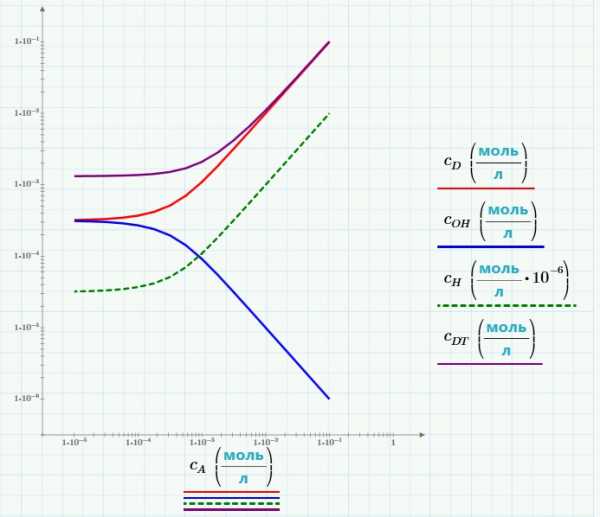
График показывает концентрацию как функцию от количества добавленной кислоты. Концентрация ионов водорода на порядки меньше, чем концентрации других элементов. Поэтому мы изменили масштаб в миллион раз, чтобы показать этот график в тех же осях:
Если концентрация кислоты мала, решение содержит низкую концентрацию DOH, которая диссоциирует только частично. При увеличении концентрации кислоты, все больше и больше вещества диссоциирует.
Резюме
- Если есть уравнение или система уравнений, Вы можете дать приближенное решение, а Mathcad улучшит эту оценку. Такой способ используется в Блоке решения.
- Первая часть блока решения – начальные приближения, т.е. Ваши оценки. Здесь используется знак присваивания «:=». Эти значения могут быть помещены и до блока.
- В области «Ограничения» (уравнения) нужно использовать булево равенство [Ctrl+=]. Это единственный знак, по обе стороны от которого могут быть выражения.
- Блок решения заканчивается функцией для решения. Мы рассмотрели Find(), которая содержит неизвестные, которые нужно найти.
- Чтобы использовать результат решения в дальнейших расчетах, присвойте Find() переменной. Это может быть как одна переменная, так и вектор.
- Для решения системы нелинейных уравнений нужно быть внимательным. Число уравнений должно быть равно числу неизвестных. Кроме того, приближенные значения должны быть как можно ближе к решению.
- Если решение не было найдено, не спешите обвинять Mathcad. Нелинейные уравнения являются головной болью для любого языка программирования. Попробуйте понять поведение Ваших уравнений, прежде чем приступать – часто уравнения могут не иметь решения.
Другие интересные материалы
sapr-journal.ru