Как в меню по дереву найти

Оглавление (нажмите, чтобы раскрыть)

Добавление и удаление строк

Пример добавления и удаления строк дерева значений

Должности = Новый ДеревоЗначений;
Должности.Колонки.Добавить("Должность");

ГенДир = Должности.Строки.Добавить();
ГенДир.Должность = "Ген. директор";

ФинДир = ГенДир.Строки.Добавить();
ФинДир.Должность = "Фин. директор";

КомДир = ГенДир.Строки.Добавить();
КомДир.Должность = "Ком. директор";

//удаляем строку "Фин. директор"
ГенДир.Строки.Удалить(0);

//удаляем все строки ветки "Ген. директор"
ГенДир.Строки.Очистить();

//удаляем все строки дерева
Должности.Строки.Очистить();

Загрузка и выгрузка колонок

Примеры загрузку и выгрузки колонок дерева значений

Должности = Новый ДеревоЗначений;
Должности.Колонки.Добавить("Должность");

ГенДир = Должности.Строки.Добавить();
ГенДир.Должность = "Ген. директор";

ФинДир = ГенДир.Строки.Добавить();
ФинДир.Должность = "Фин. директор";

КомДир = ГенДир.Строки.Добавить();
КомДир.Должность = "Ком. директор";

Массив = Должности.Строки.ВыгрузитьКолонку(0);
//Массив = ["Ген. директор"]

Массив = ГенДир.Строки.ВыгрузитьКолонку(0);
//Массив = ["Фин. директор", "Ком. директор"]

Массив[0] = "Тех. директор";
ГенДир.Строки.ЗагрузитьКолонку(Массив, 0);

Инициализация

Пример создания дерева значений

Должности = Новый ДеревоЗначений;
Должности.Колонки.Добавить("Должность");
Должности.Колонки.Добавить("Количество");

ГенДир = Должности.Строки.Добавить();
ГенДир.Должность = "Ген. директор";
ГенДир.Количество = 1;

ФинДир = ГенДир.Строки.Добавить();
ФинДир.Должность = "Фин. директор";
ФинДир.Количество = 1;

КомДир = ГенДир.Строки.Добавить();
КомДир.Должность = "Ком. директор";
КомДир.Количество = 1;

Торг = КомДир.Строки.Добавить();
Торг.Должность = "Торг. представитель";
Торг.Количество = 3;

Обход дерева значений

Пример обхода дерева значений

Должности = Новый ДеревоЗначений;
Должности.Колонки.Добавить("Должность");
Должности.Колонки.Добавить("Количество");

ГенДир = Должности.Строки.Добавить();
ГенДир.Должность = "Ген. директор";
ГенДир.Количество = 1;

ГлБух = ГенДир.Строки.Добавить();
ГлБух.Должность = "Гл. бухгалтер";
ГлБух.Количество = 1;

ЗамГлБух = ГлБух.Строки.Добавить();
ЗамГлБух.Должность = "Зам. гл. бухгалтера";
ЗамГлБух.Количество = 1;

БухРасчет = ГлБух.Строки.Добавить();
БухРасчет.Должность = "Бух. расч. отдела";
БухРасчет.Количество = 3;

ПоказатьДЗ(Должности);

КонецПроцедуры

&НаСервере
Процедура ПоказатьДЗ(Дерево, Уровень = 1)
    Пробелы = "          ";
    Для Каждого Строка из Дерево.Строки Цикл
        Стр = Строка.Должность + ": " +
        Строка.Количество + " ед.";
        //отступ для подчиненных строк
        Стр = Лев(Пробелы, (Уровень - 1)*2) + Стр;
        Сообщить(Стр);
        ПоказатьДЗ(Строка, Уровень + 1);
    КонецЦикла;
КонецПроцедуры

Перемещение строк

Пример перемещения строк в дереве значений

Должности = Новый ДеревоЗначений;
Должности.Колонки.Добавить("Должность");

ГенДир = Должности.Строки.Добавить();
ГенДир.Должность = "Ген. директор";

ФинДир = ГенДир.Строки.Добавить();
ФинДир.Должность = "Фин. директор";

КомДир = ГенДир.Строки.Добавить();
КомДир.Должность = "Ком. директор";

//сдвигаем фин. дир. на строчку ниже
ГенДир.Строки.Сдвинуть(0, 1);

//возвращаем обратно
ГенДир.Строки.Сдвинуть(1, -1);

Перечисление колонок

Пример перечисления колонок в дереве значений

Товары = Новый ДеревоЗначений;
Товары.Колонки.Добавить("Товар");
Товары.Колонки.Добавить("Цена");

Для Каждого Колонка Из Товары.Колонки Цикл
    Сообщить(Колонка.Имя);
КонецЦикла;

Поиск по дереву значений

Пример поиска по дереву значений

Должности = Новый ДеревоЗначений;
Должности.Колонки.Добавить("Должность");
Должности.Колонки.Добавить("Количество");

Директор = Должности.Строки.Добавить();
Директор.Должность = "Директор";
Директор.Количество = 1;

Бухгалтер = Директор.Строки.Добавить();
Бухгалтер.Должность = "Бухгалтер";
Бухгалтер.Количество = 1;

Продавец = Директор.Строки.Добавить();
Продавец.Должность = "Продавец";
Продавец.Количество = 3;

//поиск по всем колонкам и подчиненным строкам
Строка1 = Должности.Строки.Найти("Продавец", Неопределено, Истина);
//Строка = Продавец : 3

//поиск по колонке "Должность", включая подчиненные строки
Строка2 = Должности.Строки.Найти("Продавец", "Должность", Истина);
//Строка = Продавец : 3

//поиск по колонке "Количество", включая подчиненные строки
Строка3 = Должности.Строки.Найти("Продавец", "Количество", Истина);
//Строка = Неопределено

//поиск по колонке "Должность"
Строка4 = Должности.Строки.Найти("Продавец", "Должность");
//Строка = Неопределено

//поиск по всем колонкам в строке "директор"
строка5 = директор.Строки.Найти("Продавец");
//строка = Продавец : 3

ПараметрыОтбора = Новый Структура;
ПараметрыОтбора.Вставить("Количество", 1);
строки = должности.Строки.НайтиСтроки(ПараметрыОтбора, Истина);
//массив из строк "Директор" и "Бухгалтер"

Получение индекса строки

Пример получения индекса строки дерева значений

Должности = Новый ДеревоЗначений;
Должности.Колонки.Добавить("Должность");

ГенДир = Должности.Строки.Добавить();
ГенДир.Должность = "Ген. директор";

ФинДир = ГенДир.Строки.Добавить();
ФинДир.Должность = "Фин. директор";

КомДир = ГенДир.Строки.Добавить();
КомДир.Должность = "Ком. директор";

Индекс = Должности.Строки.Индекс(КомДир);
//Индекс = -1

Индекс = ГенДир.Строки.Индекс(КомДир);
//Индекс = 1

Создание копии дерева значений

Пример создания копии дерева значений

Должности = Новый ДеревоЗначений;
Должности.Колонки.Добавить("Должность");

ГенДир = Должности.Строки.Добавить();
ГенДир.Должность = "Ген. директор";

ФинДир = ГенДир.Строки.Добавить();
ФинДир.Должность = "Фин. директор";

КомДир = ГенДир.Строки.Добавить();
КомДир.Должность = "Ком. директор";

//полная копия дерева
Копия = Должности.Скопировать();

Сортировка данных в дереве значений

Пример сортировки данных в дереве значений

Должности = Новый ДеревоЗначений;
Должности.Колонки.Добавить("Должность");
Должности.Колонки.Добавить("Количество");

ГлБух = Должности.Строки.Добавить();
ГлБух.Должность = "Гл. бухгалтер";
ГлБух.Количество = 1;

ЗамГлБух = ГлБух.Строки.Добавить();
ЗамГлБух.Должность = "Зам. гл. бухгалтера";
ЗамГлБух.Количество = 1;

БухРасчет = ГлБух.Строки.Добавить();
БухРасчет.Должность = "Бух. расч. отдела";
БухРасчет.Количество = 3;

//сортировка подчиненных строк строки глБух
ГлБух.Строки.Сортировать("Должность Возр");

//сортировка всех строк дерева значений
Должности.Строки.Сортировать(
    "Количество Убыв, Должность Возр", Истина);

От автора: приветствую Вас дорогой друг. Меню — это неотъемлемая часть любого сайта и даже в том случае, если он состоит всего лишь из одной страницы. И так сложилось, что, как правило, редко встречаются меню одного уровня. Наибольшее распространение получили как раз многоуровневые меню, так как они позволяют расположить большее количество ссылок на значительно меньшем пространстве. Поэтому в данном уроке мы рассмотрим формирование древовидной структуры данных для отображения на экран меню указанного типа.

Уже достаточно давно на нашем сайте был опубликован урок по данной теме. И собственно, решение, которое представлено в уроке, очень неплохое и отлично справляется с поставленной задачей, но в некоторых случаях все же не совершенно. Так как, по сути, структура данных, которая формируется – не древовидная и подходит лишь к той функции, которая показана и используется для вывода ссылок на экран.

Если же потребуется передать данную структуру в определенное место для последующей обработки, то могут возникнуть определенные проблемы. Поэтому в текущем видео я хотел бы предложить несколько иное решение по формированию массива данных и собственно выводу его на экран.

Для начала, хотел бы немного остановиться на заготовке того скрипта с которым мы будем работать. Собственно он состоит всего лишь из двух файлов – index.php и functions.php.

Код файла index.php:

Как Вы видите все предельно просто – подключаем файл functions.php, в котором определены и будут сегодня определяться функции. Далее вызываем функцию подключения к базе данных и после этого вызываем на исполнение функцию getCategories(), которая вернет в виде массива выборку информации из таблицы базы данных, с которой мы будем сегодня работать, в вот таком виде:

Для данного урока я использую ту же базу данных, что и в указанном выше видео.

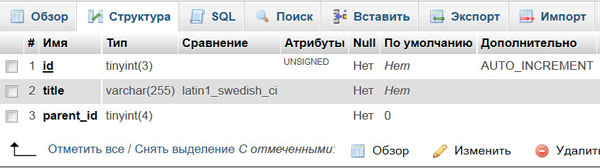
Напомню, что в поле title содержится заголовок категории или ссылки меню, в поле parent_id – идентификатор родительской категории, причем элементы самого верхнего уровня в данном поле содержат 0 и наконец, поле id – это идентификатор таблицы.

Далее, код файла functions.php:

Код приведенных функцию, думаю, не нуждается в комментариях. Теперь мы можем приступить к работе и по большому счету мы с Вами напишем ровно три функции и парочку шаблонов для отображения данных на экран. Итак, начинаем писать первую функцию, часть которой будет знакома тем, кто смотрел вышеуказанный урок:

Хотел бы заметить, что код еще не завершен – это только начало. Обратите внимание, что в качестве аргумента мы будем передавать массив из которого будет сформирована древовидная структура. Как Вы видите в коде, используя цикл foreach, мы обходим массив, переданный в виде аргумента, и формируем новый — $parents_arr, ключами которого, являются идентификаторы родительских категорий. И в каждой ячейке данного массива, содержится дополнительный подмассив – всех категорий (дочерних), у которых идентификатор родительской категории равен ключу соответствующего массива.

В итоге при вызове данной функции и распечатки на экран возвращаемого значения, мы получим следующий результат:

Теперь, мы подготовили данные и наша задача, состоит в том, что бы сформировать такой многоуровневый массив, в котором на первом уровне вложенности присутствовали только родительские элементы высшего уровня, далее в каждом из них будет определен элемент children, в котором будет содержаться массив дочерних элементов. Которые в свою очередь, если содержат потомков, так же будут их хранить в указанном элементе. Таким образом, нам нужно получить массив вот такого вида:

А значит, мы можем продолжить писать код функции и несколько изменим возвращаемое значение:

Обратите внимание, что мы создаем новый массив $treeElem, который далее возвращается как результат работы функции. И по умолчанию сохраняем в него элементы самого высокого уровня, которые содержатся в ключе с индексом 0, массива $parents_arr. По сути, сейчас мы получили массив элементов верхнего уровня, в который нужно добавить дочерние элементы, непосредственно в ячейку с ключом children. И сделает это дополнительная функция generateElemTree(), которую мы сейчас с Вами напишем.

Итак, код функции generateElemTree():

Важно! Первый аргумент функции – это ссылка на массив $treeElem , так как нам нужно его изменить – доработать и вернуть как результат работы функции createTree(). Второй же аргумент это массив который мы с Вами получили в выше указанной функции. Собственно работа функции хоть и кажется сложной, но на самом деле очень проста.

Для начала, проверяем есть ли в переданном массиве элемент с ключем ‘children’ и если его нет то мы его создаем и инициализируем пустым массивом:

А далее мы проверим, есть ли в массиве $parents_arr, элемент с ключом $key. При этом, напомню что в $key – содержится идентификатор текущего элемента, а в массиве $parents_arr, ключи это идентификаторы родительских элементов. Соответственно если условие выполнилось, значит, мы нашли дочерние элементы для текущего элемента. Соответственно массив дочерних элементов записываем я ячейку с ключом children. Затем рекурсивно вызываем эту же функцию, передавая при этом как раз найденный массив дочерних элементов, ведь они так же в свою очередь могут быть родителями для других элементов.

Вот собственно и все, если распечатать на экран содержимое массива $treeElem, мы получим желаемую древовидную структуру данных, которая показана на рисунке выше. Теперь необходимо вывести на экран полученные данные. Для этого напишем функцию шаблонизатор:

Код данной функции я позаимствовал из урока по созданию собственного шаблонизатора, а значит, комментировать ее я не буду, так как в уроке приведено подробнейшее описание.

Теперь, думаю, стоит привести код файла index.php, так как именно в нем мы будем использовать только что написанную функцию:

Как Вы видите, с помощью шаблонизатора, подключается файл template.php , код которого приведен ниже:

Внутри шаблоны мы опять же обращаемся к функции шаблонизатора и подгружаем дополнительный шаблон в который передается все та же переменная cats. Хотел бы отметить что так как мы не знаем сколько уровней вложенности в нашей древовидной структуре, соответственно нам нужно рекурсивно обрабатывать ее, а значит рекурсивно подгружать шаблон который будет выводить один уровень вложенности, что собственно и реализовано, используя дополнительный шаблон, код которого приведен ниже:

Логика работы шаблона сводится к следующему: используя цикл foreach() обходим элементы одного уровня и если у элемента в ячейке ‘children’, содержится массив дочерних элементов – рекурсивно, вызываем функцию renderTemplate(), подгружаем этот же шаблон, но при этом передаем в качестве переменной ‘cats’ ,массив дочерних элементов. При этом на экране, в качестве результата мы увидим следующее:

Вот собственно и все. Всего Вам доброго и удачного кодирования!!!

Дерево – структура данных, представляющая собой древовидную структуру в виде набора связанных узлов.

• A — корень дерева
• В — корень левого поддерева
• С — корень правого поддерева

Способы обхода дерева

Пусть имеем дерево, где A — корень, B и C — левое и правое поддеревья.

Существует три способа обхода дерева:

• Обход дерева сверху вниз (в прямом порядке): A, B, C — префиксная форма.
• Обход дерева в симметричном порядке (слева направо): B, A, C — инфиксная форма.
• Обход дерева в обратном порядке (снизу вверх): B, C, A — постфиксная форма.

Реализация дерева

Узел дерева можно описать как структуру:

При этом обход дерева в префиксной форме будет иметь вид

Обход дерева в инфиксной форме будет иметь вид

Обход дерева в постфиксной форме будет иметь вид

Бинарное (двоичное) дерево поиска – это бинарное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):

• оба поддерева – левое и правое, являются двоичными деревьями поиска;
• у всех узлов левого поддерева произвольного узла X значения ключей данных меньше, чем значение ключа данных самого узла X;
• у всех узлов правого поддерева произвольного узла X значения ключей данных не меньше, чем значение ключа данных узла X.

Добавление узлов в дерево

Удаление поддерева

Пример Сортировка элементов массива с помощью дерева

Пример Написать программу, подсчитывающую частоту встречаемости слов входного потока.

Поскольку список слов заранее не известен, мы не можем предварительно упорядочить его. Неразумно пользоваться линейным поиском каждого полученного слова, чтобы определять, встречалось оно ранее или нет, т.к. в этом случае программа работает слишком медленно.

Один из способов — постоянно поддерживать упорядоченность уже полученных слов, помещая каждое новое слово в такое место, чтобы не нарушалась имеющаяся упорядоченность. Воспользуемся бинарным деревом.

В дереве каждый узел содержит:

• указатель на текст слова;
• счетчик числа встречаемости;
• указатель на левого потомка;
• указатель на правого потомка.

 
Рассмотрим выполнение программы на примере фразы

now is the time for all good men to come to the aid of their party

При этом дерево будет иметь следующий вид

Пример реализации

Результат выполнения

Назад: Структуры данных

Время на прочтение
3 мин

Количество просмотров 18K

В процессе работы над одним из проектов передо мной встала задача создания сворачиваемого дерева папок на основе сведений о нем в базе данных. Для уточнения, это выглядит примерно так:

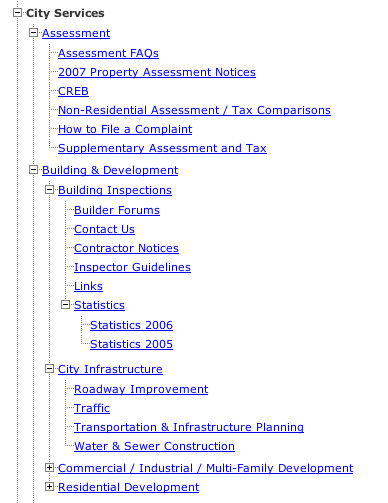
Собственно, задача стояла следующая: на сервере в таблице базы данных хранится структура дерева каталогов, которая после определенных преобразований должна отобразиться в вышеуказанном виде.

Мы имеем следующую структуру таблицы в БД:
id — идентификатор строки
level — уровень элемента
left_key — левый ключ
right_key — правый ключ
caption — название каталога.
Более подробно о создании такой таблицы вы можете узнать здесь.
Посредством AJAX эти данные, отсортированные по значению поля left_key, поступают на клиента, где мы должны построить на их основе вложенный список.
Список должен иметь следующую структуру:

Элемент <ul>, содержащий:
    элемент <li>, представляющий собой каталог. 
        Далее, в нем всегда есть элемент <span>, содержащий название каталога. 
        При условии наличия дочерних папок, в нем есть элемент <ul>
            и так далее...
    и так далее... 

Приступим к генерации дерева.
В первую очередь, необходимо создать функцию, возвращающую дочерние элементы или пустой массив в случае их отсутствия.

var getChilds = function(trgt, arr){
    var childs = Array();
    var length = arr.length;
    for (var i = 0; i < length; i++){
        var curr = getInts(arr[i]);
        var under = (curr.level > trgt.level) ;
        var l_in =  (curr.left_key > trgt.left_key);
        var r_in =  (curr.right_key < trgt.right_key);
        if (under && l_in && r_in) childs.push(arr[i]);
    }
    return childs;
}

Эта функция делает не что иное, как проверку каждого элемента массива по заданному элементу этого же массива, то есть: если уровень рассматриваемого элемента ниже уровня заданного элемента, при том что левые и правые ключи соответственно находятся в промежутке между левым и правым ключом заданного элемента, то записываем рассматриваемый элемент в массив дочерних элементов.
Функция getInts в данном случае занимается преобразованием значений полей level, left_key и right_key в числовые значения. Нужно это для того, чтобы происходило сравнение чисел, а не строк.

var getInts = function(arr){
    temp = Object();
    for (var i in arr){
        if (i!='name') temp[i] = parseInt(arr[i])
        else temp[i] = arr[i]
    return temp
}

После получения дочерних элементов, необходимо очистить от них исходный массив. Я не придумал ничего лучше, чем написать еще одну функцию.

var cleanDuplicates = function(from, elements){
    var length = arr.length;
    for (var i = 0; i < length; i++){
        if ($.inArray(from[i], elements) > -1)
            delete from[i]
    }
    return from;
}

Здесь массив elements содержит элементы, которые требуется удалить из массива from.
И, наконец, строим список, используя вышеприведенные функции.

var ul = function(arr){
    if (!arr[0]) return ''
    else{
        var html = '<ul>';
        var length = arr.length;
        for (var i = 0; i < length; i++){
            var el = arr[i];
            var childs = getChilds(el, arr);
            arr = cleanDuplicates(arr, childs)
            html += '<li>'+'<span id="cat_'+el.id+'">'+el.name+'</span>'
            html += ul(childs)
            html += '</li>'
        }
        return html + '</ul>'
    }
}

Пример использования:

'<div class="tree">' + ul(data) + '</div>'

где data — данные, полученные с сервера.
Для конечного преобразования этого списка в древовидное меню существует достаточно большое количество плагинов для jQuery, к примеру jQuery Treeview.
Работа с ним достаточно проста. Необходимо сперва подключить сам jQuery, затем этот плагин. После подключения достаточно просто натравить его на блок, содержащий ваш сгенерированный список. Если брать из примера, то это элемент $(‘.tree’).

$('.tree').treeview();

В результате мы имеем древовидное меню, которое поддерживает сворачивание/разворачивание по клику на папке (по умолчанию строится развернутое дерево папок, но благодаря настройкам плагина возможны варианты, подробнее читайте здесь).

P. S. Обратите внимание, что плагин jQuery Treeview больше не развивается, но для построения простого древовидного меню функций этого плагина более чем достаточно. Сам разработчик предлагает использовать плагин JqTree.