Информация по назначению калькулятора
Прямоугольник – это двумерная геометрическая фигура, имеющая 4 стороны и 4 угла. Две его стороны сходятся под прямым углом. Таким образом, прямоугольник имеет 4 угла, каждый из которых равен 90 градусов. Противоположные стороны прямоугольника имеют одинаковую длину и параллельны. Две стороны называются параллельными, когда расстояние между ними остается одинаковым во всех точках.
Поскольку все углы прямоугольника равны, его можно назвать равноугольным четырехугольником.
Некоторые свойства прямоугольника отмечены далее:
⇒ Прямоугольник – это четырехугольник.
⇒ Противоположные стороны прямоугольника равны и параллельны друг другу.
⇒ Внутренний угол прямоугольника в каждой вершине равен 90°.
⇒ Сумма всех внутренних углов равна 360°.
⇒ Диагонали делят пополам друг друга.
⇒ Длина диагоналей равна.
⇒ Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
⇒ Все прямоугольники являются параллелограммами, но не все параллелограммы являются прямоугольниками.
Онлайн калькулятор поможет найти параметры прямоугольника, такие как:
- Длины сторон
- Периметр
- Площадь
- Диагонали
- Углы
- Радиус Описанной окружности
- Диаметр Описанной окружности
- Длина Описанной окружности
- Площадь Описанной окружности
– равен сумме всех 4х сторон (P=AB+BC+CD+DA)
– равна произведению двух сторон (S=AB*BC)
– Диагональ разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а две смежные стороны прямоугольника образуют две другие стороны треугольника.(AC=√(AB2 + BC2))
– всегда равны 90 градусов
Диаметр описанной окружности прямоугольника равен длине его диагонали
Как найти угол, если известны стороны
Многоугольником называется фигура на плоскости, состоящая из трёх и более сторон, которые пересекаются в трёх и более точках. Многоугольник называется выпуклым, если каждый его угол меньше 180º. Обычно, в качестве многоугольников рассматривают именно выпуклые многоугольники. Для нахождения углов многоугольника нужно иметь минимально необходимый набор исходных данных. Пусть для многоугольника известны длины всех его сторон.

Инструкция
Многоугольник называется правильным, если его стороны равны между собой, а так же все углы равны между собой.
Если заранее известно, что многоугольник является правильным, то углы можно высчитать по формуле
?? = 180? * (n – 2)/n, где n – количество сторон многоугольника.
Например, в случае правильного восьмиугольника
?? = 180? * (8 – 2)/8 = 135?
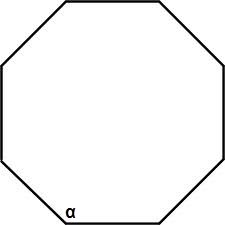
Для неправильного треугольника с известными сторонами, углы можно рассчитать по теореме косинусов, например, для угла ?? в приведённом рисунке формула примет вид
cos?? = (b? + c? – a?) / 2 • b • c

Для нахождения углов неправильных многоугольников с количеством сторон больше 3 наличие длин сторон не является достаточным условием.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Диагонали прямоугольника равны между собой. Диагональ делит прямоугольник на два равных прямоугольных треугольника ABC и ACD. Диагональ равна диаметру описанной окружности.
1. Формулы длины диагонали в прямоугольнике.
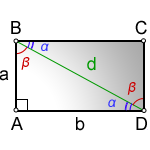
d – диагональ прямоугольника
a, b – стороны
α, β – углы полученные от деления, диагональю, прямого угла
Формула диагонали через стороны, (d):
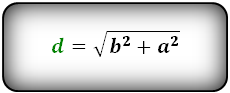
Формулы диагонали через сторону и угол, (d):
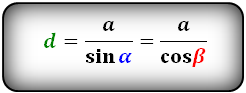
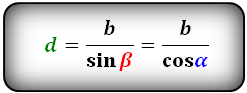
Формулы величины углов через диагональ и стороны, (α, β):


2. Формулы углов между диагоналями в прямоугольнике.
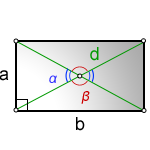
d – диагонали прямоугольника
a, b – стороны
α, β – углы между диагоналями
Формулы углов между диагоналями через стороны и диагональ, (α, β ):


- Подробности
-
Опубликовано: 27 октября 2011
-
Обновлено: 13 августа 2021
Как найти углы прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти углы прямоугольного треугольника
Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для угла α:
- угол β
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
- для угла β:
- угол α
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
Введите их в соответствующие поля и получите результат.
Найти угол α зная угол β и наоборот
Если ∠β = , то ∠α =
0
Если ∠α = , то ∠β =
0
Формула
α = 90° – β
β = 90° – α
Найти углы прямоугольного треугольника зная катеты
Катет a =
Катет b =
∠α =
0
∠β =
0
Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?
Формулы
или так:
α = arctg(a/b)
β = arctg(b/a)
Пример
Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:
∠α = arctg(5/2) = arctg(2.5) ≈ 68.2°
∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°
Найти углы прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет =
∠α =
0
∠β =
0
Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?
Формулы
sin(α) = a/c
sin(β) = b/c
cos(α) = b/c
cos(β) = a/c
или так:
α = arcsin(a/c) = arccos(b/c)
β = arcsin(b/c) = arccos(a/c)
Пример
Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:
∠α = arccos(3/6) = arccos(0.5) = 60°
∠β = arcsin(3/6) = arcsin(0.5) = 30°
См. также
Зная стороны прямоугольника, можно вычислить все остальные его параметры, используя следующий ход действий. Периметр прямоугольника представляет собой удвоенную сумму его сторон, поэтому его можно сразу вычислить.
P=2(a+b)
Площадь прямоугольника равна произведению его сторон, поэтому ее также можно найти сразу.
S=ab
Диагонали в прямоугольнике являются конгруэнтными, каждая из них образует прямоугольный треугольник со сторонами прямоугольника. Из теоремы Пифагора каждая диагональ будет равна квадратному корню из суммы квадратов сторон прямоугольника. (рис. 56.1)
d_1=d_2=√(a^2+b^2 )
Из этого же прямоугольного треугольника можно найти углы α и β при диагоналях, зная только стороны прямоугольника. Отношения катетов друг к другу дают тангенс или котангенс углов треугольника, поэтому α и β будут равны арктангенсу отношений сторон, а дальше значение в градусах можно найти, используя таблицы тангенсов.
α=arc tan〖b/a〗
β=arc tan〖a/b〗
Углы γ и δ, образованные пересечением диагоналей, как видно из чертежа, через прямоугольный треугольник с полуосью, равны удвоенным значениям α и β соответственно. (рис.56.2)
γ=2α
δ=2β
Так как углы у прямоугольника все равны друг другу, вокруг него можно описать окружность. Центр окружности будет находиться в точке пересечения диагоналей, и следовательно, радиус описанной окружности будет равен половине диагонали. (рис.56.3)
R=d/2=√(a^2+b^2 )/2
