Как в треугольнике найти третью координату

Здравствуйте, уважаемые форумчане. Помогите пожалуйста с формулой

Как найти координаты третьей вершины треугольника по длинам трёх сторон и двум координатам вершин?

Известны координаты точек А(x1,y1), С(x2,y2).
длины сторон а, в, с
необходимо вычислить координаты точки В(x3,y3)

Использовать для вычислений Косинус и Синус угла АСВ и смещение прямой АС относительно системы координат нельзя из-за получающейся огромной погрешности при вычислениях. Я про формулу такого вида: x3 = x2 + a*cosС, y3 = y2 + a*sinС

Точка А – центр окружности радиусом с

Точка С – центр окружности радиусом a

Пересечение двух окружностей дадут точку B, то есть ее координаты.

Всего-то нужно решить систему относительно [math]x,[/math] и [math]y[/math]

[math](y-y_1)^2+(x-x_1)^2=c^2[/math]

[math](y-y_2)^2+(x-x_2)^2=a^2[/math]

Получим два решения при допустимых соотношениях параметров (при которых треугольник может существовать)

Формулы я получил. Но они такие громоздкие, что писать полчаса надо. Вот численно элементарно делается. Например, зададим параметры пифагорова треугольника:
[math]x_1=0,;, y_1=0, ; , x_2=4,;, y_2=3 ,;, a=3, ;, c=4[/math]

Тогда по команде Maple

solve({(y-y1)^2+(x-x1)^2 = c^2, (y-y2)^2+(x-x2)^2 = a^2}, [x, y]);

получим два решения:

1) [math]x=4 , ; , y=0[/math]

2) [math]x=frac{28}{25}, ; , y=frac{96}{25}[/math]

Графическое представление этой задачи:

Я добавил рисунок…
Вот формулы только для одного из решений:

x:=(1/2)*((y1-y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+(x1^3-x1^2*x2+(y2^2-2*y1*y2-c^2+y1^2+a^2-x2^2)*x1-x2*(a^2-c^2-x2^2-y2^2+2*y1*y2-y1^2))*(x1-x2))/((x1-x2)*(x1^2-2*x2*x1+x2^2+(y1-y2)^2));

y := (-sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2);

Второе решение:

x := (1/2)*((-y1+y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2)))+(x1-x2)*(x1^3-x1^2*x2+(y1^2-2*y1*y2+y2^2+a^2-c^2-x2^2)*x1-x2*(-c^2-x2^2+a^2-y1^2+2*y1*y2-y2^2)))/((x1^2-2*x2*x1+x2^2+(y1-y2)^2)*(x1-x2));

y := (sqrt(-(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a+y1-y2)*(c+a-y1+y2))*(-x1^2+2*x2*x1-x2^2+(-c+a+y1-y2)*(-c+a-y1+y2)))+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2);

Формулы проверил – работают отлично. Вот если бы их суметь упростить!

Уважаемые математики
Чтобы не плодить темы, разрешить поднять текущую.

Пишу программу, но к сожалению не очень силен в математических науках. Нужно как раз вершины треугольника
Но исходные данные немного другие.
Есть длина стороны равностороннего треугольника и угол между ними.
Строится всё из начала координат в сторону x (вверх)

Вообще в итоге мне нужно написать симуляцию работы вентилятора. Крутится то я его заставлю.
Нарисовать не могу ((

вот такой должен получится.
Стороны 70
Угол лопасти 30 град
Угол между лопастями 120
Три лопасти.
У меня получается есть только координаты центра.
Чтобы нарисовать треугольники мне нужны остальные координаты вершин

Пытался сам найти, но видимо не так запрос формирую.

vvvv
Большое спасибо за потраченное время.
К сожалению ваше решение только добавило мне вопросов ((

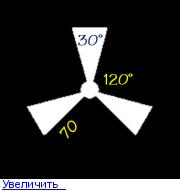
Координат всего должно быть 9 для каждой оси, но в таблице их 10
Так же вижу на графике что есть координата с х = -70 но в таблице для Х такого значения нет.

В итоге я пошёл по другому пути
Нарисовал первую лопасть вверх от начала координат и посчитал основание равнобедренного треугольника зная его стороны и угол между ними

a = 70
b = a * sin(30) / 2

и разделил её пополам. Получил координату по Y в обе стороны
Лопасть это два прямоугольных треугольника в которых по теореме пифагора нашёл вторую сторону которая и является второй коорлинатой

y1 = sqrt(a ** 2 – b ** 2)

А потом по формуле окружности просто сдвинул на 120 градусов влево и вправо

xn1 = sin(120 – 15) * a
yn1 = cos(120 – 15) * a
xn2 = sin(120 + 15) * a
yn2 = cos(120 + 15) * a

xn1 = sin(-120 – 15) * a
yn1 = cos(-120 – 15) * a
xn2 = sin(-120 + 15) * a
yn2 = cos(-120 + 15) * a

От меня вам всё равно спасибо что откликнулись!