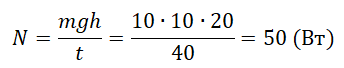Как зная импульс найти работу

Как зная импульс найти работу

Механическая работа

О чем эта статья:

Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.

Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.

Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.

Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.

Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.

Механическая работа

А = FScosα

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

α — угол между векторами силы и перемещения [°]

Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.

Для совершения работы необходимы два условия:

  • чтобы на тело действовала сила,
  • чтобы происходило перемещение тела.

Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.

Полезная и затраченная работа

Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».

Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.

Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.

Потенциальная энергия

Еп = mgh

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

h — высота [м]

На планете Земля g ≈ 9,8 м/с 2

Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

И как же достоверно определить, какая работа полезная, а какая затраченная?

Все очень просто! Задаем два вопроса:

За счет чего происходит процесс?

Ради какого результата?

В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).

Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.

Мощность

На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.

Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.

Мощность

N = A/t

N — мощность [Вт]

A — механическая работа [Дж]

t — время [с]

Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.

Также для мощности справедлива другая формула:

Мощность

N = Fv

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.

Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:

Мощность

N = Fvcosα

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

α — угол между векторами силы и скорости [°]

Примеры решения задач

Задача 1

Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:

Сила вязкого трения.

Ни одна из перечисленных сил.

Решение

Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.

Ответ: 3.

Задача 2

Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?

Решение

Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:

Ответ: 3200 Дж.

Задача 3

Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?

Решение

В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.

Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:

A = Fl = 30 * 5 = 150 Дж

Ответ: 150 Дж.

Задача 4

Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?

Решение

На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.

Мощность можно найти по формуле N = Fv.

N = FV = 2×5 = 10 Вт

Ответ: 10 Вт.

Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!

Работа силы через векторы

4.1. Работа силы

Рассмотрим абсолютно неупругий удар двух шаров одинаковой массы, сделанных из пластилина. Если эти шары летят друг на друга с одной и той же скоростью, то при соударении они прилипнут друг к другу и остановятся. В этом случае суммарный импульс обоих шаров остался равным нулю, хотя состояние системы изменилось. Шары при этом нагрелись. Этот пример показывает, что импульс не всегда может служить мерой движения. Такой мерой является энергия. В данном случае механическая энергия при ударе перешла в другой вид энергии (тепловую).

Сначала рассмотрим важную характеристику — работу. Пусть материальная точка движется по траектории AB (рис. 1). На точку во время движения действует в общем случае переменная сила F. На участке ds (настолько малом, что модуль перемещения равен пройденному пути) силу F можно считать постоянной.

Рис 4.1. Элементарная работа

Элементарная работа силы 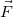равна скалярному произведению вектора силы на вектор перемещения её точки приложения

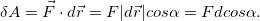
Работа — скалярная величина, ее знак зависит от знака . Положительная работа совершается силой, если ее направление составляет острый угол 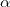с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол 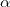с направлением движения, при этом сила тормозит это движение. Величина

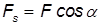
— это проекция силы F на направление перемещения. Следовательно,

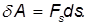
Полная работа силы находится как сумма (интеграл) элементарных работ по всей траектории L точки:

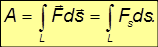
При перемещении вдоль оси x работу графически можно представить как площадь под кривой Fx(x) (рис. 4.2), причем площади под осью абсцисс следует приписывать отрицательное значение.

Рис. 2. Графическая интерпретация работы силы. Здесь для краткости положено F = Fx(x)

Если перемещение ортогонально силе, то = 0 и работа равна нулю:

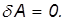
Последнее показывает, что понятие работы в механике отлично от обыденного представления о работе. Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и = 0. Здесь и ниже и 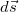означают одно и то же — бесконечно малое перемещение, а ||=||=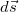 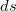— соответствующий бесконечно малый путь.

Если на тело действует несколько сил, то

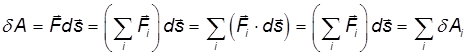
то есть работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой из сил в отдельности.

Рассмотрим для примера работу, совершаемую внешней силой по сжатию и растяжению пружины с жесткостью 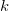. Направим ось 0x вдоль пружины, причем за начало координат 0 выберем положение свободного конца пружины, находящейся в ненагруженном состоянии. Процесс сжатия/растяжения представляем как последовательность равновесных состояний: в каждый момент времени прилагаем внешнюю силу, равную по величине силе упругости со стороны пружины. Тогда согласно закону Гука

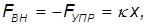
где x — удлинение пружины. При положительных x (растяжение пружины) внешняя cила направлена направо, при отрицательных (сжатие) — налево (рис. 4.3).

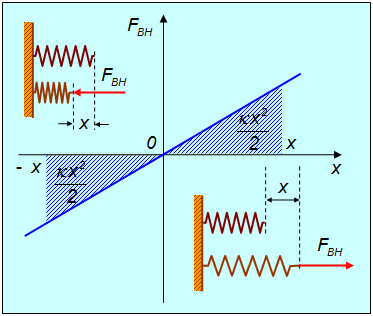
Рис. 4.3. Работа, совершаемая при сжатии/растяжении пружины

Скалярное произведение для элементарной работы внешней силы имеет в этом случае вид

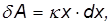
так что для полной работы упругой деформации пружины получаем

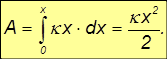
Заметим, что A не зависит от знака x: и при растяжении, и при сжатии пружины внешняя сила совершает одну и ту же положительную работу.

Механическая работа

О чем эта статья:

Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.

Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.

Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.

Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.

Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.

Механическая работа

А = FScosα

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

α — угол между векторами силы и перемещения []

Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.

Для совершения работы необходимы два условия:

  • чтобы на тело действовала сила,
  • чтобы происходило перемещение тела.

Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Полезная и затраченная работа

Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».

Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.

Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.

Потенциальная энергия

Еп = mgh

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

h — высота [м]

На планете Земля g ≈ 9,8 м/с 2

Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

И как же достоверно определить, какая работа полезная, а какая затраченная?

Все очень просто! Задаем два вопроса:

  1. За счет чего происходит процесс?
  2. Ради какого результата?

В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).

Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.

Мощность

На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.

Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.

Мощность

N = A/t

N — мощность [Вт]

A — механическая работа [Дж]

t — время [с]

Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.

Также для мощности справедлива другая формула:

Мощность

N = Fv

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.

Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:

Мощность

N = Fvcosα

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

α — угол между векторами силы и скорости []

Примеры решения задач

Задача 1

Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:

  1. Выталкивающая сила.
  2. Сила вязкого трения.
  3. Сила тяжести.
  4. Ни одна из перечисленных сил.

Решение

Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.

Ответ: 3.

Задача 2

Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?

Решение

Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:

Ответ: 3200 Дж.

Задача 3

Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?

Решение

В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.

Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:

A = Fl = 30 * 5 = 150 Дж

Ответ: 150 Дж.

Задача 4

Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?

Решение

На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.

Мощность можно найти по формуле N = Fv.

N = FV = 2×5 = 10 Вт

Ответ: 10 Вт.

Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!

Механическая работа и мощность

теория по физике 🧲 законы сохранения

Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:

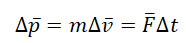
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.

Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).

Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:

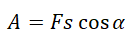
Важно!

Механическая работа совершается, если:

  1. На тело действует сила.
  2. Под действием этой силы тело перемещается.
  3. Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).

Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.

Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.

Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:

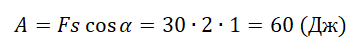
Работа различных сил

Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.

Модуль силы тяжести: Fтяж = mg

Работа силы тяжести: A = mgs cosα

Модуль силы трения скольжения: Fтр = μN = μmg

Работа силы трения скольжения: A = μmgs cosα

Модуль силы упругости: Fупр = kx

Работа силы упругости:

Работа силы тяжести
Работа силы трения скольжения
Работа силы упругости

Работа силы упругости

Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:

Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя

Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.

A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)

Знак работы силы

Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:

  1. Если α = 0 о , то cosα = 1.
  2. Если 0 о o , то cosα > 0.
  3. Если α = 90 о , то cosα = 0.
  4. Если 90 о o , то cosα о , то cosα = –1.

Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180 о ). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0 о ). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.

Геометрический смысл работы

Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

Мощность

Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.

Мощность при равномерном прямолинейном движении тела

Работа при равномерном прямолинейном движении определяется формулой:

Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:

Мощность при равномерном подъеме груза

Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:

Мгновенная мощность при неравномерном движении

Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:

Мощность силы трения при равномерном движении по горизонтали

Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180 о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:

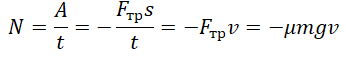
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?

Коэффициент полезного действия

Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.

  • Работа затраченная — полная работа силы, совершенной над телом (или телом).
  • Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
  • Коэффициент полезного действия(КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.

КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:

Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:

Устройство

Работа полезная и полная

Неподвижный блок, рычаг

Наклонная плоскость

l — совершенный путь (длина наклонной плоскости).

Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.

В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:

Механическая работа и мощность

теория по физике 🧲 законы сохранения

Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:

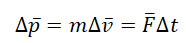
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.

Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).

Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:

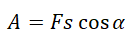
Важно!

Механическая работа совершается, если:

  1. На тело действует сила.
  2. Под действием этой силы тело перемещается.
  3. Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).

Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.

Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.

Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:

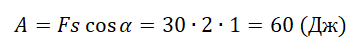
Работа различных сил

Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.

Модуль силы тяжести: Fтяж = mg

Работа силы тяжести: A = mgs cosα

Модуль силы трения скольжения: Fтр = μN = μmg

Работа силы трения скольжения: A = μmgs cosα

Модуль силы упругости: Fупр = kx

Работа силы упругости:

Работа силы тяжести
Работа силы трения скольжения
Работа силы упругости

Работа силы упругости

Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:

Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя

Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.

A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)

Знак работы силы

Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:

  1. Если α = 0 о , то cosα = 1.
  2. Если 0 о o , то cosα > 0.
  3. Если α = 90 о , то cosα = 0.
  4. Если 90 о o , то cosα о , то cosα = –1.

Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180 о ). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0 о ). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.

Геометрический смысл работы

Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

Мощность

Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.

Мощность при равномерном прямолинейном движении тела

Работа при равномерном прямолинейном движении определяется формулой:

Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:

Мощность при равномерном подъеме груза

Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:

Мгновенная мощность при неравномерном движении

Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:

Мощность силы трения при равномерном движении по горизонтали

Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180 о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:

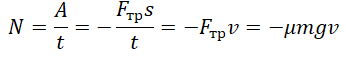
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?

Коэффициент полезного действия

Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.

  • Работа затраченная — полная работа силы, совершенной над телом (или телом).
  • Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
  • Коэффициент полезного действия(КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.

КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:

Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:

Устройство

Работа полезная и полная

Неподвижный блок, рычаг

Наклонная плоскость

l — совершенный путь (длина наклонной плоскости).

Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.

В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:

[spoiler title=”источники:”]

http://b4.cooksy.ru/articles/rabota-sily-cherez-vektory

Механическая работа и мощность

[/spoiler]

Источник

ИМПУЛЬС. РАБОТА. МОЩНОСТЬ

В формулах (1.29) сила действующая на тело, разложена на составляющие по координатным осям. Однако при решении некоторых задач удобно использовать другое разложение. В § 1 было указано, что полное ускорение тела а целесообразно разложить на два ускорения: тангенциальное вызывающее изменение скорости тела только по величине, и нормальное вызывающее изменение скорости только по направлению. В связи с этим силу, действующую на тело, также можно разложить на две составляющие:

1) тангенциальную силу ориентированную по направлению движения (по касательной к траектории движения), и

2) нормальную силу перпендикулярную направлению скорости движения (т. е. ориентированную по нормали к траектории).

Сила (которую иногда называют движущей силой) сообщает телу тангенциальное ускорение

Сила сообщает телу нормальное (центростремительное) ускорение

радиус кривизны траектории в данной точке На рис. 1.9 показано разложение сил и ускорений на тангенциальную и нормальную составляющие; сила используется для расчета изменения величины скорости, а сила для расчета радиуса кривизны траектории.

Законы механики в виде (1.29) или (1.30) связывают между собой значения сил и ускорений в каждый рассматриваемый момент времени. Пользуясь ими, можно найти изменение скорости или кинетической

энергии тела за конечный промежуток времени или на конечном участке траектории. Допустим, что на тело массой действует сила величина и направление которой измелется со временем. Разделим время наблюдения на такие малые промежутки в течение которых эту силу можно было бы с удовлетворительной точностью полагать постоянной (по величине и направлению). Тогда для каждого из этих промежутков времени можно написать или

Рис. 1.9

Суммируя эти соотнощения, получим (при постоянной массе тела)

где начальная скорость тела в момент Для точности расчета промежутки времени должны быть бесконечно малыми, поэтому

Для постоянной по величине и направлению силы это соотношение можно написать и в скалярном виде:

Формула (1.31) позволяет рассчитать изменение скорости тела за время если известно, как изменяется действующая на нее сила с течением времени.

Аналогичным образом можно получить формулы для расчета изменений скорости вдоль каждой из координатных осей:

где проекции начальной скорости на координатные оси. Если на тело действуют несколько сил (включая силы тяготения, трения, упругости и т. д.), то в эти формулы должна быть подставлена их равнодействующая, т. е. их векторная сумма.

Для иллюстрации формулы (1.31) рассмотрим один пример. Допустим, что на тело действует сила всегда перпендикулярная скорости движения и постоянная по величине (с такой силой действует, например, однородное магнитное поле на движущийся электрический заряд). Очевидно, что такая сила будет сообщать телу только

нормальное ускорение и не будет изменять величину скорости, т. е. тело будет двигаться по окружности с постоянной скоростью. Применим к такому движению формулу (1.31) и выберем промежуток времени в течение которого тело совершает четверть оборота. Разделим это время на элементарные промежутки и проведем суммирование векторов (на рис. 1.10, а они обозначены Эти векторы будут направлены к центру окружности. Для нахождения их равнодействующей совместим их начала в общую точку, как это показано на рис. 1.10, б. Векторная сумма будет вектором I, также направленным к центру окружности. Так как скорость тела, оставаясь постоянной по величине, изменяется по направлению, то изменение скорости за время наблюдения будет равно вектору показанному на рис. 1.10, в.

Рис. 1.10

Формула (1.31) утверждает, что равнодействующая всех элементарных векторов т. е. равна по величине и направлению вектору Если тело сделает один оборот, то равнодействующая I будет равна нулю; так как вектор скорости тела при этом вернется к первоначальному направлению, то изменение скорости также будет равно нулю.

Произведение массы тела на скорость его движения называется импульсом (количеством движения) тела. Формула (1.31) показывает, что изменение импульса тела за время наблюдения равно интегралу где равнодействующая всех сил, действующих на данное тело.

Воздействие силы на тело можно определить в зависимости не только от времени наблюдения, но и от пути, пройденного движущимся телом. Будем интересоваться изменением скорости только по величине, т. е. выведем формулу, которая показывала бы воздействие силы на тело независимо от формы траектории. Так как величина скорости изменяется только тангенциальной силой, то второй закон механики

перепишем в скалярном виде:

где а — угол между направлениями силы и ее тангенциальной составляющей (см. рис. 1.9). Выразим время через пройденный путь и перепишем это уравнение в виде

Если тело прошло по траектории (любой формы) путь то

Произведение силы на пройденный путь и на косинус угла между направлением силы и направлением движения (скорости) называется работой силы на этом участке траектории. Формула (1.33) показывает, что работа, совершаемая силой на некотором конечном участке траектории, равна изменению кинетической энергии тела, к которому эта сила приложена. Разумеется, есть равнодействующая всех сил, действующих на данное тело.

Если вдоль траектории (любой формы) сила остается постоянной по величине и направлению (например, при движении тела в поле тяготения Земли по траекториям небольших размеров), то работа этой силы будет равна

где проекция пройденного пути на направление силы.

Работа, совершенная переменной силой на элементарном участке пути, может быть записана в виде скалярного произведения векторов силы и перемещения

Нормальная составляющая действующей силы не изменяет численного значения скорости тела и поэтому работы не совершает. Работа совершается только тангенциальной составляющей действующей силы, ибо только она изменяет величину скорости тела. Отметим, что:

1) работа а может быть положительной, если и отрицательной, если с 0. Если сила совершает отрицательную работу, то скорость тела уменьшается:

2) при горизонтальном движении тела сила тяжести работы не совершает

3) работа, совершаемая силой тяжести при движении тела в поле тяготения, не зависит от формы траектории, а определяется только разностью высот начальной и конечной точек траектории (рис. 1.11). На малом отрезке траектории

суммарная работа

Здесь предполагается, что высота невелика и поэтому сила тяжести остается в процессе движения тела постоянной;

4) если в поле тяготения тело описывает замкнутую траекторию, то суммарная работа силы тяжести равна нулю, так как положительная работа, совершаемая при опускании тела, компенсируется отрицательной работой при подъеме;

5) при движении тела по криволинейной траектории центростремительная сила работы не совершает

Рис. 1.11

6) работа, совершаемая несколькими силами, приложенными к данному телу, равна работе равнодействующей этих сил, найденной путем их векторного сложения.

Работа и энергия выражаются в СИ в джоулях и в СГС – в эргах: 1 джоуль

Работу силы на участке пути можно представить как сумму работ, совершаемых компонентами этой силы по осям координат, т. е.

Действительно, если в эту формулу подставить также и учесть, что получим тождество. Формулу (1.34) можно получить также из выражения для работы:

Мощностью источника энергии (или работы) называется отношение работы совершаемой этим источником за время времени

Для конечных промежутков времени это отношение определяет среднюю мощность. Мощность в СИ выражается в ваттах

Подставим в формулу (1.35) вместо произведение тогда мощность

В общем случае, когда угол между векторами силы и скорости отличен от нуля, мощность равна скалярному произведению этих векторов:

Источник

Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:

Работа силы

В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.

Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).

Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:


Важно!

Механическая работа совершается, если:

  1. На тело действует сила.
  2. Под действием этой силы тело перемещается.
  3. Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).

Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.

Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.

Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:

Работа различных сил

Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.

Работа силы тяжести

Модуль силы тяжести: Fтяж = mg

Работа силы тяжести: A = mgs cosα
Работа силы трения скольжения

Модуль силы трения скольжения: Fтр = μN = μmg

Работа силы трения скольжения: A = μmgs cosα
Работа силы упругости

Модуль силы упругости: Fупр = kx

Работа силы упругости:

Работа силы упругости

Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:

s = x1 – x2

Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя

Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.

A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)

Знак работы силы

Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:

  1. Если α = 0о, то cosα = 1.
  2. Если 0о < α < 90o, то cosα > 0.
  3. Если α = 90о, то cosα = 0.
  4. Если 90о < α < 180o, то cosα < 0.
  5. Если α = 180о, то cosα = –1.

Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.

Геометрический смысл работы

Графическое определение

Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

A = Sфиг

Мощность

Определение

Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.

Мощность при равномерном прямолинейном движении тела

Работа при равномерном прямолинейном движении определяется формулой:

A = Fтs

Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:

Мощность при равномерном подъеме груза

Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:

Мгновенная мощность при неравномерном движении

Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:

Мощность силы трения при равномерном движении по горизонтали

Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:

Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?

Коэффициент полезного действия

Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.

Определения:

  • Работа затраченная — полная работа силы, совершенной над телом (или телом).
  • Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
  • Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.

КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:

A = Nt

Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:

Устройство

Работа полезная и полная

КПД
Неподвижный блок, рычаг

Aполезн = mgh

Асоверш.
Наклонная плоскость

Aполезн = mgh

Асоверш. = Fl

l — совершенный путь (длина наклонной плоскости).

Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.

В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:

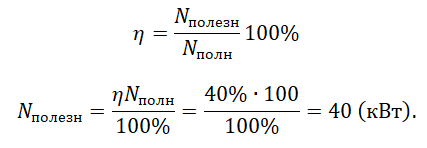
Задание EF17557

Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?

Ответ:

а) 916 Вт

б) 3300 Вт

в) 82500 Вт

г) 297000 Вт

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Записать формулу для расчета мощности.

3.Выполнить общее решение задачи.

4.Подставить известные данные и выполнить вычисления.

Решение

Запишем исходные данные:

• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.

• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.

Переведем единицы измерения в СИ:

16,5 кН = 16,5∙103 Н

18 км/ч = 18000/3600 м/с = 5 м/с

Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:

N=At

Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:

A = Fs

Тогда мощность равна:

N=Fst=Fv=16,5·103·5=82500 (Вт)

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17574

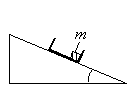С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Время движения

Ускорение

Модуль работы силы трения

Алгоритм решения

1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.

2.Вывести формулу для модуля работы силы трения.

3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.

Решение

При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:

x=xo+v0xt+axt22

y=yo+v0yt+ayt22

Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.

Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:

Fтр = μmg

Известно, что работа определяется формулой:

A = Fs cosα

Тогда работа силы трения равна:

A = μmgs cosα

Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:

A = μmgs

Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.

Поэтому правильная последовательность цифр в ответе: 332.

Ответ: 332

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18646

В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.

Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?

Для каждой величины определите соответствующий характер её изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.

Сила натяжения нити Коэффициент трения

Алгоритм решения

  1. Определить, какая величина изменилась во второй серии опытов.
  2. Определить, как зависит от этой величины сила натяжения нити.
  3. Определить, как зависит от этой величины коэффициент трения.

Решение

Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:

T = mg

Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.

Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.

Верная последовательность цифр в ответе: 13.

Ответ: 13

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18271

Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.

Алгоритм решения

1.Записать исходные данные и перевести их в СИ.

2.Записать формулу для определения КПД атомной электростанции.

3.Решить задачу в общем виде.

4.Подставить известные данные и вычислить искомую величину.

5.Массовое число: A = 235.

6.Зарядовое число: Z = 92.

Решение

Запишем исходные данные:

• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.

• Масса урана-235: m = 1,4 кг.

• Время, в течение которого происходит деление: t = 1 неделя.

• Мощность атомной электростанции: N = 38 МВт.

Переведем все единицы измерения в СИ:

1 эВ = 1,6∙10–19 Дж

200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж

1 неделя = 7∙24∙60∙60 с = 604,8∙103 с

38 МВт = 38∙106 Вт

КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:

η=AполезнQ100%

Полезную работу мы можем вычислить по формуле:

A=Nt

Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.

Количество атомов равно произведению количество молей на постоянную Авогадро:

Nкол.атомов = νNA

Количество молей равно отношения массы вещества к его молярной массе, следовательно:

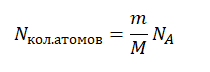
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:

M = A (г/моль) = A∙10–3 (кг/моль)

Отсюда количество атомов равно:

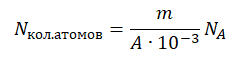
Энергия, выделенная всеми атомами, равна:

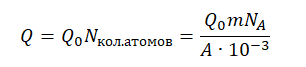
Теперь можем вычислить КПД:

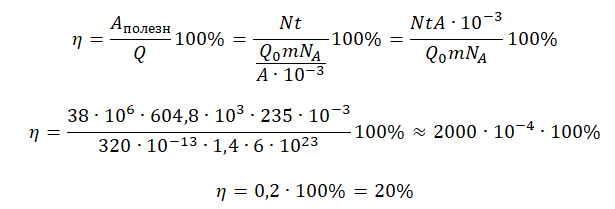
pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 11.8k

Источник

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

P1_11_2012.pdf

Скачиваний:

91

Добавлен:

03.06.2015

Размер:

772.96 Кб

Скачать

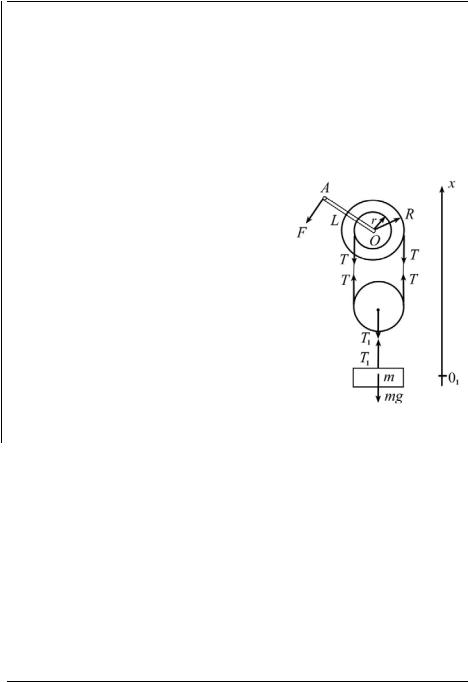
2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики

Массами цилиндров, рукоятки, троса, подвижного блока и трением в

осях пренебречь.

Ускорение

свободного падения принять

равным

g =10 м/с2 .

F, которую необходимо приложить к

Найдите минимальную силу

рукоятке ворота,

чтобы поднимать груз массой m =140 кг.

(МФТИ,

2008г.)

Решение. Изобразим на рис. 17 силы, действующие на цилиндры и груз, где через T обозначена сила натяжения троса, связывающего под-

вижный блок с дифференциальным воротом, через T1 − сила натяжения троса, на котором к подвижному блоку подвешен груз, а через mg −

сила тяжести груза.

Поскольку массой подвижного блока можно пренебречь, то в проекциях на ось

O1 x можно записать

2T −T1 = 0.

Для груза, находящегося в равновесии, в проекциях на ту же ось имеем:

T1 −mg = 0.

Для моментов сил, действующих на дифференциальный ворот, относительно оси ворота, проходящей через точку O, спра-

ведливо уравнение:

TR −Tr − FL = 0.

Решая совместно три написанных уравнения, найдём

F =

R −r

mg = 70 H.

Рис. 17

2L

Решение механических задач часто облегчается применением законов изменения и сохранения импульса и энергии тела. Особенно эффективным является использование этих законов в тех случаях, когда действующие силы переменны во времени и непосредственное решение уравнений динамики с помощью методов элементарной математики затруднительно. r

Напомним, что импульсом тела называется векторная величина p, равная произведению массы m тела на его скорость v : p = mvr.

Импульсом системы тел P называют векторную сумму импульсов всех тел, составляющих этуrсистему. Например, если система состоит из

трёх тел с импульсами pr1 , p2 и pr3 , то импульс такой системы тел равен

© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич

18

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики

Pr = pr1 + pr2 + pr3.

В общем случае импульс тела в процессе движения может изменяться как по величине, так и по направлению. При этом справедлив закон изменения импульса тела: приращение импульса тела равно произве-

дению равнодействующей силы F на промежуток времени t, в тече-

ние

которого она действует на

тело: pr = F t.

Произведение

Fr

t называют импульсом силы.

Аналогичное соотношение спра-

ведливо и для системы тел, только в этом случае под F надо понимать

равнодействующую только внешних сил: приращение

P импульса си-

стемы тел равно импульсу равнодействующей F внешних сил, дей-

ствующих на систему: P = Fr t.

Внутренние силы взаимодействия

между телами, входящими в систему, не могут изменить импульс системы.

Из сказанного следует закон сохранения импульса системы тел (или отдельноr взятого тела). Импульс системы тел (тела) сохраняется (т.

е. P =0 ) при любых взаимодействиях тел системы, если импульс рав-

нодействующей F внешних сил F t равен нулю. Это возможно в ка-

ком-либо из трёх случаев:

1) если внешние силы на систему (тело) не действуют вообще (система изолированная);

2) если равнодействующая F внешних сил, действующих на систему (тело), равна нулю;

3) если промежуток времени t, в течение которого на систему (теr– ло) действуют внешние силы, мал ( t →0), а равнодействующая F ограничена по модулю (не бесконечно большая).

Встречаются ситуации, когда импульс системы тел (тела) в целом не сохраняется, но сохраняется проекция Px импульса на некоторое на-

правление Ox ( Px =0). Это возможно в трёх случаях:

1) если внешние силы, действующие на систему (тело), направлены перпендикулярно оси Ox;

2) если проекция Fx на ось Ox равнодействующей F внешних сил равна нулю;

3) если промежуток времени t мал, а проекция Fx ограничена по

модулю (Fx ≠ ∞).

Часто при решении задач для определения импульса системы тел бывает удобно воспользоваться понятием центраr масс рассматрива-емой

системы. Можно показать, что импульс P системы тел равен

© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич

19

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики

произведению массы M

системы (т.

е. суммы масс тел, входящих в

систему)

и скорости

vrc движения

её центра масс (точки C ):

Pr = M vrc .

В связи с этим справедлива теорема о движении центра

масс: центр масс системы тел движется так, как двигалась бы материальная точка, масса которой равна массе системы, под действием силы, равной векторной сумме всех внешних сил, действующих на систему. Использование сформулированной теоремы позволяет порой существенно упростить процесс решения задачи.

Изменение импульса тела (системы) характеризует действие силы в течение конкретного промежутка времени. Для характеристики действия силы на определённом перемещении служит физическая величина,

называемая механической работой.

Пусть материальная точка движется по некоторой

не обязательно

прямолинейной траектории (рис. 18). Пусть также на

материальную

точку действует сила F, которая в общем случае в процессе движения

FS

может меняться как по модулю, так и по на-

правлению. Разобьём траекторию на множество

сколь угодно малых участков, каждый из котоr–

Si

рых можно считать прямолинейным, а силу

F

F

на каждом таком участке можно считать посто-

i =1,2,…

янной. Рассмотрим малое перемещение

Sri ,

Sr

Рис. 18

Работой

Ai силы F на малом перемещении

называют величину, равную скалярному произведению векторов Fr

i

r

r

r

и Si :

Ai = F

Si .

По определению скалярного произведения можно записать:

Ai = F Si cosαi = FS ,i Si = F Si,F ,

где αi – rугол между векторами F и

Si , FS ,i − проекция F на направ-

ление

Si ,

Si,F − проекция Si на направление F.

Работа

A силы F на всём участке траектории равна алгебраической

сумме работ

Ai , совершаемых силой Fr на каждом из малых участ-

ков, на которые разбита траектория:

A = ∑ Ai . Когда на материальную

точку действуют n сил, их общая работа i A равна алгебраической сум-

ме работ каждой из сил в отдельности: A = ∑n Ai , j =1,2,…, n.

j=1

Если мы имеем дело не с материальной точкой, а с твёрдым телом или системой тел, то данное выше определение работы остаётся спра-

© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич

20

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики

ведливым, но в этом случае надо только иметь в виду, что под S сле-

дует понимать перемещение точки приложения силы F. Игнорирова-

ние этого обстоятельства зачастую приводит к ошибочным результатам. Часто говорят о работе, которую совершает или может совершить над телом какое-либо другое тело. Здесь, во избежание недоразумений, надо чётко понимать, что по определению работу над телом совершает

сила, действующая на него со стороны рассматриваемого другого тела.

Способность конкретного тела совершать работу характеризуют с помощью энергии. Кинетической энергией K движущейся материальной точки называют половину произведения массы m точки на квадрат

её скорости v, т. е. K = mv2 / 2.

Для определения кинетической энергии конкретного твёрдого тела его следует мысленно разбить на множество материальных точек. Ки-

нетическая энергия K тела будет равна алгебраической сумме кине-

тических энергий Ki этих материальных точек: K = ∑Ki = ∑

m v2

i i

.

2

i

В случае, когда тело массой m движется поступательно (не вращаясь), скорости vi составляющих его материальных точек в каждый кон-

кретный момент времени одинаковы и равны скорости v поступательного движения тела. Тогда кинетическая энергия K такого тела в соответствии со сказанным выше в каждый момент времени равна

K = ∑Ki = ∑

m v2

=

v2

∑mi .

i

2

2

i

i

i

Очевидно, что ∑mi = m,

где m − масса тела. Следовательно, кине-

i

тическая энергия K тела массой m, движущегося поступательно со скоростью v, равна K = m2v2 . Если движение тела не поступательное

(присутствует вращение), то для нахождения его кинетической энергии эта формула непосредственно не применима!

Так, например, в случае, когда однородный обруч массой m катится без проскальзывания со скоростью v по горизонтальной поверхности,

его кинетическая энергия равна K = mv2 .

Кинетическая энергия тела есть мера его движения. Приращение ки-

нетической энергии K рассматриваемого тела равно суммарной работе A всех сил, действующих на тело:

K = A.

(13)

Здесь K − разность между конечным K2 и начальным K1 значения-

ми кинетической энергии K = K2 − K1. Утверждение (13)

называется

© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич

21

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики

теоремой об изменении кинетической энергии.

Силы, действующие на тело, могут различаться по своей природе и свойствам. В механике сложилось, в частности, разделение сил на консервативные и неконсервативные. Консервативными (или потенциальными) называются силы, работа которых не зависит от траектории движения тела, а определяется только начальным и конечным его положением. Такими силами являются, например, сила тяжести и сила упругости. В общем случае работа любых консервативных сил может быть представлена как убыль некоторой величины П, которую называют по-

тенциальной энергией тела:

А= П1 − П2 .

(14)

(Убыль величины отличается от приращения знаком:

П1 − П2 = − П. )

Например, потенциальная энергия тела массы m,

находящегося на

высоте h

над поверхностью земли, равна П = mgh,

если за «нулевой

уровень»

условно принята поверхность земли. Потенциальная энергия

тела, находящегося под действием упругой силы деформированной пружины равна П = kx2 / 2, где x − величина деформации (сжатия или растяжения) пружины, k − коэффициент жёсткости пружины.

Неконсервативными называются силы, работа которых зависит от формы траектории и пройденного пути. Для таких сил равенство (14) несправедливо (понятие потенциальной энергии не применяется). Неконсервативными являются, например, сила трения скольжения, силы сопротивления воздуха или жидкости (зависящие от скорости).

Физическую величину, равную сумме кинетической и потенциальной энергий тела, называют его механической энергией E = K + П. Можно показать, что приращение механической энергии равно суммарной работе А неконсервативных сил, действующих на тело в процессе движе-

ния. Следовательно, если неконсервативные силы отсутствуют или таковы, что не совершают работы над телом в течение интересующего нас времени, то механическая энергия тела остаётся постоянной за это время: E =const. Это утверждение известно как закон сохране-

ния механической энергии.

Взаимодействия тел, изучаемые в механике, отличаются большим разнообразием. Частным случаем таких взаимодействий являются столкновения тел. Среди них выделяют так называемые упругие и неупругие столкновения. Следует отметить, что в учебной литературе наблюдается некоторая неопределённость терминологии на этот счёт. Здесь мы будем называть столкновения, при которых сохраняется суммарная механическая энергия тел, абсолютно упругими (или просто

упругими). Так, например, в большинстве случаев можно считать абсо-

© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич

22

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики

лютно упругим центральное столкновение двух стальных шаров. Столкновения, при которых изменяется суммарная механическая

энергия взаимодействующих тел, будем называть неупругими. Изменение суммарной механической энергии при таких столкновениях характеризуется её убылью и сопровождается, например, выделением тепла. Причём количество выделившейся теплоты в точности равно убыли механической энергии системы. Если тела после столкновения движутся как единое целое (с одинаковыми по величине и направлению скоростями), то такое столкновение будем называть абсолютно неупругим.

Задача 10. С наклонной плоскости одновременно без начальных скоростей начинают соскальзывать брусок и скатываться без проскальзывания обруч. При каком коэффициенте трения скольжения между бруском и наклонной плоскостью оба тела будут двигаться, не обгоняя друг друга? Угол наклона плоскости к горизонту равен α.

Решение. Из динамики известно, что ускорение a1 бруска, скользя-

щего по наклонной плоскости вниз, равно a1 = g (sinα −μcosα).

Пусть обруч скатывается с наклонной плоскости в течение времени t. За это время его центр масс пройдёт путь l, равный длине наклонной плоскости. Пусть скорость центра масс обруча в конце этого пути равна

v. Из кинематики известно,

что

l =

a t

2

, v = a t

(где

a −

ускорение

2

2

2

2

центра масс обруча).

обруча

за

время

t

равно

Приращение

кинетической энергии

K = K

2

− K . Поскольку K = 0

(по условию),

а

K

2

= M v2 ,

где

M −

1

1

С другой стороны,

масса обруча, то

K = M v2 .

по теореме об измене-

нии кинетической энергии эта величина равна работе всех сил, действующих на обруч в течение времени t. С учётом этого имеем:

M v2 = Mgl sinα,

где Mgl sinα − работа силы тяжести (покажите это самостоятельно).

Сила нормальной реакции опоры работы не совершает, так как направлена перпендикулярно перемещению центра масс обруча. Работа силы трения также равна нулю, так как обруч катится без проскальзывания и, следовательно, в каждый момент времени скорость точки касания обруча с наклонной плоскостью (точки приложения силы трения) равна ну-

лю. Учитывая кинематические уравнения, найдём a2 = g2 sinα. Тела не будут обгонять друг друга, если a1 = a2 . Отсюда μ = 12 tgα.

© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич

23

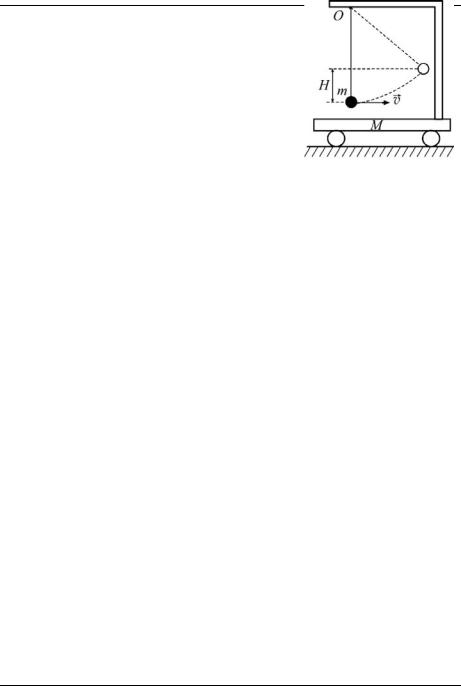
2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики

Задача 11. На подвижной тележке массой

M , находящейся на горизонтальной плоско-

сти, с помощью лёгкого стержня, который

может свободно вращаться вокруг точки O

(рис. 19), подвешен маленький шарик массой

m. Вначале система покоилась. Шарику крат-

ковременным ударом сообщают горизонталь-

ную скорость v. На какую наибольшую вы-

соту H по сравнению с первоначальным уро-

Рис. 19

внем поднимется шарик? Считать, что угол

отклонения стержня от вертикали не превышает 90o. Трением и массой колёс тележки пренебречь. (Институт криптографии, связи и информатики Академии ФСБ РФ, 2005 г.)

Решение. В горизонтальном направлении на систему «шарик– тележка» никакие силы не действуют (трения нет). Сила упругости стержня, на котором подвешен шарик, является внутренней силой и импульса системы изменить не может. Таким образом, проекция импульса системы «шарик – тележка» на горизонтальное направление сохраняется. В начальный момент она была равна mv, а в момент

достижения шариком максимальной высоты H шарик и тележка движутся с одинаковой скоростью v1 в горизонтальном направлении (на

рис. 19 – вправо). С учётом сохранения проекции импульса на направление движения тележки имеем:

mv =(m + M )v1.

Считая потенциальную энергию шарика в поле силы тяжести в начальный момент равной нулю, можно записать по закону сохранения

механической энергии:

mv2

= mgH +

(m + M )v12

.

2

2

M v2

Из двух написанных уравнений получаем ответ:

H =

.

2(M + m)g

Задача 12. Тело движется со скоростью v1 = 6мс и догоняет такое же тело, движущееся со скоростью v2 =3мс (вдоль той же прямой).

Определите скорости тел после центрального абсолютно упругого уда-

ра. (МИЭМ, 2006 г.)

Решение. Удар называется центральным, если скорости тел до удара направлены вдоль линии, соединяющей центры масс тел (рис. 20 а). За-

© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич

24

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики

данные скорости v1 и v2 направлены вдоль одной прямой. Направим ось Ox параллельно этой прямой в сторону движения тел. Пусть скоро-

сти тел после удара равны u1 и u2 . Эти скорости в данном случае могут

быть только параллельными оси Ox. Предположительно направим их так, как показано на рис. 20 б.

Систему тел будем считать замкнутой (в условии иного не оговорено). По закону сохранения импульса суммарный импульс тел до удара равен суммарному импульсу тел после удара. В проекциях на ось Ox можно, следовательно, записать:

mv1 + mv2 = mu1x + mu2x ,

(15)

Рис. 20 а Рис. 20 б

где u1x и u2x − проекции на ось Ox векторов u1 и u2 соответственно. (Если направления векторов u1 и u2 выбраны правильно, то u1x =u1, а u2 x =u2 . ) По условию удар абсолютно упругий, следовательно суммарная механическая энергия тел сохраняется. Тогда

mv

2

+

mv

2

2

=

mu

2

+

mu

2

.

(16)

1

1

2

2

2

2

2

При этом, в связи с выше сказанным, независимо от знака проекций

u1x и u2 x

u 2

= u

2 и

u 2

= u 2 .

(17)

1

1x

2

2x

Перегруппируем слагаемые в (15) и сократим на m. Тогда получим:

v1 −u1x

=u2x

−v2 .

(18)

Аналогично уравнение (16) преобразуем к виду:

v 2

−u 2

=u 2 −v 2 .

Или с учётом (17)

1

1

2

2

v 2

−u 2

= u 2

−v 2 .

1

1x

2x

2

Воспользовавшись алгебраической формулой для разности квадратов, можно записать: (v1 −u1x )(v1 +u1x )=(u2x −v2 )(u2x + v2 ).

Поскольку v1 −u1x =u2x −v2 (см. выше) и, очевидно, v1 −u1x ≠ 0 и

© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич

25

Рис. 21

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики

u2x − v2 ≠ 0, то, сократив на эти выражения, получим:

v1 +u1x

= u2x

+ v2 .

(19)

Вычитая (18) из (19), найдём u1x

= v2 .

Складывая (18) и (19), получим

u2x = v1. Видим, что u1x

и u2x

получились положительными.

Значит

направления скоростей u1

и u2 указаны на рис. 20 б верно. В рассмат-

риваемом случае тела в результате удара «обмениваются» скоростями: u1 = v2 =3мс, u2 = v1 = 6мс.

Задача 13. Лёгкий пластилиновый шарик массы m летит со скоро-

стью vr и сталкивается с массивной плитой, дви-

u

жущейся навстречу шарику со скоростью u

(рис. 21). Какое количество теплоты выделится

v

m

при абсолютно неупругом столкновении шарика с

плитой? Массу M плиты считать много большей

M

массы шарика (M >> m).

.

x

Решение. Направим ось Ox в сторону движния

0

плиты, как показано на рис. 21. Пусть u1−совмест-

ная скорость плиты с шариком после столкновения (на рис. 21 не показана). Считая, что после столкновения плита с шариком движутся в том же направлении, что и плита до столкновения, по закону сохранения импульса (система тел замкнута) можно записать в проекциях на ось Ox уравнение:

Mu −mv =(M +m)u1.

Отсюда скорость

u равна: u

=

Mu −mv

=

M

u −

m

v.

1

1

M

+ m

M + m

M + m

Преобразуем это выражение следующим образом:

m

M

m

1

u =

u −

v =

u −

M

v.

m

1

M

1+

m

M

1+

m

1+

1+

m

M

M

M

M

Считая отношение

m

близким к нулю (по условию M >> m ) и пре-

M

m

небрегая им по сравнению с единицей

<<1

в знаменателе умень-

M

шаемого, а вычитаемое по той же причине отбрасывая вовсе, получим u1 =u, то есть после столкновения шарик с плитой движутся с той же

скоростью, что и плита до столкновения. Иными словами, скорость плиты не изменилась. Перейдём в систему отсчёта, связанную с пли-

© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич

26

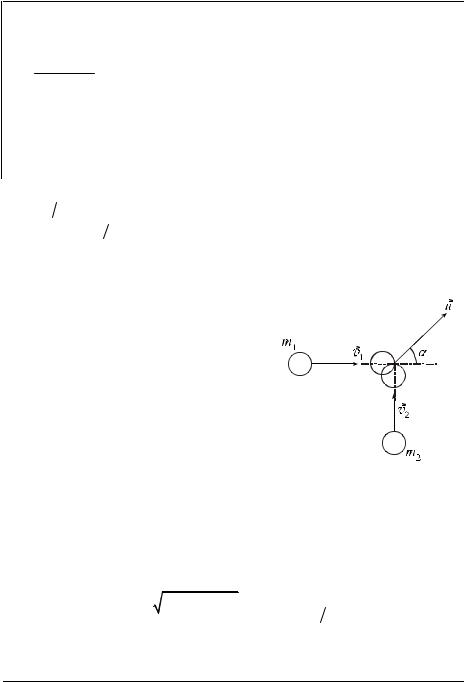
. После столкновения в выбранной системе отсчёта плита

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики

той. В свете сказанного эту систему отсчёта можно считать инерциальной. В ней плита покоится, а шарик до удара движется навстречу плите со скоростью v +u. Следовательно, перед столкновением

K = m(u + v)2

2

и шарик покоятся, их суммарная механическая энергия равна нулю. Убыль суммарной механической энергии тел равна искомому количеству теплоты

Q =

m(v +u)2

.

2

Задача

14. Шар массой m1 = 2 кг,

движущийся со скоростью

v1 = 2м с,

сталкивается с шаром массой m2 =1 кг, движущимся со ско-

ростью v2

=3м с. В результате столкновения шары слипаются. Опре-

делите количество выделившейся при столкновении теплоты и совместную скорость шаров после столкновения. В момент столкновения скорости шаров взаимно перпендикулярны.

Решение. Из условия задачи следует,

что столкновение абсолютно неупругое,

и после него шары будут двигаться как

одно целое (рис. 22). Считая систему тел

замкнутой, по закону сохранения им-

пульса имеем:

m1vr1 +m2 vr2 =(m1 + m2 )ur,

где

ur − совместная скорость слипшихся

шаров после столкновения.

Написан-

ное

уравнение

проиллюстрировано на

рис. 22. Возведём обе части этого урав-

нения в квадрат:

m12 vr12 + 2m1m2 vr1 vr2 +m22 vr2

2=(m1 + m2 )2 ur2.

Рис. 22

Поскольку по условию скорости v

и v

взаимно перпендикулярны, то

1

2

r

r

их скалярное произведение равно нулю: v1

v2 =0. Учитывая также, что

vr12

= v12 , vr2

2 = v22 ,

ur2 =u2 ,

получим

m12 v12 + m22 v22 =(m1 + m2 )2 u2 .

Откуда модуль искомой скорости u равен

u =

m12 v12 + m22 v22

=

5 м

≈1,7 м с.

m + m

3 с

Направление скорости u

1

2

составляет угол α с направлением скорости

© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич

27

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #

Источник

Законы сохранения в механике

Содержание

  • Импульс тела
  • Импульс системы тел
  • Закон сохранения импульса
  • Работа силы
  • Мощность
  • Работа как мера изменения энергии
  • Кинетическая энергия
  • Потенциальная энергия
  • Закон сохранения механической энергии
  • Основные формулы по теме «Законы сохранения в механике»

Импульс тела

Импульс тела – это векторная физическая величина, равная произведению массы тела на его скорость:

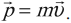
Обозначение – ​( p )​, единицы измерения – (кг·м)/с.

Импульс тела – это количественная мера движения тела.
Направление импульса тела всегда совпадает с направлением скорости его движения.
Изменение импульса тела равно разности конечного и начального значений импульса тела:

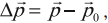
где ​( p_0 )​ – начальный импульс тела,
​( p )​ – конечный импульс тела.

Если на тело действует нескомпенсированная сила, то его импульс изменяется. При этом изменение импульса тела равно импульсу подействовавшей на него силы.

Импульс силы – это количественная мера изменения импульса тела, на которое подействовала эта сила.

Обозначение – ​( F!Delta t )​, единицы измерения — Н·с.
Импульс силы равен изменению импульса тела:

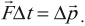
Направление импульса силы совпадает по направлению с изменением импульса тела.

Второй закон Ньютона (силовая форма):

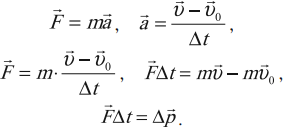
Важно!
Следует всегда помнить, что совпадают направления векторов:

• силы и ускорения: ​( vec{F}uparrowuparrowvec{a} )​;
• импульса тела и скорости: ( vec{p}uparrowuparrowvec{v} )​;
• изменения импульса тела и силы: ( Deltavec{p}uparrowuparrowvec{F} );
• изменения импульса тела и ускорения: ( Deltavec{p}uparrowuparrowvec{a} ).

Импульс системы тел

Импульс системы тел равен векторной сумме импульсов тел, составляющих эту систему:

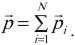
При рассмотрении любой механической задачи мы интересуемся движением определенного числа тел. Совокупность тел, движение которых мы изучаем, называется механической системой или просто системой.

Рассмотрим систему, состоящую из трех тел. На тела системы действуют внешние силы, а между телами действуют внутренние силы.
​( F_1,F_2,F_3 )​ – внешние силы, действующие на тела;
​( F_{12}, F_{23}, F_{31}, F_{13}, F_{21}, F_{32} )​ – внутренние силы, действующие между телами.
Вследствие действия сил на тела системы их импульсы изменяются. Если за малый промежуток времени сила заметно не меняется, то для каждого тела системы можно записать изменение импульса в виде уравнения:

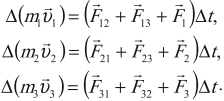
В левой части каждого уравнения стоит изменение импульса тела за малое время ​( Delta t )​.
Обозначим: ​( v_0 )​ – начальные скорости тел, а ​( v^{prime} )​ – конечные скорости тел.
Сложим левые и правые части уравнений.

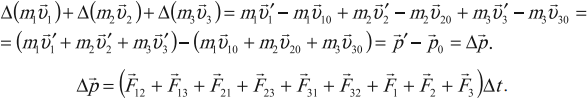
Но силы взаимодействия любой пары тел в сумме дают нуль.

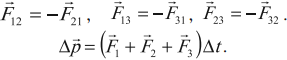
Важно!
Импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.

Закон сохранения импульса

Закон сохранения импульса
Векторная сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой:

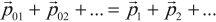
Замкнутая система – это система, на которую не действуют внешние силы.
Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций.
При абсолютно упругом ударе взаимодействующие тела до и после взаимодействия движутся отдельно.

Закон сохранения импульса для абсолютно упругого удара:

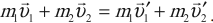
Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.

Закон сохранения импульса для абсолютно неупругого удара:

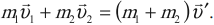
Реактивное движение – это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-то его части.
Принцип реактивного движения основан на том, что истекающие из реактивного двигателя газы получают импульс. Такой же по модулю импульс приобретает ракета.
Для осуществления реактивного движения не требуется взаимодействия тела с окружающей средой, поэтому реактивное движение позволяет телу двигаться в безвоздушном пространстве.

Реактивные двигатели
Широкое применение реактивные двигатели в настоящее время получили в связи с освоением космического пространства. Используются они также для метеорологических и военных ракет различного радиуса действия. Кроме того, все современные скоростные самолеты оснащены воздушно-ракетными двигателями.
Реактивные двигатели делятся на два класса:

  • ракетные;
  • воздушно-реактивные.

В ракетных двигателях топливо и необходимый для его горения окислитель находятся непосредственно внутри двигателя или в его топливных баках.

Ракетный двигатель на твердом топливе
При горении топлива образуются газы, имеющие очень высокую температуру и оказывающие давление на стенки камеры. Сила давления на переднюю стенку камеры больше, чем на заднюю, где находится сопло. Выходящие через сопло газы не встречают на своем пути стенку, на которую могли бы оказать давление. В результате появляется сила, толкающая ракету вперед.

Сопло – суженная часть камеры, служит для увеличения скорости истечения продуктов сгорания, что, в свою очередь, повышает реактивную силу. Сужение струи газа вызывает увеличение его скорости, так как при этом через меньшее поперечное сечение в единицу времени должна пройти такая же масса газа, что и при большем поперечном сечении.

Ракетный двигатель на жидком топливе

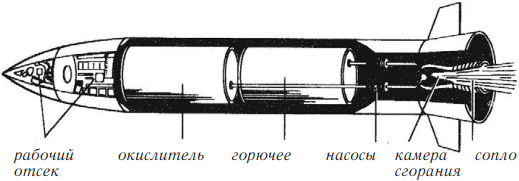
В ракетных двигателях на жидком топливе в качестве горючего используют керосин, бензин, спирт, жидкий водород и др., а в качестве окислителя – азотную кислоту, жидкий кислород, перекись водорода и пр.
Горючее и окислитель хранятся отдельно в специальных баках и с помощью насосов подаются в камеру сгорания, где температура достигает 3000 0С и давление до 50 атм. В остальном работает так же, как и двигатель на твердом топливе.

Воздушно-реактивный двигатель

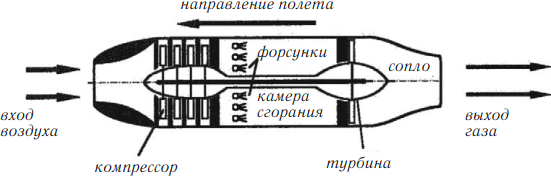
В носовой части находится компрессор, засасывающий и сжижающий воздух, который затем поступает в камеру сгорания. Жидкое горючее (керосин) попадает в камеру сгорания с помощью специальных форсунок. Раскаленные газы выходят через сопло, вращают газовую турбину, приводящую в движение компрессор.
Основное отличие воздушно-реактивных двигателей от ракетных двигателей состоит в том, что окислителем для горения топлива служит кислород воздуха, поступающего внутрь двигателя из атмосферы.

Алгоритм применения закона сохранения импульса к решению задач:

  1. Запишите краткое условие задачи.
  2. Определите характер движения и взаимодействия тел.
  3. Сделайте рисунок, на котором укажите направление векторов скоростей тел до и после взаимодействия.
  4. Выберите инерциальную систему отсчета с удобным для нахождения проекций векторов направлением координатных осей.
  5. Запишите закон сохранения импульса в векторной форме.
  6. Спроецируйте его на выбранные координатные оси (сколько осей, столько и уравнений в системе).
  7. Решите полученную систему уравнений относительно неизвестных величин.
  8. Выполните действия единицами измерения величин.
  9. Запишите ответ.

Работа силы

Механическая работа – это скалярная векторная величина, равная произведению модулей вектора силы, действующей на тело, вектора перемещения и косинуса угла между этими векторами.

Обозначение – ​( A )​, единицы измерения – Дж (Джоуль).

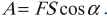
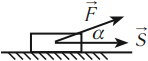
1 Дж – это работа, которую совершает сила в 1 Н на пути в 1 м:

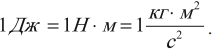
Механическая работа совершается, если под действием некоторой силы, направленной не перпендикулярно, тело перемещается на некоторое расстояние.

Зависимость механической работы от угла ​( alpha )​

  • ​( alpha=0^{circ},, cosalpha=1,, A=FS,,A>0; )​

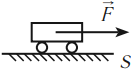
  • ​( 0^{circ}<alpha<90^{circ},, A=FScosalpha,,A>0; )

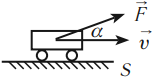
  • ( alpha=90^{circ},, cosalpha=0,, A=0; )​

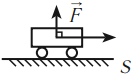
  • ​( 90^{circ}<alpha<180^{circ},, A=FScosalpha,,A<0; )


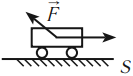
( alpha=180^{circ},, cosalpha=-1,, A=-FS,,A<0; )​

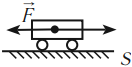
Геометрический смысл механической работы

На графике зависимости ​( F=F(S) )​ работа силы численно равна площади фигуры, ограниченной графиком, осью перемещения и прямыми, параллельными оси силы.

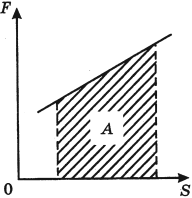
Формулы для вычисления работы различных сил

Работа силы тяжести:

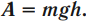
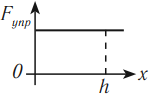
Работа силы упругости:

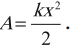
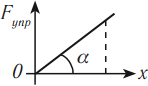
Коэффициент полезного действия механизма (КПД) — это физическая величина, равная отношению полезной работы, совершенной механизмом, ко всей затраченной при этом работе.
Обозначение – ​( eta )​, единицы измерения – %.

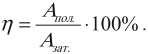
​( A_{mathit{пол.}} )​ – полезная работа – это та работа, которую нужно сделать;
​( A_{mathit{зат.}} ) – затраченная работа – это та работа, что приходится делать на самом деле.

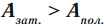
Важно!
КПД любого механизма не может быть больше 100%.

Мощность

Мощность – это количественная мера быстроты совершения работы.

Обозначение – ​( N )​, единицы измерения – Вт (Ватт).
Мощность равна отношению работы к времени, за которое она была совершена: .

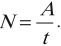
1 Вт – это мощность, при которой за 1 с совершается работа в 1 Дж:

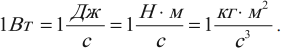
1 л. с. (лошадиная сила) = 735 Вт.

Связь между мощностью и скоростью равномерного движения:

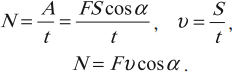
Таким образом, мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между направлениями этих векторов.

Важно!
Если интервал времени стремится к нулю, то выражение представляет собой мгновенную мощность, определяемую через мгновенную скорость.

Работа как мера изменения энергии

Если система тел может совершать работу, то она обладает энергией.

Работа и изменение кинетической энергии (теорема о кинетической энергии)

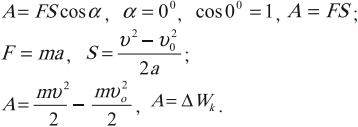
Если под действием силы тело совершило перемещение и вследствие этого его скорость изменилась, то работа силы равна изменению кинетической энергии.
Силы, работа которых не зависит от формы траектории, называются консервативными.

Работа и изменение потенциальной энергии тела, поднятого над землей

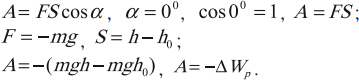
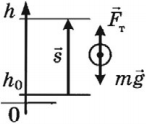
Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

Работа и изменение потенциальной энергии упруго деформированного тела

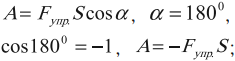
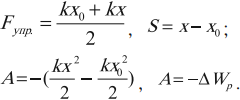
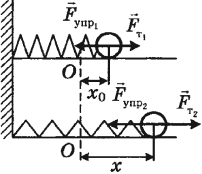
Работа силы упругости равна изменению потенциальной энергии, взятому с противоположным знаком.

Кинетическая энергия

Кинетическая энергия – это энергия, которой обладает тело вследствие своего движения.

Обозначение – ​( W_k (E_k) )​, единицы измерения – Дж.

Кинетическая энергия равна половине произведения массы тела на квадрат его скорости:

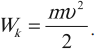
Важно!
Так как кинетическая энергия отдельного тела определяется его массой и скоростью, то она не зависит от того, взаимодействует ли это тело с другими телами или нет. Значение кинетической энергии зависит от выбора системы отсчета, как и значение скорости. Кинетическая энергия системы тел равна сумме кинетических энергий отдельных тел, входящих в эту систему.

Потенциальная энергия

Потенциальная энергия – это энергия взаимодействия тел или частей одного и того же тела.

Обозначение – ​( W_p (E_p) )​, единицы измерения – Дж.

Потенциальная энергия тела, поднятого на некоторую высоту над землей, равна произведению массы тела, ускорения свободного падения и высоты, на которой он находится:

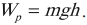
Потенциальная энергия упруго деформированного тела равна половине произведения жесткости на квадрат удлинения:

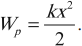
Важно!
Величина потенциальной энергии зависит от выбора нулевого уровня. Нулевым называется уровень, на котором потенциальная энергия равна нулю. Нулевой уровень выбирается произвольно, исходя из удобства решения задачи.

Закон сохранения механической энергии

Полная механическая энергия – это энергия, равная сумме кинетической и потенциальной энергий.

Обозначение – ​( W (E) )​, единицы измерения – Дж.

Закон сохранения механической энергии
В замкнутой системе тел, между которыми действуют только консервативные силы, механическая энергия сохраняется, т. е. не изменяется с течением времени:

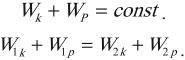
Если между телами системы действуют кроме сил тяготения и упругости другие силы, например сила трения или сопротивления, действие которых приводит к превращению механической энергии в тепловую, то в такой системе тел закон сохранения механической энергии не выполняется.

Важно!
В случае, если кроме консервативных сил (тяжести, упругости, тяготения) существуют еще и неконсервативные силы, например сила трения, а также внешние силы, то

Теорема о кинетической энергии справедлива для сил любой природы:

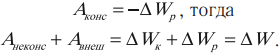
Если на систему тел действуют неконсервативные и внешние силы, то изменение полной энергии равно сумме работ неконсервативных и внешних сил.

Закон сохранения и превращения энергии
Энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой или передается от одного тела к другому.

Основные формулы по теме «Законы сохранения в механике»

Законы сохранения в механике

3.1 (62.98%) 47 votes

Источник

Добавить комментарий