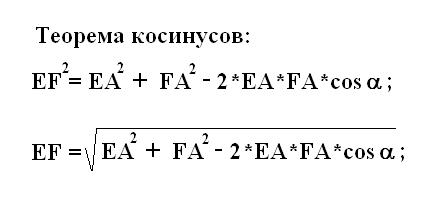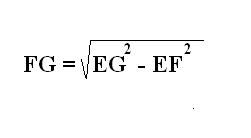Как зная периметр найти площадь неровной фигуры

Как вычислить площадь неправильного многоугольника зная периметр?

Формула для нахождения площади правильного многоугольника: Площадь = 1/2 х периметр х апофема.

1. Периметр – сумма сторон многоугольника.
2. Апофема – отрезок, соединяющий центр многоугольника и середину любой из его сторон (апофема перпендикулярна стороне).

Как найти площадь неправильного треугольника?

Площадь треугольника через гипотенузу и по радиусу вписанной окружности. S = r * (r + c), где c — гипотенуза, r — радиус вписанной окружности.

Как найти площадь треугольника если известны все его стороны?

h = 2/a √p(p-a)(p-b)(p-c), где h – длина высоты треугольника, p – полупериметр, a – длина стороны, на которую падает высота (основание), b и c – длины двух других сторон треугольника.

Как высчитать квадратуру треугольника?

что обозначает, что площадь треугольника равна произведению длины его основания и высоты поделенной на два.

Как считается площадь?

В помещении, которое представляет собой прямоугольник или квадрат, нужно измерить длину и ширину и умножить значения между собой. Вы получите площадь комнаты в квадратных метрах. Формула по которой можно высчитать площадь: S комнаты = А х B, где A – длина, B – ширина.

Как посчитать Площу Трикутника?

Формула Герона Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

Как найти площадь равностороннего треугольника 4 класс?

Многоугольник, который имеет три вершины и три стороны, называется треугольником. Треугольник называется равносторонним, если все его три стороны равны. Площадь равностороннего треугольника вычисляется как половина как половина произведения его основания на высоту.

Как найти высоту равностороннего треугольника зная сторону?

Если подставить вместо угла альфа 60 градусов, получится, что высота равностороннего треугольника равна половине стороны, умноженной на корень из трех.

Как найти высоту равностороннего треугольника?

Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами «а» и «b» гипотенуза «с» равна: a2+b2=c2. Эту теорему можно использовать, чтобы найти высоту равностороннего треугольника! Разделите равносторонний треугольник на два прямоугольных треугольника (для этого проведите высоту).

Как найти высоту треугольника через площадь?

С другой стороны та же площадь треугольника через высоту равна половине произведения стороны треугольника на высоту, на нее опущенную. Отсюда высота будет равна отношению удвоенной площади к стороне треугольника. Из предыдущей формулы можно выразить площадь через три стороны треугольника и заменить ее в формуле высоты.

Как найти высоту треугольника 7 класс?

из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к ней (перпендикуляр — это отрезок, проведённый из точки к прямой, составляющей с ней угол 90 ° ) — это и будет высота. Так же как медианы и биссектрисы, треугольник имеет три высоты. Высоты треугольника пересекаются в одной точке.

Как вычислить высоту треугольника если известны стороны?

В зависимости от входных данных, высоту треугольника можно найти разными способами. h = 2/a √p(p-a)(p-b)(p-c), где h – длина высоты треугольника, p – полупериметр, a – длина стороны, на которую падает высота (основание), b и c – длины двух других сторон треугольника.

Как найти H в треугольнике?

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

1. H – высота треугольника
2. p – полупериметр, p=(a+b+c)/2.
3. R – радиус описанной окружности

Чему равна высота в треугольнике?

Высота в формулах обозначается буквой h, нижний индекс которой соответствует стороне, на которую она опущена. Пояснения к формулам. Высота треугольника равна частному от деления произведения сторон, прилежащих к углу, из которого опущена эта высота, на удвоенный радиус описанной вокруг него окружности (Формула 4).

Как определить наибольшую высоту в треугольнике?

Чтобы найти наибольшую высоту треугольника, можно площадь треугольника разделить на длину стороны, к которой проведена эта высота (то есть на длину наименьшей из сторон треугольника).

Как найти площадь параллелограмма по высоте?

Площадь параллелограмма, формула. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h): 1.

Как найти вторую высоту у параллелограмма?

высота параллелограмма равняется корню квадратному из разности квадратов длины прилежащей стороны и отсекаемой высотой части основания. Например, если длина прилегающей стороны равняется 5 см., а длина отсекаемой части основания равна 3 см, то длина высоты будет: h=?(5^2-3^2)=4 (см).

Как найти периметр параллелограмма зная одну сторону и высоту?

Формулы определения длины периметра параллелограмма:

1. Формула периметра параллелограмма через стороны параллелограмма: P = 2a + 2b = 2(a + b)
2. Формула периметра параллелограмма через одну сторону и две диагонали: P = 2a + √2d12 + 2d22 – 4a2 …
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:

Периметр фигуры – это общее расстояние вокруг нее, а площадь – это количество поверхности, которую фигура использует или покрывает. Методы расчета периметра и площади отличаются для каждого вида фигуры. Например, хотя вы можете найти площадь прямоугольника, просто умножив его длину на ширину, круг требует более сложных вычислений. Научитесь преобразовывать периметры самых основных фигур в области, и в дальнейшем вы сможете переходить к составным фигурам.

Квадратные Периметры

1. Разделите периметр на четыре

Разделите периметр на четыре, чтобы получить длину каждой стороны, так как все четыре стороны квадрата равны. Например, квадрат с периметром 36 дюймов будет иметь стороны размером 9 дюймов каждая, потому что 36 ÷ 4 = 9.

2. Квадрат длина стороны

Квадрат длины одной стороны. Для квадрата с 9-дюймовыми сторонами, получится 9 х 9 = 81.

3. Добавить единицу измерения

Добавьте правильную единицу измерения к области. Квадрат с периметром 36 дюймов имеет площадь 81 квадратный дюйм.

Периметры прямоугольника

1. Отработка длины основания и высоты

Определите длину как основания, так и высоты. Это стороны, которые не параллельны друг другу. Например, скажем, у вас есть прямоугольник с основанием 6 см и высотой 7 см.

2. Умножить базу на высоту

Умножьте базу на высоту. Тренируйся 6 х 7 = 42.

3. Добавить единицу измерения

Добавьте правильную единицу измерения. В этом примере площадь прямоугольника составляет 42 см квадратных сантиметров.

Периметры треугольника

1. Отработать длину базы

Определите длину основания треугольника. Например, скажем, у вас есть треугольник с основанием 3 фута.

2. Высота тренировки

Рассчитайте высоту треугольника. Скажем, у вас есть треугольник с высотой 12 футов.

3. Умножить базу на высоту

Умножьте длину основания на длину высоты. Тренируй 3 х 12 = 36.

4. Разделить на два

Разделите на два. Отработать 36 ÷ 2 = 18.

5. Добавить единицу измерения

Добавьте правильную единицу измерения. Площадь треугольника составляет 18 квадратных футов.

Окружность окружности

1. Разделить периметр на пи

Разделите периметр круга, также известный как окружность, на pi (3.14159265), чтобы получить диаметр круга. Например, скажем, у вас есть круг с окружностью 40 дюймов. Отработка 40 ÷ 3.14159265 = 12.732.

2. Разделите диаметр на два

Разделите диаметр на два, чтобы получить длину радиуса. Отработать 12, 732 ÷ 2 = 6, 366.

3. Умножить радиус

Умножьте радиус на себя. В этом примере получится 6, 366 х 6, 366 = 40, 526.

4. Умножить на пи

Умножьте на pi (3.14159265). Отработка 40, 526 х 3, 14159265 = 127, 316.

5. Добавить единицу измерения

Добавьте правильную единицу измерения. Площадь круга составляет 127, 316 квадратных дюймов.

Как найти площадь, зная периметр

Площадь и периметр фигуры являются основными ее геометрическими параметрами. Их нахождение и описание с учетом известных величин составляет значительную долю в обучающем процессе. В общем смысле периметр – это длина всех границ фигуры. Для прямоугольника он равен сумме длин его сторон. А площадь представляет собой всю внутреннюю часть фигуры, измеренной в определенных единицах. Согласно свойствам фигур, а также формулам площади и периметра, можно найти соотношения между этими параметрами фигуры и выразить одно значение из другого. Для определения площади прямоугольника с известным периметром необходимо дополнительно знать одну его сторону.

Инструкция

Запишите известные параметры прямоугольной фигуры. Помимо периметра, для нахождения площади должна быть известна еще одна величина – любая сторона прямоугольника.

Согласно формуле, периметр прямоугольника находится, как сумма всех его сторон. Так как в прямоугольнике противолежащие стороны равны, можно записать формулу периметра: Р = (d+c)*2, где d и c являются прилегающими сторонами фигуры.

Площадь прямоугольной фигуры определяется произведением двух ее прилегающих сторон: S = d*c. Таким образом, зная одну из сторон можно легко найти площадь фигуры.

Подставьте в формулу периметра известные величины: одну из сторон и периметр. Выразите из полученного уравнения вторую неизвестную сторону и вычислите ее. Подставьте полученное значение в формулу площади. Вычислите искомое значение S – площади фигуры.

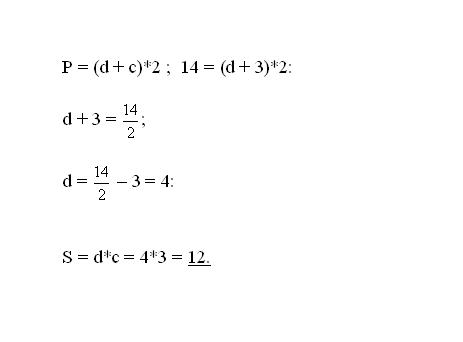
Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Площадь
и периметр
фигуры являются основными ее геометрическими параметрами. Их нахождение и описание с учетом известных величин составляет значительную долю в обучающем процессе. В общем смысле периметр
– это длина всех границ фигуры. Для прямоугольника он равен сумме длин его сторон. А площадь представляет собой всю внутреннюю часть фигуры, измеренной в определенных единицах. Согласно свойствам фигур, а также формулам площади и периметр
а, можно найти соотношения между этими параметрами фигуры и выразить одно значение из другого. Для определения площади прямоугольника с известным периметр
ом необходимо дополнительно знать одну его сторону.

Инструкция

Запишите известные параметры прямоугольной фигуры. Помимо периметр
а, для нахождения площади должна быть известна еще одна величина – любая сторона прямоугольника.

Согласно формуле, периметр
прямоугольника находится, как сумма всех его сторон. Так как в прямоугольнике противолежащие стороны равны, можно записать формулу периметр
а: Р = (d+c)*2, где d и c являются прилегающими сторонами фигуры.

Площадь
прямоугольной фигуры определяется произведением двух ее прилегающих сторон: S = d*c. Таким образом, зная одну из сторон можно легко найти площадь фигуры.

Подставьте в формулу периметр
а известные величины: одну из сторон и периметр
. Выразите из полученного уравнения вторую неизвестную сторону и вычислите ее. Подставьте полученное значение в формулу площади. Вычислите искомое значение S – площади фигуры.

Т.е. Р = a + b + c + d

Второе определение будет звучать так: периметр прямоугольника – это удвоенная сумма его длины и ширины.

Длиной является более длинная пара его сторон (обозначим их буквой a), а шириной – более короткая пара его сторон (обозначим буквой b). Противоположные стороны прямоугольника равны. Т.е. периметр можно вычислить так: Р = (a + b)* 2 или Р = а*2 + b*2

Периметром плоской фигуры называют сумму длин всех ее сторон. Но найти стороны фигуры, зная только периметр – не всегда выполнимая задача. Часто требуются дополнительные данные.

Спонсор размещения P&G
Статьи по теме “Как найти стороны, если известен периметр”
Как найти периметр прямоугольной трапеции
Как найти углы треугольника по сторонам
Как найти сторону квадрата
Как найти площадь поверхности пирамиды
Как найти сумму длин всех рёбер параллелепипеда

Инструкция

Для квадрата или ромба задача найти стороны из периметра решается очень просто. Известно, что у этих двух фигур по 4 стороны и все они равны между собой, поэтому периметр p квадрата и ромба равен 4a, где a – сторона квадрата или ромба. Тогда длина стороны равна одной четвертой периметра: a = p/4.

Легко разрешима эта задача и для равностороннего треугольника. У него три одинаковых по длине стороны, поэтому периметр p равностороннего треугольника равен 3a. Тогда сторона равностороннего треугольника a = p/3.

Для остальных фигур понадобятся дополнительные данные. Например, можно найти стороны прямоугольника, зная его периметр и площадь. Предположим, что длина двух противолежащих сторон прямоугольника равна a, а длина двух других сторон – b. Тогда периметр p прямоугольника равен 2(a+b), а площадь s равна ab. Получим систему уравнений с двумя неизвестными:
p = 2(a+b)
s = ab.

Выразим из первого уравнения а: а = p/2 – b. Подставим во второе уравнение и найдем b: s = pb/2 – b?. Дискриминант этого уравнения D = p?/4 – 4s. Тогда b = (p/2±D^1/2)/2. Отбросьте тот корень, который будет меньше ноля, и подставьте в выражение для стороны a.

Как просто

Другие новости по теме:

Площадь и периметр – основные числовые характеристики любых геометрических фигур. Нахождение этих величин упрощается благодаря общепринятым формулам, согласно которым можно также вычислить одно через другое с минимумом или полным отсутствием дополнительных начальных данных. Спонсор размещения P&G

Равносторонний треугольник наряду с квадратом является, пожалуй, самой простой и симметричной фигурой в планиметрии. Разумеется, все соотношения, справедливые для обычного треугольника, верны также и для равностороннего. Однако для правильного треугольника все формулы становятся намного проще. Вам

Часто при решении геометрических задач в условии даётся периметр фигуры, а длину сторон, диагоналей, диаметр и другие размеры фигур при этом требуется выразить самостоятельно. Периметр равен суммарной длине внешней границы геометрической фигуры. Единицей измерения периметра являются те же единицы,

По 4 стороны
и все они равны между собой, поэтому периметр p квадрата и ромба равен 4a, где a – сторона квадрата или ромба. Тогда длина стороны
равна одной четвертой периметра: a = p/4.

Легко разрешима эта задача и для равностороннего треугольника. У него три одинаковых по длине стороны
, поэтому периметр p равностороннего треугольника равен 3a. Тогда сторона равностороннего треугольника a = p/3.

Для остальных фигур понадобятся дополнительные данные. Например, можно найти стороны
прямоугольника , зная его периметр и площадь. Предположим, что длина двух противолежащих сторон прямоугольника равна a, а длина двух других сторон – b. Тогда периметр p прямоугольника равен 2(a+b), а площадь s равна ab. Получим систему уравнений с двумя неизвестными:
p = 2(a+b)
s = ab.Выразим из первого уравнения а: а = p/2 – b. Подставим во второе уравнение и найдем b: s = pb/2 – b². Дискриминант этого уравнения D = p²/4 – 4s. Тогда b = (p/2±D^1/2)/2. Отбросьте тот корень, который будет меньше ноля, и подставьте в выражение для стороны
a.

Если вы знаете значение дискриминант а, то вы можете сказать, что решили квадратное уравнение, потому как его корни будут найдены очень легко.

Вам понадобится

• -формула дискриминанта квадратного уравнения;
• -знание таблицы умножения

Инструкция

Видео по теме

Полезный совет

Дискриминант квадртаного уравнения может быть положительным, отрицательным, или равняться 0.

Источники:

• Решение квадратных уравнений
  
• дискриминант четный

Частный случай параллелограмма – прямоугольник – известен только в геометрии Евклида. У прямоугольника
равны все углы, и каждый из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника
, а также из свойств параллелограмма о параллельности противолежащих сторон можно найти стороны
фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника
основывается на дополнительных построениях и применении свойств получаемых фигур.

Инструкция

Буквой А отметьте точку пересечения диагоналей. Рассмотрите образованный построениями треугольник EFА. Согласно свойству прямоугольника
его диагонали равны и делятся пополам точкой пересечения А. Вычислите значения FА и EА. Так как треугольник EFА является равнобедренным и его стороны
EА и FА равны между собой и соответственно равны половине диагонали EG.

Далее вычислите первую сторону EF прямоугольника
. Данная сторона является третьей неизвестной стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле найдите сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА равна EА и косинус известного угла между ними α. Вычислите и запишите полученное значение EF.

Найдите вторую сторону прямоугольника
FG. Для этого рассмотрите другой треугольник EFG. Он является прямоугольным, где известны гипотенуза EG и катет EF. Согласно теореме Пифагора найдите второй катет FG по соответствующей формуле.

Совет 4: Как найти периметр равностороннего треугольника

Равносторонний треугольник наряду с квадратом является, пожалуй, самой простой и симметричной фигурой в планиметрии. Разумеется, все соотношения, справедливые для обычного треугольника, верны также и для равностороннего. Однако для правильного треугольника все формулы становятся намного проще.

Вам понадобится

• калькулятор, линейка

Инструкция

Чтобы найти периметр равностороннего треугольника измерьте длину одной из его сторон и умножьте результат измерения на три. В виде формулы это правило можно записать следующим образом:

Прт = Дс * 3,

Прт – периметр равностороннего треугольника,
Дс – длина любой из его сторон.

Периметр треугольника получится в тех же

Contrary to all other answers, I say yes you can find the area $a$ of a known shape (clover leaf) from the length of its perimeter $p$.

Taking a similar model of the clover leaf, measure its area $A$ and perimeter $P$, using a curvimeter and a planimeter. You can also do that from a digital image (photoscan), but I don’t know of ready-made tools for that.

Then, for any clover leaf (of the same shape), this proportionality rule holds:

$$frac aA=left(frac pPright)^2,$$
so that
$$a=Aleft(frac pPright)^2=F_{clover}p^2.$$

For any shape there is a corresponding conversion factor that you can compute once for all.

For instance, with the picture below, you can estimate an area of $19852$ pixels and a perimeter of $750$ pixels (this is an inaccurate measurement).

Then $F_{clover3hearts}approx0.0353$, and your leaf has an area of $325$ square units.